Static Analysis for ECMAScript String Manipulation Programs
Abstract
:1. Introduction
2. Background
2.1. String Notation
2.2. Regular Languages and Finite State Automata
2.3. Abstract Interpretation
3. The Core Language
Semantics
- substring:
- It extracts the substring between two indexes from a string. The semantics is defined by the function Ss as:
- charAt:
- It returns the character, i.e., the string of unitary length, at a specified index in a string . The semantics is the function Ca defined as follows:
- length:
- It returns the length of a string . Its semantics is the function Le defined as .
- concat:
- It returns the concatenation between two strings and its concrete semantics Cc : relies on the concatenation operator reported in Section 2.
- startsWith:
- It determines whether a specified string starts with . The semantics is the function Sw : defined as:
- repeat:
- It returns the given string repeated n times. The semantics is the function Rt defined as .
- includes:
- It determines whether a string is a substring of . The semantics is the function In defined as:
- toLowerCase:
- It returns the given string in all lowercase letters. The semantics is the function Lc defined as .
- trimLeft:
- It removes all the white-spaces at the beginning of a string. The semantics is the function Tl defined as:
- trimRight:
- It removes all the white-spaces at the end of a string. The semantics is the function Tr defined as:
- trim:
- It removes all the white-spaces at the end and beginning of a string. The semantics is the function Tm defined as: .
Implicit Type Conversion
4. An Abstract Domain for String Manipulation
4.1. The Finite State Automata Abstract Domain for Strings
Widening
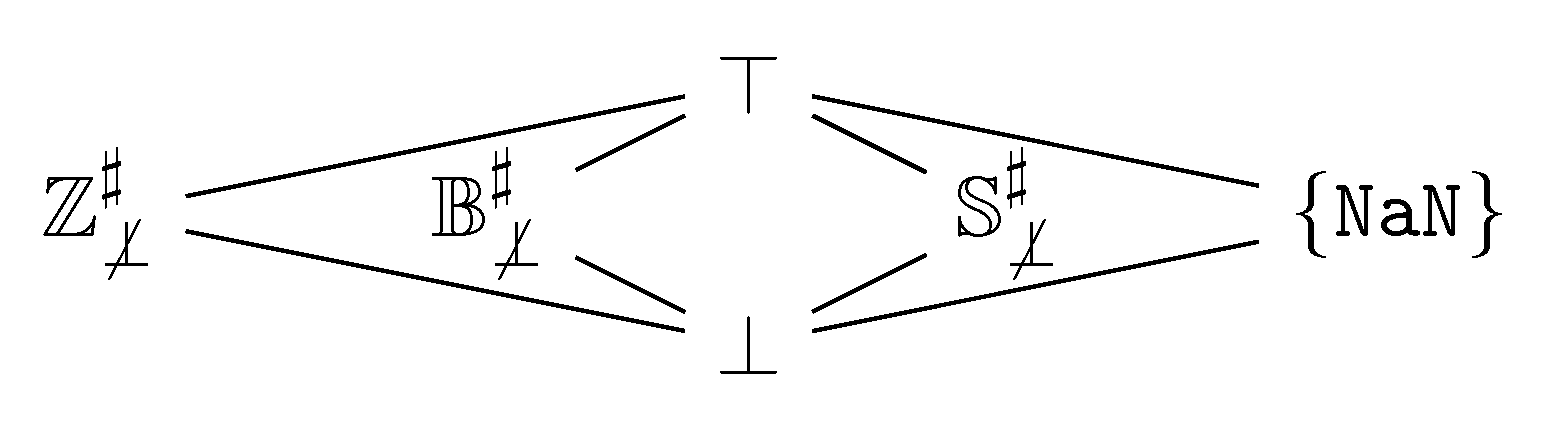
4.2. An Abstract Domain for
4.2.1. Coalesced Sum
4.2.2. Cartesian Product
5. Abstract Semantics of ECMAScript String Operations
5.1. Abstract Semantics of Substring
- If (second row, second column of Table 1) we have to compute the language of all the substrings between the initial index i and a final index in j, i.e., . For example, let , the set of its substrings from 1 to 3 is . When , as in the example, the automaton accepting this language is computed by the operatorIf , the integer arguments are simply swapped, as in the Table 1.
- When both integer parameters correspond to , the result is the automaton of all possible factors of (third row, third column), i.e., .
- When i is defined and (second row, third column), we have to compute the automaton recognizing all the substrings of from 0 to i and any substring starting from i. For example, let us consider . Due to the semantics of substring reported in Section 3, we need to compute the substring from to 5 and then any substring with initial index equal to 5. The automata recognizing any substring starting at a specific index l is defined as . The abstract semantics returns the least upper bound of all the automata of substrings from a in to the automata recognizing any substring with initial index equals to i.
- Similarly to the previous case, when j is defined and (third row, second column), we have to compute the automaton recognizing all the substring of from 0 to j and any substring starting from j. Let us consider . Similarly to the previous case, we compute the substrings from to 5 and then any substring with initial index equal to 5. The abstract semantics therefore returns the least upper bound of all the automata of substrings from a in to the automata recognizing any substring with initial index equal to j.
5.2. Abstract Semantics of charAt
5.3. Abstract Semantics of length
| Algorithm 1: algorithm |
 |
5.4. Abstract Semantics of Concat
5.5. Abstract Semantics of StartsWith
| Algorithm 2: algorithm |
 |
5.6. Abstract Semantics of ToLowerCase
| Algorithm 3: algorithm |
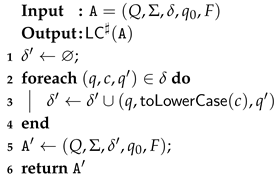 |
5.7. Abstract Semantics of Includes
| Algorithm 4: algorithm |
 |
5.8. Abstract Semantics of Repeat
| Algorithm 5: algorithm |
 |
5.9. Abstract Semantics of TrimLeft, TrimRight and Trim
| Algorithm 6: algorithm |
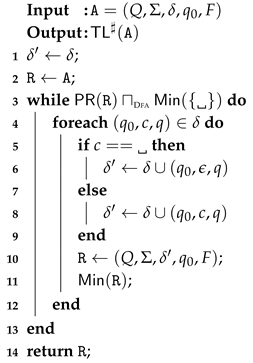 |
5.10. Concerning Abstract Implicit Type Conversion
6. Implementation
6.1. Theoretical Concerns
6.2. Implementation
6.3. Extension to Interval Abstract Domain
length Abstract Semantics with Intervals
6.4. Qualitative Evaluation of
| Algorithm 7: Algorithm |
 |
6.4.1. Obfuscated Malware
6.4.2. String Manipulation Program
7. Discussion and Related Work
7.1. Analysis vs. Verification
7.2. Main Related Works
7.3. Future Ideas
Author Contributions
Funding
Conflicts of Interest
Appendix A. Selected Proofs
- and : let us suppose, w.l.o.g., that (otherwise the indexes are swapped).
- , with
- Let us suppose that , hence , where .
- Let us suppose that , hence . It is worth noting that the function we used in the abstract semantics of charAt is complete. Let be the function that given a set of strings returns the set of characters inside any string of the input string set. It holds that .
- , s.t. :This condition checks whether the size of any path of is n. This check is performed by Algorithm 1 at lines 5–8.
- , s.t. : this means thatIf is cyclic, then the condition at line 1 is successful and is returned. Let us suppose that is not cyclic.This condition is checked by lines 5–8 of Algorithm 1.
- Let us suppose that .
- Let us suppose that . We split the proof in the following cases:
- -
- if : Algorithm 2 verifies the condition () at lines 1–3 and returns .
- -
- if or are cyclic: Algorithm 2 verifies the condition () at lines 7–9 and returns .
- -
- if is not a single-path automaton: in this case, we check if is not a single path automaton at line 10 of Algorithm 2 and, if so, is returned at line 17.
- -
- if is a single path automaton: let us denote by the longest string recognized by . As we already highlighted, if is single path, the longest string is unique. Clearly, we have that . Let us denote by .
- Let us suppose that . We split the proof in the following cases:
- -
- or are cyclic: Algorithm 2 verifies the condition () at lines 7–9 and returns .
- -
- if is not single path automaton: the check at line 10 of Algorithm 2 fails and is returned at line 17.
- -
- is single-path automaton: as before, if is single path, the longest string is unique. Let us denote by .The condition is verified at lines 13 of Algorithm 2, it fails, hence at line 17 is returned.
- Let us suppose that .
- Let us suppose that . Thus, consider the following cases:
- -
- : Algorithm 4 verifies the condition () at lines 1–3 and returns {.
- -
- or are cyclic: Algorithm 2 verifies the condition () at lines 7–9 and returns .
- -
- and are not cyclic:This condition is verified in lines 11–15 of Algorithm 4 and in this case the algorithm returns .
- Let us suppose that . Thus, consider the following cases:
- -
- or are cyclic: Algorithm 4 verifies the condition () at lines 7–9 and returns .
- -
- and are not cyclic:
This condition is verified in lines 11–15 of Algorithm 4 and in this case the algorithm returns .
- Let us suppose that , hence , where . We split the proof in the following cases:
- -
- : and Algorithm 5 checks this condition and returns at lines 1–3.
- -
- :
- *
- if is s.t. : since , Algorithm 5 checks this condition and returns at lines 1–3.
- *
- if is cyclic: and Algorithm5 checks this condition and returns at lines 4–6.
- *
- is not cyclic:In this case, Algorithm 5 returns the above automaton at lines 8–15.
- Let us suppose that , hence we have that .In this case, Algorithm 5 returns , guaranteeing the soundness of .
References
- Pradel, M.; Sen, K. The Good, the Bad, and the Ugly: An Empirical Study of Implicit Type Conversions in JavaScript. In Proceedings of the 29th European Conference on Object-Oriented Programming, ECOOP 2015, Prague, Czech Republic, 5–10 July 2015; Boyland, J.T., Ed.; LIPIcs. Schloss Dagstuhl- Leibniz-Zentrum für Informatik: Wadern, Germany, 2015; Volume 37, pp. 519–541. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F.; Zhu, S. The power of obfuscation techniques in malicious JavaScript code: A measurement study. In Proceedings of the 7th International Conference on Malicious and Unwanted Software, MALWARE 2012, Fajardo, PR, USA, 16–18 October 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 9–16. [Google Scholar] [CrossRef] [Green Version]
- Jensen, S.H.; Møller, A.; Thiemann, P. Type Analysis for JavaScript. In Proceedings of the 16th International Symposium on Static Analysis, SAS 2009, Los Angeles, CA, USA, 9–11 August 2009; Palsberg, J., Su, Z., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2009; Volume 5673, pp. 238–255. [Google Scholar] [CrossRef] [Green Version]
- Kashyap, V.; Dewey, K.; Kuefner, E.A.; Wagner, J.; Gibbons, K.; Sarracino, J.; Wiedermann, B.; Hardekopf, B. JSAI: A static analysis platform for JavaScript. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, (FSE-22), Hong Kong, China, 16–22 November 2014; Cheung, S., Orso, A., Storey, M.D., Eds.; ACM: New York, NY, USA, 2014; pp. 121–132. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Won, S.; Jin, J.; Cho, J.; Ryu, S. SAFE: Formal specification and implementation of a scalable analysis framework for ECMAScript. In Proceedings of the 19th International Workshop on Foundations of Object-Oriented Languages (FOOL’12), Tucson, AZ, USA, 19–26 October 2012. [Google Scholar]
- Hauzar, D.; Kofron, J. Framework for Static Analysis of PHP Applications. In Proceedings of the 29th European Conference on Object-Oriented Programming, ECOOP 2015, Prague, Czech Republic, 5–10 July 2015; Boyland, J.T., Ed.; LIPIcs. Schloss Dagstuhl-Leibniz-Zentrum für Informatik: Wadern, Germany, 2015; Volume 37, pp. 689–711. [Google Scholar] [CrossRef]
- Arceri, V.; Mastroeni, I. A sound abstract interpreter for dynamic code. In Proceedings of the SAC ’20: The 35th ACM/SIGAPP Symposium on Applied Computing, Brno, Czech Republic, 30 March–3 April 2020; Hung, C., Cerný, T., Shin, D., Bechini, A., Eds.; ACM: New York, NY, USA, 2020; pp. 1979–1988. [Google Scholar] [CrossRef]
- Arceri, V.; Mastroeni, I. Static Program Analysis for String Manipulation Languages. In Proceedings of the Seventh International Workshop on Verification and Program Transformation, VPT@Programming 2019, Genova, Italy, 2 April 2019; Volume 299, pp. 19–33. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R. Abstract Interpretation: A Unified Lattice Model for Static Analysis of Programs by Construction or Approximation of Fixpoints. In Proceedings of the Conference Record of the Fourth ACM Symposium on Principles of Programming Languages, Los Angeles, CA, USA, 17–19 January 1977; Graham, R.M., Harrison, M.A., Sethi, R., Eds.; ACM: New York, NY, USA, 1977; pp. 238–252. [Google Scholar] [CrossRef] [Green Version]
- ECMA. Standard ECMA-262 Language Specification, 9th ed. Available online: https://www.ecma-international.org/publications/files/ECMA-ST/Ecma-262.pdf (accessed on 6 December 2018).
- Hopcroft, J.E.; Ullman, J.D. Introduction to Automata Theory, Languages and Computation; Addison-Wesley: Reading, MA, USA, 1979. [Google Scholar]
- Davis, M.D.; Sigal, R.; Weyuker, E.J. Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science; Academic Press Professional, Inc.: Cambridge, MA, USA, 1994. [Google Scholar]
- Cousot, P.; Cousot, R. Systematic Design of Program Analysis Frameworks. In Proceedings of the Conference Record of the Sixth Annual ACM Symposium on Principles of Programming Languages, San Antonio, TX, USA, 29–31 January 1979; Aho, A.V., Zilles, S.N., Rosen, B.K., Eds.; ACM Press: New York, NY, USA, 1979; pp. 269–282. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R. Abstract Interpretation Frameworks. J. Log. Comput. 1992, 2, 511–547. [Google Scholar] [CrossRef]
- Giacobazzi, R.; Quintarelli, E. Incompleteness, Counterexamples, and Refinements in Abstract Model-Checking. In Proceedings of the Static Analysis, 8th International Symposium, SAS 2001, Paris, France, 16–18 July 2001; Cousot, P., Ed.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2001; Volume 2126, pp. 356–373. [Google Scholar] [CrossRef]
- Giacobazzi, R.; Mastroeni, I. Making abstract models complete. Math. Struct. Comput. Sci. 2016, 26, 658–701. [Google Scholar] [CrossRef]
- Giacobazzi, R.; Mastroeni, I. Transforming Abstract Interpretations by Abstract Interpretation. In Proceedings of the Static Analysis, 15th International Symposium, SAS 2008, Valencia, Spain, 16–18 July 2008; Alpuente, M., Vidal, G., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2008; Volume 5079, pp. 1–17. [Google Scholar] [CrossRef]
- Arceri, V.; Maffeis, S. Abstract Domains for Type Juggling. Electron. Notes Theor. Comput. Sci. 2017, 331, 41–55. [Google Scholar] [CrossRef]
- Park, C.; Im, H.; Ryu, S. Precise and scalable static analysis of jQuery using a regular expression domain. In Proceedings of the 12th Symposium on Dynamic Languages, DLS 2016, Amsterdam, The Netherlands, 1 November 2016; Ierusalimschy, R., Ed.; ACM: New York, NY, USA, 2016; pp. 25–36. [Google Scholar] [CrossRef]
- Choi, T.; Lee, O.; Kim, H.; Doh, K. A Practical String Analyzer by the Widening Approach. In Proceedings of the 4th Asian Symposium on Programming Languages and Systems, APLAS 2006, Sydney, Australia, 8–10 November 2006; Kobayashi, N., Ed.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2006; Volume 4279, pp. 374–388. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Bultan, T.; Cova, M.; Ibarra, O.H. Symbolic String Verification: An Automata-Based Approach. In Proceedings of the 15th International SPIN Workshop on Model Checking Software, Los Angeles, CA, USA, 10–12 August 2008; Havelund, K., Majumdar, R., Palsberg, J., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2008; Volume 5156, pp. 306–324. [Google Scholar] [CrossRef]
- Câmpeanu, C.; Paun, A.; Yu, S. An Efficient Algorithm for Constructing Minimal Cover Automata for Finite Languages. Int. J. Found. Comput. Sci. 2002, 13, 83–97. [Google Scholar] [CrossRef]
- Domaratzki, M.; Shallit, J.O.; Yu, S. Minimal Covers of Formal Languages. In Proceedings of the 5th International Conference Developments in Language Theory, DLT 2001, Vienna, Austria, 16–21 July 2001; Revised Papers. Kuich, W., Rozenberg, G., Salomaa, A., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2001; Volume 2295, pp. 319–329. [Google Scholar] [CrossRef]
- Mohri, M.; Nederhof, M. Regular Approximation of Context-Free Grammars through Transformation. In Robustness in Language and Speech Technology; Springer: Dordrecht, The Netherlands, 2001; pp. 153–163. [Google Scholar]
- Cousot, P.; Halbwachs, N. Automatic Discovery of Linear Restraints Among Variables of a Program. In Proceedings of the Conference Record of the Fifth Annual ACM Symposium on Principles of Programming Languages, Tucson, AZ, USA, 23–25 January 1978; Aho, A.V., Zilles, S.N., Szymanski, T.G., Eds.; ACM Press: New York, NY, USA, 1978; pp. 84–96. [Google Scholar] [CrossRef] [Green Version]
- Costantini, G.; Ferrara, P.; Cortesi, A. A suite of abstract domains for static analysis of string values. Softw. Pract. Exp. 2015, 45, 245–287. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R. Comparing the Galois Connection and Widening/Narrowing Approaches to Abstract Interpretation. In Proceedings of the 4th International Symposium on Programming Language Implementation and Logic Programming, PLILP’92, Leuven, Belgium, 26–28 August 1992; Bruynooghe, M., Wirsing, M., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 1992; Volume 631, pp. 269–295. [Google Scholar] [CrossRef]
- D’Silva, V. Widening for Automata. Ph.D. Thesis, Institut Fur Informatick, UZH, Zurich, Switzerland, 2006. [Google Scholar]
- Bartzis, C.; Bultan, T. Widening Arithmetic Automata. In Proceedings of the 16th International Conference on Computer Aided Verification, CAV 2004, Boston, MA, USA, 13–17 July 2004; Alur, R., Peled, D.A., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2004; Volume 3114, pp. 321–333. [Google Scholar] [CrossRef] [Green Version]
- Cousot, P. Types as Abstract Interpretations. In Proceedings of the Conference Record of POPL’97: The 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Paris, France, 15–17 January 1997; Lee, P., Henglein, F., Jones, N.D., Eds.; ACM Press: New York, NY, USA, 1997; pp. 316–331. [Google Scholar] [CrossRef]
- Reynolds, J.C. Theories of Programming Languages; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Giacobazzi, R.; Ranzato, F.; Scozzari, F. Making abstract interpretations complete. J. ACM 2000, 47, 361–416. [Google Scholar] [CrossRef]
- Fromherz, A.; Ouadjaout, A.; Miné, A. Static Value Analysis of Python Programs by Abstract Interpretation. In Proceedings of the 10th International Symposium on NASA Formal Methods, NFM 2018, Newport News, VA, USA, 17–19 April 2018; Dutle, A., Muñoz, C.A., Narkawicz, A., Eds.; Lecture Notes in Computer Science. Springer: Berin, Germany, 2018; Volume 10811, pp. 185–202. [Google Scholar] [CrossRef] [Green Version]
- Bordihn, H.; Holzer, M.; Kutrib, M. Determination of finite automata accepting subregular languages. Theor. Comput. Sci. 2009, 410, 3209–3222. [Google Scholar] [CrossRef] [Green Version]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Holzer, M.; Jakobi, S. Brzozowski’s Minimization Algorithm - More Robust than Expected-(Extended Abstract). In Proceedings of the 18th International Conference on Implementation and Application of Automata, CIAA 2013, Halifax, NS, Canada, 16–19 July 2013; Konstantinidis, S., Ed.; Springer: Berlin, Germany, 2013. Lecture Notes in Computer Science. Volume 7982, pp. 181–192. [Google Scholar] [CrossRef]
- Park, C.; Ryu, S. Scalable and Precise Static Analysis of JavaScript Applications via Loop-Sensitivity. In Proceedings of the 29th European Conference on Object-Oriented Programming, ECOOP 2015, Prague, Czech Republic, 5–10 July 2015; LIPIcs. Boyland, J.T., Ed.; Schloss Dagstuhl-Leibniz-Zentrum für Informatik: Wadern, Germany, 2015; Volume 37, pp. 735–756. [Google Scholar] [CrossRef]
- Mozilla. MDN Web Docs-Useful String Methods. Available online: https://developer.mozilla.org/en-US/docs/Learn/JavaScript/First_steps/Useful_string_methods (accessed on 20 April 2020).
- Abdulla, P.A.; Atig, M.F.; Chen, Y.; Holík, L.; Rezine, A.; Rümmer, P.; Stenman, J. Norn: An SMT Solver for String Constraints. In Proceedings of the Computer Aided Verification-27th International Conference, CAV 2015, San Francisco, CA, USA, 18–24 July 2015; Part I. Kroening, D., Pasareanu, C.S., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2015; Volume 9206, pp. 462–469. [Google Scholar] [CrossRef]
- Liang, T.; Reynolds, A.; Tsiskaridze, N.; Tinelli, C.; Barrett, C.W.; Deters, M. An efficient SMT solver for string constraints. Form. Methods Syst. Des. 2016, 48, 206–234. [Google Scholar] [CrossRef]
- Cousot, P.; Giacobazzi, R.; Ranzato, F. Program Analysis Is Harder Than Verification: A Computability Perspective. In Proceedings of the Computer Aided Verification-30th International Conference, CAV 2018, Held as Part of the Federated Logic Conference, FloC 2018, Oxford, UK, 14–17 July 2018; Part II. Chockler, H., Weissenbacher, G., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2018; Volume 10982, pp. 75–95. [Google Scholar] [CrossRef] [Green Version]
- Midtgaard, J.; Nielson, F.; Nielson, H.R. A Parametric Abstract Domain for Lattice-Valued Regular Expressions. In Proceedings of the Static Analysis-23rd International Symposium, SAS 2016, Edinburgh, UK, 8–10 September 2016; Rival, X., Ed.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2016; Volume 9837, pp. 338–360. [Google Scholar] [CrossRef]
- Lin, A.W.; Barceló, P. String solving with word equations and transducers: Towards a logic for analysing mutation XSS. In Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2016, St. Petersburg, FL, USA, 20–22 January 2016; Bodík, R., Majumdar, R., Eds.; ACM: New York, NY, USA, 2016; pp. 123–136. [Google Scholar] [CrossRef]
- Abdulla, P.A.; Atig, M.F.; Chen, Y.; Holík, L.; Rezine, A.; Rümmer, P.; Stenman, J. String Constraints for Verification. In Proceedings of the Computer Aided Verification-26th International Conference, CAV 2014, Held as Part of the Vienna Summer of Logic, VSL 2014, Vienna, Austria, 18–22 July 2014; Biere, A., Bloem, R., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2014; Volume 8559, pp. 150–166. [Google Scholar] [CrossRef]
- Bouajjani, A.; Habermehl, P.; Vojnar, T. Abstract Regular Model Checking. In Proceedings of the 16th International Conference on Computer Aided Verification, CAV 2004, Boston, MA, USA, 13–17 July 2004; Alur, R., Peled, D.A., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2004; Volume 3114, pp. 372–386. [Google Scholar] [CrossRef] [Green Version]
- Bouajjani, A.; Habermehl, P.; Holík, L.; Touili, T.; Vojnar, T. Antichain-Based Universality and Inclusion Testing over Nondeterministic Finite Tree Automata. In Proceedings of the 13th International Conference on Implementation and Applications of Automata, CIAA 2008, San Francisco, CA, USA, 21–24 July 2008; Ibarra, O.H., Ravikumar, B., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2008; Volume 5148, pp. 57–67. [Google Scholar] [CrossRef]
- Alur, R.; Madhusudan, P. Visibly pushdown languages. In Proceedings of the 36th Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–16 June 2004; Babai, L., Ed.; ACM: New York, NY, USA, 2004; pp. 202–211. [Google Scholar] [CrossRef] [Green Version]
- Holík, L.; Janku, P.; Lin, A.W.; Rümmer, P.; Vojnar, T. String constraints with concatenation and transducers solved efficiently. Proc. ACM Program. Lang. 2018, 2, 4. [Google Scholar] [CrossRef] [Green Version]
- Balakrishnan, G.; Reps, T.W. Recency-Abstraction for Heap-Allocated Storage. In Proceedings of the 13th International Symposium on Static Analysis, SAS 2006, Seoul, Korea, 29–31 August 2006; Yi, K., Ed.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2006; Volume 4134, pp. 221–239. [Google Scholar] [CrossRef] [Green Version]
- Jensen, S.H.; Jonsson, P.A.; Møller, A. Remedying the eval that men do. In Proceedings of the International Symposium on Software Testing and Analysis, ISSTA 2012, Minneapolis, MN, USA, 15–20 July 2012; Heimdahl, M.P.E., Su, Z., Eds.; ACM: New York, NY, USA, 2012; pp. 34–44. [Google Scholar] [CrossRef] [Green Version]
- Sharir, M.; Pnueli, A. Two Approaches to Interprocedural Data Flow Analysis; NYU CS: New York, NY, USA, 1978. [Google Scholar]


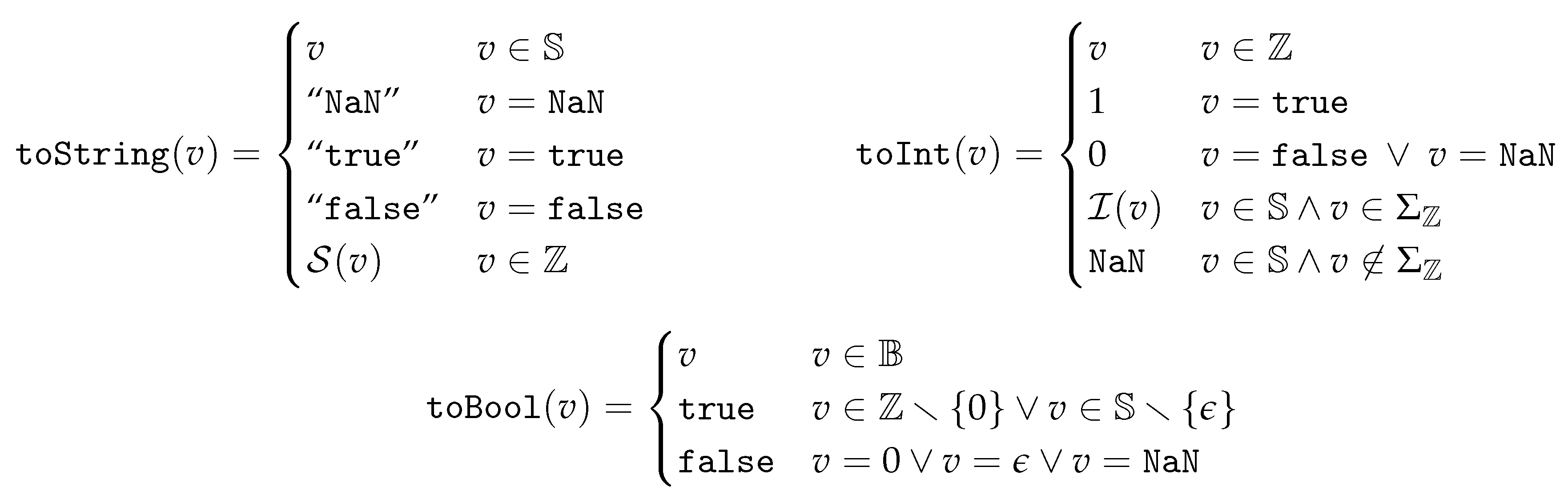
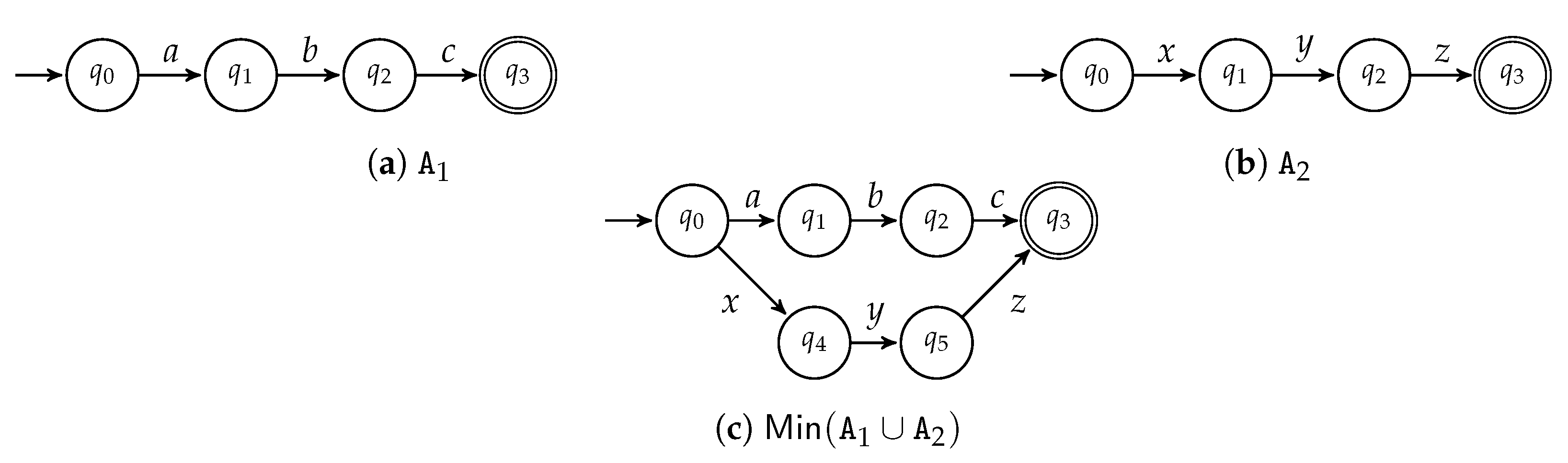
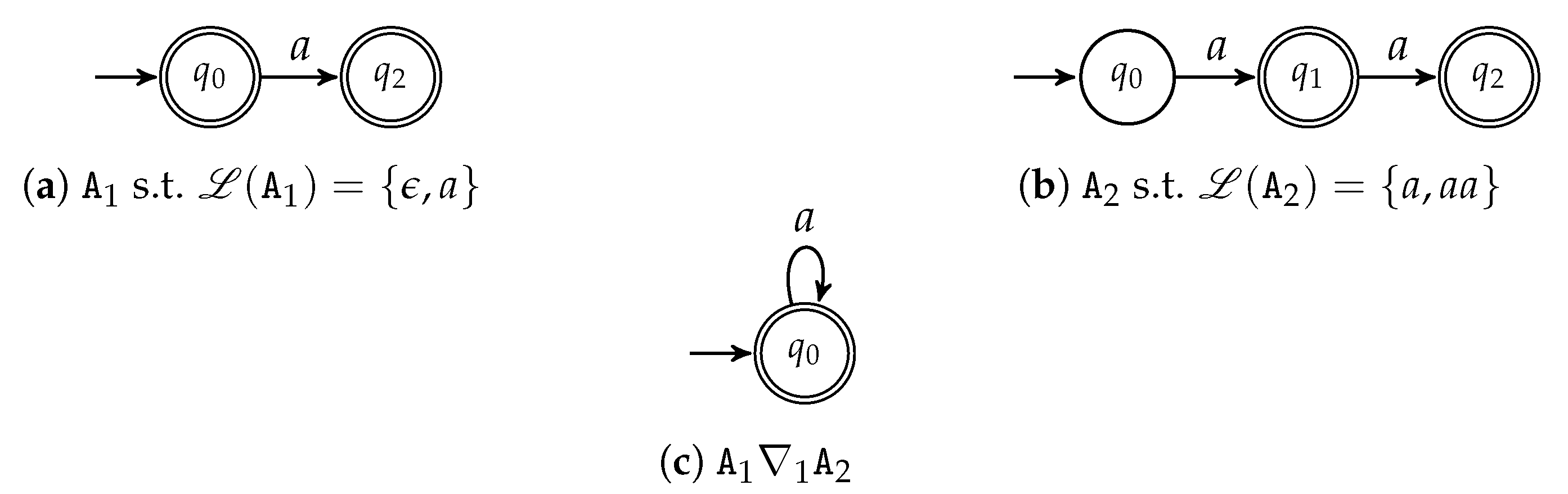


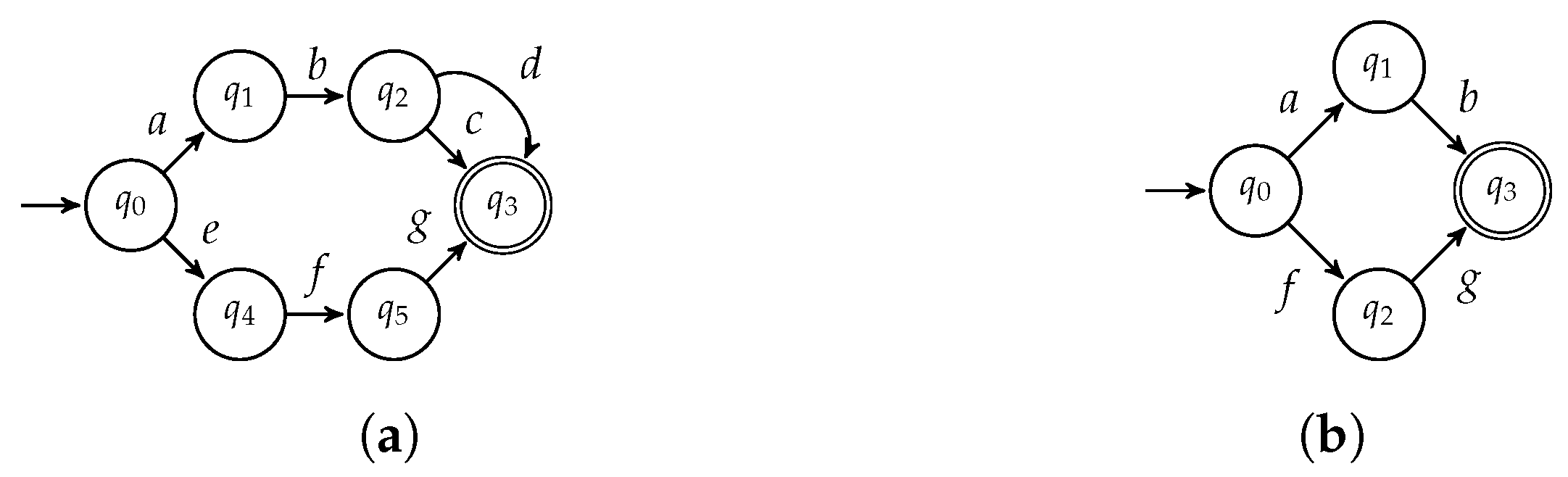
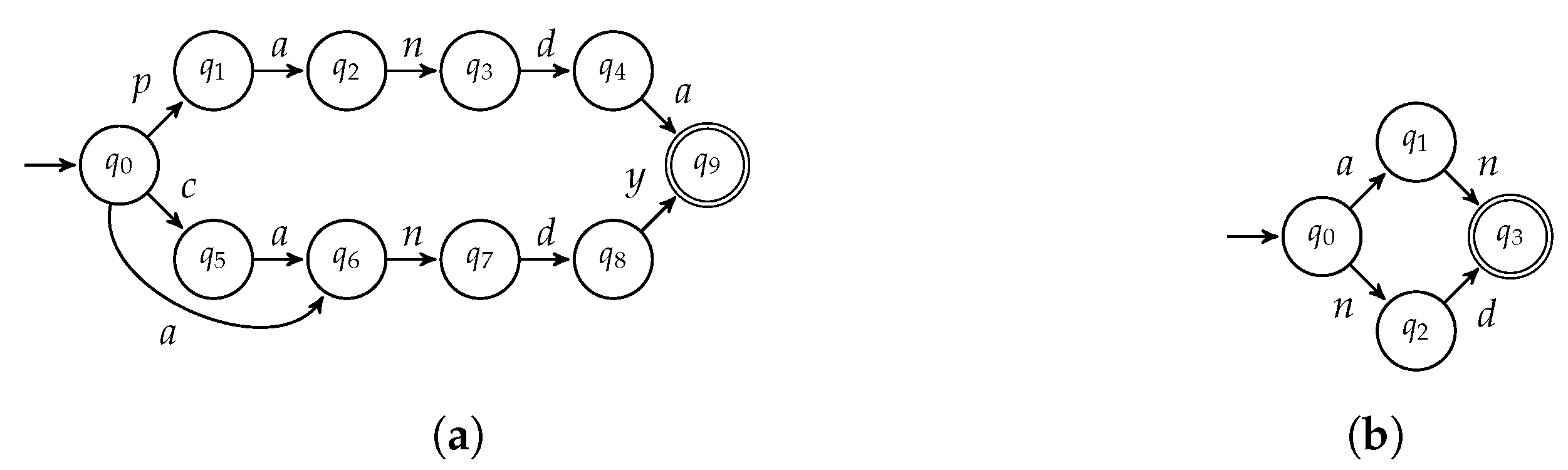
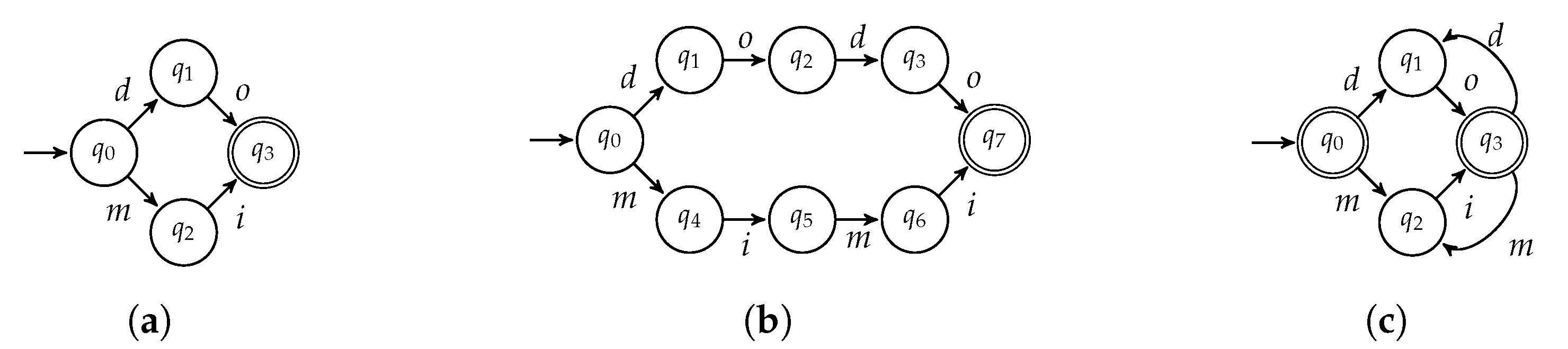

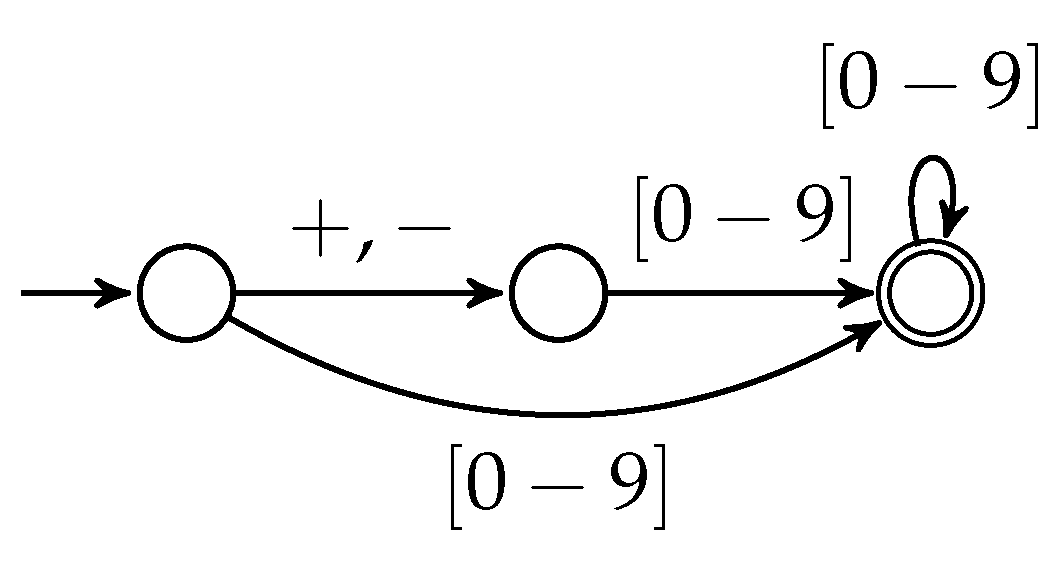
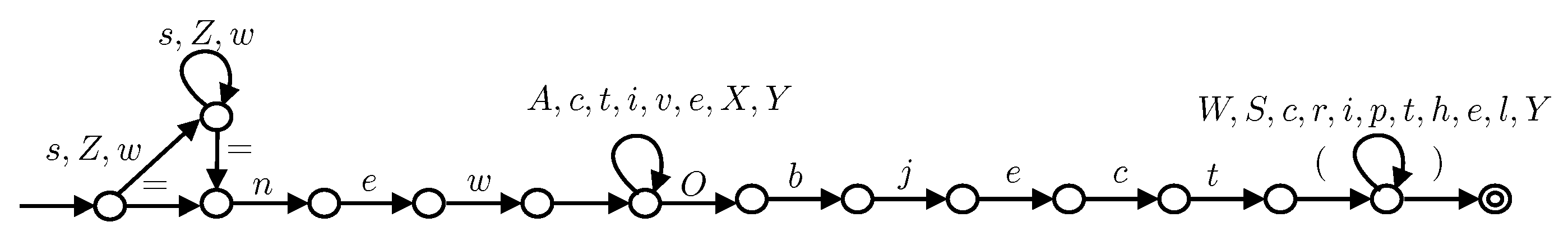

⊔ | ||
⊔ |
| String Operation | Soundness | Completeness | Average Complexity |
|---|---|---|---|
| substring | ✓ | ✓ | |
| charAt | ✓ | ✓ | |
| length | ✓ | ✓ | |
| concat | ✓ | ✓ | |
| startsWith endsWith | ✓ | ✗ | |
| toLowerCase toUpperCase | ✓ | ✓ | |
| includes | ✓ | ✗ | |
| repeat | ✓ | ✗ | |
| replace | ✓ | ✗ | |
| indexOf | ✓ | ✗ | |
| slice | ✓ | ✗ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arceri, V.; Mastroeni, I.; Xu, S. Static Analysis for ECMAScript String Manipulation Programs. Appl. Sci. 2020, 10, 3525. https://doi.org/10.3390/app10103525
Arceri V, Mastroeni I, Xu S. Static Analysis for ECMAScript String Manipulation Programs. Applied Sciences. 2020; 10(10):3525. https://doi.org/10.3390/app10103525
Chicago/Turabian StyleArceri, Vincenzo, Isabella Mastroeni, and Sunyi Xu. 2020. "Static Analysis for ECMAScript String Manipulation Programs" Applied Sciences 10, no. 10: 3525. https://doi.org/10.3390/app10103525
APA StyleArceri, V., Mastroeni, I., & Xu, S. (2020). Static Analysis for ECMAScript String Manipulation Programs. Applied Sciences, 10(10), 3525. https://doi.org/10.3390/app10103525





