Development and Characterization of a DC-Driven Thermal Oscillator Using Acrylate-Based Composites
Abstract
1. Introduction
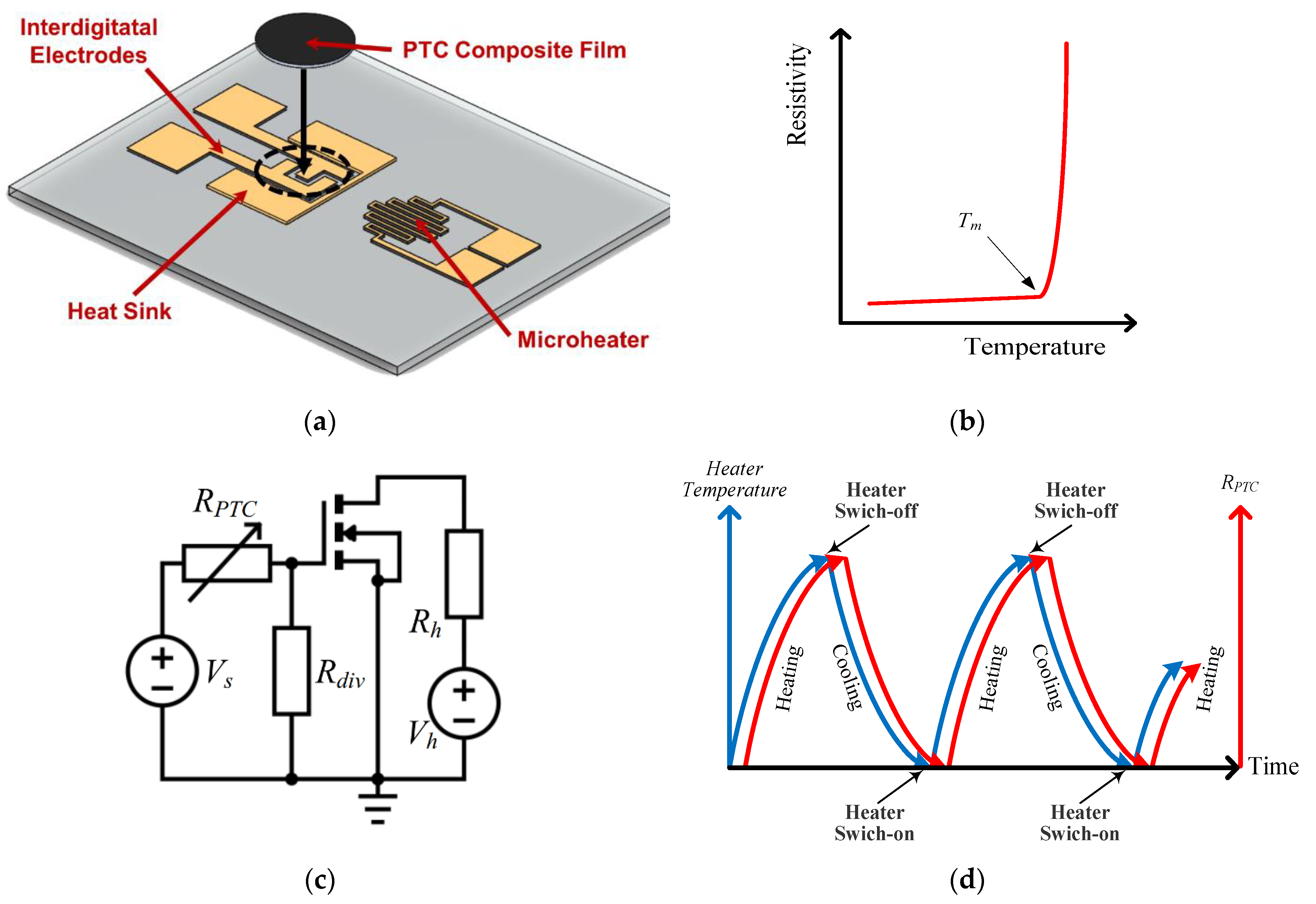
2. Working Principle and Device Design
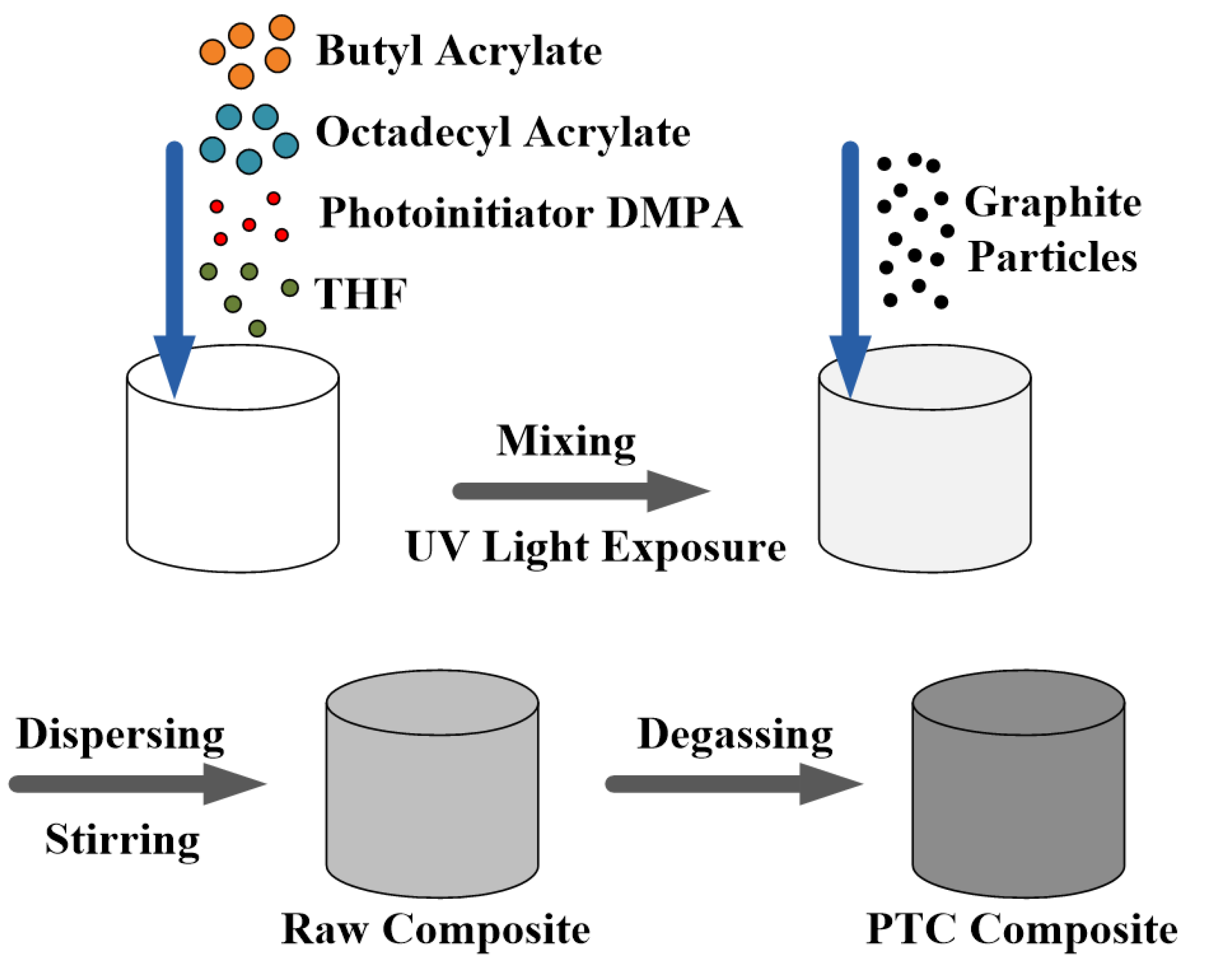
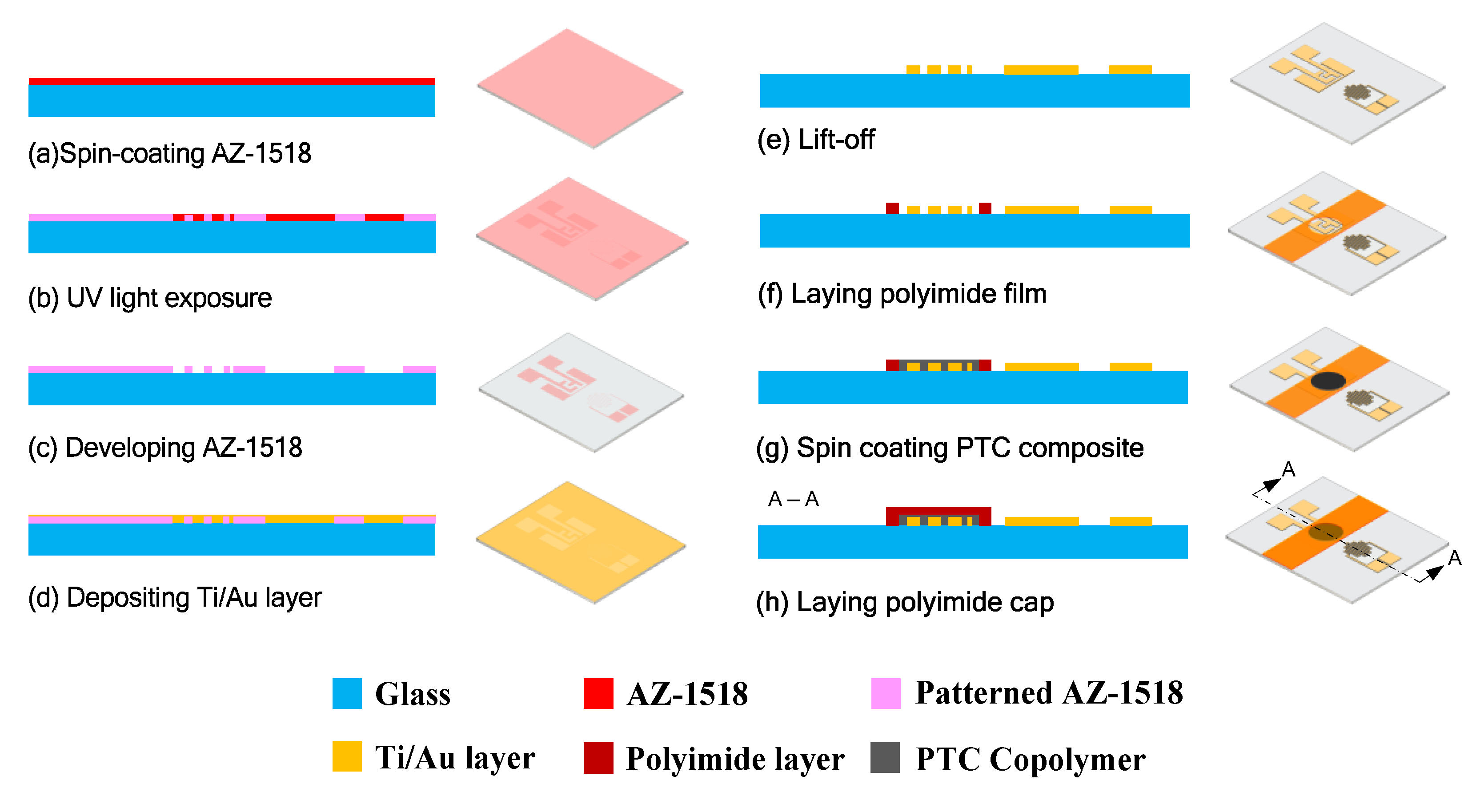
3. Device Fabrication
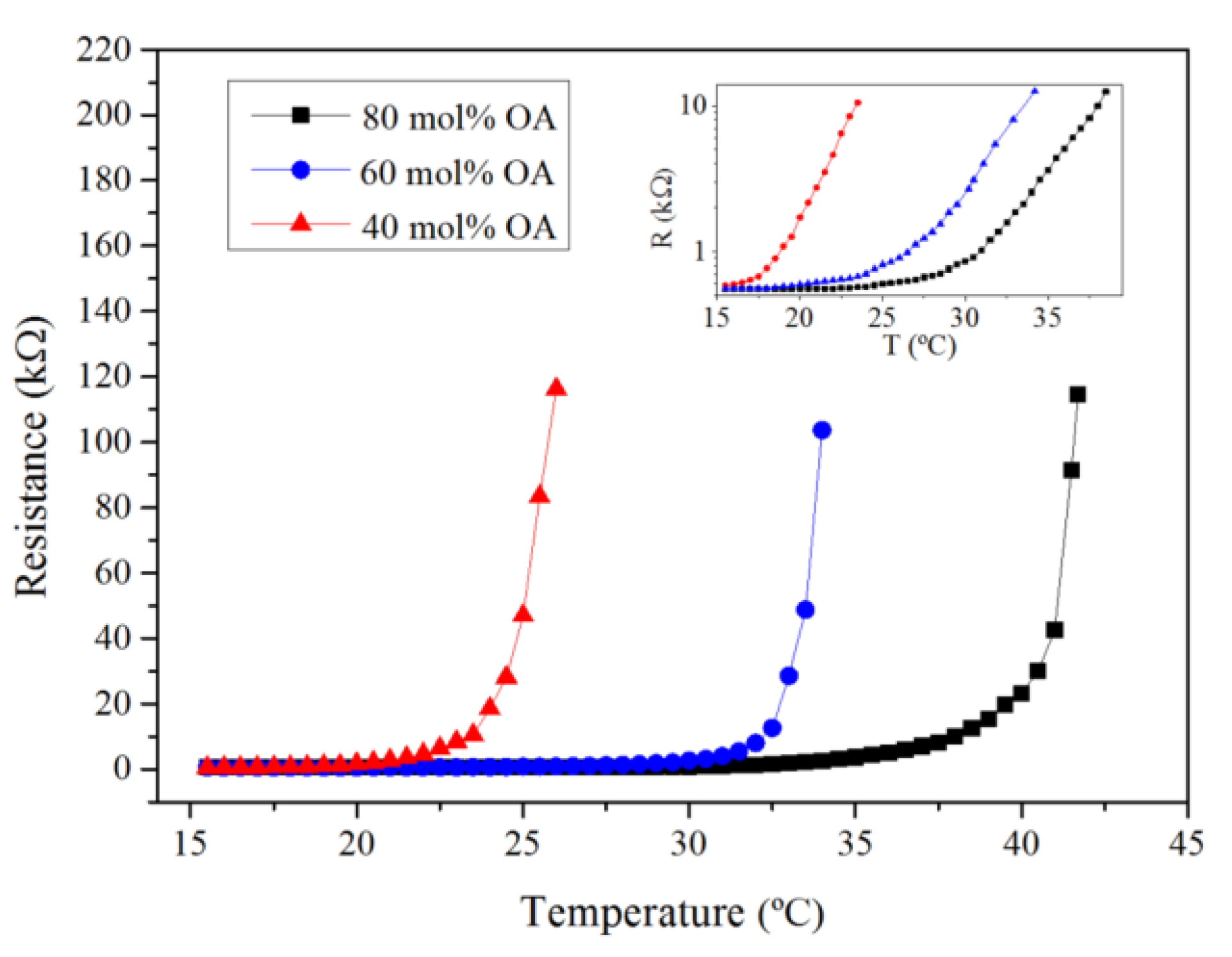
4. Measurement Results and Discussion
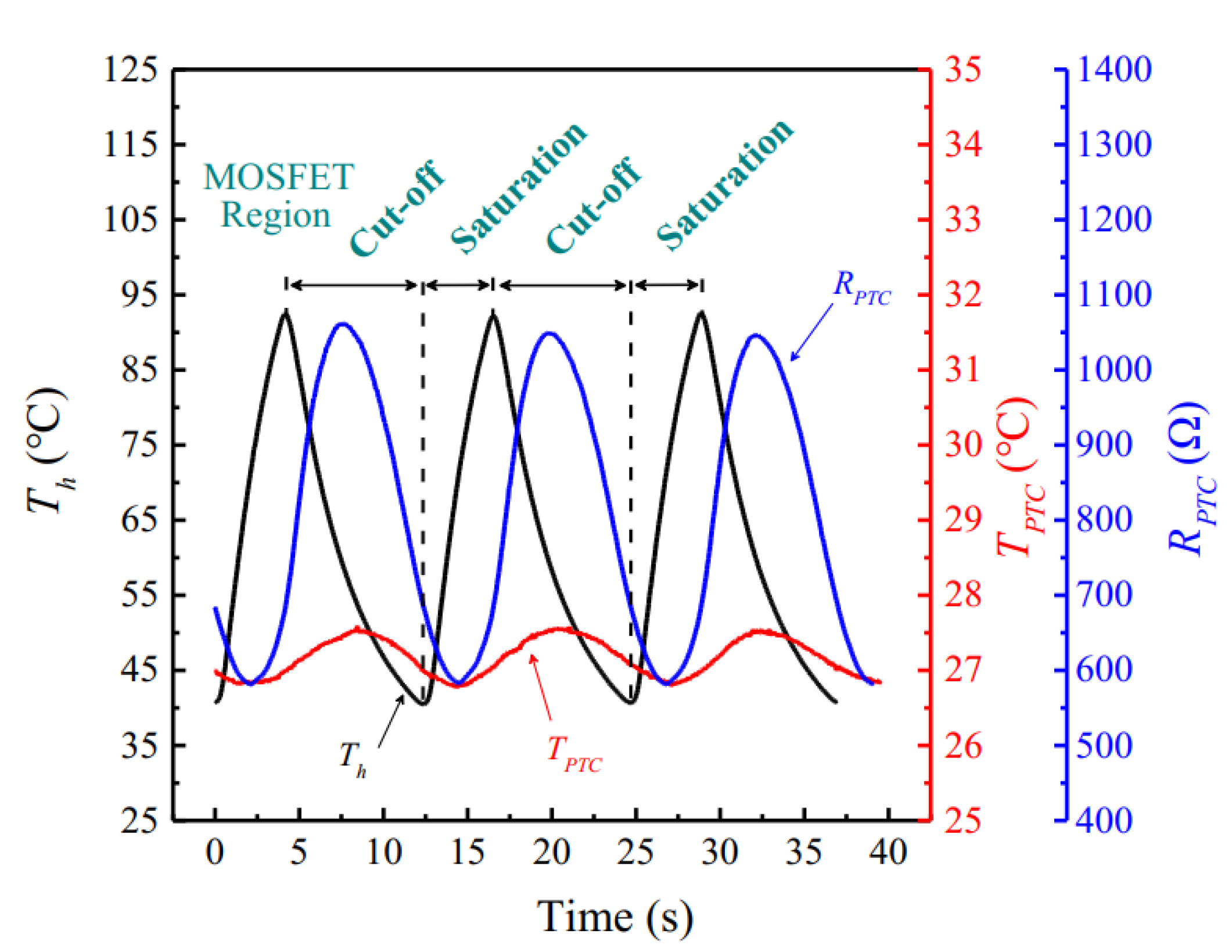
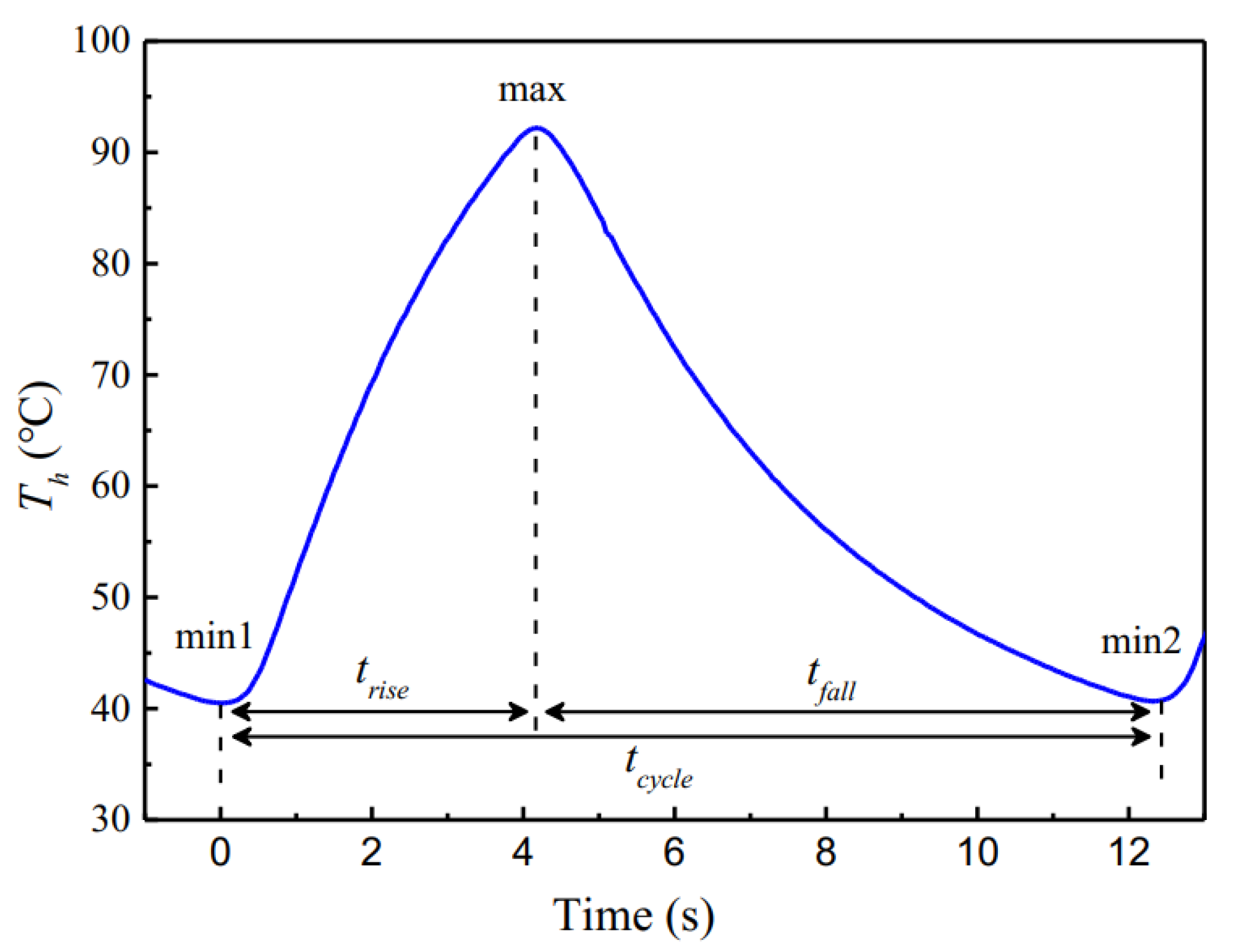
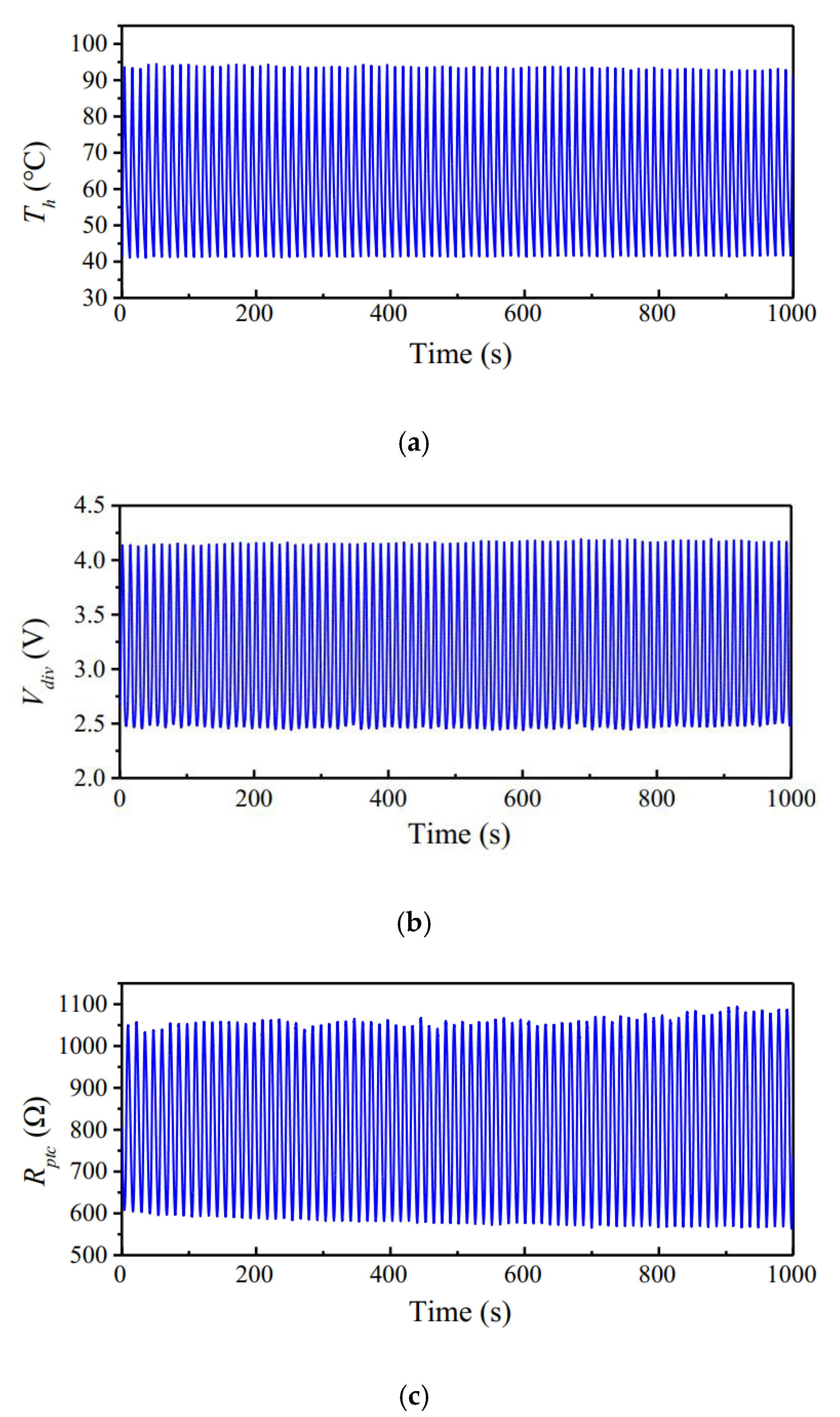
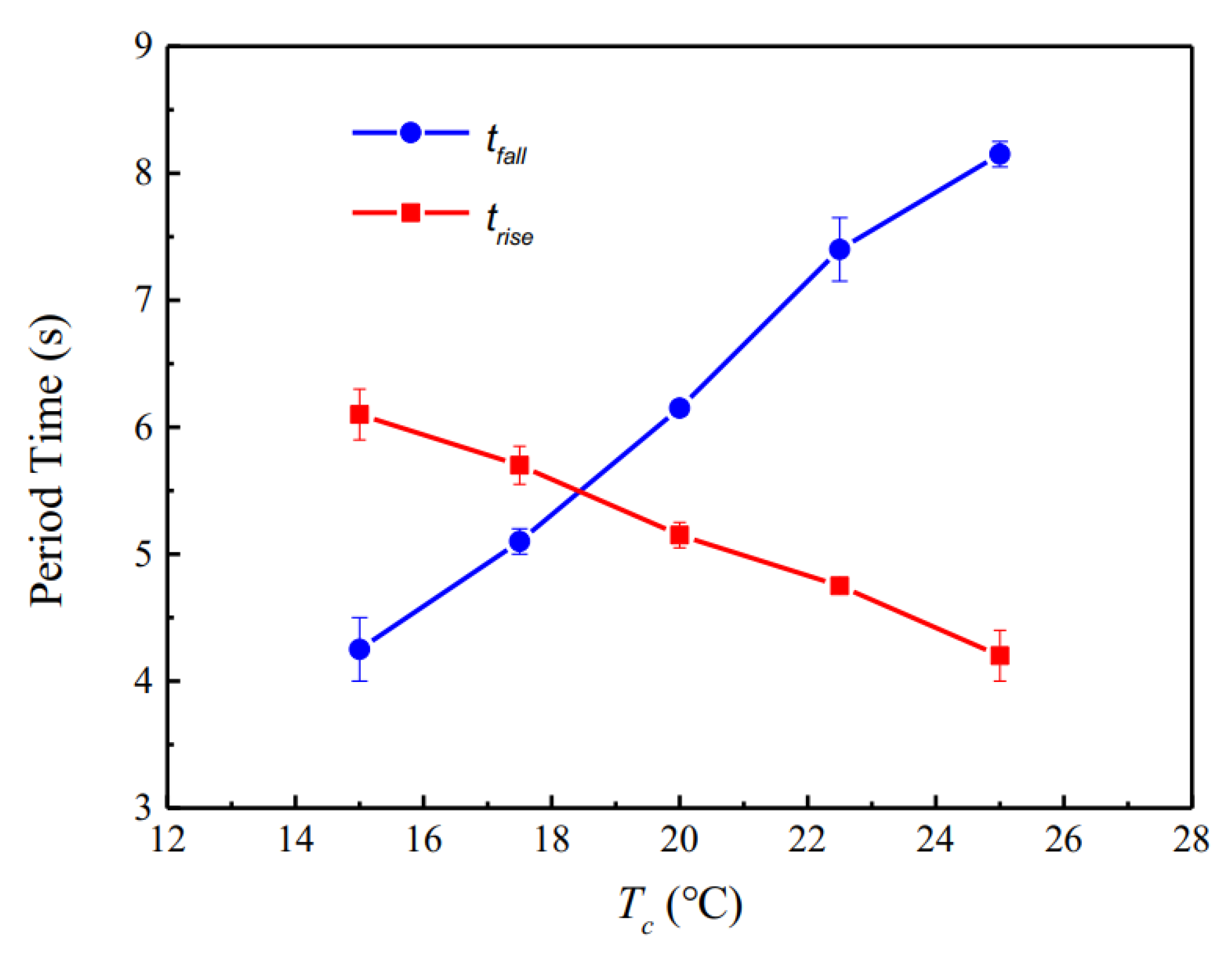
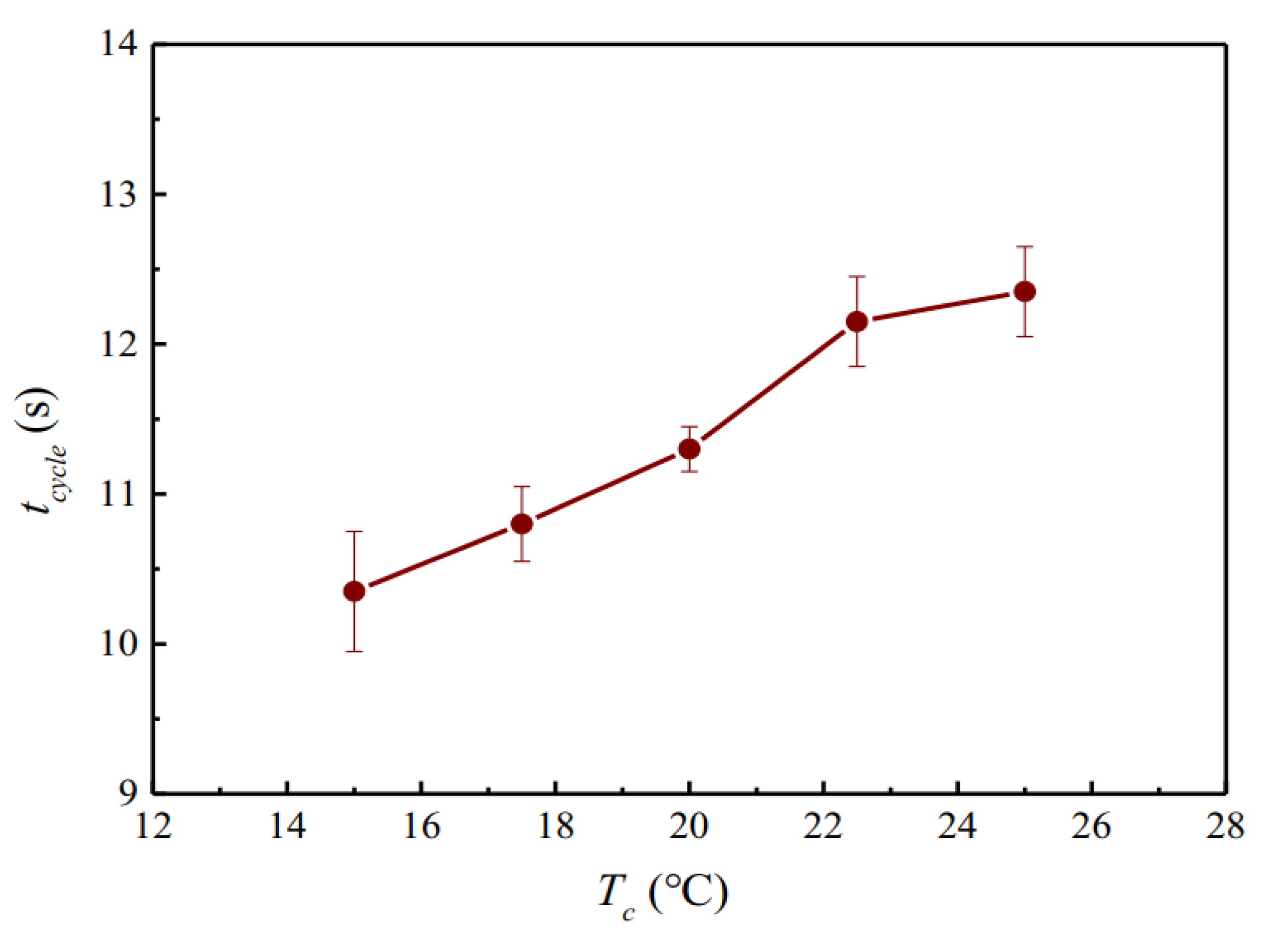
4.1. Transient Behaviors
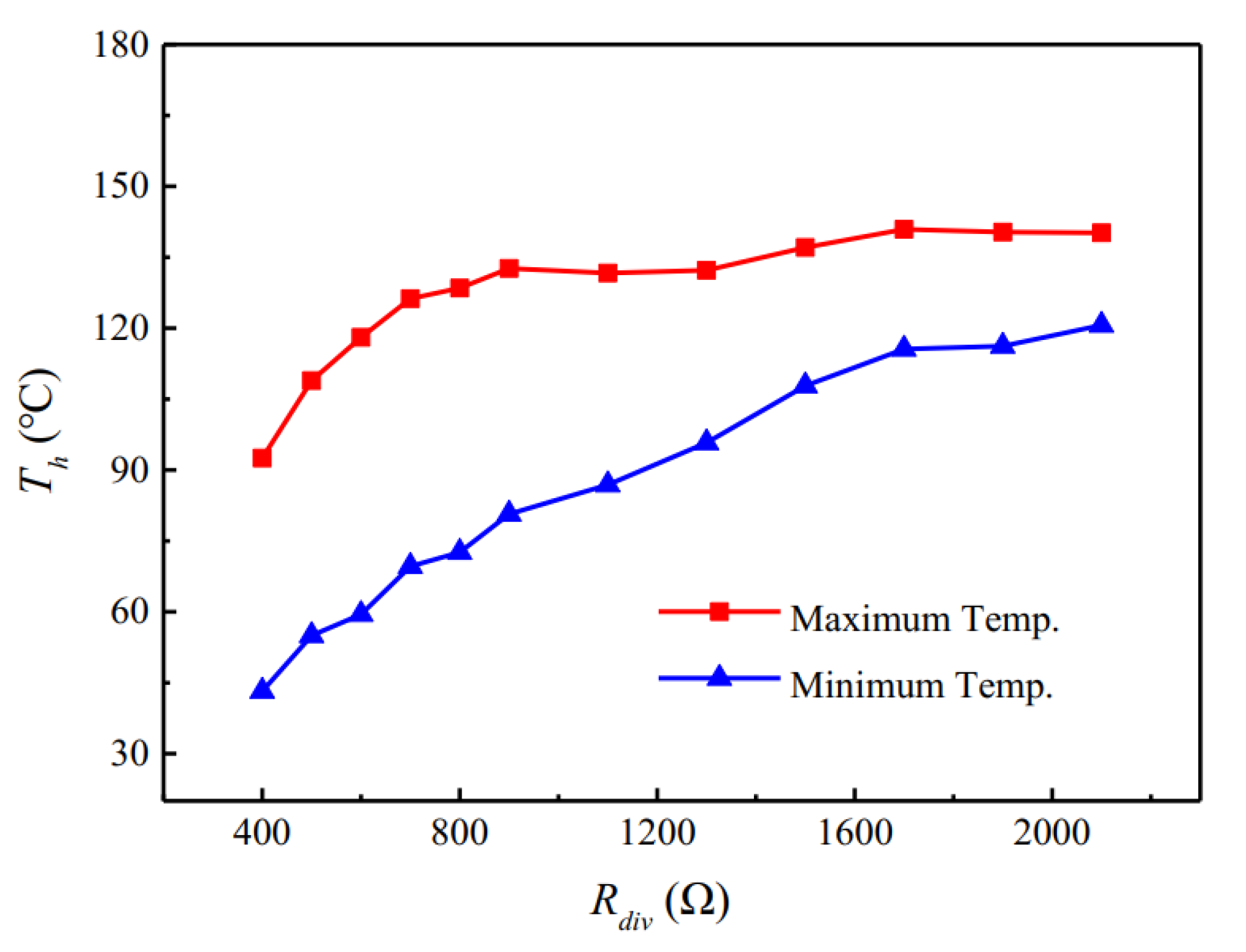
4.2. Discussions on Divider Resistance and Active Cooling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zha, J.-W.; Zhang, B.; Li, R.K.Y.; Dang, Z.-M. High-performance strain sensors based on functionalized graphene nanoplates for damage monitoring. Compos. Sci. Technol. 2016, 123, 32–38. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Liu, Y.; Zheng, G.; Liu, C.; Shen, C.; Yan, X.; Guo, J.; Guo, Z. Electrically conductive thermoplastic elastomer nanocomposites at ultralow graphene loading levels for strain sensor applications. J. Mater. Chem. C 2016, 4, 157–166. [Google Scholar] [CrossRef]
- Wu, X.; Han, Y.; Zhang, X.; Lu, C. Highly sensitive, stretchable, and wash-durable strain sensor based on ultrathin conductive Layer@Polyurethane yarn for tiny motion monitoring. ACS Appl. Mater. Interfaces 2016, 8, 9936–9945. [Google Scholar] [CrossRef] [PubMed]
- Yurddaskal, M.; Erol, M.; Celik, E. Carbon black and graphite filled conducting nanocomposite films for temperature sensor applications. J. Mater. Sci. Mater. Electron. 2017, 11, 9514–9518. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Liu, Y.; Zheng, G.; Liu, C.; Chen, J.; Shen, C. Tuning of vapor sensing behaviors of eco-friendly conductive polymer composites utilizing ramie fiber. Sens. Actuators B Chem. 2015, 221, 1279–1289. [Google Scholar] [CrossRef]
- Song, W.-L.; Cao, M.-S.; Lu, M.-M.; Bi, S.; Wang, C.-Y.; Liu, J.; Yuan, J.; Fan, L.-Z. Flexible graphene/polymer composite films in sandwich structures for effective electromagnetic interference shielding. Carbon 2014, 66, 67–76. [Google Scholar] [CrossRef]
- Ma, P.-C.; Siddiqui, N.A.; Marom, G.; Kim, J.-K. Dispersion and functionalization of carbon nanotubes for polymer-based nanocomposites: A review. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1345–1367. [Google Scholar] [CrossRef]
- Mamunya, Y.; Davydenko, V.; Pissis, P.; Lebedev, E. Electrical and thermal conductivity of polymers filled with metal powders. Eur. Polym. J. 2002, 38, 1887–1897. [Google Scholar] [CrossRef]
- Jiang, H.; Moon, K.-S.; Li, Y.; Wong, C.P. Surface functionalized silver nanoparticles for ultrahigh conductive polymer composites. Chem. Mater. 2006, 18, 2969–2973. [Google Scholar] [CrossRef]
- Pang, H.; Xu, L.; Yan, D.-X.; Li, Z.-M. Conductive polymer composites with segregated structures. Prog. Polym. Sci. 2014, 39, 1908–1933. [Google Scholar] [CrossRef]
- Frydman, E. Improvements in or Relating to Resistance Elements Having Positive Temperature/Resistance Characteristics. U.K. Patent 604,695, 16 November 1945. [Google Scholar]
- Kohler, F. Resistance Element. U.S. Patent 3,243,753, 29 March 1966. [Google Scholar]
- Ohe, K.; Naito, Y. A new resistor having an anomalously large positive temperature coefficient. Jpn. J. Appl. Phys. 1971, 10, 99–108. [Google Scholar] [CrossRef]
- Klason, C.; Kubát, J. Anomalous behavior of electrical conductivity and thermal noise in carbon black-containing polymers at Tg and Tm. J. Appl. Polym. Sci. 1975, 19, 831–845. [Google Scholar] [CrossRef]
- He, X.J.; Du, J.H.; Ying, Z.; Cheng, H.-M. Positive temperature coefficient effect in multiwalled carbon nanotube/high-density polyethylene composites. Appl. Phys. Lett. 2005, 86, 62112. [Google Scholar] [CrossRef]
- Chen, R.; Bin, Y.; Zhang, R.; Dong, E.; Ougizawa, T.; Kuboyama, K.; Mastuo, M. Positive temperature coefficient effect of polymer-carbon filler composites under self-heating evaluated quantitatively in terms of potential barrier height and width associated with tunnel current. Polymer 2012, 53, 5197–5207. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Porwal, H.; Tu, W.; Evans, J.; Newton, M.; Busfield, J.J.C.; Peijs, T.; Bilotti, E. Universal control on pyroresistive behavior of flexible self-regulating heating devices. Adv. Funct. Mater. 2017, 27, 1702253. [Google Scholar] [CrossRef]
- Skindhoj, J.; Glatz-Reichenbach, J.; Strumpler, R. Repetitive current limiter based on polymer PTC resistor. IEEE Trans. Power Deliv. 1998, 13, 489–494. [Google Scholar] [CrossRef]
- Yokota, T.; Inoue, Y.; Terakawa, Y.; Reeder, J.; Kaltenbrunner, M.; Ware, T.; Yang, K.; Mabuchi, K.; Murakawa, T.; Sekino, M.; et al. Ultraflexible, large-area, physiological temperature sensors for multipoint measurements. Proc. Natl. Acad. Sci. USA 2015, 112, 14533–14538. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Tsubokawa, N. Novel gas sensor from polymer-grafted carbon black: Vapor response of electric resistance of conducting composites prepared from poly(ethylene-block-ethylene oxide)-grafted carbon black. J. Appl. Polym. Sci. 2000, 77. [Google Scholar] [CrossRef]
- Le, A.V.; Wang, M.; Noelle, D.J.; Shi, Y.; Qiao, Y. Mitigating thermal runaway of lithium-ion battery by using thermally sensitive polymer blend as cathode binder. J. Appl. Polym. Sci. 2017, 135, 45737. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Yeh, C.-C.; Chen, S.-W.; Yang, Y.-J. Development and Characterization of a DC-Driven Thermal Oscillator Using Acrylate-Based Composites. Appl. Sci. 2020, 10, 3825. https://doi.org/10.3390/app10113825
Xu M, Yeh C-C, Chen S-W, Yang Y-J. Development and Characterization of a DC-Driven Thermal Oscillator Using Acrylate-Based Composites. Applied Sciences. 2020; 10(11):3825. https://doi.org/10.3390/app10113825
Chicago/Turabian StyleXu, Mingxin, Chao-Chi Yeh, Syuan-Wen Chen, and Yao-Joe Yang. 2020. "Development and Characterization of a DC-Driven Thermal Oscillator Using Acrylate-Based Composites" Applied Sciences 10, no. 11: 3825. https://doi.org/10.3390/app10113825
APA StyleXu, M., Yeh, C.-C., Chen, S.-W., & Yang, Y.-J. (2020). Development and Characterization of a DC-Driven Thermal Oscillator Using Acrylate-Based Composites. Applied Sciences, 10(11), 3825. https://doi.org/10.3390/app10113825




