1. Introduction
Day by day the number of mobile users exceptionally increases and approximately surpasses the 2.5 billion users worldwide [
1]. Android is an operating system manufactured using a Linux-based kernel for cellular phones. Recently, it has been considerably popular for smartphones and the Internet of things devices. Even that, it constitutes a favorable environment for malicious applications to disseminate. Malware is a malicious software accesses and hijacks computer or mobile systems, which eventually could damage, steal, encrypt, or disable the system files or data. Malware software comes in different forms such as spyware, ransomware, trojans, worms, viruses, or others. In [
2], it had been reported that a single family of mobile ransomware had a negative effect on one million Android users in one month. Ransomware is a kind of malware software that hinders the user with the infected mobile from accessing their data due to either data encryption or device locking, while the attacker waits for a ransom to decrypt the data or unlock the cellular device. Even that its source code is available online but safeguarding against it is hard [
3]. Indeed, it is a requirement to design an effective ransomware detection approach.
In the literature, the research community developed different solutions to combat ransomware, such as the use of honeypots, or the use of statistical methods. These approaches are facing challenges such as the high false positive rates, or a limited capacity to detect complex, persistently-evolved ransomware attacks [
4,
5] ideally before the files are encrypted or the system is damaged. Artificial intelligence, machine learning, and deep learning tools have been elucidating very efficient abilities in capturing hidden patterns of information and inferring useful knowledge that would be capable of unraveling intricate attacks. Machine learning approaches that are devoted to malware detection rely on utilizing a learning algorithm that learns discriminating characteristics of a malicious application and successfully classifies it into a malware application or a benign application. However, the constantly increasing number of mobile applications as well as the rapid growth of malware families, in particular, the ransomware; have led to the requirement of developing a more resilient and robust detection algorithm.
The performance of machine learning algorithms is significantly affected by various factors; such as the settings of the hyperparameters or the presence of irrelevant, redundant features. Thereby, developing an efficient malware detection algorithm requires handling the variable, high-dimensional attributes of malwares, while setting the hyperparameters properly. A fundamental preprocessing step during modeling a machine learning algorithm is the feature selection. Feature selection is concerned with removing the irrelevant redundant features which deteriorate the performance of a learning algorithm. Three major approaches are identified for performing feature selection; filter-based, wrapper-based, and embedded-based approaches. Filter methods assess and rank the features independently from the learning algorithm like the correlation filter. Whereas, the wrapper methods depend on a learning algorithm to evaluate potential subsets of features and score the best one that has the highest prediction power. Embedded approaches search for the best features during the training procedure as in the genetic programming algorithm [
6].
Feature selection is a discrete optimization problem that attempts to find an optimal value (“optimum”) of an objective function based on the optimal subset of features. Primarily, optimization problems can optimize the respective set of features, as well as searching for the best values of the hyperparameters. A well-regarded type of optimization algorithms is the metaheuristic algorithms which demonstrated an eminent ability in finding feasible solutions in a reasonable amount of time [
7].
Metaheuristic algorithms are a kind of random and global search algorithms that evolved to tackle hard-optimization problems in a feasible amount of time. For example, feature selection in classification problems is a typical optimization problem where the objective is to find the minimal best set of features as well as to maximize the classification performance. In other words, given a dataset with (
n) number of features yields a large search space of
potential features subsets, which increases the complexity of the search process, yet becomes more challenging. Remarkably, metaheuristics had shown prominent capacity in approaching hard-optimization problems due to the capability of performing stochastically local and global searches, interchangeably [
8,
9,
10]. Owing to their random natural behavior, they can traverse various areas in the search space, which promotes solutions diversity and quality. An efficient metaheuristic strategy can regularize evenly between searching globally which is known as exploration or diversification, and locally that is referred to as exploitation or intensification. The Exploration and exploitation search schemes are two principal components of metaheuristic algorithms. Exploration corresponds to producing more diversified solutions that reside in less-visited regions in the search space, as well as it avoids the trapping in a local best solution during the search of global optima. Whereas, exploitation implies to search at the local regions that potentially can create good solutions [
7].
Nature-inspired algorithms are a type of metaheuristics that are inspired by several natural phenomena including the evolution and natural selection, the cooperative foraging behaviors, or physical and chemical observations in ecological systems. Typically, nature-inspired algorithms are widely used to solve optimization, modeling, and simulation problems in various fields of science. Generally, they are grouped into two taxonomies; the population-based or the trajectory-based. Population-based evolutionary algorithms are more common for performing exploration and search at a global scale, which is contrary to the trajectory-based algorithms that are more suitable for exploiting the current region and search at a local scale. In consequence, the Salp Swarm Algorithm (SSA) is a relatively new population-based algorithm that is inspired by the foraging behavior of salps in deep oceans [
11]. SSA algorithm has proved efficacy in dealing with feature selection problems and hyperparameter tuning [
12,
13].
In this work, we propose a hybrid machine learning model that combines a modified recent swarm intelligent algorithm which is the SSA algorithm with Kernel Extreme Learning Machine (KELM) for Android ransomware detection. The SSA is modified at the level of the swarm structure and the binarization level. The SSA is used to optimize the hyperparameters of the KELM and feature selection, simultaneously. The proposed model is developed for the task of Android ransomware detection based on features that are extracted from 1000 Android applications’ permissions and API calls. The goal is to detect Android ransomware with high prediction power with the minimum possible number of features.
This paper is structured into six major sections, as follows: the next
Section 2 reviews recent works in the area of ransomware detection methods and techniques.
Section 3 briefly describes the algorithms used in the proposed detection model.
Section 4 presents the proposed classification framework covering an architectural overview, dataset description, the proposed SSA-KELM classification system, and the evaluation measures. The experiments and results are discussed in
Section 5. Finally, the main findings and conclusion of this work are given in
Section 6.
2. Related Works
In recent years, the ransomware attacks of mobile devices have grown dramatically, which lead to a significant need for developing efficient protective and defensive solutions. However, in the literature, several research studies have concerned with tackling the problem of ransomware detection over cellular or mobile networks and in particular over Android mobile networks. This section discusses thoroughly the recently proposed solutions for the detection of such a serious problem.
One of the early implementations of Android ransomware recognition is HelDroid that developed by Andronio et al. [
14]. HelDroid used three criteria for the detection of ransomware, where one of them is a text classification technique to detect either ransomware or scareware, However, HelDroid is an offline detection method that is computationally expensive. While in [
15], implemented a ransomware detection called GreatEatlon, which consists of multiple detection modules like the text analysis and encryption detection methods. Even that GreatEatlon showed improved and faster identification of Android ransomware, but it is computationally demanding and relies heavily on the text classifier that might be broken by string encryption. Nonetheless, Song et al. [
16] implemented a system to identify ransomware and goodware by observing continuously the conducted processes. While interestingly in [
17], Gharib and Ghorbani designed a hybrid of static-based and dynamic-based environment for the detection of ransomware on Android, which is called Dna-Droid. The static part of the system depended on the classification of texts and images, as well as, analyzing the APIs calls and permissions. On the other hand, the dynamic part used a deep learning approach (autoencoder neural network) to detect the presence of ransomware by analyzing and classifying system call sequences. However, the Dna-Droid was not tested on real ransomware samples as well as did not consider the scalability issues. The process of scanning Android apps to conduct both static and dynamic analysis was detailed in [
18,
19]. Nonetheless, Chen et al. [
20] deployed a ransomware detection system (RansomProper) that observes the execution of applications and the usage of user interface (UI) widgets to extract valuable features and perform real-time detection. Although, RansomProper showed a high-performance ability in detecting the malicious encryption of files but failed to achieve relatively low execution time.
Furthermore, [
21], Canfora et al. [
21] introduced the use of Hidden Markov Models (HMM) and structural entropy for the detection of Android malware. The integration of HMM is for the recognition of the malware application, while the structural entropy is for identifying the malware family. Additionally, Chen et al. [
22] designed StormDroid system which is a machine learning-oriented approach for the detection of Android malware. StormDroid extracted four types of features; sequences and dynamic features, as well as API calls and permissions. However, the authors did not consider the influence of the number of collected features in the performance of the proposed approach.
In [
23], Ahmadi et al. [
23] proposed IntelliAV that is an anti-malware system for Android. IntelliAV stands mainly on extracting a set of features (e.g. permissions, APIs, intents, and statistical features), which then are used by a TensorForest algorithm to differentiate the malware class from the benign class. However, the authors stated some limitations of the proposed system as the inability to detect malware that uses javascript. Moreover, Garcia et al. [
24] proposed a machine learning approach for Android malware detection (RevealDroid). RevealDroid extracts the features from applications’ binaries and APIs, which then used by the support vector machines (SVMs) for the recognition of the malware. Meanwhile, the classification and regression trees (CART) algorithm was used for the identification of the malware family. Markedly, RevealDroid achieved high performance in terms of accuracy, efficiency, and resilience. However, since this work collected a high-dimensional dataset; studying the effect of features on the algorithm performance will be of great importance. In [
25], Cimitile et al. [
25] proposed TALOS, which is a ransomware detector for Android based on formal detection methods. TALOS used logical rules to spot the ransomware. Even though it obtained high detection accuracy, it requires long execution time. Su et al. [
26] designed an approach for the detection of Android locker-ransomware. Where Su et al. [
26] extracted six sets of discriminating features including background behaviors like the permissions and system calls, as well as text features. The model was trained by using an ensemble of classical machine learning algorithms, which showed efficient performance capability.
Sharma et al. [
27] created a RansomwareElite android application for the detection of ransomware. It monitors the device for any malicious textual codes, or permissions using the natural language processing toolkit (NLTK). However, the authors did not perform real experiments with reliable performance results. In essence, a more recent study [
28] has proposed a multi-stage framework for android ransomware detection. The designed approach used natural language processing techniques and machine learning to extract multiple types of features, and then detect the ransomware. In which, the logistic regression classifier with the term frequency-inverse document frequency for feature representation achieved the best detection accuracy. Even the authors relied only on the accuracy measure to compare the algorithms, but other evaluation measures, as well as the time requirements, are essential.
In [
29], Scalas et al. proposed a learning-based approach for the detection of ransomware for Android devices. In which, the proposed approach relied on the application programming interface (APIs) information to recognize ransomware attacks and the generic malware. An R-PackDroid package is implemented which showed competitive results in comparison with previously suggested solutions. Even that it merely depends on the APIs information, which might affect its reliability in case of large-scale and online detection frameworks. Remarkably, Alzahrani and Alghazzawi [
30] performed a survey of deep learning techniques for the detection of Android ransomware. The authors stated that there are very few research studies concerned with the deployment of deep learning during the period (2014-2019). In addition, most of the used deep learning models were based on autoencoders and deep belief networks. However, roughly speaking, most of them have long execution time which makes them impractical. Alsoghyer and Almomani [
31,
32] conducted a machine learning approach for Android ransomware detection. Mainly, the features extracted statistically (API calls, permissions, operation code) and dynamically (user interaction and phone events). Using several evaluation metrics to assess the used machine learning methods; the results showed very effective accuracy (96.5%) in comparison with state-of-the-art methods.
Since ransomware attacks are exponentially growing with various characteristics; a more resilient approach is a demand to overcome their variable signatures. In [
33], a two-level system is implemented for the detection of Android ransomware. The first level tracks Windows API calls sequences to build a Marcov model that captures the attributes of ransomwares. Whereas, the second level is a random forest classifier to detect the ransomware. Impressively, the proposed approach achieved promising results regarding the false positive rate and the false negative rate. However, the authors did not report how much the proposed approach is demanding, where the resources and time requirements are fundamental for automatic ransomware detection. In [
34], Abdullah et al. proposed a machine learning approach for dynamically capturing the features and detecting Android ransomware. The features were dynamically extracted and analyzed using systems calls, where the results exhibited a very low false positive rate.
4. Proposed Framework for Android Ransomware Detection
This section exhibits the developed classification framework that targets ransomware over Android devices. The section introduces a general architecture for ransomware detection, describes the collected dataset, presents the design issues of the proposed classification approach (SSA-KELM), as well as its procedure. In addition, it points out to the utilized evaluation measures.
4.1. Overview
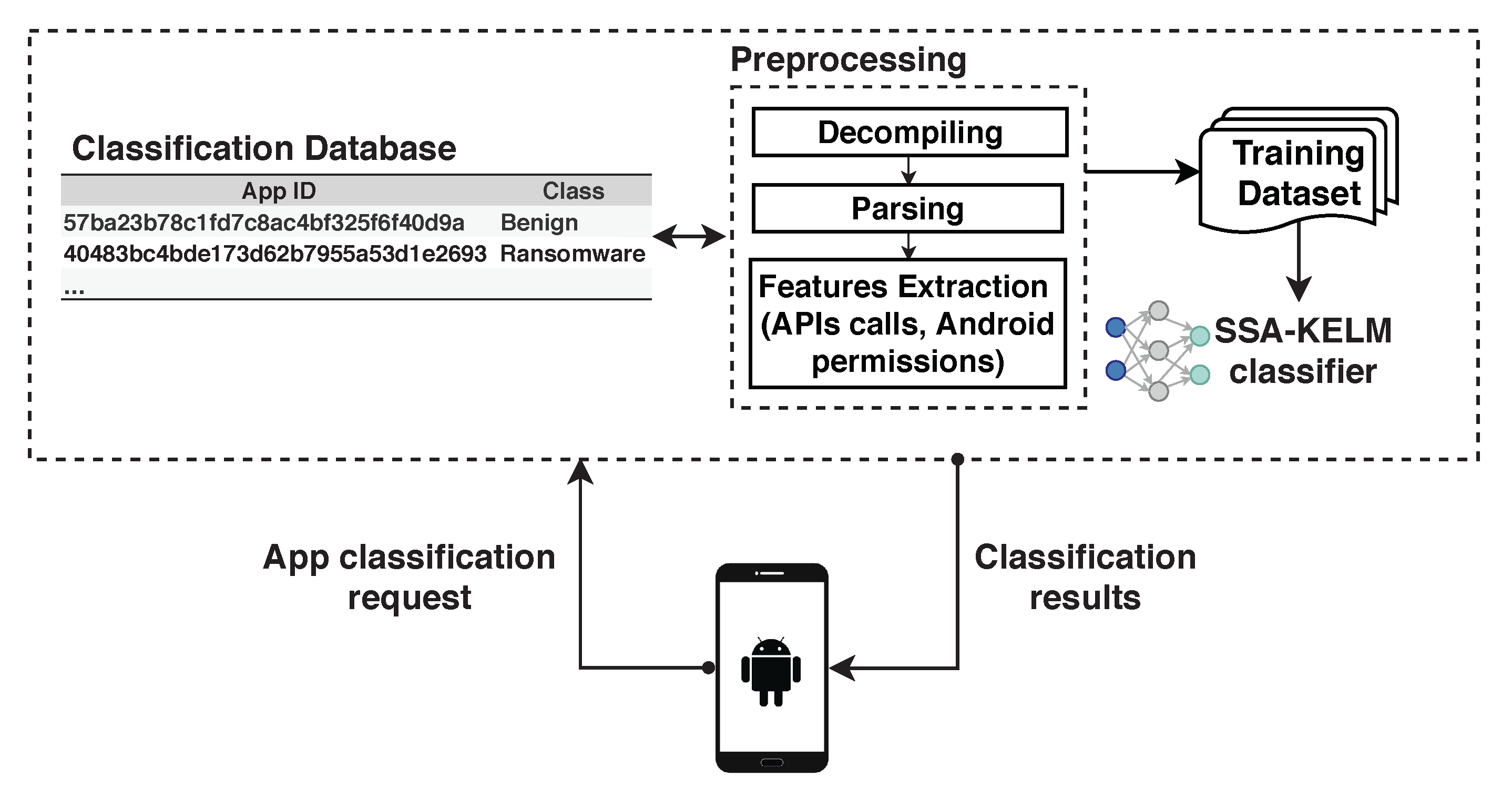
Providing ransomware detection service to Android devices is one of the main stages of the overall ransomware detection system. However, this research focuses on building an efficient predictive model to detect ransomware apps with high accuracy. Building the predictive model is a core component of any ransomware detection system. In this work, building a smart predictive model (SSA-KELM) will be executed over the cloud, not on the local Android devices. Only the app info (such as the application’s hash) will be sent from the mobile to the Ransomware detection system in order to classify the respective app as benign or ransomware. In case the app was tested before by our detection system, then its classification result will be found and sent immediately to the Android device. But if this is the first time this app is tested, then it will be decompiled and parsed to extract its features and pass them to the proposed classifier which is the role of our proposal in this paper. The result of detection will be sent to the Android device and at the same time will be logged in the system’s classification database for future use by other users’ requests. Therefore, the detection service will be lightweight as it is only called by the Android mobile devices as shown in
Figure 3.
4.2. Datasets Description and Preparation
Primarily, the constructed dataset encompasses features of the application permissions and API calls that were obtained by a reverse engineering procedure. Executable mobile applications come in the Android package kit (
) extended file, which is a package file that is used by end-users to install mobile applications on the Android operating system. Mainly, it contains all the needed files during development including classes, resources, assets, certificates, libraries, and the manifest file. Two essential types of files are needed to extract the features of permissions and the API calls; which are the (AndroidManifest.xml) and (“.smali”) files. The (AndroidManifest.xml) file is a fundamental file that consists of all the permissions that were used by the corresponding application. Whereas, the (“.smali”) files acquired by disassembling (baksmaling) the binary executable files (“.dex”). The Apktool software is a tool that automates the process of unpacking the APK files and attains the manifest and Smali files [
41].
The creation of the dataset was performed by collecting 1000 (
) files from benign and ransomware mobile applications. The benign applications were downloaded from the Google Play store, whereas, the ransomware apps were collected from HelDroid project, RansomProper project, Virus Total, and Koodous tools [
14,
20,
42,
43]. In order to unpack the AndroidManifest files and Smali files from all used applications; the Apktool (version = 2.3.1) was employed. Afterward, regarding the permissions features, the extracted files were scanned to report the presence of 131 types of permissions. The objective of the Android permissions is to inform the user and to have an acceptance to use sensitive data from the user’s mobile or access some system features (such as the camera). Typically, by default, the applications do not have permission to execute actions that might have a negative effect on the user, the system, or the installed mobile applications. Such permissions prevent the applications from accessing a user’s emails, keeping the device awake, or writing on the files of other applications. All the permissions which are (131) were scanned from the thousand AndroidManifest files and documented for further analysis. However, (16) permission features were removed from the original dataset since they are not used by the benign or ransomware classes.
Regarding the features from the API calls, they were considered from the Oreo Android release (Android API 27), which contains (199) API packages. All the respective applications were decompiled using the Apktool and the files with (“.smali”) extension were extracted. The “.smali” files were scanned to find the occurrences rate of API calls from both benign and ransomware applications; hence to be handled as distinguishing features. For instance, examples of used features of the API calls are Android Animation and Android Content. In consequence, the total dataset accounts for (1000) applications; where (500) are benign and (500) are ransomware. The total number of features is (314) of both the permissions and the API calls.
Frequency analysis is performed on the extracted features to indicate the occurrences of features with regard to the benign and ransomware classes,
Figure 4 shows the frequency of permission features in benign and ransomware applications, where the features with a frequency less than or equal to 2% were eliminated. Obviously, the top four features observed by benign applications were the access_network_state, Internet, wake_lock, and write_external_storage, even that they were highly witnessed by the ransomware apps, too. On the other hand, the receive_boot_completed, and the read_phone_state were considerably occurred by the ransomware applications. Nonetheless, the figure shows (6) features used slightly just by the benign apps, while (12) features used only by the ransomware.
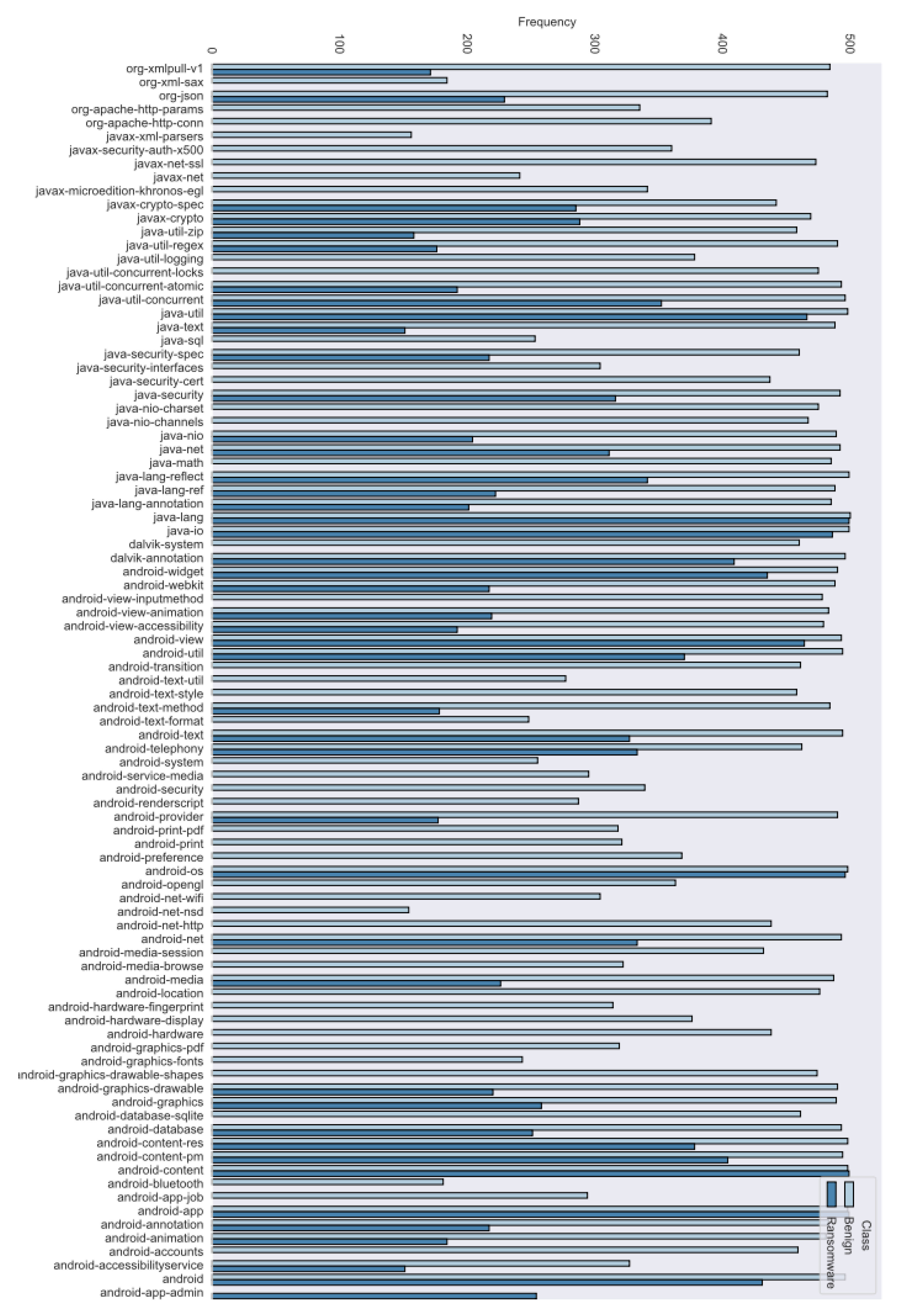
Figure 5 presents the frequency of the API features in benign and ransomware applications. In which, the features with frequency less than or equal to 30% were removed. Notably, android-app, android-content, android-os, java-io, and java-lang were the most frequent features in ransomware apps.
4.3. SSA-KELM Classifier
4.3.1. Design Issues
In this subsection, three main issues related to the design of the proposed SSA-KELM are discussed, which are the representation of the salps (solutions), the fitness function, and the binarization mechanism.
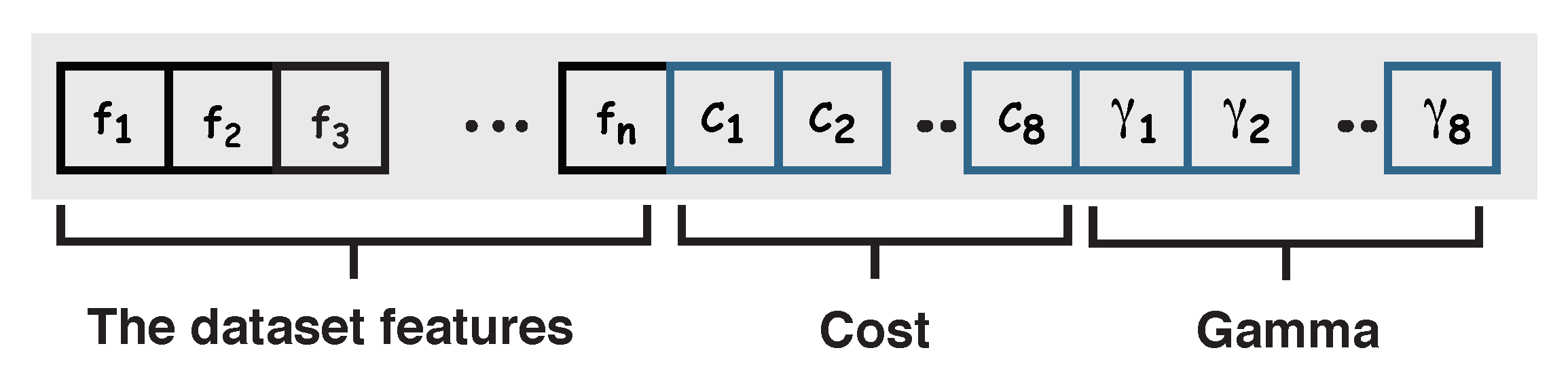
Salp representation: each salp chain is represented as a binary vector. The length of this vector is
elements, where
d is the number of features in the training data. The 16 additional elements are used to encode the values of the hyperparameters of the KELM;
C and
, where 8 elements are used for each hyperparameter. Five elements are allocated for the whole number part and three elements are allocated for the fractional part.
Figure 6 depicts an example of a salp’s vector.
Figure 6.
A vector representation of an individual salp that encompasses the features of the dataset, the hyperparameters of the KELM algorithm (C, ). (n) is the total number of features, () represent the digits of the cost value, and () are the digits of the value.
Figure 6.
A vector representation of an individual salp that encompasses the features of the dataset, the hyperparameters of the KELM algorithm (C, ). (n) is the total number of features, () represent the digits of the cost value, and () are the digits of the value.
Fitness function: to evaluate the effectiveness of the salps, the elements of each salp are decoded as described previously and a KELM algorithm is built based on the selected features and the values of the hyperparameters obtained by the decoding process. The resulted KELM is trained on the training folds from the training dataset, then the accuracy rate which is the ratio of the correctly classified instances to the total number of instances in the training data is calculated. The accuracy rate is combined with the number of the selected features as shown in Equation (
12) and returned to main procedure of the SSA as the fitness of the salp.
in Equation (
12) is the selected number of features, while
F is the total number of features.
Binarization mechanism: In the proposed approach, we utilize a sigmoidal
s-shaped function to covert the SSA to a binary optimization algorithm. The
s-shaped function is one of the most successful variants of transfer functions used in the literature in binary optimization algorithms [
44]. The conversion process by the transfer functions is based on the probability assigned by them for each element in the solution vector. When the probability is greater than one, the element is rounded to 1, and vice versa as given in Equation (
13). This process was first described by Kennedy and Eberhart [
45] to convert the classical Particle Swarm Optimization to a binary optimizer.
where
is the
element in
x solution in the
dimension, and
t is the current iteration.
The rounding process of the elements of the solution vector
x is made as given in Equation (
14).
where
is the
element at
dimension in
X solution,
is the probability given in Equation (
13).
4.3.2. Procedure
The main procedure of the SSA-KELM can be summarized in the following steps:
Initialize a random swarm of N binary salps.
Evaluate the fitness of each salp as described in the previous subsection by relying on the fitness achieved by the KELM.
Modify the position of the leading salp as in Equation (
2).
Modify the position of the followers as in Equation (
4).
Guarantee that all salps located inside the search space specified by the upper and lower bounds.
Return to step (2) if the termination criterion is not satisfied. Otherwise, return the best solution that encompasses the optimal subset of features and the best hyperparameters values.
Figure 7 describes the steps of the proposed approach.
4.4. Model Evaluation Metrics
Algorithm evaluation is a significant aspect of developing a successful classification model. Relying on one evaluation criterion might indicate a very good model, while in terms of another, it might reflect a deterioration in the algorithm performance capability. Typically, to properly measure the performance of the algorithms in handling the variable characteristics of the data, and for a fair comparison, as well; several evaluation metrics were considered.
Herein, assessing the algorithm’s ability in distinguishing between benign data or malware, generally, depends on a set of metrics derived from the confusion matrix. The confusion matrix reveals the potential of the algorithm in truly classifying the data with respect to its actual labels. It is expressed by four types of counts (given a binary classification problem); the true positive (TP), the true negative (TN), the false positive (FP), and the false negative (FN), as represented by
Table 1. Therefore, this paper incorporates the accuracy, recall, false positive rate, specificity, precision, g-mean, and the area under the curve (AUC) for measuring the performance of the proposed algorithms. Mainly, those metrics are defined as follows by considering that the positive class is the class of interest, which is the Ransomware class.
The accuracy is the ratio of the total number of classifications that were correctly labeled, it is shown by Equation (
15).
Recall expresses the true positive rate, and formulated by the percentage of the relevant instances that have been identified over the total number of relevant instances. It is presented by Equation (
16)
False positive rate (FPR) also known as the false alarm rate, which is the ratio of classifying the benign instances as ransomware instances (Equation (
17)).
True negative rate (TNR) or the specificity, it exhibits the strength of the classifier in distinguishing the negatively classified instances of data (benign) from the positively labeled (ransomware) instances. The TNR is defined as in (Equation (
18)).
Precision is the proportion of the relevant data instances over the retrieved instances. It is mathematical description is given by Equation (
19).
The geometric mean (G-mean) represents the mean of the recalls in case of the multiple classes, or the mean of the recall and specificity in case of the of binary classification, it is defined by Equation (
20).
The area under the curve (AUC) is defined as the area under the receiver operating characteristic (ROC) curve. AUC is deemed as a metric for evaluating the ability of the classifier in discriminating between the respective classes. Thereby, obtaining a high value of AUC is an indication of the power of the model in differentiating between the ransomware and the benign classes. Whereas, in the case of low AUC value that is approaching (0,) it means that the classifier identifies the benign data as ransomware, and counterintuitively, the ransomware as benign. The AUC is described by Equation (
21).
5. Experiments and Results
The performed experiments consist mainly of two parts; analysis of the influence of leaders’ salps percentage, and the analysis of the SSA’s swarm size. Thereby, the best SSA variant with the KELM was employed for the ransomware detection and compared with conventional machine learning algorithms. In addition, a feature importance analysis has been applied to reinforce the distinguishing features of the ransomware applications. The best-obtained results in subsequent sections are marked with a bold typeface.
5.1. Experiments Setup
This sub-section presents the environmental and experimental settings for all conducted experiments. Where they were implemented using the Matlab R2016b platform over Windows server 2012. In which, the random-access memory (RAM) is 64 GB, the processor is Intel(R) Xeon(R) CPU E5-2609 v4, while the speed of the two processors is 1.70 GHz.
Initially, the proposed approach is evaluated using 10 folds cross-validation. Since the adopted SSA algorithm is used as wrapper-based feature selection; it used the KELM as a learning algorithm where its hyperparameters (C and
) were optimized using SSA. The KELM is responsible for assessing the fitness of solutions; therefore, it returns the weighted-sum of (1-accuracy) and the ratio of features, as given by Equation (
12).
The SSA algorithm is a stochastic swarm-based algorithm as mentioned before; hence, diminishing the randomness effect of the algorithm requires executing it multiple times. Herein, (10) independent runs were performed with the maximum number of iterations is 50. In essence, the population size and the number of leaders are controlling parameters of the SSA that play a vital role in escalating the performance of the algorithm or degrade it if not set properly. The following subsections present a sensitivity analysis for selecting the best values of the leaders’ ratio and the population size.
5.2. Effect of Leaders Ratio
In this experiment, we study the effect of the ratio of the number of leaders to the swarm size on the performance of the proposed SSA-KELM.
Table 2 and
Table 3 show the evaluation results of the SSA-KELM at different ratios of leaders. From the results, it can be seen that the best results in terms of most evaluation measures are obtained at a ratio of 50%. Remarkably, it can be noticed that all ratios achieved approximately a high reduction rate which is around (44%), while the difference between the reduction rates is slight. For instance, when the leaders’ ratio is (20%), the algorithm obtained the maximal reduction rate of 49%, where the number of features was 160 out of 314. However, there is no obvious relation between the reduction rate and the number of leaders; this is demonstrated at the ratio (80%) where the reduction rate was 44.8%. In contrast, at leaders’ ratio (50%), even that the algorithm achieved the minimal reduction rate, but it markedly exhibited the best performance as it is shown by
Table 3.
In this table, average accuracy, recall, FPR, TNR, Precision, G-mean, and AUC were reported at different ratios of leaders. At 50% of leaders’ ratio, the SSA performed the best results and gained superior results in terms of accuracy, TNR, precision, g-mean, and AUC, which was (98%), which is reinforced by reasonable standard deviation values. Additionally, in regards to the FPR, accomplished the minimal false positive rate (0.020), whereas at the other ratios from the highest to the lowest, they were 0.032, 0.032, 0.034, 0.024, and 0.028, respectively. Notably, regarding the recall, at all ratios, the recall was relatively close, while ratio (80%) achieved the highest recall value (98.4%). Overall, the SSA algorithm performed the best in terms of all evaluation metrics when the proportion of leaders was half the swarm. As the number of leaders has tested next is to study the influence of the SSA population size.
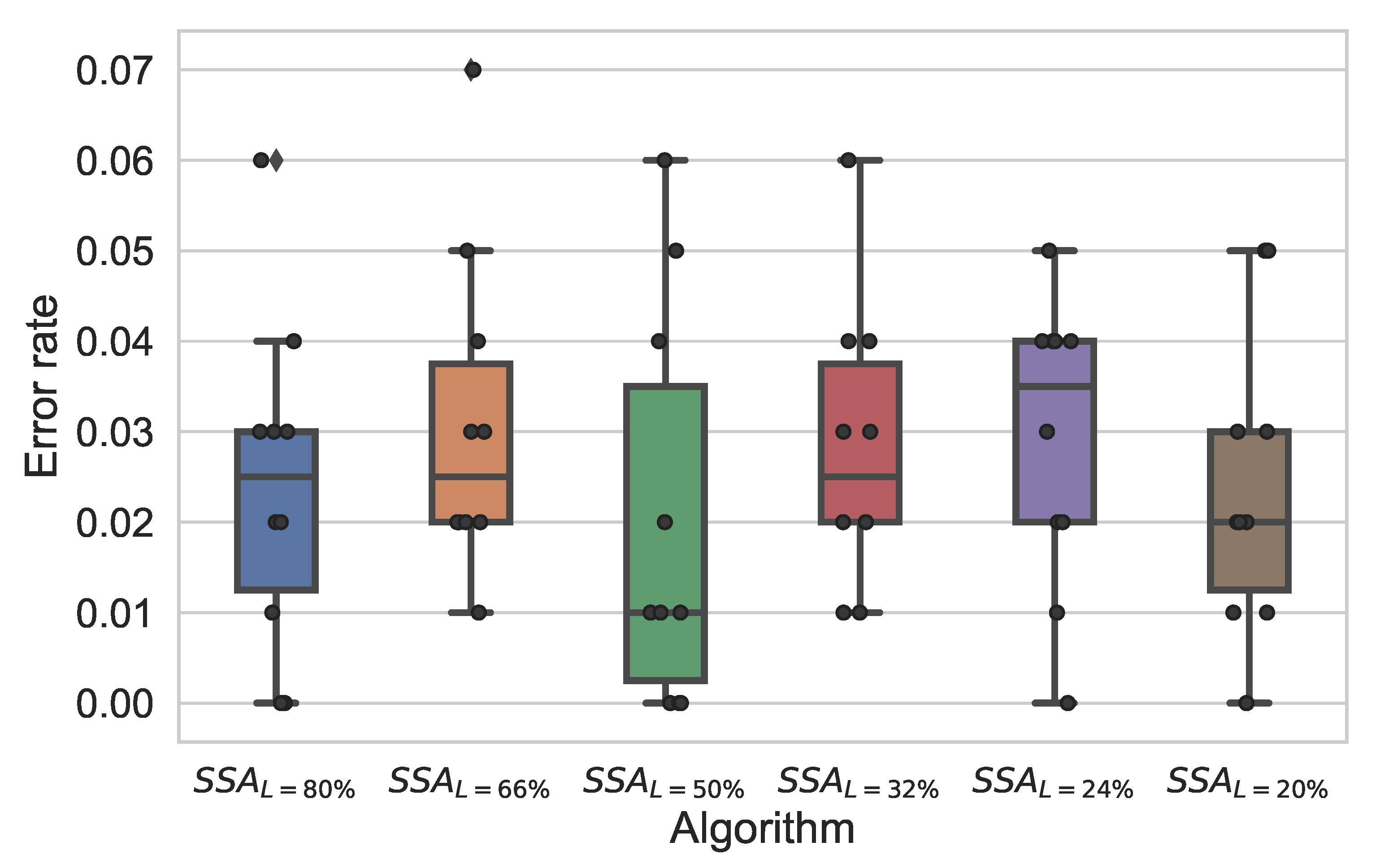
Figure 8 shows a box plot presentation of the error rate of the SSA algorithm at the six different ratios of leaders. Obviously, when the ratio (L) is 50%, the algorithm obtained the minimal error rate.
In terms of the convergence rate,
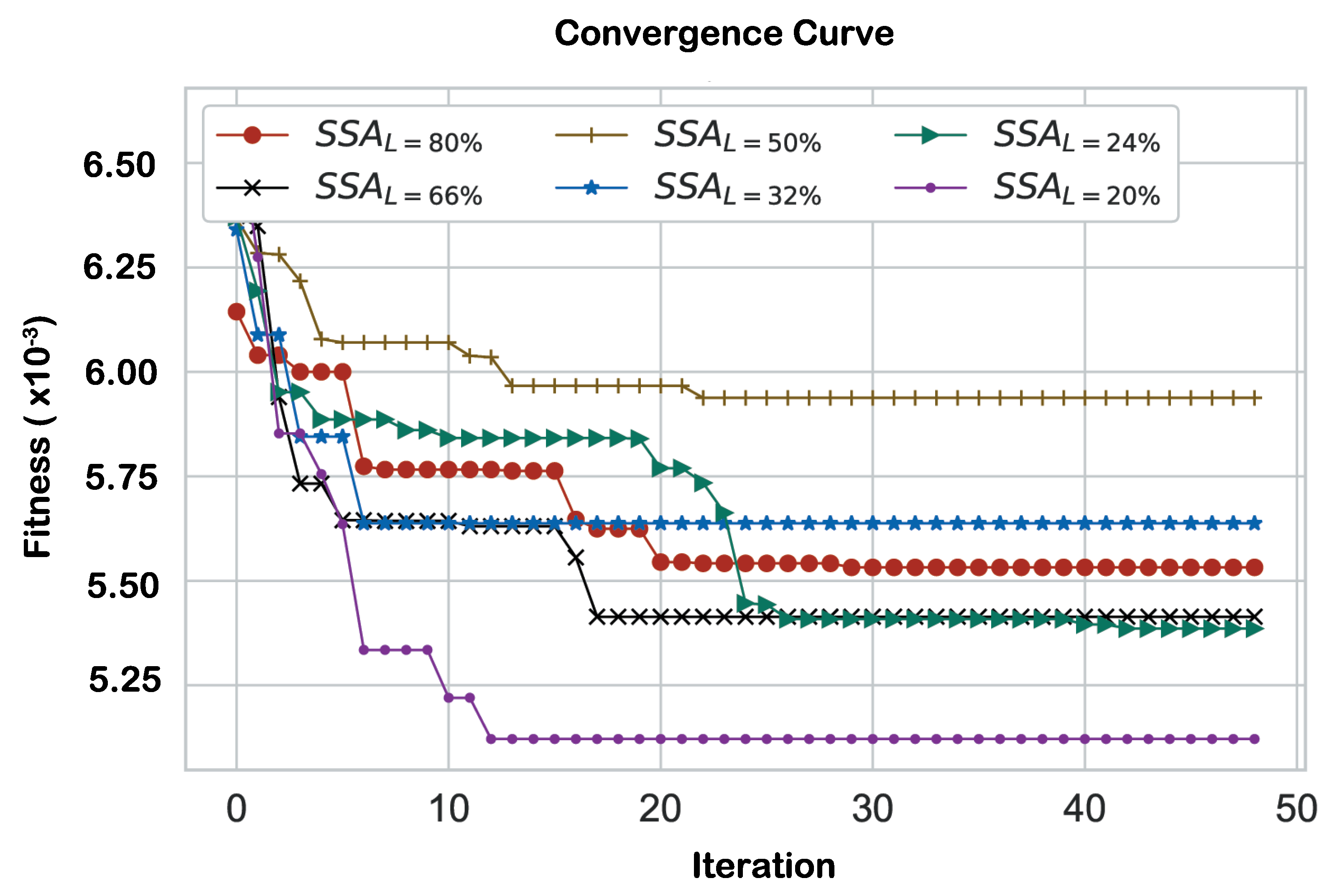
Figure 9 presents the convergence plot by depicting the obtained fitness value of the SSA algorithm at each iteration of the algorithm and at six ratios of the leaders. In which, the y-axis is the fitness, and the x-axis is the iterations. It is clear from the plot that when (L=20%), the algorithm experiences a premature convergence rate, that converges very fast to the best fitness value at the eleventh iteration and then remains constant over the rest of iterations. Whereas, the other variants of leaders’ ratios exhibited different trends of convergence over the course of iterations reaching relatively optimal minimal fitness values.
5.3. Effect of Swarm Size
It has been long argued that population-based metaheuristic algorithms can achieve reasonable good results compared to other search algorithms if they have a good-enough large population size with enough time. However, the swarm or the population size parameter has a considerable influence on the performance of evolutionary algorithms whether in promoting or degrading it. This experiment is conducted to study and substantiate the effect of the swarm size on the performance of the proposed SSA-KELM. Hence, the swarm size of the SSA has been investigated at different values; 50, 60, 70, 80, 90, and 100, as discussed in
Table 4 and
Table 5.
Table 4 illustrates the effect of the population size on the features reduction rate. It is clear from the table that increasing the population size not necessarily results in a better reduction rate. To illustrate, when the population size is 50, the obtained average number of features was 220.3 which yields nearly a 30% reduction in the features. However, at the swarm size of 100, it is obvious that the number of features dramatically decreased with the best-accomplished reduction rate that is 52%. On the other hand, when the swarm size was 60, 70, 80, and 90, the average number of features was higher than what is obtained by the swarm size of 100. For example, at the swarm size of (80), the average number of features was 172.3 and the reduction rate was 49.5%. Even that at all experimented swarm sizes, the SSA algorithm has decreased the number of features relatively efficiently that justified with a prominent performance results as represented by
Table 5.
Table 5 compares the average performance of the SSA algorithm at different population sizes regarding the accuracy, recall, FPR, TNR, precision, g-mean, and AUC with the average standard deviation values. It is obvious from the table that the superior performance obtained when the swarm size was 50. At which, the accuracy, TNR, precision, g-mean, and AUC were 98%, while the FPR was the minimal that accounted for 0.020 with standard deviation (0.028). Examining the accuracy results, when the swarm size is greater than 50, the algorithms achieved high results with the slight difference among all, where they accomplished 97.3%, 97.0%, 96.7%, 97.5%, and 97.4%, in ascending order. Regarding the recall, even that the SSA algorithm at the size (50) achieved 98%, but at sizes (90, 100) the SSA algorithm could perform 98.2%, while in contrast, the SSA at (90, 100) performed worst in terms of FPR. For instance, when the size=90, the FPR=0.032, and when it was 100, the FPR=0.034, however, at 50, the FPR=0.020. Nonetheless, regarding the TNR, the SSA at (50, 60, 70, 80, 90, and 100) achieved 98%, 96.8%, 97%, 96%, 96.8%, and 96.6%, respectively. Similarly, at the precision, at 50, the algorithm achieved the best (98%), whereas, at 80, it achieved the minimal precision (96.1%). Additionally, at both g-mean and AUC, the best performance attained at swarm size of (50) with a performance of (98%) and with feasible standard deviation, however, (80) achieved the minimum, which is (96.7%). To sum up, the SSA algorithm accomplished striking results with a considerable feature reduction ratio. To support the superiority of the proposed SSA-KELM, it has been compared with well-known classical machine learning algorithms as given by the following sub-section.
Figure 10 describes the error rate at various swarm sizes of SSA. Markedly, when the swarm size (P) is 50, the
outperformed the other variants and attained the best error rate results, while when (P = 80), the algorithm performed the worst performance regarding the error rate.
Nonetheless,
Figure 11 shows the convergence plots of the SSA algorithm at various population sizes. It can be noticed that at all the experimented population sizes, the SSA algorithm exhibits similar, good convergence rates that eventually could reach such best fitness values. For instance,
at iteration (22), it reached a minimal fitness of (0.00059), while at
, the algorithm optimally minimized the fitness to (0.00045). Generally speaking, the SSA algorithm has a successful convergence trend toward optimal solutions over the course of iterations with slight difference in relation to the population size effect.
5.4. Sensitivity Analysis of Fitness Parameters
Table 6 presents a sensitivity analysis of the (
) parameter of the fitness function of the SSA algorithm. In Equation (
12), the fitness constitutes a weighted-sum of the accuracy and the ratio of the selected subset of features. The weighted-sum approach is a classical methodology to handle a multi-objective optimization problem as a single-objective problem. Where the aim is to optimize the weighted-sum of the utilized objectives. Herein, two objectives were considered; the accuracy, and the ratio of the selected features. In which, the accuracy is weighted by the (
) parameter, and the ratio of selected features was weighted by the multiplier (1-
). The coefficient (
) has a controlling behavior for selecting the optimal salp solution, which quantifies the importance of the corresponding objectives. However, there is no guarantee that the randomly chosen value of (
) will produce the optimal solution; therefore, tuning the (
) parameter is imperative.
Table 6 shows performance of the SSA algorithm at five different values of (
), where it belongs to
. It is clear from the table that when
, it obtained the best results in terms of accuracy, recall, TNR, precision, g-mean, and AUC, which all attained (98.0%). The minimal FPR value was obtained at a percentage of (2%). Although, when
, the algorithm could achieve drastically better performance. In contrast, in terms of the reduction rate of features, when
equals 0.2, the algorithm achieved extremely better. So, the best reduction rate is obtained when (
) with percentage of 54.4%. Whereas, when (
), it achieved a reduction rate of 29.9%, and 28.7%, respectively.
5.5. Comparison Results
In this subsection, the performance of the SSA-KELM is compared with the performance of a set of well-known classifiers; which are Naive Bayes (NB), Decision Tree C4.5 (J48), very powerful ensemble classifiers which are Random Forests (RF), AdaBoost, Bagging, and XGBoost. In addition, it is compared with another well-established swarm intelligence algorithm which is the particle swarm optimization (PSO). For which the inertia weight (
), the constraints (
) are set to value (2), and the maximum velocity is (6). The hyperparameters of XGBoost are optimized using a grid search algorithm, which determines a range of values (search space) for each hyperparameter. The grid search is used to optimize a five hyperparameters of XGBoost; which are the minimum-child-weight: [2, 5, 8], gamma: [0.1, 1, 1.5], number-of-estimators: [50, 120, 323], learning-rate: [0.3, 0.5, 0.9], and the maximum-depth: [6, 10, 15]. The XGBoost-Grid is evaluated based on 10-folds cross-validation, where the best results obtained at gamma = 0.1, min-child-weight = 2, number-of-estimators = 50, learning-rate = 0.9, and the maximum-depth = 6. Mainly, all classifiers evaluated using 10-folds cross-validation and implemented using Weka workbench [
46].
The results of this comparison are shown in
Table 7. The evaluation results show that the SSA-KELM outperforms all the other classifiers and swarm intelligence methods regarding the majority of the measures. Although some classifiers like Bagging and AdaBoosting showed very competitive results, they used the full set of features without any reduction like in the SSA-KELM. Moreover, the SSA-KELM outperformed the PSO-KELM in terms of all evaluation measures indicating its powerful capability. Therefore, the SSA-KELM has merits over conventional machine learning classifiers, where it exhibited efficacy in performance and in minimizing the selected subset of features.
Features Importance
Feature importance analysis has a fundamental role in identifying to what extent the features play a part in the predictive power of the model. In this regard, the frequencies of selected subsets of features generated by the SSA algorithm were utilized to investigate the importance of features. In other words, as the SSA algorithm generates a new subset of features at each iteration; the frequency of the feature selection for all features is calculated over the number of iterations. Hence, the importance (FI) of a feature (i) is given by Equation (
22), where
L is the maximum number of iterations.
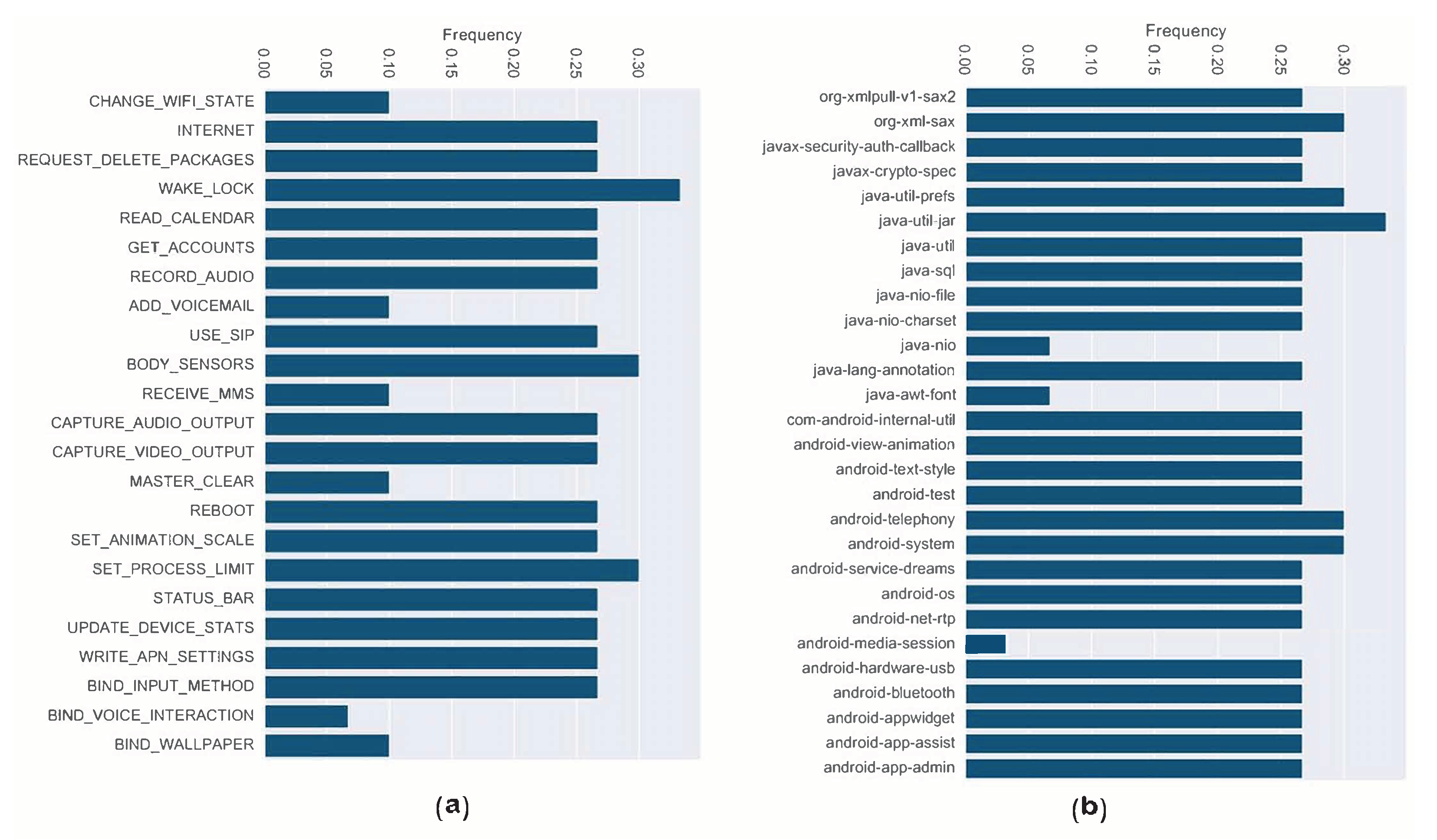
Figure 12 presents the most important features of the API calls and permissions while training the SSA-KELM at the ratio of leaders (L=50%), and swarm size (P=50). In sub-figure (a), the plot shows the most and least occurred permissions features. In which, the most important features were reported when the importance
, while the least important, were reported when the importance
. It is obvious from sub-figure (a) that WAKE_LOCK, BODY_SENSORS, and the SET_PROCESS_LIMIT were the most important features. These permissions allow the ransomware attackers to stop the processors and screens from sleeping, or to grant them access for collecting personal data such as the sensors’ readings. Such information could be targeted by ransomwares to be encrypted or locked as they are considered private and important. Additionally, as ransomware runs processes behind the scene, it might modify the state of the SET_PROCESS_LIMIT permission to change the maximum number of concurrently running processes. Whereas, sub-figure (b) represents the most important API features. Where org-xml-sax, java-util-prefs, java-util-jar, android-telephony, and android-system were the most contributed features to the prediction efficacy. These API calls allow the attacker to read user-related data that existed in different formats including the Extensible Markup Language (XML) format, and the Java Archive format (Zip format). Also, they allow ransomwares to monitor basic phone information including network type, connection state, and manipulating phone number strings which could be an indication of invasion [
31]. Moreover, andorid.system API can grant the attackers access to low-level system functionalities, which makes them more powerful due to the ability to access the underlying primitives used to implement high-level APIs.