Featured Application
THz thin film sensing.
Abstract
In this paper, we studied the sensing performance of metasurfaces comprised by spiral-disk-shaped metallic elements patterned on polypropylene substrates, which exhibited localized surface plasmon resonances in the low-frequency region of the terahertz (THz) spectrum (0.2–0.5 THz). Optimal designs of spiral disks with C-shaped resonators placed near the disks were determined and fabricated. The experimentally measured transmittance spectra of the samples coated with very thin photoresistive layers (d ~ 10−4–10−3 λ) showed good agreement with the simulations. The resonance frequency shift Δf increases with increasing d, while saturating near d = 50 µm. The narrow-band magnetic dark modes excited on symmetrical spiral disks with a 90° C-resonator demonstrated very high figure of merit (FOM) values reaching 1670 (RIU·mm)−1 at 0.3 μm thick analyte. The hybrid high order resonances excited on asymmetrical densely packed spiral disks showed about two times larger FOM values (up to 2950 (RIU·mm)−1) compared to symmetrical distantly spaced spirals that resembled the best FOM results found in the literature for metasurfaces fabricated with a similar technique. The demonstrated high sensing performance of spiral disks is evaluated to be promising for bio-sensing applications in the THz range.
1. Introduction
Localized plasmon resonance (LPR) is the resonant oscillation of the charge density of free electrons in conducting particles of sub-wavelength size in an oscillating external field, accompanied by the enhancement of the near field at the surface of the particles []. LPRs exhibit strong spatial localization and amplification of the electromagnetic field near the particle surface with the resonance frequency depending on the shape, size and conductivity of the particle and its environment. These properties have wide applications in the visible frequency range: in chemical sensors and biosensors [], surface-enhanced Raman spectroscopy [], fluorescence amplification [], second harmonic generation [], solar cells [] and photocatalysis [].
The terahertz (THz) spectral range (covering the frequency domain from 0.1 to 10 THz) is of great importance for biology due to the nonionizing nature of THz waves and the fact that the rotational and vibrational modes of complex intra- and extra-molecule bonds of many important chemical and biological substances lie in this region [,,]. This explains the high prospects of using plasmon resonances in the THz range for sensing and spectroscopy. It is worth noting, however, that the THz frequencies (ωTHz ~ 1012 Hz) are several orders of magnitude lower than the plasma frequency of free electrons in metal (ωp ~ 1016 Hz) and their collision frequency (ωc ~ 1014 Hz []) and therefore, plasmon resonances cannot formally be excited in this spectral region. To overcome these limitations, Pendry and his colleagues suggested making a periodic corrugation of the flat surface [] that leads to forming bound surface states with a high confinement of the electromagnetic field, so called “spoof surface plasmon resonances”. It has been shown that sub-wavelength metallic structures [] are able to support spoof localized surface plasmon resonances (LSPRs) in the long-wave region. This idea was elaborated in detail in the metamaterial community through the concept of plasmonic metasurfaces (PMSs) [,], which are understood as thin metallic screens with periodically patterned subwavelength apertures or substrate-backed arrays of subwavelength metallic elements. It is essential that LSPRs excited on a PMS are directly related to the geometry of the PMS unit cells that provides high flexibility in engineering the electromagnetic (EM) properties of the structures both in far- and near-field. Alongside with the feasibility of versatile frequency-selective and polarization-transforming devices, this approach enables creating high-performance PMS-based sensors of thin-film analytes. Exploiting the LSPR-induced effect of near-field confinement, which enhances light–matter interaction, such sensors exhibit high sensitivity to the dielectric environment and allow the determining of analytes with thicknesses several orders of magnitudes smaller than the LSPR wavelength via tracking a frequency shift of the LSPR relative to that of a bare PMS (without a deposited analyte).
Applicable to THz, a comprehensive review of thin film sensing with metasurfaces is given in []. From a technological viewpoint, the THz range is attractive due to its relatively large (compared to VIS and IR domains) wavelengths as it allows one to use well mastered and inexpensive micromachining technologies, such as photolithography, in the PMS fabrication. Furthermore, the Ohmic losses in metal and dielectric losses in substrates, which serve as an obstacle at shorter wavelengths, do not play such a crucial role at THz frequencies and can be neglected in many cases. Plasmon resonances with lower losses have higher Q-factors which facilitate high-sensitivity sample detection via the precise measurement of small resonant shifts. In this work, we proposed using PMSs with spiral-disk-shaped metallic elements patterned on low-loss polypropylene substrates for the THz sensing of thin dielectric films.
For the first time, a design of the LSPR-structure with azimuthally patterned (grooved) metal disks (see Figure 1a) was proposed and studied in the microwave region [,]. The grooves were filled with a dielectric material and the surrounding medium was air. For the efficient confinement of the surface mode on the structure, the period of grooves at the outer radius R must be much less than the radiation wavelength in the air: G = 2π R/n << λ0, where n is a total number of grooves. Lately, numerical simulations in the THz region for a periodic structure of azimuthally grooved golden disks on dielectric substrates [,,,] showed that high-order (multipole) electric and magnetic LSPRs can be excited under oblique illumination or when combining the grooved disk with a C-shaped resonator. As compared to dipole resonances, the multipole ones have higher Q-factors and are more sensitive to the presence of dielectric materials on the structure, i.e., more promising for sensing applications.
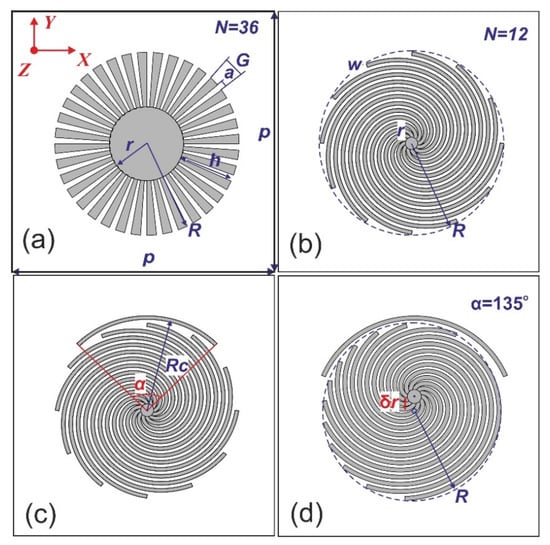
Figure 1.
Four different designs of plasmonic metasurfaces (PMSs) with the metal disk elements (the unit cells are shown; p is the lattice constant): (a) the azimuthally patterned disk; (b) the spiral disk; (c) the spiral disk with a C-shaped resonator (α is the resonator’s arch angle); (d) the spiral disk with a C-shaped resonator and a shifted center (δr is center shift).
An azimuthally grooved disk supports the resonances up to the asymptotic frequency fa, which depends on the groove depth h and the refractive index n in the groove as fa = c/(4h·n), where c is the light speed []. An increase in the depth h shifts the asymptote frequency (and the resonance spectrum) towards lower frequencies and consequently, enhances the confinement of LSPR modes. Thus, the lowest resonant frequency is governed by the size of the disk. To improve the mode confinement of spoof LSPRs, it was suggested to use long spiral grooves (Figure 1b) []. The extension of spirals allows shifting the LSPR resonances towards longer wavelengths, exceeding by far the structure size, which yields a stronger EM field localization near the surface. Thus, a spiral disk design is expected to be very promising for sensing applications at THz, whereas this kind of structures is still understudied. It is worth mentioning that numerical calculations, theoretical analysis and experimental tests of spiral grooves were reported in literature mainly for the microwave region [] and we know only one paper on the experimental implementation of a simple design of spiral disks in the THz range [].
In this paper, we present the results of numerical simulations and the experimental testing of spiral metal disks patterned on a dielectric substrate to excite electric and magnetic multipole LSPRs in the spectral region of 0.2–0.5 THz. The packing density of the disks in the array, the addition of a C-shaped resonator, the asymmetric design of the spirals and the oblique illumination were studied. The testing of the optimal designs showed that the spiral metal disks are very promising for the THz sensing of thin-film analytes.
2. Materials and Methods
Figure 1b–d presents the schematic drawings of the Archimedes spiral disk designs under study. Using the investigation results for similar structures in the microwave region [] and taking into account our technological limitations, we rescaled the spiral disk parameters to the range of 0.2–0.5 THz, which was compatible with our instrumentation capabilities: the inner radius r = 18 µm, the outer radius R = 192 µm, the spiral arm line width w = 8 µm, the number of arms n = 12. We considered two types of arrays differed in the lateral periodicity p of the single spirals in the X and Y directions: (1) p = 768 µm, distantly spaced disks; and (2) p = 408 µm, closely spaced disks with a “hybridization effect” (excitation of hybridized plasmon modes).
The transmittance spectra of a periodic array of spiral disks in the range of 0.2–0.5 THz were simulated using the commercial CST Microwave Studio Suite software, wherein the regime of Floquet ports, periodic boundary conditions applied to the structure’s unit cell were employed. In this regime, the oblique illumination of the structure was modeled through specifying the orientation angles (θ, φ) of the incident wave vector k in the XYZ coordinate system: the polar angle θ describes the angle between k and the Z axis, while the azimuthal angle φ defines the angle between the orthogonal projection of k on the XY plane measured from the X direction. Since a THz beam was horizontally polarized in our experiments and a rotary stage afforded the rotation of the sample only around a vertical axis, our investigations were limited by TM-polarized excitation. Two marginal cases were considered: φ = 0 and φ = 90°. The former was of primary importance since it enabled the proper excitation of the C-shaped resonator (Ein-plane || X), as elucidated in Section 3.1.
The spirals were modeled as 0.35 µm-thick aluminum layers with dispersionless conductivity σ = 1.5 × 107 S/m [,] placed on top of a 15 µm-thick polypropylene (PP) film with the dielectric permittivity εpp = 2.25·(1 − j·10−3) [,]. PP has low absorption in the THz range and was intentionally chosen as a substrate material to minimize the dielectric losses in the structure; we also used the thinnest PP substrate available to diminish interference effects in the PP layer.
The designed structures were fabricated with a standard contact photolithography technique, which was specifically adapted for operations on flexible polymeric substrates [,,]. Each 15 µm PP film sample was carefully tightened onto a bearing Al ring with a clear aperture diameter of 3 inches which specified the optical diameter of the output PMS. Al metallization was sputtered onto the PP films by means of a vacuum thermal deposition method. Prior to sputtering, the PP substrates were treated with a glow discharge in O2 atmosphere to improve the adhesion of Al to PP.
The sensing performance of the structure was tested by depositing a photoresistive material (AR-P 3250 produced by ALLRESIST (GmbH, Strausberg, Germany) []) of variable thickness (from 0.3 to 10 µm) on the PP film using a standard spin coating deposition technique. The photoresist was considered as a nondispersive and lossless analyte with εa = 2.65 (na ≈ 1.63), experimentally evaluated in the spectral range considered [].
To measure the complex transmission coefficient of the fabricated samples in the range of 230–540 GHz, a sub-terahertz quasi-optical backward wave oscillator (BWO) spectrometer developed in the Prokhorov General Physics Institute RAS (Moscow, Russia) [] was used. This frequency-domain (continuous-wave, CW) instrument was equipped with a Golay cell to detect the THz signal and exploited the arrangement of the dual-path polarizing Mach–Zehnder interferometer for phase-sensitive measurements []. We employed a classical scheme with a collimated THz beam (i.e., without focusing it onto the sample under test) to mimic the plane wave illumination. The THz beam was linearly polarized in a horizontal direction, having a beam width at half the maximum ~16 mm (see also []) that suited well to measuring 3″ samples both at normal and oblique incidence (with θ at least up to 40°). The spectral resolution of the BWO spectrometer was around 50 MHz. The step of the frequency scanning in our experiments was 0.5 GHz.
3. Results and Discussion
3.1. Symmetric Spiral Disks
In the beginning of our study, we searched for the optimal design of spiral disks having narrow-band resonances in the region of 0.2–0.5 THz to allow the testing of the fabricated structures with the BWO spectrometer. Under the normal illumination of distantly spaced (p = 768 µm) spiral disks, the azimuthal symmetry of the disk enables the excitation of the only dipole LSPR modes []. To produce high order localized “dark” modes (electric or magnetic []), we proposed to break the symmetry by placing a C-shape resonator near the disk (see Figure 1c). The C-resonator exhibited a “bright” mode resonance, which excited the nearby dark spectral modes of the disk. We fixed the resonator radius at RC = 204 µm, while the resonator arch angle α was a variable parameter. Figure 2a shows the calculated transmittance spectra of the spiral disks with different α for normal illumination (θ = 0°) by an X-polarized EM wave. Starting from α = 90°, the new dark mode narrow resonances were well excited (see red circles in Figure 2b). With increasing α, the resonances move towards the lower frequencies due to the decrease in the bright mode frequency of the C-resonator. For the following simulations we selected α = 90°, at which there were several narrowband resonances in the region of 0.2–0.5 THz (see the highlighted region in Figure 2a).
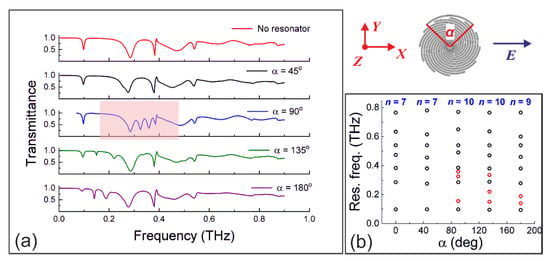
Figure 2.
(a) Transmittance spectra of the distantly spaced (p = 768 µm) spiral disks with different C-resonator angles α. Normal incidence (θ = 0°), E || X; (b) The resonance frequencies vs. α (n—number of resonances), the red circles—the resonances produced by the bright mode of the C-resonator.
Another way to excite multipole resonances with a high Q-factor is through the oblique illumination of the structure, which also breaks the excitation symmetry [,]. The TM-transmittance spectra of distantly spaced spiral disks with a 90° C-resonator at oblique incidence with θ = 0, 20° and 40° simulated for two orthogonal orientations (φ = 0 and φ = 90°) are plotted in Figure 3a. The analysis shows that the bright mode of the C-resonator in the vicinity of frequency ≈0.5 THz (see Figure 2, α = 90°) was excited most efficiently when in the XY plane projection of the incident E-field was parallel to the resonator (φ = 0: EX ≠ 0, EY = 0); in the opposite case (φ = 90°: EX = 0, EY ≠ 0), the bright mode was not revealed. For both orientations, upon increasing θ, the main resonances shifted a little and became weaker due to the decreasing E-projection on the PMS plane. We may also track new resonances arising above 0.38 THz, whose positions depend on the incidence angle and probably originate from the hybridized nature of these modes.
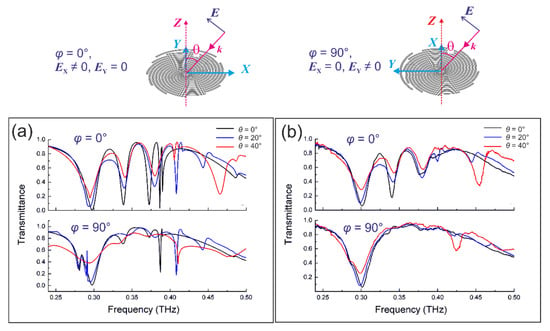
Figure 3.
TM-transmittance spectra of the distantly spaced spiral disks with a 90° C-resonator under oblique illumination: θ = 0, 20 and 40°: (a) the simulations and (b) the experiments. Azimuthal angles φ = 0 and φ = 90° correspond to the zero projections of the incident E-field on the Y and X axes, respectively.
The experimentally measured TM-transmittance spectra of the distantly spaced spiral disks with a 90° C-resonator patterned on the 15 µm PP substrate are shown in Figure 3b. Reasonable mutual agreement was demonstrated between the experimental and simulated data. There are some discrepancies in the spectral region near 0.38 THz. In the simulations, there were two narrowband resonances which were degraded in the experiment. We attributed these differences to several factors: (a) the higher THz absorption in the real metal–dielectric structures; (b) the non-ideal collimation of the probing THz beam in the spectrometer that yields its non-zero angular divergence; (c) some technological spread in the dimensions of the PMS micro-pattern upon its lithographic fabrication, which we observed with the optical microscope.
To characterize the sensing performance of the fabricated metasurfaces, we covered the metallized face of the samples with thin layers of photoresist used as the analyte. The analyte thicknesses after deposition were d = 0.3, 1, 5 and 10 µm (from 2 10−4 λ to 7 10−3 λ). Depositing thicker layers was not feasible due to the insufficient viscosity of the employed photoresist. The transmittance spectra of the samples measured with the BWO spectrometer are shown in Figure 4b. The simulated spectra (see Figure 4a) are in good accordance with the experiments. With increasing d, all the resonances were gradually shifted towards lower frequencies. We evaluated the resonance shifts Δf (GHz) from the spectra at 0.297, 0.339 and 0.373 THz as a function of the photoresist thickness d (see Figure 5a). The errors for Δf in the experiments and simulations were determined with the inaccuracy (≈0.5–1 GHz) of identifying the resonance frequency for the minima of the transmittance spectra. The experimental errors depended on the step of the frequency scanning (0.5 GHz). The experimental and simulated results were in qualitative agreement. Additional simulations for the larger thicknesses showed that Δf tended to saturation at d > 50 µm, at which the sensor was insensitive to the thickening of the photoresist layer.
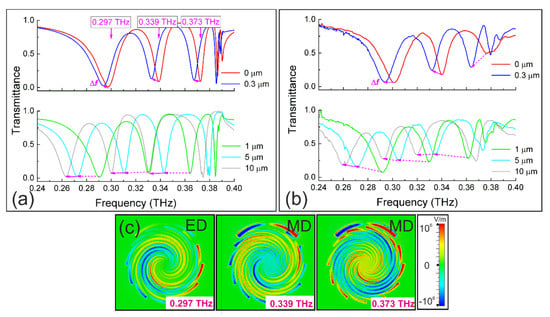
Figure 4.
Transmittance spectra of the distantly spaced (p = 768 µm) spiral disks with a 90° C-resonator and photoresist coatings of different thicknesses: (a) the numerical simulations; (b) the experiments; (c) the EZ-field distributions at the resonances (0.297 THz–natural electric dipole mode (ED), 0.339 THz and 0.373 THz–magnetic dipoles (MDs)). Normal incidence (θ = 0°), E || X.
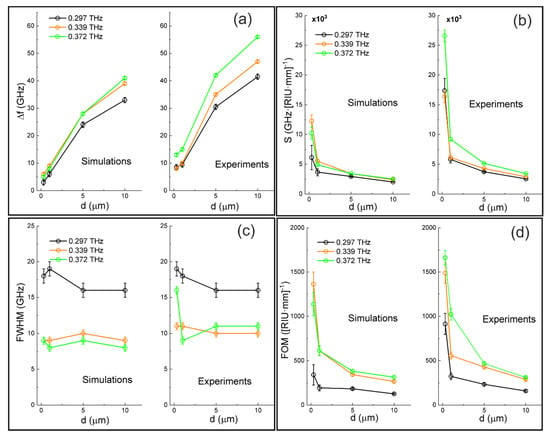
Figure 5.
Sensor parameters for the distantly spaced (p = 768 µm) spiral disks with 90° C-resonator, evaluated from the transmittance spectra in Figure 4: (a) the frequency shifts Δf of resonances at 0.297, 0.339 and 0.372 THz vs. photoresist thickness d (left—simulations, right—experiments); (b) the sensitivity of S vs. d; (c) the full width at the half minimum (FWHM) vs. d; (d) figure of merit (FOM) vs. d.
According to [], the frequency sensitivity of the sensor was defined as the ratio of the resonance frequency variation to the product of the analyte thickness and the refractive index na: S = Δf/(d·na), with the units of GHz·(the refractive index unit (RIU)·mm)−1. The dependencies S(d) plotted in Figure 5b are almost consistent with each other, except for d = 0.3 µm at which the experimental value S is larger than the simulated one. The reason for this discrepancy presumably lies in a deviation of the real thickness (averaged over a THz-illuminated area) of the photoresist layer deposited on a flexible 15 µm PP substrate of our PMS sensor.
In sensing applications, the full width at the half minimum (FWHM) in the units of frequency is another important characteristic related with the Q-factor of the resonance. The FWHM vs. d is plotted in Figure 5c. The FWHM values were determined with the accuracy of 0.5–1 GHz depending on the resonance bandwidth. It is worth noticing that the resonance at 0.297 THz has about two times larger FWHM compared to the other two resonances. This effect is explained by their different nature: the mode excited at 0.297 THz is electric dipole, while the modes at 0.339 THz and 0.373 THz are magnetic dipole, as illustrated in Figure 4c by the EZ-field distributions simulated at the resonant frequencies at a distance of 2 µm from the metallized layer. According to [], the magnetic modes potentially have higher Q-factors than the electric ones.
In many cases, the sensitivity alone is not enough to determine the sensor quality. It is clear that to minimize the overlapping between the detection thresholds upon shifting the resonance, resonances with a narrower bandwidth can be distinguished better in the experiment. From this viewpoint, it is preferable to use sensors with higher values of the figure of merit (FOM), which is defined as the ratio FOM = S/FWHM, with the units of (RIU·mm)−1. The calculated graphs of the FOM as a function of d depicted in Figure 5d show that magnetic resonances were more sensitive than electric ones, especially for very thin analyte layers. The highest FOM was attained at d = 0.3 µm: FOM ≈ 1670 (RIU·mm)−1.
Measurements under the oblique illumination of the samples demonstrated that the main resonances (see Figure 3) had the same sensitivity and FOM to the analyte as at normal incidence.
3.2. Asymmetric Spiral Disks with Shifted Center
Another way to produce high-order resonances is to break the symmetry of the disk by shifting its center at some value δr (see Figure 1d). The δr magnitude affects the number and frequencies of the dark modes. For the new design we took spiral disks with δr = 35 µm, at which multiple resonances were excited in the spectral region of interest 0.2–0.5 THz, and arranged them in the array with higher density packing (p = 408 µm). The advantage of densely packed structures lies in red shifting the LSPRs relative to the diffraction lobes’ onset point that improves the angular stability of the resonances []. Furthermore, in the case of closely spaced disks, new strong plasmon modes can be excited due to hybridizing the EM fields of nearby disks [,]. The results of simulating the transmittance spectra for the closely spaced spiral disks with a 135° C-resonator and δr = 35 µm covered with photoresist films of different thicknesses are shown in Figure 6a.
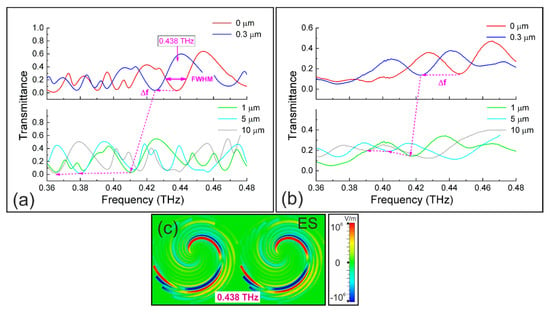
Figure 6.
Transmittance spectra of the closely spaced (p = 408 µm) spiral disks with centers shifted at δr = 35 µm, covered by photoresist films of different thicknesses: (a) the numerical simulations; (b) the experiments; (c) the EZ-field distribution at resonance (0.438 THz). Normal incidence (θ = 0°), E || X.
For clarity, the graphs in Figure 6 are plotted in a reduced spectral region of 0.36–0.48 THz. There are many narrow resonances, which are red shifted when increasing the photoresist thickness (the shifts are indicated by arrows). The experimental results of the fabricated samples with the same parameters are presented in Figure 6b. As compared with the simulations, there is only one distinct wideband resonance at 0.438 THz in the spectral range considered; other narrow resonances are broadened and disappeared due overlapping with adjacent resonances. The EZ-field distribution of two nearby disks at 0.438 THz (Figure 6c) presumably corresponds to an electric sextupole hybrid mode. The FWHM(d) values plotted in Figure 7c are approximately the same as for the distantly spaced disks without shifted centers (see Figure 5c), while Δf(d) and S(d) (Figure 7a,b) are significantly larger. The greater sensitivity can be explained by the high-density arrangement of the disks, which enhances EM field localization near the PMS. The larger sensitivity yields the greater FOM. The highest FOM ≈ 2950 (RIU·mm)−1 is reached at the smallest analyte thickness (d = 0.3 µm), which is ≈77% bigger than in the case of the distantly spaced disks. This result is comparable with the best FOM value (3450 (RIU·mm)−1) obtained at the same analyte thickness for a labyrinth metasurface absorber implemented with a similar fabrication techniques [,].
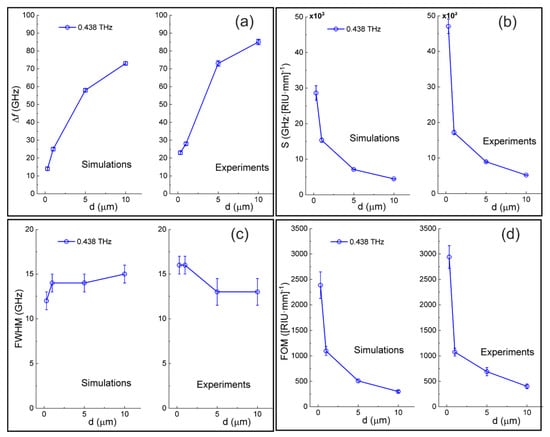
Figure 7.
Sensor parameters for the closely spaced (p = 408 µm) spiral disks with centers shifted by δr = 35 µm, evaluated from the transmittance spectra in Figure 7: (a) the frequency shift Δf of resonance at 0.438 THz vs. the photoresist thicknesses d (left—simulations, right—experiments); (b) the sensitivity S vs. d; (c) FWHM vs. d; (d) FOM vs. d.
As seen from numerical simulations in Figure 6a, the illumination of the array of asymmetrical disks excites multiple narrow resonances as compared with only several peaks excited in the symmetrical disks (Figure 4a). The sharp resonances arising in asymmetrical structures originate from the physics of bound states in the continuum (BIC) []. The number of BIC resonances and their Q-factors depend on the level of asymmetry. In our case, this level defined by the δr value (see Figure 1d) effect on the number, as well as the width and depth of the resonances. Comparing the results obtained for symmetrical and asymmetrical disks (Figure 4 and Figure 6), we can assume that the number of resonances, their widths and depths increase with increasing δr. Besides, the augmentation of a packing density of the disks produces new hybrid modes. However, in our experiments (Figure 6b), the adjacent resonances overlap with each other which leads to the formation of broad resonances with lower Q-factors. A possible way to partially prevent the resonance broadening is to reduce δr and the packing density of the disks. Taking into account that a decrease in a packing density reduces the sensor sensitivity (see Figure 5b and Figure 7b), an optimal packing density and δr value could be found to reach the maximal FOM for the spiral disk metasurface.
4. Conclusions
In summary, we demonstrated the high sensing performance of metasurfaces consisting of spiral metallic disks patterned on thin PP substrates, which operate in the low-frequency region of the THz range (0.2–0.5 THz). High Q-factor localized surface plasmon dark modes were excited by placing a C-shaped resonator near the disk. Metasurfaces with optimal design were fabricated by the photolithographic technique and tested with a sub-terahertz CW BWO spectrometer. The experimental transmittance showed good agreement with the simulations. The resonance frequency shifts Δf arising from very thin (d ≈ 10−4 λ) photoresist coatings increased with d, while approaching a constant at d = 50 µm. Dark magnetic modes excited on symmetric spiral disks with 90° C-resonators demonstrated very high FOM values, especially for the smallest thicknesses (1670 (RIU·mm)−1 at d = 0.3 µm) due to a narrow resonance width. The hybrid high order mode resonances of asymmetrical densely packed spiral disks (with a shift of the disk center) showed about two times larger FOMs (up to 2950 (RIU·mm)−1) then symmetrical spirals, which is comparable with the best FOM values obtained for alternative metasurfaces with densely packed unit cells fabricated with a similar technique. The attained results allow us to highlight the spiral disks design as promising for bio-sensing applications in the THz range.
Author Contributions
Conceptualization, V.V.G.; methodology, V.V.G. and S.A.K.; software, R.R.H. and S.A.K..; validation, V.V.G., R.R.H. and P.A.L.; formal analysis, V.V.G. and S.A.K.; investigation, V.V.G. and R.R.H.; resources, S.A.K.; data curation, V.V.G.; writing—original draft preparation, V.V.G.; writing—review and editing, S.A.K.; visualization, V.V.G. and R.R.H.; supervision, V.V.G.; project administration, V.V.G.; funding acquisition, V.V.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 18-72-00112.
Acknowledgments
This work was done using the infrastructure of the Shared Research Facility “Siberian Synchrotron and Terahertz Radiation Centre” of BINP SB RAS and the Shared Equipment Center CKP “VTAN” (ATRC) of the NSU Physics Department. Authors thanks A. V. Gelfand and N. I. Fedorinina for the sample preparation.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Stiles, P.L.; Dieringer, J.A.; Shah, N.C.; Van Duyne, R.P. Surface-enhanced Raman spectroscopy. Annu. Rev. Anal. Chem. 2008, 1, 601–626. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R.; Ray, K.; Chowdhury, M.; Szmacinski, H.; Fu, Y.; Zhang, J.; Nowaczyk, K. Plasmon-controlled fluorescence: A new paradigm in fluorescence spectroscopy. Analyst 2008, 133, 1308–1346. [Google Scholar] [CrossRef] [PubMed]
- Valev, V.K.; Silhanek, A.V.; Verellen, N.; Gillijns, W.; Van Dorpe, P.; Aktsipetrov, O.A.; Vandenbosch, G.A.; Moshchalkov, V.V.; Verbiest, T. Asymmetric optical second-harmonic generation from chiral G-shaped gold nanostructures. Phys. Rev. Lett. 2010, 104, 127401. [Google Scholar] [CrossRef] [PubMed]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Tatsuma, T.J. Mechanisms and applications of plasmon-induced charge separation at TiO2 films loaded with gold nanoparticles. J. Am. Chem. Soc. 2005, 127, 7632–7637. [Google Scholar] [CrossRef] [PubMed]
- Son, J.H. (Ed.) Terahertz Biomedical Science and Technology; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Peiponen, K.E.; Zeitler, J.A.; Kuwata-Gonokami, M. (Eds.) Terahertz Spectroscopy and Imaging. Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 171. [Google Scholar]
- Lee, Y.-S. Principles of Terahertz Science and Technology; Springer: New York, NY, USA, 2009. [Google Scholar]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef]
- Pendry, J.B.; Martin-Moreno, L.; Garcia-Vidal, F.J. Mimicking surface plasmons with structured surfaces. Science 2004, 305, 847–848. [Google Scholar] [CrossRef]
- Pors, A.; Moreno, E.; Martin-Moreno, L.; Pendry, J.B.; Garcia-Vidal, F. Localized spoof plasmons arise while texturing closed surfaces. Phys. Rev. Lett. 2012, 108, 223905. [Google Scholar] [CrossRef]
- Glybovski, S.B.; Tretyakov, S.A.; Belov, P.A.; Kivshar, Y.S.; Simovski, C.R. Metasurfaces: From microwaves to visible. Phys. Rep. 2016, 634, 1–72. [Google Scholar]
- Al-Naib, I.; Withayachumnankul, W. Recent progress in terahertz metasurfaces. J. Infrared Millim. Terahertz Waves 2017, 38, 1067–1084. [Google Scholar] [CrossRef]
- Beruete, M.; Jáuregui-López, I. Terahertz sensing based on metasurfaces. Adv. Opt. Mater. 2020, 8, 1900721. [Google Scholar] [CrossRef]
- Liao, Z.; Shen, X.; Pan, B.C.; Zhao, J.; Luo, Y.; Cui, T.J. Combined system for efficient excitation and capture of LSP resonances and flexible control of SPP transmissions. ACS Photonics 2015, 2, 738–743. [Google Scholar] [CrossRef]
- Chen, L.; Wei, Y.M.; Zang, X.F.; Zhu, Y.M.; Zhuang, S.L. Excitation of dark multipolar plasmonic resonances at terahertz frequencies. Sci. Rep. 2016, 6, 22027. [Google Scholar] [CrossRef] [PubMed]
- Bulgakova, V.; Gerasimov, V.; Lemzyakov, A.; Milekhin, I.A. Infrared localized surface plasmon resonances on subwavelength corrugated metal disks. In Proceedings of the 43th International Conference IRMMW-THz, Nagoya, Japan, 9–14 September 2018. [Google Scholar]
- Gerasimov, V.V.; Kuznetsov, S.A.; Lemzyakov, A.G.; Hafizov, R.R. Multipole terahertz localized plasmon resonances on spiral structures. In Proceedings of the 44th International Conference IRMMW-THz, Paris, France, 1–6 September 2019. [Google Scholar]
- Huidobro, P.A.; Shen, X.; Cuerda, J.; Moreno, E.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Cui, T.J.; Pendry, J.B. Magnetic localized surface plasmons. Phys. Rev. X 2014, 4, 021003. [Google Scholar]
- Gao, Z.; Wu, L.; Gao, F.; Luo, Y.; Zhang, B. Spoof Plasmonics: From metamaterial concept to topological description. Adv. Mater. 2018, 30, 1706683. [Google Scholar] [CrossRef]
- Liao, Z.; Fernández-Domínguez, A.I.; Zhang, J.; Maier, S.A.; Cui, T.J.; Luo, Y. Homogenous metamaterial description of localized spoof plasmons in spiral geometries. ACS Photonics 2016, 3, 1768–1775. [Google Scholar]
- Liao, Z.; Liu, S.; Ma, H.F.; Li, C.; Cui, J.; Cui, T.J. Electromagnetically induced transparency metamaterial based on spoof localized surface plasmons at terahertz frequencies. Sci. Rep. 2016, 6, 27596. [Google Scholar] [CrossRef]
- Kuznetsov, S.A.; Paulish, A.G.; Navarro-Cía, M.; Arzhannikov, A.V. Selective pyroelectric detection of millimetre waves using ultra-thin metasurface absorbers. Sci. Rep. 2016, 6, 21079. [Google Scholar] [CrossRef]
- Navarro-Cia, M.; Kuznetsov, S.A.; Aznabet, M.; Beruete, M.; Falcone, F.; Ayza, M.S. Route for bulk millimeter wave and terahertz metamaterial design. IEEE J. Quantum. Electron. 2011, 47, 375–385. [Google Scholar] [CrossRef]
- Aznabet, M.; Navarro-Cía, M.; Kuznetsov, S.A.; Gelfand, A.V.; Fedorinina, N.I.; Goncharov, Y.G.; Beruete, M.; El Mrabet, O.; Sorolla, M. Polypropylene-substrate-based SRR- And CSRR-metasurfaces for submillimeter waves. Opt. Express 2008, 16, 18312–18319. [Google Scholar] [CrossRef]
- Kuznetsov, S.A.; Arzhannikov, A.V.; Kubarev, V.V.; Kalinin, P.V.; Sorolla, M.; Navarro-Cía, M.; Aznabet, M.; Beruete, M.; Falcone, F.; Goncharov, Y.G.; et al. Development and characterization of quasi-optical mesh filters and metastructures for subterahertz and terahertz applications. Key Eng. Mater. 2010, 437, 276–280. [Google Scholar] [CrossRef]
- ALLRESIST GmbH. Available online: https://www.allresist.com (accessed on 21 May 2020).
- Jauregui-López, I.; Rodriguez-Ulibarri, P.; Kuznetsov, S.A.; Nikolaev, N.A.; Beruete, M. THz sensing with anomalous extraordinary optical transmission hole arrays. Sensors 2018, 18, 3848. [Google Scholar] [CrossRef]
- Kozlov, G.; Volkov, A. Coherent source submillimeter wave spectroscopy. In Millimeter and Submillimeter Wave Spectroscopy of Solids. Topics in Applied Physics; Grüner, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 74, pp. 51–109. [Google Scholar]
- Sayanskiy, A.; Kuznetsov, S.A.; Tanygina, D.S.; Risco, J.P.; Glybovski, S.; Baena, J.D. Frequency controllable polarization rotation of THz waves with an SCMS. IEEE Trans. Antennas Propag. 2019, 68, 1491–1502. [Google Scholar] [CrossRef]
- Kuznetsov, S.A.; Paulish, A.G.; Gelfand, A.V.; Lazorskiy, P.A.; Fedorinin, V.N. Bolometric THz-to-IR converter for terahertz imaging. Appl. Phys. Lett. 2011, 99, 023501. [Google Scholar] [CrossRef]
- Rodríguez-Ulibarri, P.; Kuznetsov, S.A.; Beruete, M. Wide angle terahertz sensing with a cross-dipole frequency selective surface. Appl. Phys. Lett. 2016, 108, 111104. [Google Scholar] [CrossRef]
- Jáuregui-López, I.; Rodríguez-Ulibarri, P.; Urrutia, A.; Kuznetsov, S.A.; Beruete, M. Labyrinth metasurface absorber for ultra-high-sensitivity terahertz thin film sensing. Phys. Status Solidi 2018, 12, 1800375. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, Z.; Luo, Y.; Shen, X.; Maier, S.A.; Cui, T.J. Spoof plasmon hybridization. Laser Photonics 2017, 11, 1600191. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).