Parameter Selection of Local Search Algorithm for Design Optimization of Automotive Rubber Bumper

Abstract

In rubber bumper design, the most important mechanical property of the product is the force–displacement curve under compression and its fulfillment requires an iterative design method. Design engineers can handle this task with the modification of the product shape, which can be solved with several optimization methods if the parameterization of the design process is determined. The numerical method is a good way to evaluate the working characteristics of the rubber product; furthermore, automation of the whole process is feasible with the use of Visual Basic for Application. An axisymmetric finite element model of a rubber bumper was built with the use of a calibrated two-term Mooney–Rivlin material model. A two-dimensional shape optimization problem was introduced where the objective function was determined as the difference between the initial and the optimum characteristics. Our goal was to integrate a surrogate model-based parameter selection of local search algorithms for the optimization process. As a metamodeling technique, cubic support vector regression was selected and seemed to be suitable to accurately predict the nonlinear objective function. The novel optimization procedure which applied the support vector regression model in the parameter selection process of the stochastic search algorithm proved to be an efficient method to find the global optimum of the investigated problem.

1. Introduction

Rubber bumpers built into air spring structures perform several critical tasks, such as working together with the air spring as a secondary spring, thus modifying the original characteristics of the air spring when pressed together. In the product design and development cycle, engineers are faced with several predefined requirements that are difficult to fulfill and time consuming, and thus remain a challenging task. The product investigated is applied in the air springs of lorries, where the force–displacement characteristic for the compression load is one of the most challenging technical requirements. Design engineers manage to achieve the required working characteristics by modifying the shape of the product, which leads to an iterative design process. This process is termed shape optimization whose simplest solution is to determine the optimal geometry through a series of trials with a study called “what if,” based on design engineers’ experiences. Owing to the continuum mechanics background and hyperelastic material model, available trials can be carried out by applying a finite element analysis. If there is an opportunity to parameterize the process from creating a geometry to obtaining the results, then conversion that meets the technical requirements can be automated; furthermore, there might also be an opportunity to use optimization algorithms in the design process.

Design optimization is an engineering design methodology that uses a mathematical formulation of a design problem to support the selection of the optimal design among many alternatives [1]. Several researchers have investigated shape optimization of rubber products, out of which [2,3] are the least efficient “trial and error” procedures. Many articles combined finite element analysis with a variety of optimum search methods, such as one presented by Kaya [4] involving a differential evolution algorithm-based shape optimization of the 2D rubber bushing. Interaction of a genetic algorithm and finite element code was used in the shape optimization of a rubber bumper for a new pickup vehicle [5]. A bush-type engine mount using a parameter optimization method was designed by Kim [6], and Fletcher’s method using the concept of quadratic convergence and was applied as an optimization algorithm.

Several papers can be found where metamodel-based design optimization was used for rubber product design. The problem of a rubber component design for automotive application by changing the shape with five design variables was discussed by Previati et al. [7]. The optimization of the bushing was performed concerning two objectives, mass reduction and the fatigue life of the component. The finite element model of the bushing was used to simulate about 200 different combinations of parameters for four different material models. These simulations were used to calibrate the parameters of a series of interpolating functions. A parameter optimization methodology for a rubber mount, based on finite element analysis and the genetic neural network model, was proposed by Li [8]. The orthogonal experiment table was adopted to design the geometric parameters of the samples on which the numerical analyses were run. The results of finite element analyses were used as samples to train the error backpropagation neural network model which defines the nonlinear global mapping relationship between the geometric parameters of the rubber mount and its primary stiffness in the three principal directions.. Multiobjective shape optimization of a rubber isolator of an automotive cooling module was performed to maximize fatigue life and vibration isolation. The response values of interest were evaluated with the integration of various computer-aided engineering tools. The analysis procedure was automated using a commercial process integration and design optimization tool, therefore the cycle time of the complex analysis was reduced. A regression-based sequential approximate optimizer was used successfully to obtain the optimal shapes of the rubber isolators for two different cooling module types [9].

Optimization methods can be divided into local and global optimum search procedures. Most local search procedures require the calculation of gradient while most optimum search ones are direct and belong to gradient-free optimization algorithms. Applying the latter kind of algorithms needs to meet few requirements, as they only use function value and implementing them is generally simpler. The direct optimal algorithm includes localized stochastic search, the Nelder–Mead method (simplex method), simulated annealing, tunneling, and several other methods [10]. The random search methods for optimization are based on randomly exploring the design area to find a point that minimizes the objective function. These techniques have all or some of the following advantages relative to most other search methods. The advantages, like ease of programming, inexpensive realization, flexibility, or reasonable computational efficiency, were mentioned by Karnopp [11]. In direct random search, several methods are known, depending on the field of application for noise-free or noise problems. For noise-free object function, three algorithms were presented in [12]. One of the presented methods is a simple random or blind search. In this case, uniformly distributed random numbers were created above the range of each design variable. This is a unique algorithm from the point of view that it does not contain any adjustable algorithm coefficients that need to be selected by the user. Localized and enhanced localized random search methods are slightly more sophisticated in that random sampling depends on the position of the current best-estimate object function.

The most primitive version of the localized random search was applied by Mátyás [13]. This utilizes selection of the next point from a normally distributed hyperplane or hypersphere and then moving to a better position. This technique can be improved in several ways based on observations. One of them is that if the newly selected point results in a higher function value, the opposite direction can often lead to a lower objective function. The other observation is that successive success or failure searches in a certain direction should bias or discourage subsequent searching toward that direction. It could be handled with the use of a bias term as the mean value of the random vector [14]. In [15], a modified algorithm such as enhanced localized random search was introduced with these guidelines. Luus-Jaakola [16] utilized a local search algorithm with the use of pseudorandom numbers over an exponentially decreasing search region. To test its effectiveness, mathematical, chemical, and engineering examples were chosen.

Metamodel methods applied to replace costly simulation engineering tasks are termed “surrogate models” in the English literature [17]. Generally, the main goal is to replace the original model with one very similar that requires a lower calculational time. There are several metamodels known, such as the simple and adaptive response surface, kriging method, radial basis function, multivariable adaptive spline regression, and neural network or support vector machines (SVM) [18]. In machine learning, SVM is a supervised learning algorithm that can efficiently perform a nonlinear classification using the so-called kernel trick [19]. Based on the SVM algorithm, support vector regression (SVR) was introduced in [20]. This regression technique has advantages in high dimensionality spaces because SVR optimization does not depend on the dimensionality of the input space. Therefore, it is widely used for function approximation, regression estimation, and signal processing [21,22].

Three mathematical problems and two engineering design problems were solved with SVR efficiency and accuracy of which were compared with other metamodels such as kriging, radial basis function (RBF), and polynomial regression. Latin hypercube design was used as a design of the experiment technique. The results showed that in all problems the introduced SVR method performed more efficiently than the other methods [23]. A two-variable aerodynamic problem was introduced in [24] where the quasi-Monte Carlo algorithm was used to determine eight sample points. Poor space-filling properties of the quasi-Monte Carlo sampling left a noticeable gap in the data. In this area, inaccuracies were found in the prediction of the kriging and RBF model, and only the SVR method mitigated this problem. In [25,26], vehicle crashworthiness designs were presented, where SVR was utilized to construct crashworthiness responses. It was demonstrated that SVR models with Gaussian RBF and exponential RBF have good generalization performance compared to other types of kernels. SVR outperforms polynomial response surface, radial basis neural network, and kriging with good accuracy in approximating the crashworthiness responses. A multiobjective crashworthiness design of a tailor-rolled blank thin-walled structure was constructed based on the ε-support vector regression (ε-SVR) technique and nondominated sorting genetic algorithm-II. The SVR parameters were further optimized with a genetic algorithm to improve the predictive accuracy of ε-SVR [27,28]. Shape optimization of rubber bumpers, where obtaining data with finite element simulation is independent on the optimization algorithm, was investigated [29,30,31,32]. Optimal shape was determined by minimizing the objective function by calculating differences in work energy. Design options obtained from design space, such as learning points, were applied. The SVR model was applied to determine the given values of the objective functions of further constructions. Through this metamodel, the optimal shape was determined. 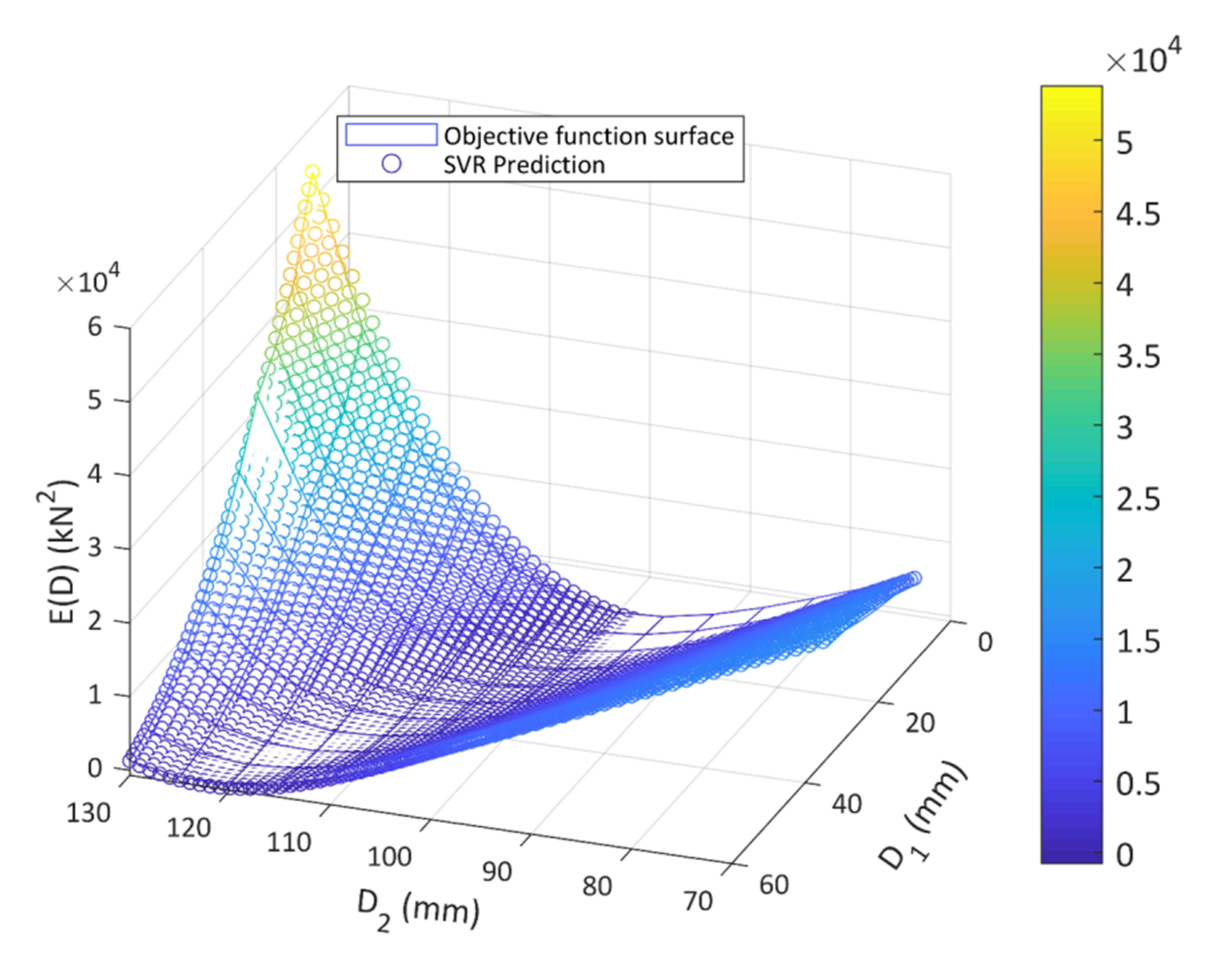The SVR method was investigated by Huri and Mankovits [33] to predict the optimum shape of a rubber jounce. From the results, the cubic kernel function showed the best match, therefore it was chosen for the prediction of each combination of design variables. From the predicted values, the optimum shape was selected, which was sufficiently accurate if the number of the learning points was at least 22. This observation is used in the current rubber product optimization process.

Based on the professional papers, the local stochastic search method is suitable for finding the global optimum of engineering optimization tasks. However, it is vital to find the right size of the search space to achieve good results. Due to the stochastic procedure, it is to be noted that one cannot conclude whether the adjustment is correct by simply running one instance. From the literature review, it can be seen that none of the research deals with setting the parameters of the applied optimization algorithms. The parameters highly influence the required finite element run and the accuracy of the determined optimum. All the case studies indicated that if enough set of training vectors are supported, the SVR is a promising metamodel technique for highly nonlinear engineering applications. The selection of the appropriate type of kernel function and hyperparameter choice is of vital importance for the right assessment. This article first introduces what considerations are necessary for the finite element analysis of axisymmetric rubber products, especially when exposed to pressure with special attention to the selected material model type and its parameters. The rubber bumper investigated in the paper is a case study based on an industrial design problem. Secondly, the task of two-variable shape optimization of a rubber bumper is described where the objective function values of 22 uniformly distributed samples from the design area were determined from the results of finite element analysis. The SVR surrogate model with cubic kernel function was trained utilizing the sampled experiments, whereby the relationship between the design variables and objective function values was described. The pre- and postprocessing of the model were automated in the Visual Basic for Applications (VBA) language. Owing to this method, the local stochastic search algorithm was implemented and run with basic options for the shape optimization task. This research aims to investigate the parameter selection of local search algorithms for design optimization of an automotive rubber bumper. The novelty of our research is that the trained SVR surrogate model was integrated into the size selecting process of the search space of the algorithm. Finally, using the stochastic search algorithm and the adjusted parameter, the finite element model was directly run to solve the shape optimization of the rubber bumper. Later on, to validate the goodness of the procedure, it is compared with the initial algorithm in terms of precision and efficiency.

2. Materials and Methods

2.1. Hyperelastic Material Model of the Investigated Rubber Product

Rubber behaves as a nonlinear, elastic, isotropic, and incompressible material, which can be described accurately with a hyperelastic constitutive model. Within this model, several material models and material constants can be found. The material models for rubbers are generally given by the strain energy potential. A successful finite element simulation of rubber parts hinges on the selection of an appropriate strain energy function and the accurate determination of material constants. Because of material incompressibility, the strain energy function can be divided into two parts [34]:

$$W=W_D\left({\overline{I}}_1,{\overline{I}}_2\right)+W_b\left(J\right),$$

(1)

where $W_b\left(J\right)$ denotes the volumetric terms of the strain energy function and $J$ is for the Jacobian and $W_D\left({\overline{I}}_1,{\overline{I}}_2\right)$ is for the deviatoric terms of the strain energy function. The polynomial form of the strain energy potential is based on the first ${\overline{I}}_{1 }$ and second ${\overline{I}}_{2 }$ strain invariants of the right Cauchy–Green tensor [35]

$$W={\displaystyle \sum }_{i+j=1}^N{c}_{ij}{\left({\overline{I}}_1-3\right)}^i{\left({\overline{I}}_2-3\right)}^j+{\displaystyle \sum }_{k=1}^N\frac{1}{d_k}{\left(J-1\right)}^{2k},$$

(2)

where determination of $c_{ij}$ and $d_k$ material constants are required in a material model. The $d_k$ material compressibility parameter can be calculated as

$$d_k=\frac{2}{\mathsf{\kappa }} ,$$

(3)

where κ is the bulk modulus.

Mooney–Rivlin, Yeoh, and neo-Hookean material models are available within the polynomial form of the strain energy potential. There are two-, three-, five- and nine-term Mooney–Rivlin models. With N = 1 substitution, the expression of the polynomial form is equivalent to the two-term Mooney–Rivlin model:

$$W_{MR}=c_{10}\left({\overline{I}}_1-3\right)+c_{01}\left({\overline{I}}_2-3\right)+\frac{1}{d}{\left(J-1\right)}^2.$$

(4)

The exact mixture of the styrene–butadiene rubber (SBR) material is unknown for the investigated product; the manufacturing instruction prescribes 90 ± 5 Shore A hardness. Measurements on the base material are needed to determine the material constants used for finite element analysis. The main load of the rubber bumper is pressure, therefore a compression test and curve-fitting process were performed by us on rubber specimens according to [36,37]. The two-term Mooney–Rivlin model with $c_{10}=1.28801 \mathrm{MPa}$, $c_{01}=1.1371 \mathrm{MPa},$ and $\kappa =1000 \mathrm{MPa}$ values were selected for the finite element investigation of the rubber part. The determined models were used for the finite element analysis of the specimen and the exactness of parameters was compared with experimental data.

2.2. Finite Element Model of the Rubber Bumper Under Compression Load Set

The geometry of the investigated rubber specimen is axisymmetric; furthermore, the boundary conditions are symmetric as well, thereby the deformation of the shape is independent of the φ axis. In such a case, it is worth choosing the axisymmetric element (isoparametric quadrilateral elements) for meshing. The size of the element was 1 mm. The investigated geometry can be seen in Figure 1 and it was created with $H=40 \mathrm{mm}, \alpha =3°,D_1=77 \mathrm{mm}$ and $D_2=15 \mathrm{mm}$ dimensions. Under working conditions, the rubber bumper comes into contact on the bottom and on the top with flat steel plates. Therefore, frictional contact was defined between the surfaces of the product and the steel parts. The coefficient of static friction ${\mu }_s=0.6$ was selected according to [38]. For boundary conditions, it was given 12 mm prescribed displacement for the top edge of the upper one steel plate; furthermore, the bottom curve nodes on the lower steel one were constrained along the z axis. Finally, finite element analysis was run. As a result, Figure 1 shows the deformation state of the rubber bumper while the curve named "Initial characteristics" in Figure 2 shows the load–displacement characteristics of the investigated product.

2.3. Two-Dimensional Shape Optimization Problem

In many cases, the dimensions of the rubber bumper built-in air spring are constrained by other parts. During the current investigation, the product’s height $H=40 \mathrm{mm}$ and draft angle $\alpha =3°$ were fixed while the outer diameter $D_1$ and hole diameter $D_2$ were design variables (Figure 1). Thus, in the shape optimization, the design variables are defined in mm, according to the following conditions:

$$\mathit{D}=\left(D_1;D_2\right), where \{\begin{array}{c}{D}_1\in \left[70,71,\dots 130\right]\\ D_2\in \left[10,11,\dots 60\right]\end{array}and x_1-\frac{D_2}{2}\ge 15,$$

(5)

where vector $\mathit{D}$ contains design variables of possible construction and $x_1$ is the coordinate of point $P$ (Figure 1):

$$x_1=\frac{D_1}{2}-Htan\alpha .$$

(6)

The goal of the shape optimization process is to minimize the difference between the initial characteristics and the optimum characteristics (Figure 2). This research investigated the applicability of localized random search algorithm in the optimization process, therefore the desired characteristics determined from predefined an optimum shape ${\mathit{D}}_{opt}=\left(108;33\right) \mathrm{mm}$.

The finite element analysis was solved in 100 steps with every 10th step created as output. The difference was calculated as the sum of the square error (SSE):

$$E{\left(\mathit{D}\right)}_{FEA}={{\displaystyle \sum }}_{i=1}^{10}{\left(F_i\left({\mathit{D}}_{opt}\right)-F_i\left(\mathit{D}\right)\right)}^2 \left(k{N}^2\right),$$

(7)

where $E{\left(\mathit{D}\right)}_{FEA}$ is the error value in an investigated design point, $F_i\left({\mathit{D}}_{opt}\right)$ is the $i\mathrm{th}$ results of required compression force value in the optimal design point, and $F_i\left(\mathit{D}\right)$ is the $i\mathrm{th}$ results of the required compression force value in the initial design point.

Table 1. Calculated cost function value in different design points.

	${\mathit{D}}_{1 }\left(\mathbf{mm}\right)$	${\mathit{D}}_{2 }\left(\mathbf{mm}\right)$	$\mathit{E}{\left(\mathit{D}\right)}_{\mathit{F}\mathit{E}\mathit{A}} \left(\mathbf{k}{\mathbf{N}}^2\right)$
Optimum Shape	108	33	0
Initial Shape	77	15	7911.2
$D_{opt}$, best from 128 DP	120	55	3.267

contains the calculated error value for the initial design point $\mathit{D}=\left(77;15\right) \mathrm{mm}.$ Function $E\left(\mathit{D}\right)$ is considered on $\Omega \in {\mathbb{R}}^n$, the set of possible design variables vectors $\mathit{D}$. The objective function of the shape optimization process is to minimize this error value:

$$E\left({\mathit{D}}_{opt}\right)=\underset{D\in \Omega }{\min }E\left(\mathit{D}\right).$$

(8)

3. Results and Discussion

3.1. Investigating the Shape of The Objective Function above the Design Area

With the increment of $5 \mathrm{mm}$ along with the design variables, $128$ vertex pairs (Design Points, DP) were selected from $\Omega$. With the use of the introduced finite element model of the rubber bumper, it was possible to calculate the $E{\left(\mathit{D}\right)}_{FEA}$ values for each vertex pair. To accelerate the finite element model pre- and postprocessing, the parameterization of these processes was necessary. Automation of the whole process was feasible with the use of Visual Basic for Applications (VBA), which allowed us to directly access Femap from Excel. Thereby, the finite element model pre- and postprocessing were controlled with a macro running in Excel, and $E{\left(\mathit{D}\right)}_{FEA}$ values were determined for each vertex pair.

The objective function values are plotted above the design area, which is shaped like a valley (Figure 3). Table 1 contains the best design point ${\mathit{D}}_{opt}=\left(120;55\right) \mathrm{mm}$ relating to the smallest objective function $E{\left({\mathit{D}}_{opt}\right)}_{FEA}=3.267 {\mathrm{kN}}^2$ value from the $128$ vertex pairs investigated. As it can be seen, the error value was small compared to the initial shape, however, and the determined optimum point was far away from the known optimum. This indicated that convergence to the global optimum was not a trivial task.

3.2. Train Support Vector Regression Model

The objective of machine learning is to discover a function $E{\left(\mathit{D}\right)}_{FEA}=E{\left(\mathit{D}\right)}_{SVM}$ that best predicts the value of $E{\left(\mathit{D}\right)}_{FEA}$ associated with each value of $\mathit{D}$. At the first step, $22$ vertex pairs (Learning Points, LP) were selected from $\Omega$ according to Figure 4, then $E{\left(\mathit{D}\right)}_{FEA}$ values were determined by the use of finite element analysis. Thereby, the training set was produced for the machine learning algorithm.

With the use of Regression Learner application built into Matlab, it is possible to perform an automated training to search for the best regression model type, including linear regression models, regression trees, Gaussian process regression models, support vector machines, and ensembles of regression trees. Manual regression model training was run without a validation data set for the support vector machine. The goodness of the prediction highly hinges on the kernel function type. According to [32], the cubic kernel function was selected because this method’s root mean square error (RMSE) value was the lowest on the predicted set. For the fitting process ε = 0.001 and kernel scale = 1 values were selected while the rest of the hyperparameters were selected automatically by the Regression Learner application. The predicted response $E_{SVM}$ of the cubic SVM model is plotted against the true response $E_{FEA}$, see Figure 4b. A perfect regression model has a predicted response equal to the true response, so all the points lay on the diagonal line. The vertical distance from the line to any point is the error of the prediction for that point. The predictions are scattered near the diagonal line, which means the SVR model accurately predicts the nonlinear objective function values.

Using the trained cubic SVM model, predictions were made for each combination of integer values of design variables.

Table 2. The predefined and the support vector machines (SVM) model-based optimum point.

	${\mathit{D}}_1 \left(\mathbf{mm}\right)$	${\mathit{D}}_2 \left(\mathbf{mm}\right)$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{F}\mathit{E}\mathit{A} }\left(\mathbf{k}{\mathbf{N}}^2\right)$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}\left(\mathbf{k}{\mathbf{N}}^2\right)$
Optimum Shape	108	33	0	-
SVM	95	10	390.91	−772.83

shows the smallest predicted object function value and the associated design variables. Based on the results, the SVM-based design optimization is not feasible to find the global optimum of a valley function. Predicted objective function values are illustrated above the design space according to Figure 5. It can be pointed out that the trained SVM model overlaps with the objective function values calculated by finite element analysis in point 128. The SVM model with the cubic kernel function was trained by using 22 support vectors. As a result, it seemed suitable for approaching the values of the nonlinear objective function.

3.3. Local Search Algorithm Applied for Shape Optimization

Program for pre- and postprocessing of the finite element model written in Visual Basic language contains values of parametric geometric variables. This language facilitates implementation of local stochastic search algorithm whose pseudocode follows:

(1)

Select a starting point ${\mathit{D}}_0\in \mathsf{\Omega }$ randomly;

(2)

${\mathit{D}}_m\to {\mathit{D}}_{m+1}$—generate a random direction ${\mathit{a}}_m\in {\mathbb{R}}^n$, if ${\mathit{D}}_m+{\mathit{a}}_m\notin \mathsf{\Omega }$ then generate a new ${\mathit{a}}_m$ direction and repeat it. If ${\mathit{D}}_m+{\mathit{a}}_m\in \mathsf{\Omega }$ then ${\mathit{D}}_{new}={\mathit{D}}_m+{\mathit{a}}_m$;

(3)

If $E{\left({\mathit{D}}_{new}\right)}_{SVM}<E{\left({\mathit{D}}_m\right)}_{SVM}$, then ${\mathit{D}}_{m+1}={\mathit{D}}_{new}$, otherwise ${\mathit{D}}_{m+1}={\mathit{D}}_m$, further $m=m+1$;

(4)

Stopping criterion—if the maximum iteration number is reached.

To generate ${\mathit{a}}_m$ direction, a normally distributed random number with mean zero is selected in all directions of the design variables. This algorithm contains two parameters to be determined, which are the $\sigma$ standard deviation belonging to random number and $m_{max}$ maximum iteration number should be provided as a precondition of stopping criterion, meaning cost of the algorithm. To investigate the operation of the algorithm, $\sigma =20 \mathrm{mm}$ and $m_{max}=5000$ values were selected. The search method was run for the two-variable shape optimization task for the rubber bumper as outlined in the previous section. The program written was operated for running the shape optimization task in an automatized closed system by providing the parameters. As a result, it determined the optimal objective function value as well as its other relevant values.

Table 3. Better function values accepted by the local search algorithm.

$\mathit{m}$	${\mathit{D}}_1\left(\mathbf{mm}\right)$	${\mathit{D}}_2\left(\mathbf{mm}\right)$	$\mathit{E}{\left(\mathit{D}\right)}_{\mathit{F}\mathit{E}\mathit{A}}\left(\mathbf{k}{\mathbf{N}}^2\right)$
0	89.851	31.215	4828.676
2	109.522	25.262	748.357
4	113.054	44.676	25.124
17	113.506	43.719	1.057
427	111.375	39.416	0.654
514	107.389	31.960	0.267
1250	109.184	35.372	0.051

contains better function values accepted in $m$ iteration by the algorithm and its related geometric variable values. Figure 6 visualizes the change in the location of the better function accepted by the optimization method in design space, as well as the starting and end points. Considering the results, the efficiency of the algorithm was low, as it was not suitable for identifying better value than $E{\left({\mathit{D}}_{opt}\right)}_{FEA}=0.051{ \mathrm{kN}}^2$ even after passing $m=1250$ iterations. The optimum revealed, based on Figure 6, could not approach the global optimum even after $m=5000$ function calculation, although it managed to approach it.

3.4. Adjustment of Local Search Algorithm Parameters

The optimization algorithm run in the previous section is suitable for solving shape optimization tasks. However, the question arises if there is an adjustment appropriate for increasing the precision and efficiency of the algorithm. The main goal of this section is to adjust the parameters of the local search algorithm for the investigated shape optimization task. The stochastic search algorithm can only find the acceptable environment of the global optimum with an appropriately high number of iterations, which means a computationally expensive procedure. Calculation of the finite element model is a time-consuming task, which makes it impossible to investigate the search algorithm parameters. Model SVM, which was trained before, provides a suitable approach for describing the relation between the design variables and objective function values, while running it is less time consuming. By running model SVM, there is an opportunity to test the effects of adjusting the algorithm parameters in terms of optimal search precision and efficiency. By doing so, we can observe the behavior of the original model on a well-approximating function. While training the algorithm, the $\sigma \in \left[ 1; 5; 10; 30\right]$ standard deviation is selected parameter by parameter.

Table 4. Different settings of local search algorithms.

	P-I	P-II	P-III	P-IV
maximum iteration number, $m_{max}$	5000	5000	5000	5000
standard deviation, $\sigma (\mathrm{mm}$)	1	5	10	30

includes algorithms of different settings between P-I and P-IV.

The starting point is chosen at random from the design area, while the search direction of the algorithm is stochastic too, whereby each adjustment is run ten times. The number of the better function accepted after the starting point should be marked by $k$.

Table 5. Optimal objective function values with search algorithms run with different adjustments.

	P-I			P-II			P-III			P-IV
Test No.	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$
1	14	2578	−707.86	17	3202	−707.86	13	2523	−767.65	9	4528	−754.88
2	4	107	−707.85	10	280	−707.81	14	3992	−707.81	12	3123	−755.79
3	19	1762	−707.86	10	474	−707.73	4	21	−707.77	5	3723	−755.96
4	47	2412	−707.86	15	2588	−771.93	5	723	−707.78	15	4847	−747.06
5	59	2209	−707.86	12	4288	−770.20	12	2679	−767.12	11	4076	−771.67
6	69	4838	−707.86	14	4635	−772.15	8	1626	−707.78	5	2165	−741.28
7	13	1812	−772.86	19	515	−707.70	18	3224	−707.77	9	4601	−756.77
8	47	2385	−707.86	12	424	−707.71	15	2626	−766.46	3	370	−757.06
9	38	1311	−772.87	15	1122	−771.10	11	911	−707.81	8	470	−752.52
10	48	2437	−772.60	10	945	−707.83	10	4490	−707.85	11	4935	−753.29

includes the last accepted $k$ value and $m$ iteration number belonging to it, as well as the target function value $E{\left({\mathit{d}}_{opt}\right)}_{SVM}$ belonging to the optimum location that can be found on the surrogate model. Based on the results, it can be pointed out that the algorithms got stuck in the local optimum while being run several times. The search process adjusted by P-IV found the optimum environment expected in all ten cases of being run, but not in a sufficiently good environment. This proves the fact that it lags behind the minimum values found during the P-I adjustment. There were even cases when the algorithm did not manage to find a single better solution after iteration 370. This was mainly caused by the big search space, due to which the chance to find a better solution while approaching global optimum converges to zero. The only solution seems to tighten the search space. By applying P-IV adjustment, the algorithm moves out its local minimum environment during 1000 iterations in 8 cases out of 10, whereas it occurred in 9 cases out of 10 during 2000 iterations.

3.5. Local Search Algorithms with Search Space Tightening

Based on research carried out in the previous section, it can be pointed out that no optimal value can be defined for the size of the search space. In the beginning, a large space is needed for mapping the design space and avoiding getting stuck in the local optimum. On the other hand, a smaller space is needed in the environment of the global optimum for the algorithm to have a better chance to find an optimal solution. Decreasing search space may happen through various functions such as an exponential function or after a manually selected iteration number. Based on Table 5, the method adjusted by the P-IV option was the only one suitable to move out its local environment during every instance of being run, which took place in most cases following 1000 iterations. As a result of the iteration number exceeding it, it was possible to decrease the search space as the algorithm had possibly managed to move out of its local environment, looking for a better solution in a global optimum environment. The main objective of this section, therefore, was to decrease $\sigma =30 mm$ value of standard deviation exceeding the prescribed iteration number, as long as it is still being run according to cases of P-V to P-VIII, as seen in

Table 6. Adjusting local stochastic search algorithm by tightening search space.

	P-V		P-VI		P-VII		P-VIII
iteration number start, $m_{start}$	1	2001	1	1001	1	2001	1	1001
iteration number stop, $m_{stop}$	2000	5000	1000	5000	2000	5000	1000	5000
standard deviation, $\sigma \left(1\right) (\mathrm{mm}$)	30	1	30	1	30	0.5	30	0.5
standard deviation, $\sigma \left(2\right)\left(\mathrm{mm}\right)$	30	1	30	1	30	0.5	30	0.5

.

Table 7. The values of the optimal objective function with algorithms run by different adjustments.

	P-V			P-VI			P-VII			P-VIII
Test No.	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$	$\mathit{k}$	$\mathit{m}$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{S}\mathit{V}\mathit{M}}$ ${\left(\mathbf{kN}\right)}^2$
1	18	3566	−772.50	13	4752	−707.86	13	2454	−772.82	18	3800	−772.84
2	20	4884	−772.67	10	3379	−772.87	16	3729	−772.84	14	4615	−772.52
3	15	2212	−772.29	22	2378	−772.32	14	2319	−772.80	17	1266	−772.89
4	9	2022	−771.61	17	3601	−707.86	11	3097	−772.49	11	3270	−707.86
5	15	2549	−772.78	8	4125	−707.86	19	3892	−707.86	13	3004	−707.86
6	9	3682	−707.86	13	2810	−772.63	11	4643	−772.86	18	1144	−772.72
7	19	3851	−772.67	10	4120	−707.86	21	2600	−772.77	16	2462	−772.72
8	20	2825	−772.76	13	1770	−772.67	16	3268	−772.73	23	3227	−707.86
9	15	3756	−772.80	16	4896	−772.39	21	3889	−772.60	13	2591	−772.89
10	17	3768	−772.36	16	4844	−772.01	11	2173	−772.74	19	1758	−772.85
avg.	16	3312	−766.03	14	3668	−746.64	15	3206	−766.25	16	2714	−753.3

suggests that algorithms P-V and P-VII were suitable for finding the global optimum in the adjustments. The value of the smallest objective function was determined by algorithm P-VIII, and yet performance of algorithm P-VII was best by far in terms of average values. It proved the most precise procedure out of the algorithms investigated. Concerning the results of running this algorithm, it reached the objective function value $E{\left({\mathit{d}}_{opt}\right)}_{SVM}<-772 {\mathrm{kN}}^2$ during the 2319 iteration, even in the worst case. It is worth noting that the random number generated with a standard deviation $\sigma =0.5 \mathrm{mm}$ after 4000 iterations means a too large a search space near-global optimum, as the algorithm only managed to find a better function value only after one case of being run.

3.6. Direct Optimization by Running the Parameterized Finite Element Model

The main goal of this section is to run directly the local stochastic search algorithm trained on the parameterized finite element model created for shape optimization. For adjustments of the algorithm based on cases of it being run in the previous section, see

Table 8. Adjustment of local stochastic search algorithm by tightening search space.

	P-IX
iteration number start, $m_{start}$	1	2001
iteration number stop, $m_{stop}$	2000	3000
standard deviation, $\sigma \left(1\right) \left(\mathrm{mm}\right)$	30	0.5
standard deviation, $\sigma \left(2\right) \left(\mathrm{mm}\right)$	30	0.5

.

Table 9. Better function values accepted by P-IX adjusted local search algorithm.

$\mathit{m}$	${\mathit{D}}_1\left(\mathbf{mm}\right)$	${\mathit{D}}_2\left(\mathbf{mm}\right)$	$\mathit{E}{\left(\mathit{D}\right)}_{\mathit{F}\mathit{E}\mathit{A}}$
0	73.237	36.540	14624.63333
1	76.240	20.204	9106.38117
2	90.939	42.385	7081.81690
3	119.767	46.106	603.32863
4	105.709	37.932	482.39861
6	114.168	38.937	249.21546
18	108.312	32.409	8.77936
89	119.990	54.945	3.30837
204	115.371	46.689	2.16783
338	109.392	35.507	0.54223
410	106.942	30.752	0.06769
1056	108.970	34.950	0.03469
2073	108.861	34.704	0.03287
2158	108.738	34.448	0.02950
2178	108.562	34.174	0.01972
2202	108.511	34.070	0.01649
2219	108.338	33.685	0.00402
2307	107.900	32.816	0.00258
2373	107.966	32.937	0.00025

includes better function values and their geometry variable values accepted by the algorithm, while Figure 7 visualizes the path done by the algorithm. Based on the results of it being run, we managed to find an appropriate environment for the global optimum when the function was run 3000 times. Based on the results, the objective function values were equal until three decimals were reached, even when the variables were within one decimal to the known optimum value. The effect of tightening search space coincided with what was experienced with the surrogate model. The optimum found by the algorithm occurred in the $m=2373$ iteration, which involves the fact that the random number generated with the $\sigma =0.5 \mathrm{mm}$ standard deviation meant a search space that was too large while on the way to a global optimum.

Optimal variable values found by the basic adjustment local search methods were compared with ones found by the local search method trained on surrogate models, and they were related to optimal design variable values (

Table 10. Calculated cost function values in different design points.

	$\mathit{m}$	${\mathit{D}}_1\left(\mathbf{mm}\right)$	${\mathit{D}}_2\left(\mathbf{mm}\right)$	$\mathit{E}{\left({\mathit{D}}_{\mathit{o}\mathit{p}\mathit{t}}\right)}_{\mathit{F}\mathit{E}\mathit{A} }\left(\mathbf{k}{\mathbf{N}}^2\right)$
Optimum Shape		108	33	0
Stochastic Search	5000	109.184	35.372	0.051
Stochastic Search, P-IX	3000	107.966	32.937	0.00025

). Regarding the results, the algorithm adjusted by P-IX was several orders of magnitude more precise in determination of the objective function value, even with a lower iteration number.

4. Conclusions

Foremost, the axisymmetric finite element model for the compression test of the automotive rubber bumper was built with the use of a calibrated two-term Mooney–Rivlin material model. A two-dimensional shape optimization problem was introduced where the objective function was determined as the difference between the initial characteristics and the optimum characteristics. As a metamodeling technique, SVM was selected and 22 support vectors were supported for the training process, which proved to be enough. Using the trained cubic SVM model, predictions were made for each combination of integer values of design variables. Based on the results, the SVR model with a cubic kernel function was found to be suitable to accurately predict the nonlinear objective function in case of rubber bumper engineering design. Running the trained SVM model required a lot less calculation than the finite element model, so the right adjustment of the stochastic search method parameters happened on this surrogate model. The method described above (surrogate model-based parameter selection of the optimization algorithm) was suitable for determining the local search algorithm parameters by running 22 extra functions. The algorithm adjusted in this way was more suitable for determining the objective function values, despite being run 2000 times less frequently than the optimization run at basic adjustment. The algorithm was capable of carrying out similar tasks without human interaction to determine the optimum, while in other cases readjustment of parameters might be justified. Owing to the opportunity of axisymmetric simplification, the running time of the finite element model only took 25 s on an Intel Core i5-8250U CPU. This computational need with 3000 iterations is below 21 h. This time allows a design engineer to solve axisymmetric two-variable rubber shape optimization tasks.

The introduced optimization process can be implemented in design practice relatively simply. The results can be obtained in an engineering sense, with accuracy and calculation efficiency; therefore, the applicability can be considered by other researchers. The SVR model-based parameter selection is a relatively new method that can be automated, thus it can be a useful tool for engineers. The algorithm with the adjusted parameters can be used directly in the shape optimization of rubber bumpers.