Mutation Rate Model Used in the DNA VIEW Program

Abstract

The first problem considered in this paper is the problem of correctness of a mutation model used in the DNA VIEW program. To this end, we theoretically predict population allele frequency changes in time according to this and similar models (we determine the limit frequencies of alleles—they are uniformly distributed). Furthermore, we evaluate the speed of the above changes using computer simulation applied to our DNA database. Comparing uniformly distributed allele frequencies with these existing in the population (for example, using entropy), we conclude that this mutation model is not correct. The evolution does not follow this direction (direction of uniformly distributed frequencies). The second problem relates to the determination of the extent to which an incorrect mutation model can disturb DNA VIEW program results. We show that in typical computations (simple paternity testing without maternal mutation) this influence is negligible, but in the case of maternal mutation, this should be taken into account. Furthermore, we show that this model is inconsistent from a theoretical viewpoint. Equivalent methods result in different error levels.

1. Introduction

Nowadays, DNA polymorphism is widely used in genetic expertise for fixing biological paternity and consanguinity of people. Results of DNA profiling are based on probabilistic and statistical interpretation. This interpretation leads to obtaining the probability of paternity or another relationship determined by Bayesian analysis (likelihood ratio). This probability depends on three factors:

(i)

a priori probability (usually assumed to be equal to 0.5),

(ii)

allele frequencies (main factor), and

(iii)

mutation rate.

The last factor, i.e., mutation rate, is usually small, but in some situations essential. From a viewpoint of population, mutation is the primary generator of genetic diversity, whereas drift tends to reduce the genetic diversity. Most of the human genome has a very low mutation rate: for a typical nucleotide site $\omega =2\times {10}^{-8}$ (the probability that a mutation will occur during gene transmission from a parent to a child). Short Tandem Repeat (STR) (also known as a microsatellite) mutation rates are even higher (approximately 1 or 2 mutations per locus per thousand generations). However, the key problem is that statistical analysis of the observed mutation cases is therefore almost impossible, because there is not a sufficient amount of observations (cf. [1,2]). Some observations suggest taking the Stepwise Mutation Model (SMM; cf. [3,4,5]) in which a mutant allele has either $k-1$ or $k+1$ repeats, each with a probability of $\frac{1}{2},$ where k is the current repeat number. The SMM is known to be false because the mutation rate increases with allele length and occasionally two-step mutations occur. In [6,7,8], other defects of the SMM are shown.

Like the Mendel law, the Hardy–Weinberg hypothesis (sometimes called Hardy–Weinberg model/equilibrium/theorem/state of balance) is one of well known genetic laws. The Hardy– Weinberg model describes the genotype and allele frequencies in a non-evolving population. This model has seven basic assumptions (cf. [9,10]):

• organisms are diploid;
• only sexual reproduction occurs;
• generations are nonoverlapping;
• mating is random;
• population size is infinitely large;
• each sex has the same allele frequencies;
• there is no migration, gene flow, admixture, mutation, and selection.

Despite these assumptions, as we show below, there exist mutation models (Model 4) in which the Hardy–Weinberg hypothesis holds. Given these assumptions, the population’s genotypes and allele frequencies remain unchanged over successive generations, and the population is said to be in the Hardy–Weinberg equilibrium (cf. [11]). In practice, if we consider loci with $\{A_1,A_2,\dots A_k\}$ possible alleles and we observe the frequencies of a pair of alleles $(A_i,A_j)$ in the population $P_{i,j},1\le i\le j\le k,$ then the good approximation (as the right-hand side values are estimated only from our database sample, and, as a consequence, these values in the whole population can slightly differ) of allele frequencies is

$$p_i\approx \sum _{1\le j\le k,j\ne i}{P}_{i,j}+2P_{i,i},1\le i\le k.$$

(1)

The Hardy–Weinberg equilibrium can be stated as

$$P_{i,j}\approx \left\{\begin{array}{cc}{p}_i^2,\hfill & \mathrm{if} i=j,\hfill \\ 2p_i{p}_j,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.1\le i\le j\le k.$$

(2)

The above approximation is usually (cf. [12] Chapter 3 and [13] Section 3.2) verified by Pearson’s ${\chi }^2$ goodness-of-fit test (cf. [14,15], here arises the problem of rare alleles whose frequencies must be bound together), Fisher’s exact test [16,17,18], or the likelihood ratio test or permutation test (known as the G-test, cf. [19]). Large deviations from the Hardy–Weinberg equilibrium are a consequence of errors in the STR amplification procedure, whereas the small ones follow from the departure from the above assumptions.

In most genetic laboratories, the interpretation of forensic investigations is obtained as a result of computations of Brenner’s DNA VIEW computer program [20,21]. In this paper, we concentrate on the considerations of the consequences of the mutation model used in this program which is a generalization of the SMM model in three aspects:

• The problem of satisfying the Hardy–Weinberg hypothesis and some mathematical inconsistency as a consequence of the assumed mutation model
• Paternity testing application. We show that in some cases the assumed different mutation models affect different paternity results (exclusion or acceptance of a putative father).
• The influence of the assumed mutation model on the long-time simulations of a population’s behavior.

The aspect of satisfying the Hardy–Weinberg hypothesis is essentially theoretical, whereas the other two are numeric. The considered models are described in Section 2; the materials and methods are described in Section 3; Section 4, Section 5 and Section 6 are devoted to Problems 1, 2, and 3, respectively; whereas the last section presents conclusions.

Our considerations are similar to those presented in [22]. The main differences are

(i)

they consider similar but not the same mutation models;

(ii)

they state nonstationarity on the basis of the computation of allele frequencies in the consecutive generations, whereas we give a mathematical proof of this assertion;

(iii)

they state some problems in the case of paternity testing, we evaluate them;

(iv)

we focus on some mathematical inconsistency, which they do not deal with; and

(v)

we consider the behavior of a population under the assumed mutation model in the long distance of sequential generations, while they do not consider this problem.

Thus, our approach is wider and deeper than that taken in [22].

2. Materials and Methods

All computations were performed using large database of allelic DNA frequencies obtained from the Medical University of Lublin. This database contains DNA results of 7076 individuals, including personal information such as names, dates, places of birth etc. From this database we took 4410 unrelated persons and computed the distribution of allele frequencies of this sample (for example

Table 1. Allele (indicated by the number of gene repetition); $n_i$ frequencies; $v_i$ at the D5S818 locus $N=17,$ ${\omega }_M=0.00025, {\omega }_F=0.0012, \omega =0.0011$ (cf. [24]).

i	${\mathit{n}}_{\mathit{i}}$	${\mathit{\nu }}_{\mathit{i}}$	i	${\mathit{n}}_{\mathit{i}}$	${\mathit{\nu }}_{\mathit{i}}$	i	${\mathit{n}}_{\mathit{i}}$	${\mathit{\nu }}_{\mathit{i}}$
1	9	$0.00022$	7	15	$0.15693$	13	20	$0.02359$
2	10	$0.00730$	8	16	$0.17187$	14	21	$0.00999$
3	11	$0.01404$	9	17	$0.13188$	15	22	$0.00550$
4	12	$0.09717$	10	$17.3$	$0.00011$	16	23	$0.00157$
5	13	$0.09998$	11	18	$0.08324$	17	24	$0.00056$
6	14	$0.15850$	12	19	$0.03752$

presents the frequencies for the D5S818 locus). Three-thousand-nine-hundred-and-seventy-three individuals were typed using the classical electrophoresis method and 437 by NGS (next generation sequencing). All individuals were genotyped within 17 STR (short tandem repeat) markers located on the autosomal chromosomes. The techniques of DNA amplification are well described in Butler’s book [23] in Section 1.

The loci of 3973 individuals were amplified using commercial kits: PowerPlex 16Hs System and PowerPlex 17ESX System (Promega Corporation, Madison, WI, USA). PCR products were separated and detected on the ABI 3130 Genetic Analyzer (Applied Biosystems, Foster City, CA, USA). Data were analyzed with the Gene Mapper ID software (v3.2, Applied Biosystems, Foster City, CA, USA, 2005). Laser-induced fluorescence was used in CE systems (Capillary Electrophoresis) with detection (by sensors) as low as ${10}^{-18}$ to ${10}^{-21}$ mol. The sensitivity of the techniques is attributed to the high intensity of incident light and the ability to accurately focus the light on the capillary. Multi-color fluorescence detection can be achieved by including multiple dichroic mirrors and bandpass filters to separate the fluorescence emission among multiple detectors (e.g., photomultiplier tubes) or by using a prism or grating to project spectrally resolved fluorescence emission onto a position-sensitive detector (sensor) such as a CCD (Charge Coupled Device) array. CE systems with 4- and 5-color LIF (Laser-Induced Fluorescence) detection systems are used routinely for capillary DNA sequencing and genotyping (DNA fingerprint) applications.

The 437 individuals were profiled by next-generation sequences (NGS). Libraries were prepared using the ForenSeq DNA Signature Prep. Kit (Illumina) according to the manufacturer’s protocol. Sequencing was performed on MiSeq FGx using the Miseq FGx Reagent Kit v.3 (600 cycles) and the ForenSeq Universal Analysis Software package. Following cluster generation, clusters were imaged using LED and filter combinations specific to each of four fluorescently labeled dideoxynucleotides. After the imaging of a tile was complete, the flow cell was moved into place to expose the nest tile. The process was repeated for each cycle of sequencing. Following image analysis, the software performed base calling, filtering, and quality scoring.

All amplification results were stored in a database. All computations were performed in the R-3.6.0 language on a RSTUDIO platform (v1.2.1335, RStudio, Boston, MA, USA, 2019).

The starting point for our considerations is the following allele frequencies table (for example, for locus $D5S818$).

Here, and in what follows, N denotes the number of alleles; $n_i$ denotes the number of gene repetitions; i denotes the number of alleles; and ${\omega }_M,{\omega }_F,\omega ,v_i$ denote the maternal, paternal, and overall mutation rate and the frequency of i-th allele, respectively. It is worthwhile to remark that $n_i$ is not a number but rather a name ($17.3$ means, 17 full repetitions of gene, and 3 additional pairs of alkali), but throughout the paper, as in [20,21], we will consider $n_i$ as a number.

3. Mutation Models

Throughout this paper, the notation $(i\to j)$ means allele i was given by parents and arises as allele j in descendant. Although the maternal and the paternal mutations are generally different, we do not take this aspect into account, therefore we do not specify how the parent gives allele i.

Some assumptions (usually assumed) on equal chance of every allele to be transmitted are fulfilled too. Depending on whether mutation takes place or not, the following formula is used to describe the transmission of alleles,

$$(i\to j)=\left\{\begin{array}{cc}1-\omega +\omega {\omega }_{i,i},\hfill & 1\le i=j\le N,\hfill \\ \omega {\omega }_{i,j},\hfill & 1\le i,j\le N,i\ne j,\hfill \end{array}\right.$$

(3)

where ${\omega }_{i,j},1\le i,j\le N$ indicates how frequently i mutates into j, provided that i mutates. The different mutation models are derived from a different evaluation of ${\omega }_{i,j},1\le i,j\le N.$ The value ${\omega }_{i,i}$ means that there was mutation, but the number of gene repetition does not change (it is almost not possible to determine this value from observations). Historically, two models were considered:

Model 1.

$${\omega }_{i,j}=\frac{1}{N}.$$

(4)

Model 2.

$${\omega }_{i,j}=\left\{\begin{array}{cc}\frac{1}{N-1},\hfill & 1\le i,j\le N,i\ne j,\hfill \\ 0,\hfill & 1\le i=j\le N.\hfill \end{array}\right.$$

(5)

In the description of the DNA VIEW program (Mutation model implemented in DNA VIEW [20]), one can read the following.

Rule A.

Therefore, as a rule of thumb, I suggest assuming that

50% of all mutations increase by one step

50% decrease by one step

5% increase by two steps

5% decrease by two steps

0.5% increase by three steps

0.5% decrease by three steps

… etc.

Never mind that these numbers add to more than 100%.

This description leads us to the following model of mutation.

Model 3.

$${\omega }_{i,j}=\left\{\begin{array}{cc}\frac{{10}^{\lfloor -|n_i-n_j|\rfloor }}{{\alpha }_i},\hfill & 1\le i,j\le N,i\ne j,\hfill \\ 0,\hfill & 1\le i=j\le N,\hfill \end{array}\right.$$

(6)

where

$${\alpha }_i=\sum _{\genfrac{}{}{0pt}{}{1\le j\le N}{j\ne i}}{10}^{\lfloor -|n_i-n_j|\rfloor },1\le i\le N.$$

(7)

Previously, in the case of Variable Number of Tandem Repeat (VNTR) investigations, the most popular model of mutation was

Model 4.

$${\omega }_{i,j}={\nu }_j,1\le i,j\le N.$$

(8)

What assumptions should the mutation model satisfy? At first, we remark that a correctly defined mutation model should be such that

$${\forall }_{1\le i\le N}\sum _{j=1}^N(i\to j)=1,$$

(9)

because the i-th allele must be transmitted “to somebody”. On the other hand, the second condition deals with the allele frequencies in parent and child populations. At first, allele j has the frequencies ${\nu }_j$, whereas after transmission, it has the frequency ${\sum }_{i=1}^N(i\to j){\nu }_i.$ Thus, we have

$${\forall }_{1\le j\le N}\sum _{i=1}^N(i\to j){\nu }_i={\nu }_j.$$

(10)

The last condition is a formulation of the Hardy–Weinberg hypothesis described in the Introduction.

Using (3), these conditions can be formulated in an equivalent form:

Condition I.

$${\forall }_{1\le i\le N}\sum _{j=1}^N{\omega }_{i,j}=1,$$

(11)

Condition II.

$${\forall }_{1\le j\le N}\sum _{i=1}^N{\omega }_{i,j}{\nu }_i={\nu }_j.$$

(12)

Furthermore, it is easy to check that in some models (1 and 4) the computed total mutation is not equal to the observed $\omega$. In Model 1 it is $(1-\frac{1}{N})\omega$ and for the i-th allele in Model 4 $(1-{\nu }_i)\omega$ (instead of $\omega$ in both cases). This is a small disturbance in the observed mutation rate.

4. Hardy–Weinberg Equilibrium

In this section, we consider how the above mutation models satisfy conditions I and II (Hardy–Weinberg hypothesis).

Theorem 1.

Let us consider the sequence of positive numbers $\{{\alpha }_i,1\le i\le N\}$ and the array of non-negative numbers $\{{\beta }_{i,j},1\le i,j\le N\}$ such that

(i) 

${\beta }_{i,j}>0,{\beta }_{i,i}\ge 0,1\le i\ne j\le N,$

(ii) 

${\beta }_{i,j}={\beta }_{j,i},1\le i,j\le N,$

(iii) 

${\alpha }_i={\sum }_{j=1}^N{\beta }_{i,j}={\sum }_{j=1}^N{\beta }_{j,i},1\le i\le N.$

Let us define a matrix

$$A_N=\left[\begin{array}{ccccc}-{\alpha }_1+{\beta }_{1,1}\hfill & {\beta }_{1,2}\hfill & {\beta }_{1,3}\hfill & \dots \hfill & {\beta }_{1,N}\hfill \\ {\beta }_{2,1}\hfill & -{\alpha }_2+{\beta }_{2,2}\hfill & {\beta }_{2,3}\hfill & \dots \hfill & {\beta }_{2,N}\hfill \\ {\beta }_{3,1}\hfill & {\beta }_{3,2}\hfill & -{\alpha }_3+{\beta }_{3,3}\hfill & \dots \hfill & {\beta }_{3,N}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ {\beta }_{N,1}\hfill & {\beta }_{N,2}\hfill & {\beta }_{N,3}\hfill & \dots \hfill & -{\alpha }_N+{\beta }_{N,N}\hfill \end{array}\right],$$

(13)

then $rank\left(A_N\right)=N-1.$

Proof of Theorem 1.

Let $A_k,1\le k\le N$ denote the k-th main minor of the matrix $A_N.$ Assume contrary that $det\left(A_k\right)=0$ for some $1\le k<N$ (cf. Exercise 11 (e) p. 48 [25]). It means that there exist numbers ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{k-1}$ such that

$$\sum _{i=1}^{k-1}\left|{\lambda }_i\right|>0,$$

(14)

and

$$v_k=\sum _{i=1}^{k-1}{\lambda }_i{v}_i,$$

(15)

where $v_i$ denotes the i-th column of the matrix $A_k$. It can be rewritten (after renaming rows and columns in the minor) precisely as

$$\left\{\begin{array}{ccc}{\beta }_{k,1}\hfill & =\hfill & (-{\alpha }_1+{\beta }_{1,1}){\lambda }_1+{\beta }_{1,2}{\lambda }_2+\dots +{\beta }_{1,k-1}{\lambda }_{k-1},\hfill \\ {\beta }_{k,2}\hfill & =\hfill & {\beta }_{2,1}{\lambda }_1+(-{\alpha }_2+{\beta }_{2,2}){\lambda }_2+\dots +{\beta }_{2,k-1}{\lambda }_{k-1},\hfill \\ ⋮\hfill & \hfill & ⋮\hfill \\ -{\alpha }_k+{\beta }_{k,k}\hfill & =\hfill & {\beta }_{k,1}{\lambda }_1+{\beta }_{k,2}{\lambda }_2+\dots +{\beta }_{k,k-1}{\lambda }_{k-1}.\hfill \end{array}\right.$$

(16)

Among the numbers ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{k-1}$ there are positive and non-positive ones. By $I_1$ we denote a set of positive numbers. This set is nonempty. Indeed, if $I_1=\varnothing ,$ then summing up both sides of (16), we get

$$-{\alpha }_k+\sum _{i=1}^k{\beta }_{k,i}=\sum _{j=1}^{k-1}(-{\alpha }_j+\sum _{i=1}^k{\beta }_{i,j}){\lambda }_j,$$

(17)

and on the left-hand side we have a negative number, whereas on the right hand side it is non-negative.

Let t be an index of the maximal ${\lambda }_i$ (if there is more than one such index, we take the smallest one),

$$t=min\{i:{\lambda }_i=\underset{j}{max}{\lambda }_j\}.$$

(18)

Then, taking the t-th equation in (16), we get

$${\beta }_{k,t}=(-{\alpha }_t+{\beta }_{t,t}){\lambda }_t+\sum _{i<k,i\ne t}{\beta }_{t,i}{\lambda }_i\le (-{\alpha }_t+\sum _{i=1}^{k-1}{\beta }_{t,i}){\lambda }_t$$

(19)

and we have a positive number on the left-hand side of the above inequality and a non-positive number on its right-hand side. Thus, this contradiction leads us to $det\left(A_k\right)\ne 0,$ for every $1\le k<N.$

Now we prove that $det\left(A_N\right)=0$. It follows from assumption (iii) which can be rewritten as

$$\left\{\begin{array}{ccc}-{\beta }_{N,1}\hfill & =\hfill & -{\alpha }_1+{\beta }_{1,1}+{\beta }_{1,2}+\dots +{\beta }_{1,N-1},\hfill \\ -{\beta }_{N,2}\hfill & =\hfill & {\beta }_{2,1}+-{\alpha }_2+{\beta }_{2,2}+\dots +{\beta }_{2,N-1},\hfill \\ ⋮\hfill & \hfill & ⋮\hfill \\ {\alpha }_N-{\beta }_{N,N}\hfill & =\hfill & {\beta }_{N,1}+{\beta }_{N,2}+\dots +{\beta }_{N,N-1}.\hfill \end{array}\right.$$

(20)

□

Corollary 1.

(p. 62 in [26] or Definitions 7.1.2 and 7.1.4 and Theorem 7.1.3 in [27]) Let $A_N$ be a matrix satisfying the assumptions of Theorem 1. Let the matrix $A_N^{\prime }$ be obtained from $A_N$ by multiplying the rows of $A_N$ by positive numbers possibly different for different rows. Then,

$$rank\left(A_N^{\prime }\right)=N-1.$$

(21)

The same result can be obtained if we multiply columns instead of rows.

Corollary 2.

Mutation models 1–3 satisfy Condition I, but Condition II is only satisfied when ${\bigwedge }_{1\le i\le N}{\nu }_i=\frac{1}{N}.$ Mutation model 4 always satisfies both conditions.

Proof of Corrollary 2.

Let us consider the following matrices.

$$A_N^{\left(1\right)}=\left[\begin{array}{ccccc}\frac{1}{N}\hfill & \frac{1}{N}\hfill & \frac{1}{N}\hfill & \dots \hfill & \frac{1}{N}\hfill \\ \frac{1}{N}\hfill & \frac{1}{N}\hfill & \frac{1}{N}\hfill & \dots \hfill & \frac{1}{N}\hfill \\ \frac{1}{N}\hfill & \frac{1}{N}\hfill & \frac{1}{N}\hfill & \dots \hfill & \frac{1}{N}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ \frac{1}{N}\hfill & \frac{1}{N}\hfill & \frac{1}{N}\hfill & \dots \hfill & \frac{1}{N}\hfill \end{array}\right],A_N^{\left(2\right)}=\left[\begin{array}{ccccc}0\hfill & \frac{1}{N-1}\hfill & \frac{1}{N-1}\hfill & \dots \hfill & \frac{1}{N-1}\hfill \\ \frac{1}{N-1}\hfill & 0\hfill & \frac{1}{N-1}\hfill & \dots \hfill & \frac{1}{N-1}\hfill \\ \frac{1}{N-1}\hfill & \frac{1}{N-1}\hfill & 0\hfill & \dots \hfill & \frac{1}{N-1}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ \frac{1}{N-1}\hfill & \frac{1}{N-1}\hfill & \frac{1}{N-1}\hfill & \dots \hfill & 0\hfill \end{array}\right],$$

(22)

and

$$A_N^{\left(3\right)}=\left[\begin{array}{ccccc}0\hfill & \frac{{10}^{\lfloor -|n_1-n_2|\rfloor }}{{\alpha }_{n_1}}\hfill & \frac{{10}^{\lfloor -|n_1-n_3|\rfloor }}{{\alpha }_{n_1}}\hfill & \dots \hfill & \frac{{10}^{\lfloor -|n_1-n_N|\rfloor }}{{\alpha }_{n_1}}\hfill \\ \frac{{10}^{\lfloor -|n_2-n_1|\rfloor }}{{\alpha }_{n_2}}\hfill & 0\hfill & \frac{{10}^{\lfloor -|n_2-n_3|\rfloor }}{{\alpha }_{n_2}}\hfill & \dots \hfill & \frac{{10}^{\lfloor -|n_2-n_N|\rfloor }}{{\alpha }_{n_2}}\hfill \\ \frac{{10}^{\lfloor -|n_3-n_1|\rfloor }}{{\alpha }_{n_3}}\hfill & \frac{{10}^{\lfloor -|n_3-n_2|\rfloor }}{{\alpha }_{n_3}}\hfill & 0\hfill & \dots \hfill & \frac{{10}^{\lfloor -|n_3-n_N|\rfloor }}{{\alpha }_{n_3}}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ \frac{{10}^{\lfloor -|n_N-n_1|\rfloor }}{{\alpha }_{n_N}}\hfill & \frac{{10}^{\lfloor -|n_N-n_2|\rfloor }}{{\alpha }_{n_N}}\hfill & \frac{{10}^{\lfloor -|n_N-n_3|\rfloor }}{{\alpha }_{n_N}}\hfill & \dots \hfill & 0\hfill \end{array}\right].$$

(23)

Now, if $v_o$ denotes the vector of allele frequencies of parents’ population, then Condition II (Hardy–Weinberg hypothesis) can be rewritten as

$$(A_N^{\left(k\right)}-I_N)v_o=0,k=1,2,3,$$

(24)

where $I_N$ denotes the $N\times N$ unit matrix. From Corollary 1 we have $rank(A_N^{\left(k\right)}-I_N)=N-1,k=1,2,3.$ Thus, the subspace of solutions of $A_N^{\left(k\right)}x=x,k=1,2,3$ is one-dimensional. On the other hand, it is easy to see that the vector ${\overline{v}}_N={[\frac{1}{N},\frac{1}{N},\dots ,\frac{1}{N}]}^T$ satisfies $A_N^{\left(k\right)}{\overline{v}}_N={\overline{v}}_N,k=1,2,3,$ thus it is a unique solution (among the vectors with non-negative coordinates such that ${\left|\right|x\left|\right|}_{l_1}=1$). □

Theorem 2.

Let us define the sequence of vectors $\{v_k,k\ge 1\}$ by

$$v_{k+1}=\left((1-\omega )I_N+\omega A_N^{\left(i\right)}\right)v_k=T_i{v}_k,k=0,1,2,\dots ,i=1,2,3,$$

(25)

where $v_o$ denotes the vector of starting allele frequencies in some loci, N is the number of alleles, and $i=1,2,3$ is the selected model of mutations ($v_k$ denotes the frequencies of alleles in the k-th population applying the i-th model of mutation). Then,

$$\underset{k\to \infty }{lim}{T}_i^k{v}_o=\underset{k\to \infty }{lim}(\underset{ktimes}{\underbrace{T_i\circ T_i\circ \dots \circ T_i}})v_o=\underset{k\to \infty }{lim}{v}_k={\overline{v}}_N,i=1,2,3.$$

(26)

Proof of Theorem 2.

Let us consider the Banach space ${\Re }^N$ with the norm ${\left|\right|x\left|\right|}_{l_1}={\sum }_{i=1}^N\left|x_i\right|$. Furthermore, let $K=\{x\in {\Re }^N:|\left|x\right|{|}_{l_1}=1,0\le x_i\le 1,i=1,2,3,\dots ,N\}$ be a compact, separable subset of the space ${\Re }^N.$ Obviously, the fixed point of the mapping $T_i$ on K is the same as the fixed point of $A_N^{\left(i\right)}$ and from Corollary 3 this point is ${\overline{v}}_N.$ The mapping $T_i$ is not a contraction because $\left|\right|T_1\left|\right|=\left|\right|A_N^{\left(i\right)}\left|\right|=1,$ as the matrix $T_i$ consists of non-negative numbers such that their sums are equal to 1 in each row and each column. The norm is achieved for an arbitrary vector x with ${\left|\right|x\left|\right|}_{l_1}=1$ and all non-negative or all non-positive coordinates. Thus, we cannot apply the Banach Contraction Theorem. However, Theorem 9.4 (and Corollary 9.1) in [28] considers the matrix such as $T_i$. As a conclusion we get a thesis. □

More information about the determinants and algebra of matrices can be found in [29,30].

5. Mutation Models and Paternity Testing

Let us denote unordered pairs $P=\{p_1,p_2\},M=\{m_1,m_2\},D=\{d_1,d_2\}$ of alleged paternal, maternal, and child’s STR profile, respectively, ($V=\{P,D,M\}$). As usual in paternity testing, we consider two hypotheses:

Hypothesis 1

($H_1$). Man P is a father of D assuming that M is a mother of D.

Hypothesis 2

($H_2$). A man different than P is a father of D assuming that M is a mother of D.

Now, from the Bayesian formula we get

$$P\left[H_1\right|V]=\frac{1}{1+\frac{P\left[V\right|H_2]}{P\left[V\right|H_1]}\frac{P\left[H_2\right]}{P\left[H_1\right]}},$$

(27)

and by putting a priori probabilities equal to $0.5$ we obtain

$$P\left[H_1\right|V]=\frac{1}{1+\frac{P\left[V\right|H_2]}{P\left[V\right|H_1]}},$$

(28)

(for more details of the computations see [10,23,31,32]).

However, the computed probability depends on the mutation model (we will write $P_i\left[V\right|H_1],i=1,2,3,4$). Thus, we compute

$${\rho }_{i,j}=|P_i\left[H_1\right|V]-P_j\left[H_1\right|V]|,1\le i<j\le 4.$$

(29)

The frequency of each result V is a frequency of alleles P and M and from Mendel’s law, the probability of achieving from such a pair of parents the child’s profile D (it also depends on a mutation, but the differences are negligible). We consider two different situations:

• Maternal mutation situation, i.e., when $\{m_1,m_2\}\cap \{d_1,d_2\}=\varnothing .$
• Without maternal mutation when $\{m_1,m_2\}\cap \{d_1,d_2\}\ne \varnothing .$

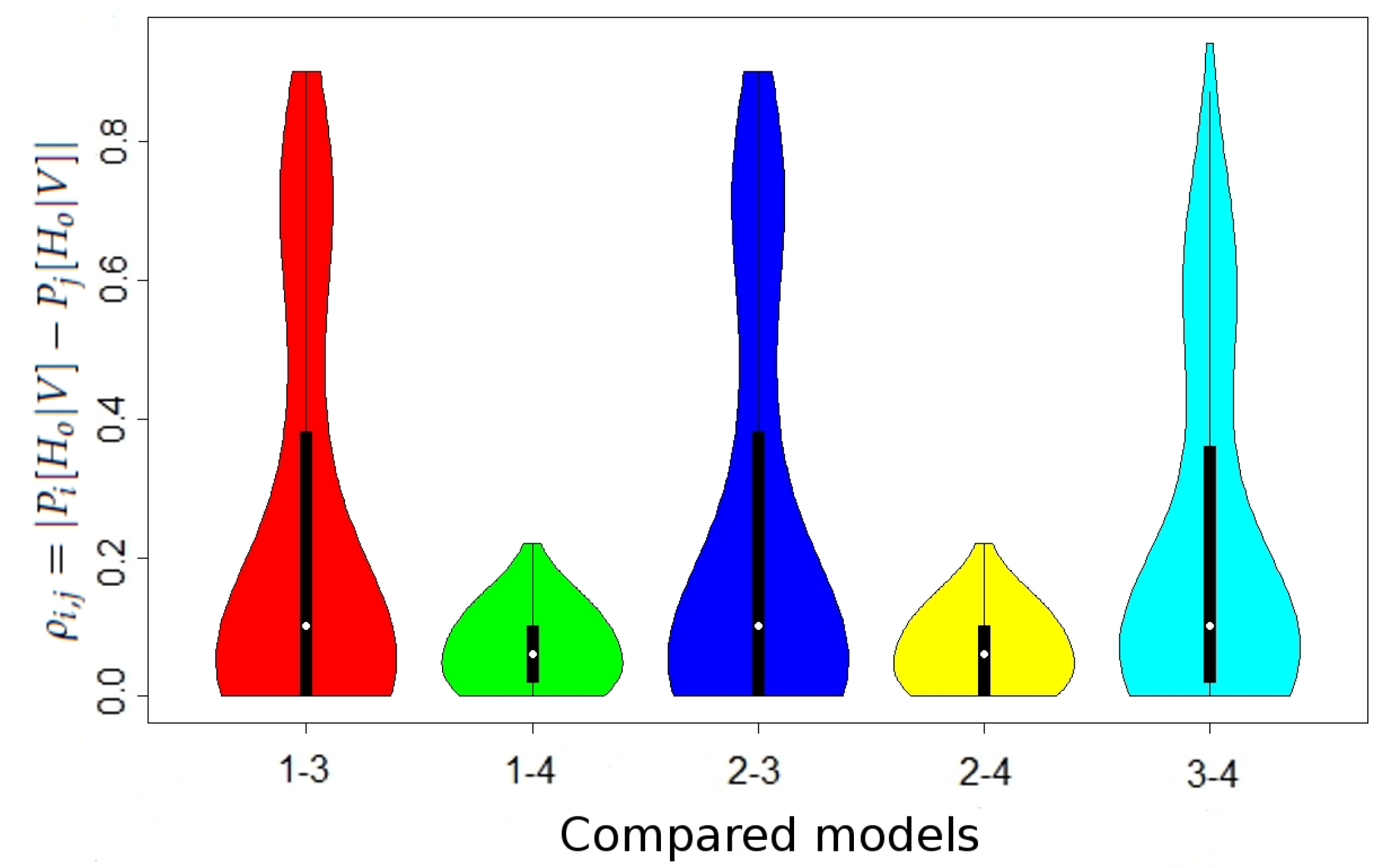
We show the maximal values of ${\rho }_{i,j}$ in

Table 2. Maximal difference of probability of paternity values between i-th and j-th model (${\rho }_{i,j}$) in two cases: with maternal mutation and without it, at the D5S818 locus.

	Maternal Mutation			No Maternal Mutation
	Model 2	Model 3	Model 4	Model 2	Model 3	Model 4
Model 1	0.00003	0.9977	0.4237	0.00003	0.0005	0.0003
Model 2		0.9977	0.4237		0.0005	0.0003
Model 3			0.9985			0.0006

and the distribution of ${\rho }_{i,j}$ in Figure 1 (the differences in the case without maternal mutation between all models and in the case when maternal mutation takes place between Models 1 and 2 were lower than $0.02$, thus negligible).

For example, the maximal value $0.9985$ was achieved for $P=(15,15),D=(7,15),M=(14,14).$ In this case, we have the overall mutation rate $\omega =0.001,$ and the frequencies of alleles $7,14,$ and 15 are equal to $0.002718,0.009399,$ and $0.000566,$ respectively. Thus, we have the

Table 3. Probability that we achieve DNA profiles V, providing man P is a father of D ($P\left[V\right|H_1]$), probability that we achieve DNA profiles V, providing P is not a father of D ($P\left[V\right|H_2]$), and probability that P is a father of D ($P\left[H_1\right|V]$) in the case of $(P,D,M)=\left(\right(15,15),(7,15),(14,14\left)\right)$ at locus D5S818.

Value	Model 1	Model 2	Model 3	Model 4
$P\left[V\right|H_1]$	$2.8308\times {10}^{-15}$	$3.1450\times {10}^{-15}$	$1.2801\times {10}^{-20}$	$7.6925\times {10}^{-17}$
$P\left[V\right|H_2]$	$9.3044\times {10}^{-18}$	$1.0338\times {10}^{-17}$	$3.4825\times {10}^{-17}$	$8.7205\times {10}^{-20}$
$P\left[H_1\right|V]$	$0.9967239$	$0.9967236$	$0.0003674$	$0.9988676$

.

The above result follows from the fact that in the case of Model 3, allele 15 is significantly more likely to be a mutation of allele 14 than a transfer from a putative father.

Finally, we verify some remarks on the inconsistency of theoretical equations and their practical application. Let $P(p,s)$ be the probability that two alleles p and s are transferred from the same allele (they are brothers). Then, we have

$$P(p,s)=\left\{\begin{array}{cc}{(1-\omega )}^2\ast {\nu }_s,\hfill & \mathrm{if} p=s,\hfill \\ (1-{(1-\omega )}^2){\nu }_s{\nu }_p,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(30)

but, on the other hand, we have

$$P(p,s)=\sum _t(t\to p)(t\to s){\nu }_t.$$

(31)

In the formula (31), the assumed mutation model plays an important role, whereas in (30), only the overall mutation rate $\omega$ is important. The maximal differences for locus $D5S818$ between the values computed using these formulas for different p and s are equal to $0.000172,0.000164,$ and $0.000123$, and for the same $p=s=12$, are equal to $0.000197,0.000271,$ and $0.000271$ for Models 1, 2, and 3, respectively. Model 4 always gives an error of 0. All of them are small, smaller than the mutation rate. Which equation should be chosen by the investigator? With very complicated computations, this difference may become considerable. What about other similar situations?

6. Speed of Convergence of Allele Frequencies

Obviously, the speed of convergence depends on the matrix $A_N^{\left(i\right)},i=1,2,3,$ the starting point $v_o$, and the number of alleles. We measure the speed of convergence by the entropy of frequencies in a population’s sequential generations. By entropy we denote

$$H_k^{\left(i\right)}=-{\nu }_1^{\left(k\right)}{log}_2{\nu }_1^{\left(k\right)}-{\nu }_2^{\left(k\right)}{log}_2{\nu }_2^{\left(k\right)}-\dots -{\nu }_N^{\left(k\right)}{log}_2{\nu }_N^{\left(k\right)},$$

(32)

where $v_k={[{\nu }_1^{\left(k\right)},{\nu }_2^{\left(k\right)},{\nu }_3^{\left(k\right)},\dots ,{\nu }_N^{\left(k\right)}]}^T$ denotes the vector of allele frequencies in the k-th generation of a population submitted to action by the i-th model of mutation. From Theorem 4, we have

$$\underset{k\to \infty }{lim}{H}_k^{\left(i\right)}=H_{\infty }={log}_{2}N,$$

(33)

for $i=1,2,3.$ The speed of convergence is described by an approximation in a mean-square sense of behavior of entropy in sequential generations.

Another measure of distance between two probability measures is the so-called Kolmogorov distance. For frequencies of sequential generations, we define the Kolmogorov distance between the k-th generation and the 1st generation:

$$K_k^{\left(i\right)}=\underset{1\le l\le N}{max}|\sum _{j=1}^l({\nu }_j-{\nu }_j^{\left(k\right)})|,k\ge 1,$$

(34)

and investigate the behavior of the sequence $K_k^{\left(i\right)}$.

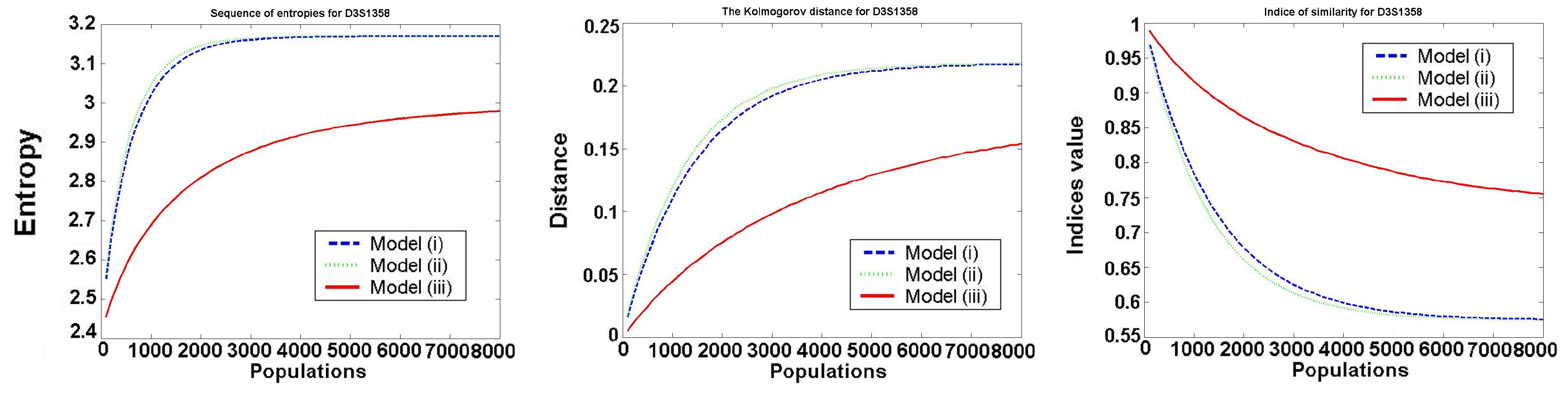
The third measure of distance of probability distribution is called a similarity index. We investigate

$$I_k^{\left(i\right)}=\sum _{j=1}^{N}min\{{\nu }_j,{\nu }_j^{\left(k\right)}\},k\ge 1.$$

(35)

The behavior of the investigated values for one typical locus D3S1358 is presented in the following Figure 2.

We only consider Models 1–3, because in Model 4 all values are constant (it satisfies the Hardy–Weinberg hypothesis). We see that Models 1 and 2 (almost identical in the figures) are worse than Model 3, as the entropy of frequencies increases much faster in Model 1 and Model 2. In all models, the speed of convergence decreases with increasing the number of generations. Thus, the increase is the biggest in the first generation.

For all the investigated values $H_k^{\left(i\right)},K_k^{\left(i\right)}$, and $I_k^{\left(i\right)}$ for $i=1,2,3$, the best in a mean-square sense is the logarithmic function:

$$f\left(k\right)=aln\left(k\right)+b,k\in \mathcal{N}.$$

(36)

The optimal values for $H_k$ belong to the intervals $a\in \left(0.097\right(VWA),0.197(FESFPS\left)\right)$, $b\in \left(2.2\right(TPOX),4.156(FESFPS\left)\right)$, for $K_k$ to $a\in \left(0.021\right(TH01),0.062(CSF1PO\left)\right),$ $b\in \left(0.099\right(VWA),0.243(D5S818\left)\right)$, and for $I_k$ to $a\in (-0.107(CSF1PO),-0.037(TH01\left)\right),$ $b\in \left(0.460\right(FGA),0.824(VWA\left)\right).$ This means that after about 8000 generations, we obtain almost uniformly distributed allele frequencies.

7. Conclusions

(i)

The mutation model assumed in the DNA VIEW program is not correct. After a long-time simulation (~8000 generations), this model results in almost uniformly distributed frequencies (the value of entropy in the D3S1358 locus case is over 93% its maximal value, much more than the value observed in human population, and the trend is still growing, however much slower than in earlier generations) of alleles but in reality no such uniform distribution at any locus can be observed. The uniformly distributed allele frequencies give the maximal entropy, but in reality, the entropy at different loci is smaller than the maximal one (between $62.9\%$ of the maximal entropy in the case of LPL and $87.9\%$ in the case of Penta E).

(ii)

The speed of convergence $H_k^{\left(3\right)}$ is directly proportional to the number of allele N and inversely proportional to the difference between the uniform distribution and the distribution of ${\nu }^{\left(o\right)}$ (expressed by $H_1$). A statistical analysis gives the formula $H_{\infty }-H_k^{\left(3\right)}=0.33923+0.013062\times N-0.138466\times H_1$ ($p=0.0146$ for N and $p=0.00229$ for $H_1$). In the case of the Kolmogorov distance and indices of similarity, this dependence is not statistically significant.

(iii)

Among the considered models: Models 1, 2, and 3, Model 3 is the best. However, from a viewpoint of the Hardy–Weinberg hypothesis, Model 4 is the best. On the other hand, Models 1 and 4 “change” the observed mutation rate; however, this change is very small. Model 3 is preferred from the viewpoint of genetic observation.

(iv)

The choice of model taken for paternity testing has an essential influence in the case of maternal mutation. The only cause why it is hard to detect is that maternal mutations occur rarely. However, if they do, the differences can be enormous, as it was shown in Table 3 ($P\left[H_1\right|V]$ value 0.0003674 in Model 3 suggests that the man almost sure is not a father while values over 0.9967 in other models contradict this statement). In this case, we may get a different conclusion dependent on the taken mutation model (the defendant is accepted or excluded as a father).

(v)

By choosing a model different than Model 4, the researcher can omit the difference between two theoretically identical equations (see (30) and (31)). From a theoretical viewpoint, this is a significant lack of cohesion.