Statistical Analysis of Acoustic Emission in Uniaxial Compression of Tectonic and Non-Tectonic Coal
Abstract
:1. Introduction
2. Experiment
2.1. Materials for the Experiment
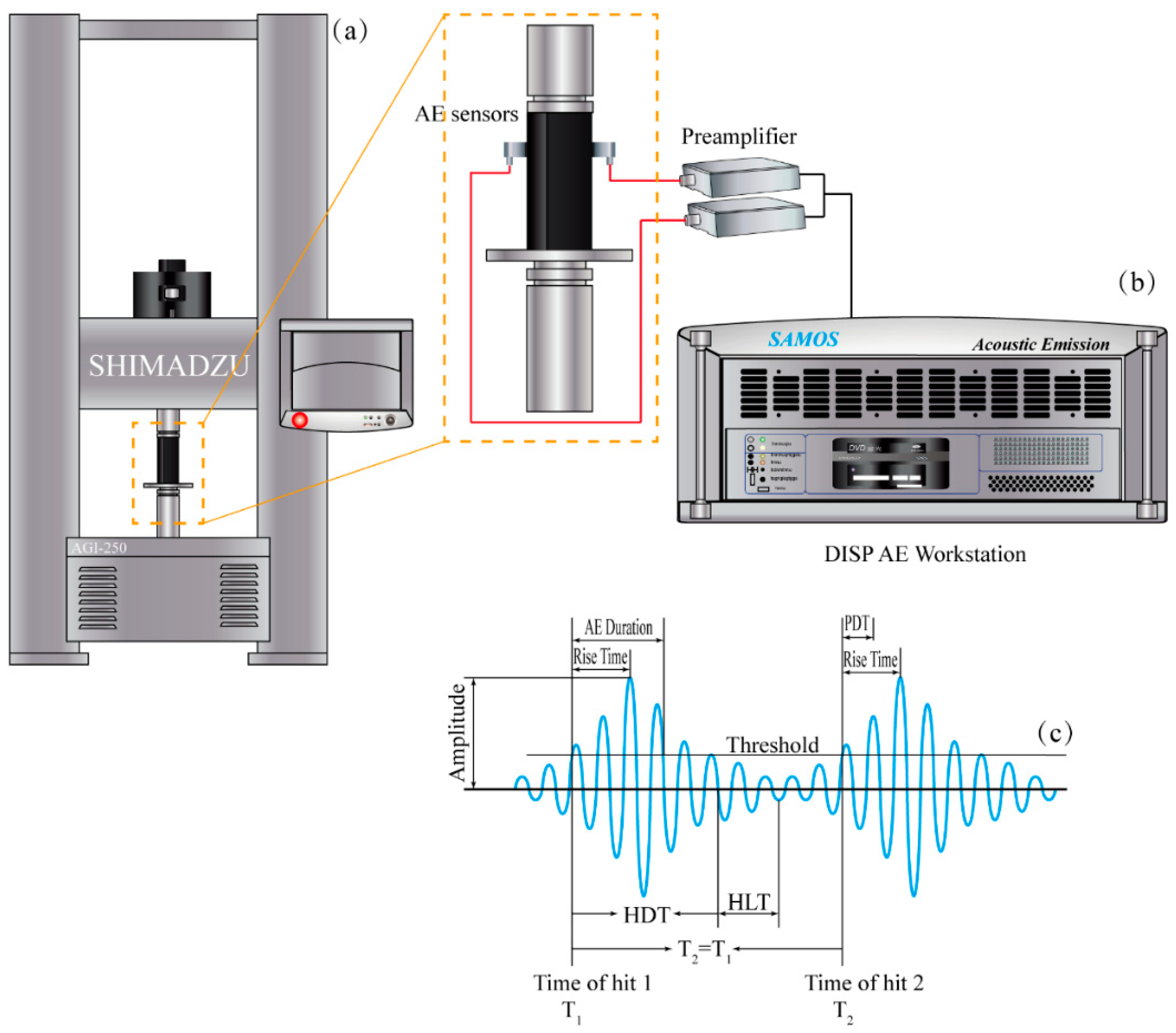
2.2. Experimental Facilities
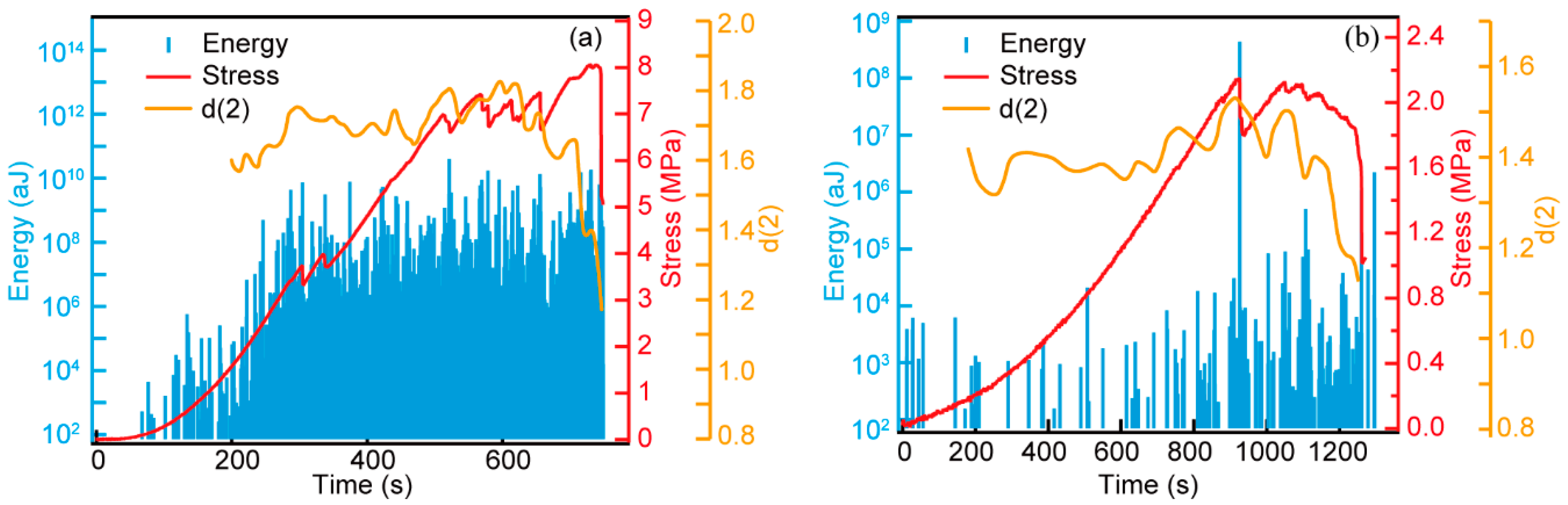
3. Results
4. Analysis and Discussion
4.1. Probability Density Function Distribution of AE Absolute Energy
4.2. Waiting Time Analysis of AE
4.3. Analysis of Aftershock and Båth’s Law
4.4. Multi-Fractal Analysis of AE
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cheng, Y.; Pan, Z. Reservoir properties of Chinese tectonic coal: A review. Fuel 2020, 260, 116350. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, Y.; Jiang, H.; Jin, K.; Wang, H.; Wang, L. Role of the rapid gas desorption of coal powders in the development stage of outbursts. J. Nat. Gas Sci. Eng. 2016, 28, 491–501. [Google Scholar] [CrossRef] [Green Version]
- Hou, Q.L.; Li, P.J.; Li, J.L. Foreland Fold Thrust Belt in Southwest Fujian; Geology Press: Beijing, China, 1995; pp. 1–107. [Google Scholar]
- Lu, S.; Wang, C.F.; Liu, Q.Q.; Zhang, Y.L.; Liu, J.; Sa, Z.Y.; Wang, L. Numerical assessment of the energy instability of gas outburst of deformed and normal coal combinations during mining. Process Saf. Envrion. Prot. 2019, 132, 351–366. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, Y.; Sa, Z.; Si, S.; Shu, L.; Wang, L. Damage-induced permeability model of coal and its application to gas predrainage in combination of soft coal and hard coal. Energy Sci. Eng. 2019, 7, 1352–1367. [Google Scholar] [CrossRef]
- Tu, Q.; Cheng, Y.; Ren, T.; Wang, Z.; Lin, J.; Lei, Y. Role of Tectonic Coal in Coal and Gas Outburst Behavior During Coal Mining. Rock Mech. Rock Eng. 2019, 52, 4619–4635. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, Y.; Wang, L.; Zhou, H.; He, X.; Yi, M.; Xi, C. Characterization of pore structure and the gas diffusion properties of tectonic and intact coal: Implications for lost gas calculation. Process Saf. Envrion. Prot. 2020, 135, 12–21. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, Y.; Wang, L.; Wang, C.; Lei, Y.; Jiang, Z. Analysis of pulverized tectonic coal gas expansion energy in underground mines and its influence on the environment. Environ. Sci. Pollut. Res. 2020, 27, 1508–1520. [Google Scholar] [CrossRef]
- Alpern, B. Tectonics and gas deposit in coalfields a bibliographical study and examples of application. Int. J. Rock Mech. Min. 1970, 7, 67–76. [Google Scholar] [CrossRef]
- Evans, H.; Brown, K.M. Coal structures in outbursts of coal and firedamp conditions. Min. Eng. 1973, 148, 171–179. [Google Scholar]
- Bustin, R.M.; Ross, J.V.; Rouzaud, J.N. Mechanisms of graphite formation from kerogen: Experimental evidence. Int. J. Coal Geol. 1995, 28, 1–36. [Google Scholar] [CrossRef]
- Gamson, P.D.; Beamish, B.; Johnson, D.P. Effect of coal microstructure and secondary mineralization on methane recovery. Geol. Soc. Lond. Spec. Publ. 1996, 109, 165–179. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Bustin, R.M. Variation in permeability with lithotype and maceral composition of Cretaceous coals of the Canadian Cordillera. Int. J. Coal Geol. 1997, 33, 135–151. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Bustin, R.M. Binary gas adsorption/desorption isotherms: Effect of moisture and coal composition upon carbon dioxide selectivity over methane. Int. J. Coal Geol. 2000, 42, 241–271. [Google Scholar] [CrossRef]
- Gürdal, G.; Yalçın, M.N. Pore volume and surface area of the Carboniferous coals from the Zonguldak basin (NW Turkey) and their variations with rank and maceral composition. Int. J. Coal Geol. 2001, 48, 133–144. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Dahmen, K.A. Crackling Noise in Disordered Materials. Annu. Rev. Condens. Matter Phys. 2014, 5, 233–254. [Google Scholar] [CrossRef]
- Sethna, J.P.; Dahmen, K.A.; Myers, C.R. Crackling noise. Nature 2001, 410, 242–250. [Google Scholar] [CrossRef] [Green Version]
- Salje, E.K.H.; Saxena, A.; Planes, A. Avalanches in Functional Materials and Geophysics; Springer: Berlin, Germany, 2017; pp. 1–58. [Google Scholar] [CrossRef]
- Baró, J.; Corral, Á.; Illa, X.; Planes, A.; Salje, E.K.H.; Schranz, W.; Soto-Parra, D.E.; Vives, E. Statistical Similarity between the Compression of a Porous Material and Earthquakes. Phys. Rev. Lett. 2013, 110, 088702. [Google Scholar] [CrossRef]
- Xie, K.; Jiang, D.; Sun, Z.; Chen, J.; Zhang, W.; Jiang, X. NMR, MRI and AE Statistical Study of Damage due to a Low Number of Wetting–Drying Cycles in Sandstone from the Three Gorges Reservoir Area. Rock Mech. Rock Eng. 2018, 51, 3625–3634. [Google Scholar] [CrossRef]
- Jiang, D.; Xie, K.; Chen, J.; Zhang, S.; Tiedeu, W.N.; Xiao, Y.; Jiang, X. Experimental Analysis of Sandstone Under Uniaxial Cyclic Loading through Acoustic Emission Statistics. Pure Appl. Geophys. 2019, 176, 265–277. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, H.; Xie, K.; Salje, E.; Jiang, X. Avalanches in Compressed Sandstone: Crackling Noise under Confinement. Crystals 2019, 9, 582. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Jiang, D.; Chen, J.; Salje, E.K.H. Collapsing minerals: Crackling noise of sandstone and coal, and the predictability of mining accidents. Am. Mineral. 2016, 101, 2751–2758. [Google Scholar] [CrossRef] [Green Version]
- Kun, F.; Varga, I.; Lennartz-Sassinek, S.; Main, I.G. Approach to failure in porous granular materials under compression. Phys. Rev. E 2013, 88, 062207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kun, F.; Varga, I.; Lennartz-Sassinek, S.; Main, I.G. Rupture Cascades in a Discrete Element Model of a Porous Sedimentary Rock. Phys. Rev. Lett. 2014, 112, 065501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nataf, G.F.; Castillo-Villa, P.O.; Baro, J.; Illa, X.; Vives, E.; Planes, A.; Salje, E.K.H. Avalanches in compressed porous SiO2-based materials. Phys. Rev. E 2014, 90, 022405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
- Salje, E.K.H.; Planes, A.; Vives, E. Analysis of crackling noise using the maximum-likelihood method: Power-law mixing and exponential damping. Phys. Rev. E 2017, 96, 042122. [Google Scholar] [CrossRef]
- Soto-Parra, D.; Vives, E.; Botello-Zubiate, M.E.; Matutes-Aquino, J.A.; Planes, A. Acoustic emission avalanches during compression of granular manganites. Appl. Phys. Lett. 2018, 112, 251906. [Google Scholar] [CrossRef]
- Xie, K.; Jiang, X.; Jiang, D.; Xiao, Y.; Chen, S.; Dahmen, K.A.; Vives, E.; Planes, A.; Salje, E.K.H. Change of crackling noise in granite by thermal damage: Monitoring nuclear waste deposits. Am. Mineral. 2019, 104, 1578–1584. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Lampronti, G.I.; Soto-Parra, D.E.; Baro, J.; Planes, A.; Vives, E. Noise of collapsing minerals: Predictability of the compressional failure in goethite mines. Am. Mineral. 2013, 98, 609–615. [Google Scholar] [CrossRef]
- Davidsen, J.; Stanchits, S.; Dresen, G. Scaling and Universality in Rock Fracture. Phys. Rev. Lett. 2007, 98, 125502. [Google Scholar] [CrossRef] [Green Version]
- Utsu, T.; Ogata, Y.; Matsuura, R.S. The Centenary of the Omori Formula for a Decay Law of Aftershock Activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Bath, M. Lateral inhomogeneities of the upper mantle. Tectonophysics 1965, 2, 483–514. [Google Scholar] [CrossRef]
- Console, R.; Lombardi, A.M.; Murru, M.; Rhoades, D. Bath’s law and the self-similarity of earthquakes. J. Geophys. Res. Atmos. 2013, 108. [Google Scholar] [CrossRef] [Green Version]
- Lapenna, V.; Macchiato, M.; Piscitelli, S.; Telesca, L. Scale-invariance Properties in Seismicity of Southern Apennine Chain (Italy). Pure Appl. Geophys. 2000, 157, 589–601. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Helmstetter, A. Is earthquake triggering driven by small earthquakes? Phys. Rev. Lett. 2003, 91, 058501. [Google Scholar] [CrossRef] [Green Version]
- Kiyashchenko, D.; Smirnova, N.; Troyan, V.; Saenger, E.; Vallianatos, F. Seismic hazard precursory evolution: Fractal and multifractal aspects. Phys. Chem. Earth Parts A/B/C 2004, 29, 367–378. [Google Scholar] [CrossRef]
- Kiyashchenko, D.; Smirnova, N.; Troyan, V.; Vallianatos, F. Dynamics of multifractal and correlation characteristics of the spatio-temporal distribution of regional seismicity before the strong earthquakes. Nat. Hazards Earth Syst. Sci. 2003, 3, 285–298. [Google Scholar] [CrossRef]
- Vidya Sagar, R.; Raghu Prasad, B.K. Fracture analysis of concrete using singular fractal functions with lattice beam network and confirmation with acoustic emission study. Theor. Appl. Fract. Mech. 2011, 55, 192–205. [Google Scholar] [CrossRef]
- Hidalgo, R.C.; Grosse, C.U.; Kun, F.; Reinhardt, H.W.; Herrmann, H.J. Evolution of percolating force chains in compressed granular media. Phys. Rev. Lett. 2002, 89, 1–4. [Google Scholar] [CrossRef]







| Parameters | Tectonic | Non-Tectonic | |
|---|---|---|---|
| Moisture contents | Ma | 2.17% | 2.72% |
| Ash content | Aa | 8.50% | 9.24% |
| Volatile matter content | Vdaf | 10.67% | 31.24% |
| Elemental C content | Ca | 79.63% | 73.73% |
| Elemental H content | Ha | 2.02% | 3.85% |
| Elemental N content | Na | 2.62% | 2.56% |
| Elemental S content | Sa | 1.96% | 1.17% |
| Parameters | Tectonic | Non-Tectonic |
|---|---|---|
| Vitrinite | 83.1% | 58.2% |
| Liptinite | 5.3% | 9.0% |
| Inertinite | 10.4% | 31.2% |
| Diameter | Tectonic | Non-Tectonic |
|---|---|---|
| 100~0.1 mm | 38.97% | 70.34% |
| 10~100 nm | 61.03% | 29.66% |
| Parameters | Tectonic | Non-Tectonic |
|---|---|---|
| 1000~2000 Å | 0.000918 cm3/g | 0.000186 cm3/g |
| 100~1000 Å | 0.001668 cm3/g | 0.000468 cm3/g |
| 14~100 Å | 0.001548 cm3/g | 0.000689 cm3/g |
| BET Surface Area | 3.2650 m2/g | 1.1130 m2/g |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; He, Y.; Zhao, Y.; Jiang, X.; Ren, S. Statistical Analysis of Acoustic Emission in Uniaxial Compression of Tectonic and Non-Tectonic Coal. Appl. Sci. 2020, 10, 3555. https://doi.org/10.3390/app10103555
Liu R, He Y, Zhao Y, Jiang X, Ren S. Statistical Analysis of Acoustic Emission in Uniaxial Compression of Tectonic and Non-Tectonic Coal. Applied Sciences. 2020; 10(10):3555. https://doi.org/10.3390/app10103555
Chicago/Turabian StyleLiu, Rong, Yi He, Yunfeng Zhao, Xiang Jiang, and Song Ren. 2020. "Statistical Analysis of Acoustic Emission in Uniaxial Compression of Tectonic and Non-Tectonic Coal" Applied Sciences 10, no. 10: 3555. https://doi.org/10.3390/app10103555
APA StyleLiu, R., He, Y., Zhao, Y., Jiang, X., & Ren, S. (2020). Statistical Analysis of Acoustic Emission in Uniaxial Compression of Tectonic and Non-Tectonic Coal. Applied Sciences, 10(10), 3555. https://doi.org/10.3390/app10103555





