An Entropy Weight-Based Lower Confidence Bounding Optimization Approach for Engineering Product Design
Abstract
:1. Introduction
2. Background
2.1. Kriging Model
2.2. Review of the Typical Adaptive Surrogate-Based Design Optimization Methods
2.2.1. The Lower Confidence Bounding Method
2.2.2. The Parameterized Lower Confidence Bounding Method
2.2.3. The Expected Improvement Method
2.2.4. The Weighted Expected Improvement Method
3. Proposed Approach
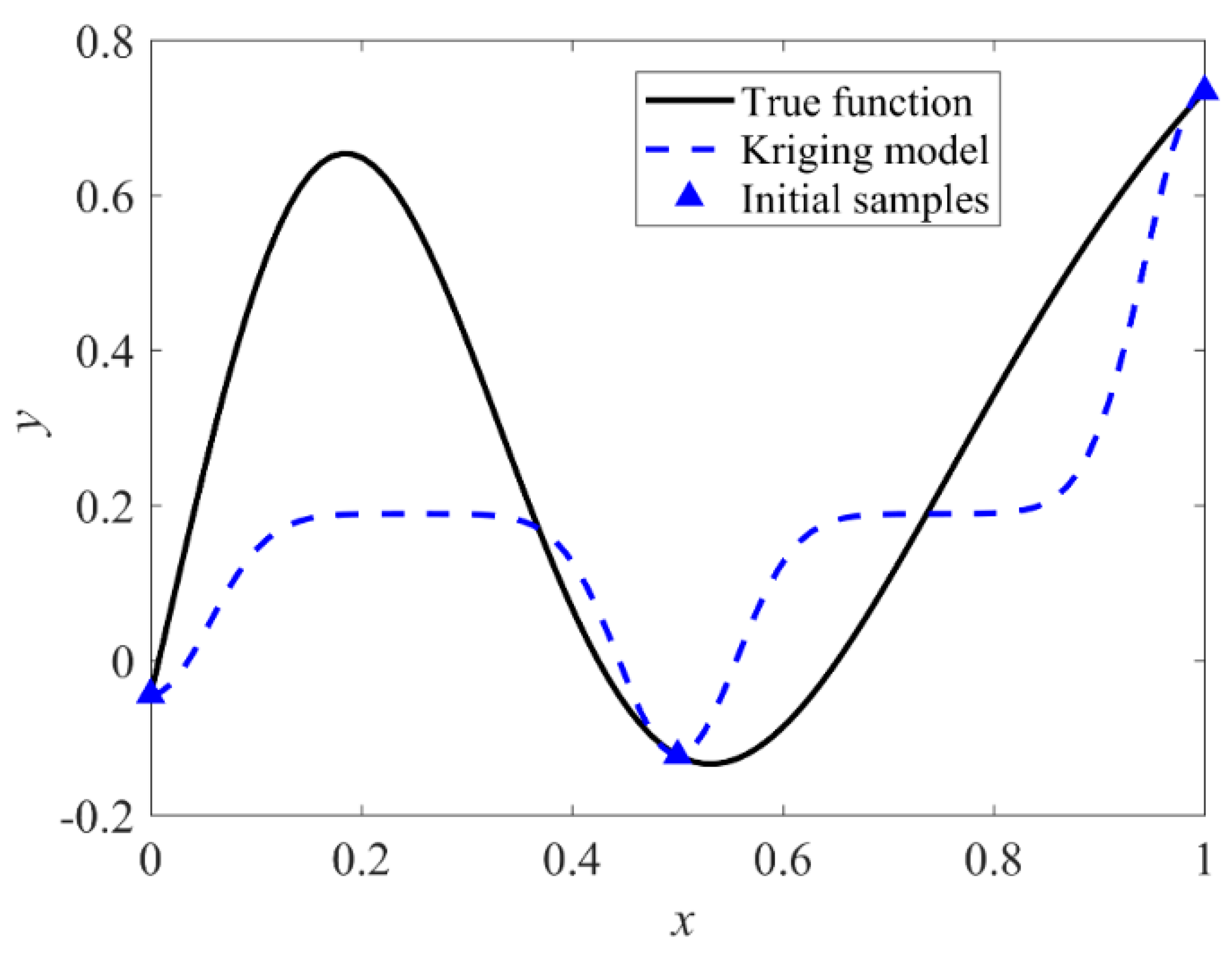
3.1. Step 1: Generate the Initial Sample Set
3.2. Steps 2 and 3: Constructing the Kriging Model and Obtaining the Current Optimal Solution
3.3. Step 4: Check the Terminal Condition
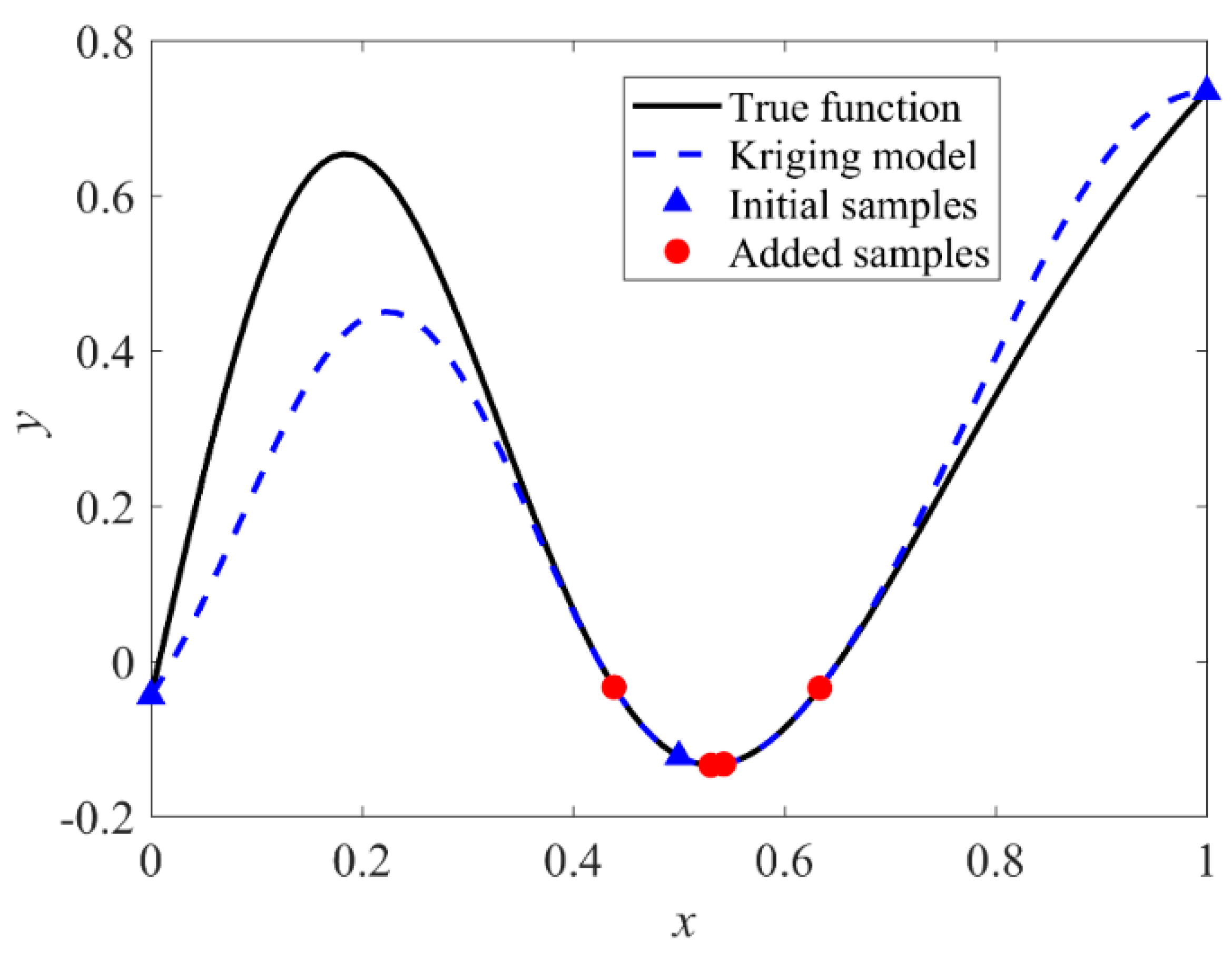
3.4. Steps 5: Update the Sample Set through the Proposed EW-LCB
3.5. Step 6: Output the Optimal Solution
4. Tested Cases
4.1. Numerical Examples
- Peaks function (PK)
- Banana function (BA)
- Sasena function (SA)
- Six-hump camp-back function (SC)
- Himmelblau function (HM)
- Goldstein–Price function (GP)
- Generalized polynomial function (GF)
- Levy 3 function (L3)
- Hartmann 3 function (H3)
- Leon (LE)
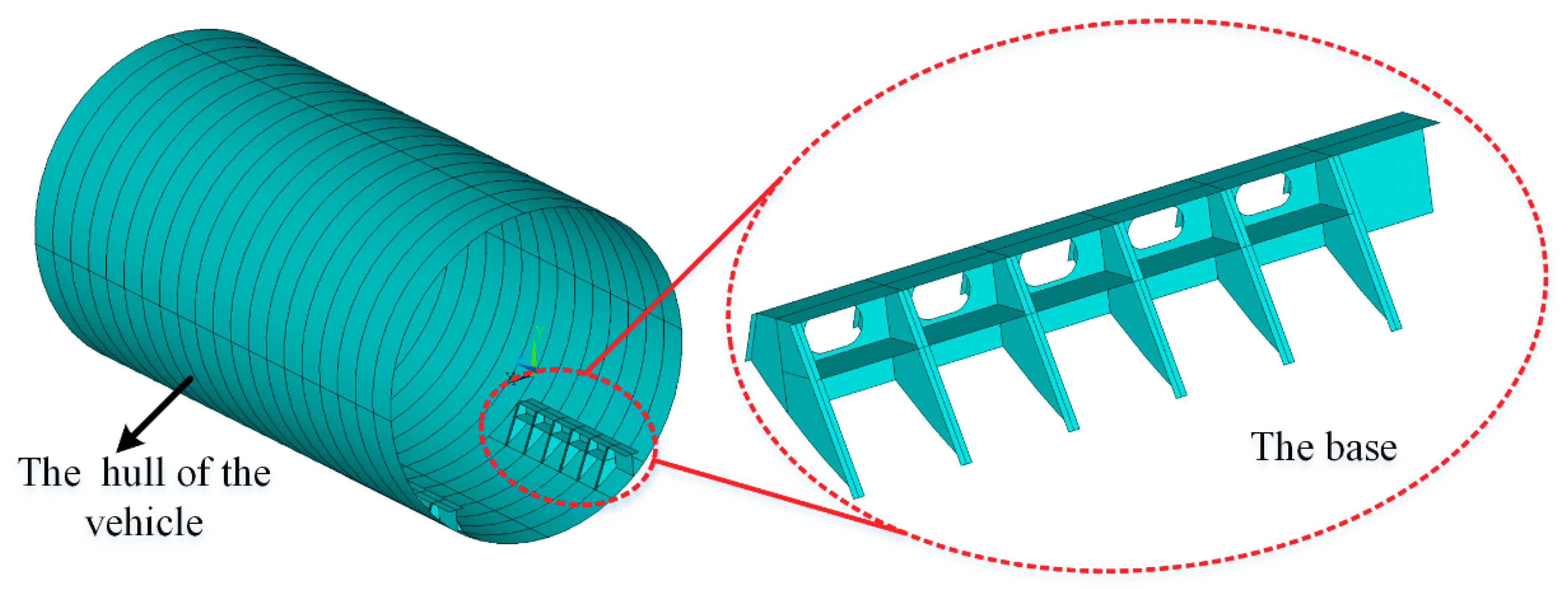
4.2. Engineering Application
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Methods | Variables (Rounded) | Weight (t) | ||||||
|---|---|---|---|---|---|---|---|---|
| t1 mm | t3 mm | t5 mm | t2 mm | t4 mm | t6 mm | Allowance 3.0327 | ||
| EI | 88 | 59 | 12 | 40 | 16 | 12 | 3.945 | 3.0058 |
| 90 | 60 | 12 | 40 | 13 | 13 | 3.991 | 3.0151 | |
| 90 | 60 | 12 | 40 | 14 | 12 | 4.020 | 3.0136 | |
| 90 | 59 | 12 | 40 | 15 | 12 | 4.031 | 3.0125 | |
| 83 | 60 | 12 | 40 | 20 | 12 | 4.004 | 3.0158 | |
| 88 | 59 | 12 | 40 | 16 | 12 | 3.945 | 3.0058 | |
| 90 | 60 | 12 | 40 | 13 | 13 | 3.991 | 3.0151 | |
| 90 | 60 | 12 | 40 | 14 | 12 | 4.020 | 3.0136 | |
| 90 | 59 | 12 | 40 | 15 | 12 | 4.031 | 3.0125 | |
| 83 | 60 | 12 | 40 | 20 | 12 | 4.004 | 3.0158 | |
| 88 | 59 | 12 | 40 | 16 | 12 | 3.945 | 3.0058 | |
| 90 | 60 | 12 | 40 | 13 | 13 | 3.991 | 3.0151 | |
| 90 | 60 | 12 | 40 | 14 | 12 | 4.020 | 3.0136 | |
| 90 | 59 | 12 | 40 | 15 | 12 | 4.031 | 3.0125 | |
| 83 | 60 | 12 | 40 | 20 | 12 | 4.004 | 3.0158 | |
| 88 | 59 | 12 | 40 | 16 | 12 | 3.945 | 3.0058 | |
| 90 | 60 | 12 | 40 | 13 | 13 | 3.991 | 3.0151 | |
| 90 | 60 | 12 | 40 | 14 | 12 | 4.020 | 3.0136 | |
| 90 | 59 | 12 | 40 | 15 | 12 | 4.031 | 3.0125 | |
| 83 | 60 | 12 | 40 | 20 | 12 | 4.004 | 3.0158 | |
| WEI | 88 | 59 | 12 | 40 | 16 | 13 | 3.919 | 3.0172 |
| 89 | 60 | 12 | 40 | 14 | 12 | 4.042 | 3.0047 | |
| 88 | 60 | 12 | 40 | 16 | 12 | 4.013 | 3.0172 | |
| 83 | 60 | 13 | 40 | 20 | 12 | 3.974 | 3.0266 | |
| 82 | 60 | 13 | 40 | 21 | 12 | 3.964 | 3.0281 | |
| 88 | 59 | 12 | 40 | 16 | 13 | 3.919 | 3.0172 | |
| 89 | 60 | 12 | 40 | 14 | 12 | 4.042 | 3.0047 | |
| 88 | 60 | 12 | 40 | 16 | 12 | 4.013 | 3.0172 | |
| 82 | 60 | 13 | 40 | 21 | 12 | 3.964 | 3.0281 | |
| 83 | 60 | 13 | 40 | 20 | 12 | 3.974 | 3.0266 | |
| 88 | 59 | 12 | 40 | 16 | 13 | 3.919 | 3.0172 | |
| 89 | 60 | 12 | 40 | 14 | 12 | 4.042 | 3.0047 | |
| 88 | 60 | 12 | 40 | 16 | 12 | 4.013 | 3.0172 | |
| 83 | 60 | 13 | 40 | 20 | 12 | 3.974 | 3.0266 | |
| 82 | 60 | 13 | 40 | 21 | 12 | 3.964 | 3.0281 | |
| 88 | 59 | 12 | 40 | 16 | 13 | 3.919 | 3.0172 | |
| 89 | 60 | 12 | 40 | 14 | 12 | 4.042 | 3.0047 | |
| 88 | 60 | 12 | 40 | 16 | 12 | 4.013 | 3.0172 | |
| 83 | 60 | 13 | 40 | 20 | 12 | 3.974 | 3.0266 | |
| 82 | 60 | 13 | 40 | 21 | 12 | 3.964 | 3.0281 | |
| LCB | 81 | 58 | 16 | 42 | 18 | 12 | 3.808 | 3.0203 |
| 78 | 58 | 20 | 40 | 18 | 14 | 3.857 | 3.0457 | |
| 75 | 52 | 17 | 46 | 17 | 21 | 3.676 | 3.0409 | |
| 69 | 51 | 25 | 43 | 20 | 19 | 3.688 | 3.0617 | |
| 76 | 50 | 21 | 44 | 15 | 22 | 3.647 | 3.0499 | |
| 81 | 58 | 16 | 42 | 18 | 12 | 3.808 | 3.0203 | |
| 78 | 58 | 20 | 40 | 18 | 14 | 3.857 | 3.0457 | |
| 75 | 52 | 17 | 46 | 17 | 21 | 3.676 | 3.0409 | |
| 69 | 51 | 25 | 43 | 20 | 19 | 3.688 | 3.0617 | |
| 76 | 50 | 21 | 44 | 15 | 22 | 3.647 | 3.0499 | |
| 81 | 58 | 16 | 42 | 18 | 12 | 3.808 | 3.0203 | |
| 78 | 58 | 20 | 40 | 18 | 14 | 3.857 | 3.0457 | |
| 75 | 52 | 17 | 46 | 17 | 21 | 3.676 | 3.0409 | |
| 69 | 51 | 25 | 43 | 20 | 19 | 3.688 | 3.0617 | |
| 76 | 50 | 21 | 44 | 15 | 22 | 3.647 | 3.0499 | |
| 81 | 58 | 16 | 42 | 18 | 12 | 3.808 | 3.0203 | |
| 78 | 58 | 20 | 40 | 18 | 14 | 3.857 | 3.0457 | |
| 75 | 52 | 17 | 46 | 17 | 21 | 3.676 | 3.0409 | |
| 78 | 47 | 21 | 47 | 14 | 20 | 3.651 | 3.0303 | |
| 70 | 51 | 25 | 49 | 12 | 21 | 3.632 | 3.0461 | |
| PLCB | 78 | 55 | 12 | 40 | 11 | 12 | 3.892 | 2.8243 |
| 84 | 47 | 17 | 46 | 12 | 21 | 3.769 | 3.0154 | |
| 84 | 47 | 24 | 42 | 12 | 19 | 3.748 | 3.0331 | |
| 45 | 51 | 33 | 46 | 35 | 17 | 3.533 | 3.1076 | |
| 84 | 38 | 28 | 44 | 15 | 19 | 3.684 | 3.0270 | |
| 78 | 55 | 12 | 40 | 11 | 12 | 3.892 | 2.8243 | |
| 84 | 47 | 17 | 46 | 12 | 21 | 3.769 | 3.0154 | |
| 84 | 47 | 24 | 42 | 12 | 19 | 3.748 | 3.0331 | |
| 45 | 51 | 33 | 46 | 35 | 17 | 3.533 | 3.1076 | |
| 84 | 38 | 28 | 44 | 15 | 19 | 3.684 | 3.0270 | |
| 78 | 55 | 12 | 40 | 11 | 12 | 3.892 | 2.8243 | |
| 84 | 47 | 17 | 46 | 12 | 21 | 3.769 | 3.0154 | |
| 84 | 47 | 24 | 42 | 12 | 19 | 3.748 | 3.0331 | |
| 45 | 51 | 33 | 46 | 35 | 17 | 3.533 | 3.1076 | |
| 84 | 38 | 28 | 44 | 15 | 19 | 3.684 | 3.0270 | |
| 78 | 55 | 12 | 40 | 11 | 12 | 3.892 | 2.8243 | |
| 84 | 47 | 17 | 46 | 12 | 21 | 3.769 | 3.0154 | |
| 84 | 47 | 24 | 42 | 12 | 19 | 3.748 | 3.0331 | |
| 67 | 59 | 39 | 40 | 11 | 12 | 3.645 | 3.0369 | |
| 45 | 51 | 35 | 47 | 33 | 16 | 3.524 | 3.1050 | |
| EW-LCB | 88 | 60 | 12 | 40 | 15 | 12 | 4.015 | 3.0065 |
| 87 | 60 | 12 | 40 | 17 | 12 | 4.017 | 3.0187 | |
| 87 | 60 | 12 | 40 | 17 | 12 | 4.016 | 3.0187 | |
| 85 | 60 | 12 | 40 | 18 | 12 | 4.016 | 3.0118 | |
| 84 | 60 | 12 | 40 | 18 | 12 | 4.015 | 3.0034 | |
| 88 | 60 | 12 | 40 | 15 | 12 | 4.015 | 3.0065 | |
| 87 | 60 | 12 | 40 | 17 | 12 | 4.017 | 3.0187 | |
| 87 | 60 | 12 | 40 | 17 | 12 | 4.016 | 3.0187 | |
| 85 | 60 | 12 | 40 | 18 | 12 | 4.016 | 3.0118 | |
| 84 | 60 | 12 | 40 | 18 | 12 | 4.015 | 3.0034 | |
| 88 | 60 | 12 | 40 | 15 | 12 | 4.015 | 3.0065 | |
| 87 | 60 | 12 | 40 | 17 | 12 | 4.017 | 3.0187 | |
| 87 | 60 | 12 | 40 | 17 | 12 | 4.016 | 3.0187 | |
| 85 | 60 | 12 | 40 | 18 | 12 | 4.016 | 3.0118 | |
| 84 | 60 | 12 | 40 | 18 | 12 | 4.015 | 3.0034 | |
| 89 | 59 | 12 | 40 | 16 | 12 | 4.061 | 3.0143 | |
| 89 | 58 | 12 | 40 | 16 | 12 | 4.056 | 3.0026 | |
| 88 | 60 | 12 | 40 | 16 | 12 | 4.062 | 3.0172 | |
| 89 | 60 | 12 | 40 | 14 | 12 | 4.060 | 3.0047 | |
| 89 | 60 | 12 | 40 | 15 | 12 | 4.059 | 3.0155 | |
References
- Han, Z.; Xu, C.; Zhang, L.; Zhang, Y.; Zhang, K.; Song, W. Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids. Chin. J. Aeronaut. 2020, 33, 31–47. [Google Scholar] [CrossRef]
- Zhou, Q.; Wu, J.; Xue, T.; Jin, P. A two-stage adaptive multi-fidelity surrogate model-assisted multi-objective genetic algorithm for computationally expensive problems. Eng. Comput. 2019, 1–17. [Google Scholar] [CrossRef]
- Velayutham, K.; Venkadeshwaran, K.; Selvakumar, G. Process Parameter Optimization of Laser Forming Based on FEM-RSM-GA Integration Technique. Appl. Mech. Mater. 2016, 852, 236–240. [Google Scholar] [CrossRef]
- Gutmann, H.M. A radial basis function method for global optimization. J. Glob. Optim. 2001, 19, 201–227. [Google Scholar] [CrossRef]
- Zhou, Q.; Rong, Y.; Shao, X.; Jiang, P.; Gao, Z.; Cao, L. Optimization of laser brazing onto galvanized steel based on ensemble of metamodels. J. Intell. Manuf. 2018, 29, 1417–1431. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, Y.; Choi, S.-K.; Jiang, P.; Shao, X.; Hu, J.; Shu, L. A robust optimization approach based on multi-fidelity metamodel. Struct. Multidiscip. Optim. 2018, 57, 775–797. [Google Scholar] [CrossRef]
- Shu, L.; Jiang, P.; Song, X.; Zhou, Q. Novel Approach for Selecting Low-Fidelity Scale Factor in Multifidelity Metamodeling. AIAA J. 2019, 57, 5320–5330. [Google Scholar] [CrossRef]
- Zhou, Q.; Shao, X.; Jiang, P.; Zhou, H.; Shu, L. An adaptive global variable fidelity metamodeling strategy using a support vector regression based scaling function. Simul. Model. Pract. Theory 2015, 59, 18–35. [Google Scholar] [CrossRef]
- Jiang, C.; Cai, X.; Qiu, H.; Gao, L.; Li, P. A two-stage support vector regression assisted sequential sampling approach for global metamodeling. Struct. Multidiscip. Optim. 2018, 58, 1657–1672. [Google Scholar] [CrossRef]
- Qian, J.; Yi, J.; Cheng, Y.; Liu, J.; Zhou, Q. A sequential constraints updating approach for Kriging surrogate model-assisted engineering optimization design problem. Eng. Comput. 2019, 36, 993–1009. [Google Scholar] [CrossRef]
- Shishi, C.; Zhen, J.; Shuxing, Y.; Apley, D.W.; Wei, C. Nonhierarchical multi-model fusion using spatial random processes. Int. J. Numer. Methods Eng. 2016, 106, 503–526. [Google Scholar] [CrossRef]
- Hennig, P.; Schuler, C.J. Entropy search for information-efficient global optimization. J. Mach. Learn. Res. 2012, 13, 1809–1837. [Google Scholar]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Shu, L.; Jiang, P.; Wan, L.; Zhou, Q.; Shao, X.; Zhang, Y. Metamodel-based design optimization employing a novel sequential sampling strategy. Eng. Comput. 2017, 34, 2547–2564. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, Y.; Choi, S.-K.; Jiang, P.; Shao, X.; Hu, J. A sequential multi-fidelity metamodeling approach for data regression. Knowl.-Based Syst. 2017, 134, 199–212. [Google Scholar] [CrossRef]
- Dong, H.; Song, B.; Dong, Z.; Wang, P. SCGOSR: Surrogate-based constrained global optimization using space reduction. Appl. Soft Comput. 2018, 65, 462–477. [Google Scholar] [CrossRef]
- Dong, H.; Song, B.; Dong, Z.; Wang, P. Multi-start Space Reduction (MSSR) surrogate-based global optimization method. Struct. Multidiscip. Optim. 2016, 54, 907–926. [Google Scholar] [CrossRef]
- Serani, A.; Pellegrini, R.; Wackers, J.; Jeanson, C.-E.; Queutey, P.; Visonneau, M.; Diez, M. Adaptive multi-fidelity sampling for CFD-based optimisation via radial basis function metamodels. Int. J. Comput. Fluid Dyn. 2019, 33, 237–255. [Google Scholar] [CrossRef]
- Pellegrini, R.; Iemma, U.; Leotardi, C.; Campana, E.F.; Diez, M. Multi-fidelity adaptive global metamodel of expensive computer simulations. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 4444–4451. [Google Scholar]
- Jones, D.; Schonlau, M.; Welch, W. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Cox, D.D.; John, S. A statistical method for global optimization. In Proceedings of the 1992 IEEE International Conference on Systems, Man, and Cybernetics, Chicago, IL, USA, 18–21 October 1992; Volume 1242, pp. 1241–1246. [Google Scholar]
- Li, G.; Zhang, Q.; Sun, J.; Han, Z. Radial basis function assisted optimization method with batch infill sampling criterion for expensive optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1664–1671. [Google Scholar]
- Diez, M.; Volpi, S.; Serani, A.; Stern, F.; Campana, E.F. Simulation-based design optimization by sequential multi-criterion adaptive sampling and dynamic radial basis functions. In Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Sciences; Springer: Berlin/Heidelberg, Germany, 2019; pp. 213–228. [Google Scholar]
- Boukouvala, F.; Ierapetritou, M.G. Derivative-free optimization for expensive constrained problems using a novel expected improvement objective function. AIChE J. 2014, 60, 2462–2474. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Ruan, S.; Li, Z.; Shen, C.; Zeng, Y. A modified hypervolume based expected improvement for multi-objective efficient global optimization method. Struct. Multidiscip. Optim. 2018, 58, 1961–1979. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Trautmann, H.; Jing, N.; Emmerich, M. Multiobjective evolutionary algorithms based on target region preferences. Swarm Evol. Comput. 2018, 40, 196–215. [Google Scholar] [CrossRef]
- Xiao, S.; Rotaru, M.; Sykulski, J.K. Adaptive Weighted Expected Improvement With Rewards Approach in Kriging Assisted Electromagnetic Design. IEEE Trans. Magn. 2013, 49, 2057–2060. [Google Scholar] [CrossRef] [Green Version]
- Zhan, D.; Cheng, Y.; Liu, J. Expected improvement matrix-based infill criteria for expensive multiobjective optimization. IEEE Trans. Evol. Comput. 2017, 21, 956–975. [Google Scholar] [CrossRef]
- Sasena, M.J. Flexibility and Efficiency Enhancements for Constrained Global Design Optimization with Kriging Approximations. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2002. [Google Scholar]
- Forrester, A.I.J.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Zheng, J.; Li, Z.; Gao, L.; Jiang, G. A parameterized lower confidence bounding scheme for adaptive metamodel-based design optimization. Eng. Comput. 2016, 33, 2165–2184. [Google Scholar] [CrossRef]
- Cheng, J.; Jiang, P.; Zhou, Q.; Hu, J.; Yu, T.; Shu, L.; Shao, X. A lower confidence bounding approach based on the coefficient of variation for expensive global design optimization. Eng. Comput. 2019, 36, 1–21. [Google Scholar] [CrossRef]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M.W. Information-Theoretic Regret Bounds for Gaussian Process Optimization in the Bandit Setting. IEEE Trans. Inf. Theory 2012, 58, 3250–3265. [Google Scholar] [CrossRef] [Green Version]
- Desautels, T.; Krause, A.; Burdick, J.W. Parallelizing exploration-exploitation tradeoffs in Gaussian process bandit optimization. J. Mach. Learn. Res. 2014, 15, 3873–3923. [Google Scholar]
- Yondo, R.; Andrés, E.; Valero, E. A review on design of experiments and surrogate models in aircraft real-time and many-query aerodynamic analyses. Prog. Aerosp. Sci. 2018, 96, 23–61. [Google Scholar] [CrossRef]
- Candelieri, A.; Perego, R.; Archetti, F. Bayesian optimization of pump operations in water distribution systems. J. Glob. Optim. 2018, 71, 213–235. [Google Scholar] [CrossRef] [Green Version]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the witwatersrand. J. South. Afr. Inst. Min. Metall. 1952, 52, 119–139. [Google Scholar]
- Guo, Z.; Song, L.; Park, C.; Li, J.; Haftka, R.T. Analysis of dataset selection for multi-fidelity surrogates for a turbine problem. Struct. Multidiscip. Optim. 2018, 57, 2127–2142. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Schutte, J.F.; Reinbolt, J.A.; Fregly, B.J.; Haftka, R.T.; George, A.D. Parallel global optimization with the particle swarm algorithm. Int. J. Numer. Methods Eng. 2004, 61, 2296–2315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volpi, S.; Diez, M.; Gaul, N.J.; Song, H.; Iemma, U.; Choi, K.; Campana, E.F.; Stern, F. Development and validation of a dynamic metamodel based on stochastic radial basis functions and uncertainty quantification. Struct. Multidiscip. Optim. 2015, 51, 347–368. [Google Scholar] [CrossRef]
- Liu, J.; Han, Z.; Song, W. Comparison of infill sampling criteria in kriging-based aerodynamic optimization. In Proceedings of the 28th Congress of the International Council of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012; pp. 23–28. [Google Scholar]
- Loeppky, J.L.; Sacks, J.; Welch, W.J. Choosing the sample size of a computer experiment: A practical guide. Technometrics 2009, 51, 366–376. [Google Scholar] [CrossRef] [Green Version]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Søndergaard, J. DACE: A Matlab Kriging Toolbox, Version 2.0; Technical Report Informatics and Mathematical Modelling, (IMM-TR)(12); Technical University of Denmark: Lyngby, Denmark, 2002; pp. 1–34. [Google Scholar]
- Homaifar, A.; Qi, C.X.; Lai, S.H. Constrained optimization via genetic algorithms. Simulation 1994, 62, 242–253. [Google Scholar] [CrossRef]
- Gadre, S.R. Information entropy and Thomas-Fermi theory. Phys. Rev. A 1984, 30, 620. [Google Scholar] [CrossRef]
- de Boer, P.-T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A Tutorial on the Cross-Entropy Method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Jiang, P.; Cheng, J.; Zhou, Q.; Shu, L.; Hu, J. Variable-Fidelity Lower Confidence Bounding Approach for Engineering Optimization Problems with Expensive Simulations. AIAA J. 2019, 57, 5416–5430. [Google Scholar] [CrossRef]
- Zhou, Q.; Shao, X.Y.; Jiang, P.; Gao, Z.M.; Zhou, H.; Shu, L.S. An active learning variable-fidelity metamodelling approach based on ensemble of metamodels and objective-oriented sequential sampling. J. Eng. Des. 2016, 27, 205–231. [Google Scholar] [CrossRef]
- Toal, D.J.J. Some considerations regarding the use of multi-fidelity Kriging in the construction of surrogate models. Struct. Multidiscip. Optim. 2015, 51, 1223–1245. [Google Scholar] [CrossRef] [Green Version]
- Jiao, R.; Zeng, S.; Li, C.; Jiang, Y.; Jin, Y. A complete expected improvement criterion for Gaussian process assisted highly constrained expensive optimization. Inf. Sci. 2019, 471, 80–96. [Google Scholar] [CrossRef]
- Bali, K.K.; Gupta, A.; Ong, Y.S.; Tan, P.S. Cognizant Multitasking in Multiobjective Multifactorial Evolution: MO-MFEA-II. IEEE Trans. Cybern. 2020, 1–13. [Google Scholar] [CrossRef]
- Pellegrini, R.; Serani, A.; Liuzzi, G.; Rinaldi, F.; Lucidi, S.; Campana, E.F.; Iemma, U.; Diez, M. Hybrid Global/Local Derivative-Free Multi-objective Optimization via Deterministic Particle Swarm with Local Linesearch. In Proceedings of the Machine Learning, Optimization, and Big Data, Third International Conference, MOD 2017, Cham, Switzerland, 14–17 September 2017; pp. 198–209. [Google Scholar]
- Pellegrini, R.; Serani, A.; Leotardi, C.; Iemma, U.; Campana, E.F.; Diez, M. Formulation and parameter selection of multi-objective deterministic particle swarm for simulation-based optimization. Appl. Soft Comput. 2017, 58, 714–731. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, C.; Chen, H.; Sun, L.; Deng, K. Multi-objective optimization operation of the green energy island based on Hammersley sequence sampling. Energy Convers. Manag. 2020, 204, 112316. [Google Scholar] [CrossRef]
- Zheng, J.; Shao, X.; Gao, L.; Jiang, P.; Qiu, H. A prior-knowledge input LSSVR metamodeling method with tuning based on cellular particle swarm optimization for engineering design. Expert Syst. Appl. 2014, 41, 2111–2125. [Google Scholar] [CrossRef]
- Garcia, S.; Herrera, F. An extension on “statistical comparisons of classifiers over multiple data sets” for all pairwise comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]







| Parameter | Values |
|---|---|
| Population Size | 100 |
| Maximum generation | 100 |
| Crossover probability | 0.95 |
| Mutation probability | 0.01 |
| Methods | EI | WEI | LCB | PLCB | EW-LCB |
|---|---|---|---|---|---|
| Mean Value | 7.64 | 7.86 | 7.98 | 7.66 | 6.48 |
| Standard deviations | 1.352 | 1.498 | 1.301 | 1.780 | 0.505 |
| Functions | Items | EI | WEI | LCB | PLCB | EW-LCB |
|---|---|---|---|---|---|---|
| PK | FEmean | 29.82/3 | 30.13/4 | 29.68/2 | 31.99/5 | 26.97/1 |
| FEstd | 2.435/2 | 2.884/3 | 2.068/1 | 5.107/4 | 5.34/5 | |
| BA | FEmean | 33.23/3 | 32.15/2 | 33.88/4 | 34.34/5 | 26.33/1 |
| FEstd | 3.989/3 | 3.777/2 | 5.664/4 | 6.144/5 | 2.78/1 | |
| SA | FEmean | 32.12/3 | 36.15/5 | 34.88/4 | 31.23/2 | 27.92/1 |
| FEstd | 4.674/3 | 4.865/4 | 2.813/2 | 5.241/5 | 2.722/1 | |
| SC | FEmean | 39.30/4 | 40.66/5 | 39.20/3 | 36.41/2 | 33.42/1 |
| FEstd | 3.965/3 | 3.634/1 | 3.785/2 | 5.292/4 | 5.320/5 | |
| HM | FEmean | 45.76/4 | 46.22/5 | 44.12/3 | 41.34/2 | 35.22/1 |
| FEstd | 3.456/3 | 2.973/2 | 1.894/1 | 5.157/5 | 3.49/4 | |
| GP | FEmean | 117.66/5 | 115.67/4 | 105.27 /3 | 97.77/2 | 89.27/1 |
| FEstd | 19.11/5 | 11.81/2 | 17.55/4 | 14.44/3 | 9.99/1 | |
| GF | FEmean | Failed/5 | Failed/5 | Failed/5 | 140.42/2 | 116.67/1 |
| FEstd | Failed/5 | Failed/5 | Failed/5 | 75.66/2 | 30.63/1 | |
| L3 | FEmean | 300.4/3 | 534.6/4 | 540.4/5 | 167.1/1 | 199.2/2 |
| FEstd | 119.1/3 | 147.0/4 | 159.4/5 | 55.21/1 | 88.89/2 | |
| H3 | FEmean | 37.50/3 | 37.62/2 | 38.20/4 | 39.34/5 | 36.58/1 |
| FEstd | 3.50/4 | 3.46/3 | 3.29/2 | 3.64/5 | 2.56/1 | |
| H6 | FEmean | 107.03/4 | 105.13/3 | 103.67/2 | 114.1/5 | 101.16/1 |
| FEstd | 44.50/2 | 50.39/5 | 48.26/3 | 49.30/4 | 43.43/1 |
| Metrics | EI | WEI | LCB | PLCB | EW-LCB | |
|---|---|---|---|---|---|---|
| Average rank | FEmean | 3.70 | 4.00 | 3.22 | 3.10 | 1.10 |
| FEstd | 2.50 | 3.40 | 2.90 | 3.70 | 2.30 |
| i | Hypothesis | p-Values |
|---|---|---|
| 1 | EI vs. EW-LCB | 0.0028 |
| 2 | WEI vs. EW-LCB | 0.0001 |
| 3 | LCB vs. EW-LCB | 0.0016 |
| 4 | PLCB vs. EW-LCB | 0.0056 |
| Functions | Initial Sample Size | EI | WEI | LCB | PLCB | EW-LCB |
|---|---|---|---|---|---|---|
| SA | 27.55/4 | 28.98/5 | 27.02/3 | 24.12/2 | 23.34/1 | |
| 32.12/3 | 36.15/5 | 34.88/4 | 31.23/2 | 27.92/1 | ||
| 41.67/4 | 43.98/5 | 41.12/3 | 40.20/2 | 38.03/1 | ||
| L3 | 393.6/3 | 524.5/5 | 513.4/4 | 142.5/1 | 173.2/2 | |
| 300.4/3 | 534.6/4 | 540.4/5 | 167.1/1 | 199.2/2 | ||
| 403.4/3 | 525.4/4 | 536.5/5 | 166.6/1 | 206.1/2 |
| Fixed Parameters | Values |
|---|---|
| Elastic modulus | |
| Density | |
| Poisson’s ratio | 0.3 |
| The length of the Hull | 12,000 mm |
| The radius of the Hull | 3300 mm |
| Rib space | 600 mm |
| Size of the ribs’ | mm |
| The radius of the base web opening | 75 mm |
| Width of the base web opening | 210 mm |
| Design Variables | Ranges | |
|---|---|---|
| Former half | The thickness of the base panel | 40–90 mm |
| The thickness of the base web | 10–60 mm | |
| The thickness of the base bracket | 12–40 mm | |
| Remaining half | The thickness of the base panel | 40–90 mm |
| The thickness of the base web | 10–60 mm | |
| The thickness of the base bracket | 12–40 mm | |
| Methods | ||||
|---|---|---|---|---|
| Max | Mean | Std | Succeeded | |
| EI | 4.031 | 3.998 | 0.03060 | 20/20 |
| WEI | 4.042 | 3.983 | 0.04316 | 20/20 |
| LCB | 3.857 | 3.733 | 0.08629 | 5/20 |
| PLCB | 3.892 | 3.723 | 0.12230 | 11/20 |
| EW-LCB | 4.062 | 4.027 | 0.01953 | 20/20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Yi, J.; Zhang, J.; Cheng, Y.; Liu, J. An Entropy Weight-Based Lower Confidence Bounding Optimization Approach for Engineering Product Design. Appl. Sci. 2020, 10, 3554. https://doi.org/10.3390/app10103554
Qian J, Yi J, Zhang J, Cheng Y, Liu J. An Entropy Weight-Based Lower Confidence Bounding Optimization Approach for Engineering Product Design. Applied Sciences. 2020; 10(10):3554. https://doi.org/10.3390/app10103554
Chicago/Turabian StyleQian, Jiachang, Jiaxiang Yi, Jinlan Zhang, Yuansheng Cheng, and Jun Liu. 2020. "An Entropy Weight-Based Lower Confidence Bounding Optimization Approach for Engineering Product Design" Applied Sciences 10, no. 10: 3554. https://doi.org/10.3390/app10103554
APA StyleQian, J., Yi, J., Zhang, J., Cheng, Y., & Liu, J. (2020). An Entropy Weight-Based Lower Confidence Bounding Optimization Approach for Engineering Product Design. Applied Sciences, 10(10), 3554. https://doi.org/10.3390/app10103554




