Abstract
Simulating groups and their behaviors have been one of the important topics recently. This paper proposes a novel velocity-based method to simulate the realistic behavior of groups moving in a specific formation in a virtual environment including other groups and obstacles. The proposed algorithm, we called “DGB—Discretionary Group Behavior”, takes advantage of ORCA (Optimal Reciprocal Collision Avoidance) half-planes for both grouping and collision avoidance strategy. By considering new half-planes for each agent, we can have more reasonable and intelligent behavior in front of challenging obstacles and other agents. Unlike recent similar works, independent members in a group do not have predefined connections to each other even though they can keep the group’s formation while moving and trying to follow their best neighbors discretionarily in critical situations. Through experiments, we found that the proposed algorithm can yield more human-like group behavior in a crowd of agents.
1. Introduction
Group formation in crowd simulation has gotten huge attention in recent years due to its wide range of usage in virtual environments such as video games and movies. This work can be beneficial for bringing about more reasonable movements of groups in the simulation of video games. Also, this topic can be useful in training systems such as the study of human behaviors in emergency evacuation situations or common urban environments. Groups in a crowd have a significant effect on presenting a realistic simulated crowd. Thus, a realistic motion of groups in each of these situations can help to improve the quiality of the training systems. This topic can easily be defined by a crowd of robots navigating in the environment while trying to maintain their specific formation as a group.
The concept of group behaviors has been well studied recently. However, they do not take into account that, usually real people in a group can individually decide how to avoid other people and obstacles while trying to keep the group’s formation. In other words, it is better to not have any pre-connection between agents to make them stay in their formation [1]. Furthermore, sometimes an agent may get out of the band or falls behind the group for some reason while it can later return to its predefined and desired spot in the group. Put it differently, people are not always following a subgroup during their motion in the entire group [1]. In this paper, we present a new method (Discretionary Group Behavior—DGB) for having more realistic group formation and behavior in front of other agents and complicated obstacles in which the behavior of agents in groups is discretionary, meaning that members do not have mandatory connections to each other. This method can be useful in human-like multi-robot navigation or group formation of crowds in video games such as the collision-free motion of armies passing through each other, keeping their uniform cohesion.
In this paper, we address a velocity-based method, implemented from Optimal Reciprocal Collision Avoidance (ORCA) half-planes [2], to make each agent move with its group members in a particular formation while avoiding collisions and having no unnecessary connection to other members. The goals of our work are as follows.
Our method presents usual and familiar scenarios for a group of agents starting from the initial position, moving to their target position. We can consider a leader and the group’s followers that try to reach themselves to their target area. There are other groups, individual agents and obstacles which are on the group’s way, simultaneously. Each agent has its unique style to avoid others, like a real human. Meanwhile, all agents try their best to keep the group’s formation and cohesion. In this context, group formation is a specific shape that can be made by aggregation of several agents together (which in our work is a specific uniform formation) and consequently, keeping the formation means that members of a group adjust their directions and positions while moving to maintain at that specific shape as a whole group. Let’s describe the two main scenarios. First, if an agent is not in its proper location, by adding two more half-planes and limiting the set of allowable velocities, the agent will change its direction toward that position. And second, if there are obstacles on the agent’s way, the agent tries to pick one of the other members of the group as its subleader and then again by producing more half-planes, the agent can follow the subleader until passes the challenging environment. After passing obstacles, agents will recover from the destroyed formation to the main formation of the group. We should notice the fact that there is no time requirement for agents to do that. However, each member will increase its speed to return to its proper location and help the group to transform into the previous formation as soon as possible.
In our case, we define the challenging or complex environment as an area with different kinds of obstacles such as walls that provide limitations and difficulty for a group to pass through. For example, one of these kinds of environments can be a narrow corridor, which we proposed in this work, in front of a large group that requires the agents to pass it while trying to keep their formation and move collision-free as much as possible.
Through our analysis from the experiments, we came to this conclusion that our approach provides smooth and realistic motion for a group of agents in a crowd. Agents can take more human-like decisions between keeping the group’s formation or changing their position to avoid colliding with the others. For a better understanding of the “human-like” expression, let’s focus on the limitations of humans’ vision. One of these constraints is the range of distance that our eyes can see and is dependent on some factors like the presence of any obstructions in our line of sight [3]. Normally, in a crowded group, the front members have a good vision for moving properly so they have this ability to guide their back neighbors who have less clear visions. Put it differently, usually, agents in a large group will rely on their front neighbors to find their path, especially in critical situations such as a tightened space that requires destruction in the group’s formation and alteration in moving direction. This process continues until the members at the last lines of the group. Therefore, in this paper, we define the “human-like group behavior” as the movement of members in a group that takes into account this characteristic of humans’ vision. In our work, we propose two common cases for simulating groups of people in a virtual environment. However, this method can be easily expanded in other scenarios.
2. Related Work
This section overviews the most related works to this paper considering avoidance strategies and focusing on group modeling. We divide related works by their collision avoidance algorithm on the subject of velocity-based approaches (Section 2.1) or other kinds of methods (Section 2.2).
2.1. Velocity-Based Avoidance Methods
Some methods [4,5] use the Social Force Model (SFM) [6] for their collision avoidance strategy. These methods provide an ability for the group to change its formation in critical situations. For example, Nasir et al. [5] proposed the techniques for simulating group behavior in a dense crowd. According to this model, agents can switch between two formations based on the density of other agents around the group, which are the wide and narrow formation for the small and large density, respectively. The SFM is not providing a collision-free motion for agents; besides, this strategy is limited to a fixed number of agents and formations. Also, there is no path planning algorithm used for the leader to find the best way to the target position. Furthermore, with this method, agents do not have realistic and human-like behavior in front of obstacles due to their limited behavior confronting the other components in the environment (all of our claims are explicit in their provided video).
As with the previously proposed model [5], Karamouzas and Overmars [7] also demonstrate specific formations for agents to make the group transform into them in crowded areas. In their approach, they introduce three basic formations for the movement of small social groups in a virtual world which are line-abreast, V-like and river shapes that are inspired by a study from Moussaïd et al. [8], stating that real people tend to walk in small groups in common situations. Also, they used a velocity-selection approach for both collision avoidance and grouping behaviors, which is inspired by their previous work [9]. Qiu and Hu used two predefined matrixes for setting the member-to-member and group-to-group influences during the simulation [10].
The RVO2 [2] is one of the most accepted models for the collision avoidance idea in crowd simulation and is an extension of their previous work called Reciprocal Velocity Obstacle (RVO) [11]. The new method is innovative in that it aims to create ORCA half-planes in the velocity space and reduce the problem to be solved with three linear programs. Then, by picking a velocity from the intersection of all half-planes which is the nearest one to the preferred velocity, the agent can find the best and collision-free way among other agents and obstacles to go to its target position (we encourage the reader to see the referenced paper for having a better understanding of our method). Our method is built on the half-planes concept and we introduce a modified model of this work for grouping issues.
Some existing works [1,12] take advantage of the velocity obstacle and some others [13,14] consider the RVO2 library [15] to provide collision-free motion for groups of agents. He et al. [12] use the velocity obstacle to perform agent-agent and group-group collision avoidance by adding a velocity obstacle to the whole group. This method provides collision avoidance constraints for group maintenance and navigation. Park et al. allege that members in a group can keep their cohesion by communicating and adapting their behaviors in a virtual environment [13]. Additionally, it aims to have several subgoals assigned on the path of each agent to help it reach the main goal. Also, agents can respond to events and scenarios during their motion. On the other hand, Zhang et al. [14] use ORCA half-planes to perform the collision-free motion of small groups with equal or less than 3 members. This paper provides a method based on attraction rules and communication of agents in a group.
Another velocity-based approach for modeling groups of agents is introduced by Van Den Berg et al. [1]. This model is a unified solution for diverse types of groups by modifying the Velocity Obstacle approach and having Velocity Connection for each agent which is the set of velocities that keep agents moving together while avoiding the collision. This process, by using a relation matrix, forces agents to be connected to the fixed nearby members. As a result, agents cannot have individual behavior when confronted with obstacles or other agents since real people are not always connected to specific members and can make their own decision to avoid other people while trying to maintain in their group formation. Our approach has this capability for agents to avoid others individually, maintaining in their formation.
The work by Gu et al. [16] shows a user interactive freestyle group formation that allows users to control the shape of the group. By computing the distribution of target formation, the group will start moving to make that specific shape. However, this strategy does not have enough concentration on the collision avoidance method in situations with a large density of the crowd. Furthermore, the group’s interaction with challenging obstacles which is noticeable in our method is not considered in their work. A similar method has proposed by Zhang et al. for having user interactive freestyle formations by generating an optimum path for each individual from the initial position to the target, without any collision [17].
Some other works have benefitted from physically-based models (using velocities) to provide group maintenance and avoidance in a dense crowd. For instance, Braun et al. [18] is inspired by a method proposed by Helbing et al. [19] to simulate group behaviors. This model aims to simulate individual agents with different characteristics performing group motion in panic situations.
2.2. Other Avoidance Methods
The work by Rojas et al. [20] which has inspired by previously described methods [7,10], proposes a ray casting technique for the collision avoidance strategy of small groups. In their paper, the possible formation of a group is taken from three different shapes which are limited to abreast, U/V-like and river formations [7].
Other recent works [21,22,23] use Finite State Machines (FSM) to provide the avoidance feature to the agents navigating through the environment. In the first model [21], Groups are composed of five fixed agents in line formation. Rojas and Yang’s method [22] which is an extension of Reference [21], has expanded groups’ formations to not just line shape but in the three specific formations that have introduced previously [7].
Ennis et al. focus on determining the distance and orientation of a group, consists of talkers and listeners in a virtual conversation to make more realistic background groups of talkers in a virtual environment like video games and movies [24]. This work benefits from special cameras for capturing real actors’ motion.
In our paper, we demonstrate a new algorithm for simulating groups of agents not limited to the specific number of members with more believable animation in their motion toward their goals confronting with other groups or challenging obstacles.
3. Algorithm: Discretionary Group Behavior
3.1. Overview
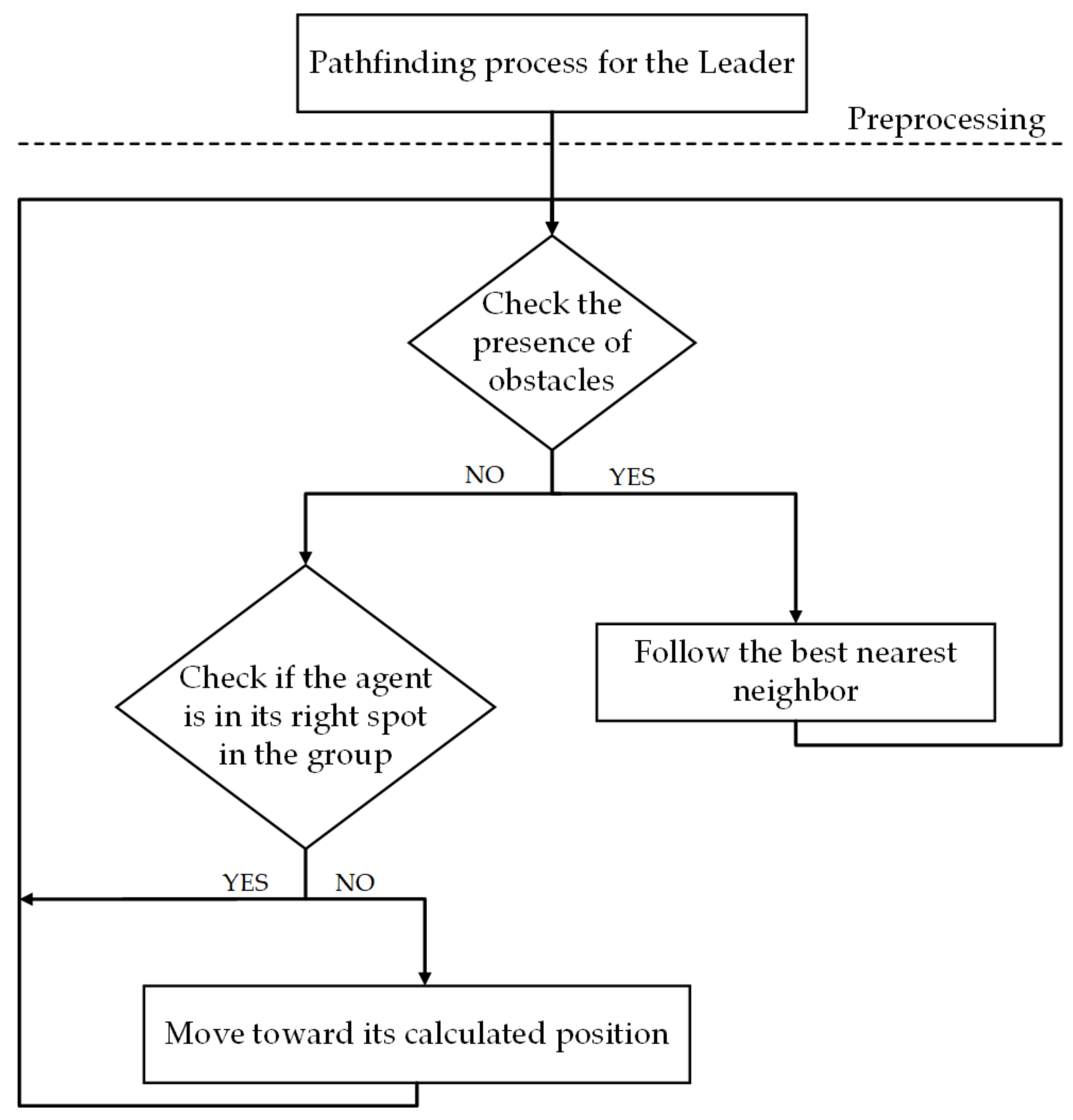
Our simulation can handle both group-group and group-obstacle interactions. There is a preprocessing step for the leader to calculate the best path to its target position using A* pathfinding algorithm [25] due to the simplicity and ability of this method to find the minimum cost solution. In our implementation, this algorithm works in a grid space with units (see Section 4 for more details) as the grid value that makes a smooth motion for all agents while not having large memory consumption. The proper position for each agent to follow, considering the group’s shape, will be calculated based on the leader and agents’ unit velocity. Meanwhile, in the moving direction, each agent can sense the density of obstacles around itself. If there is no obstacle in front of the agent and if the agent is not in its acceptable area, it will move toward the calculated location by adding two other half-planes toward the right direction, continuously. Finally, if the calculation of density around the agent determines the presence of obstacles, the agent will find its best neighbor which is more near to the leader and will follow the selected subleader until there is no obstacle near it (Figure 1). The stage of the flowchart that evaluates the position of agents depends on their proper locations in the group is simply done by computing the relative position for each agent (subtraction of them) and then, comparing the value with “T” as a predefined threshold (see Section 4 for more details). We clarify each step individually.
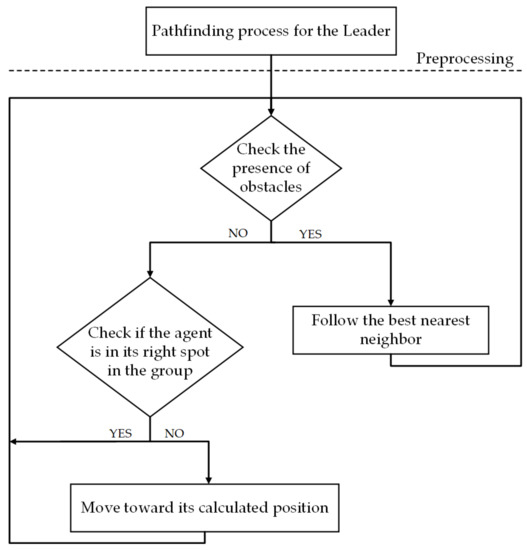
Figure 1.
The flowchart of the Discretionary Group Behavior (DGB) algorithm. The preprocessing step happens once and the other parts repeat in each time step.
3.2. Formation Model
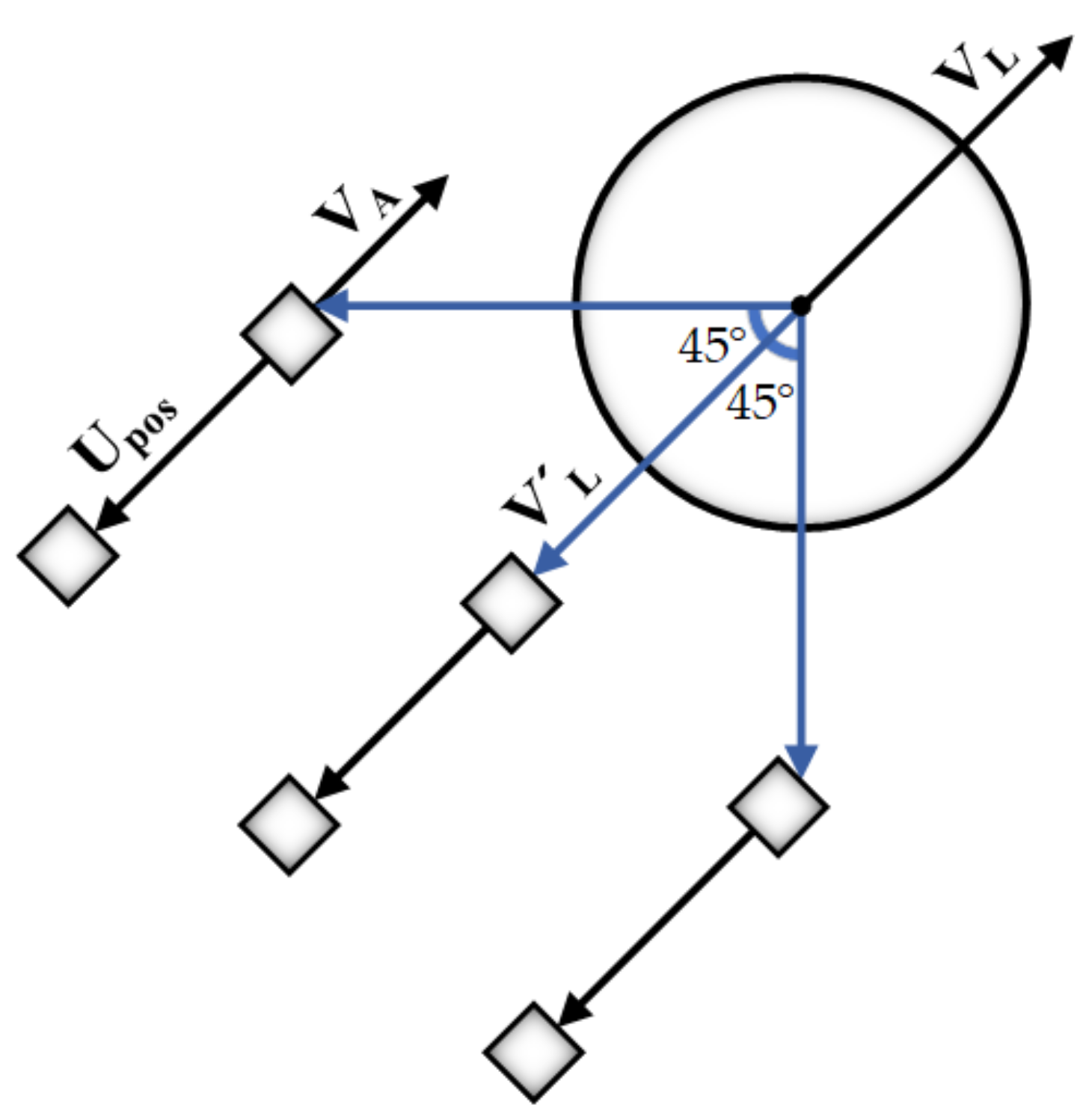
Depending on what kind of formation is required, this part can be easily changed while we considered a uniform formation for our approach. For example, in Figure 2, and are the unit velocity and the reverse unit velocity of the leader, respectively. For having a three-column uniform shape, two steps are required. First, the reverse direction of the leader’s unit velocity produces the first line positions in the way that will be rotated in 45 degrees clockwise and vice versa. Second, the other locations in the formation will be calculated by the weighted sum of the reverse unit velocity of other members and the leader (Equation (1)). The final unit vector Upos that specifies the new position is defined by , the reverse unit velocity of the agent at the position in upper line of the formation, and , the reverse unit velocity of the leader. We considered more weight for the agents’ unit velocity (W1) and it makes a more realistic motion for the whole group in orientations. This process can easily be adapted to have any other formations.
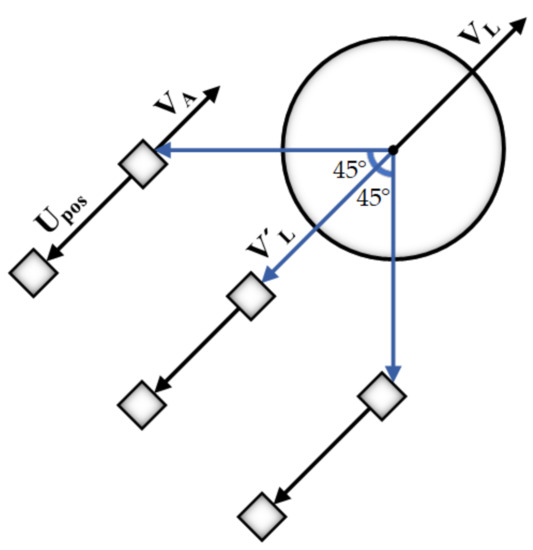
Figure 2.
An approximate sample of position production for a uniform formation. The first line will be computed directly from the leader’s unit velocity and other positions by the weighted sum of the velocities related to the leader () and the agent () in the upper line of the formation.
3.3. Sensing the Presence of Obstacles
In this part of the process, each agent can measure the density of obstacles by generating an ellipse around itself. The center of the ellipse, , is determined at units direction ahead of the agent’s trajectory. To expound it in more details, we placed at the . and (see Section 4 for more details) are the agent’s location and a constant coefficient for moving the ellipse’s center respectively. The reason for moving the ellipse in the lead of the agent’s position is to make the agent focuses more on its forward way for detecting obstacles. An obstacle falls into the ellipse if the condition of Equation (2) is satisfied [5]. In the equation below, are the ellipse’s major and minor radiuses through the process.
3.4. Maintaining in the Right Position
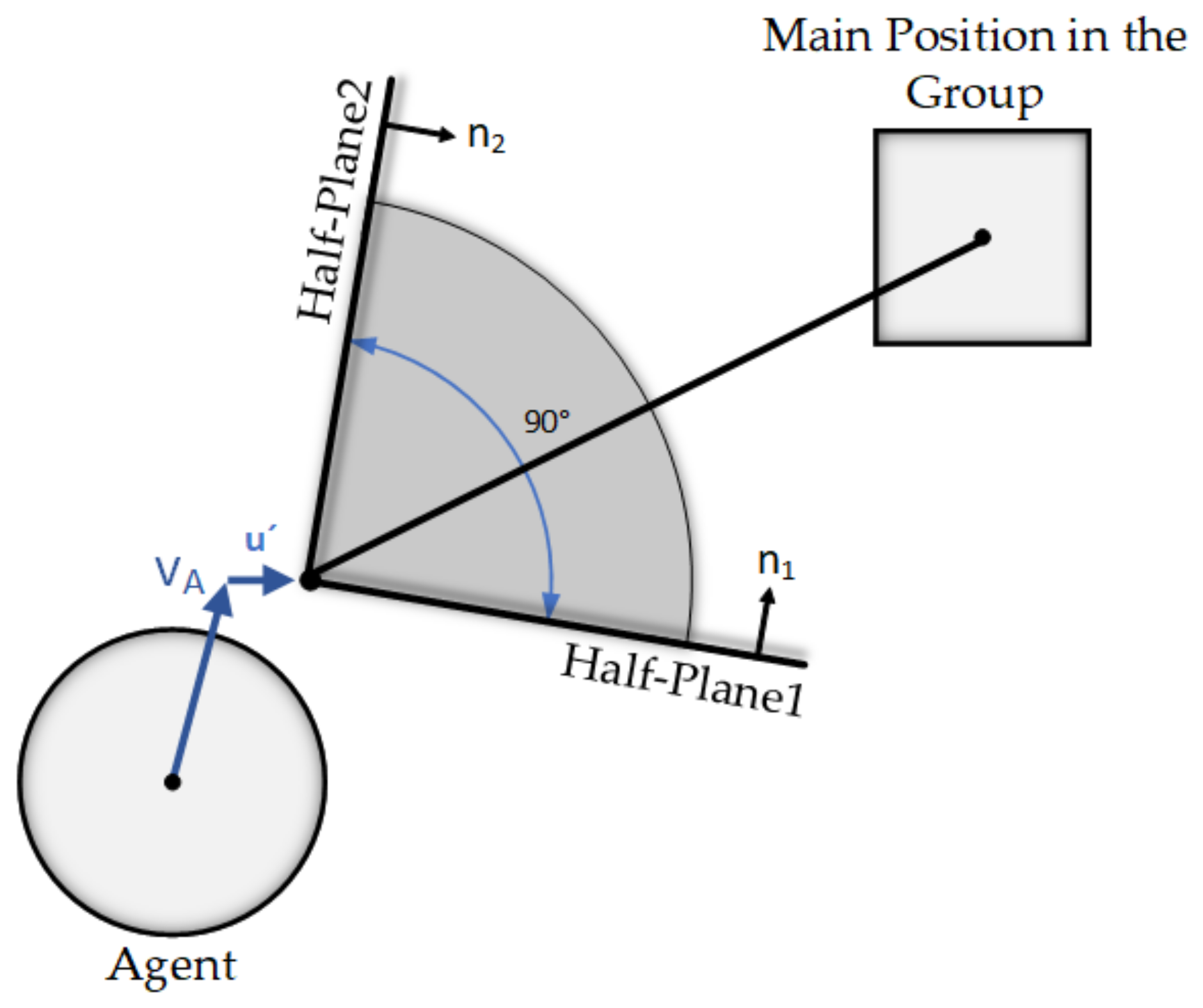
This section is for a situation when the calculated density is zero and the agents are forced to leave their proper area across the group to avoid other agents and obstacles from colliding. Having the right location for the agent, two half-planes will be added by rotating the vector calculated from the relative position between the agent and the right spot, with 45 degrees in two directions (Figure 3). Relative position (RP) calculates by the subtraction of the agent’s position from the proper position. The rotation of RP in two-dimensional space can simply calculate by the two matrixes for clockwise (Equation (3)) and counterclockwise (Equation (4)) rotations. For determining each half-planes, it is required to have three main vectors—the agent’s unit velocity, the normal vector of the half-plane toward the desired direction and a unit vector in one of the left or right directions of the moving path. Since in our case, the rotation degree () is 45, there is no need to calculate normal vectors because the two half-planes are perpendicular to each other. If the rotation degree changes to other values, the calculation of normal vectors is necessary.
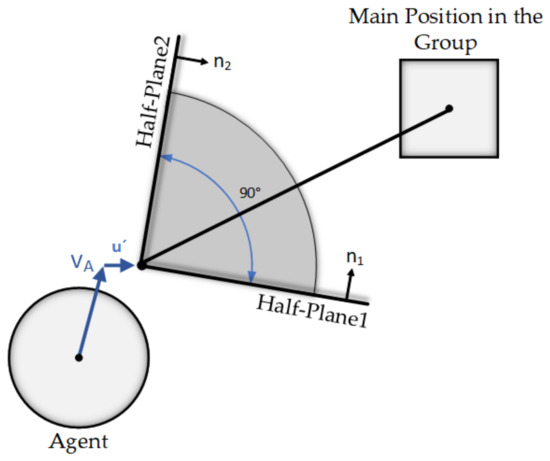
Figure 3.
Producing additional half-planes in the direction of the proper location, in each time step of the algorithm.
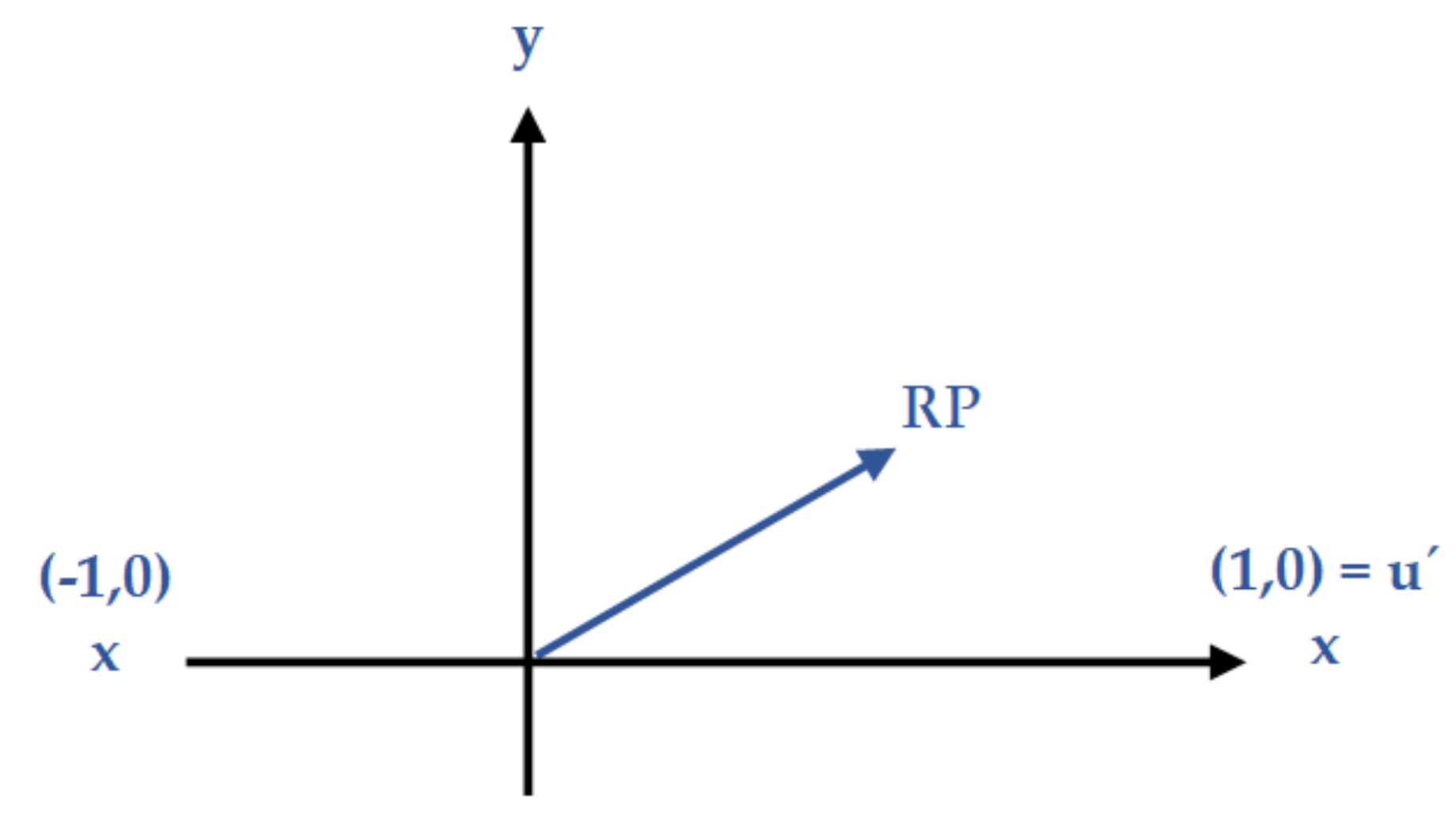
Let and be normals of the rotated vectors (our half-planes) from RP and let be the unit vector in the left or right directions considering the moving side. For a better understanding of how calculates, let’s consider vector RP () as the desired moving direction for agent A (Figure 4). So according to this direction, will be equal to . This tactic helps the starting point of all half-planes including collision avoidance [2] and the two other half-planes created in this section be so close to each other. Therefore, it facilitates solving linear programs during the algorithm.
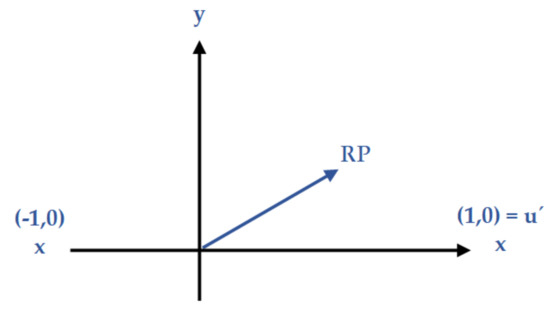
Figure 4.
A simple method for calculating that has been used for defining the points of the half-planes. In this special case, the moving direction of the group considers in Y coordinate.
Hence, is a half-plane defining a set of allowed velocities leading agent A toward its proper position. This half-plane is pointing in the direction of or starting at the point of (Equations (5) and (6)).
The intersection of all half-planes leads the agent to move in a direction that provides both collision-free motions for all members and a well-constructed formation for the group during the movement. After calculating the two half-planes in the direction of the accurate spot in the group, the agent that is far away from its position because of the avoidance function against some contrary components can adjust (increase) its speed for being able to get back in the proper location in the group. Once the agent gets to the right place, it will change the speed to be the same as the leader. This important feature of agents that can change their speed depending on the situation, has been used in a few methods [20,23] and is missing in some other works for simulating large groups or small groups.
3.5. Confronting with Obstacles
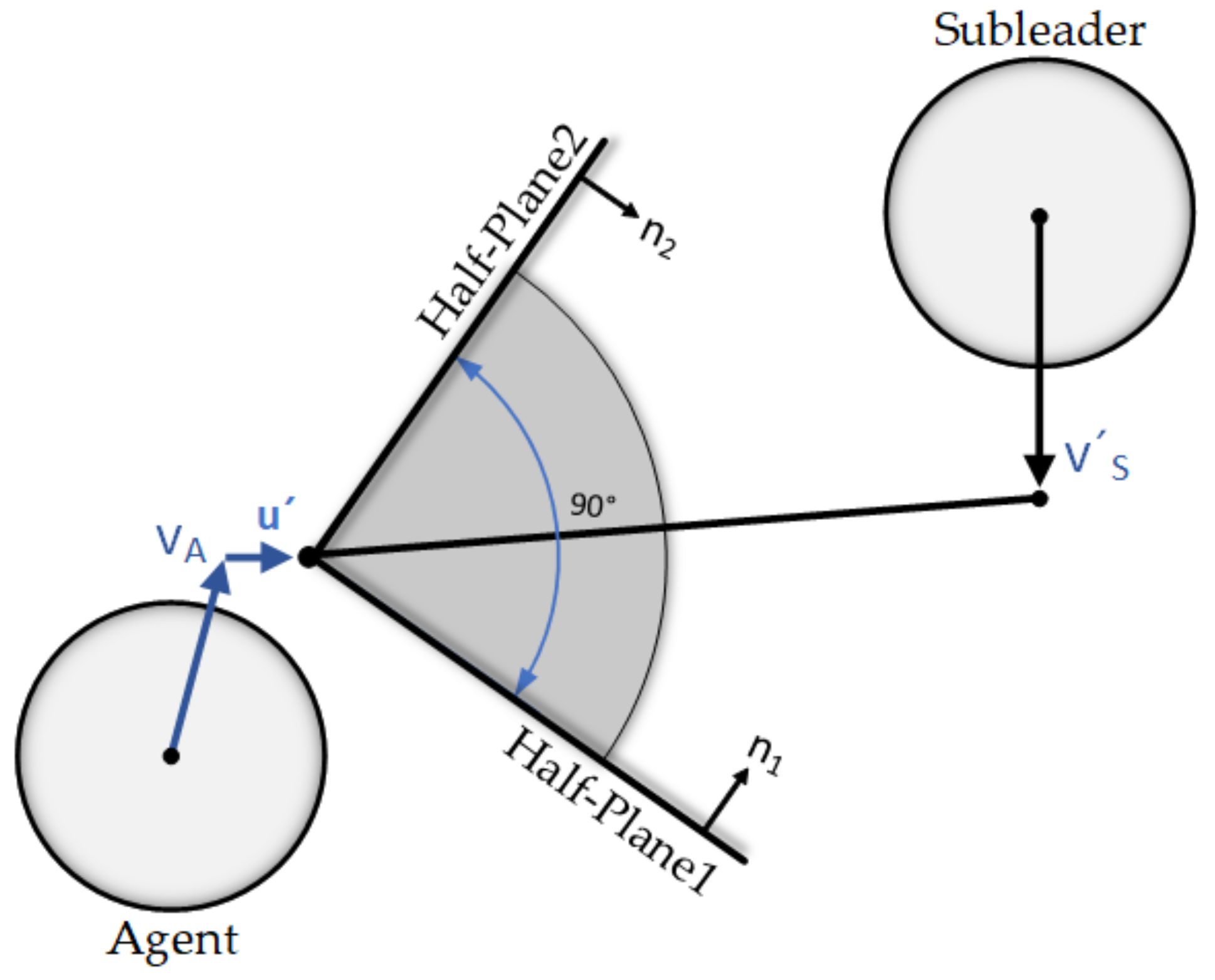
The situation in which the measured density expresses the existence of obstacles, makes the agent find the nearest neighbor that is closer to the leader (we will discuss further in more details) and then, changes its direction toward one unit vector of the reverse velocity behind the subleader (Figure 5). The reason for doing this is that it leads the agent in an appropriate distance from its subleader and makes a narrow formation for the group when it is necessary for being able to pass through narrow spaces easier and it can help agents to find the path through tight and challenging obstacles. For agents to find their direction toward the subleader, we simply rotate the relative position between the agent and the subleader by 45 degrees clockwise and vice versa. Except for the calculation of relative position (), all other steps are similar to Equation (3)–(6).
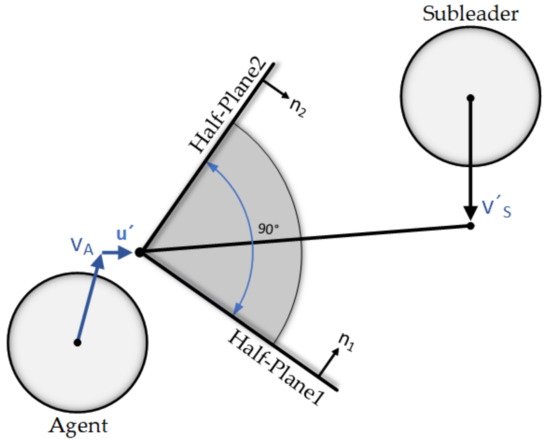
Figure 5.
Producing additional half-planes in the direction of the subleader. is the reverse unit velocity of the subleader.
The algorithm that finds the best neighbor as the subleader for each agent is shown in Algorithm 1. (see Section 4 for more details) which is used in Line 9 for deciding whether to skip that neighbor or keep it as one of the subleader candidates, is remarkable. It’s a factor that helps to determine the maximum distance a good subleader can have from the main leader based on the distance of the agent from the leader. For understanding the reason, let’s consider a situation when the agent’s nearest neighbor has more or equal distance from the leader than the agent itself. So, it is obvious that this neighbor cannot be a good choice for being the subleader. In our experiment, makes the agents choose a better neighbor. The function used in Line 1 which is called obstacleDensity, is related to the part discussed in Section 3.3. It takes the position of the agent and its unit velocity to compute the density of obstacles around that area. The purpose of Line 18 and 19 is that if no subleader is found, the agent chooses the main leader as its subleader. It happens for members in the first line of the formation.
| Algorithm 1: Finding the best subleader for each agent in challenging situations. |
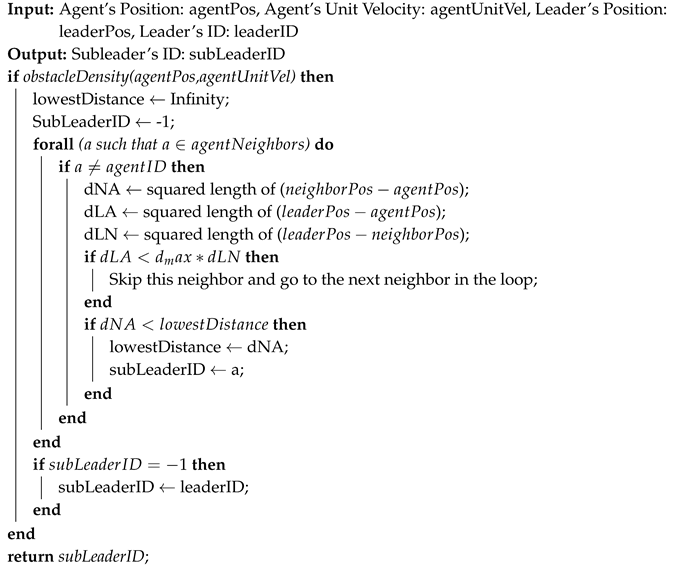 |
4. Experiments
For a better understanding of our method, the experimental results for our simulation are available in a video which is located at the following link—https://youtu.be/2JlQ3MJ8mcw (Supplementary Materials).
For experimentation, our method has been tested on a machine with the intel core i5-8265U processor, 8 GB RAM, and 1.80 GHz. In our algorithm, we specified the values for the parameters that we have discussed in previous sections as follows: (Section 3.1), (Section 3.1), (Section 3.2), (Section 3.3) and (Section 3.5). However, these values might be changed for new scenarios and purposes.
We have two main demonstrations here; the first one is the agents’ effort to maintain in their position in the group to make a specific shape while moving. For this issue, based on the leader and other agents’ velocity, some positions will be computed. If an agent is not in its estimated position while moving, they will select their optimal velocities from the intersection of all half-planes consisting of half-planes for collision avoidance (ORCA) and additional half-planes that guide the agent to the right spot in the group (DGB). Agents are performing this action continuously since the leader is moving and the positions for making the group formation are updating in each time step.
The second illustration is the agents’ behavior in the face of challenging obstacles like a tightened corridor for a big group of people to pass through. In this case, first, the density of obstacles in front of the agent will be computed using an ellipse and if it shows the presence of obstacles, the agent tries to find its nearest neighbor which is more near to the leader. Then simply by adding two half-plane restricting valid velocities and guiding the agent to follow its subleader, we will have more realistic and human-like behavior in this common situation.
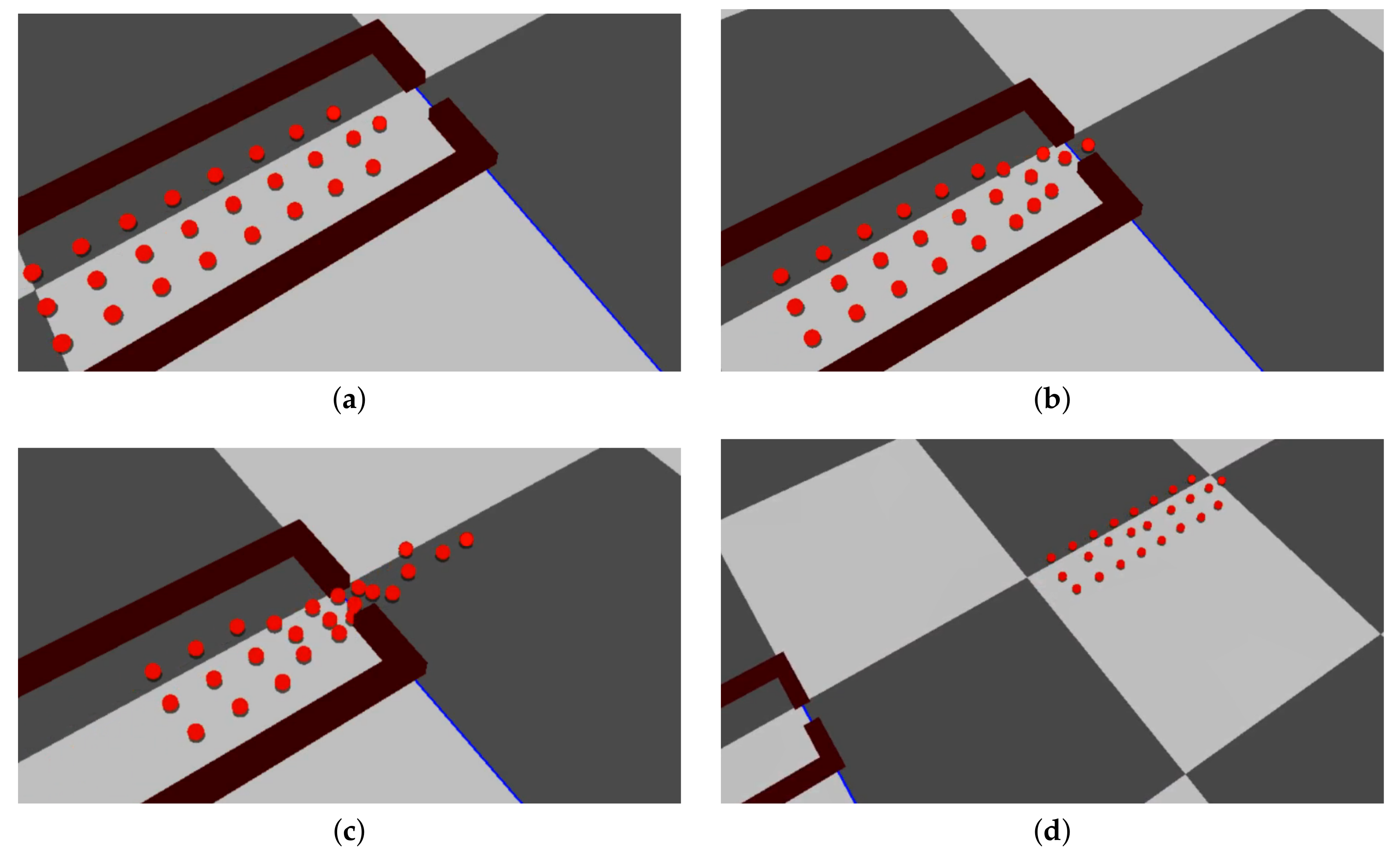
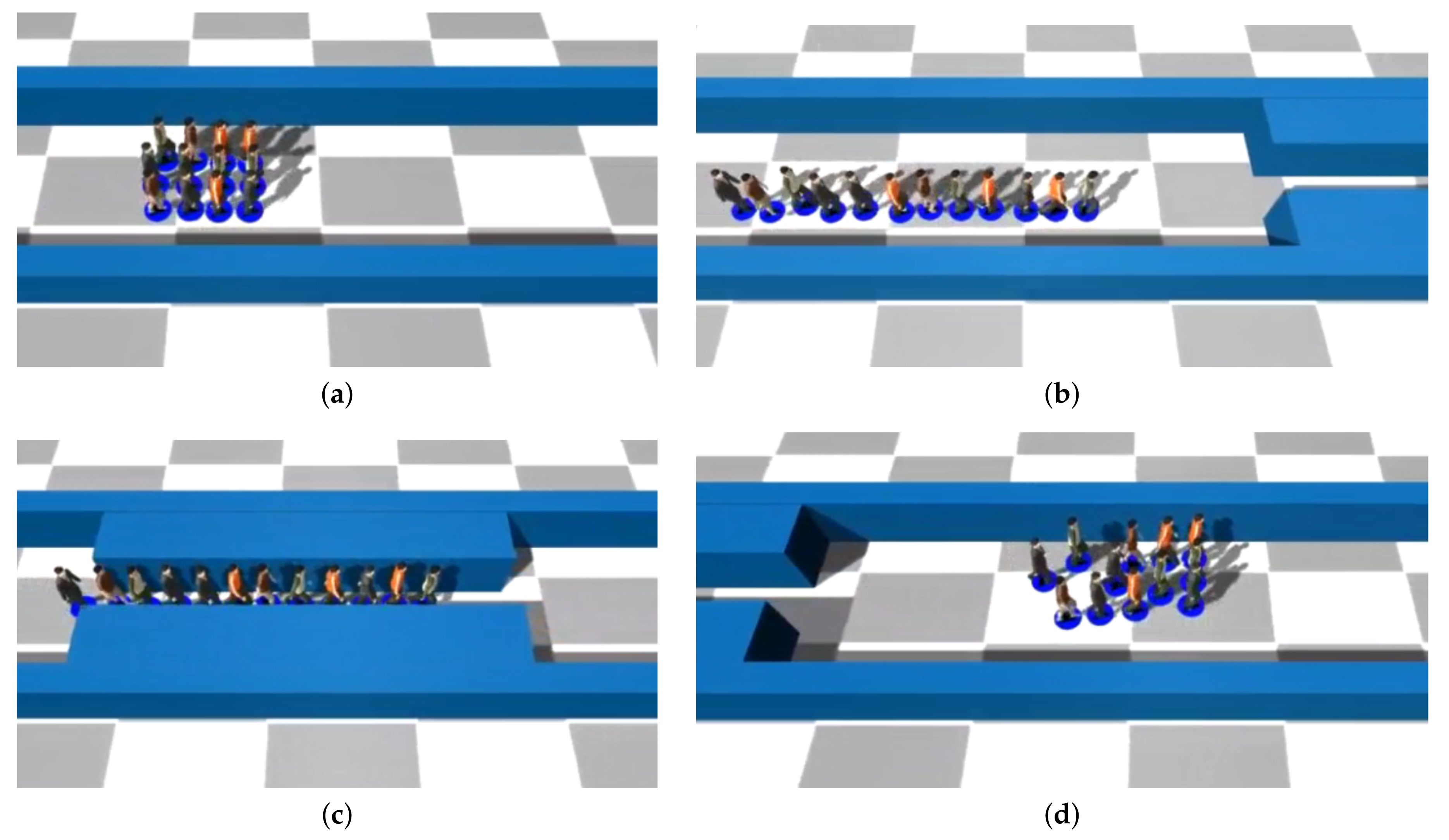
Experiments show that each agent’s behavior in front of other agents and obstacles is more realistic due to their independent and discretionary manner confronting avoidable components in the environment. We compare our method with one of the most related and recent works. According to Figure 6, for passing through a narrow corridor, just at the time when obstacles are visible for the agent, it will move toward its selected subleader to be able to find the best path easier; like what would happen if it was a real human. Notice the fact that the vision of humans is limited to a range of distances and it is going to be more limited when people are in groups. In our work, this characteristic of humans has been considered and agents will not change their formation unless they see some obstacles that have blocked their front path. While in Figure 7 [1], all agents in the group, at the same time, change their original formation and make a line shape before reaching to the obstacles. This event is not usual among a group of people passing through a tighten area like a doorway and can be time-consuming for a large number of agents in a group. Furthermore, their work requires changing the preprocessing step in the algorithm which is not doing automatically. Also, storing the relationship between all of the members in the group in a matrix [1] for having this transformation in the group’s shape, can make a lot of memory usage especially for large groups.
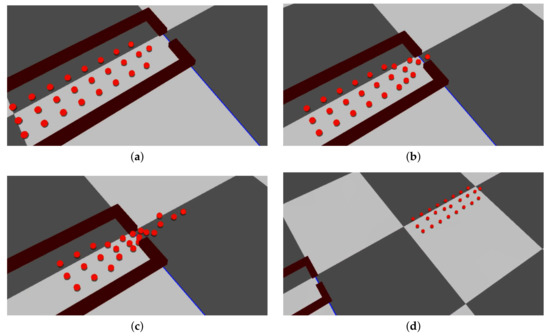
Figure 6.
A demonstration of our approach in four frames. The members of a group keep their formation as much as possible: (a) A group of agents in a uniform formation approaching a narrow doorway. (b,c) Each agent, when realizes that its front path has been blocked by obstacles, will follow the selected subleader until passes that area completely (d) When the density of obstacles for agents is zero, they return to their previous formation.
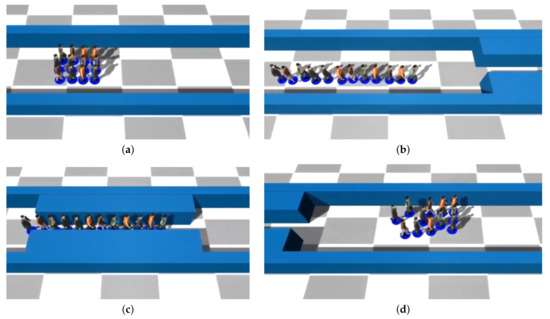
Figure 7.
The behavior of a group in front of a narrow space according to Reference [1]: (a) Agents in a uniform formation are approaching the corridor. (b,c) All of the agents will change their formation to the line shape at the same time for being able to pass through the narrow space. (d) They change to their previous formation all together after passing the corridor.
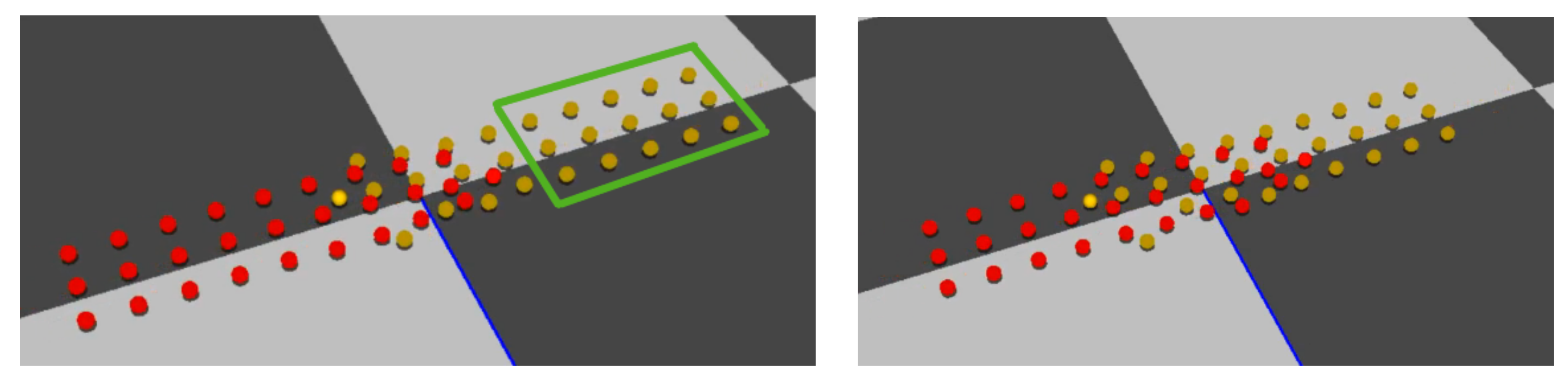
Another controversial feature of Reference [1] is that, in each cycle, each agent chooses some other members as its connection-agents among a predefined set called connection-neighbors. connection-agents is another subset of neighbors that the agent tries to stay close to. Making agents always being close to others yields to none-realistic avoidance behavior. In Figure 8, our method, agents have their independent manner for collision avoidance and formation maintenance. As it is noticeable, agents in one group that are far away from other avoidable agents in the opposite direction, will not disturb the group’s formation (the green rectangle). In our opinion, keeping the group’s formation should have a high priority. While in Figure 9, the marked agent (with the red circle around it) changes its direction and follows another agent although nearby its position, there are no avoidable agents in its front way and no reason to change the moving direction. Thus, there will be unnecessary movements for members in a group avoiding a small number of individual agents coming from the opposite direction. Accordingly, we can conclude that the process of keeping formation that should have a high priority for a group, has been given less attention in their work. However, in our work, groups try their best to not destroy their formation unless they have to.
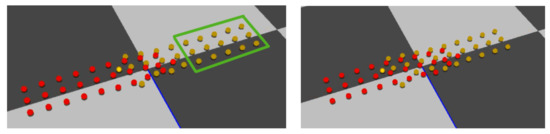
Figure 8.
Our model containing two groups of agents confronting each other in opposite directions. Agents remain in their formation when there is no danger of colliding with other agents. In another word, while the agents in the first lines of the group are changing their position for collision avoidance behavior, other agents in the last lines keep the group’s formation independently (agents in the green rectangle).

Figure 9.
A group confronting individual agents coming from the opposite direction, according to [1]: (a) Although the agent in the red square has enough space to walk without any change in the group’s formation, it just follows its connected-agents without awareness of the surrounded area. This behavior makes unnecessary movements for all agents. (b) The big gap between the subgroups resulting from a small number of opposite agents is noticeable in this frame.
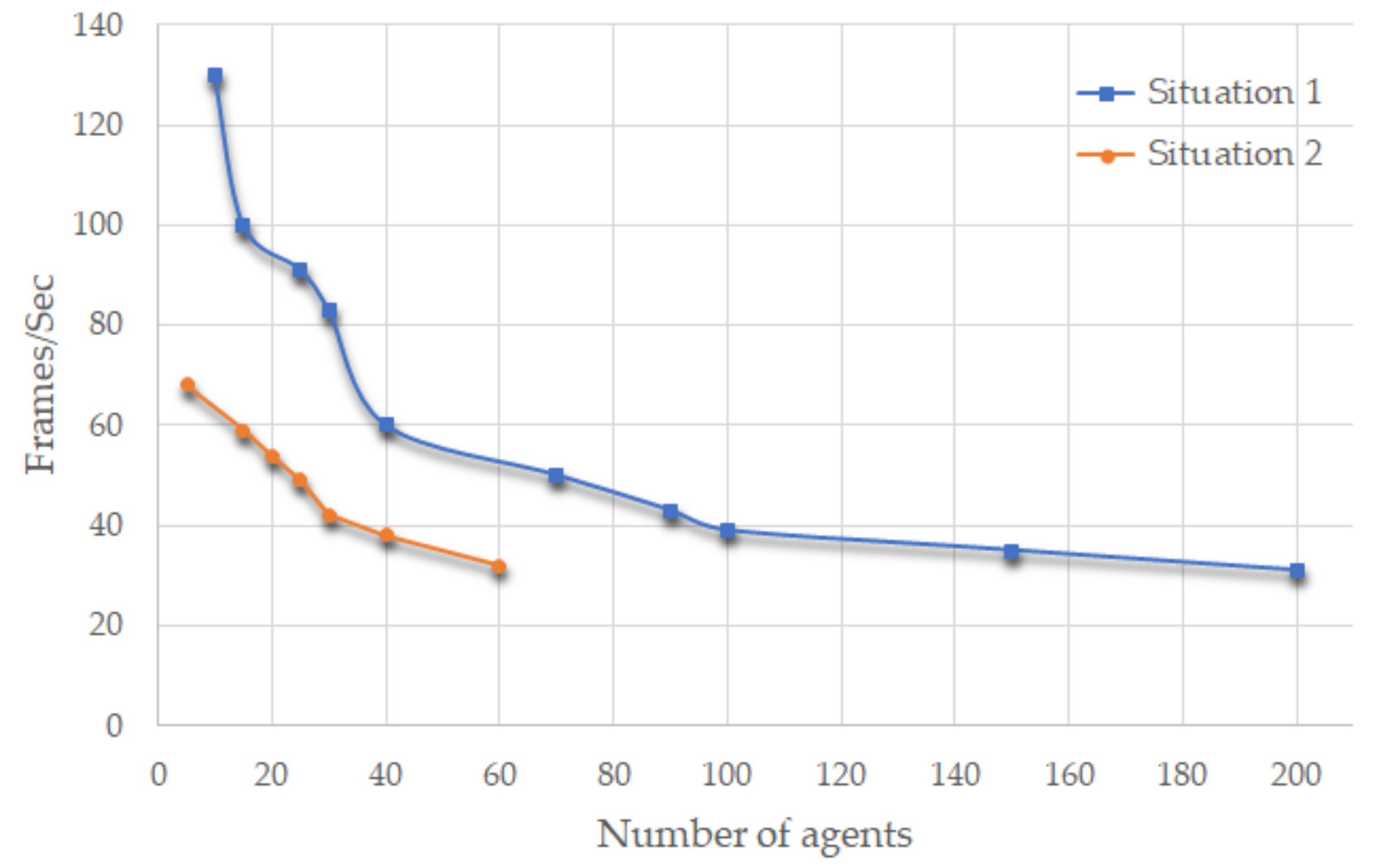
We compared the average of frames/second (fps) for the different number of agents in our two main situations separately (Figure 10). The situation in which agents are dealing with each other without any obstacles is shown in the upper (blue) graph and the lower graph is for a situation with both agents and static obstacles. Therefore, we should notice that in the second situation the fps decrease due to the presence of obstacles. In the case of using a more powerful machine for testing the algorithm, we can get higher values for fps in Figure 10. But for our simulation, it was not necessary. Also, we have made a comparison between our DGB algorithm and the most recent and relevant models (Table 1). The last two columns of the table present the main differences in our method from the others. First, for keeping any formation by members of a group, it is not always necessary that each individual has connections to his/her neighbors. In other words, having all of the members connected can make unnecessary movements, which are obvious in Figure 9. Second, in critical situations, like a narrow corridor, other methods provide one or a limited set of formations for a group to change into it/them when there is a large density of agents around the group or when the group is confronting with tough areas. However, by examining a crowd of real people more carefully, we can notice that it is rare that a group, having an original formation that is trying to keep it while moving, changes its whole shape just for passing the challenging situation. While it is usual that a group that has a goal formation tries its best to maintain in that original formation even in hard situations. To conclude, because keeping the original formation is the main goal for a group, changing formation in some specific situations can be unrealistic and might take a lot of time, especially for large groups.
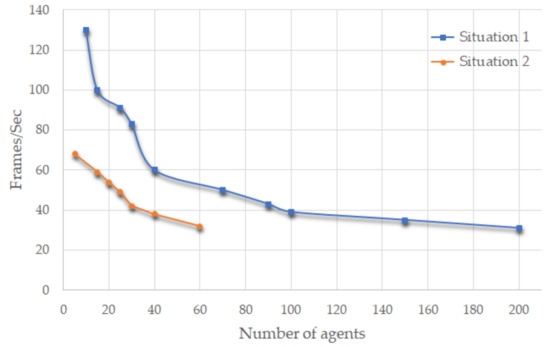
Figure 10.
Frame rates for the different number of agents in a group based on two main situations. Situation 1 is the confrontation of two groups or one group with individual agents (without any obstacle). Situation 2 is the group in a challenging area (with obstacles).

Table 1.
Comparison between our method and the three recent similar models.
5. Conclusions and Future Works
This paper has presented a new algorithm called “Discretionary Group Behavior (DGB)” for simulating more realistic group behaviors in virtual environments. We take advantage of RVO2 for the collision avoidance strategy and extend it to work for grouping purposes. We have two usual cases—firstly, the group’s attitude toward keeping its formation while moving. Secondly, the group’s effort to avoid challenging obstacles in the best way that does not have effects on the group’s shape as much as possible. In both cases, by adding computed half-planes to the list of other collision avoidance half-planes, we can have a more realistic and discretionary motion of agents in a group compared to the previous works.
While our method has shown acceptable group behaviors, there can be other tasks for possible improvements. First, A* has been used for the pathfinding algorithm. During the process, this algorithm makes a grid partition from the environment and tries to discover the best partition in each cycle to find the closest path. The problem is that it cannot return to the previous partition if the current one and its neighbors are not possible to take. Therefore, implementing other intelligent algorithms for path planning can help the leader to not stock over obstacles in any different kinds of complicated environments.
Second, our method has been tested in two main scenarios. Thus, we have a plan to expand its usage into all possible scenarios consisting of all kinds of agents and static or dynamic obstacles.
Third, our other idea for future works is to simulate groups of agents during protests situations. In this kind of model, the formation and the number of agents are not fixed. Thus, it makes the modeling process more difficult. Imagine a person who starts the protest and, during walking, other people in that way join the group over time. Then, the group’s formation is going to change depending on the number of agents.
Finally, as mentioned by Peters C. and Ennis [26], during a more believable behavior, the group’s formation may not strictly be maintained when there are no other agents or obstacles for avoiding them. Like a situation when a group of people is walking together and some of them walk faster or slower. Hence, in our future work, we shall introduce a new version of our method which is more intelligent and human-like during groups’ movements.
Supplementary Materials
The accompanying video is available online at https://youtu.be/2JlQ3MJ8mcw.
Author Contributions
Methodology, N.S. and M.S.; software, N.S.; investigation, N.S.; writing—original draft preparation, N.S.; writing—review and editing, M.S. and N.S.; supervision, M.S.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2018R1D1A1B07048414).
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, Z.; Charalambous, P.; Bruneau, J.; Peng, Q.; Pettré, J. Group Modeling: A Unified Velocity-Based Approach. Comput. Graph. Forum 2017, 36, 45–56. [Google Scholar] [CrossRef]
- Van Den Berg, J.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-body collision avoidance. Robot. Res. 2011, 3–9. [Google Scholar] [CrossRef]
- How Far Can We See and Why. Available online: https://www.healthline.com/health/how-far-can-the-human-eye-see (accessed on 25 April 2020).
- Takahashi, S.; Yoshida, K.; Kwon, T.; Lee, K.H.; Lee, J.; Shin, S.Y. Spectral-based group formation control. Comput. Graph. Forum 2008, 639–648. [Google Scholar] [CrossRef]
- Nasir, F.M.; Noma, T.; Oshita, M.; Yamamoto, K.; Sunar, M.S.; Mohamad, S.; Honda, Y. Simulating group formation and behaviour in dense crowd. In Proceedings of the 15th ACM SIGGRAPH Conference on Virtual-Reality Continuum and Its Applications in Industry, Zhuhai, China, 3–4 December 2016; Volume 1, pp. 289–292. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Karamouzas, I.; Overmars, M. Simulating and evaluating the local behavior of small pedestrian groups. IEEE Trans. Vis. Comput. Graph. 2011, 18, 394–406. [Google Scholar] [CrossRef] [PubMed]
- Moussaïd, M.; Perozo, N.; Garnier, S.; Helbing, D.; Theraulaz, G. The walking behaviour of pedestrian social groups and its impact on crowd dynamics. PLoS ONE 2010, 5, e10047. [Google Scholar] [CrossRef] [PubMed]
- Karamouzas, I.; Overmars, M. Simulating human collision avoidance using a velocity-based approach. Eurograph. Assoc. 2010. [Google Scholar] [CrossRef]
- Qiu, F.; Hu, X. Modeling group structures in pedestrian crowd simulation. Simul. Model. Pract. Theory 2010, 18, 190–205. [Google Scholar] [CrossRef]
- Van den Berg, J.; Lin, M.; Manocha, D. Reciprocal velocity obstacles for real-time multi-agent navigation. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1928–1935. [Google Scholar]
- He, L.; Pan, J.; Manocha, D. Reciprocal Multi-Agent Navigation with Dynamic Group Behaviors. Available online: https://www.andrew.cmu.edu/user/gswagner/workshop/IJCAI_2016_WOMPF_paper_3.pdf (accessed on 1 April 2020).
- Park, S.I.; Quek, F.; Cao, Y. Simulating and animating social dynamics: Embedding small pedestrian groups in crowds. Comput. Animat. Virtual Worlds 2013, 24, 155–164. [Google Scholar] [CrossRef]
- Zhang, Y.; Pettre, J.; Qin, X.; Donikian, S.; Peng, Q. A local behavior model for small pedestrian groups. In Proceedings of the 2011 12th International Conference on Computer-Aided Design and Computer Graphics, Jinan, China, 15–17 September 2011; pp. 275–281. [Google Scholar]
- RVO2 Library Documentation. Available online: http://gamma.cs.unc.edu/RVO2/documentation/2.0 (accessed on 1 April 2020).
- Gu, Q.; Deng, Z. Generating freestyle group formations in agent-based crowd simulations. IEEE Comput. Graph. Appl. 2011, 33, 20–31. [Google Scholar]
- Zhang, P.; Liu, H.; Ding, Y.-H. Crowd simulation based on constrained and controlled group formation. Vis. Comput. 2015, 31, 5–18. [Google Scholar] [CrossRef]
- Braun, A.; Musse, S.R.; de Oliveira, L.P.L.; Bodmann, B.E. Modeling individual behaviors in crowd simulation. In Proceedings of the 11th IEEE International Workshop on Program Comprehension, Portland, OR, USA, 10–11 May 2003; pp. 143–148. [Google Scholar]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef] [PubMed]
- Rojas, F.; Tarnogol, F.; Yang, H.S. Dynamic social formations of pedestrian groups navigating and using public transportation in a virtual city. Vis. Comput. 2016, 32, 335–345. [Google Scholar] [CrossRef]
- Rojas, F.A.; Park, J.H.; Yang, H.S. Group agent-based steering for the realistic corner turning and group movement of pedestrians in a crowd simulation. In Proceedings of the Computer Animation and Social Agents (CASA 2013), Istanbul, Turkey, 4 February 2013. [Google Scholar]
- Rojas, F.A.; Yang, H.S. Immersive human-in-the-loop HMD evaluation of dynamic group behavior in a pedestrian crowd simulation that uses group agent-based steering. In Proceedings of the 12th ACM SIGGRAPH International Conference on Virtual-Reality Continuum and Its Applications in Industry, Hong Kong, China, 17–19 November 2013; pp. 31–40. [Google Scholar] [CrossRef]
- Curtis, S.; Guy, S.J.; Zafar, B.; Manocha, D. Virtual tawaf: A case study in simulating the behavior of dense, heterogeneous crowds. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 128–135. [Google Scholar]
- Ennis, C.; O’Sullivan, C. Perceptually plausible formations for virtual conversers. Comput. Animat. Virtual Worlds 2012, 23, 321–329. [Google Scholar] [CrossRef]
- Cui, X.; Shi, H. A*-based pathfinding in modern computer games. Int. J. Comput. Sci. Netw. Secur. 2011, 11, 125–130. [Google Scholar]
- Peters, C.; Ennis, C. Modeling groups of plausible virtual pedestrians. IEEE Comput. Graph. Appl. 2009, 29, 54–63. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).