Walsh Transform and Empirical Mode Decomposition Applied to Reconstruction of Velocity and Displacement from Seismic Acceleration Measurement
Abstract
:1. Introduction
2. The Proposed Method
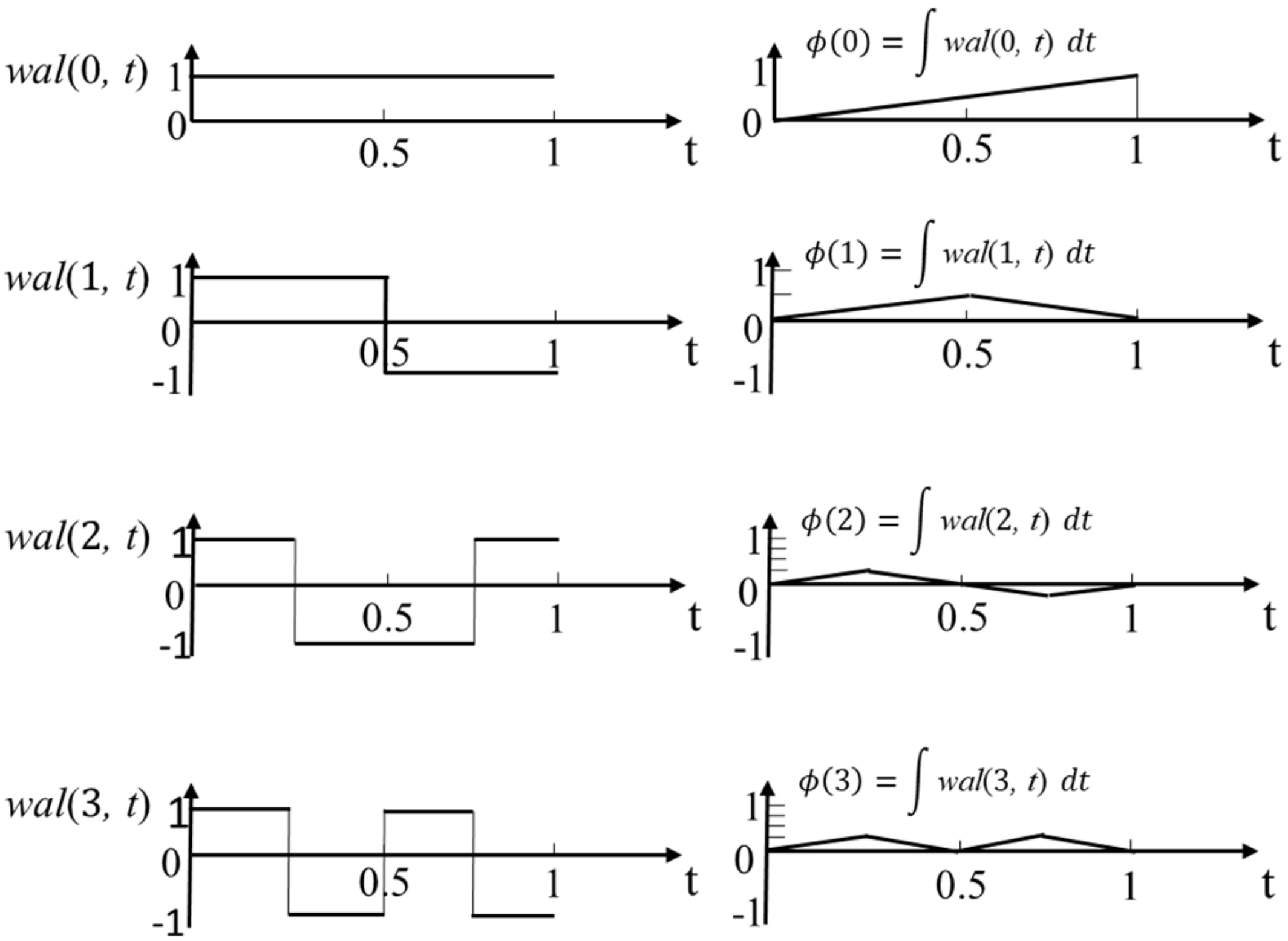
2.1. Walsh Series and Transform
2.2. Walsh Transform Versus Fourier Transform
2.3. Empirical Mode Decomposition (EMD)
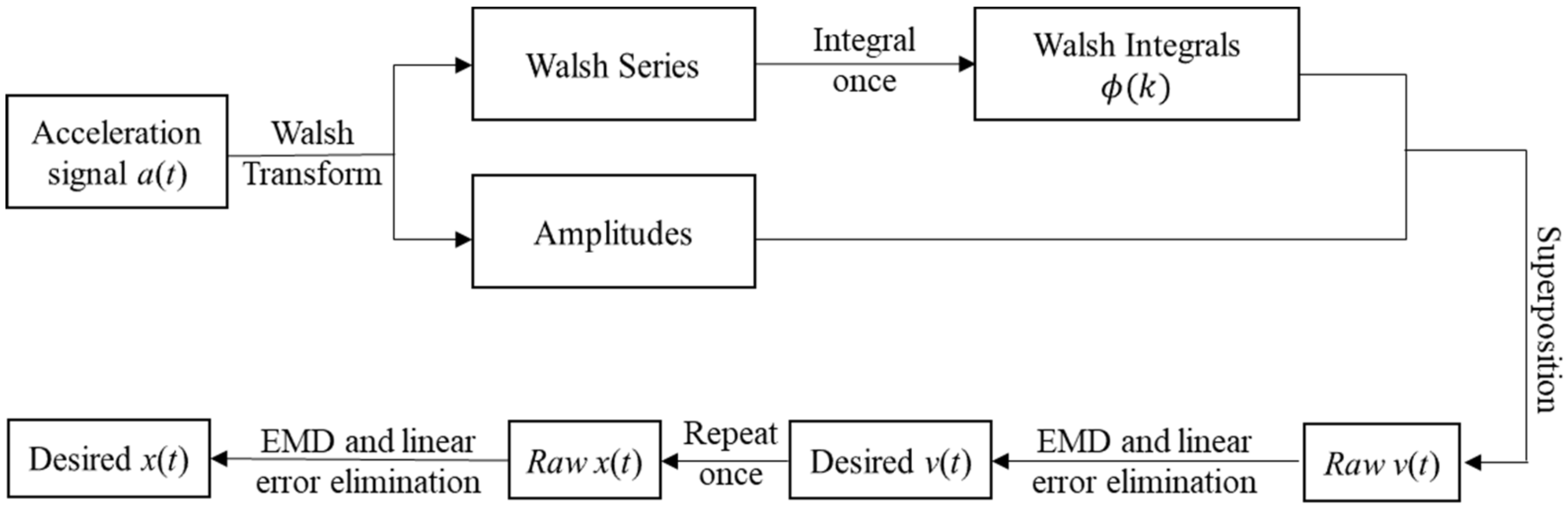
2.4. Signal Reconstruction
2.5. Numerical Effectiveness and Elimination of Trend Error
3. Case Studies and Analyses
3.1. Case 1: Vibration of a SDOF System
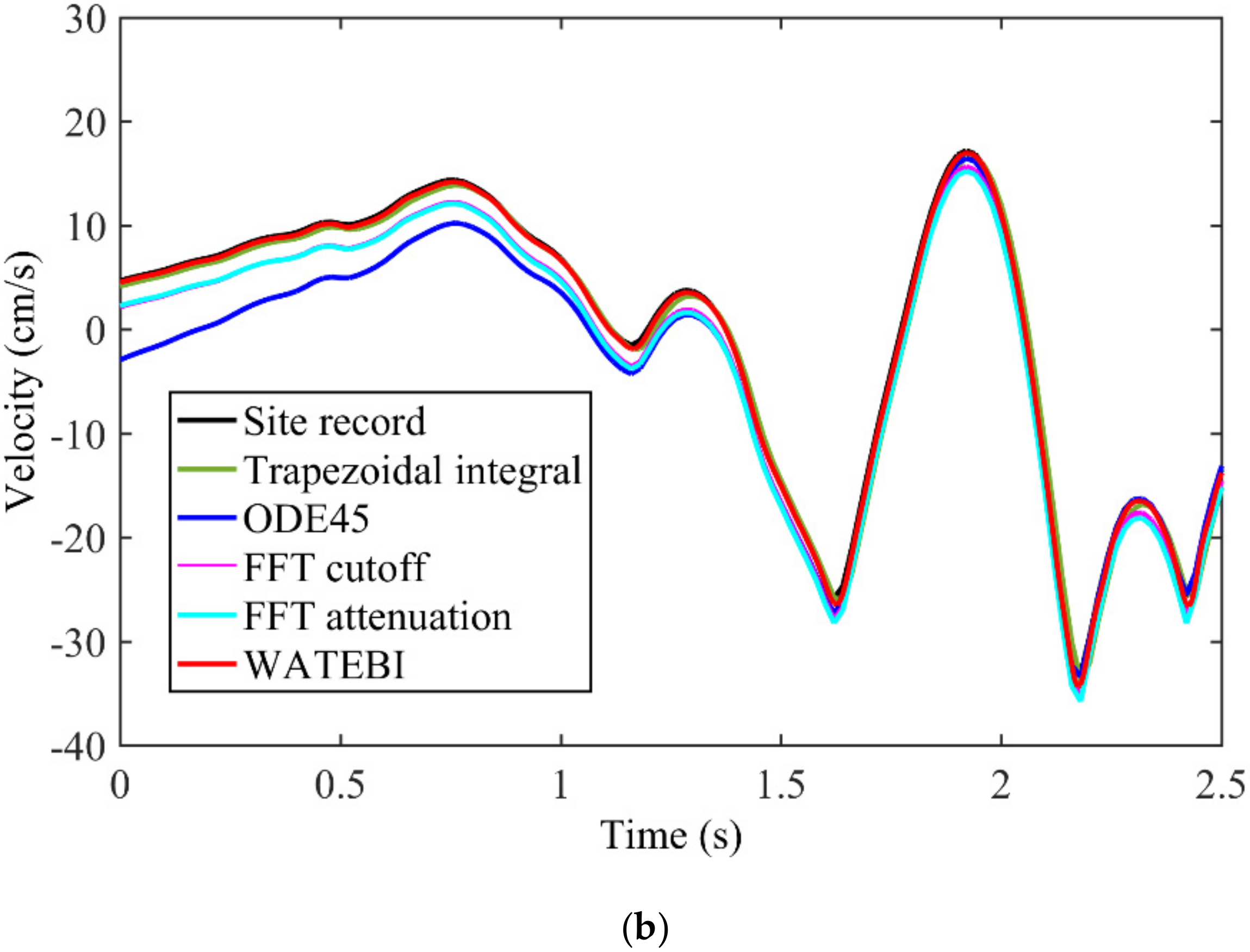
3.2. Case 2: El Centro Earthquake Ground Motion
3.3. Case 3: Kaikoura Earthquake in The South Island of New Zealand
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, Y.J. A Study on Integral Algorithm for Acceleration Test to Get Displacement and Application. Master’s Thesis, Chongqing University, Chongqing, China, 2013. [Google Scholar]
- Housner, G.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.; Spencer, B.; Yao, J.T. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Smyth, A.; Wu, M. Multi-rate Kalman filtering for the data fusion of displacement and acceleration response measurements in dynamic system monitoring. Mech. Syst. Signal Pr. 2007, 21, 706–723. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Earthquake magnitude, intensity, energy, and acceleration. Bull. Seismol. Soc. Am. 1942, 32, 163–191. [Google Scholar]
- Berg, G.; Housner, G. Integrated velocity and displacement of strong earthquake ground motion. Bull. Seismol. Soc. Am. 1961, 51, 175–189. [Google Scholar]
- Li, Q.; Wang, T.; Xu, Y. The Modification of the Vibration Parameter Transform Based on Frequency Domain Integration. Modular. Mach. T. Auto. Man. Tec. 2005, 9, 60–61. [Google Scholar]
- Hamming, R.W. Digital Filters, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Wang, G.Q.; Boore, D.M.; Igel, H.; Zhou, X.Y. Some observations on colocated and closely spaced strong ground-motion records of the 1999 Chi-Chi, Taiwan, earthquake. Bull. Seismol. Soc. Am. 2003, 93, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Liao, W.; Lamoureux, M.P. Antileakage least-squares spectral analysis for seismic data regularization and random noise attenuation. Geophysics 2018, 83, 157–170. [Google Scholar] [CrossRef]
- Ghaderpour, E. Multichannel antileakage least-squares spectral analysis for seismic data regularization beyond aliasing. Acta Geophys. 2019, 67, 1349–1363. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, Y.; Pham, D.; Lambaré, G. Antileakage Fourier transform for seismic data regularization. Geophysics 2005, 70, 87–95. [Google Scholar] [CrossRef]
- Guo, J.; Zheng, Y.; Liao, W. High fidelity seismic trace interpolation. In Proceedings of the SEG Annual Meeting, New Orleans, LA, USA, 18–23 October 2015. [Google Scholar]
- Zhou, X.X.; Chen, E.K.; lv, G.Q.; Liu, L.X. The Processing of Vibration Acceleration Signal Based on Numerical Integration and LMS. Process. Autom. Instrum. 2006, 9, 51–53. [Google Scholar]
- Park, K.T.; Kim, S.H.; Park, H.S.; Lee, K.W. The determination of bridge displacement using measured acceleration. Eng. Struct. 2005, 27, 371–378. [Google Scholar] [CrossRef]
- Lee, H.S.; Hong, Y.H.; Park, H.W. Design of an FIR filter for the displacement reconstruction using measured acceleration in low-frequency dominant structures. Int. J. Numer. Meth. Eng. 2009, 82, 403–434. [Google Scholar] [CrossRef]
- Hong, Y.H.; Kim, H.K.; Lee, H.S. Reconstruction of dynamic displacement and velocity from measured accelerations using the variational statement of an inverse problem. J. Sound Vib. 2010, 329, 4980–5003. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X. Application of Matlab in Processing of Vibration Signals; China Water & Power Press: Beijing, China, 2006. [Google Scholar]
- Huang, N.E.; Shen, S. Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Huang, N.E.; Attoh-Okine, N.O. The Hilbert-Huang Transform in Engineering; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inform. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Peter, W.T.; Chu, F. A comparison study of improved Hilbert-Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Pr. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D. LSWAVE: A MATLAB software for the least-squares wavelet and cross-wavelet analyses. GPS Solut. 2019, 23, 50. [Google Scholar] [CrossRef]
- Walsh, J.L. A closed set of normal orthogonal functions. Am. J. Math. 1923, 45, 5–24. [Google Scholar] [CrossRef] [Green Version]
- Horadam, K.J. Hadamard Matrices and Their Applications; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Beauchamp, K.G. Walsh Functions and Their Applications; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Corrington, M. Solution of differential and integral equations with Walsh functions. IEEE Trans. Circuit Theory 1973, 20, 470–476. [Google Scholar] [CrossRef]
- Aloui, N.; Bousselmi, S.; Cherif, A. Speech Compression Based on Discrete Walsh Hadamard Transform. Int. J. Inform. Eng. Electron. Bus. 2013, 5, 59. [Google Scholar] [CrossRef] [Green Version]
- Ashrafi, A. Walsh–Hadamard Transforms: A Review. Adv. Imag. Elect. Phys. 2017, 201, 1–55. [Google Scholar]
- Jayathilake, A.A.C.A.; Perera, A.A.I.; Chamikara, M.A.P. Discrete Walsh-Hadamard transform in signal processing. Int. J. Res. Inf. Technol. 2013, 1, 80–89. [Google Scholar]
- Press, W.H. The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. Proceedings of IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado, Italy, 8–11 June 2003. [Google Scholar]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Proc. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef] [Green Version]
- Hahn, B. Essential MATLAB for Scientists and Engineers, 3rd ed.; Pearson Education: Cape Town, South Africa, 2002. [Google Scholar]
- Travis, J.; Kring, J. LabVIEW for Everyone; Prentice-Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Lindfield, G.; Penny, J. Numerical Methods: Using MATLAB, 4th ed.; Academic Press: London, UK, 2018. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]













| Algorithms | Average Peak Error (%) | Maximum Peak Error (%) | Root-Mean-Square Error |
|---|---|---|---|
| Trapezoidal integral | 0.32 | 0.33 | 0.12 |
| Matlab Ode45 | 0.05 | 0.05 | 0.01 |
| Low-frequency cutoff | 0.83 | 0.91 | 0.04 |
| Low-frequency attenuation | - | - | - |
| WATEBI | 0.43 | 0.57 | 0.02 |
| Algorithms | Average Peak Error (%) | Maximum Peak Error (%) | Root-Mean-Square Error |
|---|---|---|---|
| Trapezoidal integral | 0.21 | 0.26 | 0.07 |
| Matlab Ode45 | 0.39 | 0.6 | 0.01 |
| Low-frequency cutoff | 0.4 | 0.47 | 0.04 |
| Low-frequency attenuation | 10.85 | 21.43 | 0.12 |
| WATEBI | 0.19 | 0.23 | 0.02 |
| Algorithms | Average Peak Error (%) | Maximum Peak Error (%) | Root-Mean-Square Error |
|---|---|---|---|
| Trapezoidal integral | 1.63 | 1.68 | 0.51 |
| Matlab Ode45 | 3.86 | 7.04 | 1.05 |
| Low-frequency cutoff | 3.33 | 6.42 | 0.64 |
| Low-frequency attenuation | - | - | - |
| WATEBI | 1.47 | 2.47 | 0.32 |
| Algorithms | Average Peak Error (%) | Maximum Peak Error (%) | Root-Mean-Square Error |
|---|---|---|---|
| Trapezoidal integral | 6.81 | 12.55 | 0.77 |
| Matlab Ode45 | 7.98 | 13.87 | 1.15 |
| Low-frequency cutoff | 11.04 | 11.09 | 1.33 |
| Low-frequency attenuation | 11.73 | 12.41 | 1.23 |
| WATEBI | 5.93 | 8.71 | 0.74 |
| Algorithms | Average Peak Error (%) | Maximum Peak Error (%) | Root-Mean-Square Error |
|---|---|---|---|
| Trapezoidal integral | 0.33 | 0.65 | 1.68 |
| Matlab Ode45 | 0.32 | 0.51 | 0.10 |
| Low-frequency cutoff | 1.77 | 2.46 | 1.38 |
| Low-frequency attenuation | - | - | - |
| WATEBI | 1.04 | 1.94 | 0.75 |
| Algorithms | Average Peak Error (%) | Maximum Peak Error (%) | Root-Mean-Square Error |
|---|---|---|---|
| Trapezoidal integral | 0.63 | 0.69 | 0.61 |
| Matlab Ode45 | 2.17 | 2.45 | 0.77 |
| Low-frequency cutoff | 4.35 | 7.80 | 1.58 |
| Low-frequency attenuation | 0.91 | 0.96 | 0.12 |
| WATEBI | 0.64 | 0.73 | 0.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zheng, X.Y. Walsh Transform and Empirical Mode Decomposition Applied to Reconstruction of Velocity and Displacement from Seismic Acceleration Measurement. Appl. Sci. 2020, 10, 3509. https://doi.org/10.3390/app10103509
Zhang Q, Zheng XY. Walsh Transform and Empirical Mode Decomposition Applied to Reconstruction of Velocity and Displacement from Seismic Acceleration Measurement. Applied Sciences. 2020; 10(10):3509. https://doi.org/10.3390/app10103509
Chicago/Turabian StyleZhang, Qi, and Xiang Yuan Zheng. 2020. "Walsh Transform and Empirical Mode Decomposition Applied to Reconstruction of Velocity and Displacement from Seismic Acceleration Measurement" Applied Sciences 10, no. 10: 3509. https://doi.org/10.3390/app10103509
APA StyleZhang, Q., & Zheng, X. Y. (2020). Walsh Transform and Empirical Mode Decomposition Applied to Reconstruction of Velocity and Displacement from Seismic Acceleration Measurement. Applied Sciences, 10(10), 3509. https://doi.org/10.3390/app10103509






