Monthly Reservoir Inflow Forecasting for Dry Period Using Teleconnection Indices: A Statistical Ensemble Approach
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
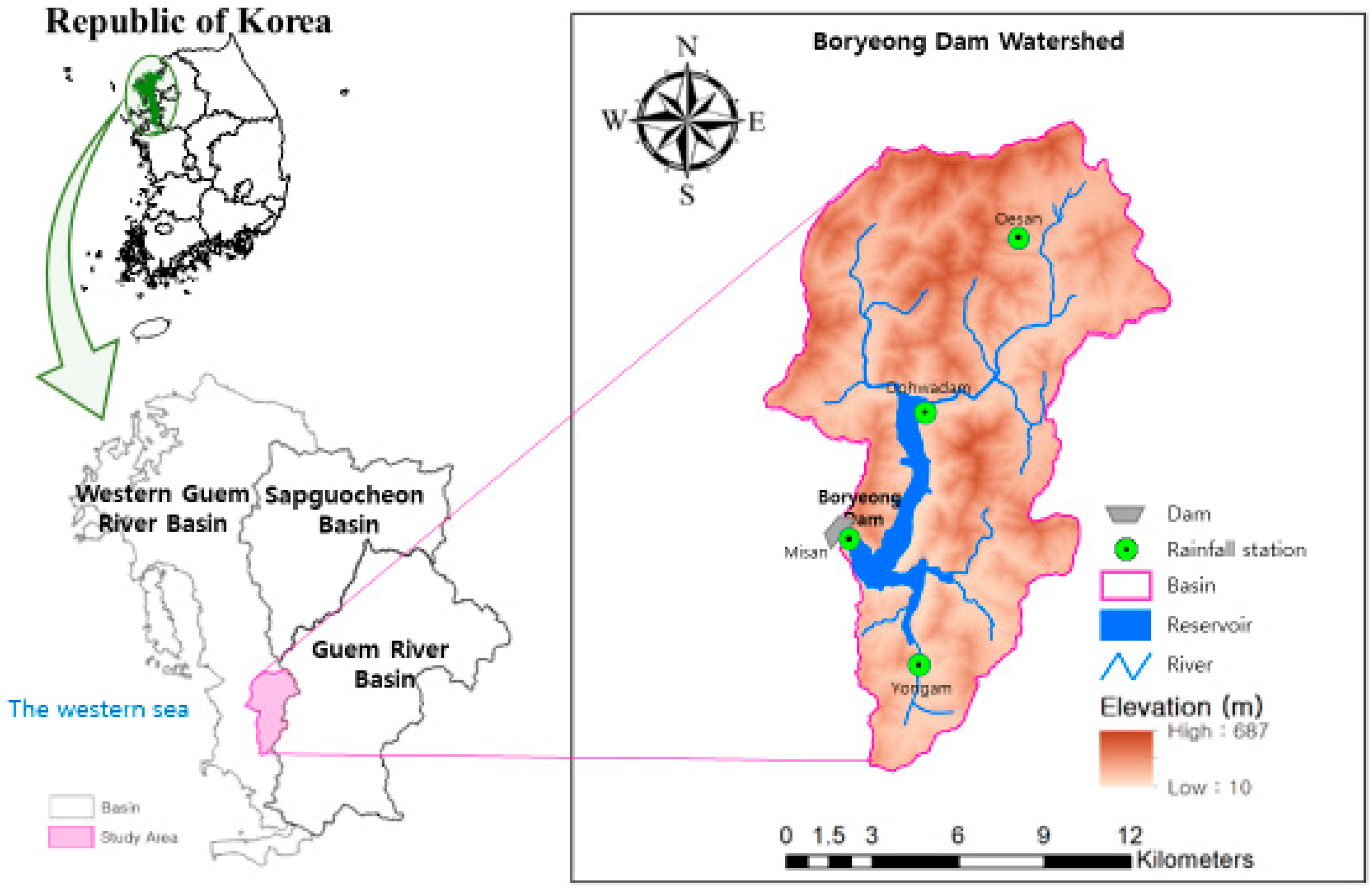
2.1. Study Site and Data Used
2.2. Methodology
2.2.1. Predictor Selection
2.2.2. Statistical Models
2.2.3. Model Validation
2.2.4. Model Evaluation
3. Results and Discussion
3.1. Selection of Oceanic-Atmospheric Indices
3.2. Individual Model Performance
3.3. Application of Ensemble Prediction
3.3.1. Ensemble Prediction Method
3.3.2. Application of Ensemble Prediction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jeong, W.; Rho, S.; Kim, Y. Assessment of Boryeong Multipurpose Dam’s Water Supply Capacity and Research on Drought Response; Chungnam Institute: Chungcheongnam-do, Korea, 2016. (In Korean) [Google Scholar]
- Lima, C.H.R.; Lall, U. Climate informed monthly streamflow forecasts for the Brazilian hydropower network using a periodic ridge regression model. J. Hydrol. 2010, 380, 438–449. [Google Scholar] [CrossRef]
- Sinha, A.; Sankarasubramanian, A.; Mazrooei, A. Decomposition of Sources of Errors in Monthly to Seasonal Streamflow Forecasts in a Rainfall–Runoff Regime. J. Hydrometeorol. 2014, 15, 2470–2483. [Google Scholar] [CrossRef] [Green Version]
- Harpold, A.A.; Sutcliffe, K.; Clayton, J.; Goodbody, A.; Vazquez, S. Does including soil moisture observations improve operational streamflow forecasts in snow-dominated watersheds? J. Am. Water Resour. Assoc. 2017, 53, 179–196. [Google Scholar] [CrossRef]
- Anderson, J.; van den Dool, H.; Barnston, A.; Chen, W.; Stern, W.; Ploshay, J. Present-day capabilities of numerical and statistical models for atmospheric extratropical seasonal simulation and prediction. Bull. Am. Meteorol. Soc. 1999, 80, 1349–1361. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. Global and Regional Scale Precipitation Patterns Associated with the El Niño/Southern Oscillation. Mon. Weather Rev. 1987, 115, 1606–1626. [Google Scholar] [CrossRef] [Green Version]
- Cayan, D.R.; Dettinger, M.D.; Diaz, H.F.; Graham, N.E. Decadal Variability of Precipitation over Western North America. J. Clim. 1998, 11, 3148–3166. [Google Scholar] [CrossRef]
- Piechota, T.C.; Dracup, J.A.; Fovell, R.G. Western US streamflow and atmospheric circulation patterns during El Nino Southern Oscillation. J. Hydrol. 1997, 201, 249–271. [Google Scholar] [CrossRef]
- McCabe, G.J.; Dettinger, M.D. Decadal variations in the strength of ENSO teleconnections with precipitation in the western United States. Int. J. Climatol. 1999, 19, 1399–1410. [Google Scholar] [CrossRef]
- Regonda, S.K.; Rajagopalan, B.; Clark, M. A new method to produce categorical streamflow forecasts. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Moss, M.E.; Pearson, C.P.; McKerchar, A.I. The Southern Oscillation index as a predictor of the probability of low streamflows in New Zealand. Water Resour. Res. 1994, 30, 2717–2723. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Piechota, T.C.; Dracup, J.A.; McMahon, T.A. El Nino/Southern Oscillation and Australian rainfall, streamflow and drought: Links and potential for forecasting. J. Hydrol. 1998, 204, 138–149. [Google Scholar] [CrossRef]
- Chen, C.-J.; Lee, T.-Y. Variations in the correlation between teleconnections and Taiwan’s streamflow. Hydrol. Earth Syst. Sci. 2017, 21, 3463–3481. [Google Scholar] [CrossRef] [Green Version]
- Chiew, F.H.S.; McMahon, T.A. Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability. Hydrol. Sci. J. 2002, 47, 505–522. [Google Scholar] [CrossRef] [Green Version]
- Xu, K.; Brown, C.; Kwon, H.-H.; Lall, U.; Zhang, J.; Hayashi, S.; Chen, Z. Climate teleconnections to Yangtze river seasonal streamflow at the Three Gorges Dam, China. Int. J. Climatol. 2007, 27, 771–780. [Google Scholar] [CrossRef] [Green Version]
- Chandimala, J.; Zubair, L. Predictability of stream flow and rainfall based on ENSO for water resources management in Sri Lanka. J. Hydrol. 2007, 335, 303–312. [Google Scholar] [CrossRef] [Green Version]
- Kalra, A.; Miller, W.P.; Lamb, K.W.; Ahmad, S.; Piechota, T. Using large-scale climatic patterns for improving long lead time streamflow forecasts for Gunnison and San Juan River Basins. Hydrol. Process. 2013, 27, 1543–1559. [Google Scholar] [CrossRef]
- Ouachani, R.; Bargaoui, Z.; Ouarda, T. Power of teleconnection patterns on precipitation and streamflow variability of upper Medjerda Basin. Int. J. Climatol. 2013, 33, 58–76. [Google Scholar] [CrossRef]
- Hidalgo-Munoz, J.M.; Gamiz, S.R.; Castro, Y.; Argueso, D.; Esteban, M.J. Long-range seasonal streamflow forecasting over the Iberian Peninsula using large-scale atmospheric and oceanic information. Water Resour. Res. 2015, 51, 3543–3567. [Google Scholar] [CrossRef] [Green Version]
- Schepen, A.; Zhao, T.; Wang, Q.J.; Zhou, S.; Feikema, P. Optimising seasonal streamflow forecast lead time for operational decision making in Australia. Hydrol. Earth Syst. Sci. 2016, 20, 4117–4128. [Google Scholar] [CrossRef] [Green Version]
- Zhao, T.; Schepen, A.; Wang, Q.J. Ensemble forecasting of sub-seasonal to seasonal streamflow by a Bayesian joint probability modelling approach. J. Hydrol. 2016, 541, 839–849. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.; Kim, J.; Kim, S. Assessment of Water Supply Stability for Drought-Vulnerable Boryeong Multipurpose Dam in South Korea Using Future Dry Climate Change Scenarios. Water 2019, 11, 2403. [Google Scholar] [CrossRef] [Green Version]
- EGIS: Environmental Geographic Information Services. Available online: https://egis.me.go.kr/main.do (accessed on 13 April 2020).
- WAMIS: Hydrologic Data of Dams. Available online: http://www.wamis.go.kr (accessed on 17 March 2020).
- Coley, D.M.; Waylen, P.R. Forecasting dry season streamflow on the Peace River at Arcadia, Florida, USA. J. Am. Water Resour. As. 2006, 42, 851–862. [Google Scholar] [CrossRef]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. The skill of seasonal ensemble low-flow forecasts in the Moselle River for three different hydrological models. Hydrol. Earth Syst. Sci. 2015, 19, 275–291. [Google Scholar] [CrossRef] [Green Version]
- Risva, K.; Nikolopoulos, D.; Efstratiadis, A. A framework for dry period low flow forecasting in Mediterranean streams. Water Resour. Manag. 2018, 32, 4911–4932. [Google Scholar] [CrossRef]
- CPC: Climate Information. Available online: http://www.cpc.ncep.noaa.gov/ (accessed on 17 March 2020).
- Mathias, S.; Merz, B.; Apel, H. Seasonal forecasting of hydrological drought in the Limpo Basin: A comparison of statistical methods. Hydrol. Earth Syst. Sci. 2017, 21, 1611–1629. [Google Scholar]
- Hair, J.F., Jr.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995; pp. 200–206. [Google Scholar]
- Zhang, Z.H.; Zhang, Q.; Singh, V.P. Univariate streamflow forecasting using commonly used data-driven models: Literature review and case study. Hydrolog. Sci. J. 2018, 63, 1091–1111. [Google Scholar] [CrossRef]
- Salas, J.; Fu, C.; Rajagopalan, B. Long-Range forecasting of Colorado streamflows based on hydrologic, atmospheric, and oceanic data. J. Hydrol. Eng. 2011, 16, 508–520. [Google Scholar] [CrossRef] [Green Version]
- Kabir, R.; Hsieh, W.; Cannon, A. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414, 284–293. [Google Scholar]
- Cheng, C.T.; Feng, Z.K.; Niu, W.J.; Liao, S.L. Heuristic methods for reservoir monthly inflow forecasting: A case study of Xinfengjiang Reservoir in Pearl River, China. Water 2015, 7, 4477–4495. [Google Scholar] [CrossRef]
- Sudheer, C.; Maheswaran, R.; Panigrahi, B.; Mathur, S. A hybrid SVM-PSO model for forecasting monthly streamflow. Neural Comput. Appl. 2014, 6, 1381–1389. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, J.Z.; Qin, H.; Zou, Q.; Li, Q.Q. Monthly streamflow forecasting based on improved support vector machine model. Expert. Syst. Appl. 2011, 10, 13073–13081. [Google Scholar] [CrossRef]
- Zhang, X.L.; Wang, H.X.; Peng, A.B.; Wang, W.C.; Li, B.J.; Huang, X.D. Quantifying the uncertainties in data-driven models for reservoir inflow prediction. Water Resour. Res. 2020, 34, 1479–1493. [Google Scholar] [CrossRef]
- Babaei, M.; Moeini, R.; Ehsanzadeh, E. Artificial neural network and support vector machine models for inflow prediction of dam reservoir (case study: Zayandehroud Dam reservoir). Water Resour. Manag. 2019, 6, 2203–2218. [Google Scholar] [CrossRef]
- Patel, S.; Hardaha, M.K.; Seetpal, M.K.; Madankar, K.K. Multiple linear regression model for stream flow estimation of Wainganga River. Am. J. Water Sci. Eng. 2016, 2, 1–5. [Google Scholar]
- Moradi, A.M.; Dariane, A.B.; Yang, G.; Block, P. Long-range reservoir inflow forecasts using large-scale climate predictors. Int. J. Clinatol. 2020, 22. [Google Scholar] [CrossRef]
- Hossain, I.; Rasel, H.M.; Imteaz, M.A.; Mekanik, F. Long-term seasonal rainfall forecasting using linear and non-linear modelling approaches: A case study for Western Australia. Meteorol. Atmos. Phys. 2020, 132, 131–141. [Google Scholar] [CrossRef]
- Esha, R.I.; Imteaz, M.A. Assessing the predictability of MLR models for long-term streamflow using lagged climate indices as predictors: A case study of Australia. Hydrol. Res. 2019, 50, 262–281. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 3rd ed.; HarperCollins College Publishers: New York, NY, USA, 1996. [Google Scholar]
- Guyon, I.; Matic, N.; Vapnik, V. Discovering informative patterns and data cleaning. In Advances in Knowledge Discovery and Data Mining; Usama, M.F., Gregory, P.S., Padhraic, S., Ramasamy, U., Eds.; American Association for Artificial Intelligence Press: Menlo Park, CA, USA, 1996; pp. 181–203. [Google Scholar]
- Müller, K.R.; Smola, A.J.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Proceedings of the Artificial Neural Networks—ICANN’97, Berlin/Heidelberg, Germany, 8–10 October 1997; pp. 999–1004. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zaefizadeh, M.; Khayatnezhad, M.; Gholamin, R. Comparison of Multiple Linear Regressions (MLR) and Artificial Neural Network (ANN) in Predicting the Yield Using its Components in the Hulless Barley. Am.-Eur. J. Agric. Environ. Sci. 2011, 11, 60–64. [Google Scholar]
- Govindaraju, R.S. Artificial Neural Networks in Hydrology. I: Preliminary Concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction; Wilks, D.S., Ed.; International Geophysics Series, 59; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Brooks/Cole Publishing: Pacific Grove, CA, USA, 1996. [Google Scholar]
- Kim, Y.; Kim, M.; Lee, W. An investigation of large-scale climate indices with the influence on temperature and precipitation variation in Korea. Atmosphere 2008, 18, 83–95. (In Korean) [Google Scholar]
- Kwon, H.H.; Brown, C.; Xu, K.Q.; Lall, U. Seasonal and annual maximum streamflow forecasting using climate information: Application to the Three Gorges Dam in the Yangtze River basin, China. Hydrol. Sci. J. 2009, 54, 582–595. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Interconnections between oceanic-atmospheric indices and variability in the US streamflow. J. Hydrol. 2015, 525, 724–736. [Google Scholar] [CrossRef]
- Hinkle, D.E.; Wiersma, W.; Jurs, S.G. Applied Statistics for the Behavioral Sciences, 5th ed.; Houghton Mifflin: Boston, MA, USA, 2003. [Google Scholar]
- Foody, G.M.; McCulloch, M.B.; Yates, W.B. The effect of training set size and composition on artificial neural-network classification. Int. J. Remote Sens. 1995, 16, 1707–1723. [Google Scholar] [CrossRef]
- Sug, H. The effect of training set size for the performance of neural networks of classification. WSEAS Trans. Comp. 2010, 9, 1297–1306. [Google Scholar]
- Sordo, M.; Zeng, Q. On Sample Size and Classification Accuracy: A Performance Comparison; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Rodriguez-Perez, R.; Vogt, M.; Bajorath, J. Influence of varying training set composition and size on support vector machine-based prediction of active compounds. J. Chem. Inf. Model. 2017, 57, 710–716. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Res. 2007, 30, 1371–1386. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A. MODELAVG: A MATLAB Toolbox for Postprocessing of Model Ensembles; Department of Civil and Environmental Engineering, University of California Irvine: Irvine, CA, USA, 2016; Available online: http://faculty.sites.uci.edu/jasper/files/2016/04/manual_Model_averaging.pdf (accessed on 15 August 2019).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wood, A.W.; Kumar, A.; Lettenmaier, D.P. A retrospective assessment of national centers for environmental prediction climate model-based ensemble hydrologic forecasting in the western United States. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S. Using oceanic-atmospheric oscillations for long lead time streamflow forecasting. Water. Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Qian, B.; Saunders, M.A.; Summer, U.K. Temperature and Its Links to Preceding Eurasian Snow Cover, North Atlantic SSTs, and the NAO. J. Clim. 2003, 16, 4108–4120. [Google Scholar] [CrossRef]
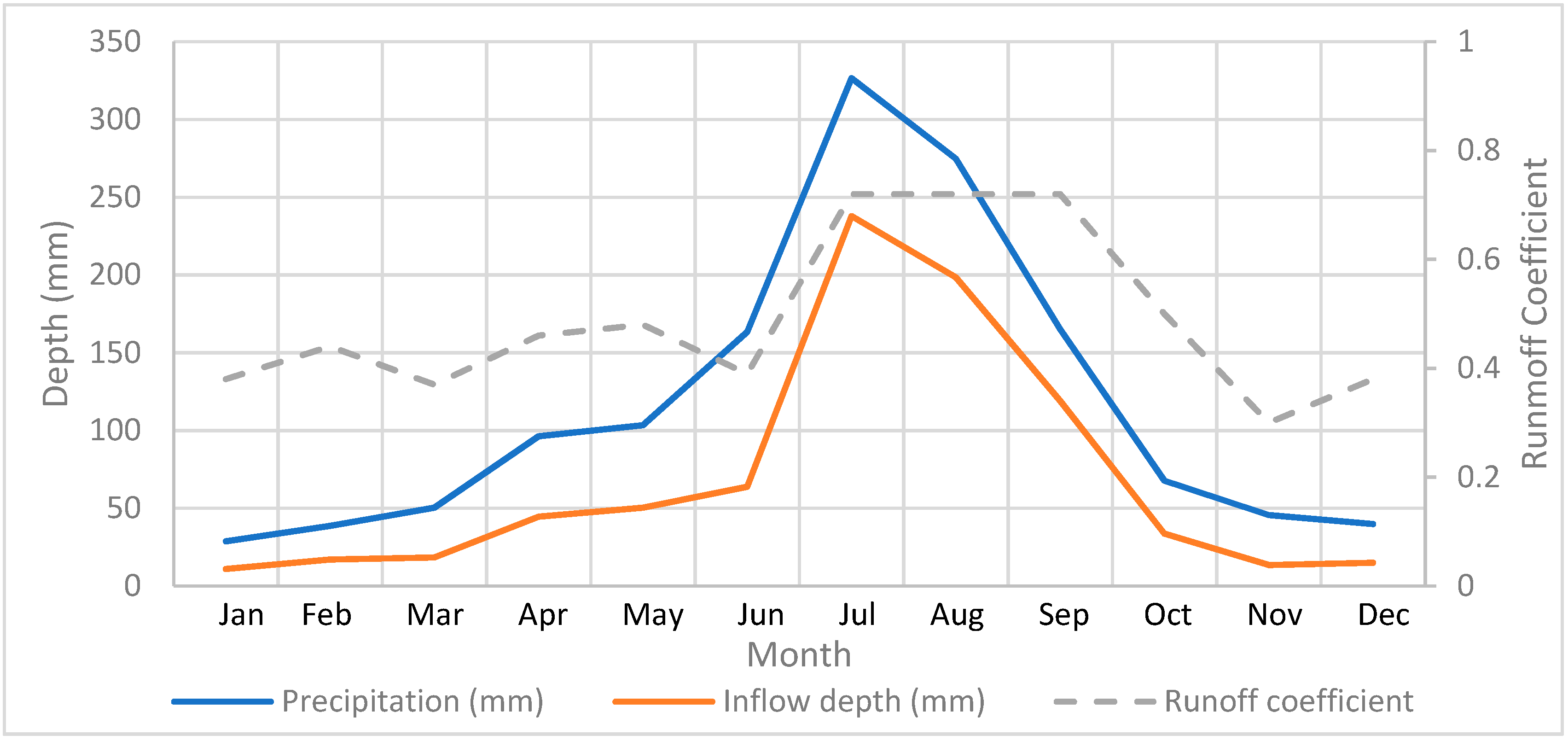









| Data | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precipitation (mm) | 28.7 | 38.6 | 50.3 | 96.3 | 103.4 | 163.4 | 326.6 | 274.8 | 165.2 | 67.7 | 45.6 | 39.9 |
| Inflow depth (mm) | 10.9 | 17.0 | 18.4 | 44.6 | 50.3 | 63.8 | 237.9 | 198.5 | 119.1 | 33.6 | 13.5 | 15.0 |
| Runoff coefficient | 0.38 | 0.44 | 0.37 | 0.46 | 0.48 | 0.39 | 0.72 | 0.72 | 0.72 | 0.50 | 0.30 | 0.38 |
| Abbreviation | Definition |
|---|---|
| AAO | Antarctic Oscillation is the first leading mode from the EOF analysis of monthly mean height anomalies at 700-hPa. |
| AMM | Atlantic Meridional Mode is the atmosphere-ocean variability in the tropical Pacific and tropical Atlantic. |
| AMO | Atlantic Multidecadal Oscillation is an index of the North Atlantic temperature. |
| AO | Arctic Oscillation is a pattern of atmospheric pressures of the Arctic and North Atlantic oceans. |
| EA | East Atlantic Pattern is associated with surface temperatures in Europe and US. |
| EAWR | Eastern Asia/Western Russia index is the second prominent mode of low-frequency variability over the North Atlantic. |
| ERSST | Extended Reconstructed Sea Surface Temperature is a global grid monthly sea surface temperature. |
| MEI | Multivariate ENSO Index is related to sea-level pressure, surface wind, sea surface temperature, surface air temperature and total cloudiness fraction of the sky. |
| NAO | North Atlantic Oscillation is a dominant teleconnection patterns ranging from North America to Europe and North Asia. |
| NINA3 | NINA3 is the average of sea surface temperature anomalies over the region from 5N to 5S and 150W to 90W. |
| PDO | Pacific Decadal Oscillation is associated with monthly SSTs across the North Pacific. |
| SOI | Southern Oscillation Index is the development and intensity of El Nino or La Nina events in the Pacific Ocean. |
| TNA | Tropical Northern Atlantic Index is the anomaly of the average of the monthly SST from 5.5N to 23.5N and 15W to 57.5W. |
| WP | Western Pacific Index is a primary mode of low-frequency variability over the North Pacific in all months. |
| Month | Climatic Indices | Correlation Coefficient | p-Value | VIF |
|---|---|---|---|---|
| Jan | TNA(10), ERSST(3) | −0.67, 0.61 | 0.001, 0.005 | <1.0 |
| Feb | WP(4), MEI(8) | −0.67, 0.68 | 0.001, 0.001 | <1.3 |
| Mar | EA(4), AO(5), AMM(3), ERSST(3) | −0.71, −0.64, −0.59, 0.45 | 0.0007, 0.002, 0.007, 0.05 | <1.7 |
| Apr | NINA3(10), SOI(5), EAWR(6), PDO(8) | 0.83, −0.57, 0.44, 0.66 | 0.0001, 0.009, 0.05, 0.001 | <4.1 |
| May | EA(9), AO(9), AAO(12), ERSST(3) | 0.67, 0.45, −0.47, 0.47 | 0.001, 0.04, 0.03, 0.03 | <1.3 |
| Nov | TNA(8), ERSST(3) | −0.54, 0.75 | 0.01, 0.0002 | <1.1 |
| Dec | NAO(8), NINO3(5), ERSST(3) | 0.46, 0.57, 0.66 | 0.04, 0.01, 0.002 | <1.3 |
| Month | Jan | Feb | Mar | Apr | May | Nov | Dec |
|---|---|---|---|---|---|---|---|
| Locations selected | 48° N, 210° E | 40° N, 150° E | 26° N, 244° E | 32° N, 198° E | 46° N, 146° E | 60° N, 152° E | 48° N, 210° E |
| Correlation coefficient | 0.61 | 0.40 | 0.45 | 0.64 | 0.47 | 0.75 | 0.66 |
| Month | MLR | ANN | SVM | |||
|---|---|---|---|---|---|---|
| r | S | r | S | r | S | |
| Jan | 0.65 | 0.21 | 0.67 | 0.20 | 0.67 | 0.26 |
| Feb | 0.69 | 0.26 | 0.83 | 0.44 | 0.62 | 0.21 |
| Mar | 0.89 | 0.55 | 0.86 | 0.49 | 0.90 | 0.56 |
| Apr | 0.86 | 0.49 | 0.76 | 0.35 | 0.83 | 0.44 |
| May | 0.78 | 0.33 | 0.81 | 0.41 | 0.71 | 0.30 |
| Nov | 0.81 | 0.41 | 0.88 | 0.52 | 0.80 | 0.32 |
| Dec | 0.75 | 0.31 | 0.75 | 0.27 | 0.76 | 0.34 |
| Year | BMA | SMA | Naive Forecast | |||
|---|---|---|---|---|---|---|
| NSE | PBIAS (%) | NSE | PBIAS (%) | NSE | PBIAS (%) | |
| 2013 | 0.78 | 6.45 | 0.77 | 14.41 | −0.02 | 37.37 |
| 2014 | 0.77 | 3.08 | 0.52 | 10.37 | −1.68 | 14.92 |
| 2015 | 0.89 | −1.33 | 0.71 | −7.11 | −1.34 | 36.41 |
| 2016 | 0.71 | −21.87 | 0.43 | −36.34 | 0.31 | 44.19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Kim, H.; Jung, I.; Yoon, J. Monthly Reservoir Inflow Forecasting for Dry Period Using Teleconnection Indices: A Statistical Ensemble Approach. Appl. Sci. 2020, 10, 3470. https://doi.org/10.3390/app10103470
Lee D, Kim H, Jung I, Yoon J. Monthly Reservoir Inflow Forecasting for Dry Period Using Teleconnection Indices: A Statistical Ensemble Approach. Applied Sciences. 2020; 10(10):3470. https://doi.org/10.3390/app10103470
Chicago/Turabian StyleLee, Donghee, Hwansuk Kim, Ilwon Jung, and Jaeyoung Yoon. 2020. "Monthly Reservoir Inflow Forecasting for Dry Period Using Teleconnection Indices: A Statistical Ensemble Approach" Applied Sciences 10, no. 10: 3470. https://doi.org/10.3390/app10103470
APA StyleLee, D., Kim, H., Jung, I., & Yoon, J. (2020). Monthly Reservoir Inflow Forecasting for Dry Period Using Teleconnection Indices: A Statistical Ensemble Approach. Applied Sciences, 10(10), 3470. https://doi.org/10.3390/app10103470





