Extended SSH Model in Non-Hermitian Waveguides with Alternating Real and Imaginary Couplings
Abstract
:1. Introduction
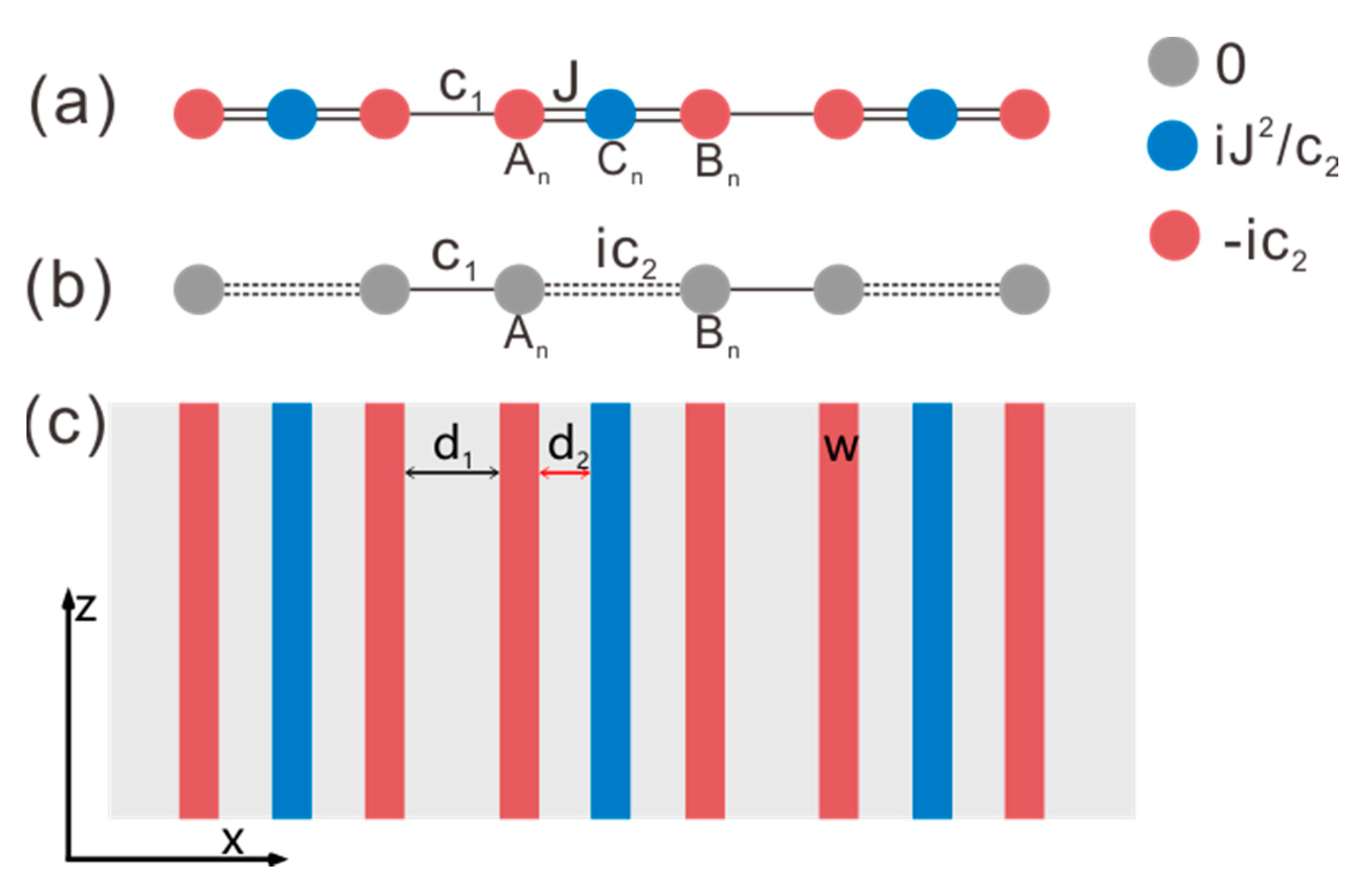
2. Geometry and Theoretical Model
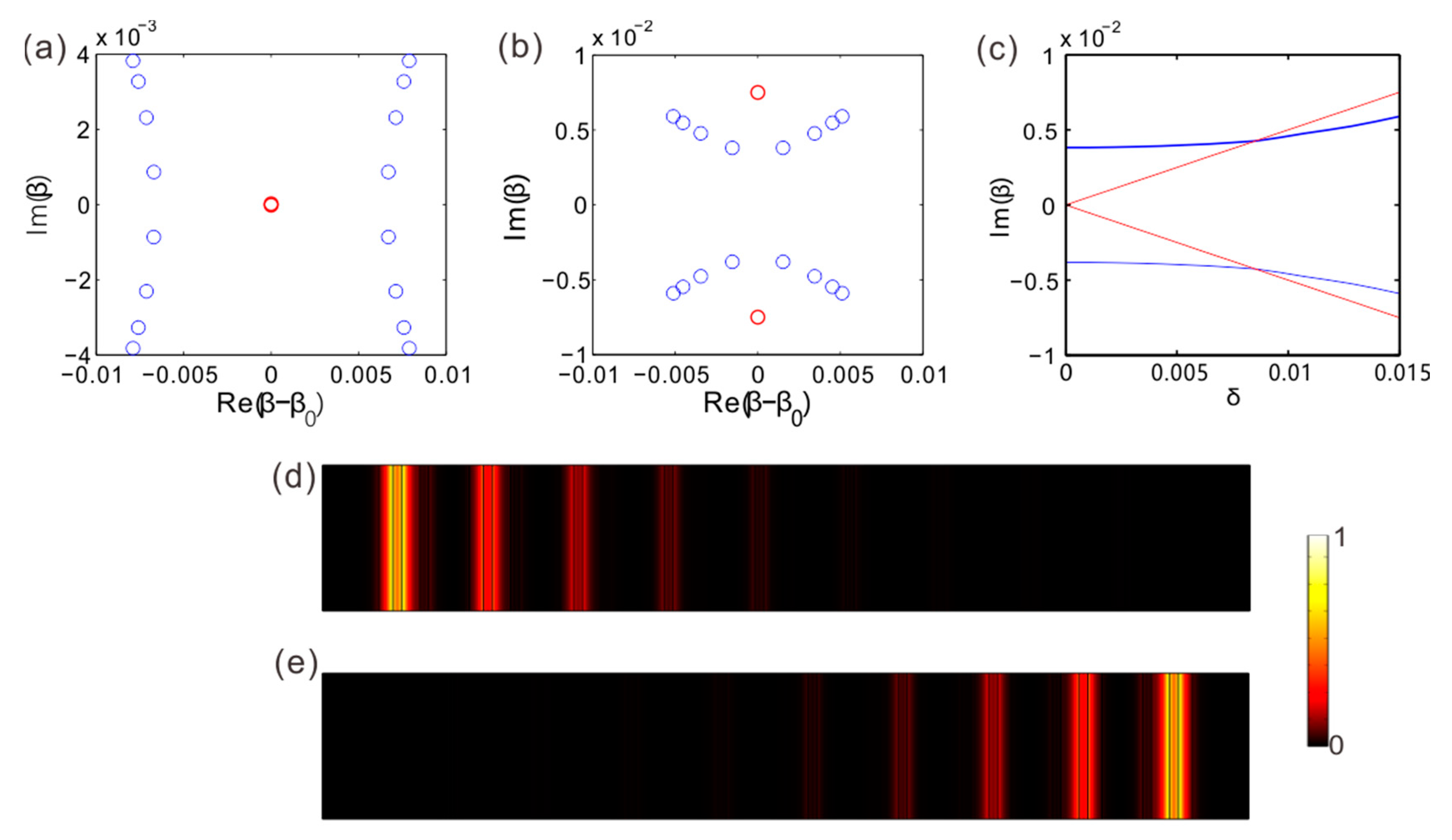
3. Bloch Mode
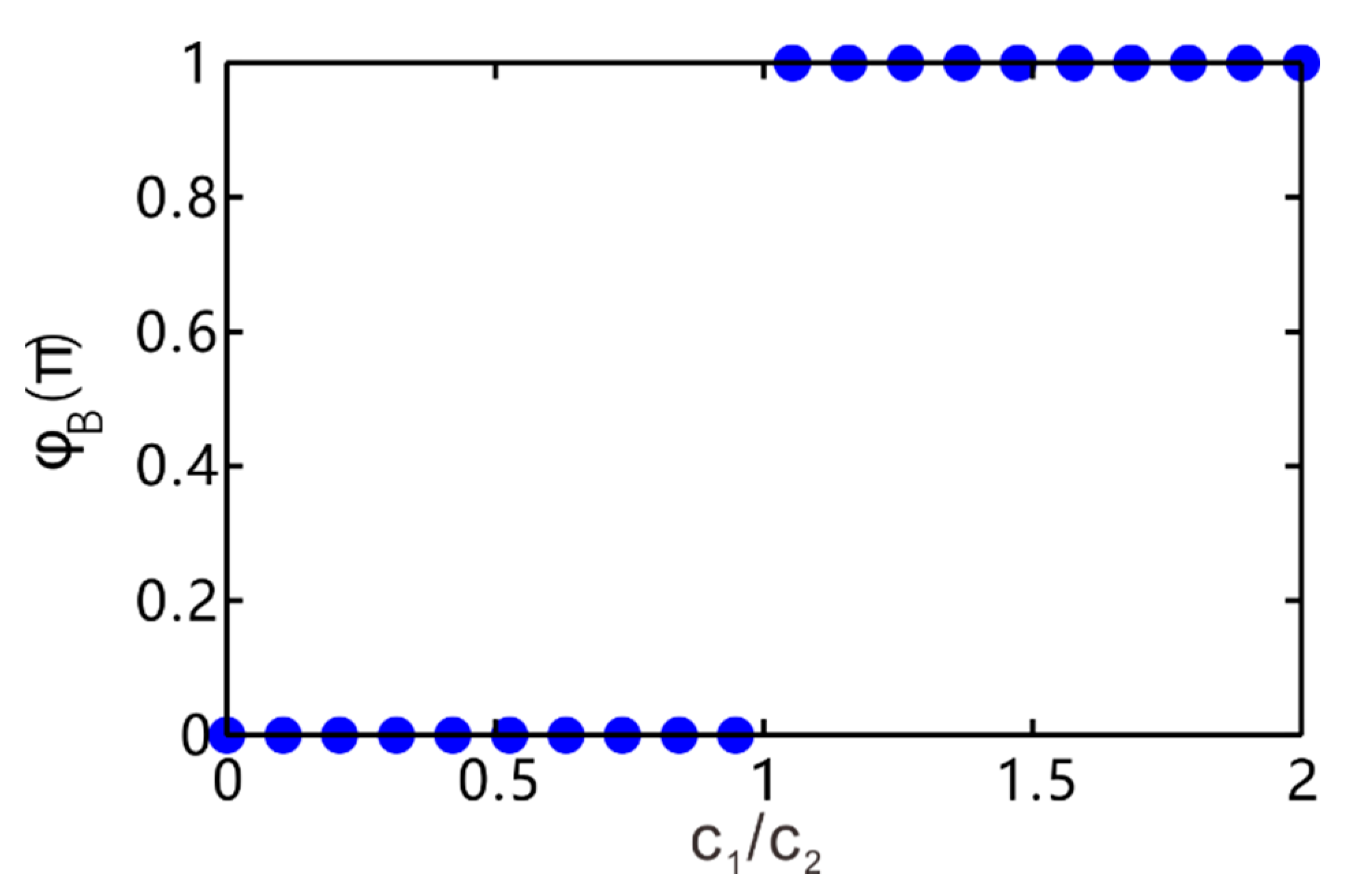
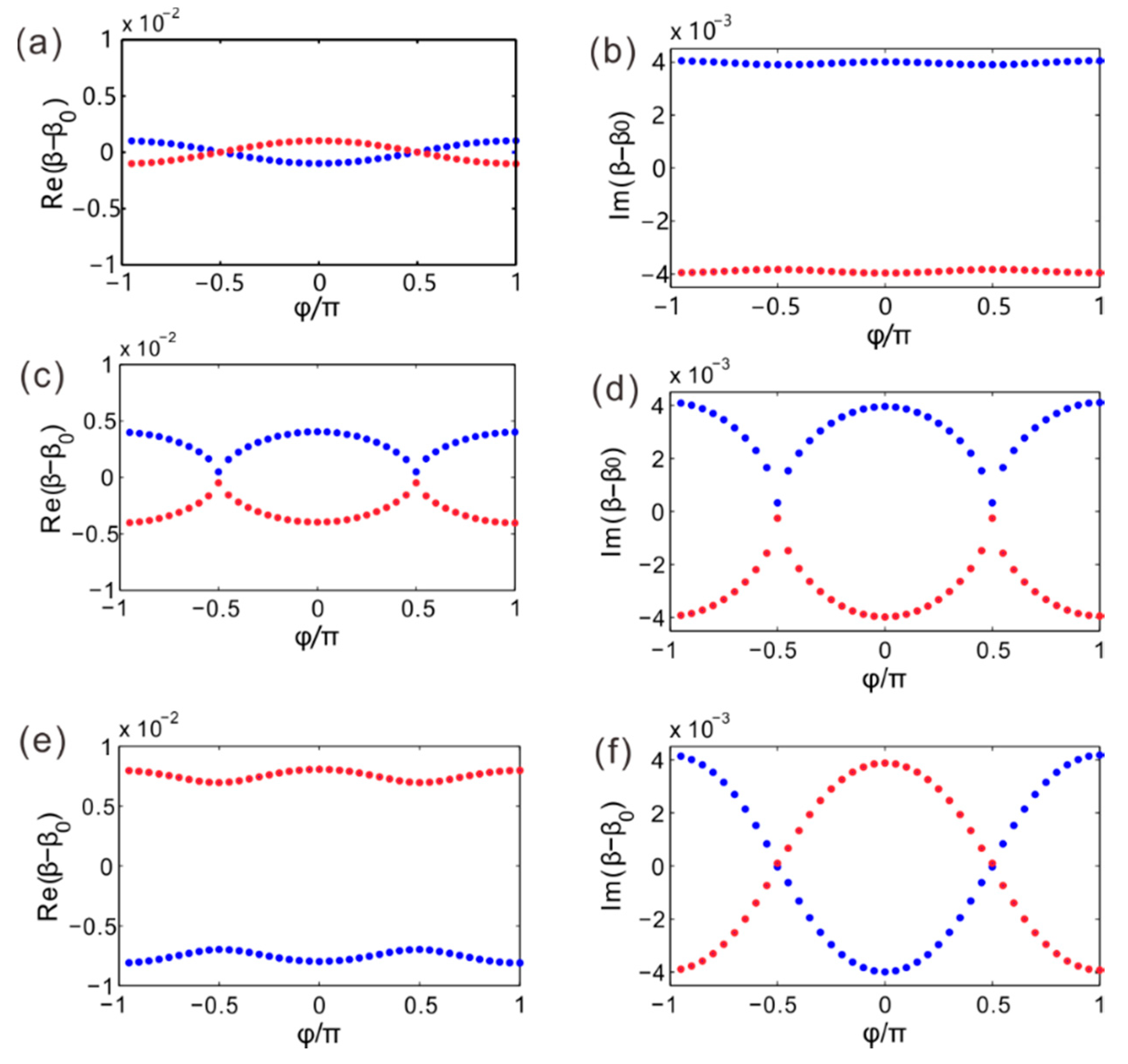
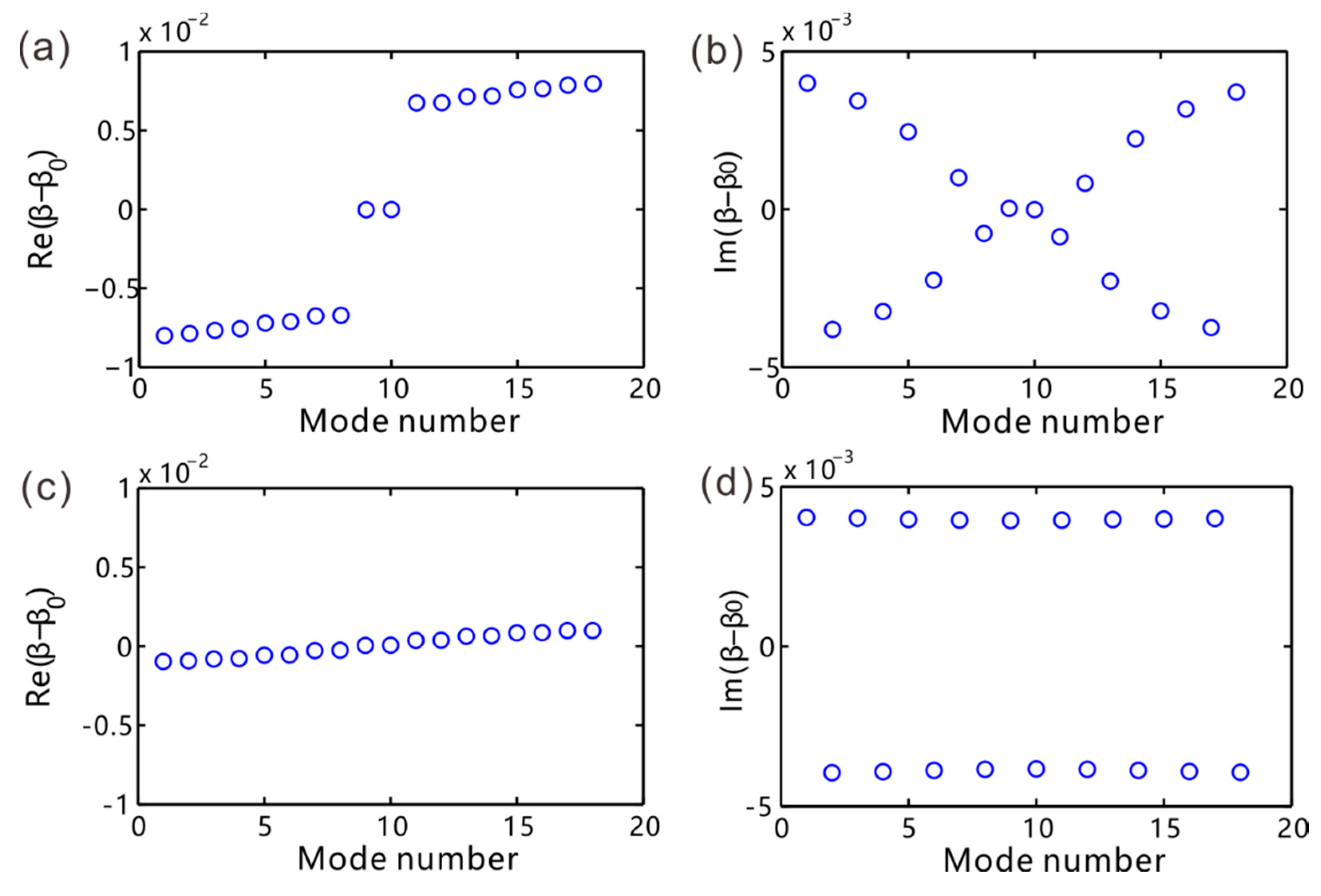
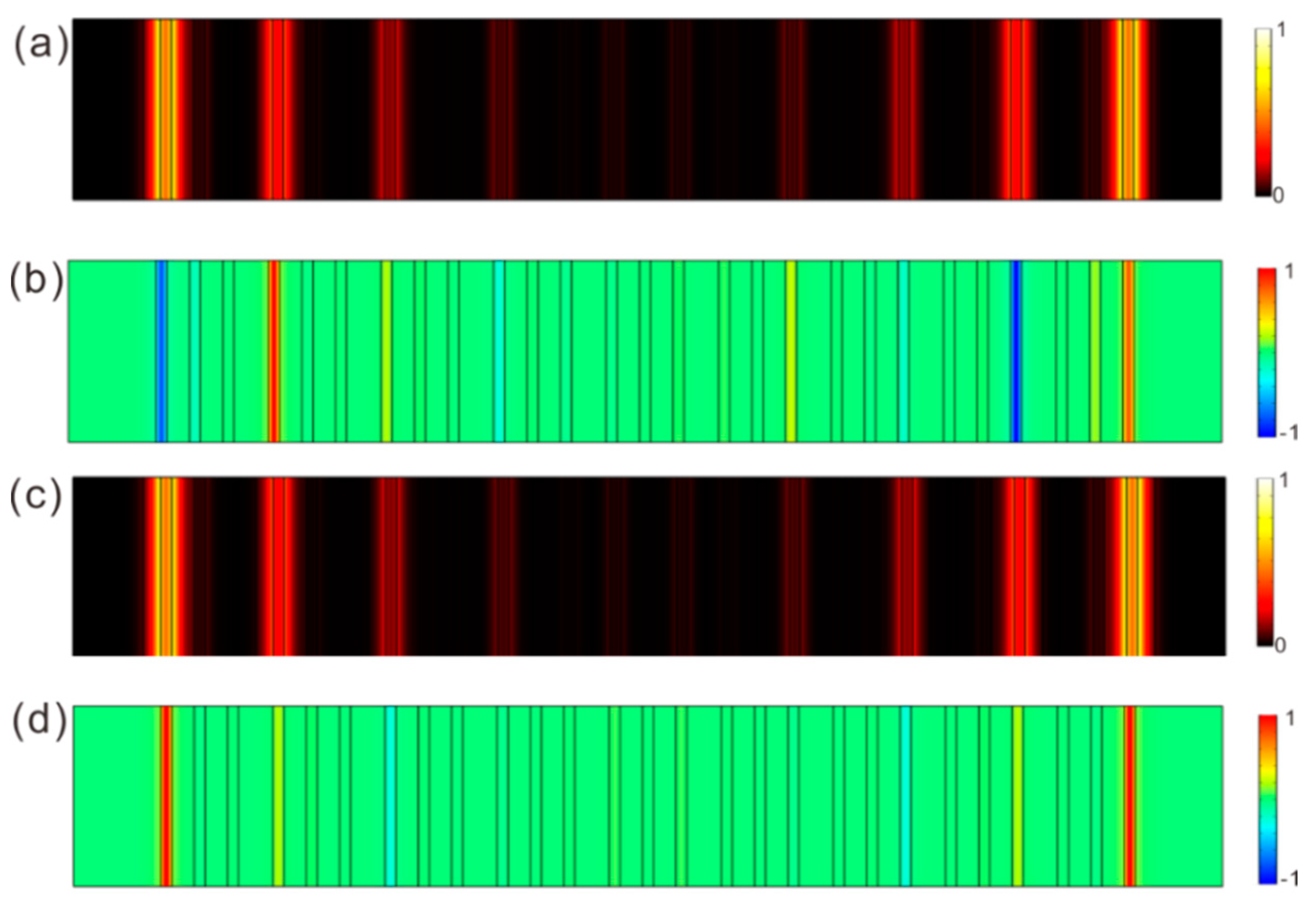
4. Topological Edge Modes
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1978, 42, 1698. [Google Scholar] [CrossRef]
- Asbóth, J.K.; Oroszlány, L.; Pályi, A. The Su-Schrieffer-Heeger (SSH) Model. In A Short Course on Topological Insulators. Lecture Notes in Physics; Springer: Cham, Switzerland, 2016; p. 919. [Google Scholar]
- Blanco-Redondo, A.; Andrea, I.; Collins, M.; Harari, G.; Lumer, Y.; Rechtsman, M.; Eggleton, B.; Segev, M. Topological optical waveguiding in silicon and the transition between topological and trivial defect states. Phys. Rev. Lett. 2016, 116, 163901. [Google Scholar] [CrossRef]
- Cheng, Q.; Pan, Y.; Wang, Q.; Li, T.; Zhu, S. Topologically protected interface mode in plasmonic waveguide arrays. Laser Photon. Rev. 2015, 9, 392–398. [Google Scholar] [CrossRef]
- Ge, L.; Wang, L.; Xiao, M.; Wen, W.; Chan, C.; Han, D. Topological edge modes in multilayer graphene systems. Opt. Express 2015, 23, 21585–21595. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.; Wang, B.; Long, H.; Wang, K.; Lu, P. Topological edge modes in non-Hermitian plasmonic waveguide arrays. Opt. Express 2017, 25, 11132–11143. [Google Scholar] [CrossRef]
- Wang, B.X.; Zhao, C.Y. Wideband tunable infrared topological plasmon polaritons in dimerized chains of doped-silicon nanoparticles. J. Appl. Phys. 2020, 127, 073106. [Google Scholar] [CrossRef]
- Peng, Y.G.; Qin, C.; Zhao, D.; Shen, Y.; Xu, X.; Bao, M.; Jia, H.; Zhu, X. Experimental demonstration of anomalous Floquet topological insulator for sound. Nat. Commun. 2016, 7, 13368. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Zhou, Q.; Zhao, D.; Belic, M.; Zhao, Y. Spatiotemporal solitons in cold Rydberg atomic gases with Bessel optical lattices. Appl. Math. Lett. 2020, 106, 106230. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, D.; Soljačić, M. Topological photonics. Nat. Photon. 2014, 8, 821–829. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Chen, X.; Panoiu, N.; Ye, F. Topological surface plasmons in superlattices with changing sign of the average permittivity. Opt. Lett. 2016, 41, 4281–4284. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, P.; Zhao, D.; Guo, H.; Huang, M.; Ke, S. Plasmonic Jackiw-Rebbi Modes in Graphene Waveguide Arrays. Appl. Sci. 2019, 9, 4152. [Google Scholar] [CrossRef] [Green Version]
- Xie, D.; Gou, W.; Xiao, T.; Gadway, B.; Yan, B. Topological characterizations of an extended Su–Schrieffer–Heeger model. npj Quantum Inf. 2019, 5, 55. [Google Scholar] [CrossRef] [Green Version]
- Fu, N.; Fu, Z.; Zhang, H.; Liao, Q.; Zhao, D.; Ke, S. Topological bound modes in optical waveguide arrays with alternating positive and negative couplings. Opt. Quantum Electron. 2020, 52, 61. [Google Scholar] [CrossRef]
- Meng, P.; Zhao, D.; Zhong, D.; Liu, W. Topological plasmonic modes in graphene-coated nanowire arrays. Opt. Quantum Electron. 2019, 51, 156. [Google Scholar] [CrossRef]
- Wang, F.; Ke, S.; Qin, C.; Wang, B.; Long, H.; Wang, K.; Lu, P. Topological interface modes in graphene multilayer arrays. Opt. Laser Technol. 2018, 103, 272–278. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Pan, H.; Wang, C.; Zhang, D.; Yu, A.; Gover, H.; Zhang, T.; Li, L.Z.; Zhu, S. Observation of Anomalous π Modes in Photonic Floquet Engineering. Phys. Rev. Lett. 2019, 122, 173901. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Wakabayashi, K. Novel Topological Phase with a Zero Berry Curvature. Phys. Rev. Lett. 2017, 118, 076803. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Deng, W.; Shi, F.; Zhao, F.; Chen, M.; Dong, J. Direct observation of corner states in second-order topological photonic crystal slabs. Phys. Rev. Lett. 2019, 122, 233902. [Google Scholar] [CrossRef] [Green Version]
- Yao, S.; Wang, Z. Edge States and Topological Invariants of Non-Hermitian Systems. Phys. Rev. Lett. 2018, 121, 086803. [Google Scholar] [CrossRef] [Green Version]
- Silveirinha, M.G. Topological theory of non-Hermitian photonic systems. Phys. Rev. B 2019, 99, 125155. [Google Scholar] [CrossRef] [Green Version]
- Yuce, C. Topological phase in a non-Hermitian PT symmetric system. Phys. Lett. A 2015, 379, 1213. [Google Scholar] [CrossRef] [Green Version]
- Yuce, C.; Ramezani, H. Topological states in a non-Hermitian two-dimensional Su-SchriefferHeeger model. Phys. Rev. A 2019, 100, 032102. [Google Scholar] [CrossRef] [Green Version]
- Miri, M.; Alù, A. Exceptional points in optics and photonics. Science 2019, 363, 6422. [Google Scholar] [CrossRef] [Green Version]
- Ke, S.; Zhao, D.; Liu, Q.; Wu, S.; Wang, B.; Lu, P. Optical imaginary directional couplers. J. Lightwave Technol. 2018, 36, 2510–2516. [Google Scholar] [CrossRef]
- Zhao, D.; Xu, B.; Guo, H.; Xu, W.; Zhong, D.; Ke, S. Low Threshold Optical Bistability in Aperiodic PT-Symmetric Lattices Composited with Fibonacci Sequence Dielectrics and Graphene. Appl. Sci. 2019, 9, 5125. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Ke, S.; Hu, Y.; Wang, B.; Lu, P. Optical bistability of graphene embedded in parity-time-symmetric photonic lattices. JOSA B 2019, 36, 1731–1737. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, D.; Cao, H.; Xu, B.; Xu, W.; Ke, S. Exceptional Points in Non-Hermitian Photonic Crystals Incorporated with a Defect. Appl. Sci. 2020, 10, 823. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Zhong, D.; Hu, Y.; Ke, S.; Liu, W. Imaginary modulation inducing giant spatial Goos–Hänchen shifts in one-dimensional defective photonic lattices. Opt. Quantum Electron. 2019, 51, 113. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, T.; Chan, C.T. Dynamically encircling an exceptional point in anti-parity time symmetric systems: Asymmetric mode switching for symmetry-broken modes. Light Sci. Appl. 2019, 8, 88. [Google Scholar] [CrossRef]
- Ke, S.; Wang, B.; Qin, C.; Long, H.; Wang, K.; Lu, P. Exceptional points and asymmetric mode switching in plasmonic waveguides. J. Lightwave Technol. 2016, 34, 5258–5262. [Google Scholar] [CrossRef] [Green Version]
- Ke, S.; Wang, B.; Long, H.; Wang, K.; Lu, P. Topological mode switching in a graphene doublet with exceptional points. Opt. Quantum Electron. 2017, 49, 1–12. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Liu, W. Adiabatic transfer of surface plasmons in non-Hermitian graphene waveguides. Opt. Quantum Electron. 2018, 50, 393. [Google Scholar] [CrossRef]
- Ke, S.; Liu, J.; Liu, Q.; Zhao, D.; Liu, W. Strong absorption near exceptional points in plasmonic waveguide arrays. Opt. Quantum Electron. 2018, 50, 31. [Google Scholar] [CrossRef]
- Parto, M.; Wittek, S.; Hodaei, H.; Harari, G.; Miguel, A.B.; Ren, J.; Mikael, C.R.; Segev, M.; Demetrios, N.C.; Khajavikhan, M. Edge-Mode Lasing in 1D Topological Active Arrays. Phys. Rev. Lett. 2018, 120, 113901. [Google Scholar] [CrossRef] [Green Version]
- Yuce, C. Non-Hermitian anomalous skin effect. Phys. Lett. A 2020, 384, 126094. [Google Scholar] [CrossRef] [Green Version]
- Ke, S.; Zhao, D.; Liu, J.; Liu, Q.; Liao, Q.; Wang, B.; Lu, P. Topological bound modes in anti-PT symmetric optical waveguide arrays. Opt. Express 2019, 27, 13858–13870. [Google Scholar] [CrossRef]
- Keil, R.; Poli, C.; Heinrich, M.; Arkinstall, J.; Weihs, G.; Schomerus, H.; Szameit, A. Universal Sign Control of Coupling in Tight-Binding Lattices. Phys. Rev. Lett. 2016, 116, 213901. [Google Scholar] [CrossRef]
- Fan, H.; Chen, J.; Zhao, Z.; Wen, J.; Huang, Y. Anti-parity-time Symmetry in Passive Nanophotonics. arXiv 2020, arXiv:2003.11151. [Google Scholar]
- Kremer, M.; Petrides, I.; Meyer, E.; Heinrich, M.; Zilberberg, O.; Szameit, A. A square-root topological insulator with non-quantized indices realized with photonic Aharonov-Bohm cages. Nat. Commun. 2020, 11, 907. [Google Scholar] [CrossRef]
- Yang, F.; Liu, Y.; You, L. Anti-PT symmetry in dissipatively coupled optical systems. Phys. Rev. B 2017, 96, 053845. [Google Scholar] [CrossRef]
- Lieu, S. Topological phases in the non-Hermitian Su-Schrieffer-Heeger model. Phys. Rev. B 2018, 9, 045106. [Google Scholar] [CrossRef] [Green Version]
- Rüter, C.; Makris, K.; El-Ganainy, R.; Christodoulides, D.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Fu, N.; Zhang, H.; Wang, Z.; Zhao, D.; Ke, S. Extended SSH Model in Non-Hermitian Waveguides with Alternating Real and Imaginary Couplings. Appl. Sci. 2020, 10, 3425. https://doi.org/10.3390/app10103425
Fu Z, Fu N, Zhang H, Wang Z, Zhao D, Ke S. Extended SSH Model in Non-Hermitian Waveguides with Alternating Real and Imaginary Couplings. Applied Sciences. 2020; 10(10):3425. https://doi.org/10.3390/app10103425
Chicago/Turabian StyleFu, Ziwei, Nianzu Fu, Huaiyuan Zhang, Zhe Wang, Dong Zhao, and Shaolin Ke. 2020. "Extended SSH Model in Non-Hermitian Waveguides with Alternating Real and Imaginary Couplings" Applied Sciences 10, no. 10: 3425. https://doi.org/10.3390/app10103425
APA StyleFu, Z., Fu, N., Zhang, H., Wang, Z., Zhao, D., & Ke, S. (2020). Extended SSH Model in Non-Hermitian Waveguides with Alternating Real and Imaginary Couplings. Applied Sciences, 10(10), 3425. https://doi.org/10.3390/app10103425




