Numerical Investigation into the Effect of Different Parameters on the Geometrical Precision in the Laser-Based Powder Bed Fusion Process Chain
Abstract
1. Introduction
2. Materials and Methods
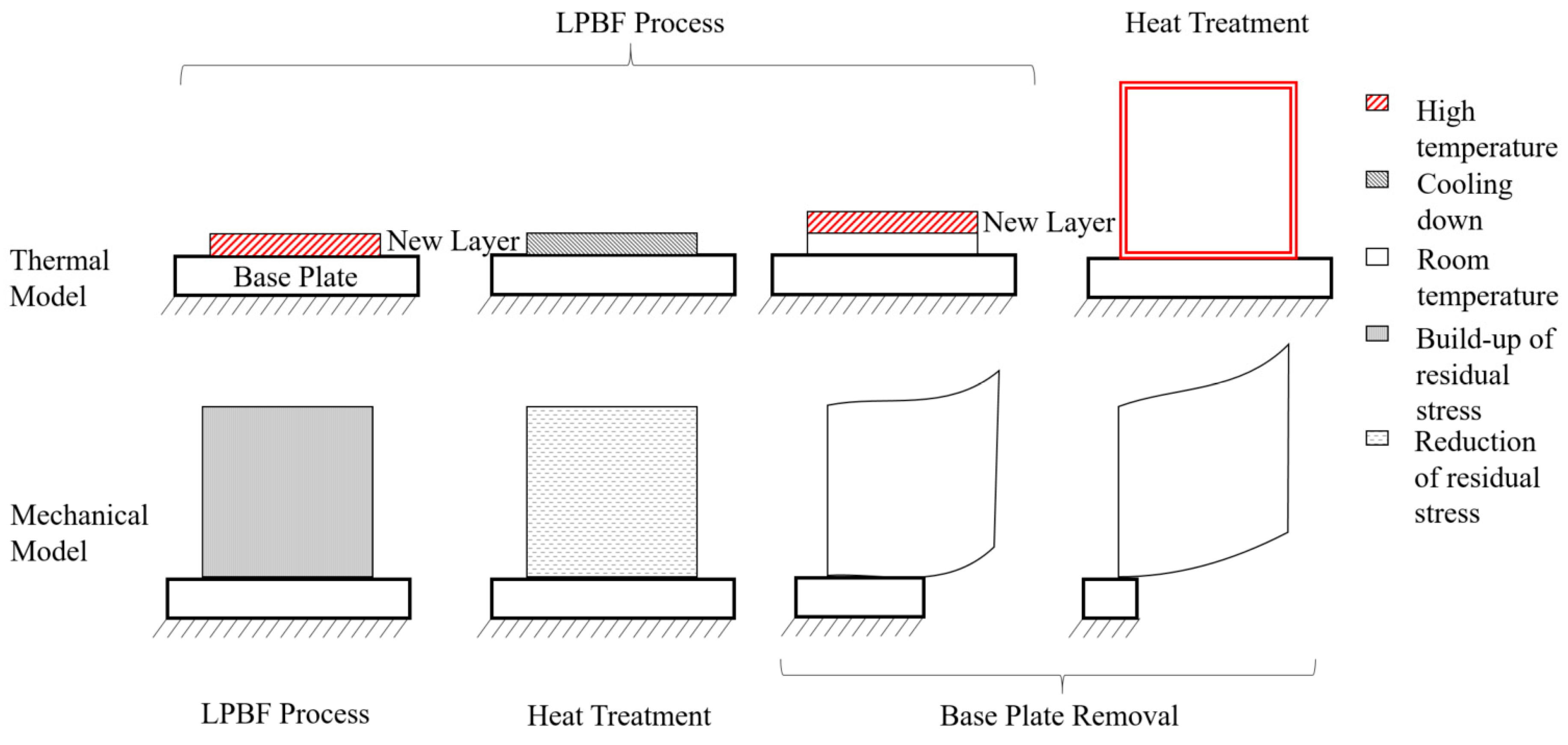
2.1. Modelling Approach
2.1.1. Thermal Model
2.1.2. Mechanical Model
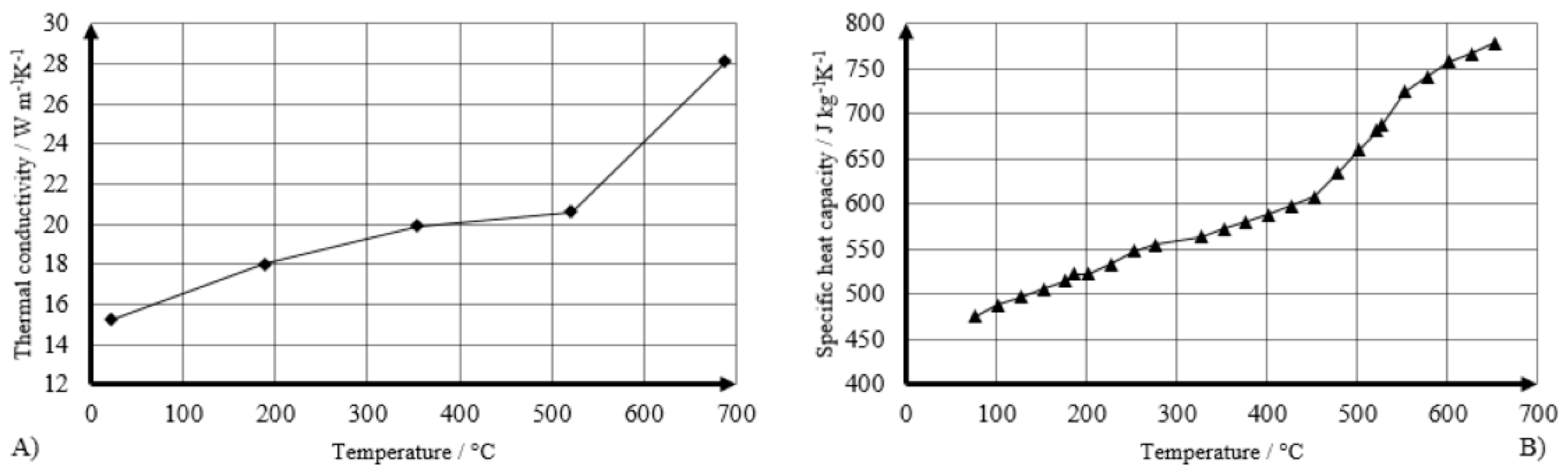
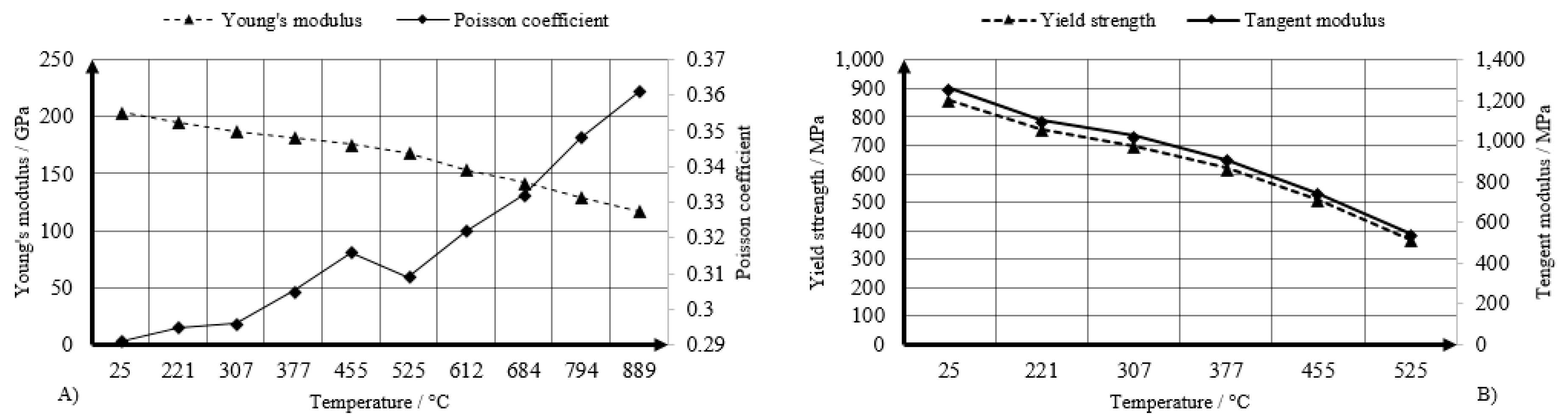
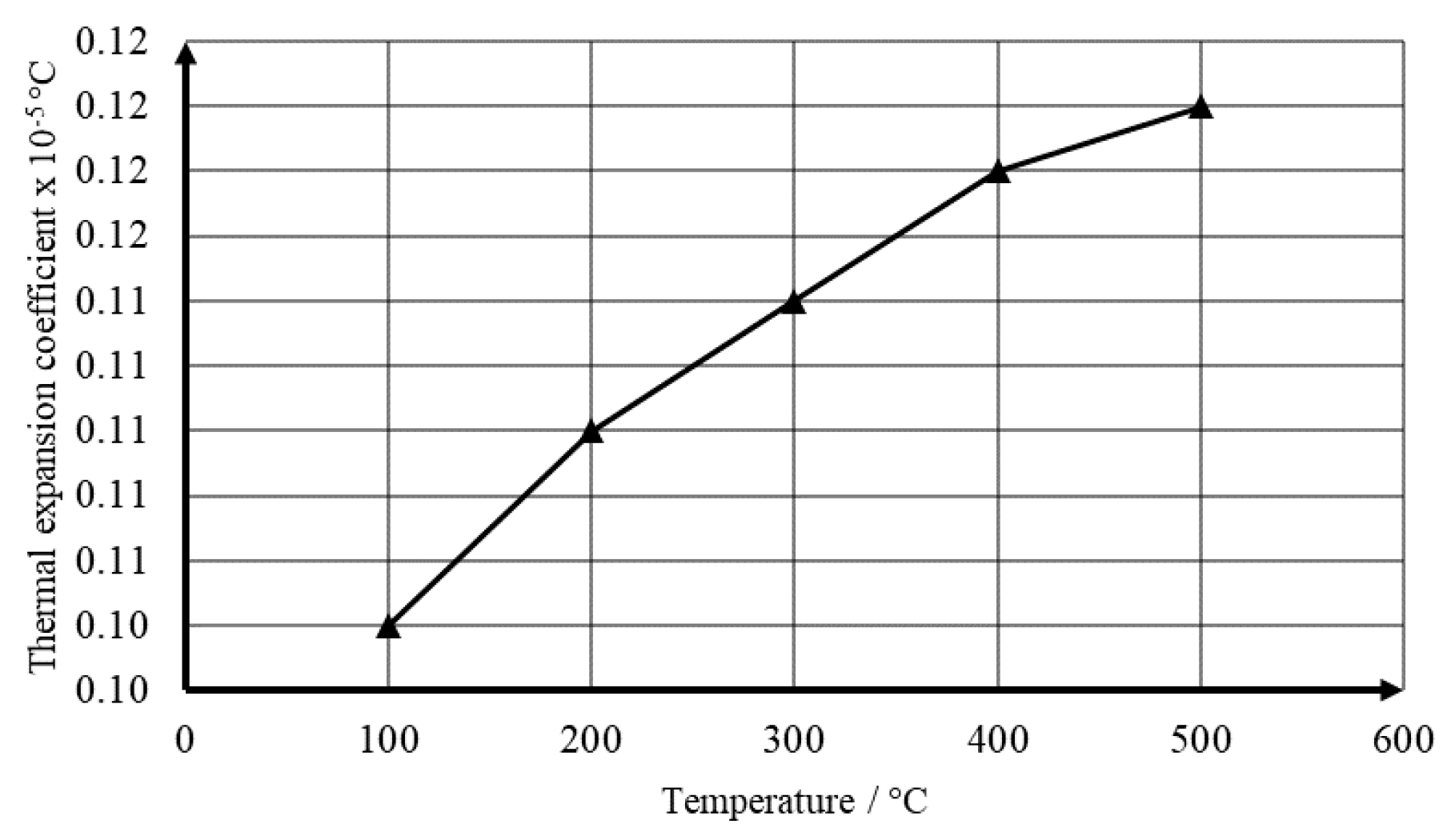
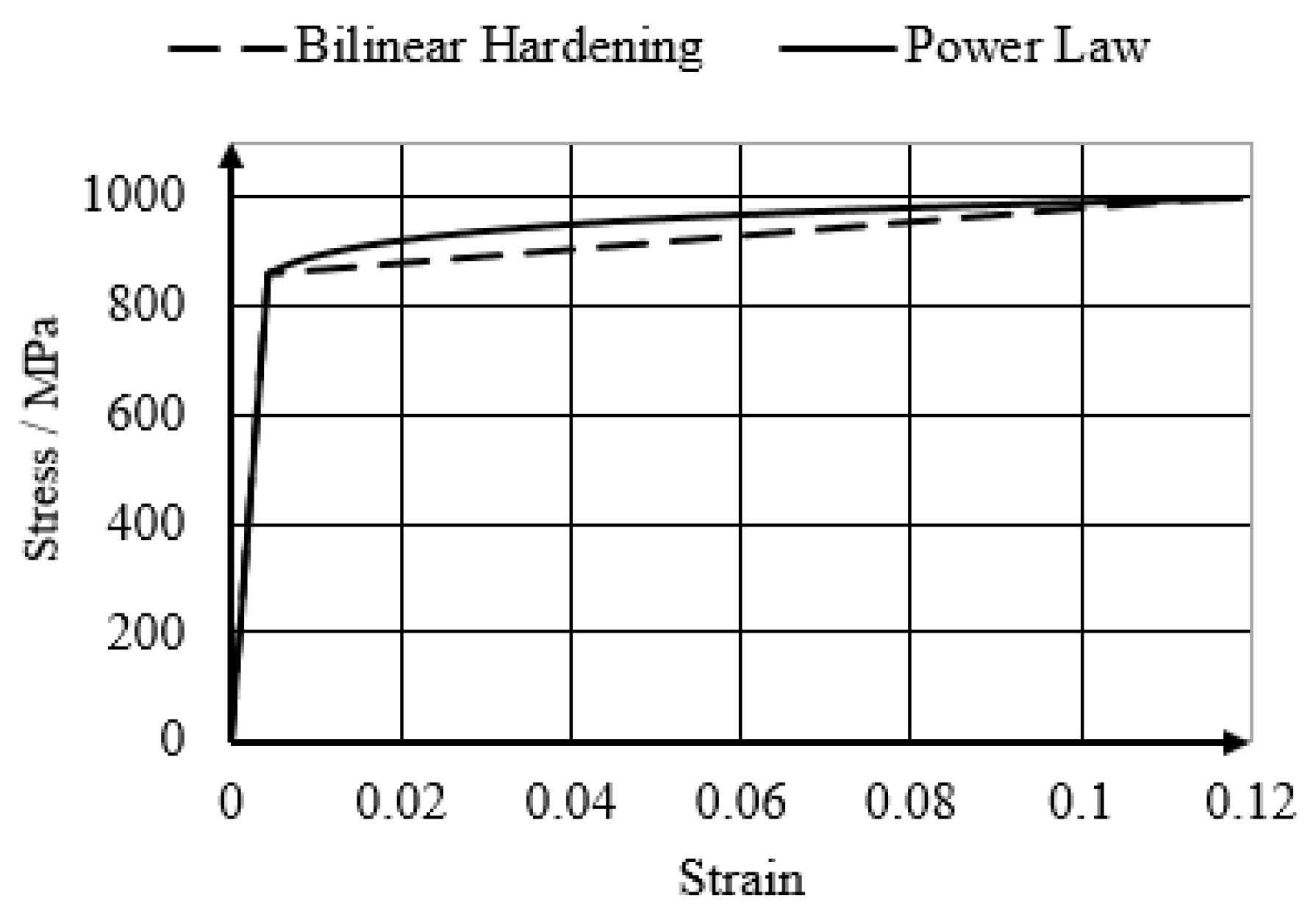
2.2. Material Properties
3. Results and Discussion
3.1. Overview of the Simulations
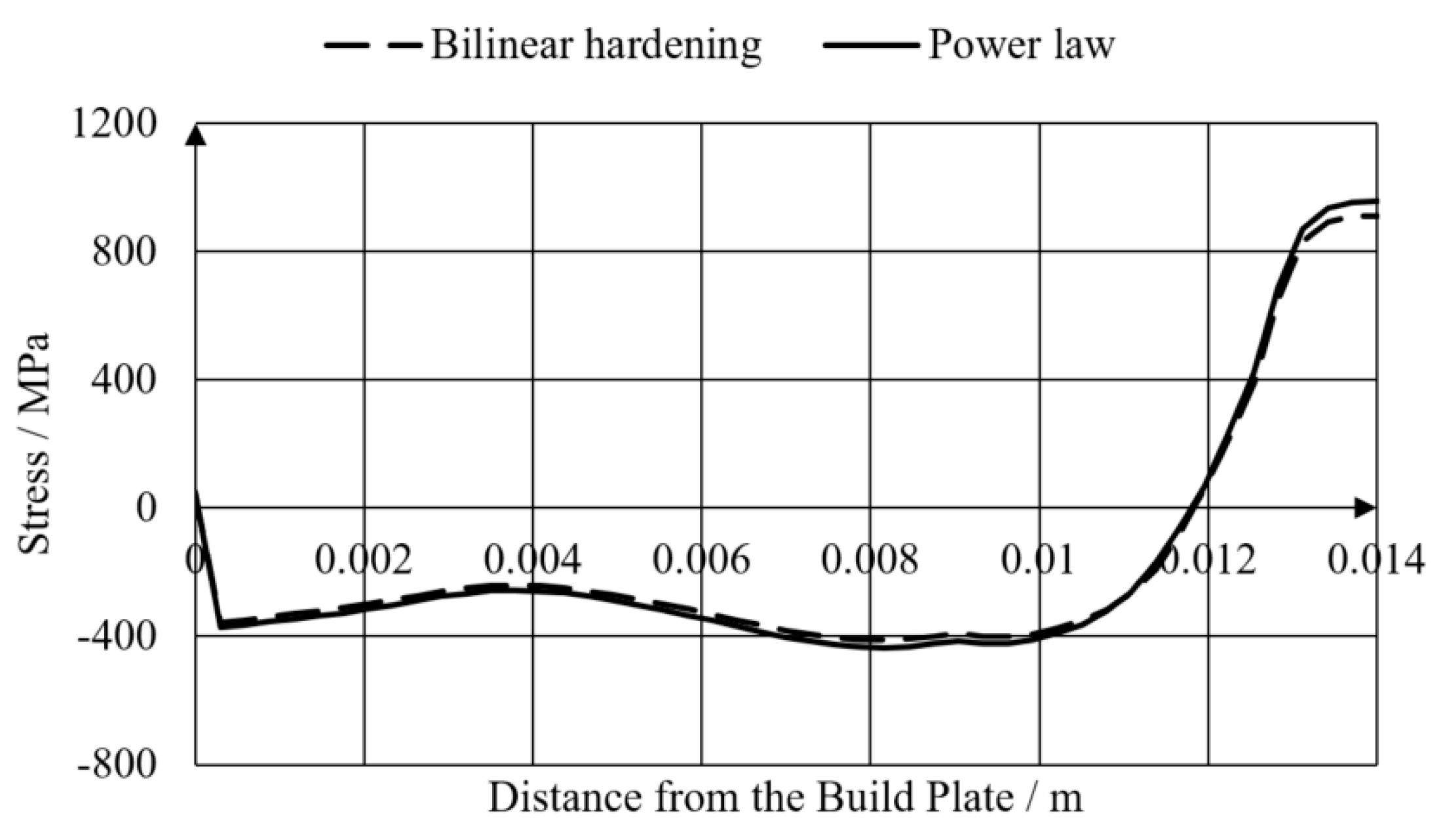
3.2. Benchmark Case: Simulation 1
3.3. Mesh Sensitivity Analysis: Simulations 1–5
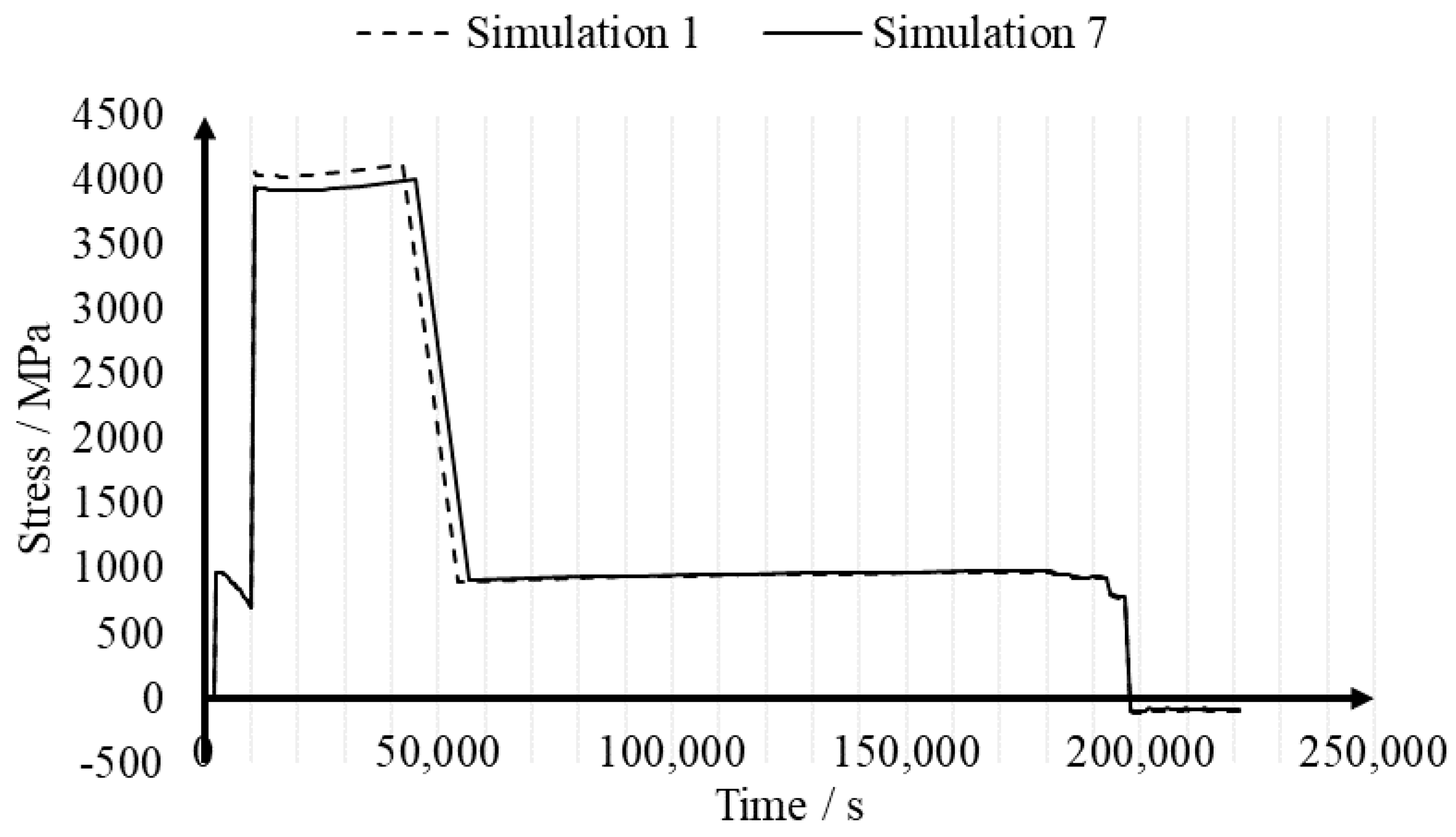
3.4. Effect of the Duration of the Heat Treatment: Simulations 6 and 7
3.5. Effect of the Heat Treatment Temperature: Simulations 8, 9 and 10
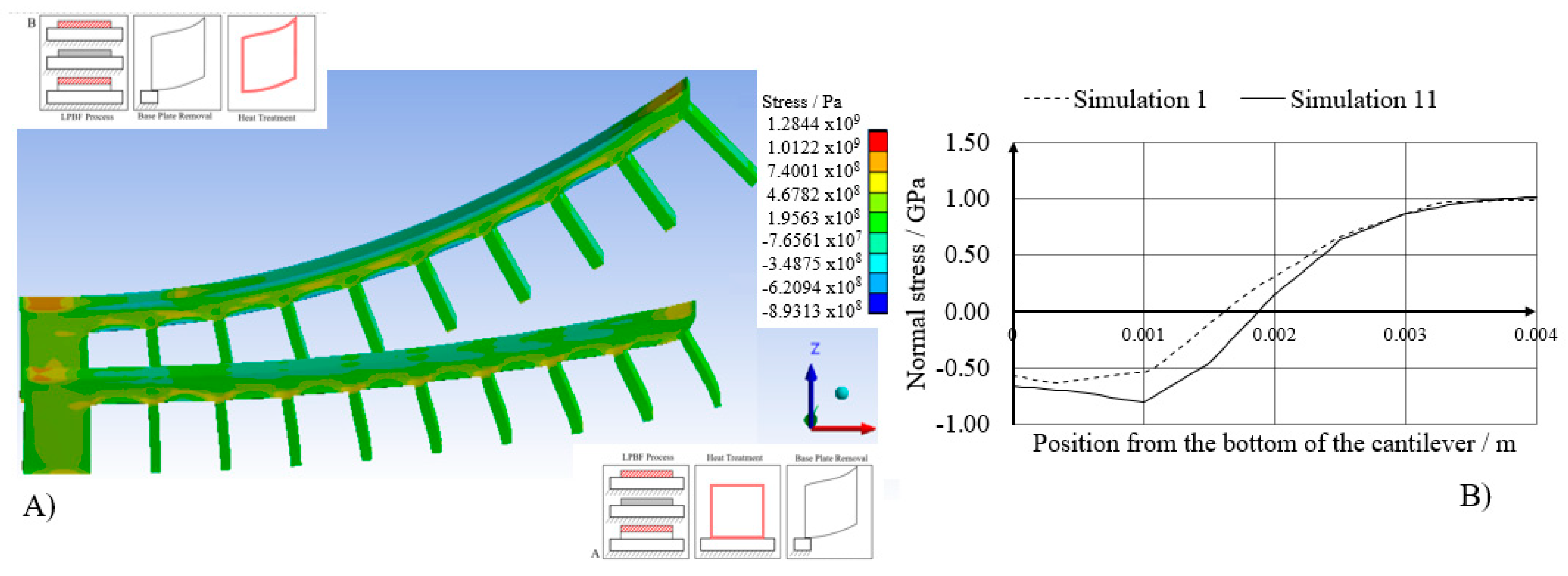
3.6. Correcting the Energy Input of the Primary Process: Simulation 11
4. Conclusions
- The model is capable of modelling the entire process in a limited amount of time and using a limited amount of computational resources. This allows a large number of simulations to be run for estimating the effect of varying certain parameters.
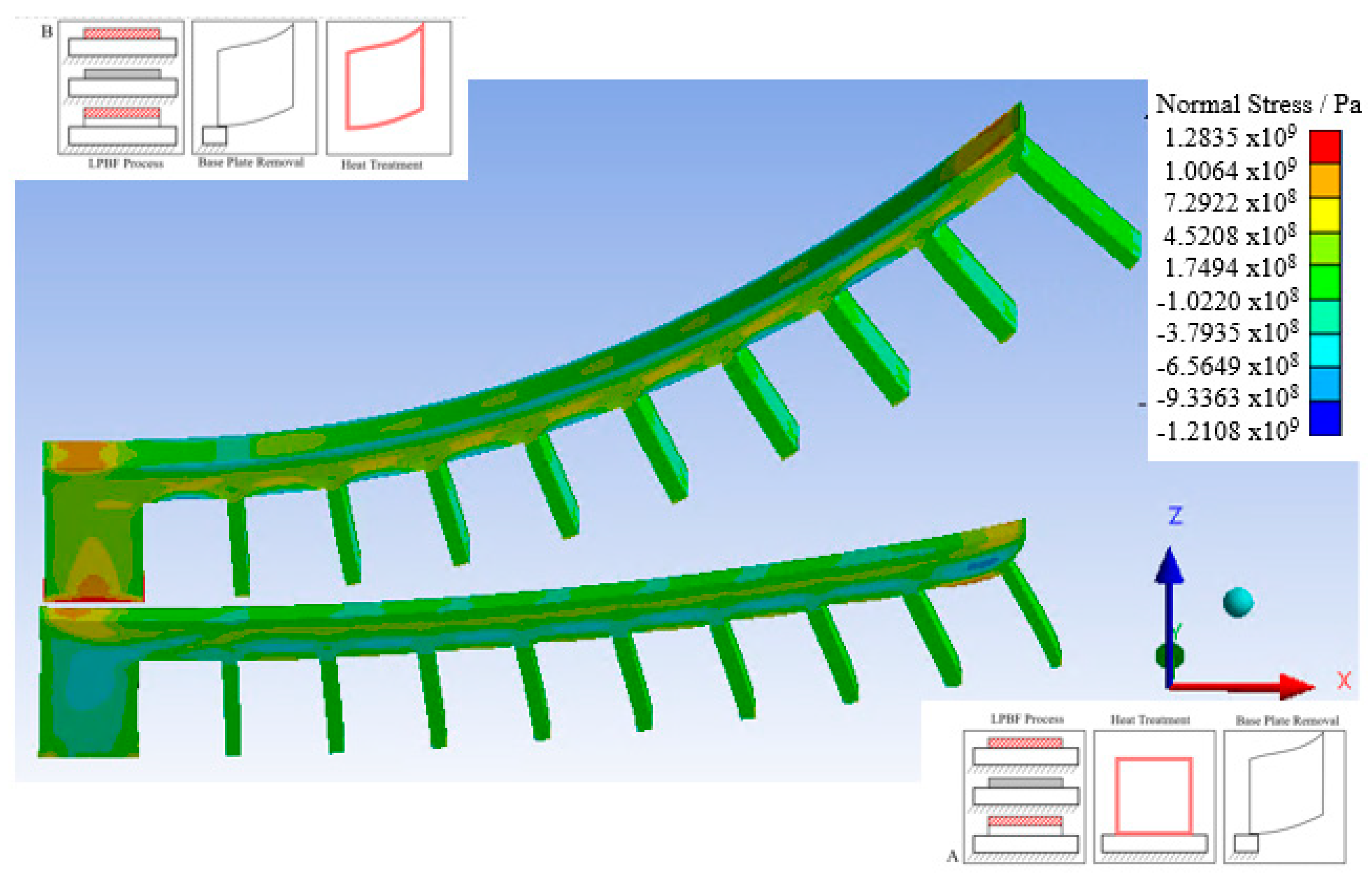
- The effect of changing the process chain sequence, from first heat treating to first removing from the base plate, leads to an increase of the deformation of the used part. This is most likely due to the stress relaxation, which causes deformation without build-up of stresses when heating up, while causing a build-up of stress and limited deformation when cooling down.
- The model also illustrates the capabilities of a generic FE solver to show the effect of the different process chain steps in the additive manufacturing process chain on the part quality.
- The model is not capable of capturing the effect of the duration of the heat treatment or the used temperature accurately due to its insensitivity to these parameters. However, when heating below the relaxation temperature a significant difference is observed in sequence B, since the stresses are no longer relaxed when heating up the beam.
- The stress relaxation does not decrease the stresses in a cantilever beam significantly but does lead to a homogenisation of this stress.
- Correcting the energy input does lead to an improved estimate for the residual stress in the part before post-processing, but since the post-processing changes the stress, the final deflection of a cantilever beam-type part does not differ significantly.
Author Contributions
Funding
Conflicts of Interest
References
- Wohlers, T. Wohlers Report 2018. Tech. Rep. 2018. [Google Scholar]
- Klocke, F.; Arntz, K.; Teli, M.; Winands, K.; Wegener, M.; Oliari, S. State-of-the-art Laser Additive Manufacturing for Hot-work Tool Steels. Procedia CIRP 2017, 63, 58–63. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Williams, R.J.; Davies, C.M.; Hooper, P.A. A pragmatic part scale model for residual stress and distortion prediction in powder bed fusion. Addit. Manuf. 2018, 22, 416–425. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.; Fang, X.; Guo, Y. Efficient predictive model of part distortion and residual stress in selective laser melting. Addit. Manuf. 2017, 17, 157–168. [Google Scholar] [CrossRef]
- Ahmad, B.; Van Der Veen, S.; Fitzpatrick, M.; Guo, H. Residual stress evaluation in selective-laser-melting additively manufactured titanium (Ti-6Al-4V) and inconel 718 using the contour method and numerical simulation. Addit. Manuf. 2018, 22, 571–582. [Google Scholar] [CrossRef]
- Markl, M.; Körner, C. Multiscale Modeling of Powder Bed–Based Additive Manufacturing. Annu. Rev. Mater. Res. 2016, 46, 93–123. [Google Scholar] [CrossRef]
- Kruth, J.; Froyen, L.; Van Vaerenbergh, J.; Mercelis, P.; Rombouts, M.; Lauwers, B. Selective laser melting of iron-based powder. J. Mater. Process. Technol. 2004, 149, 616–622. [Google Scholar] [CrossRef]
- Ferguson, B.; Li, Z.; Freborg, A. Modeling heat treatment of steel parts. Comput. Mater. Sci. 2005, 34, 274–281. [Google Scholar] [CrossRef]
- Dong, P.; Song, S.; Zhang, J. Analysis of residual stress relief mechanisms in post-weld heat treatment. Int. J. Press. Vessel. Pip. 2014, 122, 6–14. [Google Scholar] [CrossRef]
- Azizi, H.; Ghiaasiaan, R.; Prager, R.; Ghoncheh, M.; Abu Samk, K.; Lausic, A.; Byleveld, W.; Phillion, A. Metallurgical and mechanical assessment of hybrid additively-manufactured maraging tool steels via selective laser melting. Addit. Manuf. 2019, 27, 389–397. [Google Scholar] [CrossRef]
- Makoana, N.W.; Yadroitsava, I.; Moller, H.; Yadroitsev, I. Characterization of 17-4PH Single Tracks Produced at Different Parametric Conditions towards Increased Productivity of LPBF Systems—The Effect of Laser Power and Spot Size Upscaling. Metals 2018, 8, 475. [Google Scholar] [CrossRef]
- Yaghi, A.; Ayvar-Soberanis, S.; Moturu, S.R.; Bilkhu, R.; Afazov, S. Design against distortion for additive manufacturing. Addit. Manuf. 2019, 27, 224–235. [Google Scholar] [CrossRef]
- Antony, K.; Arivazhagan, N.; Senthilkumaran, K. Numerical and experimental investigations on laser melting of stainless steel 316L metal powders. J. Manuf. Process. 2014, 16, 345–355. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J. A systematic investigation of the effects of process parameters on heat and fluid flow and metallurgical conditions during laser-based powder bed fusion of Ti6Al4V alloy. Int. J. Heat Mass Transf. 2019, 139, 213–230. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J. Multiphysics modelling of lack-of-fusion voids formation and evolution in IN718 made by multi-track/multi-layer L-PBF. Int. J. Heat Mass Transf. 2019, 139, 95–114. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Parry, L.; Ashcroft, I.; Wildman, R.D. Understanding the effect of laser scan strategy on residual stress in selective laser melting through thermo-mechanical simulation. Addit. Manuf. 2016, 12, 1–15. [Google Scholar] [CrossRef]
- Hodge, N.E.; Ferencz, R.; Solberg, J.M. Implementation of a thermomechanical model for the simulation of selective laser melting. Comput. Mech. 2014, 54, 33–51. [Google Scholar] [CrossRef]
- Chen, C.; Yin, J.; Zhu, H.; Xiao, Z.; Zhang, L.; Zeng, X. Effect of overlap rate and pattern on residual stress in selective laser melting. Int. J. Mach. Tools Manuf. 2019, 145, 103433. [Google Scholar] [CrossRef]
- Denlinger, E.R. Thermomechanical Model Development and In Situ Experimental Validation of the Laser Powder-Bed Fusion Process. Thermo-Mech. Model Addit. Manuf. 2017, 16, 215–227. [Google Scholar] [CrossRef]
- Parry, L.; Ashcroft, I.; Wildman, R.D. Geometrical effects on residual stress in selective laser melting. Addit. Manuf. 2019, 25, 166–175. [Google Scholar] [CrossRef]
- Bayat, M.; Klingaa, C.; De Baere, D.; Mohanty, S.; Thorborg, J.; Skat Tiedje, N.; Hattel, J.H. Part-scale thermo-mechanical modellin of distortions in L-PBF-Analysis of the sequential flash heating method with experimental validation. Addit. Manuf. 2020. (Under review). [Google Scholar]
- Yakout, M.; Elbestawi, M.; Veldhuis, S.; Nangle-Smith, S. Influence of thermal properties on residual stresses in SLM of aerospace alloys. Rapid Prototyp. J. 2020, 26, 213–222. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Gusarov, A.; Yadroitsava, I.; Smurov, I.Y. Single track formation in selective laser melting of metal powders. J. Mater. Process. Technol. 2010, 210, 1624–1631. [Google Scholar] [CrossRef]
- Ukar, E.; Lamikiz, A.; De Lacalle, L.L.; Martinez, S.; Liebana, F.; Tabernero; Lamikiz, A.; De Lacalle, L.N.L. Thermal model with phase change for process parameter determination in laser surface processing. Phys. Procedia 2010, 5, 395–403. [Google Scholar] [CrossRef]
- Montevecchi, F.; Venturini, G.; Grossi, N.; Scippa, A.; Campatelli, G. Finite Element mesh coarsening for effective distortion prediction in Wire Arc Additive Manufacturing. Addit. Manuf. 2017, 18, 145–155. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J. Numerical modelling and parametric study of grain morphology and resultant mechanical properties from selective laser melting process of Ti6Al4V. In Proceedings of the 18th International Conference of the european Society for Precision Engineering and Nanotechnology (euspen 18), Venice, Italy, 4–8 June 2018. [Google Scholar]
- Vaverka, O.; Koutny, D.; Vrana, R. Effect of heat treatment on mechanical properties and residual stresses in additively manufactured parts. In Proceedings of the 24th International Conference Engineering Mechanics 2018, Svratka, Czech Republic, 14–27 May 2018. [Google Scholar] [CrossRef]
- Shiomi, M.; Osakada, K.; Nakamura, K.; Yamashita, T.; Abe, F. Residual Stress within Metallic Model Made by Selective Laser Melting Process. CIRP Ann. 2004, 53, 195–198. [Google Scholar] [CrossRef]
- Mutua, J.; Nakata, S.; Onda, T.; Chen, Z.-C. Optimization of selective laser melting parameters and influence of post heat treatment on microstructure and mechanical properties of maraging steel. Mater. Des. 2018, 139, 486–497. [Google Scholar] [CrossRef]
- Rohde, J.; Jeppsson, A. Literature review of heat treatment simulations with respect to phase transformation, residual stresses and distortion. Scand. J. Met. 2000, 29, 47–62. [Google Scholar] [CrossRef]
- Su, B.; Ma, Q.; Han, Z. Modeling of Austenite Decomposition during Continuous Cooling Process in Heat Treatment of Hypoeutectoid Steel with Cellular Automaton Method. Steel Res. Int. 2017, 88, 1600490. [Google Scholar] [CrossRef]
- Yan, G.; Crivoi, A.; Sun, Y.; Maharjan, N.; Song, X.; Li, F.; Tan, M.J. An Arrhenius equation-based model to predict the residual stress relief of post weld heat treatment of Ti-6Al-4V plate. J. Manuf. Process. 2018, 32, 763–772. [Google Scholar] [CrossRef]
- Alberg, H.; Berglund, D. Comparison of plastic, viscoplastic, and creep models when modelling welding and stress relief heat treatment. Comput. Methods Appl. Mech. Eng. 2003, 192, 5189–5208. [Google Scholar] [CrossRef]
- De Baere, D.; Bayat, M.; Mohanty, S.; Hattel, J. Thermo-fluid-metallurgical modelling of the selective laser melting process chain. Procedia CIRP 2018, 74, 87–91. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Michaleris, P. (Pan) Effect of stress relaxation on distortion in additive manufacturing process modeling. Addit. Manuf. 2016, 12, 51–59. [Google Scholar] [CrossRef]
- Tan, P.; Shen, F.; Li, B.; Zhou, K. A thermo-metallurgical-mechanical model for selective laser melting of Ti6Al4V. Mater. Des. 2019, 168, 107642. [Google Scholar] [CrossRef]
- Zanger, F.; Boev, N.; Schulze, V. Novel Approach for 3D Simulation of a Cutting Process with Adaptive Remeshing Technique. Procedia CIRP 2015, 31, 88–93. [Google Scholar] [CrossRef]
- Afazov, S. Modelling and simulation of manufacturing process chains. CIRP J. Manuf. Sci. Technol. 2013, 6, 70–77. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Tekkaya, A.E.; Biermann, D.; Zabel, A.; Langhorst, M.; Schober, A.; Kloppenborg, T.; Steiner, M.; Ungemach, E. Integrated simulation of the process chain composite extrusion–milling–welding for lightweight frame structures. Prod. Eng. 2009, 3, 441–451. [Google Scholar] [CrossRef]
- Gallego, A.C.; Ramos, L.M.M.; Aguirrebeitia, J.; De Lacalle, L.N.L.; De Lacalle, L.L. A Methodology to Evaluate the Reliability Impact of the Replacement of Welded Components by Additive Manufacturing Spare Parts. Metals 2019, 9, 932. [Google Scholar] [CrossRef]
- Gusarov, A.; Smurov, I.Y. Modeling the interaction of laser radiation with powder bed at selective laser melting. Phys. Procedia 2010, 5, 381–394. [Google Scholar] [CrossRef]
- Hsiao, C.; Chiou, C.; Yang, J.-R. Aging reactions in a 17-4 PH stainless steel. Mater. Chem. Phys. 2002, 74, 134–142. [Google Scholar] [CrossRef]
- Hu, Z.; Zhu, H.; Zhang, H.; Zeng, X. Experimental investigation on selective laser melting of 17-4PH stainless steel. Opt. Laser Technol. 2017, 87, 17–25. [Google Scholar] [CrossRef]
- Ansys Workbench Release 2019 R2. Available online: https://www.ansys.com/ (accessed on 5 May 2019).
- Sames, W.; List, F.A.; Pannala, S.; Dehoff, R.R.; Babu, S.S. The metallurgy and processing science of metal additive manufacturing. Int. Mater. Rev. 2016, 61, 315–360. [Google Scholar] [CrossRef]
- Hodge, N.E.; Ferencz, R.; Vignes, R. Experimental comparison of residual stresses for a thermomechanical model for the simulation of selective laser melting. Addit. Manuf. 2016, 12, 159–168. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Ghosh, S.; McReynolds, K.; E Guyer, J.; Banerjee, D.K. Simulation of temperature, stress and microstructure fields during laser deposition of Ti–6Al–4V. Model. Simul. Mater. Sci. Eng. 2018, 26, 075005. [Google Scholar] [CrossRef]
- Ganeriwala, R.; Strantza, M.; King, W.; Clausen, B.; Phan, T.; Levine, L.; Brown, D.; Hodge, N. Evaluation of a thermomechanical model for prediction of residual stress during laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 27, 489–502. [Google Scholar] [CrossRef]
- Mugwagwa, L.; Yadroitsev, I.; Matope, S. Effect of Process Parameters on Residual Stresses, Distortions, and Porosity in Selective Laser Melting of Maraging Steel 300. Metals 2019, 9, 1042. [Google Scholar] [CrossRef]
- Masoomi, M.; Shamsaei, N.; Winholtz, R.A.; Milner, J.L.; Gnäupel-Herold, T.; Elwany, A.; Mahmoudi, M.; Thompson, S.M. Residual stress measurements via neutron diffraction of additive manufactured stainless steel 17-4 PH. Data Brief 2017, 13, 408–414. [Google Scholar] [CrossRef]
- Barros, R.; Silva, F.J.G.; Gouveia, R.; Saboori, A.; Marchese, G.; Biamino, S.; Salmi, A.; Atzeni, E. Laser Powder Bed Fusion of Inconel 718: Residual Stress Analysis Before and After Heat Treatment. Metals 2019, 9, 1290. [Google Scholar] [CrossRef]
- ASM International. Atlas of Stress-Strain Curves, 2nd ed.; ASM International: Russel Township, ON, Canada, 2002. [Google Scholar]
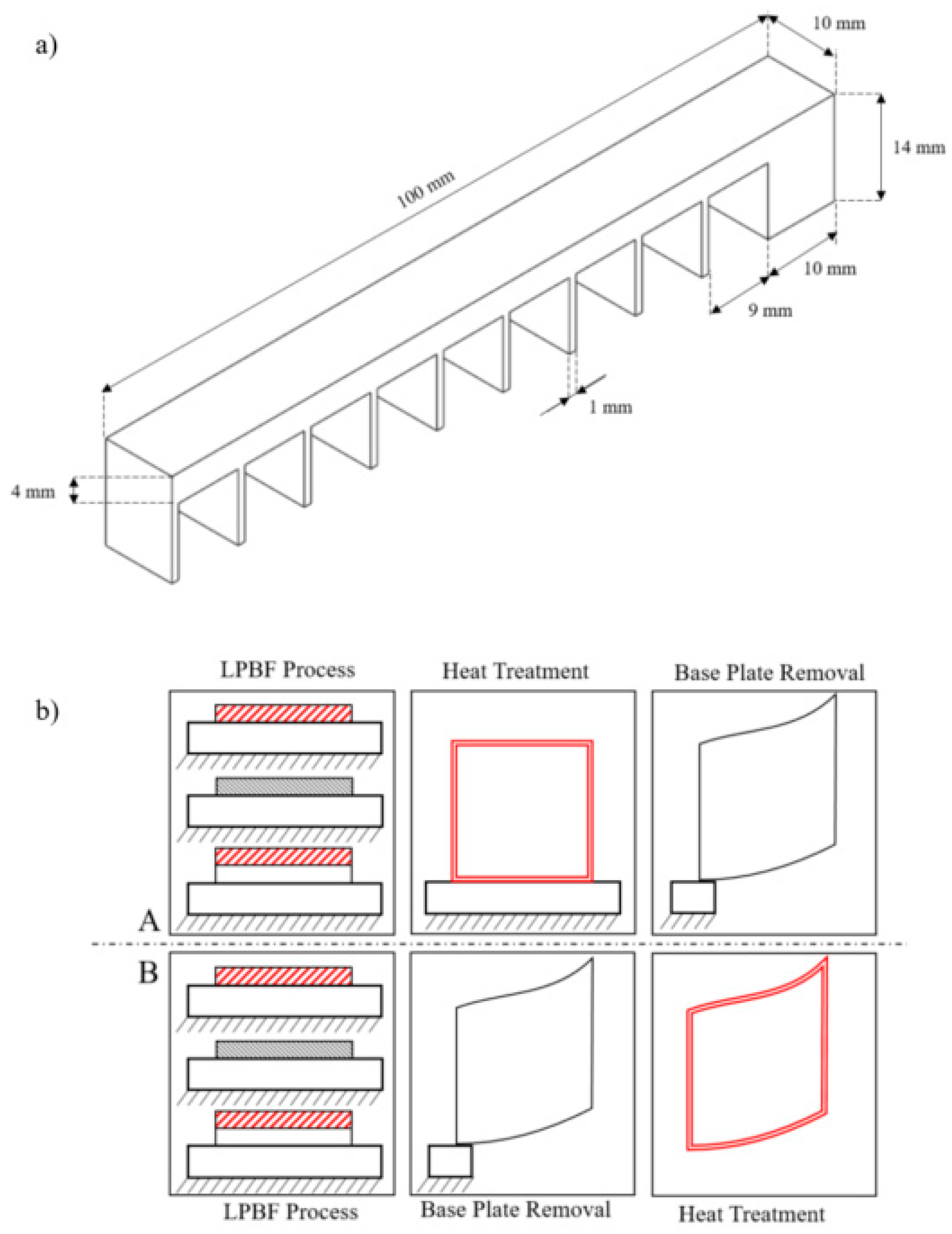
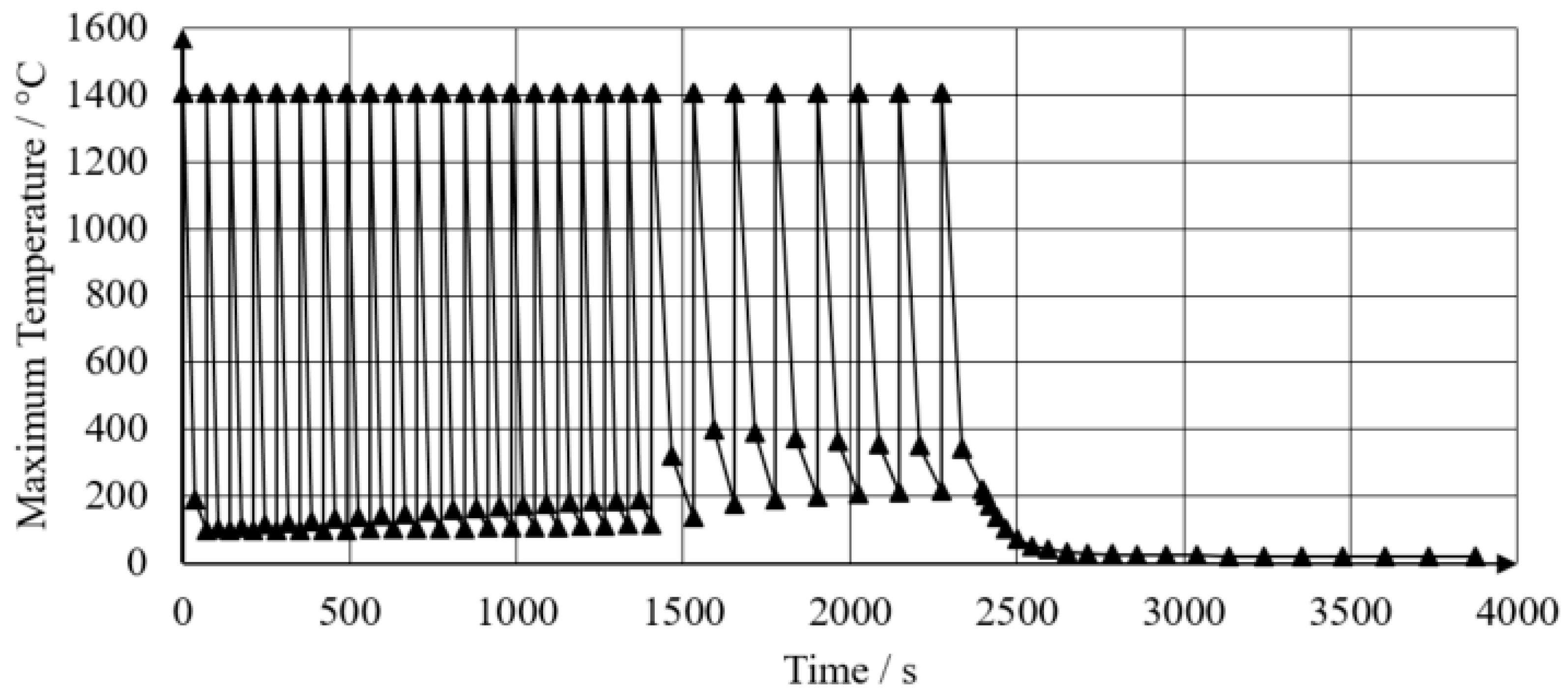

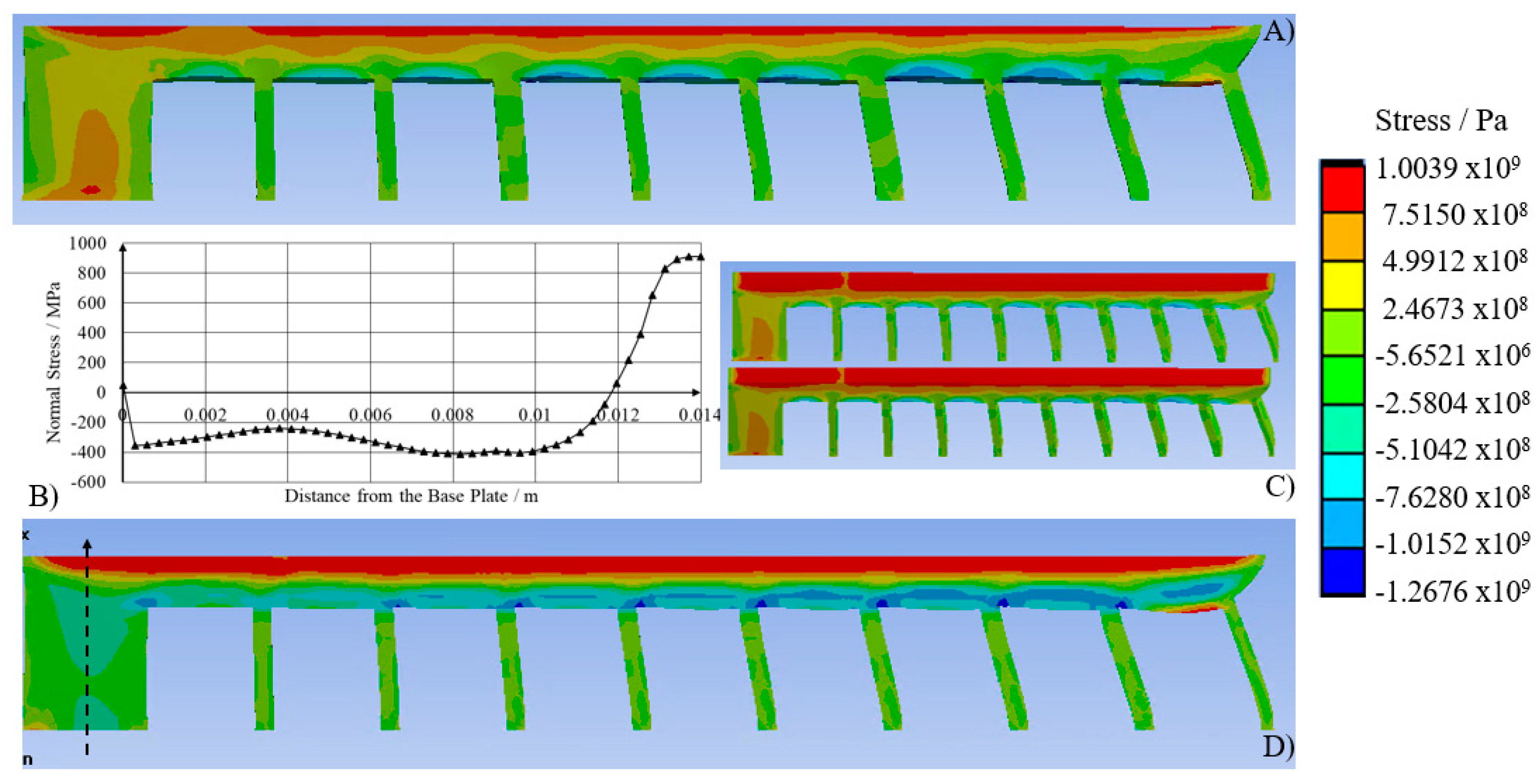
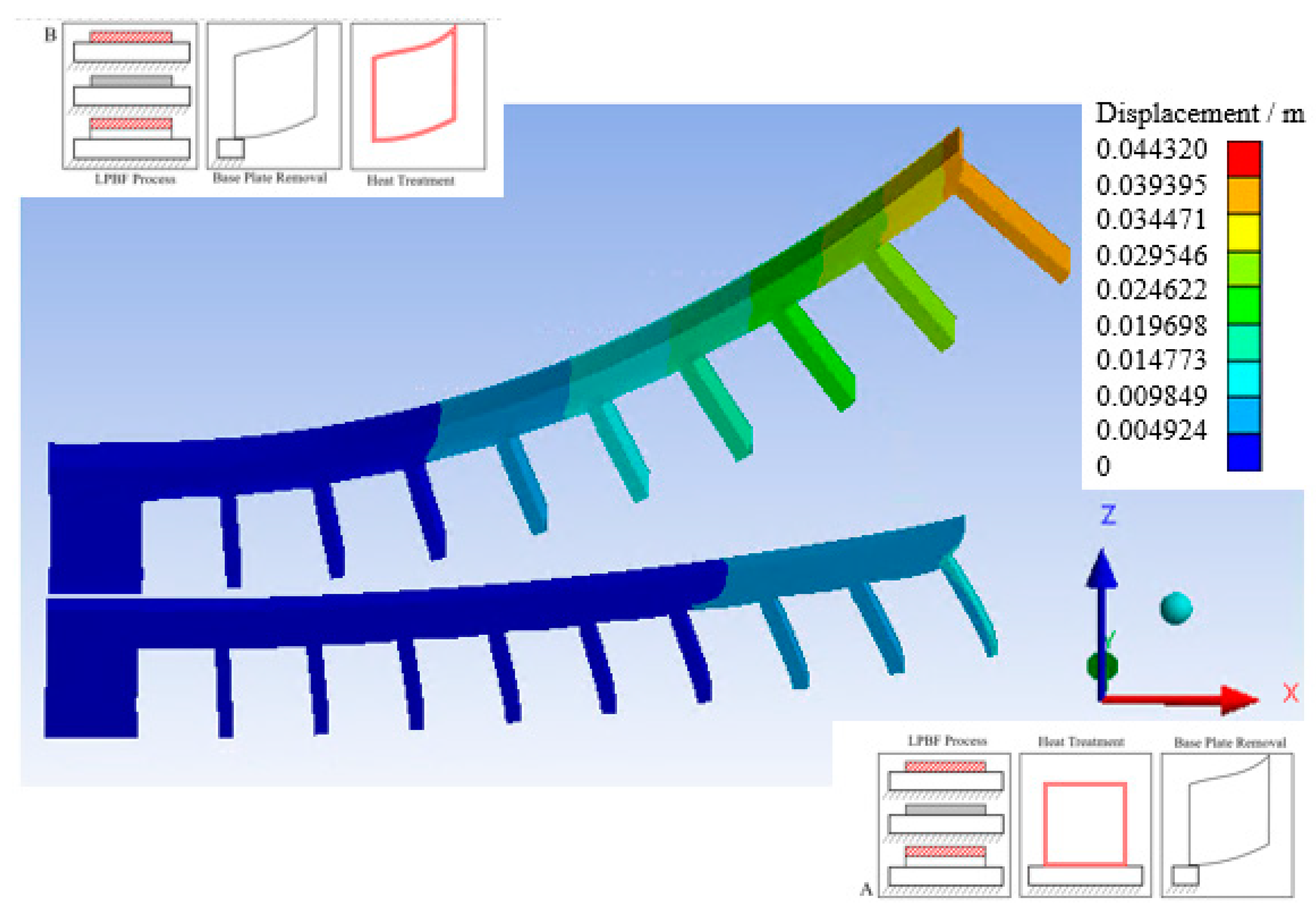
| Number | Parameters | Intentions | |||
|---|---|---|---|---|---|
| Time | Peak Temperature | Deposition Temperature | Element Size | ||
| 1 | 7200 s | 350 °C | 1405 °C | 5.00 × 10−3 m | Simulation benchmark |
| 2 | 7200 s | 350 °C | 1405 °C | 6.00 × 10−4 m | Investigation of mesh convergence |
| 3 | 7200 s | 350 °C | 1405 °C | 7.50 × 10−4 m | |
| 4 | 7200 s | 350 °C | 1405 °C | 8.00 × 10−4 m | |
| 5 | 7200 s | 350 °C | 1405 °C | 1.00 × 10−3 m | |
| 6 | 3600 s | 350 °C | 1405 °C | 5.00 × 10−4 m | Investigation of effect of dwell time during heat treatment |
| 7 | 10800 s | 350 °C | 1405 °C | 5.00 × 10−4 m | |
| 8 | 7200 s | 400 °C | 1405 °C | 5.00 × 10−4 m | Investigation of effect of heat treatment temperature |
| 9 | 7200 s | 300 °C | 1405 °C | 5.00 × 10−4 m | |
| 10 | 7200 s | 280°C | 1405 °C | 5.00 × 10−4 m | |
| 11 | 7200 s | 350 °C | 3000 °C | 5.00 × 10−4 m | Energy correction approach |
| Simulation Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Element size (m) | 5 × 10−4 | 6 × 10−4 | 7.5 × 10−4 | 8 × 10−4 | 1 × 10−3 |
| Longitudinal normal stress (MPa) | 841.6 | 840.5 | 835.1 | 832.8 | 825.7 |
| Simulation 8 | Simulation 9 | Simulation 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature | 400 °C | 300 °C | 280 °C | ||||||
| Sequence A | Sequence B | Sequence A | Sequence B | Sequence A | Sequence B | ||||
| Displacement in z (m) | 0.0102 | 0.0363 | 0.0102 | 0.0364 | 0.0102 | 0.0103 | |||
| End stress (Pa) | 1.00 × 109 | 1.28 × 109 | 1.39 × 109 | 1.28 × 109 | 1.00 × 109 | 1.10 × 109 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Baere, D.; Moshiri, M.; Mohanty, S.; Tosello, G.; Hattel, J.H. Numerical Investigation into the Effect of Different Parameters on the Geometrical Precision in the Laser-Based Powder Bed Fusion Process Chain. Appl. Sci. 2020, 10, 3414. https://doi.org/10.3390/app10103414
De Baere D, Moshiri M, Mohanty S, Tosello G, Hattel JH. Numerical Investigation into the Effect of Different Parameters on the Geometrical Precision in the Laser-Based Powder Bed Fusion Process Chain. Applied Sciences. 2020; 10(10):3414. https://doi.org/10.3390/app10103414
Chicago/Turabian StyleDe Baere, David, Mandanà Moshiri, Sankhya Mohanty, Guido Tosello, and Jesper Henri Hattel. 2020. "Numerical Investigation into the Effect of Different Parameters on the Geometrical Precision in the Laser-Based Powder Bed Fusion Process Chain" Applied Sciences 10, no. 10: 3414. https://doi.org/10.3390/app10103414
APA StyleDe Baere, D., Moshiri, M., Mohanty, S., Tosello, G., & Hattel, J. H. (2020). Numerical Investigation into the Effect of Different Parameters on the Geometrical Precision in the Laser-Based Powder Bed Fusion Process Chain. Applied Sciences, 10(10), 3414. https://doi.org/10.3390/app10103414







