Regularized Instance Embedding for Deep Multi-Instance Learning

Abstract

In the era of Big Data, multi-instance learning, as a weakly supervised learning framework, has various applications since it is helpful to reduce the cost of the data-labeling process. Due to this weakly supervised setting, learning effective instance representation/embedding is challenging. To address this issue, we propose an instance-embedding regularizer that can boost the performance of both instance- and bag-embedding learning in a unified fashion. Specifically, the crux of the instance-embedding regularizer is to maximize correlation between instance-embedding and underlying instance-label similarities. The embedding-learning framework was implemented using a neural network and optimized in an end-to-end manner using stochastic gradient descent. In experiments, various applications were studied, and the results show that the proposed instance-embedding-regularization method is highly effective, having state-of-the-art performance.

1. Introduction

Benefiting from fully labeled training datasets, supervised learning techniques such as deep neural networks [1] have obtained great success in various applications, such as image and speech recognition, and natural-language understanding. However, in most, if not all practical scenarios, it is not so easy to construct large-scale fully labeled training datasets due to the high cost of the data-labeling process. In these circumstances, multi-instance learning (MIL), which only requires inexact supervision, becomes attractive [2]. Different from conventional supervised learning in which the learner receives a set of instances and each instance is individually labeled, the learner in MIL receives of set of labeled bags and each bag contains multiple unlabeled instances. Thus, in the training stage of MIL, only the bag-level label is given, while the instance-level label is unknown.

With the emergence of deep learning techniques, the quality of representation/embedding learning has especially been greatly improved over the past few years, making it increasingly important in machine learning. As representatives, neural networks that take raw data as input and learn multi-layer features toward the final classification/regression goals have shown impressive abilities. In this paper, we attempt to equip a MIL problem with representation learning using neural networks via exploiting the relationship between instances. Despite inexact MIL (weak) supervision, if instance-level information is unknown, it would be helpful to learn instance-level representation (i.e., instance embedding). The following reasons support our idea: (1) Bag embedding heavily depends on instance embedding, and better instance embedding results in better bag-classification results. (2) Instance-level predictions are desired in many applications, for instance weakly supervised object detection [3,4]. However, learning instance embedding is very challenging due to the ambiguity of instance labels.

Thanks to the good capacity of neural networks, instance embedding can be plugged into a neural network. Recently, the authors of [5] revisited multi-instance neural networks and showed state-of-the-art bag classification performance. In [6], the authors proposed a 3D subconcept layer that was combined with a deep network to perform multi-instance multi-label classification in various domains. In these works, instance probabilities were treated as latent variables and then aggregated into bag probability via a pooling function, e.g., max pooling. Since the bag-level ground truth is given, instance probabilities can be adjusted using back-propagation. Because the max-pooling procedure omits some instance-level information, it is unnecessary to require all instances to have correct labels. As pointed out by Carbonneau et al. [7], in positive bags, some false-negative and false-positive instances barely affect bag classification. However, learning instance embedding relies on instance probabilities. Noisy instance probabilities very likely degrade instance-embedding quality.

Inspired by the classical MIL work proposed by Zhou et al. [8], in which instances from a bag are treated in a non-independent and identically distributed (i.i.d.) way that exploits relations among instances and a mi-Graph algorithm was proposed to obtain a better MIL performance, we aimed to use instance relations to promote instance-embedding quality. This is different from mi-Graph that directly compares bags without considering instance embedding, as we employed instance embedding as the MIL backbone and further distinguished positive and negative instances in a bag. Our usage of instance relations was to encourage instances from a same class to have higher similarity and instances from different classes to have less similarity, which is similar to the goal of metric learning [9]. In metric learning, the goal is to learn the similarity between a pair of objects/instances rather than classification or regression. As we had instance probabilities as hidden nodes in a neural network, we could use instance probabilities to determine instance classes. In practice, given a pair of instances in a bag or a training batch, the proposed regularizer encourages instances with similar labels to have close embedding; otherwise, their embedding should be dissimilar. In other words, the regularizer maximizes correlations between the embedding- and the label-similarity matrices of instances.

In summary, this work emphasizes the importance of instance-embedding learning in MIL. We designed an instance-embedding regularizer for taking instance relations into consideration instead of treating instances as i.i.d. samples. The regularizer was integrated into a single multi-instance neural network and optimized end-to-end. Extensive experiments on various MIL applications showed that our method outperformed previous state-of-the-art methods by a large margin.In the following parts of the paper, we first review related MIL methods and discuss the differences between the previous works in Section 2, then give details the proposed multi-instance network with regularized instance embedding learning in Section 3, perform experiments and compare our results with the state-of-the-art methods in Section 4, lastly conclude the paper in Section 5.

2. Related Work

In this section, we first review the research background of MIL, including MIL applications, MIL tasks, and MIL with multi-label learning, regression, ranking, and clustering, and then review some classical MIL methods. We finally review deep MIL methods. In each section, the relation between the proposed method and the cited methods are discussed.

2.1. Research Background of MIL

MIL deals with a dataset called a bag and only supervises the whole bag, but does not provide specific labels of instances in the bag. Especially, in recent years, the formulation of this problem has attracted much attention from the research community. The data volume of the problem is exponential and requires a lot of labeling work. As a weakly supervised learning method, MIL can effectively reduce this burden because weak supervision is usually easier to obtain. For example, you can train object detectors with images collected from the web, using their associated tags as weak supervision, rather than a dataset of local annotations, such as object bounding box annotation and pixel-wise annotation [10,11]. MIL is widely used in medical image analysis problems. A computer-aided-diagnosis (CAD) algorithm can be trained with medical images instead of expensive local annotations provided by experts. There are several types of problems that can be naturally expressed as MIL problems. For example, in a drug-activity-prediction problem [12], the goal is to predict whether a molecule induces a given effect. A molecule can have many conformations, and it is impossible to observe the influence of individual conformation without the expected effect. Therefore, the molecule must be observed as a set of conformations, so MIL formulation is used. Due to these attractive features, MIL has been increasingly used in many other applications in the past 20 years, such as image and video classification [13,14,15,16,17,18], document classification [19,20], and sound classification [21]. Motivated by the great effectiveness of MIL in real applications, the research goal of this paper is to propose a state-of-the-art MIL method.

When developing MIL algorithms, there are two tasks: bag classification task and instance classification task. Bag classification is the most common task for MIL algorithms. It involves assigning a class label to a set of instances. The single instance label is not necessarily important depending on the algorithm and the type of hypothesis. Instance classification requires predicting instance labels though the instance labels in training set are not given. As described in [22], the loss functions of the two tasks are different. When the goal is bag classification, misclassification of the instance does not necessarily affect bag-level loss. For example, in a positive bag, if there are few real negative instances that are wrongly classified as positive instances, and bag labels remain the same; therefore, in the structure of the problem, such as the number of instances per-bag, the loss function plays an important role [22]. Moreover, many methods perform bag classification in the bag space without reasoning in instance space; therefore, they are often unable to perform instance classification. The proposed method can predict both bag labels and instance labels, which makes it more useful in applications.

MIL classification is not limited to assigning a single label to an instance or bag. Assigning multiple labels to bags is particularly relevant because they can contain instances that represent different concepts. This multi-label MIL idea has been the focus of several publications [23,24,25]. Besides classification, MIL can be applied in for regression problems (see, e.g., [26,27,28]). The simplest way is to replace the bag-level classifier with a regressor [28]. Other methods proposed to rank bags instead of assigning a class tag or score. This problem is different from regression, because the goal is not to obtain accurate real-value labels, but to compare the predicted scores for sorting. Ranking can be performed at bag-level [29] or instance-level [30]. It is also possible to implement clustering tasks, including searching for clusters or structures in the set of an unlabeled bag. In some cases, clustering is performed in bag spaces using standard algorithms and set-based distance measures. For example, in [31], the algorithm identified the most relevant instances of each bag and performed the largest edge clustering on those instances. Alternatively, clustering can be executed at the instance-level. For example, Wang et al. [32] performed instance clustering for dictionary learning and Tang et al. [4] used instance clustering to stabilize the process of weakly-supervised object detection. The proposed instance embedding regularization method works on feature learning and it could be helpful for multi-label MIL, multi-instance regression, multi-instance ranking, and multi-instance clustering.

2.2. Classical MIL Methods

For MIL, many scholars carried out long-term research and made good progress. MIL was first proposed to solve the problem of drug molecular activity [3,12]. Then, many machine-learning models have emerged to solve the multiple-instance-learning problem, such as linear support vector machines (SVM) [33] that are applied in MI-SVM and mi-SVM for bag- and instance-level classification, respectively. Citation-kNN [34] solves the MIL problem in a lazy way which simply uses a k-nearest neighbor (kNN) classifier and various distance metrics. Fretcit-kNN [35] employs the minimal Hausdorff distance between frequent term sets and utilizes both the references and citers of an unseen bag in determining its label in the task of web recommendation. G3P-MI [36] solves MIL from a perspective by utilizing grammar-guided genetic programming. MI-Kernel [37] introduces kernel methods into MIL. EM-DD combines the expectation-maximization algorithm with the diverse density (DD) algorithm for MIL [38]. Multi-instance Fisher Vector (miFV) [39] is the representative algorithm to solve multi-instance learning problems from the perspective of embedded space, mapping instance features into a high-dimensional space through a pretrained Gaussian model and Fisher Vector coding. Besides Fisher Vector coding, the vector of locally aggregated descriptors (VLAD) is also applied in [39] for MIL and the method is called miVLAD. The multi-instance dissimilarity (MInD) method [40] uses bag similarities to classify bags. Zhou et al. [8] proposed a classical multiple-instance learning work. They proposed a non-independent and identically distributed method to handle instance from the bag and utilize the relationship between instances, and a mi-Graph algorithm to provide better multi-instance learning performance. Inspired by this work, we aimed to improve the quality of instance embedding by using instance relationships. Unlike mi-Graph that directly compares bags without considering instance embedding, we could also use instance embedding as the backbone of multiple-instance learning, and further distinguish positive and negative instances in the bag. Besides, mi-Graph is a non-deep learning method while our method is based on deep neural networks.

2.3. Deep MIL Methods

Before the rise of deep learning, Ramon and Raedt [41] first proposed the idea of using a traditional neural network to solve multiple-instance learning and called it a multiple-instance neural network. This network learns and predicts instance labels, and obtains bag labels by aggregating the predicted instance labels. Their ideas are undoubtedly forward-looking, but, at that time, deep learning and neural networks had not yet had a breakthrough, and this research direction has not attracted too much attention; nonetheless, it is still a pioneering work.

In recent years, deep learning has made a breakthrough in the field of artificial intelligence, and has been widely used in many fields, such as speech recognition and computer vision. Many classical neural-network architectures, such as AlexNet [42], VGG [43], GoogleNet [44], and ResNet [45], have become common means for people to solve machine-learning problems. Therefore, for multiple-instance learning, many good studies based on neural networks have emerged in recent years and instance-embedding learning can be done on a neural network due to its good capacity. Recently, Wang et al. [5] re-examined multiple-instance neural networks and achieved the most advanced bag-classification performance. Feng et al. [6] proposed a 3D subconcept layer combined with a deep network to perform multi-instance multi-label classification in various domains. In these works, instance probability was regarded as a latent variable; then, instance probabilities were aggregated in bag probability through a pooling function such as max-pooling. Since the bag-level ground truth was given, back-propagation could be used to adjust instance probability. Because the pooling process omits some instance-level information, it is not necessary for all instances to have the correct labels. As pointed out in [7], in positive bags, some false-negative and false-positive instances hardly affect bag classification. However, learning instance embedding depends on instance probabilities, and wrong instance probabilities are likely to reduce bag-classification quality.

We used the relationship between instances so that those from the same class would have higher similarity, while those from different classes smaller similarity, which is similar to the goal of metric learning. Since instance probability is a hidden node in the neural network, we could use it to determine the instance category. In practice, given a set of instances in a bag or training batch, the regularizer we designed considers that instances with similar labels should have similar embeddings; otherwise, their embeddings should be different. In other words, the regularizer maximizes the correlation between the embedded similarity matrix and the instance-label similarity matrix.

3. Method

3.1. Overview of the Proposed MIL Network

We first briefly introduces the definition of MIL. In MIL, a set of bags are given: $X=\{X_1,X_2,\dots ,X_N\}$. Each bag contains various instances, and can be conveniently expressed in $X_i=\{{\mathbf{x}}_{i1},{\mathbf{x}}_{i2},\cdots ,{\mathbf{x}}_{i{m}_i}\}$, where ${\mathbf{x}}_{ij}\in {\mathbb{R}}^d$. The numbers of bags and instances in bag $X_i$ are designated as N and $m_i$, respectively. Recall that only bag-level labels are available in training. Let $Y_i\in \{0,1\}$ be the label for bag $X_i$, where 1 means $X_i$ is positive and 0 otherwise. On the contrary, no labels are available for instances. Relations between bag labels and instance labels can be formally expressed as follows:

$$\left\{\begin{array}{c}{Y}_i=0\iff \forall y_{ij}=0;\hfill \\ Y_i=1\iff {\displaystyle \sum _{j=1}^{m_i}}{y}_{ij}\ge 1.\hfill \end{array}\right.$$

(1)

Having the above preliminary knowledge, we now discuss instance-embedding learning for MIL. As a weakly supervised classification problem, MIL methods usually have two kinds of predictive targets [7]: bag- and instance-level prediction.

The overall multi-instance neural network is illustrated in Figure 1. The instances were first fed into three fully connected (FC) layers for instance-embedding generation with 256, 128, and 64 neurons, respectively. Each FC layer was followed by a Rectified Linear Unit (ReLU) layer [46] for nonlinearity, and a dropout layer [47] (0.5 dropout ratio) to avoid overfitting. Then, learned instance embedding was fed into three streams: instance-level predictor network, bag-level predictor network, and embedding regularizer network, as described in Section 3 and Figure 1. For instance-level prediction, an FC layer with one neuron was used to predict its probability of belonging to the positive class of each instance, and a max-pooling layer was used to aggregate instance scores (i.e., positiveness) into the bag scores. For bag-level prediction, a MIL pooling function, as described in Section 3.3, was used to aggregate instance representations (i.e., instance embedding) into bag representations (i.e., bag embedding), and an FC layer with one neuron was used to obtain the bag scores. Since regularized instance embedding (RIE) is the novelty in the proposed MIL network, we call the proposed method RIE in the rest of the paper.

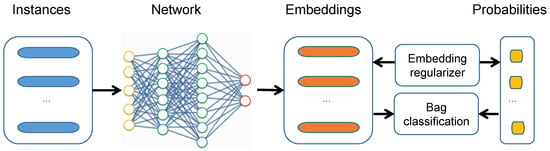
Figure 1. Framework of the proposed multi-instance network with instance embedding regularizer. Given a bag of instances as input, we use a multi-layer fully-connected neural network to extract an embedding (i.e., feature vector) for each instance. The instance embeddings are regularized and used for predicting instance probabilities. Then, the regularized instance embeddings are aggregated for predicting bag probability. The predicted bag probability and instance probabilities are both used for making the final bag classification.

3.2. Target Function

By utilizing multitask learning, the two predictive targets can be optimized together, as follows:

$$min L=L_{\mathrm{bag}}+L_{\mathrm{ins}},$$

(2)

where $L_{\mathrm{bag}}$ and $L_{\mathrm{ins}}$ are loss functions for bag prediction and instance prediction, respectively. However, different from other multi-instance neural networks, we propose a novel instance-embedding regularizer for better performance. In the following subsections, we give the details of instance-embedding learning.

3.3. Instance-Embedding Learning

Different from fully supervised learning, instance labels in MIL are unknown. Thus, performing instance-level embedding/representation learning is a very challenging task. However, instance-level learning is very important in many applications since it reveals more detailed information and makes MIL approaches more interpretable. As a result, we attempt to solve this challenging problem in this paper.

In previous MIL methods, instance-embedding learning was usually ignored, while bag embedding was extensively studied. We formulated an instance-embedding-learning framework and propose novel regularized instance embedding as follows.

Let $f\left(x_{ij}\right)$ be an embedding of instance ${\mathbf{x}}_{ij}\in {\mathbb{R}}^N$, where $f:{\mathbb{R}}^N\to {\mathbb{R}}^D$. Usually, f is a differential neural network with parameters $\Theta$. $\Theta$ contains all the parameters in the multiple layers of the network f. On the basis of instance embedding, there are two styles of prediction functions: instance- and bag-level prediction.

Instance-level prediction: Let $h\left(f\left({\mathbf{x}}_{ij}\right)\right)$ be an instance classifier, where $h:{\mathbb{R}}^D\to \mathbb{R}$ is a binary classifier that predicts the positiveness $p_{ij}$ of instance ${\mathbf{x}}_{ij}$, denoted as follows:

$$p_{ij}=h\left(f\left({\mathbf{x}}_{ij}\right)\right).$$

(3)

Then, instance-level probabilities $[p_{i1},p_{i2},\cdots ,p_{i{m}_i}]$ are aggregated into bag-level probability using a max operator, denoted as

$$P_i=\underset{j\in [1,m_i]}{max}{p}_{ij},$$

(4)

where $m_i$ is the total number of instances in the ith bag, and $P_i$ denotes the probability of the ith bag being positive. Here, max is chosen rather than $\mathrm{mean}$ for the max function, as it is more suitable with the MIL definition.

Bag-level prediction: This generates bag-level embedding/representation and directly makes bag-level predictions without considering instance-level probabilities. Given an instance-embedding set from the same bag $f\left({\mathbf{x}}_{ii}\right),f\left({\mathbf{x}}_{i2}\right),\cdots ,f\left({\mathbf{x}}_{i{m}_i}\right)$, we generated the bag embedding using a function denoted as F. There are at least two ways to define F, i.e., using a $\max$ or $\mathrm{mean}$ pooling function, which are given as follows:

$$F\left(f\left({\mathbf{x}}_{ij}\right|j\in [1,m_j])\right)={\max }_{j\in [1,m_i]}\left(f\left({\mathbf{x}}_{ij}\right)\right),$$

(5)

and

$$F\left(f\left({\mathbf{x}}_{i}j\right|j\in [1,m_j])\right)={\mathrm{mean}}_{j\in [1,m_i]}\left(f\left({\mathbf{x}}_{ij}\right)\right).$$

(6)

Here, max and $\mathrm{mean}$ are both elementwise pooling functions that operate on D-dimensional instance-embedding vectors. After that, a bag predictor is applied to generate bag probability, denoted as follows:

$$P_i=H\left(F\left(f\left({\mathbf{x}}_{ij}\right|j\in [1,m_j])\right)\right),$$

(7)

where H is a linear classifier for bag classification. In neural networks, H can be implemented as a fully connected layer, and its parameters can be optimized together with instance- and bag-level feature-extraction networks in an end-to-end manner.

The loss function for bag $X_i$ is $\mathrm{L}=\frac{1}{N}{\sum }_i^N\ell (P_i,Y_i)$. In this paper, we use cross-entropy loss

$$\ell (P_i,Y_i)=-\{Y_{i}log\left(P_i\right)+(1-Y_i)log(1-P_i)\}.$$

(8)

Other loss functions, e.g., Euclidean or softmax loss, can also be utilized. We chose cross-entropy loss following the setting in [5] and the same loss function provides fair comparison in the experiments. For instance- and bag-level predictors, the MIL loss functions of $X_i$ are given, respectively, as follows:

$${\mathrm{L}}_{\mathrm{ins}}=\frac{1}{N}\sum _{i=1}^N\ell \left({\max }_{i\in [1,m_i]}h\left(f\left({\mathbf{x}}_{ij}\right)\right),Y_i\right)$$

(9)

$${\mathrm{L}}_{\mathrm{bag}}=\frac{1}{N}\sum _{i=1}^N\ell \left(H\left({\max }_{j\in [1,m_i]}f\left({\mathbf{x}}_{ij}\right)\right),Y_i\right)$$

(10)

3.4. Regularized Instance Embedding

The above loss function learns instance embedding on the basis of max- and mean-pooling functions, which fail to consider pairwise information between instances within the same bag, since max- or min-pooling functions deal with each instance individually. Here, we propose to use pairwise information to regularize instance embedding. As a result, we could obtain more accurate instance embedding for better instance and bag classification.

In machine learning, as a common assumption, instances belonging to the same category tend to be more similar, while instances from different categories are dissimilar. However, we cannot directly judge whether instances are from the same category or not because instance labels are unavailable. To solve this problem, instance probabilities $p_{ij}$ were used as latent variables to assist in distinguishing instances categories. For learning better instance embedding, we designed a regularizer to maximize the similarity between instances from the same category and minimize similarity between instances from different categories.

Given a batch of bags $\mathcal{M}=\{X_1,X_2,\cdots ,X_M\}$, supposing there are n instances in $\mathcal{M}$, we denote a pair of instances $\{{\mathbf{x}}_{i_1{j}_1},{\mathbf{x}}_{i_2{j}_2}\}$; no matter if they are from the same bag or not, the regularization objective can be formulated as Equation (11).

$${\mathrm{R}}_{ins}=\frac{1}{C_n^2}\sum _{i_1{j}_1{i}_2{j}_2}{r}_{\mathrm{pro}}\left(p_{i_1{j}_1},p_{i_2{j}_2}\right)\left(1-r_{\mathrm{emb}}(f\left({\mathbf{x}}_{i_1{j}_1}\right),f\left({\mathbf{x}}_{i_2{j}_2}\right))\right),$$

(11)

where $C_n^2=\frac{n(n-1)}{2}$ is the total number of instance pairs, and n means the total number of instances in batch $\mathcal{M}$. $r_{\mathrm{emb}}$ calculates instance similarity; $r_{\mathrm{pro}}$ calculates instance relationship. If ${\mathbf{x}}_{i_1{j}_1}$ and ${\mathbf{x}}_{i_2{j}_2}$ belong to the same category, $r_{\mathrm{pro}}\left(p_{i_1{j}_1},p_{i_2{j}_2}\right)$ is positive; otherwise, $r_{\mathrm{pro}}\left(p_{i1j1},p_{i2j2}\right)$ is negative, which is denoted as follows.

$$r_{\mathrm{pro}}\left(p_{i_1{j}_1},p_{i_2{j}_2}\right)=\left\{\begin{array}{cc}1\hfill & (p_{i_1{j}_1}-0.5)\times (p_{i_2{j}_2}-0.5)>0\hfill \\ -1\hfill & (p_{i_1{j}_1}-0.5)\times (p_{i_2{j}_2}-0.5)\le 0\hfill \end{array}\right.$$

(12)

where $0.5$ is the probability threshold to classify whether an instance is positive or negative. Further, a weighted version of $r_{\mathrm{pro}}$ is given as follows.

$$r_{\mathrm{pro}}\left(p_{i_1{j}_1},p_{i_2{j}_2}\right)=\left(2(p_{i_1{j}_1}-0.5)\right)\times \left(2(p_{i_2{j}_2}-0.5)\right).$$

(13)

Since $P_{ij}\in [0,1]$, $r_{\mathrm{pro}}\left(p_{i_1{j}_1},p_{i_2{j}_2}\right)\in [-1,1]$. Equation (11) can be easily optimized and has a larger penalty if instance predictors have higher confidence. The similarity measure for two embedding vectors has many choices. Here, we used the simple cosine similarity described in Equation (14).

$$r_{\mathrm{emb}}\left(f\left({\mathbf{x}}_{i_1{j}_1}\right),f\left({\mathbf{x}}_{i_2{j}_2}\right)\right)=\frac{f{\left({\mathbf{x}}_{i_1{j}_1}\right)}^{T}f\left({\mathbf{x}}_{i_2{j}_2}\right)}{|f\left({\mathbf{x}}_{i_1{j}_1}\right){|}_2{\left|f\left({\mathbf{x}}_{i_2{j}_2}\right)\right|}_2}.$$

(14)

The regularizer in Equation (11) uniformly embraces three cases. The first case is two instances belonging to two different bags that are essentially different in terms of embedding and prediction. This leads to a negative value with a large magnitude. The second case is two instances coming from the same bag but different categories.

3.5. Optimization Using Stochastic Gradient Descent

In the above formulations, learned instance embedding f, instance-level predictor h, and bag-level predictor H could all be implemented using fully connected layers in a neural network, and optimized in an end-to-end manner. The overall loss function of the neural network is given as follows:

$$\mathrm{L}={\lambda }_{\mathrm{ins}}{\mathrm{L}}_{\mathrm{ins}}+{\lambda }_{\mathrm{bag}}{\mathrm{L}}_{\mathrm{bag}}+{\lambda }_{\mathrm{reg}}{\mathrm{R}}_{\mathrm{ins}}$$

(15)

where ${\lambda }_{\mathrm{ins}},{\lambda }_{\mathrm{bag}}$, and ${\lambda }_{\mathrm{reg}}$ are loss weight parameters. In the experiments, the weight parameters can simply be set by cross-validation on the training data.

After calculating the loss of the whole network, we minimized the loss function by employing back propagation with stochastic gradient descent (SGD). We used the PyTorch [48] framework to implement the whole network. SGD with automatic differentiation can be directly invoked in PyTorch.

3.6. Training and Testing Details

During training, it is natural to add losses ${\mathrm{L}}_{\mathrm{ins}}$ and ${\mathrm{L}}_{\mathrm{bag}}$ for instance- and bag-level predictions. For the embedding regularizer, we used the instance scores from the instance-level prediction and instance embedding to compute loss. During testing, the average of the bag scores from both instance- and bag-level predictions were used. In our experiments, the weights of all FC layers were initialized by truncated normal distribution [49]. Adam [50] was adopted to optimize the network. Some parameters are shown in Table 1 according to our later experiments. More specifically, we doubled the learning rate after 4000 iterations and divided it by 10 after 3000 more iterations. We trained the network for 10,000 iterations in total for all experiments.

Table 1. Detailed experiment hyperparameters. Listed are initial learning rate (LR), weight decay (WD), standard deviation of initial weights (W-Std), initial bias (B), and batch size (BS).

Dataset	LR	WD	W-Std	B	BS
Musk1	$0.001$	$0.01$	$0.05$	0	2
Musk2	$0.001$	$0.01$	$0.05$	0	2
Fox	$0.001$	$0.01$	$0.05$	0	2
Tiger	$0.001$	$0.01$	$0.05$	0	2
Elephant	$0.001$	$0.01$	$0.05$	0	2
Newsgroups	$0.001$	$0.001$	$0.1$	0	2
Web recommendation	$0.001$	$0.001$	$0.1$	0	1

4. Experiments

In this section, conducted experiments are outlined in detail to show the effectiveness of our method.

4.1. Datasets and Evaluation Metrics

We evaluated our method on a range of MIL datasets for various tasks: MUSK [12] for molecule-activity prediction; Fox, Tiger, and Elephant [15] for image classification; and Newsgroups [8] and Web Recommendation [35] for text categorization.

The detailed properties of these datasets are listed in Table 2 (Newsgroups has 20 sub-datasets, and Web Recommendation has nine sub-datasets; we only list some sub-datasets in the table for simplification). Each dataset consisted of some positive bags and negative bags. Each bag was composed of some instances, where an instance is an N-dimensional vector; N varied in different datasets. Only bag-level labels were given for training and testing.

Table 2. Detailed dataset properties, including name of MIL dataset, instance dimension (N in Section 3.3 and Section 4.1), number of positive and negative bags, total number of bags, average number of instances for each bag, and total number of instances. The Newsgroups dataset contains 20 sub-datasets, and only two sub-datasets are presented for simplification (alt.atheism and comp.graphics). The Web Recommendation dataset contains nine sub-datasets, and only one sub-dataset is presented for simplification (web1-train and web1-test for training and testing, respectively).

Dataset	Dimension	Number of Bags			Number of Instances
		Positive	Negative	Total	Average	Total
MUSK1	166	47	45	92	5	476
MUSK2	166	39	63	102	65	6598
Elephant	230	100	100	200	7	1391
Fox	230	100	100	200	7	1320
Tiger	230	100	100	200	6	1220
alt.atheism	200	50	50	100	54	5443
comp.graphics	200	49	51	100	31	3094
web1-train	5863	17	58	75	29	2212
web1-test	5863	4	34	38	29	2212
messidor	687	654	546	1200	10	12,352
UCSB_breast	708	26	32	58	35	2002

Following previous works [5,8,38,40,51], we evaluated the bag-classification results. For MUSK, Fox, Tiger, Elephant, Messidor, UCSB_Breast, and Newsgroups, we performed 10-fold cross validation and reported average classification accuracies and standard deviations ($\mathrm{mean}\pm \mathrm{std}$) for all compared methods. For Web Recommendation, we used the default training and testing sets, and report the classification accuracies for all the compared methods.

4.2. Results

We conducted extensive experiments on various datasets for different applications, such as drug-activity prediction on the MUSK dataset, image classification on the Animal dataset, text classification on the 20 Newsgroups and Web Recommendation datasets, and cancer prediction on the Messidor and Ucsb_breast datasets. The results are listed and compared with state-of-the-art methods in Table 3, Table 4, Table 5, Table 6 and Table 7, respectively.

Table 3. Classification accuracy of different methods for bag classification on MUSK1 and MUSK2 (task: molecule-activity prediction).

Dataset	MUSK1	MUSK2
mi-SVM [15]	$0.874$	$0.836$
MI-SVM [15]	$0.779$	$0.843$
MI-Kernel [37]	$0.880$	$0.893$
EM-DD [38]	$0.849\pm 0.098$	$0.869\pm 0.108$
mi-Graph [8]	$0.889\pm 0.073$	$0.903\pm 0.086$
miVLAD [51]	$0.871\pm 0.097$	$0.872\pm 0.095$
miFV [51]	$0.909\pm 0.089$	$0.884\pm 0.094$
MInD	$0.893\pm 0.019$	$0.888\pm 0.034$
MI-Net [5]	$0.893\pm 0.099$	$0.872\pm 0.096$
mi-Net [5]	$0.889\pm 0.098$	$0.868\pm 0.113$
RIE	$0.962\pm 0.060$	$0.937\pm 0.091$

Table 4. Classification accuracy of different methods for bag classification on Fox, Tiger, and Elephant (task: image classification).

Dataset	Fox	Tiger	Elephant
mi-SVM [15]	$0.582$	$0.784$	$0.822$
MI-SVM [15]	$0.578$	$0.840$	$0.843$
MI-Kernel [37]	$0.603$	$0.842$	$0.843$
EM-DD [38]	$0.609\pm 0.101$	$0.730\pm 0.096$	$0.771\pm 0.097$
mi-Graph [8]	$0.620\pm 0.098$	$0.860\pm 0.083$	$0.869\pm 0.078$
miVLAD [51]	$0.620\pm 0.098$	$0.811\pm 0.087$	$0.850\pm 0.080$
miFV [51]	$0.621\pm 0.109$	$0.813\pm 0.083$	$0.852\pm 0.081$
MInD [40]	$0.651\pm 0.011$	$0.819\pm 0.021$	$0.857\pm 0.018$
MI-Net [5]	$0.627\pm 0.080$	$0.832\pm 0.087$	$0.891\pm 0.074$
mi-Net [5]	$0.622\pm 0.137$	$0.861\pm 0.091$	$0.874\pm 0.078$
RIE	$0.686\pm 0.117$	$0.885\pm 0.100$	$0.907\pm 0.070$

Table 5. Classification accuracy of different methods for bag classification on 20 Newsgroup datasets (task: text categorization).

Dataset	MI-Kernel [37]	mi-Graph [8]	miFV [51]	MInD [40]	MI-Net [5]	mi-Net [5]	RIE
alt.atheism	$0.602$	$0.655$	$0.848$	$0.861$	$0.846$	$0.844$	$0.906$
comp.graphics	$0.470$	$0.778$	$0.594$	$0.825$	$0.831$	$0.833$	$0.857$
comp.windows.misc	$0.510$	$0.631$	$0.615$	$0.730$	$0.730$	$0.730$	$0.777$
comp.ibm.pc.hardware	$0.469$	$0.595$	$0.665$	$0.780$	$0.803$	$0.796$	$0.814$
comp.sys.mac.hardware	$0.445$	$0.617$	$0.660$	$0.835$	$0.811$	$0.801$	$0.862$
comp.window.x	$0.508$	$0.698$	$0.768$	$0.785$	$0.836$	$0.832$	$0.886$
misc.forsale	$0.518$	$0.552$	$0.565$	$0.729$	$0.707$	$0.715$	$0.773$
rec.autos	$0.529$	$0.720$	$0.667$	$0.775$	$0.812$	$0.806$	$0.835$
rec.motorcycles	$0.506$	$0.640$	$0.802$	$0.577$	$0.853$	$0.849$	$0.914$
rec.sport.baseball	$0.517$	$0.647$	$0.779$	$0.837$	$0.871$	$0.872$	$0.899$
rec.sport.hockey	$0.513$	$0.850$	$0.823$	$0.833$	$0.918$	$0.915$	$0.952$
sci.crypt	$0.563$	$0.696$	$0.760$	$0.768$	$0.808$	$0.799$	$0.843$
sci.electronics	$0.506$	$0.871$	$0.555$	$0.940$	$0.928$	$0.931$	$0.938$
sci.med	$0.506$	$0.621$	$0.783$	$0.832$	$0.862$	$0.864$	$0.895$
sci.space	$0.547$	$0.757$	$0.818$	$0.796$	$0.820$	$0.808$	$0.883$
soc.religion.christian	$0.492$	$0.590$	$0.814$	$0.841$	$0.829$	$0.823$	$0.875$
talk.politics.guns	$0.477$	$0.585$	$0.747$	$0.806$	$0.782$	$0.771$	$0.829$
talk.politics.mideast	$0.559$	$0.736$	$0.793$	$0.830$	$0.825$	$0.834$	$0.889$
talk.politics.misc	$0.515$	$0.704$	$0.697$	$0.720$	$0.748$	$0.758$	$0.848$
talk.religion.misc	$0.554$	$0.633$	$0.739$	$0.725$	$0.778$	$0.776$	$0.829$
average	$0.515$	$0.679$	$0.726$	$0.791$	$0.820$	$0.818$	$0.865$

Table 6. Classification accuracy of different methods for bag classification on Web Recommendation (task: text categorization).

Dataset	web1	web2	web3	web4	web5	web6	web7	web8	web9	Average
Citation-kNN [34]	$0.879$	$0.768$	$0.763$	$0.816$	$0.758$	$0.816$	$0.684$	$0.684$	$0.653$	$0.758$
Fretcit-kNN [35]	$0.911$	$0.868$	$0.858$	$0.847$	$0.853$	$0.863$	$0.758$	$0.690$	$0.648$	$0.811$
G3P-MI [36]	$0.842$	$0.737$	$0.842$	$0.842$	$0.842$	$0.790$	$0.842$	$0.605$	$0.684$	$0.781$
MI-Net [5]	$0.916$	$0.866$	$0.824$	$0.916$	$0.724$	$0.818$	$0.758$	$0.703$	$0.666$	$0.799$
mi-Net [5]	$0.911$	$0.905$	$0.858$	$0.803$	$0.742$	$0.811$	$0.718$	$0.598$	$0.589$	$0.771$
RIE	$0.916$	$0.937$	$0.909$	$0.934$	$0.708$	$0.829$	$0.868$	$0.747$	$0.768$	$0.846$

Table 7. Comparison of mi-net and MI-net on Messidor and ucsb_breast.

Dataset	mi-net [5]	MI-net [5]	RIE
messidor	$0.714\pm 0.044$	$0.723\pm 0.043$	$0.730\pm 0.046$
ucsb_breast	$0.773\pm 0.203$	$0.820\pm 0.160$	$0.894\pm 0.158$

Table 3 lists the results of our RIE method on the MUSK dataset compared with the experiment results of some classical methods. From the experiment results, we can see that our method was significantly improved on the MUSK dataset, which shows that our method is valid. Table 4 shows the experiment results and comparison on three datasets: Fox, Tiger, and Elephant. RIE achieved the best results in these image datasets, and had significantly better accuracy compared with the other methods of multi-instance learning. The extensive applicability of our RIE method was further proved. Table 5 lists the experiment results on 20 Newsgroups datasets. Compared with the previous methods of the 20 datasets, average accuracy was obviously improved, making our method also useful in text classification. From the results in Table 6, we can observe that our RIE method generally worked better than the other methods, having obtained the best result on average. Table 7 shows the performance of the proposed MIL method for medical image analysis on the Messidor and ucsb_breast datasets. RIE results were compared with baseline methods mi-net and MI-net, which confirmed the effectiveness of the proposed instance-embedding regularizer. Overall, the proposed RIE method had state-of-the-art performance on the tested datasets.

Besides bag classification accuracy, we report the f1 scores of our RIE method on all the tested datasets in Table 8. F1 score provides a more comprehensive evaluation to the proposed method, which is rarely used in previous MIL papers. The outstanding f1 scores confirm the high effectiveness of the proposed RIE method.

Table 8. F1 score of the our RIE method on various datasets.

Dataset	F1 Score	Dataset	F1 Score	Dataset	F1 Score
MUSK1	$0.941$	rec.autos	$0.816$	talk.religion.misc	$0.789$
MUSK2	$0.899$	rec.motorcycles	$0.922$	web1	$\mathrm{0.9.03}$
Fox	$0.693$	rec.sport.baseball	$0.859$	web2	$0.925$
Tiger	$0.899$	rec.sport.hockey	$0.939$	web3	$0.883$
Elephant	$0.911$	sci.crypt	$0.806$	web4	$0.917$
alt.atheism	$0.885$	sci.electronics	$0.786$	web5	$0.683$
comp.graphics	$0.805$	sci.med	$0.854$	web6	$0.806$
comp.windows.misc	$0.724$	sci.space	$0.841$	web7	$0.872$
comp.ibm.pc.hardware	$0.717$	soc.religion.christian	$0.852$	web8	$0.721$
comp.sys.mac.hardware	$0.813$	talk.politics.guns	$0.816$	web9	$0.749$
comp.window.x	$0.847$	talk.politics.mideast	$0.882$	messidor	$0.741$
misc.forsale	$0.660$	talk.politics.misc	$0.817$	ucsb_breast	$0.791$

5. Conclusions

Multi-instance learning is an important weakly-supervised learning method with many applications. This paper proposes a novel MIL method based on the multi-instance network framework. Different from previous multi-instance networks that learn the embedding for each instance individually, this method learns more robust instance and bag embeddings by considering the relationship between instances as a regularizer, i.e., maximizing the correlation between instance-embedding similarities and similarities of the underlying instance labels. The proposed instance-embedding regularizer together with bag classification loss and instance classification loss were optimized using the stochastic gradient descent method in an end-to-end manner. We conducted a number of experiments on datasets of drug molecular activity prediction, image classification, text classification, and cancer prediction. The results show that the proposed method achieved a significant improvement over previous multi-instance networks. In the future, we would like to explore the effectiveness of the proposed method in other machine learning applications, such as image ranking, image retrieval, and weakly-supervised object detection.