Abstract
The problem of an interface crack that approaches a three-material joint with two interfaces is analyzed in this paper. Two possible cases are considered: the crack that lies at the interface between materials A and B, approaching the joint of materials A, B, and C, deflects into the interface between materials A and C or into the interface between materials B and C. Analysis is performed within restrictions imposed by the linear elastic fracture mechanics (LEFM), linear elastic behavior of materials, and the small plastic zone around the crack tip, based on the crack deflection criterion proposed by He and Hutchinson. That criterion is applied in this paper to a joint of the three homogeneous isotropic materials. The energy release rates for the crack deflection into one interface or the other are compared to each other, and, based on this comparison, a conclusion is drawn as to which of the two interfaces the crack would deflect. If the value of the ratio of the energy release rates GBC/GAC is greater than the ratio of the corresponding fracture toughnesses of the two interfaces, the crack will deflect into the BC interface. If this ratio is smaller than the ratio of the corresponding fracture toughnesses, the crack will deflect into the AC interface. Knowing the ratio of energy release rates for deflection into one interface or the other can be used for designing the interface, namely for prediction of the direction of further crack propagation.
1. Introduction
Fracture mechanics applications to problems of cracks at bi-material interfaces is a topic that has been attractive to numerous researchers in recent years, since this is a discipline which is still developing. Since the pioneering works of Williams [1], Erdogan [2], England [3], Malyshev and Salganik [4], and Rice and Sih [5], interface fracture mechanics has developed significantly. This development has stemmed from the necessity of studying the behavior of such cracks in various engineering problems, including depositing a metal layer to a composite substrate in the airplane industry, analysis of interior damages and flaws in composite materials, or delamination of multi-layer materials like thermo-insulating coatings, as in Foraboschi [6,7,8]. In more recent times progress in research of static fractures at interfaces has been provided in the works of Hutchinson and Suo [9], Shih [10], and Nikolic, Djokovic, and Micunovic [11].
The stress and displacement field at the tip of a crack at an interface has an oscillatory character, meaning that the crack surfaces can mutually overlap or penetrate each other at the vicinity of the crack tip. One of the first analytical models of fractures at bi-material interfaces was presented in a paper by Williams [1]. The biggest contribution of this paper was an analytical expression for the stress and displacement fields in the zone of a strong singularity, which lies close to the tip of the interface crack. Erdogan [2] has investigated the case of two half-planes joined along a finite number of linear segments and determined the stress distribution close to the cracks’ ends. The paper presents an investigation of problems of interface cracks under various loading conditions. England [3] and Malyshev and Salganik [4] have analyzed the oscillatory behavior as wrinkling of two crack surfaces and material overlap. Rice and Sih [5] have solved the problem of the interface crack by combining the Eigen-function expansion method and the complex variables method of Muskhelishvili [12]. Two typical cases were considered, namely, a central crack of finite length and a semi-infinite edge crack. Both cracks lay on a joint of two dissimilar elastic planes. On the other hand, the contact zone concept in the vicinity of the interface crack was introduced by Comninou [13]. In Comninou’s paper it was shown that oscillatory behavior in the vicinity of an interfacial crack tip disappears if one assumes that the crack is not completely open and that its surfaces are in contact and close to the tip. Rice [14] has shown that the contact zone concept is dominant if the contact zone is small. He proposed that the ratio of the contact zone size and the crack length should be less than 0.01. Further contributions to studying the static interface fracture have been given in [9,10,15].
Cracks most frequently appear on the interface between two dissimilar materials, since the toughness of the interface is smaller than the toughnesses of the materials that constitute the interface. However, in some cases, the crack can appear in one of the two materials and it can be either parallel to the interface (a sub-interface crack) or it can attack the interface at a certain angle. In addition, in some cases, a crack that is propagating along the interface can kink away from it and continue to propagate in one of the two materials. The problem of the sub-interface crack has been considered by Hutchinson et al. [16], while problems of cracks kinking away from the interface have been analyzed by He and Hutchinson [17] for the static loading case and by Veljković [18] for the case of isotropic materials constituting an interface, while Nikolic et al. [11] have considered the case of a crack at the interface between two orthotropic materials. With regards to the behavior of a crack approaching an interface, there are a number of papers in which the competition between crack deflection into the interface and crack penetration of the interface has been considered. Namely, the crack attacking the interface at a certain angle can behave in one of these two ways; which of the two cases the angle follows depends on the fracture toughnesses of the two materials and the fracture toughness of the interface itself. Cook and Erdogan [19] and Erdogan and Biricikoglu [20] have studied the behavior of a crack penetrating the interface at a right angle. Goree and Venezia [21] have, on the other hand, considered cases where a crack attacking the interface at a right angle would deflect into it. An additional contribution to the investigation of these problems has been provided by Lu and Erdogan [22]. He and Hutchinson [23] have considered the behavior of a crack approaching the interface between two dissimilar elastic materials. This problem has also been investigated by Djokovic [24] and Nikolic and Djokovic [25]. Interface crack behavior in anisotropic materials has been considered in papers by Suo [26], Suo et al. [27], and Ma and Luo [28]. Nakamura [29] has conducted a three-dimensional analysis of a bi-material plate with a central crack. The material properties of the two dissimilar materials constituting the interface (shear modulus and Poisson’s ratio) were chosen in such a way as to obtain the usual oscillatory stress field in the plane strain state. Chaudhuri [30] has analyzed the three-dimensional stress field in the area close to the perimeter of a penny-shaped crack. Ayhan et al. [31] have developed an efficient computer model which, by using an enriched finite element at the crack tip, gives correct results of the asymptotic behavior at the crack tip. In this formulation of the enriched element, the stress intensity factors KI, KII, and KIII were considered as additional degrees of freedom and their values were obtained by the finite element method. Nagai et al. [32] have determined the stress intensity factors for a three-dimensional interface crack in various anisotropic materials. Saputra et al. [33] have dealt with calculations of three-dimensional fracture parameters for an interface crack and a notch using the scaled boundary finite element method. Djokovic et al. [34] have in one paper analyzed interface crack propagation from a straight corner along the joint plane between two plates made of dissimilar materials for different shapes of the crack front, namely, concave, triangular, and quarter-circular.
The possibility of being able to predict whether a bi-material interface crack will propagate along an interface, kink away from the interface, or not propagate at all, has been defined by criterion proposed by He and Hutchinson [23]. These authors analyzed interface cracksunder plane strain conditions, in which the cracks kink away from the interface between two different isotropic elastic solids. Their attention was focused on the beginning of the crack deflection, which is why it is assumed that the segment of a crack, which is leaving the interface, is small with respect to the crack at the interface. The stress intensity factors and the energy release rates for the kinked crack were determined as related to the corresponding values for the crack prior to kinking. Roughly speaking, the tough interface prevents the crack from propagating along it. A crack kinking away from the interface is possible if the ratio of the energy release rates for the kinked crack and the crack propagation along the interface is greater than the ratio of the fracture toughnesses of the material into which the crack is kinking and the interface itself.
All the aforementioned research papers dealt with the problem of a crack at the interface between two materials. The problem of a crack at the joint of three or more materials has not been considered by many researchers. Pageau et al. [35] have obtained solutions and numerical results for the stress singularity of joints of two and three materials, which are perfectly bonded along the interface, as well as for disbonded junctions. Shkarayev et al. [36] have presented analytical solutions for an asymptotic field ahead of the tip of a crack that comes from a wedge made of dissimilar materials. Carpinteri and Paggi [37] have proposed a new numerical procedure for determination of the stress singularity at multi-material interfaces. Sator and Becker [38] have considered the stress singularity for bi-material and tri-material joints of dissimilar, homogeneous, and isotropic linear elastic wedges in the plane strain state. The method proposed in this paper enables analytical calculation of all the real values of the eigen functions of any bi-material or tri-material configuration in its closed form.
In the existing literature there are no papers which deal with predictions of the further propagation of a crack at the interface between two materials that comes to a three-material joint; this is considered in this paper. The objective of this work was to check whether it is possible to apply the method proposed by He and Hutchinson [23] for a two-material joint to a three-material joint. This would involve predicting the propagation of a crack that lies at the interface between two materials and which is coming to a three-material joint, by comparing the energy release rates for propagation along the corresponding interfaces. The consideration is limited to the plane strain state of the crack propagation.
2. Problem Formulation
The problem of an interface crack between materials A and B which approaches the joint of three materials, A, B and C, as shown in Figure 1a, is considered. The crack is at a distance a from the joint. Two cases can occur: the crack could continue to propagate along the interface between materials A and C, as in Figure 1b, or it could deflect into the interface between materials B and C and continue to propagate along it, as in Figure 1c.
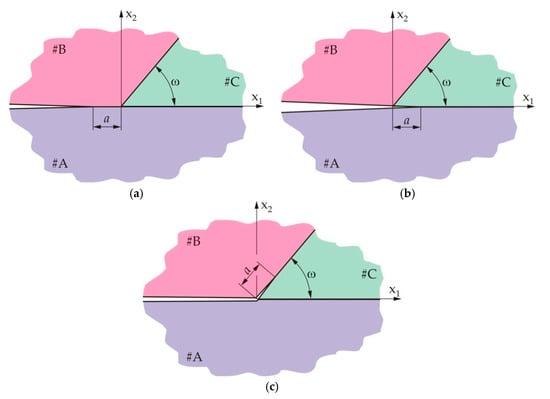
Figure 1.
(a) Interface crack approaching a three-material joint; (b) crack propagating along the AC interface; (c) crack deflecting into the BC interface.
Distance a in Figure 1a is so chosen to represent the characteristic length for the considered problem, and could be the plastic zone size, the cell size in cellular materials, or the thickness of the adhesive layer in glued materials, etc., as considered in Hutchinson and Suo [9]. For calculations in this paper, length a is selected as the size of the plastic zone in material B. In the following analysis, variables related to particular interfaces are denoted by subscripts containing notation of the two materials constituting them, i.e., variables for the interface between materials A and B have the subscript AB, variables for the interface between materials A and C have the subscript AC, and materials for the interface between materials B and C have the subscript BC.
The energy release rate for the crack at the interfaces AB, AC, and BC, expressed via the corresponding stress intensity factors, can be calculated as in Malyshev and Salganik [4] as
respectively, where Kij = K1,ij + iK2,ij is the complex stress intensity factor, with subscripts ij denoting the materials in the joint, i.e., the corresponding interface. Variables εAB, εAC, and εBC represent the oscillatory index for interfaces AB, AC, and BC, respectively, being defined as in Rice [14] as
where βij is one of the two Dundurs parameters as in Dundurs [39], which are defined as
where μi = Ei/2(1 + νi) is the shear modulus, Ei is the Young elasticity modulus, νI is the Poisson ratio of material i(i = A, B, C), κi = 3–4, νi for the plane strain state, κi = (3 − νi)/(1 + νi) for the plane stress state, and ij again stands for the corresponding interface parameter.
The mixed mode for the crack that deflected into the BC or AC interface can be calculated as the phase angle of the complex stress intensity factor (also known as the mode mixity) according to the formulation given by Hutchinson and Suo [9], i.e.,
where l is the characteristic length, which for the considered case is a. In general, the mode mixity defines the share of Mode 2 with respect to Mode 1 of the crack propagation, i.e., whether the crack will propagate in an in-plane shearing or tearing manner. Here, it represents the ratio of the imaginary and real parts of the complex stress intensity factor, which is the characteristics of the interface crack.
The criterion for the crack deflection into the BC interface can be formulated based on the He and Hutchinson [23] criterion as
where ΓBC and ΓAC are the fracture toughnesses of the BC and AC interfaces, respectively.
Considering that the analysis is performed according to the linear elastic fracture mechanics (LEFM) concept, the ratio of the interfaces’ fracture toughnesses can be determined from the stress intensity factor in the phase of the crack approaching the three-material joint. This ratio can be used in designing the interface, i.e., for prediction of further crack propagation. If the ratio of the fracture toughness of the BC and AC interfaces is smaller than the (GBC/GAC) ratio, the crack should propagate along the BC interface, and in the opposite case it should propagate along the AC interface.
Based on the linearity of the problem, dimensional analysis, and the proposition by Cotterell and Rice [40] for the bi-material problem, it follows that the stress intensity factors (their determination is presented in the Appendix A) are
where the coefficients c, d, e, and f are complex functions depending on elastic characteristics of the materials A, B, and C, namely, EA, EB, EC, νA, νB, and νC, as well as on ω, the angle of material C (Figure 1). They can be determined in a way proposed by He and Hutchinson [23]. Solutions for these complex functions, c, d, e, and f, obtained by the Mathematica® programming routine, are shown in Figure 2. The programming package Mathematica® has been used here to obtain this result, using functional programming through built-in and newly defined functions that are called as needed, as well as through symbolic programming for poorly set problems when manipulating complex expressions of multiple variables and for calculating expressions containing variables that have no set value.
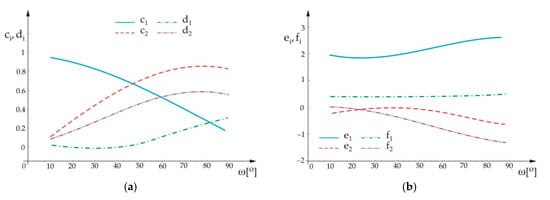
Figure 2.
(a) Solutions for the complex coefficients c and d as functions of angle ω. (b) Solutions for the complex coefficients e and f as functions of angle ω.
3. Results and Discussion
Based on Equations (1) and (6), using the Mathematica® programming routine, the ratio of the energy release rate for the crack that propagates along the BC interface and the energy release rate for the crack that propagates along the AC interface has been calculated, and its variation in terms of angle ω is shown in Figure 3. For the calculations, the following data were taken into account: εAB = 0.086, εBC = 0.061, εAC = 0.084, and KAB = 1 + i·0.672 (MPa·mm1/2−i·0.086). It is also assumed that angle ω varies within the interval 10° to 90° due to the physical nature of the considered problem.
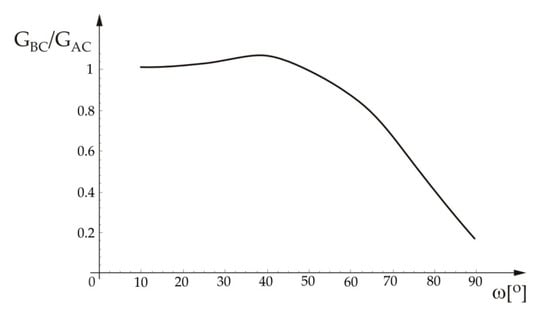
Figure 3.
Ratio GBC/GAC in terms of angle ω.
From Figure 3 it can be seen that the ratio of the energy release rates has higher values for the small values of angle ω, while when increasing the value of the angle the ratio starts to decrease. Based on Figure 3, one can determine whether the crack at the interface between materials A and B would deflect into the BC or AC interface. For values of the (GBC/GAC) ratio below the curve the crack will deflect into the interface BC, while for the values of the (GBC/GAC) ratio above the curve the crack will deflect into the AC interface.
In Figure 4 variations of the mode mixities are shown for the crack that deflects into the BC or AC interface, ψBC or ψAC, respectively, in terms of the angle ω, obtained by application of the Mathematica® programming routine.
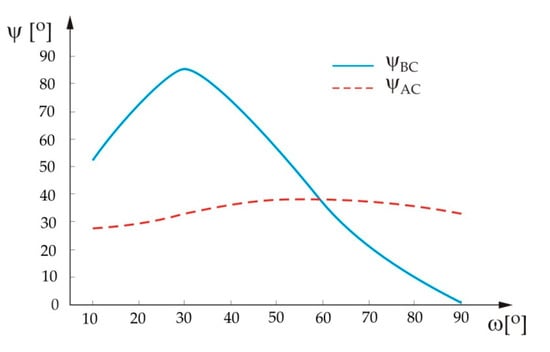
Figure 4.
Variation of the mode mixities ψBC and ψAC in terms of angle ω.
From Figure 4 it can be seen that for the small values of angle ω, the mode mixity for the case of the crack deflection into the AC interface has lower values than the mode mixity for the case of the crack deflection into the BC interface. In fact, values of the mode mixity ψAC do not vary significantly with angle ω, which is not the case for the ψBC mode mixity. It can be seen that this mixity’s values increase until angle ω reaches a value of about 30°, at which point it decreases and reaches a zero value at ω = 90°.
As mentioned, the mode mixity measures the ratio of the real and imaginary parts of the stress intensity factor. For the crack propagation along the BC interface the mode mixity increases (for up to about 30°), meaning that the imaginary part of the stress intensity factor is predominant, which would correspond to the shearing mode of the crack propagation. After reaching the maximum value, the mode mixity decreases and reaches a zero value, meaning that the share of the imaginary part of the stress intensity factor decreases, and at its zero value (for a value of the angle ω = 90°) there is only a real part of the stress intensity factor, which corresponds to a completely tearing mode of the crack propagation. For the crack propagation along the AC interface the mode mixity remains almost constant, meaning that increase of the angle ω does not influence the share of the imaginary part of the stress intensity factor, i.e., the crack propagation mode.
Variation of the real and imaginary parts of the stress intensity factors for the crack that deflects into the BC interface, K1,BC and K2,BC, respectively, in terms of angle ω for the load phase angle ψAB = 30°, was calculated based on Equation (6) by application of the programming routine Mathematica®, with the results shown in Figure 5. The units for K1,BC and K2,BC are Re(MPa·mm1/2−i·0.061) and Im(MPa·mm1/2−i·0.061), respectively.
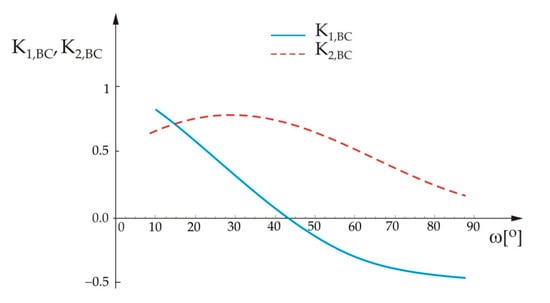
Figure 5.
Variation of the real and imaginary parts of the stress intensity factors for the crack that deflects into the BC interface, in terms of angle ω.
From Figure 5 it can be seen that the stress intensity factor for Mode 2 for the crack that propagates along the BC interface initially increases with increase of the angle ω and then starts to decrease, while the stress intensity factor for Mode 1 decreases with increase of ω. For larger values of angle ω the real part of the stress intensity factor has negative values. This is a consequence of the possible overlap of the crack surfaces, taking into account the fact that limits on the crack surfaces were not introduced in this analysis, meaning they can deform. The overlap of the crack surfaces (actual jamming) implies that the crack would not be able to propagate along the BC interface above a value of angle ω of approximately 40°. As mentioned, this is the consequence of the application of the LEFM restrictions related to the small plastic zone size. If these restrictions had not been taken into account, this problem would have to be considered within the framework of elastic–plastic fracture mechanics.
Variation of the real and imaginary parts of the stress intensity factors for the crack that deflects into the AC interface, K1,AC and K2,AC, respectively, in terms of angle ω for the load phase angle ψAB = 30°, was calculated based on Equation (6) by application of the programming routine Mathematica®, with the results shown in Figure 6. The units for K1,AC and K2,AC are Re(MPa·mm1/2−i·0.084) and Im(MPa·mm1/2−i·0.084), respectively.
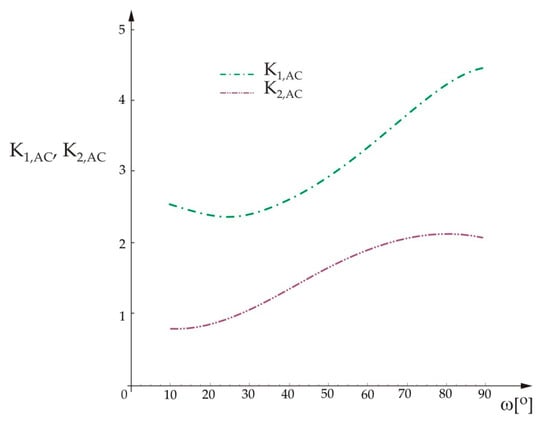
Figure 6.
Variation of the real and imaginary parts of the stress intensity factors for the crack that deflects into the AC interface, in terms of angle ω.
From Figure 6 it can be seen that the stress intensity factor for Mode 1, for the crack that propagates along the AC interface, initially decreases with increase of angle ω and then starts to increase and has positive values, unlike for the case of the crack propagation along the BC interface. The stress intensity factor for Mode 2 only displays an increasing trend with increase of angle ω. For this case of crack propagation along the AC interface, there is no overlapping (jamming) of the crack surfaces and the crack “freely” propagates along the interface with increasing load and with increasing angle ω (this is the extension of material C).
4. Conclusions
The problem of a crack at the interface between two materials approaching a three-material joint was considered in this paper. In the case considered, the crack that lies along the interface between the two materials A and B deflects into the interface between materials A and C or into the interface between materials B and C. The criterion as to which of the two interfaces the crack deflects into is defined based on a criterion proposed by He and Hutchinson [23].
Based on the calculations performed, the following conclusions were drawn:
A curve representing the variation (in terms of angle ω) of the ratio of the two energy release rates for the crack that deflects into the BC interface and into the AC interface (GBC/GAC) was obtained. For values of the (GBC/GAC) ratio above this curve, the crack deflects into the AC interface, and for values of the (GBC/GAC) ratio below this curve, the crack deflects into the BC interface.
Analysis of the curve that represents the variation of the mode mixity with angle of material C shows that the mode mixity for the case of crack deflection into the AC interface has lower values than the mode mixity for the case of crack deflection into the BC interface. For crack propagation along the BC interface the mode mixity increase (of up to about 30°) means that the imaginary part of the stress intensity factor is predominant, which corresponds to the shearing mode of the crack propagation. After reaching the maximum value, the mode mixity decreases and reaches a zero value, meaning that the share of the imaginary part of the stress intensity factor decreases, and at its zero value there is only a real part of the stress intensity factor, i.e., the crack propagation is completely in the tearing mode. For crack propagation along the AC interface the mode mixity remains almost constant, i.e., the share of the imaginary part of the stress intensity factor, (the crack propagation mode) remains almost the same.
Analysis of the curves that represent variation of the real and imaginary parts of the stress intensity factors for the crack that deflects into one interface or the other, in terms of angle ω, showed that the real part of the stress intensity factor for the case of crack deflection into the BC interface obtains negative values for larger values of angle ω, which be explained by possible overlap of the crack surfaces. This overlap can be explained by taking into account the LEFM restrictions on the crack surfaces. If one did not take into account these restrictions, the problem would have to be considered within the framework of elastic–plastic fracture mechanics.
For the case of crack propagation along the AC interface, there is no overlapping (jamming) of the crack surfaces and the crack is able to “freely” propagate along the interface with increasing load and angle ω (this is the extension of material C).
The presented theoretical considerations of the interface crack approaching a three-material joint could be used in trying to understand some micro-cracking phenomena during the fatigue loading of engineering materials, like steel or nodular cast iron, [41,42]; this might be a direction for future research.
The criterion proposed by He and Hutchinson could be used to predict the behavior of an interface crack approaching the three-material joint and to “design” interfaces between the materials to “force” the crack to deflect into one of them. This could be applied in the design of composite, cellular, or other complex materials, both at the micro and the nano levels.
Author Contributions
Conceptualization, J.M.D. and R.R.N.; methodology, B.H.; software, J.M.D.; validation, R.R.N. and R.U.; formal analysis, J.M.D.; investigation, J.M.D.; data curation, B.H; writing—original draft preparation, J.M.D. and R.R.N.; writing—review and editing, J.M.D. and R.R.N.; supervision, B.H and R.U.; project administration, B.H.; funding acquisition, B.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially financially supported by the project of Operational Program Research and Innovation “Research and development activities of the University of Žilina in industry in the 21st century in the field of materials and nanotechnologies”, No. 313011T426, co-funded by the European Regional Development Fund as well as by the European Regional Development Fund and by the Serbian Ministry of Education, Science, and Technological Development through grant ON174001.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Taking into account that the problem of a crack that approachesa three-material joint is considered from the aspect of linear elastic fracture mechanics, the stress intensity factors for the crack propagating along the BC interface can be written as
The stress intensity factors for the crack propagating along the AC interface can be written as
where , and , are the complex functions, which can be determined in the way proposed by He and Hutchinson [23]. Their results can be approximated using
Appendix B
Part of this research was published at the 7th International Congress of Serbian Society of Mechanics, Sremski Karlovci, Serbia, 24–26 June 2019, reference [43].
References
- Williams, M.L. The stresses around a fault or crack in dissimilar media. Bull. Seism. Soc. Am. 1959, 49, 199–204. [Google Scholar]
- Erdogan, F. Stress Distribution in Bonded Dissimilar Materials with Cracks. ASME J. Appl. Mech. 1965, 32, 03–410. [Google Scholar] [CrossRef]
- England, A.H. A Crack between Dissimilar Media. ASME J. Appl. Mech. 1965, 32, 400–402. [Google Scholar] [CrossRef]
- Malyshev, B.M.; Salganik, R.L. The Strength of Adhesive Joints Using the Theory of Fracture. Int. J. Fract. Mech. 1965, 1, 114–128. [Google Scholar]
- Rice, J.R.; Sih, G.C. Plane Problems of Cracks in Dissimilar Media. ASME J. Appl. Mech. 1965, 32, 418–423. [Google Scholar] [CrossRef]
- Foraboschi, P. Shear strength computation of reinforced concrete beams strengthened with composite materials. Comp. Mech. Comp. Appl. 2012, 3, 227–252. [Google Scholar] [CrossRef]
- Foraboschi, P. Effectiveness of novel methods to increase the FRP-masonry bond capacity. Comp. Part B Eng. 2016, 107, 14–232. [Google Scholar] [CrossRef]
- Foraboschi, P. Analytical model to predict the lifetime of concrete members externally reinforced with FRP. Theor. Appl. Fract. Mech. 2015, 75, 137–145. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Suo, Z. Mixed-mode cracking in layered materials. Adv. Appl. Mech. 1992, 29, 63–191. [Google Scholar]
- Shih, C.F. Cracks on bimaterial interfaces: Elasticity and Plasticity aspects. Mater. Sci. Eng. 1991, A143, 77–90. [Google Scholar] [CrossRef]
- Nikolic, R.R.; Djokovic, J.M.; Micunovic, M.V. The Competition between the Crack Kinking Away from the Interface and Crack Propagation along the Interface in Elastic Bicrystals. Int. J. Fract. 2010, 164, 73–82. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity, 1st ed.; Springer: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Comninou, M. The interface crack. ASME J. Appl. Mech. 1977, 44, 631–636. [Google Scholar] [CrossRef]
- Rice, J.R. Elastic fracture mechanics concepts for interfacial cracks. ASME J. Appl. Mech. 1988, 55, 98–103. [Google Scholar] [CrossRef]
- Nikolic, R.R.; Djokovic, J.M. Interfacial Cracks in Bicrystals and Bimaterials. In Crack Growth: Rates, Prediction and Prevention; Kubair, D., Ed.; Nova Publishers, Inc.: New York, NY, USA, 2011; pp. 101–126. [Google Scholar]
- Hutchinson, J.W.; Mear, M.E.; Rice, J.R. Crack Paralleling an Interface between Dissimilar Materials. ASME J. Appl. Mech. 1987, 54, 828–832. [Google Scholar] [CrossRef]
- He, M.Y.; Hutchinson, J.W. Kinking of a crack out of an interface. ASME J. Appl. Mech. 1989, 56, 270–278. [Google Scholar] [CrossRef]
- Veljkovic, J. The Crack Kinking Out of an Interface. Appl. Mech. 2005, 32, 208–221. [Google Scholar] [CrossRef][Green Version]
- Cook, T.S.; Erdogan, F. Stress in bonded materials with a crack perpendicular to the interface. Int. J. Eng. Sci. 1972, 10, 677–697. [Google Scholar] [CrossRef]
- Erdogan, F.; Biricikoglu, V. Two bonded half planes with a crack going through the interface. Int. J. Eng. Sci. 1973, 11, 745–766. [Google Scholar] [CrossRef]
- Goree, J.G.; Venezia, W.A. Bonded elastic half planes with an interface crack and a perpendicular intersecting crack that extends into the adjacent material. Int. J. Eng. Sci. 1977, 15, 1–17. [Google Scholar] [CrossRef]
- Lu, M.C.; Erdogan, F. Stress intensity factors in two bonded elastic layers containing cracks perpendicular to and on the interface. Eng. Fract. Mech. 1983, 18, 491–506. [Google Scholar]
- He, M.Y.; Hutchinson, J.W. Crack deflection at an interface between dissimilar elastic materials. Int. J. Sol. Struct. 1989, 25, 1053–1065. [Google Scholar]
- Djokovic, J.M. Some aspects of the crack approaching interface. Mat. Eng. 2009, 16, 41–45. [Google Scholar]
- Nikolic, R.R.; Djokovic, J.M. Influence of the Interface on Cracks Propagation along it and on Behavior of Cracks Approaching Interface. In Crack Growth: Rates, Prediction and Prevention; Kubair, D., Ed.; Nova Publishers, Inc.: New York, NY, USA, 2011; pp. 127–160. [Google Scholar]
- Suo, Z. Singularities, interfaces and cracks in dissimilar anisotropic media. Proc. Roy. Soc. Lond. 1990, 247, 331–358. [Google Scholar] [CrossRef]
- Suo, Z.; Bao, G.; Fan, B.; Wang, T.C. Orthotropy rescaling and implications for fracture in composites. Int. J. Sol. Struct. 1991, 28, 235–248. [Google Scholar] [CrossRef]
- Ma, C.C.; Luo, J.J. Plane solutions of interface cracks in anisotropic dissimilar media. J. Eng. Mech. 1996, 122, 30–38. [Google Scholar] [CrossRef]
- Nakamura, T. Three-dimensional stress fields of elastic interface cracks. ASME J. Appl. Mech. 1991, 58, 939–946. [Google Scholar] [CrossRef]
- Chaudhuri, R. Three-dimensional asymptotic stress field in the vicinity of the circumference of a bimaterial penny-shaped interfacial discontinuity. Int. J. Fract. 2006, 141, 211–225. [Google Scholar] [CrossRef]
- Ayhan, A.; Kaya, A.; Nied, H. Analysis of three-dimensional interface cracks using enriched finite elements. Int. J. Fract. 2006, 142, 255–276. [Google Scholar] [CrossRef]
- Nagai, M.; Ikeda, T.; Miyazaki, N. Stress intensity factor analysis of a three-dimensional interface crack between dissimilar anisotropic materials. Eng. Fract. Mech. 2007, 74, 2481–2497. [Google Scholar] [CrossRef]
- Saputra, A.; Birk, C.; Song, C. Computation of three-dimensional fracture parameters at interface cracks and notches by the scaled boundary finite element method. Eng. Fract. Mech. 2015, 148, 213–242. [Google Scholar] [CrossRef]
- Pageau, S.; Joseph, P.; Biggers, S. The order of stress singularities for bonded and disbonded three-material junctions. Int. J. Sol. Struct. 1994, 31, 2979–2997. [Google Scholar] [CrossRef]
- Shkarayev, S.; Madenci, E.; Ibnabdeljalil, M.; Savruk, M.P. Analytical stress singularities for a crack at a Bi-or triple junction of dissimilar materials with bilinear behavior. Eng. Fract. Mech. 2001, 68, 475–486. [Google Scholar] [CrossRef]
- Carpinteri, A.; Paggi, M. Analytical study of the singularities arising at multi-material interfaces in 2D linear elastic problems. Eng. Fract. Mech. 2007, 74, 59–74. [Google Scholar] [CrossRef]
- Sator, C.; Becker, W. Closed-form solutions for stress singularities at plane bi-and tri-material junctions. Arch. App. Mech. 2012, 82, 643–658. [Google Scholar] [CrossRef]
- Djokovic, J.; Vulovic, S.; Nikolic, R.; Hadzima, B. Analysis of Three-Dimensional Interface Corner Cracks. FME Trans. 2019, 47, 29–35. [Google Scholar] [CrossRef]
- Dundurs, J. Elastic Interaction of Dislocations with Inhomogeneities. In Mathematical Theory of Dislocations; Mura, T., Ed.; ASME: New York, NY, USA, 1969; pp. 77–114. [Google Scholar]
- Cotterell, B.; Rice, J.R. Slightly curved or kinked cracks. Int. J. Fract. 1980, 16, 155–169. [Google Scholar] [CrossRef]
- Nový, F.; Bokůvka, O.; Trško, L.; Jambor, T. Safe choice of structural steels in a region of ultra-high number of load cycles. Prod. Eng. Arch. 2019, 24, 25–28. [Google Scholar]
- Ulewicz, R.; Tomski, P. The effect of high-frequencies loading on the fatigue cracking of nodular cast iron. Metallurgy 2017, 56, 33–36. [Google Scholar]
- Djoković, J.M.; Nikolić, R.R.; Kalinović, S.M. Analysis of behavior of the interface crack that is approaching the three-material Joint. In Proceedings of the Abstracts of the 7th International Congress of Serbian Society of Mechanics, SremskiKarlovci, Serbia, 24–26 June 2019; Lazarević, M., Simić, S., Madjarević, D., Atanasovska, I., Hedrih, A., Jeremić, B., Eds.; p. 137. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).