AI-Based Modeling and Monitoring Techniques for Future Intelligent Elastic Optical Networks

Abstract

With the development of 5G technology, high definition video and internet of things, the capacity demand for optical networks has been increasing dramatically. To fulfill the capacity demand, low-margin optical network is attracting attentions. Therefore, planning tools with higher accuracy are needed and accurate models for quality of transmission (QoT) and impairments are the key elements to achieve this. Moreover, since the margin is low, maintaining the reliability of the optical network is also essential and optical performance monitoring (OPM) is desired. With OPM, controllers can adapt the configuration of the physical layer and detect anomalies. However, considering the heterogeneity of the modern optical network, it is difficult to build such accurate modeling and monitoring tools using traditional analytical methods. Fortunately, data-driven artificial intelligence (AI) provides a promising path. In this paper, we firstly discuss the requirements for adopting AI approaches in optical networks. Then, we review various recent progress of AI-based QoT/impairments modeling and monitoring schemes. We categorize these proposed methods by their functions and summarize advantages and challenges of adopting AI methods for these tasks. We discuss the problems remained for deploying AI-based methods to a practical system and present some possible directions for future investigation.

1. Introduction

The progress of 5G mobile networks, internet of things and cloud services has raised high demands and new requirements for the capacity and reliability of optical networks. To serve the rapidly increasing number of internet service users, the technologies of optical networks are continuously evolving. The development of elastic optical networks (EON) [1] enables network controllers to scale up or down resources in order to utilize spectrum resources efficiently [2]. However, the EON architecture increases network complexity because of the various configurations of links and signals, which makes it more challenging to maintain the high transmission quality of a lightpath from the beginning of life (BoL) to the end of life (EoL). Since a large amount of data is transmitted in each link, even a brief disruption of traffic flows can lead to disastrous degradation [2]. Therefore, improving the reliability of optical networks is also important.

To reach a high capacity, optical networks should better utilize network resources. In many scenarios, since a planning tool cannot accurately estimate the quality of transmissions (QoT), a high design margin is mandatory, which accounts for the difference between the planned metrics and the real value to ensure proper operations of networks [3]. A high margin can lead to the underutilization of spectrum resources. Therefore, to build a low margin optical network to increase network capacity, a more accurate planning tool is needed to estimate the QoT prior to link deployment or reconfiguration [4]. In this case, an accurate QoT model is essential and impairment models can improve the accuracy of the QoT model. On the other hand, to improve the reliability of optical networks, controllers should be capable of obtaining the real-time status of networks to prevent the serious degradation of systems. To achieve this, advanced optical performance monitoring (OPM) techniques are essential to enable needed functionalities to monitor the QoT and impairments. If failures occur in optical networks, the monitoring mechanisms should be capable of detecting, identifying and localizing them. Therefore, in summary, the modeling and monitoring techniques are the key building blocks for the next generation EON. The basic architecture of the modeling and monitoring techniques is shown in Figure 1.

For the modeling, some models are applied to judge whether one lightpath meets the requirement for establishment in terms of the QoT [4]. Some are applied to estimate the specific value of the QoT or impairments [5]. In EON, there are some challenges for traditional analytical models. Firstly, there exists typically a tradeoff between complexity and accuracy. Some sophisticated analytical models, e.g., the split-step Fourier method (SSFM) [6], are capable of capturing different impairments with great precision, but the complexity may be prohibitively high. Some approximate models, e.g., the Gaussian noise (GN) model [7], can be calculated in a short time, but the accuracy needs to be improved especially for heterogeneous and dynamic links. Moreover, because of the diversity of EON, it is difficult to obtain one specific model for all scenarios. In this case, the estimation results of models may appear a large deviation for some scenarios.

Artificial intelligence (AI) [8] technologies provide new opportunities to solve these problems. In many scenarios, machine learning (ML) methods can obtain a higher accuracy and/or a lower complexity compared to analytical models. For instance, in [5], an artificial neural network (ANN) is adopted to estimate fiber nonlinear noise more accurately and efficiently compared to the original analytical model. The accuracy of this ANN-based nonlinear estimator is higher than the incoherent GN (IGN) model and the complexity is much lower than the SSFM. Moreover, for situations where there is no suitable traditional model, ML methods can make estimations utilizing the data extracted from simulations or real scenes. For example, the filtering effect brought by reconfigurable optical add-drop multiplexers (ROADM) can be modeled with an ANN [9]. Finally, many data-driven methods with ML can be adopted to adjust analytical models to be scalable for more scenarios where they show large deviations. For instance, in [10], ML algorithms are used to improve the performance of the analytical model with data collected from an established lightpath.

The transmission performance of an established light path is not always reliable due to the various changes of link conditions. Therefore, optical performance monitoring (OPM) is a key building block, which enables network controllers to adjust link configurations according to the real-time status of a system. Moreover, monitoring results can be used to detect, identify and localize failures in EON’s. However, the heterogeneity of EON’s has also raised many new challenging requirements for the monitoring techniques, and ML shows a potential in building more intelligent and efficient monitoring schemes. Firstly, faster response time is desired for monitoring [2]. Since a monitoring agent should provide information for optimizing lightpath configurations and diagnosing the anomaly, the monitoring scheme needs to be capable of tracking the change of the network performance. According to [2], the monitoring time of some network applications is required to be at the order of milliseconds. Therefore, some traditional methods with complex data processing and a long-time window may not be compatible with dynamic real-time applications. To solve this problem, advanced ML methods with forward propagation mechanisms [11], such as ANN, convolutional neural networks (CNN) and so on, can be employed to accomplish the feature extraction and estimate real-time status in a short time period [5,12,13]. These monitoring tools can be trained offline before deployment. When estimating the signal performance, the pre-trained monitors can respond in a very short time. Secondly, monitoring techniques should be cost-effective [2]. In particular, they should not necessitate expensive external devices, and one OPM block is preferable to monitor multiple impairments. It may be difficult for analytical models to achieve these two goals simultaneously but ML-aided methods can help to fulfill these requirements. For instance, samples of received signals can be input to ML algorithms for monitoring the chromatic dispersion (CD), polarization-mode dispersion (PMD) and optical signal-to-noise ratio (OSNR) at the same time [14]. Moreover, when obtaining information from the receiver digital signal processing (DSP) modules, ML methods may be able to monitor the QoT or impairments without any external devices such as the optical spectrum analyzer (OSA) [15].

Therefore, for the next generation EON, applications of ML techniques for modeling and monitoring can provide strong support to build a reliable and intelligent optical network with lower design margins. This paper is intended to review recent progress in AI-enabled modeling and monitoring techniques for EON. Since optical networks are full of data with heterogeneous sources and various characteristics, it is possible to improve the accuracy and/or sensitivity of optical performance estimation functionalities with these data. However, the large number of data also makes it more challenging to discover useful information from them. In this case, data-driven ML methods are essential tools for network planning and management, but these methods should be improved to be cost-effective and reliable for deployment. Several previous review works have provided comprehensive summaries of the applications of ML techniques in optical networks [2,16,17,18,19]. They discuss the ML-based techniques adopted in various domains and point out many possible directions for the future deployment strategies. In this paper, we focus on the AI-based techniques specifically for link modeling and monitoring in optical networks. In addition, we discuss and summarize the advantages and challenges for adopting the AI-based modeling and monitoring methods in the future EON. This paper is organized as follows.

• In Section 2, we firstly introduce the background and challenges for modeling the QoT and impairments in EON’s. The potentials of applying ML to estimate network performance are also discussed. Then, we review many previous works on ML-based modeling techniques.
• In Section 3, we firstly review various previous works on ML-based monitoring techniques. Afterwards, the monitoring techniques specifically for failure management are elaborated.
• In Section 4, the use cases for AI-based modeling and monitoring techniques are discussed.
• In Section 5, we provide a lookout for the future of utilizing ML methods in EON by discussing both the challenges and opportunities.
• In Section 6, a conclusion for this paper is provided.

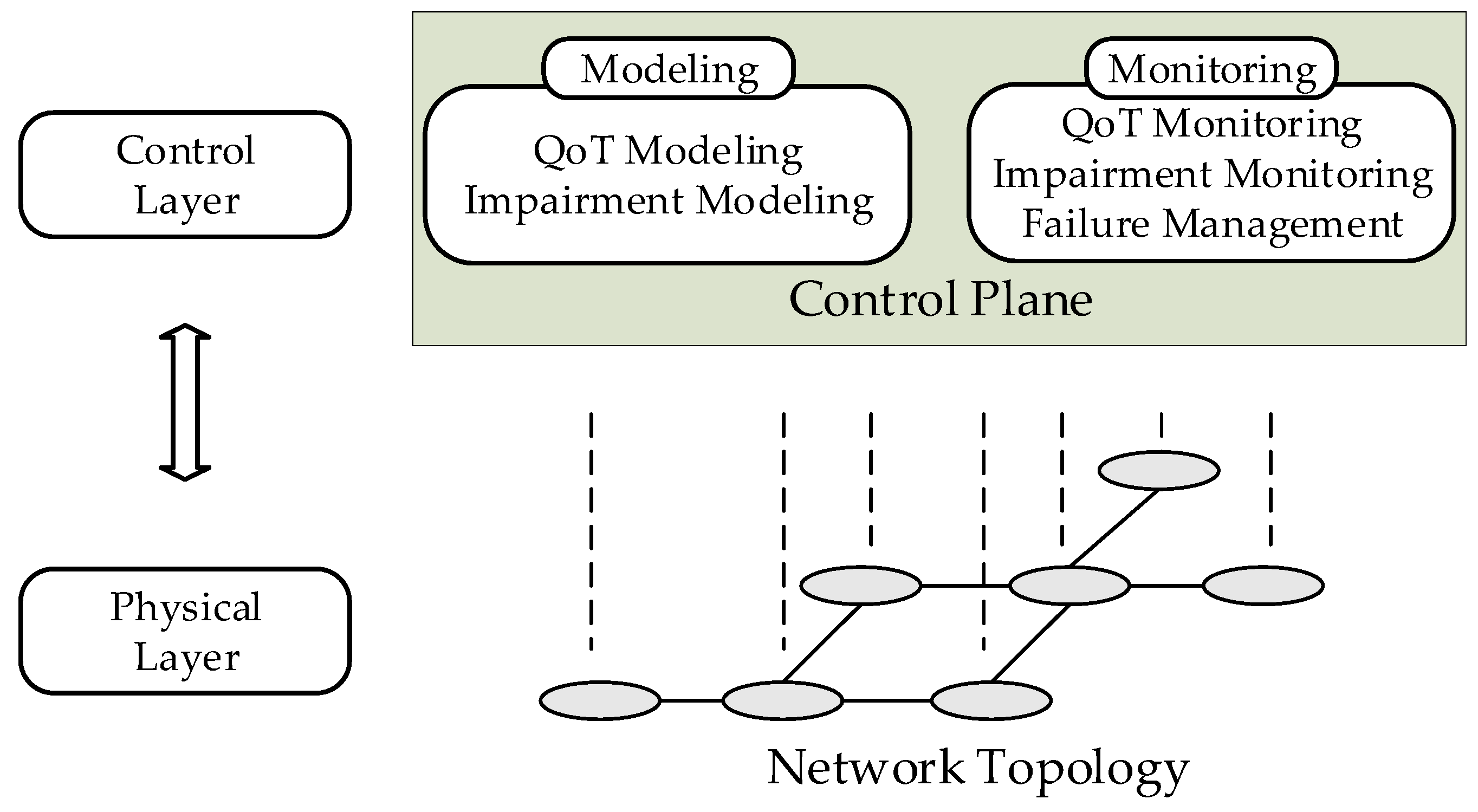
2. AI-Based QoT and Impairment Modeling

2.1. Background and Challenges

QoT modeling for an unestablished lightpath can help planning tools in the control plane to develop proper strategies of routing, wavelength assignment and signal configurations [20,21,22,23,24,25]. In EON, during the phase of network planning, the accuracy of QoT and impairment models is influenced by various configurable parameters like modulation format, symbol rate and physical path in optical networks. If these parameters are not accurate, the estimations of QoT may have deviations compared with the real value [5,26,27]. In this case, due to the inaccuracy of planning tools, a large design margin [3] is needed and networks are overutilized to avoid network degradation until the EoL. As a result, QoT models with a higher accuracy are desired and impairment models can provide an insight into the contributions of each individual impairment to help QoT estimators reach a better performance.

For the QoT modeling, some traditional methods [28] can estimate the performance of an optical link in terms of signal-to-noise ratio (SNR), pre-forward error correction (FEC) bit error rate (BER), OSNR and so forth. For the impairment modeling, traditional methods can estimate some important physical layer effects, such as fiber nonlinearity, optical filtering effect and amplified spontaneous emission (ASE) noise. The requirements for QoT and impairment modeling techniques of the next-generation EON are illustrated as follows.

• Self-adaptiveness: Analytical models are essential for estimating the QoT of unestablished lightpaths. However, they may not be scalable for all scenarios since the assumptions for these models may be inappropriate when the configuration of traffic optical paths evolves continuously. For instance, the optical amplifier gain spectrum is wavelength-dependent but some models assume the gain to be identical for all channels. This kind of improper assumption may lead to an inaccurate estimation of the ASE noise. Therefore, network planning tools with self-adaptive QoT and impairment models are highly desired to guarantee a high-quality transmission from the BoL to the EoL.
• Efficiency: For many QoT and impairment models, traditional models with high precision may incur burdensome computational requirements. For example, to model the nonlinear impairment, the SSFM [6,29,30,31] can reach a high accuracy if the step size is sufficiently small, which leads to a high complexity. The GN model [7] can provide results in a very short time but the precision is lower than that of the SSFM in most scenarios. Therefore, models that can efficiently make estimations with a high accuracy are desired.
• High tolerance to parameter uncertainty: In a practical system, link parameters can be uncertain due to inaccurate measurements and other reasons. If the uncertainty of the model input exists, there might be a significant deviation between the real value and the model estimation [5]. Therefore, models that are less sensitive to parameter uncertainty are also desired.

To fulfill these requirements, data-driven ML methods open new opportunities. Firstly, ML methods are mostly data-driven [32], which means they enable the model to learn the characteristics of the dataset, in principle even without any theoretical information [4,33,34,35,36]. This specific ability of learning adaptively with data allows ML models to be easily extended to any scenarios if the simulation, experiment or field-trial data for this situation can be obtained [13,23,37]. Secondly, for most optical networks, the number of tunable parameters for link configurations is limited. Therefore, the number of input parameters for QoT or impairment models are relatively small [5,33,38], which enables ML models to reach a good performance with simple structures such as the ANN with a small number of nodes and hidden layers [23]. In this case, these low-complexity ML models can calculate faster compared with some traditional models. Many previous works using a simple ANN or linear regression have already achieved good performances [5]. Finally, advanced ML algorithms like ensemble learning [39] and Theil-Sen regression [40] can address the drawbacks of the least squared algorithms and make models less sensitive to the outliers and fluctuations of data. Besides, training techniques like data augmentation [41,42] can improve the model robustness to parameter uncertainty and avoid overfitting by adding interference manually. In this section, we reviewed various previous works for AI-based QoT and impairment modeling techniques.

2.2. AI-Based QoT Modeling

For the QoT modeling, there are many types of metrics, such as BER, Q-factor, SNR, OSNR and margin. The aim of the QoT modeling is to precisely estimate the link performance and then build low margin networks. The requirement of the QoT estimations differs in different scenarios. Some need to judge whether one light path can be established or not [4,21,38], and some need the specific value of the QoT metrics. For the former, ML classification methods [43] can be used such as K-nearest neighbors (KNN), random forests (RF), support vector machine (SVM), logistic regression (LR), ANN and so forth. For the latter, ML regression methods [43,44] can be employed such as network Kriging (NK), Gaussian process (GP), CNN [45], ANN and so forth. We provided a review of some recent ML-based QoT modeling techniques in the literature for different metrics in this section. They are listed in

Table 1. Summary of the machine learning (ML)-based quality of transmission (QoT) modeling techniques discussed in Section 2.2.

Modeling Targets	Algorithms	Input Features
BER	K-Nearest Neighbors, Random Forest [4]	Traffic volume, modulation format, total length of links, length of the longest link, number of lightpath links
	Stochastic Gradient Descent Polynomial Regression [21]	Generalized OSNR, baud rate, modulation format, FEC, slot-size
	Deep Graph Convolutional Neural Networks [46]	Total length of the path, span length, central frequency, number of slots in each path, modulation format, number of Erbium-doped fiber amplifier (EDFA), number of links, BER
Q-factor	Case-based Reasoning [47,48]	Route, selected wavelength, total length of the path, sum of the co-propagating lightpaths per link, standard deviation of the number of total co-propagating lightpaths
	Transfer Learning [33]	Channel loading, per-channel output power
OSNR	Network Kriging, $l_2$-norm Regularization [49]	Average PMD of each link, accumulation value of CD, the self-phase modulation (SPM) quantified through the nonlinear phase of the signal
	Gaussian Process Regression [50]	Wavelength, OSNR of the established wavelength
SNR	Combination of Machine Learning and Physical Layer Model [10]	Lightpath length, link load, number of crossed EDFAs
	Gradient Decent [51]	Power, noise figure
Margin	K-Nearest Neighbors, Linear Regression, Support Vector Machine, Artificial Neural Networks [38]	Number of hops, number of spans, total link length, average link length, maximum link length, average span attenuation, average CD

and elaborated as follows.

For the BER estimation, in [4], an ML-based classifier is used to decide whether the BER of an unestablished lightpath can achieve the network requirement. Features of the model are the traffic volume, modulation format, lightpath total length, length of the longest link and number of lightpath links. The training dataset is obtained from the deployed lightpaths. The employed ML classifier algorithms are KNN and RF with various kernel settings. Moreover, this work comprehensively compare the performance of different ML algorithms. The influences of different combinations of input features and different sizes of dataset are also analyzed. The result shows that RF outperformes KNN in accuracy and efficiency in most cases. The result also shows that a bigger dataset can help to reach a higher accuracy. In [21], the generalized optical signal-to-noise ratio (gOSNR), baud rate, modulation format, FEC, slot-size and so on are used to estimate the BER and the training data is obtained from a practical system. Therefore, this model can enable controllers to find the optimum configuration of a light path for each specific network. In [46], a deep graph convolutional neural network (DGCNN) is applied to estimate the feasibility of the network state. This work considers the crosstalk between unestablished and established light paths according to historical data.

For the Q-factor estimation, in [47,48], a cognitive QoT estimator classifies lightpaths to high- or low-quality categories. The classification method is case-based reasoning (CBR), which is based on the prior experiences or cases to make estimations. Features for this model include the route, selected wavelength, total length of a path, sum of the co-propagating lightpaths per link and standard deviation of the number of total co-propagating lightpaths. To extend a pre-trained model to more scenarios, transfer learning is proposed in [52] to make use of collected data from new scenes for retraining. This method can effectively reduce the training time when configurations of the optical networks change. Methods mentioned above all use historical data from real scenes and they all achieve a good performance for estimating the QoT. Therefore, we can infer that data-driven ML methods can improve the training efficiency and the scalability of models to more systems.

For the OSNR estimation, in [49], regression methods like network Kriging (NK) and least-squares minimization with $l_2$-norm regularization are utilized. The parameters used for estimations are the average PMD of each link, accumulation value of CD, and SPM quantified through the nonlinear phase of the signal. The algorithm is based on established light paths to evaluate an unestablished path for transparent optical networks. This method successfully helps to design a reliable light path efficiently. According to [50], in some practical systems, the noise figure and gain of amplifiers and fiber loss are wavelength-dependent. In this case, the Gaussian process regression (GPR) is used to estimate the OSNR with a confidence output.

For the SNR estimation, in [10], the combination of the ML model (ML-M) and physical layer model (PLM) is applied to build a framework called ML-PLM to estimate the QoT performance. This model is based on the data from the existing connections of a network. Features used for estimation are the light path length, link load and number of crossed Erbium-doped fiber amplifiers (EDFAs). The simulation shows that, this method can reduce the influence of the uncertainty of parameters such as the fiber attenuation, dispersion, nonlinear coefficients or amplifier noise. Moreover, the more light paths the model can get from the network topology, the higher accuracy the model can achieve. In this way, ML-PLM can reach better performances and makes the model suitable for a dynamic network. In [51], gradient decent is used to correct the deviations of the input parameters for the QoT estimators. This method takes advantage of back-propagation algorithms embedded in many neural networks, which successfully reduces the uncertainty of models.

For the margin estimation, in [38], ML models such as KNN, LR, SVM and ANN are proposed to judge whether the residual margin is positive. The input features are the number of hops, number of spans, total link length, average link length, maximum link length, average span attenuation and average dispersion. To build a better classifier, those models for classification are investigated with different kinds of kernels. Then, to obtain the specific value of the residual margin an ANN is employed. In [38], the performances of the adopted ML algorithms are compared with each other and they all reach a decent performance.

2.3. AI-Based Impairment Modeling

Accurate modeling of impairments can provide more information to improve the accuracy of QoT models. Moreover, the estimation of specific impairments can help controllers design an optimum configuration of a light path. In this section, since impairments like CD and PMD can be compensated in the receiver, we focus on the impairments that may cause performance degradation. A few recent works using AI-based modeling methods for estimating fiber nonlinearity, filtering effect and ASE noise are investigated in this section. They are listed in

Table 2. Summary of the ML-based impairment modeling techniques discussed in Section 2.3.

Modeling Targets	Algorithms	Input Features
Nonlinear Noise	Artificial Neural Networks [5]	Nonlinear SNR from the GN model, span number, maximum span length, average span length, optical launch power, link length, net CD, average gamma of fiber spans, average attenuation of fiber spans, number of wavelength-division multiplexing (WDM) channels
Optical Filtering Effect	Artificial Neural Networks [9]	Number of ROADMs, OSNR, loaded noise distribution, bandwidth distribution
Gain Spectrum of EDFA	Deep Neural Networks [34]	Power levels of all WDM channels
EDFA Gain Excursion	Multilayer Perceptron [35]	Gain setting, total input power, input power of each channel

and introduced as follows.

2.3.1. Nonlinear Noise

For the nonlinear effect modeling, sophisticated analytical models such as the SSFM [6] can provide accurate estimations. However, these methods also result in a long computation time. Although approximate models can calculate much more quickly [53], they cannot guarantee the accuracy in all scenarios, thus leading to a high design margin and an inefficient utilization of network resources [3]. In [5], a combination of analytical models and ML methods is proposed to reach a higher accuracy for nonlinear noise estimation.

2.3.2. Filtering Effect

In future EON, ROADM can enable optical networks to support the flexible multiplexing and demultiplexing, which is important for build an intelligent network with more capacity and dynamicity. However, in this case, the filtering effect caused by cascaded ROADMs can also influence the QoT much more significantly because of the reduced guard band between channels. In [9], an ANN-aided approach is introduced to estimate the filtering effect. The input features of the neural network are the ROADM number, OSNR, loaded noise distribution and bandwidth distribution. A one-hidden layer ANN can estimate the SNR of the light path induced by the filtering effect with error mostly less than 1 dB. In practical systems, the filtering effect can be more significant when multiple impairments co-exist such as nonlinearity. Besides, the filtering effect is not a kind of additive noise and SNR may not be the best metric for evaluation. Therefore, problems like how to model the filtering effect together with other impairments and how to quantify the filtering effect using a proper metric should be further investigated.

2.3.3. ASE Noise

In a practical system, to accurately model the ASE noise generated by EDFAs, the noise figure (NF) of each EDFA at each wavelength should be precisely known. According to [36], the NF of an EDFA is related to the gain at each wavelength. Therefore, the ASE noise can be more accurately estimated with the aid of an accurate EDFA gain model. However, the spectral hole burning [54] (SHB) effect makes the spectral gain profile of an EDFA change dynamically under channel reconfigurations, thus leading to a power excursion. Since it is hard for the traditional model to efficiently model the gain spectrum of an EDFA with different power loadings in each channel, data-driven ML methods can be adopted. In [34], deep learning is adopted to estimate the gain of each channel individually. To simplify the structure of ML algorithms, a multilayer perceptron neural network is introduced to estimate the gain of all channels at the same time [35].

3. AI-Based Optical Performance Monitoring

OPM is key to ensure the reliability of optical networks [16]. According to [2], monitoring techniques can enable several essential and advanced network functionalities. Firstly, a precise monitoring of QoT and impairments [55,56] can make the control plane accurately assess the signal quality. Therefore, the monitoring information can guide the network self-reconfiguration and also enables receivers to adapt some impairment compensation algorithms. Secondly, the real-time monitoring can continuously obtain the condition of the physical layer. If the QoT deteriorates, monitoring agents can detect failures. Then, the controller can reconfigure the network to avoid further degradations. Finally, monitoring data from real scenes can be used to retrain the planning model. This retraining scheme can improve the accuracy of planning tools and make the design margin lower. At the same time, there are also some challenging requirements for deploying an OPM in an EON, such as how to track the real-time change of the optical networks accurately in a short response time and how to monitor multiple impairments simultaneously. These challenges have been elaborated in Section 1. ML shows its potential to fulfill these challenges. In this section, we review various works using ML for OPM. According to their different functions, these approaches are divided into two categories. We firstly introduce some use cases of monitoring the QoT and impairments of a lightpath. Then, we review the monitoring techniques for detecting, identifying and localizing soft failures in a network. These two aspects are discussed as follows.

3.1. AI-Based QoT and Impairment Monitoring

For the QoT monitoring, the evaluation of BER, SNR, Q-factor, QSNR and so forth can enable controllers to assess the transmission performance of each established light path and provide a quantitative measure to check whether the designed QoT can be ensured. At the same time, impairment monitoring is also needed to provide an insight into each specific effect in the physical layer. In this section, various applications of ML for monitoring QoT and impairment are discussed. A brief summary of methods discussed in this section is shown in

Table 3. Summary of the ML-based monitoring techniques discussed in Section 3.1.

Algorithms	Features	Monitoring Targets
Artificial Neural Networks [14]	Empirical asynchronously sampled signal amplitudes	OSNR, CD, PMD
Deep Neural Networks [57]	Asynchronously sampled raw data	OSNR
Convolutional Neural Network [58]	Constellation-diagram	OSNR, Modulation Format
Convolutional Neural Networks [13,59]	Horizontal and vertical polarization, in-phase and quadrature-phase components of optical signals	OSNR, Modulation Format
Artificial Neural Networks [37]	Launched power, EDFAs’ input powers, EDFAs’ output powers, EDFAs’ gains, EDFAs’ NFs, etc.	OSNR
Principal Component Analysis, Artificial Neural Networks [60]	Asynchronous delay-tap plots	OSNR, CD, Differential Group Delay (DGD), Joint Bit-rate and Modulation Format Identification (BR-MFI)
Principle Component Analysis, Artificial Neural Networks [61]	Asynchronous single channel sampling data	OSNR, Modulation Format
Deep Neural Networks [62]	Signals’ amplitude histograms	OSNR, Modulation Format
Kernel-based Ridge Regression [63]	Asynchronous delay-tap sampling data	CD, DGD
Long Short-Term Memory Neural Networks [64]	Four-tributary digital output	OSNR
Long Short-Term Memory Neural Networks [65]	Frequency domain signal	OSNR, Nonlinear Noise Power
Support Vector Machine [66]	Eye diagrams	CD, PMD, Noncoherent Crosstalk
Artificial Neural Networks [67]	Amplitude noise and phase noise correlation (ANC, PNC), number of WDM channel, total CD	Nonlinear SNR
Artificial Neural Networks [68]	Accumulative logarithmic ANC (ALANC), number of WDM channel, total CD, noise tangential and normal component	Nonlinear SNR
Support Vector Regression [69]	Amplitude noise correlation, logarithmic accumulated CD	Nonlinear SNR
Artificial Neural Networks [5]	Nonlinear SNR from GN model, span number, maximum span length, average span length, the launch power, link length, net CD, average gamma of fiber spans, average attenuation of fiber spans, number of WDM channels, ANC, PNC	Nonlinear SNR

and the details are elaborated as follows.

In [14], an ANN is used to monitor the OSNR, CD and PMD simultaneously with empirical asynchronously sampled signal amplitudes. In [57], to make an easier monitoring procedure without labor-intensive feature engineering, deep neural networks (DNN) are used to monitor the OSNR with asynchronously sampled raw data. For this work, neural networks with an advanced structure perform the feature extraction and monitoring calculation at the same time. Moreover, the results show that a larger training dataset and a deeper neural network can help to increase the estimation performance. As more advanced neural network structures emerge, CNN is also introduced to monitor the OSNR and modulation format simultaneously [13,58,59]. In [37], ANN is adopted to monitor the OSNR based on the historical data collected from real systems. In [60], principle component analysis (PCA) and ANN are used to monitor the OSNR, bit rate, modulation format, CD and DGD by asynchronous delay-tap plots. In this case, PCA can reduce the number of input parameters, thus reducing the complexity of the ANN. A similar approach is investigated in [61] to monitor the OSNR and identify the modulation format by asynchronous single channel sampling, which makes the algorithms simple and low-cost. In some other situations, ML-methods are also employed to monitor specific impairments. In [62], DNN is proposed to monitor the OSNR and modulation format with signals’ amplitude histograms. This method only requires few DSP blocks, which makes it cost-effective for deployment. In [63], kernel-based ridge regression is used to monitor the CD and differential group delay (DGD) simultaneously. This method is validated by simulations and experiments. In [64], the long short-term memory (LSTM) neural network is applied to monitor the OSNR with the four-tributary digital outputs. The mean absolute error can be significantly reduced from 0.4 to 0.04 dB compared with other ML algorithms. In [65], OSNR and nonlinear noise power are monitored simultaneously based on frequency domain signals. In [66], to identify the impairment causing the transmission degradation, SVM can accurately make classifications between CD, PMD and noncoherent crosstalk.

In many scenes, obtaining specific features strongly related to an impairment can improve monitoring accuracy. In [68], the amplitude noise correlation (ANC) and phase noise correlation (PNC) are proved to be related to nonlinear impairments and an ANN is applied to monitor the nonlinear SNR based on them. In [69], multiple logarithmic ANCs are directly input to an estimator using support vector regression for monitoring the nonlinear SNR, which can estimate nonlinear noise without features like the number of WDM channels. Moreover, in [5], the ANC and PNC are combined with an analytical model such as the GN model to estimate nonlinear noise. Simulation results in [5] prove that this combination can improve the monitoring accuracy.

3.2. AI-Based Failure Management

Link failures can be classified into hard failures and soft failures. Hard failures in the link cause immediate disruptions but can be easily detected and restored. Soft failures just gradually deteriorate the performance of the link and they are hard to be detected. In addition, the causes behind them are challenging to be identified. Therefore, detecting and identifying soft failures are of great importance and highly desired. In this section, we review some recent works for failure management based on AI techniques and they are listed in

Table 4. Summary of the AI-based failure management techniques discussed in Section 3.2.

Targets	Algorithms	Input Features
Detection, Identification	Finite State Machine [70]	BER, received power in receiver
Detection, Identification	Random Forests, Support Vector Machine [71]	The trend of BER
Identification	Convolutional Neural Networks [12]	Optical spectrum
Detection	Support Vector Machine, Decision Trees [15]	Optical spectrum
Detection	One-class Support Vector Machine [72]	Tap value of the adaptive filter

.

For the soft failure detection, current detection methods in a deployed network usually rely on a pre-defined threshold. However, because of the high complexity of modern optical networks, it is hard to set an accurate threshold. If it is set too loose, some soft failures may be ignored, and if too tight, false detection may occur. For soft failure identification, it is generally difficult to accomplish accurate identifications using analytic methods. To address the challenges faced by the traditional methods, many works are proposed to utilize the ML techniques to perform failure detection and identification. In [70], finite state machine (FSM) is used to detect and identify the soft failures caused by laser and wavelength selective switch (WSS). In [71], the trend of the BER is monitored and analyzed. The statistical characteristics of BER are input to the RF and SVM to detect the soft failure, and an ANN with a hidden layer is applied to identify the cause of the soft failure between EDFA and WSS. In [15], the optical spectrum is monitored using an optical spectrum analyzer (OSA). The features of it are extracted and analyzed to detect the soft failure caused by WSS. Then, controllers identify the anomaly between filter shift (FS) and filter tightening (FT). In [72], the tap value of the adaptive filter is analyzed using one-class SVM to detect the soft failure caused by laser, WSS and fiber nonlinearity. To summarize, ML techniques pave a promising way to address the problems of failure detection and identification. With the powerful learning capability of ML, the hidden patterns of the monitored data can be learned to enable various failure management functionalities. As optical networks becoming more dynamic and heterogeneous, traditional techniques for soft failure detection and identification may not be able to adapt to the complex scenarios well. Therefore, more applications of ML techniques are expected to be investigated in this field.

4. Use Cases

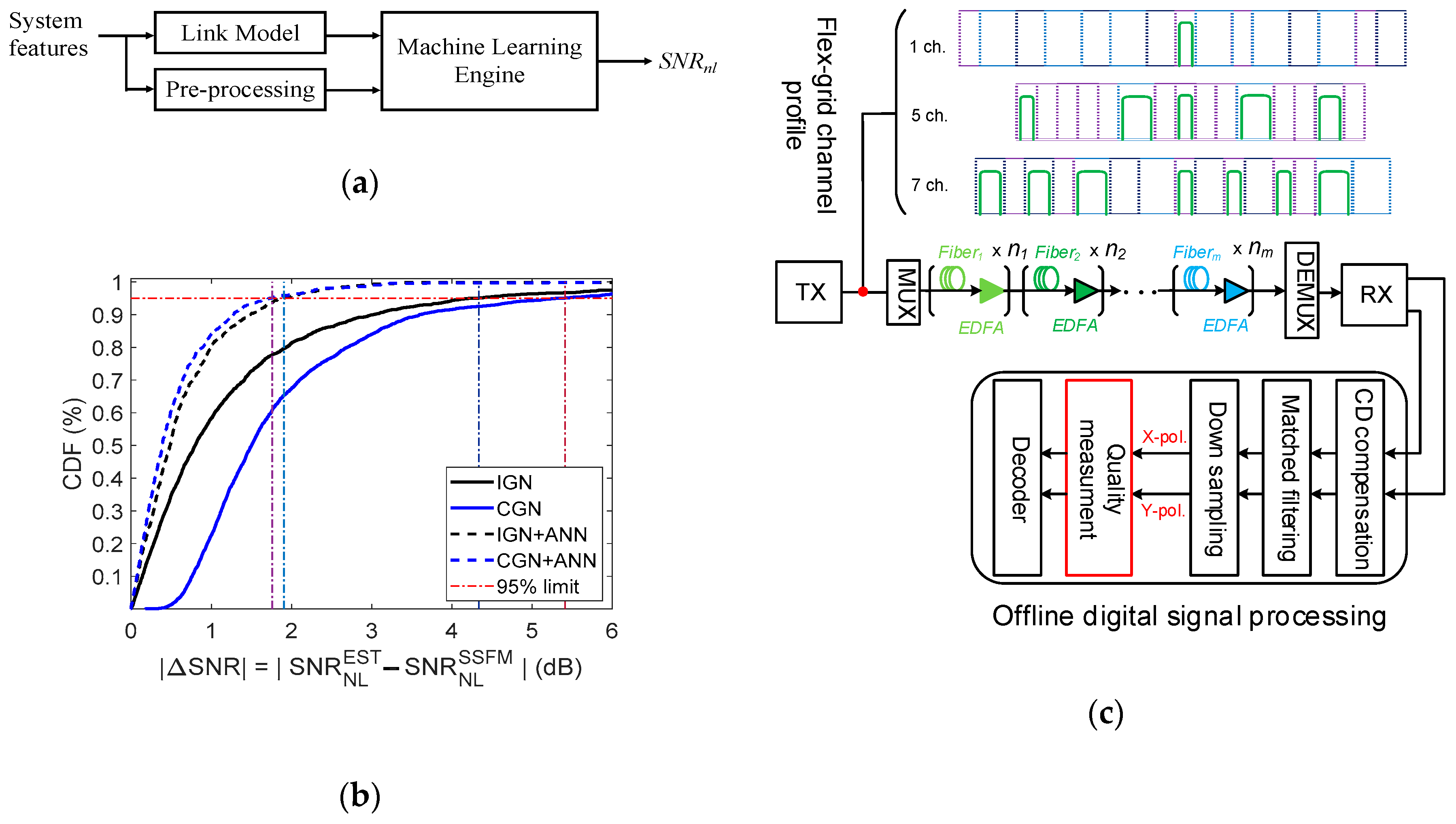
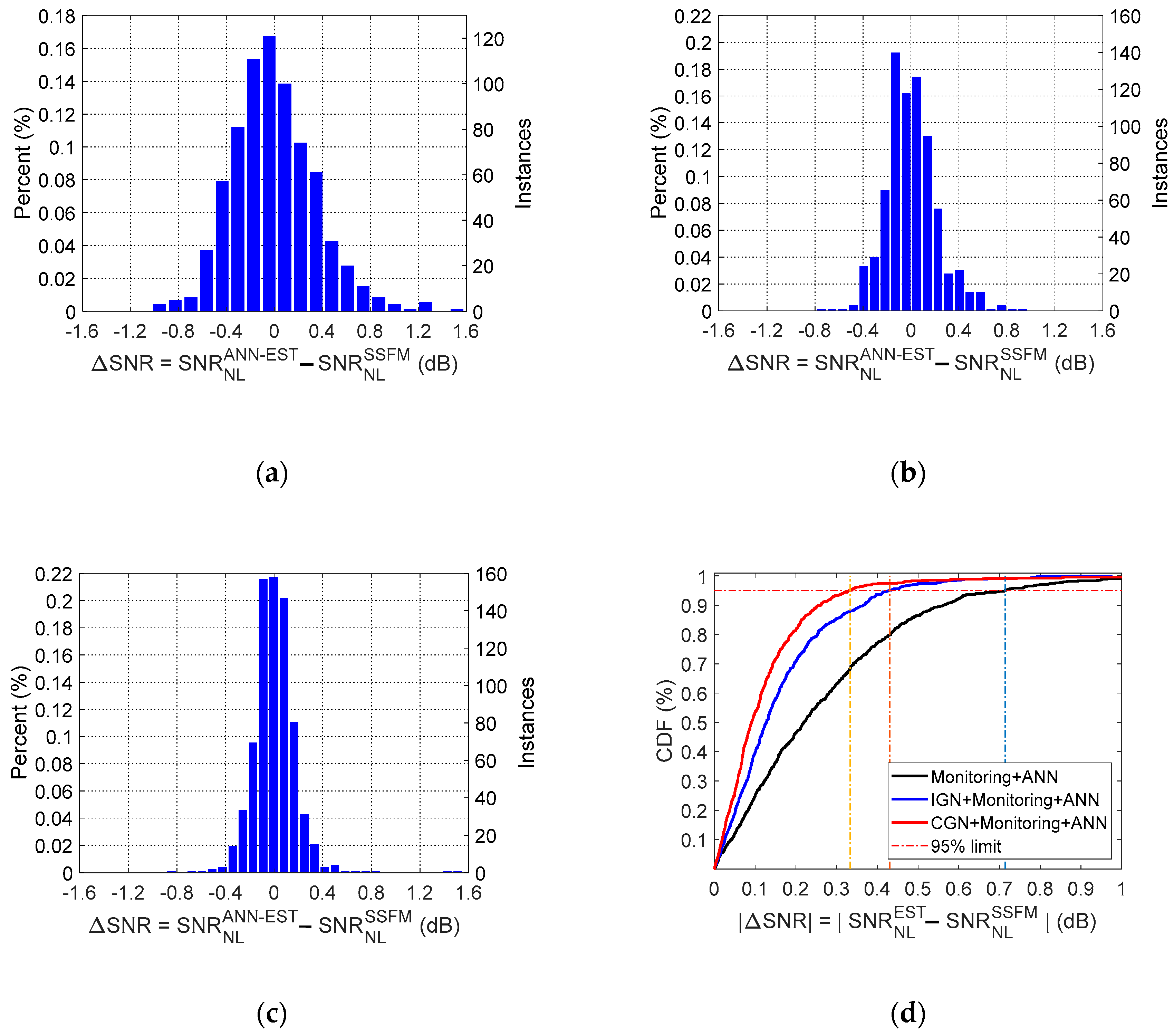
4.1. Use Case 1: AI-Based Nonlinear Noise Modeling

A use case for modeling the nonlinear SNR with ML is discussed as below. This use case is based on the methods proposed in [5]. The structure of the ML-based estimator is shown in Figure 2a. For this model, an analytical model provides a relatively low-accuracy result in a short time. Afterwards, the pre-calculated result is input to a ML engine together with the processed system features related to nonlinear interference. The system features are shown in

Table 5. Summary of the modeling input features used in [5].

Features of modeling	1. $SN{R}_{NL}$ from the GN model
	2. Span number
	3. Maximum span length
	4. Average span length
	5. Launch power
	6. Link length
	7. Net CD
	8. Average gamma of fiber spans
	9. Average alpha of fiber spans
	10. Number of WDM channels

. These features can be easily obtained by a central controller and the processing time is short. For this modeling scheme, the GN model can provide an approximate value with lower precision compared with the SSFM, and the ANN only needs to learn the residuals between the real value and the approximate one. In this way, only with a simple-structure ANN, the estimation result can be accurate. The simulation setup is shown in Figure 2c and the detailed description can be found in [5]. In Figure 2b, results show that when combining the ANN with the coherent GN model (CGN) or the IGN model, the estimation accuracy can be significantly improved.

4.2. Use Case 2: AI-Based Nonlinear Noise Monitoring

As elaborated in Section 3.1, many ML-based methods are proposed to monitor the nonlinear SNR in [66,67,72]. To improve the monitoring accuracy, in [5], the AI-based monitoring method combines the analytical models and the monitoring features such as ANC and PNC. As shown in Figure 3a–c, when combining monitoring features with analytical models, the maximum error reduces from 1.2 to 1 dB and 0.8 dB using the IGN and CGN, respectively. Moreover, the comparison of the CDF in Figure 3d also shows that the CGN model outperforms the IGN model to improve the ANN performance by 0.35 dB. In this work, the analytical model provides an approximate estimation. Afterwards, monitoring features are applied to improve the estimation accuracy based on the prior approximate estimations made by analytical models. Therefore, we can infer that ML can reach a higher accuracy if the input features are selected and processed properly.

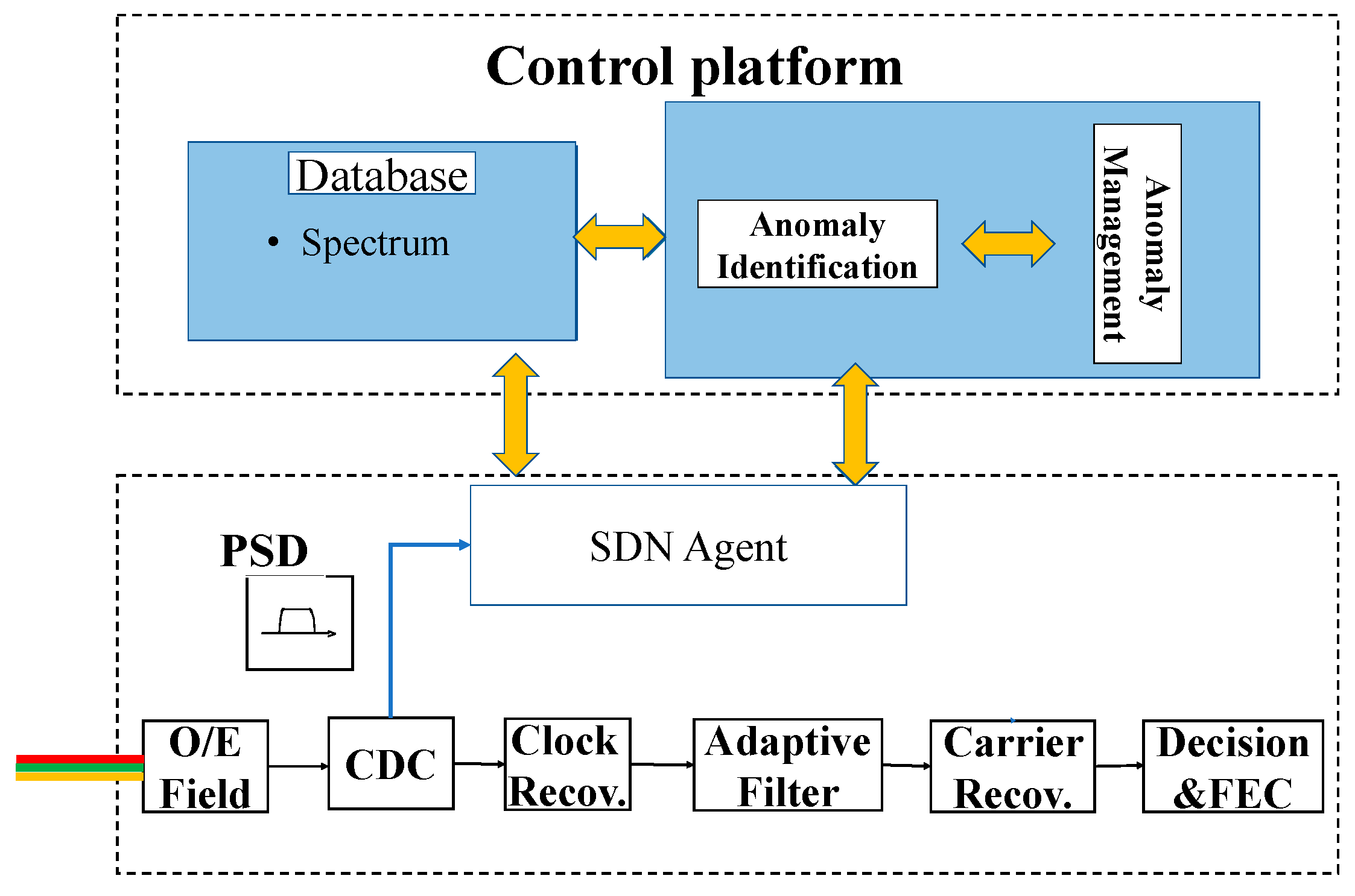
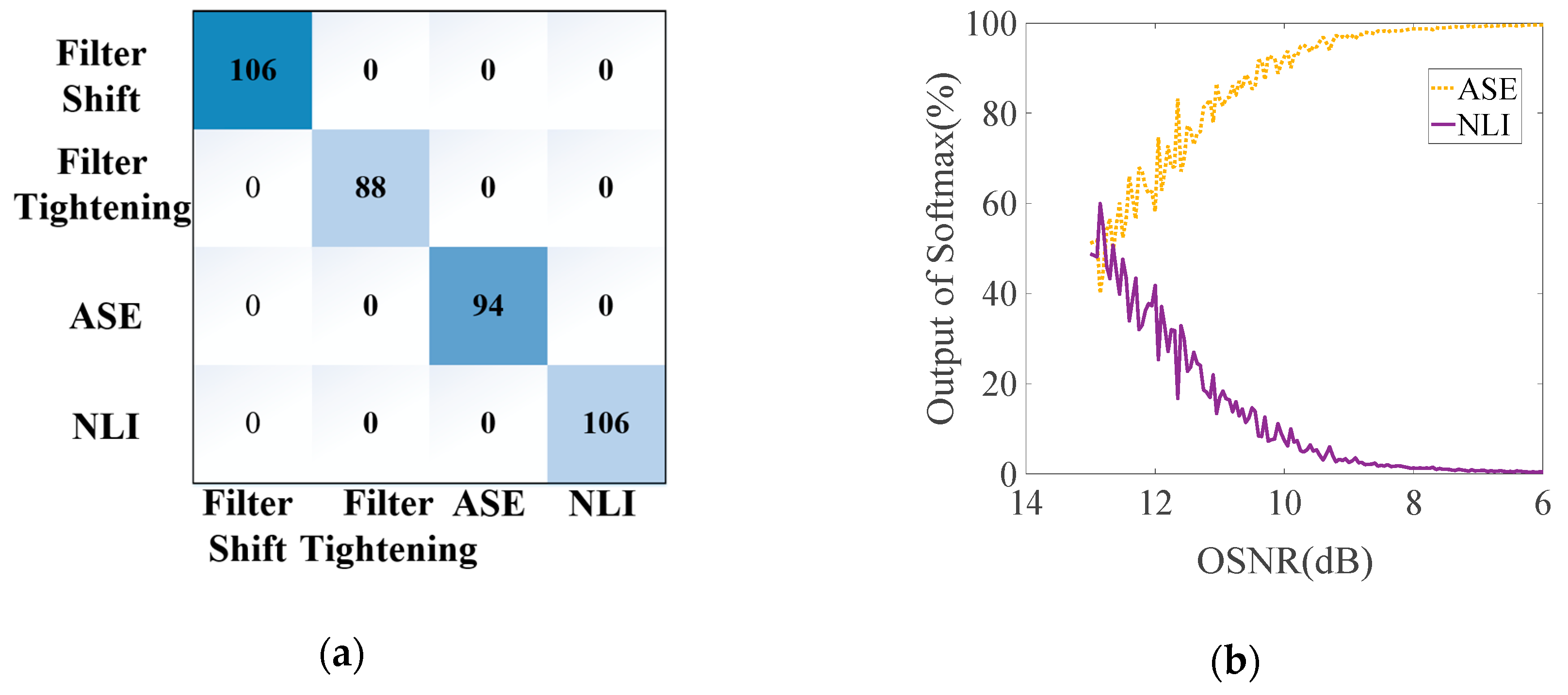
4.3. Use Case 3: AI-Based Soft Failure Identification

A use case for failure identification is elaborated in [12]. In addition to the filtering effect of WSS and ASE noise, fiber nonlinearity is also considered. Compared with the previous works, a deep learning algorithm is used and the power spectrum density (PSD) is extracted from a coherent receiver. The overall architecture is shown in Figure 4.

The SDN agent monitors the physical layer continuously and uploads the PSD to the control layer. Once the anomaly is detected, the CNN embedded in the anomaly identification module analyzes the PSD stored in the database. Finally, the identification results are output to the failure management module and proper actions are taken to restore the optical link.

The identification results are shown in Figure 5a. The results demonstrate a high accuracy of the proposed method when there exists only one type of anomaly. In the scene when multiple types of anomalies exit, the probability output by the SoftMax layer is utilized to gain insight into their respective influences on the system. The result is shown in Figure 5b. The influences of ASE and nonlinear interference (NLI) on the system are similar at first since the output probabilities of the two causes are both about 50 percent. Then, with the OSNR increasing, the NLI gradually becomes the dominant cause.

5. Future Work

To build a reliable optical network with a lower margin, ML methods provide a promising way. By reviewing the previous works using ML techniques for the modeling and monitoring, we observed that ML outperformed many traditional approaches for its scalability, efficiency and robustness. In future, more research with ML will be carried out for building an efficient, reliable and autonomous optical network. At the same time, there are also some challenges for ML-based techniques for practical deployments.

• Efficient adaptation scheme. For most of the works mentioned above, the ML-based methods are trained offline with data from simulations or lab experiments before deployment. Since the weights and parameters of the ML-based methods are fixed after training, the calculation time will be short when using these methods in a practical system. This firstly-trained-then-deployed scheme is efficient for adopting ML-based methods for situations that require a fast response time. However, the data from real scenes may be different from the simulation data. Therefore, a reasonable adaptation scheme is also needed after deployment. In EON, online learning approaches such as retraining are preferable to cope with time-evolving network scenarios [73]. Even though collecting data from the practical system for retraining has been proposed in many works, the rationality for the retraining scheme needs to be reconsidered. Since the change of the EON may be unpredictable, data collected from the real scenes may not follow the same distribution with the original training data. In this case, the collected data cannot be mixed with the pre-training data to adapt the ML-based modeling/monitoring agents. Besides, if retraining agents only use the data collected from the practical system, there are other problems. On the one hand, if retraining is performed frequently for a better adaptation, dataset collected in a short period is relatively small and overfitting may occur. On the other hand, if the retraining is not frequent, estimators may have large deviations when the network state changes at a fast pace. Therefore, how to deploy an efficient adaptation scheme should be carefully considered.
• Reasonable design of ML structure. To reach a higher accuracy, ML algorithms with more complex structures are introduced, such as DGCNN, reinforcement learning and generative adversarial network (GAN). However, these ML methods with complex structures may be hard to deploy in an optical system since they require large memories. Therefore, cost-effective ML methods are desired for EON and the structures of ML methods need to be adjusted to be tailored for the optical system.
• Interpretability of ML-based approaches. Many works discussed in this paper are based on a neural network, which is a flexible structure for classification and regression. However, those ML algorithms often cannot provide concrete explanations for their decisions to a satisfactory extent [74]. Therefore, it is difficult to guarantee the algorithmic fairness of ML methods, which is an obstacle for deploying ML techniques to real systems. More works are desired to make ML methods interpretable to scientifically make sure that these methods can perform as expected.
• Deployment of the ML engine. Many approaches for modeling and monitoring with ML have been proposed recently. Where to deploy these ML engines is another problem. Some ML engines can be embedded in receivers to build a low latency system while some need to be deployed in the control plane to obtain information from the whole optical networks [75]. Therefore, the strategies for the deployment of the ML engine can be carefully designed to reach an optimum performance of the ML-based method.

6. Conclusions

To improve the capacity of optical networks, planning tools with higher accuracy are required. To improve the reliability of optical networks, accurate optical performance monitoring is also desired. In this paper, we review many previous works on machine learning (ML) aided modeling and monitoring techniques in elastic optical networks. We firstly analyzed the requirements of QoT and impairment modeling. Then, by reviewing many ML-based modeling techniques, we analyze the advantages of applying ML methods for this task. Afterwards, we review and discuss various works for ML-based monitoring techniques for QoT/impairment estimation and failure management. Finally, we summarized the opportunities and challenges for the application of ML methods. Looking forward to the future, we can foresee a vital role played by ML-based mechanisms to build an intelligent optical network with high efficiency.