1. Introduction
Nature displays power laws in frequency distributions of diverse phenomena [
1,
2]. Scaling theories as expressed by power laws play an important role in quantification of scale invariance in Earth systems. From the classical study of earthquakes to complex geosystems analysis, the appearance of power law behavior has been seen as the signature of hierarchy. The present study is part of a systematic attempt to examine the dynamics of earth system by implementing the generalized non-extensive statistical physics (NESP) formalism. Investigation of the scaling properties of a geomorphological system strongly suggests the development of complex systems associated with their dynamics [
3,
4]. To understand this scientific challenge, we apply modern statistical physics approaches to understand the dynamics of geomorphological effects.
Analyses of power-law behavior in earth systems frequently invoke self-organized criticality (SOC) [
1,
5] to explain evolution towards the observed hierarchical structure. Geomorphologists seek to understand landscapes evolution, landform history and dynamics and to evaluate changes through a combination of field observations, physical experiments and numerical modeling. Landscape dynamics is governed mainly by slope and fluvial processes both operating in a drainage network [
6], resulting after combining a large-amplitude climatic fluctuations along with tectonic uplift/subsidence activity. As a result the complex interaction between earth’s surface and tectonic processes plays a key role in geomorphological evolution [
7]. Tectonic activity generates complex relief that controls surface processes such as erosion patterns, drainage network development, sedimentary basin growth, and local climate [
8,
9,
10,
11,
12]. Moreover, erosion, transport and sedimentation induce large mass transfer that changes the dynamical equilibrium of orogenic wedges and trigger mechanical actions [
8,
13]. The continuous evolution of the aforementioned processes, in a dynamical non-linear feedback indicates a system in a dynamical non-equilibrium stage where long-range interactions and memory effects are dominant.
In this context, geomorphologists have studied the evolution of drainages in time and found it to be driven by local conditions due to erosion, natural damming, tectonic motion, as well as volcanic activity [
14,
15,
16]. A drainage basin is an area of land that drains all the streams and rainfall to a common outlet such as the outflow of a reservoir, mouth of a bay, or any point along a stream channel. Drainage basins as conceptual or physical entities are used in water management [
17,
18], landsliding processes control [
19] and flood control [
20,
21].
According to Strahler and Strahler [
22], the development of a drainage system (i.e., a stream network and its drainage basin) can be described as follows: Initially, the stream is established on a land surface dominated by landforms of tectonic activity. In a next stage, the channels are deepening due to gradation resulting in steep gorges while the stream tributaries extend into the land carrying out a drainage basin and transforming the landscape into a fluvial landform system. Moreover, after reaching a state of balance (i.e., the supply of load becomes equal to the capacity of the stream to transport it), the stream continues to cut laterally its banks resulting in an extension of the drainage basin. The quantification of drainage geometry aims to study the underlying organization and to offer an insight to the physical processes controlling their evolution. Cumulative area distribution is a geomorphologic measure that characterizes the drainage basin hydrology and is widely used by geomorphologists to characterize the possible existence of their scale invariant structure and the scaling properties of the drainage area [
23,
24,
25,
26].
Recently, non-extensive statistical physics [
27,
28] have been becoming a valuable framework for interpreting geo-environmental complex systems [
29,
30,
31,
32,
33,
34,
35]. Drainages obtain long range interaction, multi-fractality and present a memory of the geological and physical processes involved in their evolution. Since memory and fractality are two of the key components of any geophysical process [
36,
37,
38] we can use a current generalization of Boltzmann-Gibbs (BG) statistical physics, referred as non-extensive statistical physics (NESP) [
27,
28,
36] to justify the hierarchy pattern presented in drainage area distribution.
The advantage of considering the Tsallis distribution [
28] is that, based on the fundamental principle of Tsallis entropy, scaling laws observed in phenomena that present fractality, long range interaction and memory effects [
27,
28] could be interpreted. We note that recent applications to solid earth physics (in regional or planetary scale) [
31,
32,
33,
37] and to natural hazards [
29,
30,
38] supports the applicability of non-extensive statistical physics in complex geosystems. To our knowledge, this is the first time that Tsallis entropy is used to express and interpret the drainage basins area distribution, within an effort to present scaling laws as extracted from first principles and not in an empirical basis. Scaling theories play an important role in quantification of scale invariance in geosystems, since the appearance of power-law behavior has been seen as the signature of scale invariance.
Our motivation is to suggest a new view of scaling laws observed in drainage basins of Greece in terms of Tsallis entropy. A connection between the observed power law exponent and the Tsallis entropic parameter is suggested. To demonstrate the hierarchy observed in drainage area statistical pattern, data sets for all drainages all over Greece, along with subsets of drainages in the internal and external Hellinides, that are the main tectonic structures in Greece, are constructed. Since the topographic relief is a crucial parameter in drainages formation, we classify them according to the mean value of the Topographic Position Index (TPI) and the mean elevation. Finally, the observed hierarchy within each one of the sub-datasets, is interpreted according to non extensive statistical physics. We clarify that the zonation used is the external input in our analysis, as introduced by geotectonic and geomorphological critiria. We note that the selection of TPI and of mean elevation is based on their simplicity as geomorphological measures that control a number of phenomena (e.g., erosion).
The remaining of this presentation is organized as follows. A procedure of data extraction using Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model Version 2 (GDEM V2), images is presented in
Section 2. A brief presentation of the NESP formalism will be given in
Section 3, followed by a presentation of the hierarchical drainage basin analysis applied power law formulation and along with NESP expressions. The analysis as presented in
Section 4, will focus on the drainage data set of Greece along with the subsets created by the classification of drainages in the geotectonic frame of internal or external Hellenides or using classifications based on topographic criteria as that of mean elevation or the mean Topographic Position Index (TPI).
Section 5 is devoted to the discussion of the results and to the presentation of a possible origin of the deviation from power law observed in a number of cases for large drainage area. Finally, it shall be demonstrated that drainage systems are sub-additive systems with significant long range interaction where non-extensive statistical physics could be used to understand the observed hierarchical processes.
2. Drainage Basins Extraction
It is obvious that drainage basins statistical characterization is critical for understanding the geomorphic processes.
During the last decades, geographical information systems (GIS) coupled with digital elevation models (DEMs) have been widely used for the automatical extraction of drainage networks and drainage basins as well as for landforms classification [
39,
40]. In the present work, ASTER GDEM v2, is used as downloaded from the LP DAAC at one arc sec resolution (30 m) [
41]. In comparison with other free DEMs, Aster GDEM has lower RMS errors in mountainous areas [
42,
43] and since Greece is such an area we decided to use it for the watersheds extraction. Aster GDEM was clipped to the extent of the study area of Greece and re-projected to the Hellenic Geodetic Reference System ‘87 (HGRS’87). Using ArcHydro, an extension of ArcGIS software, we were capable to efficiently delineate the drainage basins of Greece. The procedure used is as follows: firstly, the cells with elevation values abnormally low or high in comparison to their neighboring cells (known as sinks or spikes respectively) were removed. After the removal of the erroneous data, a new, hydrologically corrected (i.e., free of sinks and spikes), digital elevation model, was obtained [
44]. After that, a flow direction computation using the commonly used D8 algorithm [
45] was applied. D8 flow direction is an integer raster whose values range from 1 to 255 providing 8 different directions. It is then analyzed to find all sets of connected cells that belong to the same drainage basin. The drainage basins are delineated within the analysis window by identifying ridge lines. The drainage basins of the Greek territory were extracted in the form of a raster layer which was later converted to a vector polygonal one, containing a few thousands of basins.
From these basins only that with an area greater than 0.1 km
2 (
Figure 1) were selected for further analysis based on visual comparison with the national drainage basins dataset. For the area distribution analysis, the final drainage basin dataset was extracted into several layers (sub-datasets) according to different attributes and spatial characteristics such as, the geotectonic environment, the mean elevation value, and the mean topographic position index using the “select by attributes” and “select by location” functions of ArcGIS software.
3. The Principles of Non-Extensive Statistical Physics as Applied in Drainage Systems
A number of earth physics effects in different spatial and temporal scales, which includes rock and material properties, natural hazards, earthquake mechanics, plate tectonics, geomagnetic reversals and geological faults, have been interpreted in terms of the non-extensive statistical mechanics (NESP) view [
36]. Here we recapitulate the main principles of NESP in which a cornerstone is the introduction of the non-extensive Tsallis entropy Sq [
28] in terms of the probability distribution p(A) of a fundamental geometric parameter, A that in our case could be the watershed area A:
where k
B is Boltzmann’s constant. The index q is the degree of non-additivity. In the limit q→1, Sq→S
1 and the approach reduced to the well-known Boltzmann-Gibbs (BG) entropy, with which the Tsallis entropy shares many common properties [
28]. However, simple additivity is violated, because for a system composed of two statistically independent systems, U
A and U
B, the Tsallis entropy satisfies:
The last term on the right hand side of this equation describes the interaction between the two systems and is the origin of non-additivity. The index q accounts for the memory, multifractality and long-range interaction between the elements (drainages) of the analyzed set, and for q < 1, q = 1 and q > 1 respectively correspond to super-additivity, additivity and sub-additivity. This is the fundamental principle of non-extensive statistical mechanics.
In order to estimate the expected probability distribution p(A) of the drainage area A, in terms of NESP, we maximized the non-extensive entropy under the appropriate constraints, using the Lagrange-multipliers method with the Lagrangian [
28,
34,
37]:
The first constraint used refers to the normalization condition that reads as:
Introducing the generalized expectation value (q-expectation value), <A>
q which is defined as:
where the escort probability is given in [
28] as:
the extremization of Sq with the above constraints yields to the probability distribution of p(A) as [
34]:
where
is a normalization coefficient. We recall that the Q-exponential function introduced in NESP by Tsallis (2009) is defined as [
28]:
The normalized cumulative number of drainage with area greater than A can be obtained by integrating the probability density function p(A) as:
where N(>A) is the number of drainages with area larger than A. In the latter expression, if we define
, this leads to:
having a typical Q-exponential form.
In the frame of non extensive statistical mechanics approach for drainage with a quite large area where
Equation (4) leads to a power law description of the cumulative distribution function
with an exponent
in agreement with the power law extensively used to describe hierarchical drainage systems [
23,
25,
26,
46,
47].
4. Hierarchical Drainage Basins Analysis
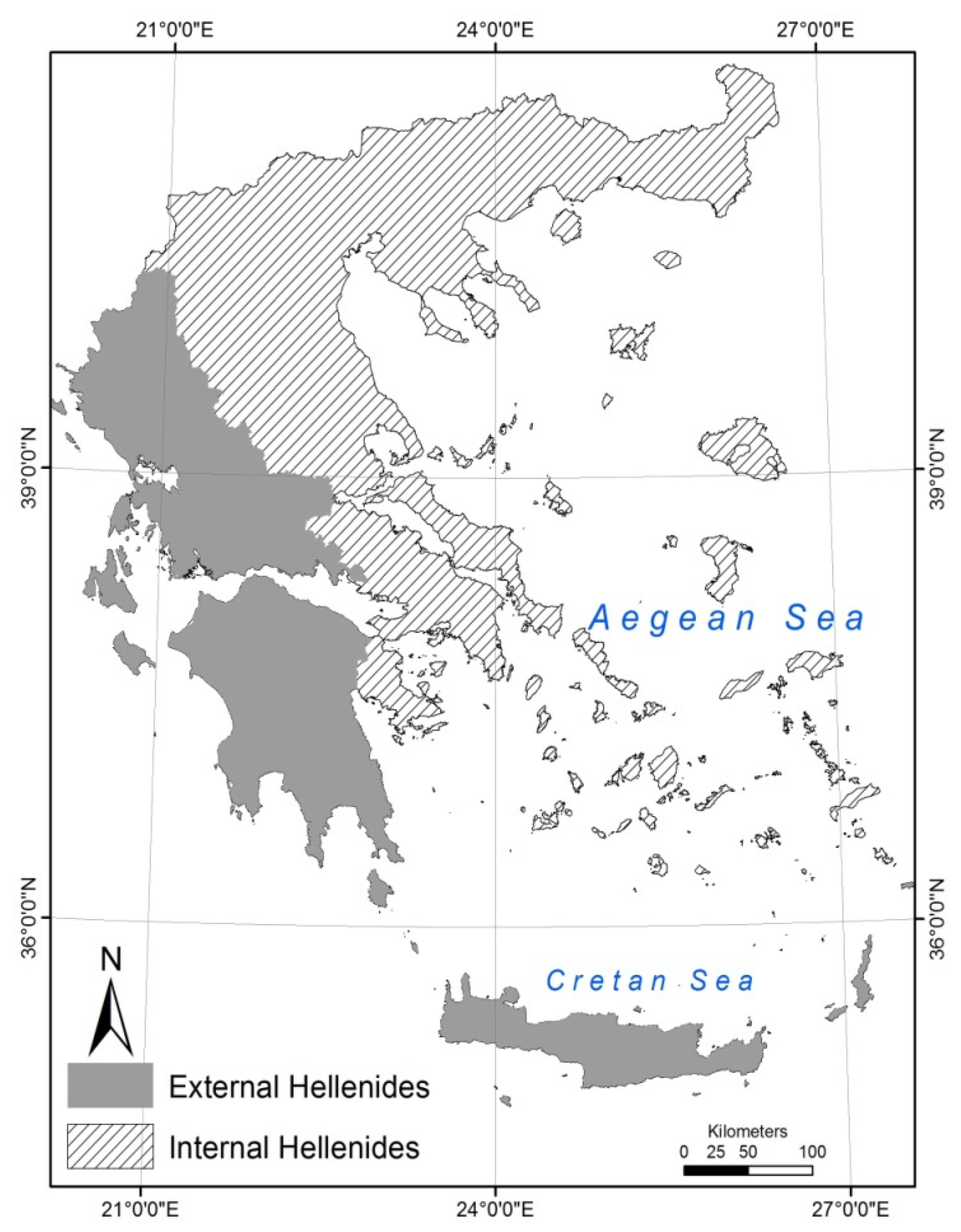
Here the drainages of Greece were selected and analyzed according to their tectonic regime, mean elevation value and mean value of Topography Position Index (TPI). In terms of geotectonics, a distinction between the non-metamorphic External Hellenides of western Greece on the one hand, characterized by Triassic-Cenozoic sedimentary sequences, and the Internal Hellenides of eastern Greece on the other, with metamorphic zones of pre-Alpine formations (
Figure 2) is used, in order to see the watershed distribution pattern in this two main geotectonic units that form Greece. The External Hellenides mainly consist of Meso- and Cenozoic sedimentary rocks deposited in a series of platforms (Pre-Apulian and Gavrovo zones) and deep basins (Ionian and Pindos zones) that formed the eastern rifted margin of the Apulian plate, bordering towards the east the Pindos Ocean [
48,
49,
50]. These units were developed during Tertiary times following the closure of the Pindos Ocean and the consequent continent–continent collision between the Apulian and Pelagonian micro-continents to the east [
51,
52]. This process induced the inversion of Mesozoic basins in the northern margin of Apulia as well as the formation of a series of thrust sheets comprising the External Hellenides thrust belt ([
48] and references therein). To search the possible connection of drainages hierarchy with the geotectonic environment as indicated in a number of previous works [
21,
23,
24,
46,
47] we select to search the drainage distribution in the two drainage subsets defined by the two main tectonic patterns of Greece.
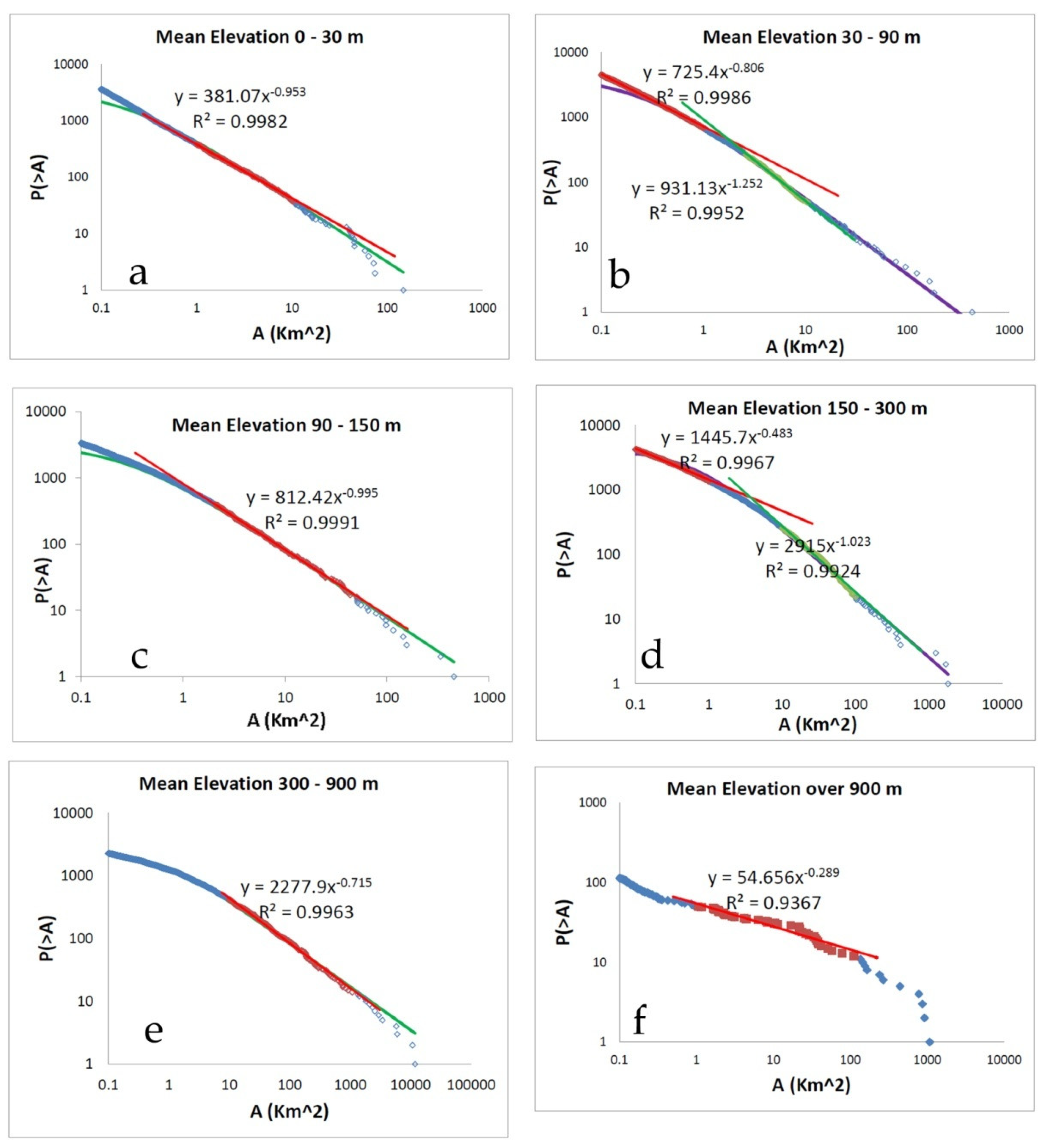
Moreover, having in mind that different elevation values may reflect different landscape dynamics probably affecting the drainage basins area distribution, zonal statistical analysis was performed on all the cells of GDEM that belong to each one drainage basin (i.e., zone). In this way, we obtained the mean elevation value of all the drainage basins in Greece. The latter were classified in 6 classes according to their mean elevation: 0–30 m, 30–90 m, 90–150 m, 150–300 m, 300–900 m and over 900 m (
Figure 3). The range of each class was adopted from Hammond’s 1964 methodology for classifying and mapping landforms [
53].
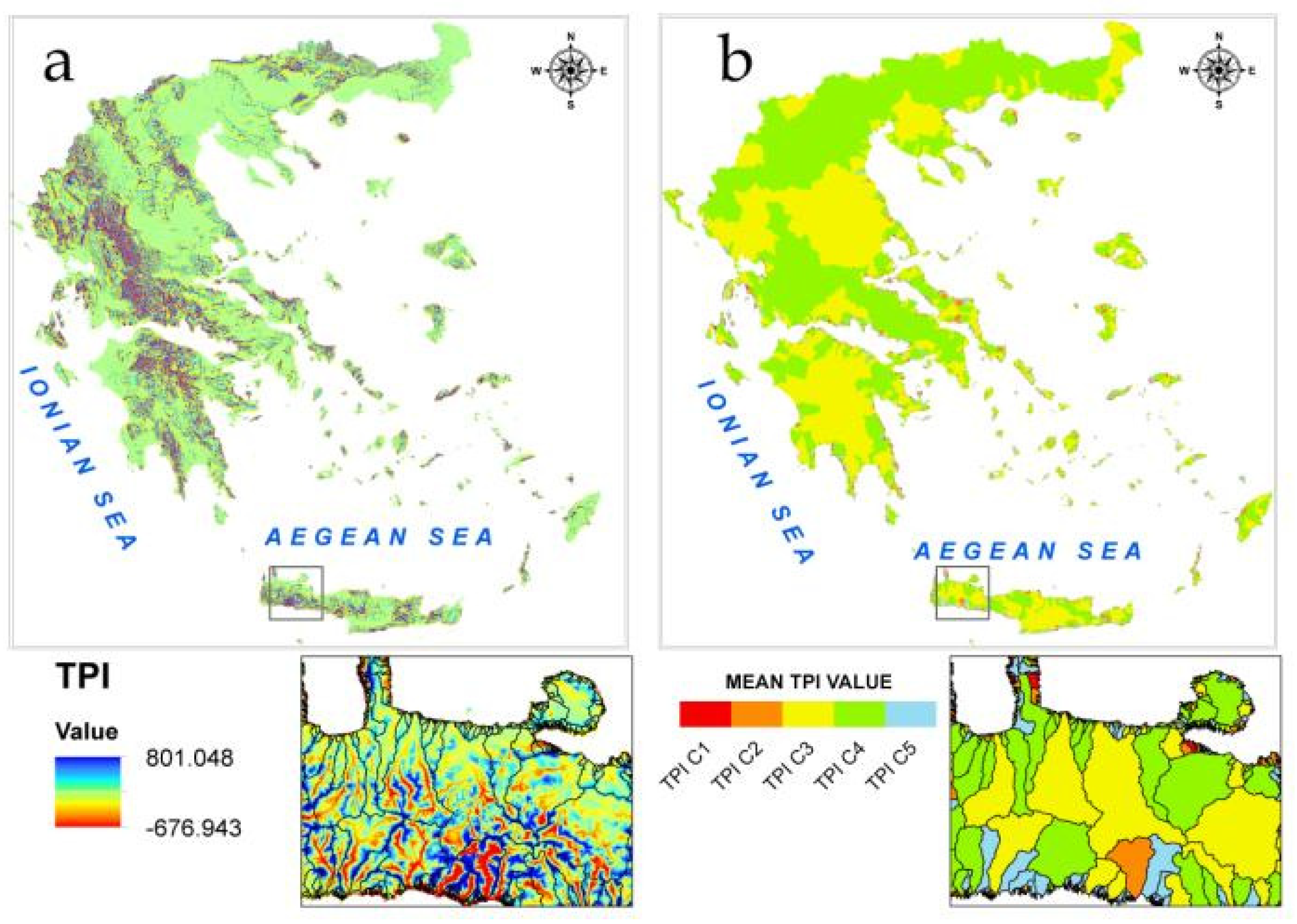
Furthermore, the size distribution of Greek drainages classified in several classes according to their mean value of the Topography Position Index (TPI) [
54] is given. The latter is a morphometric parameter derived from DEM and therefore an objective quantitative way of landform classification and watersheds characterization. The topographic position index (TPI) was introduced by Weiss (2001) as a GIS application for landform classification as well as watersheds characterization [
55]. The creation of an ESRI ArcView 3.x extension by Jenness in 2006 [
54], led to a broad application of TPI in several scientific fields, such as geomorphology [
56,
57]; geology [
58]; hydrology [
59]; geoarchaeology [
60] risk management [
61]. The TPI is defined as:
where M
0 is the elevation of the model point under evaluation, M
n the elevation of grid, and n the total number of surrounding points employed in the evaluation.
TPI compares the elevation of each cell in a DEM to the mean elevation of a specified neighborhood around that cell. Mean elevation is subtracted from the elevation value at center. The neighborhood size is substantial for the analysis and is related to the scale of landscape feature being analyzed. To identify large landforms, a large circular neighborhood is proposed [
56]. Choosing the correct neighborhood is an iterative process with several trials before the most appropriate size of neighborhood is decided. In this study, TPI generated from 2000 m neighborhoods due to the extended spatial coverage of the study area. Positive TPI values represent areas that are higher than the average of their neighborhoods (ridges), while negative TPI values represent locations with less elevation than their neighborhood (valleys). TPI values near zero are characterized as flat areas or areas of constant slope. The mean TPI value was further calculated for each drainage basin unit. At the scale of 2000 m, TPI reflects the broader valley morphology and the relative relief of streams and their surrounding topography. Drainage basins with higher mean values have a high proportion of streams in relatively deeper and narrower drainages, with narrowness defined by the spatial scale of the index [
55]. For the area distribution analysis we obtained 5 classes of drainage basins with different mean TPI values using the quantile classification method (
Figure 4a,b).
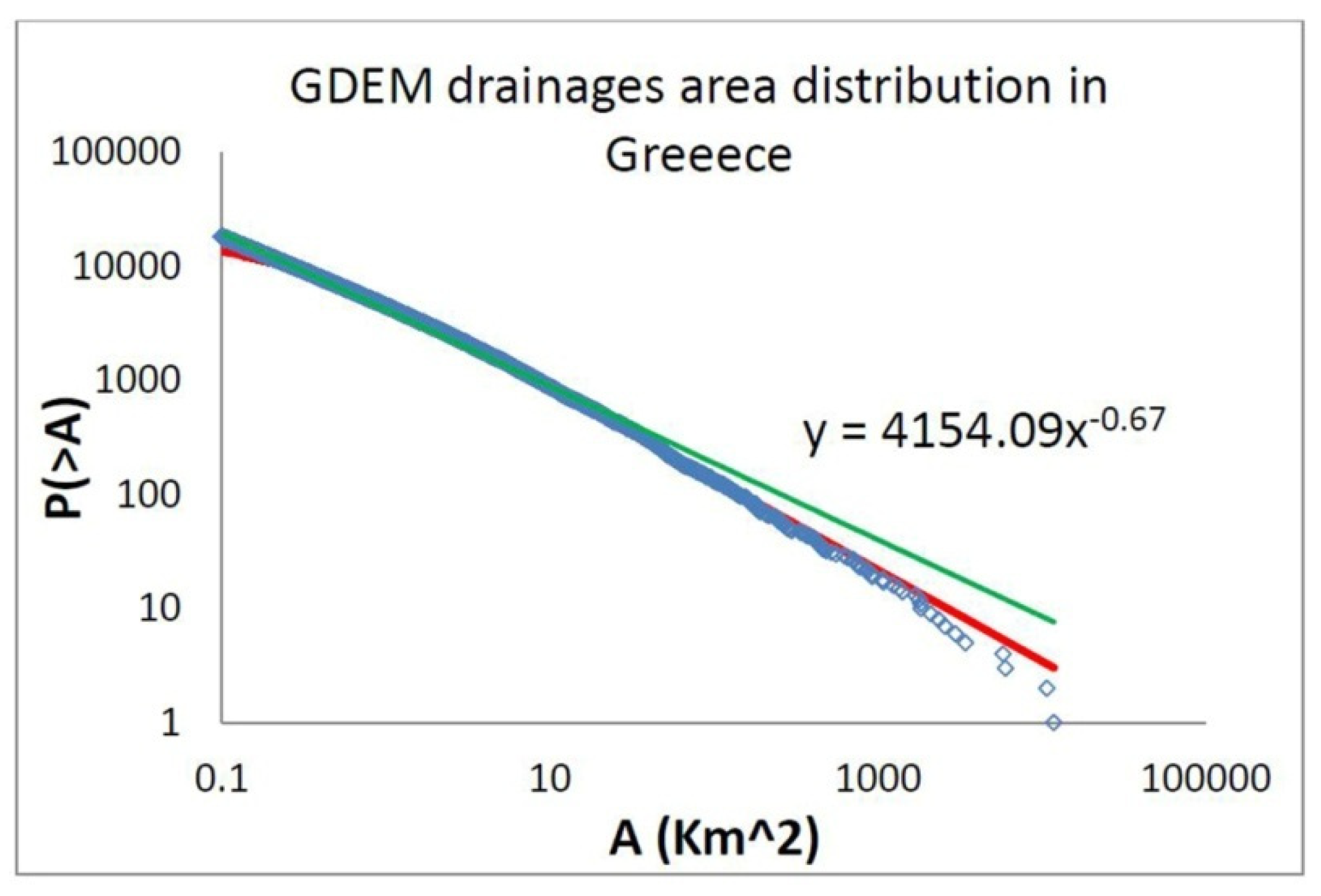
As a first step in our analysis we present the cumulative drainage area distribution for all the territory of Greece (
Figure 5). As
Figure 5 presents a power law scaling of the form [
2]
where N(>A) is the number of drainages with area greater than A, is observed with β
all≈0.67, with a deviation from power law to observed for large drainage areas.
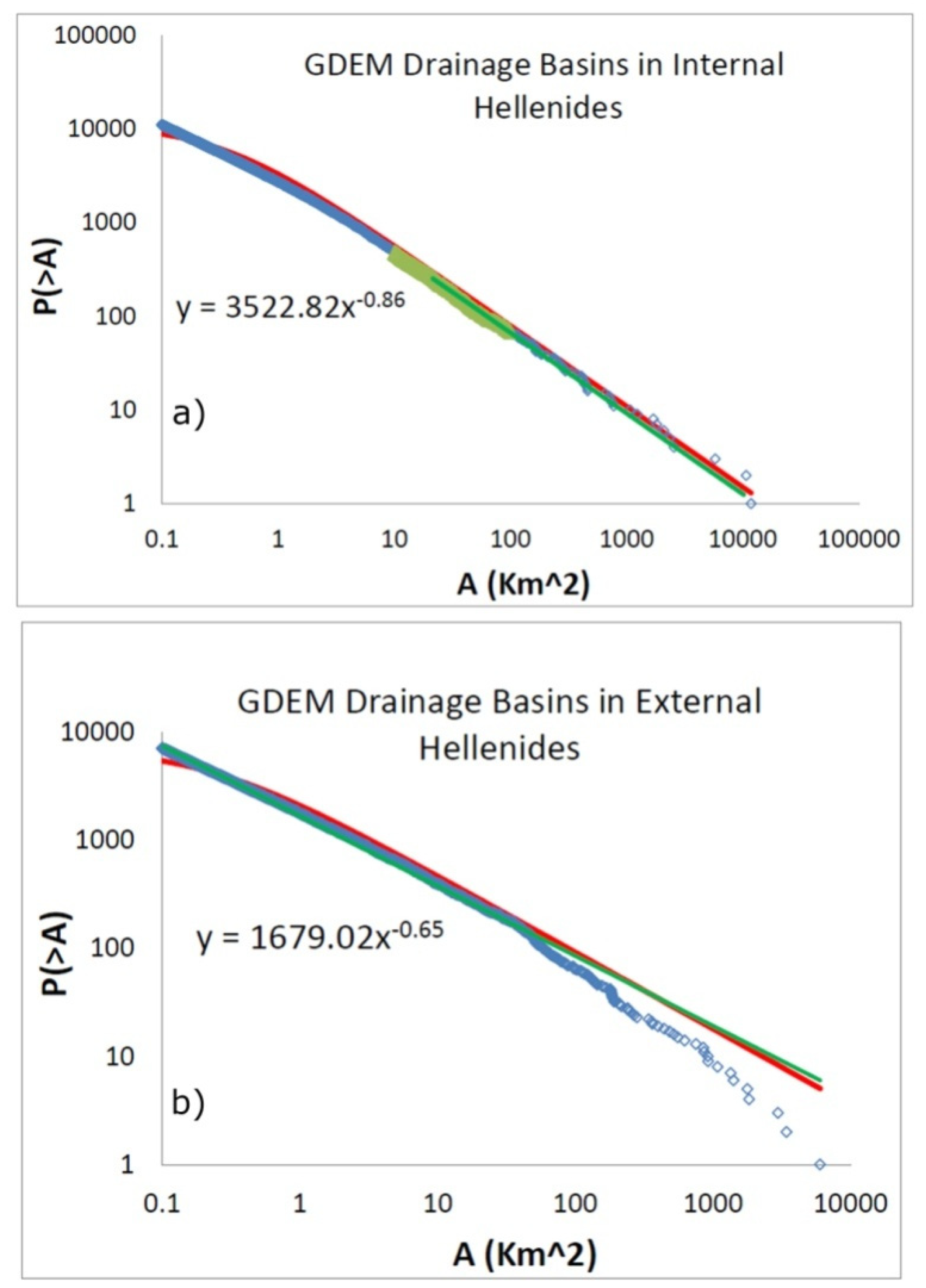
A power law (see Equation (6)) fits the data for both the data sets organized for the drainage areas in external and internal Hellenides, respectively, implying a hierarchical organization of drainage basins. For each one of the cases we have β
ext ≈ 0.65 and β
int ≈ 0.86 (see
Figure 6a,b). For the case of External Hellenides a deviation of observation from power law is observed for large drainage areas, i.e., for A > 100 km
2.
In
Table 1 we present the power law exponent β observed for each of the six elevation classes defined (
Figure 7).
In
Table 2 we present the power law exponent β observed for each of TPI defined classes (see
Figure 8).
All the above mentioned distributions are analyzed in terms of Tsallis entropy estimating the q-entropic index characterizing the distribution. To estimate the q value (or equivalently the Q one) we fit all the observed drainage areas distributions with Equation (4). In
Figure 5 and
Figure 6 the Q-exponential fitting leads to the Q (and equivalently q) values that describe the drainage distribution as Q
all ≈ 2.41, Q
int ≈ 2.16, Q
ext ≈ 2.45 or equivalently q
all = 1.58, q
int = 1.54 and q
ext = 1.59, for all the drainages of Greece, and for that in the internal and external Hellenides, respectively. Since the theoretical β value is given as
the calculated β values using the Q estimates are
≈0.71,
≈0.86 and
≈0.69 for the drainages all over Greece, and for that in the internal and external Hellenides, respectively, in agreement with that estimated fitting an empirical power law in the distribution. The same procedure is repeated for all the data subsets created by the classification of the Greece drainages. In
Table 1 and
Table 2 the Q and q parameters along with the
values are given.
5. Discussion
In the present work we study the hierarchical pattern of drainages area distribution in Greece as extracted from an ASTER GDEM v2 Digital Elevation Model, offering a 30m resolution, enabling the creation of an accurate drainage basins’ database within a GIS environment. The power law exponent β for classification of drainages based on a) the geotectonic pattern and b) on topographic characteristics are estimated. Our analysis, demonstrate that an empirical power law distribution could be used to describe, as a first approximation, the drainages’ area distribution. We study the drainage basin area-frequency distribution in the set of Greek drainages along with the subsets constructed applied different geological or geomorphological criteria. The hierarchy pattern observed for the drainage’s areas not only for all the Greece but also for the subsets of drainages in the internal and external Hellenides that are the main tectonic structures in Greece, and the drainages classified according to their elevation or the Topographic Position Index (TPI), was presented.
Furthermore the feasibility of the non-extensive statistical physics applied to the size distribution of the drainages areas is demonstrated. The estimation of the entropic parameter q which is mainly in the range 1.45–1.55, indicates a sub-additive system, with significant long range interactions. Within the view of Tsallis entropy we extract as a first approximation of Q-exponential a power law of the form
with Q the non-extensive parameter extracted from the fitting of observations with a Q-exponential. The Q parameter is related with the q entropic Tsallis parameter introduced in the definition of Tsallis Entropy as
Following NESP, the Greek drainage system could be seen as a drainage set organized by the merging of different sub-systems, according to the classification used. In view of Tsallis statistics formulation for non-extensive systems composed of non-extensive subsystems having different Q’s it is proposed in [
62] and references therein, that enables to estimate the behavior of a composite system containing subsystems, each having its own Q, using the expression [
62]:
where Q
i the Q-exponential parameter and Ni the number of elements (drainages) in each of the sub-sets formed the composite one. In this frame the Greek drainage system could be viewed as containing two Q-exponential subsystems with different Q’s as the external and internal Hellenides drainage sets are. Since Q
int < Q < Q
ext an estimation of Q is given
the number of drainages in each subset. Substituting the values of Q
int and Q
ext we lead to Q = 2.30 in a good agreement with Q ≈ 2.41 obtained with fitting a Q-exponential for all the Greek drainage system.
We now discuss the possible origin of the deviation from the power law observed in a number of cases for large values of drainage area A, where an exponential tail (i.e., q = 1) observed. According to NESP the generalized probability distribution
can be obtained by solving the nonlinear differential equation
while Boltzmann-Gibbs (BG) are approached, with the BG entropy optimized when q = 1.
We now use the above differential equation path in order to further generalize the anomalous equilibrium distribution, in such a way as to have a crossover from anomalous (q ≠ 1) to normal (q = 1) statistical mechanics, while increasing the drainage’s area. Following [
63] we consider the differential equation
whose solution is
where C is a normalization factor. For positive β
q and β
1, p(A) decreases monotonically with increasing A. It can be easily verified that in the case where β
q >> β
1, equation (7) defines three regions, according to the area A of the drainage. We will call these “drainage regions”, small, intermediate and large drainage area regions, respectively. The asymptotic behavior of the probability distributions in these areas is
where A
c1 and A
c2 are the cross-over points between the three regions.
The observed crossover from hierarchical (q ≠ 1) to exponential (q = 1) pattern, with increasing of the parameter A deserves special attention. In this case, in equation (7) expanding the exponential term in it can be easily concluded that in the case where
the asymptotic behavior of the probability distributions simplified as a q-exponential
while
where Ac is the crossover point between the hierarchical (q ≠ 1) to exponential (q = 1) statistical mechanics. Equation (8a) leads to the q-exponential of Equation (6) for a cumulative distribution function
. The latter Equation (8a,b) explain the q-exponential description of the distribution of drainage areas along with the exponential tail observed in some of the cases, as a result of generalized non-extensive statistical mechanics.
Here we state that the estimation of the entropic parameter q which is mainly in the range 1.45–1.55, indicates a sub-additive system, with significant long range interactions. The q non-extensive parameter increases as the mean elevation increases, implying that watersheds in higher elevations interact stronger than those of lower mean elevations. These strong interactions are probably related to the limited space in which they have to be developed. As a result, the area distribution between smaller and bigger basins follows a hierarchical pattern. On the other hand, watersheds of low elevation are more sensitive to tectonic (presence of faults), climatic (precipitation) and antropogenic (land use changes) factors.
As for the q parameter extracted from the TPI subdata sets, there is an obvious increase from class 1 (big negative values, showing watersheds that are relatively deeper and narrower with a broader valley morphology) to class 2 and class 3. According to [
55] watersheds of class 1 can be more sensitive to drainage wide deforestation and land use, and would likely have a stronger response to extreme weather and snowmelt events. This fact is in a good agreement with a q equal to 1.275. As the TPI values increase to class 4 and class 5, the q parameter value decreases, implying weaker interactions between basins of a broader ridge topography. The biggest q value has been estimated for class 3 (nearly flat areas or areas of constant slope) indicating that in such environments of small roughness the systems are well organized with their area distribution to follow a hierarchy (mature or old drainage basins?).
6. Concluding Remarks
Summarizing we can state that the use of non-extensive statistical physics is a suited tool to describe the drainages frequency-size (area) distribution. The obtained distribution function incorporates the characteristics of non-extensivity into the cumulative distribution of drainages’ areas and explains the observed power law behavior fitting the observed data. The presence of deviations from the power law for large areas in the frequency distribution can be regarded as the manifestation of the physical foundation of the generalized non-extensive Tsallis entropy, where the deviation of distribution from power law for large drainages area is discussed in terms of generalized non extensive statistical mechanics, introducing two mechanisms that describe hierarchical and exponential patterns. The latter implies two main mechanisms applied to form the geomorphological drainage pattern. The first one for the intermediate size drainages where a power law applies and a second one for the large drainage areas, where a significant lower frequency observed compared with that calculated by the power law extrapolation. In addition our work contributes, supporting the ideas of scaling and universality in geomorphology as presented in [
64,
65] using an entropic approach as presented in [
28].
Note that the proposed scaling is not an empirical guess for the drainages size distribution but derived from the first principle of non-extensive entropy formalism, which is completely universal and has a long range of application [
28,
34,
36]. The physical meaning underlying the non-extensive entropy formalism is that the final physical state can be considered as a collection of interacted parts which, after division, have the sum of individual entropies larger than the entropy of the initial state in a similar way as pointed out for landslides and rockfalls [
29,
30,
38]. The latter is straightforward from the concept of not additivity since [
28,
29,
36,
38,
62].
Finally, since drainage systems consists of many non-independent subareas, the non-additivity index q (q > 1) could be interpreting as an approximate measure of the long-range interactions within the drainage system. The scaling properties studied in this work and in the theory developed in order to explain the experimental evidence of power law distribution it is expected to be applied in hydrological applications and it could be proved significantly helpful for geomorphologists and engineers in order to validate water flows within a drainage basin.