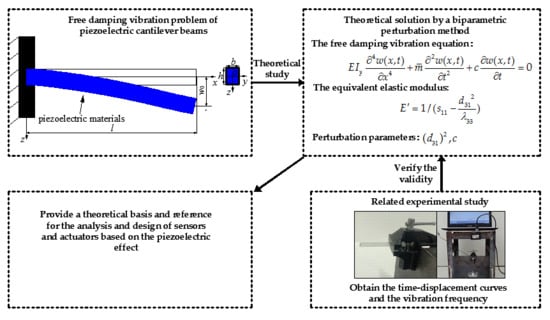
Free Damping Vibration of Piezoelectric Cantilever Beams: A Biparametric Perturbation Solution and Its Experimental Verification
Abstract
1. Introduction
2. The Basic Equations and Biparametric Perturbation Solution
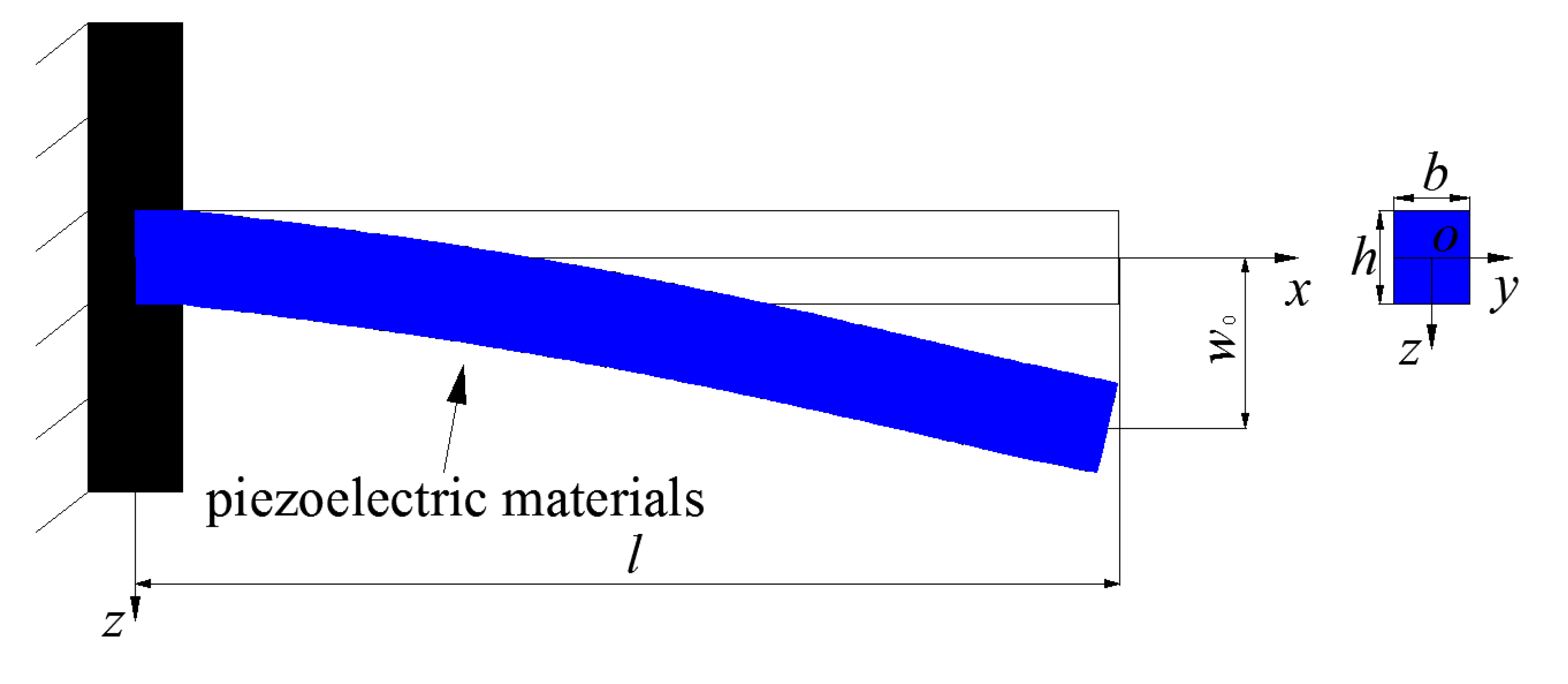
2.1. The Mechanical Model and Basic Equations
2.2. The Biparametric Perturbation Solution
3. Comparison with the Existing Theory
4. Experimental Verification and Discussion
4.1. The Experiments of Piezoelectric Cantilever Beams
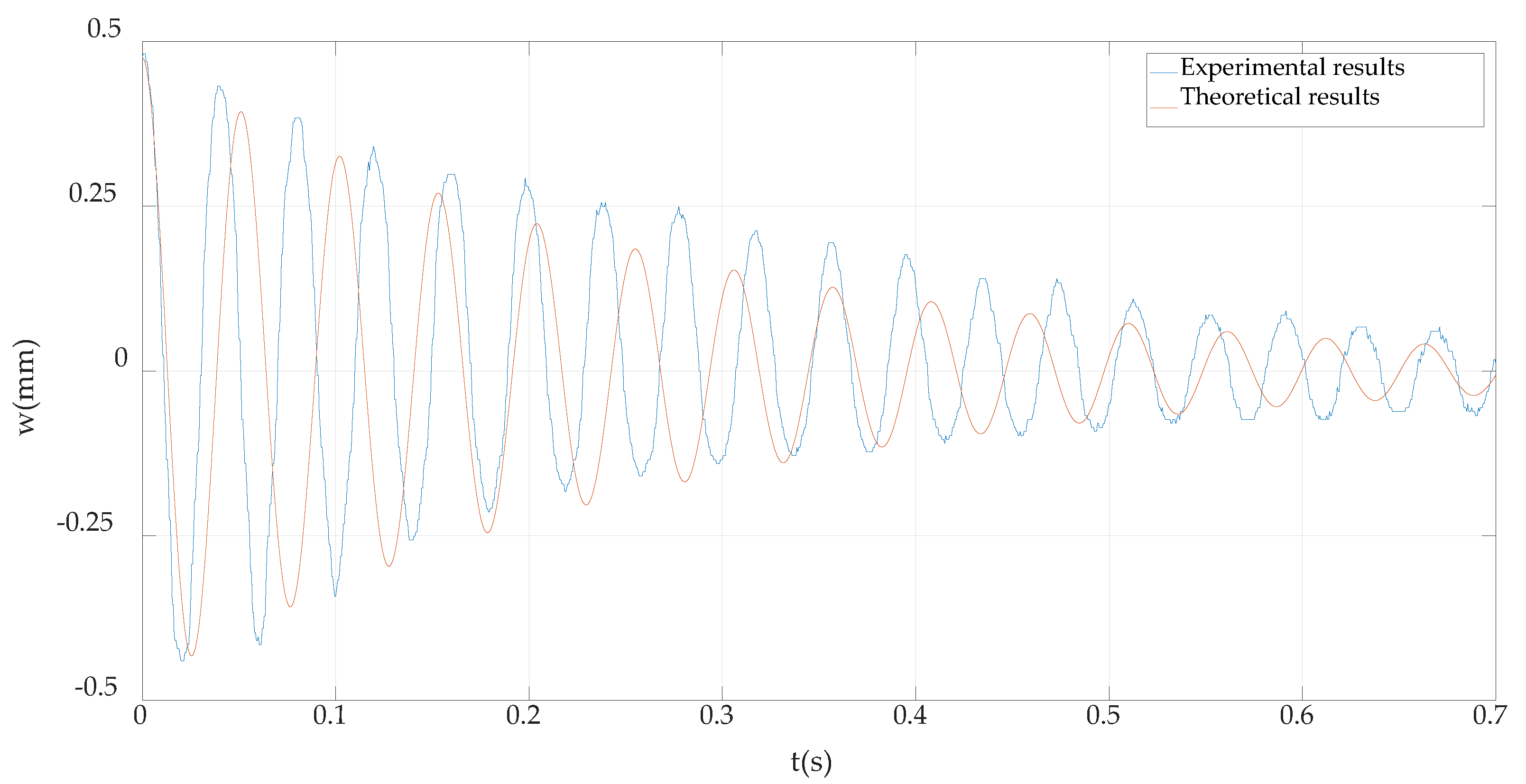
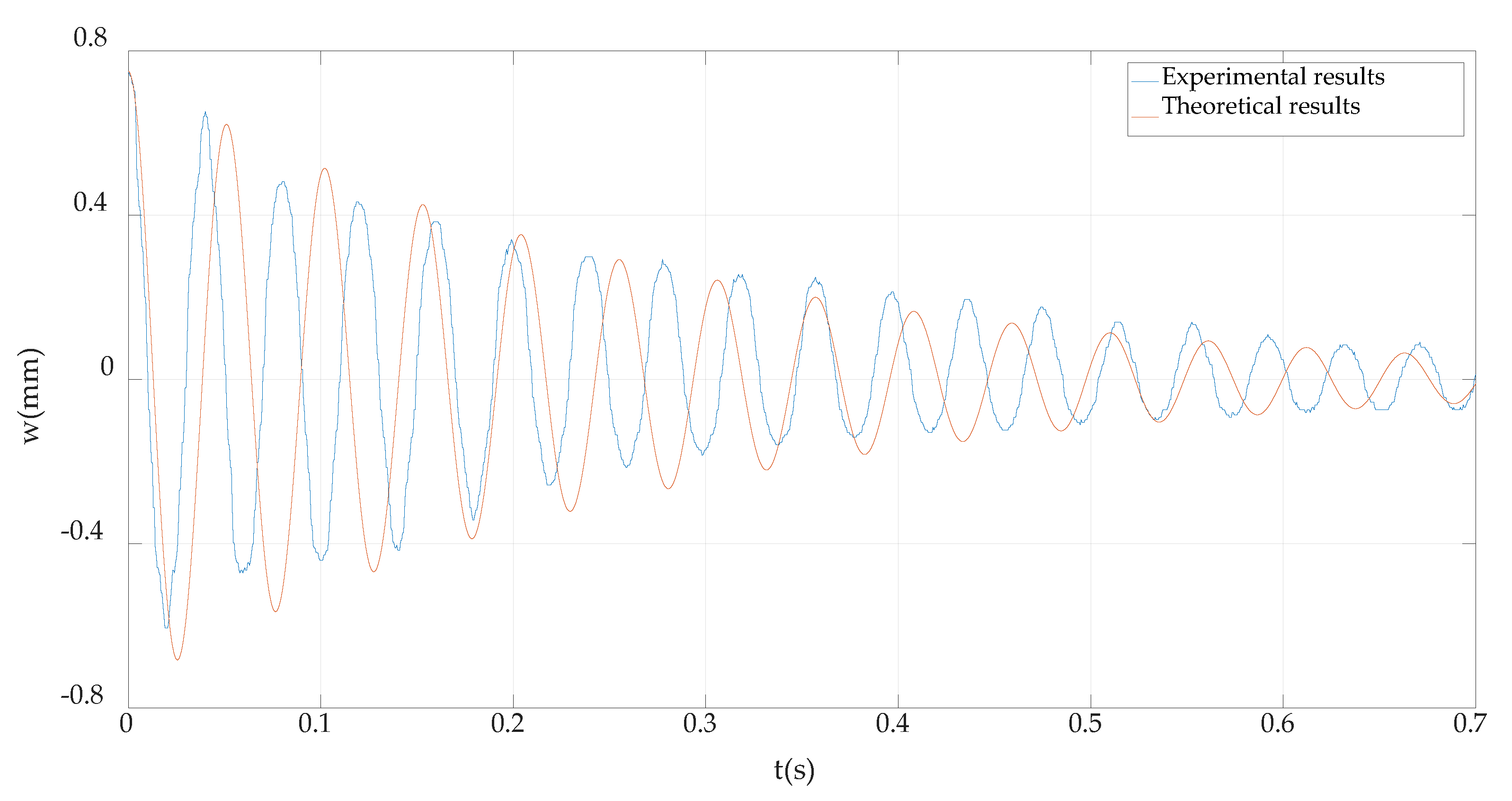
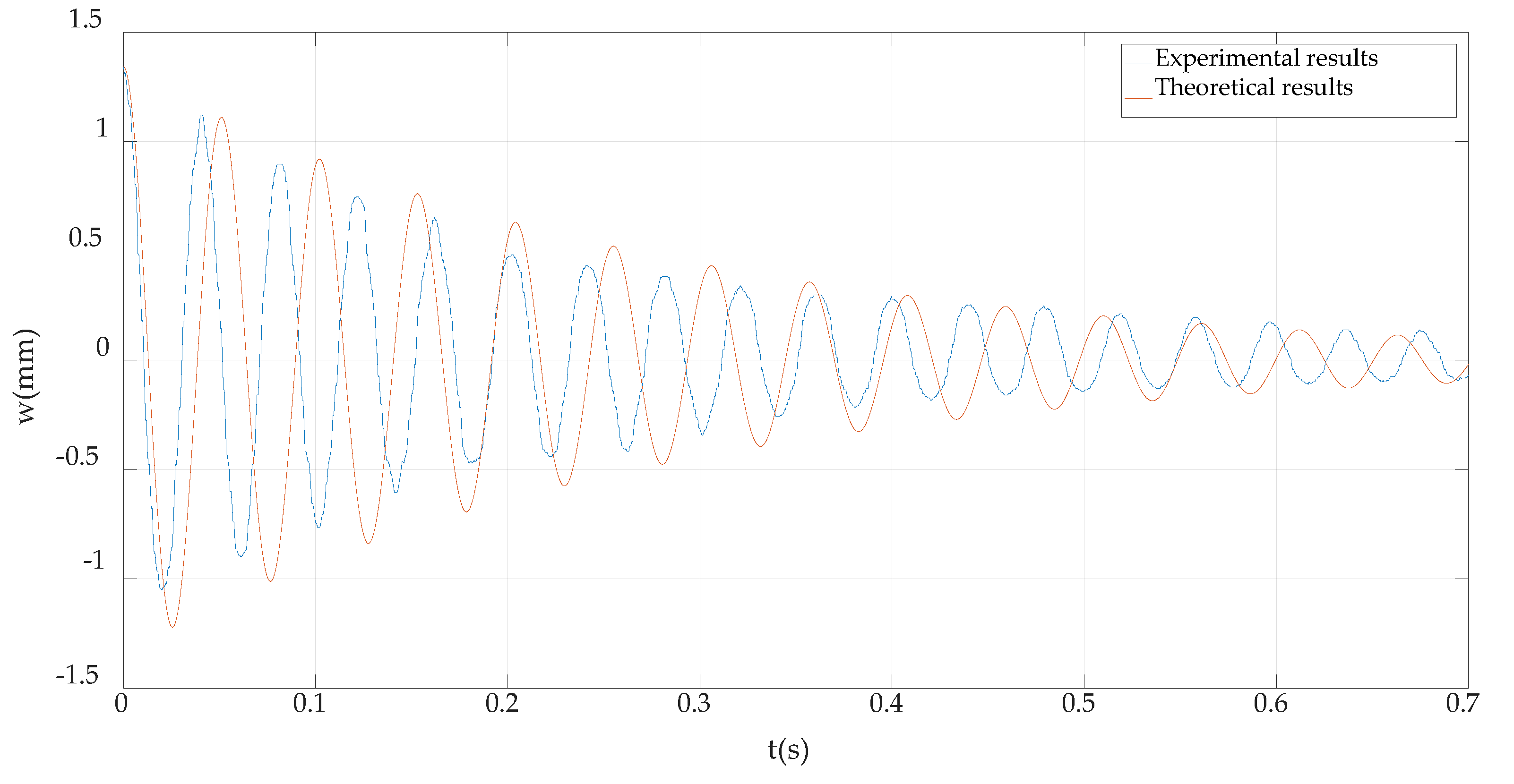
4.2. Comparison of the Experimental Results and Theoretical Results
5. Concluding Remarks
- (i)
- The theoretical solution given in this paper can be degraded to the existing vibration solution of the general cantilever beam, and the theoretical results are in good agreement with the experimental results. These indicate that the analytical solution given in this paper is correct, and the biparametric perturbation method used in this paper is effective.
- (ii)
- From Equation (11), it can be seen that the piezoelectric properties of the piezoelectric materials will increase the elastic modulus, which is usually known as the piezoelectric stiffening effect peculiar to piezoelectric materials and structures. As we all know, the greater the elastic modulus, the higher the vibration frequency. Thus, the piezoelectric properties will increase the vibration frequency of the piezoelectric cantilever beams.
- (iii)
- From the perturbation expansion, it is easy to find that the zero-order solution is the solution of the free vibration of the classical cantilever beam, without the piezoelectric properties and damping. The influences of the piezoelectric properties and the damping are reflected in the first-order and second-order perturbation solutions. The analytical characteristic and structural form of the perturbation solution are beneficial to the parameter analyses of the studied problem.
Author Contributions
Funding
Conflicts of Interest
References
- Holeczek, K.; Starke, E.; Winkler, A.; Dannemann, M.; Modler, N. Numerical and experimental characterization of fiber-reinforced thermoplastic composite structures with embedded piezoelectric sensor-actuator arrays for ultrasonic applications. Appl. Sci. 2016, 6, 55. [Google Scholar] [CrossRef]
- D’Annibale, F.; Rosi, G.; Luongo, A. Piezoelectric control of Hopf bifurcations: A non-linear discrete case study. Int. J. Non-Linear Mech. 2016, 80, 160–169. [Google Scholar] [CrossRef]
- Dell’lsola, F.; Maurini, C.; Porfiri, M. Passive damping of beam vibrations through distributed electric networks and piezoelectric transducers: Prototype design and experimental validation. Smart Mater. Struct. 2004, 13, 299–308. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Xu, T. A novel piezoelectric ceramic actuator with scissoring composite vibration for medical applications. Appl. Sci. 2019, 9, 4637. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Haris, S.M.; Nuawi, M.Z. Role of piezoelectric elements in finding the mechanical properties of solid industrial materials. Appl. Sci. 2018, 8, 1737. [Google Scholar] [CrossRef]
- Mahinzare, M.; Ranjbarpur, H.; Ghadiri, M. Free vibration analysis of a rotary smart two directional functionally graded piezoelectric material in axial symmetry circular nanoplate. Mech. Syst. Signal Process. 2018, 100, 188–207. [Google Scholar] [CrossRef]
- Przybylski, J.; Gasiorski, G. Nonlinear vibrations of elastic beam with piezoelectric actuators. J. Sound Vib. 2018, 437, 150–165. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Li, W. Dynamic analytical solution of a piezoelectric stack utilized in an actuator and a generator. Appl. Sci. 2018, 8, 1779. [Google Scholar] [CrossRef]
- Parashar, S.K.; Wagner, U.V.; Hagedorn, P. Nonlinear shear-induced flexural vibrations of piezoceramic actuators: Experiments and modeling. J. Sound Vib. 2005, 285, 989–1014. [Google Scholar] [CrossRef]
- Mukherjee, A.; Chaudhuri, A.S. Nonlinear dynamic response of piezolaminated smart beams. Comput. Struct. 2005, 83, 1298–1304. [Google Scholar] [CrossRef]
- Chen, M.F.; Chen, H.L.; Ma, X.L.; Jin, G.Y.; Ye, T.G.; Zhang, Y.T.; Liu, Z.G. The isogeometric free vibration and transient response of functionally graded piezoelectric curved beam with elastic restraints. Results Phys. 2018, 11, 712–725. [Google Scholar] [CrossRef]
- Dong, X.J.; Meng, G.; Li, H.G. Free vibration of stepped composite Timoshenko beam with piezoelectric materials. J. Vib. Eng. 2005, 18, 243–247. [Google Scholar]
- Li, S.R.; Su, H.D.; Cheng, C.J. Free Vibration of Functionally Graded Material Beams with Surface-Bonded Piezoelectric Layers in Thermal Environment. Appl. Math. Mech. 2009, 30, 907–918. [Google Scholar] [CrossRef]
- Oh, I.K.; Han, J.H.; Lee, I. Postbuckling and vibration characteristics of piezolaminated composite plate subject to thermo-piezoelectric loads. J. Sound Vib. 2000, 233, 19–40. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.F. A new method for free vibration analysis of piezoelectric-elastic laminated beams. Chin. J. Theor. Appl. Mech. 2008, 40, 564–571. [Google Scholar]
- Lu, Y.T.; He, B.W.; Guan, Q. Exact solution of dynamic for piezoelectric laminated beams. J. Anhui Jianzhu Univ. 2015, 23, 79–93. [Google Scholar]
- Chen, W.Q.; Lv, C.F.; Bian, Z.G. Free vibration analysis of generally laminated beams via state-space-based differential quadrature. Compos. Struct. 2004, 63, 417–425. [Google Scholar] [CrossRef]
- Kapuria, S.; Alam, N. Efficient layerwise finite element model for dynamic analysis of laminated piezoelectric beams. Comput. Methods Appl. Mech. Eng. 2006, 195, 2742–2760. [Google Scholar] [CrossRef]
- Chen, S.L.; Li, Q.Z. The FPPM solutions for the problems of large deflection of axisymmetric circular plate. J. Chongqing Jianzhu Univ. 2003, 25, 32–36. [Google Scholar]
- Lian, Y.S.; He, X.T.; Liu, G.H.; Sun, J.Y.; Zheng, Z.L. Application of perturbation idea to well-known Hencky problem: A perturbation solution without small-rotation-angle assumption. Mech. Res. Commun. 2017, 83, 32–46. [Google Scholar] [CrossRef]
- Nowinski, J.L.; Ismail, I.A. Application of a multi-parameter perturbation method to elastostatics. J. Theor. Appl. Mech. 1965, 2, 35–45. [Google Scholar]
- Chien, W.Z. Second order approximation solution of nonlinear large deflection problem of Yongjiang Railway Bridge in Ningbo. Appl. Math. Mech. 2002, 23, 493–506. [Google Scholar]
- He, X.T.; Chen, S.L. Biparametric perturbation solutions of the large deflection problem of cantilever beams. Appl. Math. Mech. 2006, 27, 404–410. [Google Scholar] [CrossRef]
- He, X.T.; Cao, L.; Li, Z.Y.; Hu, X.J.; Sun, J.Y. Nonlinear large deflection problems of beams with gradient: A biparametric perturbation method. Appl. Math. Comput. 2013, 219, 7493–7513. [Google Scholar] [CrossRef]
- He, X.T.; Cao, L.; Sun, J.Y.; Zheng, Z.L. Application of a biparametric perturbation method to large-deflection circular plate problems with a bimodular effect under combined loads. J. Math. Anal. Appl. 2014, 420, 48–65. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures; Wang, G.Y., Translator; China Science Publishing House: Beijing, China, 1981. [Google Scholar]
- Ruan, X.P.; Danforth, S.C.; Safari, A.; Chou, T.W. Saint-Venant end effects in piezoceramic materials. Int. J. Solids Struct. 2000, 37, 2625–2637. [Google Scholar] [CrossRef]


| Elastic Constant (10−12 m2·N−1) | Piezoelectric Constant (10−12 C·N−1) | Dielectric Constant (10−8 F·m−1) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| s11 | s12 | s13 | s33 | s44 | d31 | d33 | d15 | λ11 | λ33 |
| 16.4 | −5.74 | −7.22 | 18.8 | 47.5 | −172 | 374 | 584 | 1.505 | 1.531 |
| Initial Displacements (mm) | Vibration Frequency | ||
|---|---|---|---|
| Experimental Results (rad/s) | Theoretical Results (rad/s) | Relative Errors (%) | |
| 0.475 | 123.25 | 146.12 | 15.65 |
| 0.750 | 123.25 | 151.40 | 18.59 |
| 1.342 | 123.25 | 139.63 | 11.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.-X.; He, X.-T.; Peng, D.-D.; Sun, J.-Y. Free Damping Vibration of Piezoelectric Cantilever Beams: A Biparametric Perturbation Solution and Its Experimental Verification. Appl. Sci. 2020, 10, 215. https://doi.org/10.3390/app10010215
Yang Z-X, He X-T, Peng D-D, Sun J-Y. Free Damping Vibration of Piezoelectric Cantilever Beams: A Biparametric Perturbation Solution and Its Experimental Verification. Applied Sciences. 2020; 10(1):215. https://doi.org/10.3390/app10010215
Chicago/Turabian StyleYang, Zhi-Xin, Xiao-Ting He, Dan-Dan Peng, and Jun-Yi Sun. 2020. "Free Damping Vibration of Piezoelectric Cantilever Beams: A Biparametric Perturbation Solution and Its Experimental Verification" Applied Sciences 10, no. 1: 215. https://doi.org/10.3390/app10010215
APA StyleYang, Z.-X., He, X.-T., Peng, D.-D., & Sun, J.-Y. (2020). Free Damping Vibration of Piezoelectric Cantilever Beams: A Biparametric Perturbation Solution and Its Experimental Verification. Applied Sciences, 10(1), 215. https://doi.org/10.3390/app10010215