An Improved Dynamic Model of the Vanadium Extraction Process in Steelmaking Converters

Abstract

The production process from iron ore to steel can be divided into several stages, among which the processes of vanadium extraction and steelmaking are two key technological sections. The products of vanadium extraction are important strategic resources for modern industrial countries, and the remaining molten iron after vanadium extraction provides the material used in the subsequent steelmaking processes. In some mechanism models of vanadium extraction and the steelmaking process, the contact area of the reactions is considered to be constant in the empirical formula; furthermore, even the masses of the molten steel and slag are taken to be constants. This paper presents an important improvement to the existing models, in which the contact areas of the slag–metal interface and the emulsion system are considered to be non-constant. The improved model is simple and easy to analyze theoretically. Theoretical analysis of the model equations can be used to explain the competitive oxidation between each element, as well as the oxygen conservation of the system. The numerical simulations are consistent with existing production data, showing that the mass fraction of vanadium can be reduced to the specified threshold after about 3.5 min of blowing, which provides an important reference for production control. Furthermore, it is shown that the model captures the “trapezoid” structure of the decarburization rate. This paper also considers the relationship between FeO and O, the numerical simulation partly reflecting the dependence between the concentrations of FeO and O. The improved model can be used to describe and predict the change of the molten steel and slag composition in the process of vanadium extraction, which provides a mathematical foundation for the automatic control of the vanadium extraction process.

1. Introduction

Many researchers have studied mathematical models of the steelmaking process, aiming to predict and automatically control the complicated steelmaking process using computers. An appropriate mathematical model can help us understand the essence of the steelmaking process and improve the techniques used; this is the foundation of automatic control in the steelmaking process. China is one of the main countries which produces steel through vanadium extraction [1]. The Panzhihua Iron and Steel Group (PISG), located in the Sichuan Province, is one of the most important steel industry bases in China. The region is rich in vanadium–titanium magnetite, whose vanadium content accounts for 61% of the proven reserves in China [2].

The industrial uses of vanadium–titanium magnetite mainly includes vanadium extraction and steelmaking. At first, vanadium is extracted from the vanadium-containing molten steel in a converter, following which the resultant semi-steel is smelted to steel. Currently, the vanadium extraction process still depends on manual operation and control of the production relies on the experience of operators. Therefore, it is important to establish mathematical models to predict the changes of composition in molten steel and slag.

There have been many studies focused on mathematical models of the steelmaking process. Shukla et al. [3] studied the converter steelmaking process from thermodynamic and kinetic standpoints, obtained the reaction trend when the process was regarded at thermodynamic equilibrium, and compared it with the actual process. Takawa et al. [4] proposed a mathematical model that can be applied to an automatic blowing process and gave an estimate of the content of some components in the molten steel by sampling analysis of the blowing process. Reichel and Szekely [5] established a mathematical model of the AOD (Argon Oxygen Decarburization) and VOD (Vacuum Oxygen Decarburization) refining processes. According to their model, in the case of high carbon, the decarburization rate is proportional to the oxygen supply rate; while, in the case of low carbon, the decarburization rate is related to both the carbon content and oxygen supply rate. Johansson et al. [6] established a non-linear model to consider the estimation of carbon content in the process of steelmaking and proved that the error is locally asymptotically stable. Konno et al. [7] developed a general dynamic system simulator as a tool to analyze dynamic systems, represented by differential equations, difference equations, and algebraic equations. Han Min et al. [8] proposed an endpoint prediction model based on correlation vector machines to predict the carbon content and temperature of an oxygen converter. Fruehan [9] put forward some hypotheses on the oxidation mechanisms of C and Cr under different conditions and developed a reaction model to predict the oxidation rates of C and Cr in the AOD process. Deb Roy and Robertson [10,11] proposed a mathematical model for stainless steel refining and validated the model with data obtained from a 45-ton converter producing 304 stainless steel. Asai and Szekely [12,13] put forward a mathematical model of the stainless steel decarbonizing process, based on the mass and heat balance of the system. Wang et al. [14] obtained a multiple linear regression model to predict the oxygen blowing quantity by analyzing the factors that affect oxygen consumption during the basic oxygen furnace steelmaking process. The Nippon steel corporation [15] has developed an expert system for converter steelmaking. Li et al. [16] established a prediction model and control model based on a neural network by analyzing BOF steelmaking characteristics. Wei and Zhu [17,18] believed that the distribution ratio of oxygen which is blown to the molten pool across various elements is proportional to its Gibbs free energy of reaction. However, few studies have focused on mathematical models of vanadium extraction. Xu et al. [19] proposed a series of kinetic models of reactions in the oxygen converter, based on the results of the experiments and a parameter estimation method, in which the dynamic behaviors of vanadium, silicon, and carbon in the oxygen converter bath are described. In addition, there have been a few penetrating studies on mathematical models of the vanadium extraction process.

In this paper, based on the relevant theories of physics and chemistry, mathematical models of the vanadium extraction process are established to describe and predict the changes of composition in molten steel and slag during vanadium extraction. The numerical simulation results of the model are compared with the existing results, and its advantages over existing models are discussed. Theoretical analysis of the model explains the contradiction between “vanadium extraction” and “carbon protection”; furthermore, the model is used to analyze the competitive oxidation among elements.

2. Improved Mathematical Model of the Vanadium Extraction Process

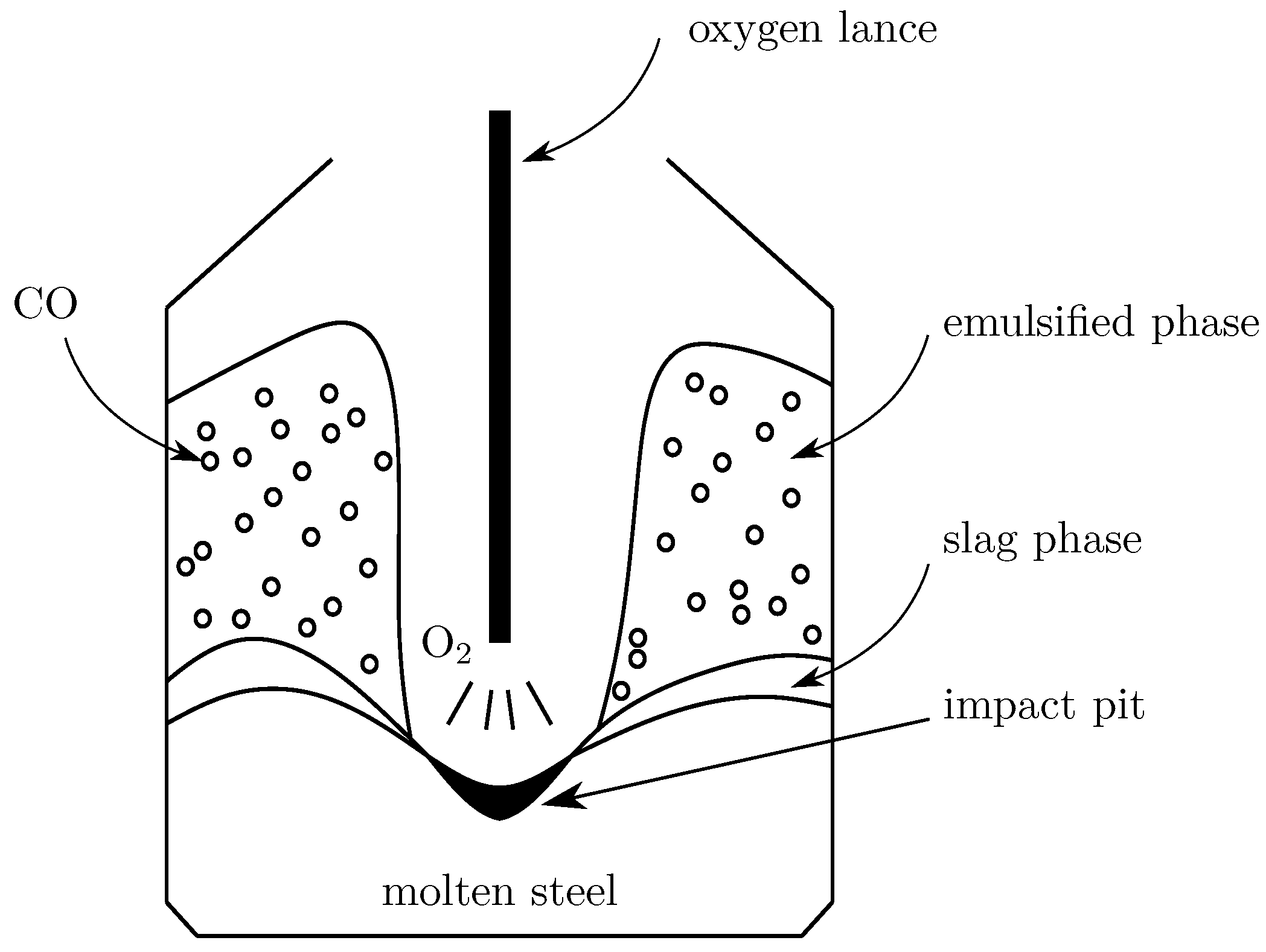
When extracting vanadium in a converter (Figure 1), vanadium-containing molten steel and a coolant are put together into the converter, following which an oxygen lance is inserted into the converter to blow oxygen at a high pressure. The high-speed oxygen jets interact with the metal melt in the converter, reacting with the elements in the molten steel which, in turn, oxidizes the vanadium to stable vanadium oxides, causing them to group into slag. The element oxidization process in the converter mainly consists of three series links: the diffusion of the reactants to the phase interfaces, interfacial chemical reactions, and the diffusion of the resultants away from the phase interfaces. Among these steps, the one with the lowest rate is called the rate limiting step.

As the slag in the vanadium extraction process is acidic, and as phosphorus and sulfur in the molten pool have been shown to not be involved in the reaction [20], we mainly consider the elements iron, carbon, vanadium, titanium, silicon, manganese, and oxygen in the molten steel. In this paper, substances in the metal phase (molten steel) are denoted by $\left[\mathrm{M}\right]$, where $\mathrm{M}$ represents $\mathrm{Fe},\mathrm{C},\mathrm{V},\mathrm{Ti},\mathrm{Si},\mathrm{Mn},\mathrm{O}$; the substances in the gaseous phase (gas) are denoted by $\left\{\mathrm{G}\right\}$, where $\mathrm{G}$ represents ${\mathrm{O}}_2$ and $\mathrm{CO}$; and the substances in the slag phase (slag) are denoted by $\left(\mathrm{S}\right)$, where $\mathrm{S}$ represents $\mathrm{FeO},{\mathrm{V}}_2{\mathrm{O}}_3,\mathrm{Ti}{\mathrm{O}}_2,\mathrm{Si}{\mathrm{O}}_2,\mathrm{MnO}$. Note that vanadium has many oxidation states; however, vanadium mainly has been shown to have a valence of $+3$ in the slag [21], which we assume for convenience.

2.1. The Gas–Liquid Interface of the Impact Pit

Due to the impact of the top-blown oxygen jet, an impact pit forms on the surface of the molten pool. at the gas–liquid interface of the impact pit, the oxygen is absorbed at the surface of the impact pit, and $\left[\mathrm{Fe}\right]$, $\left[\mathrm{C}\right]$, $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$ in the molten steel are oxidized. Although the dissolved elements in molten steel have an affinity for oxygen, the number of iron atoms at the surface of molten pool is much larger than other elements and, so, the oxidation of $\left[\mathrm{Fe}\right]$ is still at an absolute advantage [22]. For convenience, it is assumed that the oxidation reaction of $\left[\mathrm{Fe}\right]$ only occurs on the interface of impact pit, and all oxidation products of $\left[\mathrm{Fe}\right]$ are $\left(\mathrm{FeO}\right)$; which oxidizes other elements as an oxidant. The oxidation reaction equation of $\left[\mathrm{Fe}\right]$ is

$$\left[\mathrm{Fe}\right]+\frac{1}{2}\left\{{\mathrm{O}}_2\right\}=\left(\mathrm{FeO}\right).$$

(1)

If the oxygen pressure, flow, and oxygen lance position remain unchanged, the shape and size of the impact pit remain almost constant. Therefore, the contact area of $\left[\mathrm{Fe}\right]$ and $\left\{{\mathrm{O}}_2\right\}$ is basically unchanged. The chemical reaction (1) is carried out rapidly at a high temperature and, so, the chemical reaction process does not become a rate limiting step. Assuming that the oxidation rate of $\left[\mathrm{Fe}\right]$ in the impact pit is proportional to the oxygen blowing rate, then the oxidation rate of $\left[\mathrm{Fe}\right]$ at the gas–liquid interface of the impact pit is

$$\frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}^{\mathrm{cav}}}{\mathrm{d}t}=-M_{\mathrm{Fe}}\frac{2{\eta }_{{\mathrm{O}}_2}{Q}_{{\mathrm{O}}_2}}{V_{\mathrm{mol}}},$$

(2)

where $\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{cav}}}{\mathrm{d}t}$ is the mass change rate of $\left[\mathrm{M}\right]$ at the interface of the impact pit, $M_{\mathrm{M}}$ is the molar mass of substance $\mathrm{M}$, ${\eta }_{{\mathrm{O}}_2}$ is the utilization of oxygen, $Q_{{\mathrm{O}}_2}$ is the flow rate of top-blown oxygen gas, and $V_{\mathrm{mol}}$ is the molar volume of the gas.

2.2. The Slag–Metal Interface

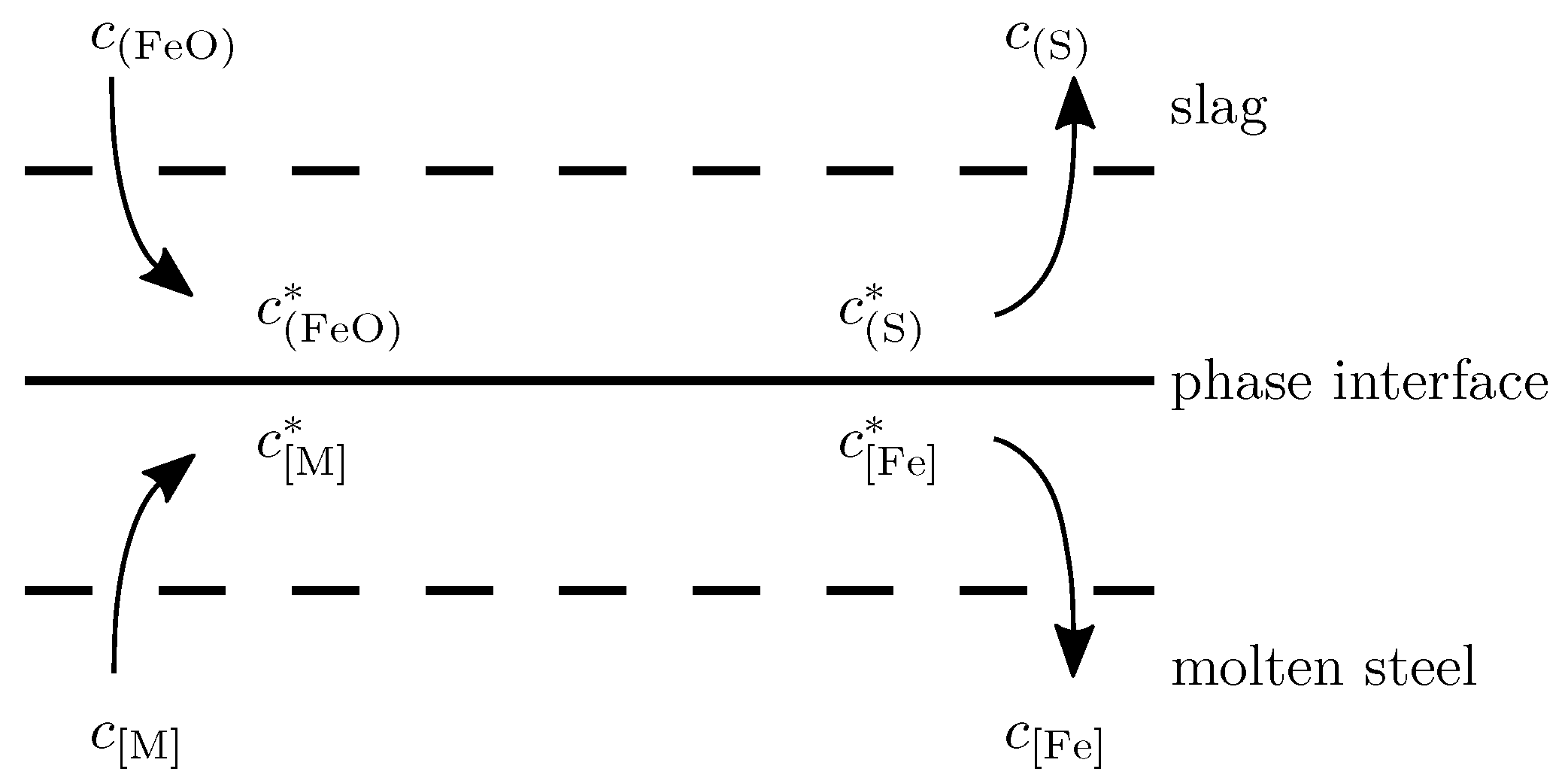
When the molten pool is strongly stirred, the slag is broken and incorporated into the molten steel to form the slag–metal interface. Within the system composed of molten metal and slag, due to different physical properties or flow velocities, there exist boundary layers [22] representing the mass transfer resistances on both sides of the phase interface. As shown in Figure 2, due to the concentration difference, each component $\left[\mathrm{M}\right]$ (with a concentration of $c_{\left[\mathrm{M}\right]}$) and $\left(\mathrm{FeO}\right)$ (with a concentration of $c_{\left(\mathrm{FeO}\right)}$) diffuse to the phase interface, where their concentrations are denoted by $c_{\left[\mathrm{M}\right]}^{*}$ and $c_{\left(\mathrm{FeO}\right)}^{*}$, respectively. Similarly, each component $\left(\mathrm{S}\right)$ (with a concentration of $c_{\left(\mathrm{S}\right)}^{*}$) and $\left[\mathrm{Fe}\right]$ (with a concentration of $c_{\left[\mathrm{Fe}\right]}^{*}$) in the phase interface diffuse to the slag and molten steel, where their concentrations are denoted by $c_{\left(\mathrm{S}\right)}$ and $c_{\left[\mathrm{Fe}\right]}$, respectively. The whole chemical reaction process consists of reactant diffusion, interface reaction, and product diffusion.

As an oxidant, the $\left(\mathrm{FeO}\right)$ generated by top-blown oxygen oxidizes $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$ at the slag–metal interface. The corresponding chemical reaction equations are

$$\begin{array}{cc}\hfill \left[\mathrm{V}\right]+\frac{3}{2}\left(\mathrm{FeO}\right)& =\frac{1}{2}\left({\mathrm{V}}_2{\mathrm{O}}_3\right)+\frac{3}{2}\left[\mathrm{Fe}\right],\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \left[\mathrm{Ti}\right]+2\left(\mathrm{FeO}\right)& =\left(\mathrm{Ti}{\mathrm{O}}_2\right)+2\left[\mathrm{Fe}\right],\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \left[\mathrm{Si}\right]+2\left(\mathrm{FeO}\right)& =\left(\mathrm{Si}{\mathrm{O}}_2\right)+2\left[\mathrm{Fe}\right],\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \left[\mathrm{Mn}\right]+\left(\mathrm{FeO}\right)& =\left(\mathrm{MnO}\right)+\left[\mathrm{Fe}\right].\hfill \end{array}$$

(6)

In order to establish the rate equation of the chemical reactions (3)–(6), the rate limiting elements of the chemical reactions are analyzed from the two following aspects:

• Interface Chemical Reaction: The interface chemical reaction is carried out rapidly at a high temperature, and the chemical reaction process does not become the rate limiting step.
• Mass Transfer of Reactant and Resultant: Generally, the concentrations of the reactant $\left(\mathrm{FeO}\right)$ and the resultant $\left[\mathrm{Fe}\right]$ are high, and their mass transfer processes will not be the rate limiting step.

Therefore, the mass transfer processes of the reactants $\left[\mathrm{M}\right]$ and the products $\left(\mathrm{S}\right)$ are the rate limiting steps. The rates of the interface reactions are regulated by each other. It is generally considered that the diffusion processes on both sides of the slag–metal interface satisfy the steady-state principle [22]. According to the definition of a rate limiting step, the diffusion rates of $\left[\mathrm{M}\right]$ can reveal the rates of the interface reactions (3)–(6). By Fick’s law [23], we have

$$\begin{array}{cc}\hfill J_{\left[\mathrm{V}\right]}^{\mathrm{sm}}& =-\frac{1}{A^{\mathrm{sm}}}\frac{\mathrm{d}{n}_{\left[\mathrm{V}\right]}^{\mathrm{sm}}}{\mathrm{d}t}={\beta }_{\left[\mathrm{V}\right]}(c_{\left[\mathrm{V}\right]}-c_{\left[\mathrm{V}\right]}^{*\mathrm{sm}}),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill J_{\left[\mathrm{Ti}\right]}^{\mathrm{sm}}& =-\frac{1}{A^{\mathrm{sm}}}\frac{\mathrm{d}{n}_{\left[\mathrm{Ti}\right]}^{\mathrm{sm}}}{\mathrm{d}t}={\beta }_{\left[\mathrm{Ti}\right]}(c_{\left[\mathrm{Ti}\right]}-c_{\left[\mathrm{Ti}\right]}^{*\mathrm{sm}}),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill J_{\left[\mathrm{Si}\right]}^{\mathrm{sm}}& =-\frac{1}{A^{\mathrm{sm}}}\frac{\mathrm{d}{n}_{\left[\mathrm{Si}\right]}^{\mathrm{sm}}}{\mathrm{d}t}={\beta }_{\left[\mathrm{Si}\right]}(c_{\left[\mathrm{Si}\right]}-c_{\left[\mathrm{Si}\right]}^{*\mathrm{sm}}),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill J_{\left[\mathrm{Mn}\right]}^{\mathrm{sm}}& =-\frac{1}{A^{\mathrm{sm}}}\frac{\mathrm{d}{n}_{\left[\mathrm{Mn}\right]}^{\mathrm{sm}}}{\mathrm{d}t}={\beta }_{\left[\mathrm{Mn}\right]}(c_{\left[\mathrm{Mn}\right]}-c_{\left[\mathrm{Mn}\right]}^{*\mathrm{sm}}),\hfill \end{array}$$

(10)

where $J_{\left[\mathrm{M}\right]}^{\mathrm{sm}}$ is the diffusion rate of $\left[\mathrm{M}\right]$, $A^{\mathrm{sm}}$ is the contact area for chemical reactions at the slag–metal interface, $\frac{\mathrm{d}{n}_{\left[\mathrm{M}\right]}^{\mathrm{sm}}}{\mathrm{d}t}$ is the mol change rate of $\left[\mathrm{M}\right]$ at the slag–metal interface, ${\beta }_{\left[\mathrm{M}\right]}$ is the mass transfer coefficient of $\left[\mathrm{M}\right]$, $c_{\left[\mathrm{M}\right]}$ is the concentration of $\left[\mathrm{M}\right]$, and $c_{\left[\mathrm{M}\right]}^{*\mathrm{sm}}$ is the concentration of $\left[\mathrm{M}\right]$ at the slag-metal interface. According to (7)–(10), the rate change equation of $\left[\mathrm{M}\right]$ can be derived, as long as $c_{\left[\mathrm{M}\right]}^{*\mathrm{sm}}$ can be determined.

According to the literature, the interfacial concentration equations are obtained by assuming that the interface reaction is in thermodynamic equilibrium [20,24] or by usng the distribution ratio of oxygen [17]. However, the key idea of these different modeling ideas is to give an estimate of the interface concentration, either directly or indirectly. As the oxidation rate of the element $\left[\mathrm{M}\right]$ is related to the Gibbs free energy $\Delta G_{\left[\mathrm{M}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}$ of (3)–(6), the concentration $c_{\left[\mathrm{M}\right]}$, and the mass transfer coefficient ${\beta }_{\left[\mathrm{M}\right]}$, we can assume that the oxidation rate of the element is proportional to the product of $\Delta G_{\left[\mathrm{M}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}$, $c_{\left[\mathrm{M}\right]}$ and ${\beta }_{\left[\mathrm{M}\right]}$; that is,

$$\frac{{\beta }_{\left[{\mathrm{M}}_1\right]}(c_{\left[{\mathrm{M}}_1\right]}-c_{\left[{\mathrm{M}}_1\right]}^{*\mathrm{sm}})}{{\beta }_{\left[{\mathrm{M}}_1\right]}{c}_{\left[{\mathrm{M}}_1\right]}\Delta G_{\left[{\mathrm{M}}_1\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}=\frac{{\beta }_{\left[{\mathrm{M}}_2\right]}(c_{\left[{\mathrm{M}}_2\right]}-c_{\left[{\mathrm{M}}_2\right]}^{*\mathrm{sm}})}{{\beta }_{\left[{\mathrm{M}}_2\right]}{c}_{\left[{\mathrm{M}}_2\right]}\Delta G_{\left[{\mathrm{M}}_2\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}},$$

(11)

where ${\mathrm{M}}_1,{\mathrm{M}}_2=\mathrm{V},\mathrm{Ti},\mathrm{Si},\mathrm{Mn}$. Under the typical temperature used for vanadium extraction, the Gibbs free energy of $\left[\mathrm{Ti}\right]$ is much greater than that of $\left[\mathrm{V}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$. Therefore, $\left[\mathrm{Ti}\right]$ will be oxidized preferentially. Only when the interfacial concentration of $\left[\mathrm{Ti}\right]$ is very low, will the other elements begin to be oxidized. The temperature in the converter is very high and, so, the rate of each chemical reaction is very fast. Therefore, once the reactant $\left[\mathrm{Ti}\right]$ diffuses to the interface, it will be consumed rapidly.

So, we take

$$c_{\left[\mathrm{Ti}\right]}^{*\mathrm{sm}}=0$$

(12)

as an estimate for the interface concentration.

At the slag–metal interface, part of the $\left(\mathrm{FeO}\right)$ generated by the top-blown oxygen enters into the molten steel in the form of dissolved oxygen atoms $\left[\mathrm{O}\right]$; the chemical reaction equation for this is

$$\left(\mathrm{FeO}\right)=\left[\mathrm{Fe}\right]+\left[\mathrm{O}\right].$$

(13)

By Fick’s law, the diffusion fluxes of the reactant $\left(\mathrm{FeO}\right)$ and resultant $\left[\mathrm{O}\right]$ are

$$\begin{array}{cc}\hfill J_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}& =-\frac{1}{A^{\mathrm{sm}}}\frac{\mathrm{d}{n}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\mathrm{d}t}={\beta }_{\left(\mathrm{FeO}\right)}(c_{\left(\mathrm{FeO}\right)}-c_{\left(\mathrm{FeO}\right)}^{*\mathrm{sm}}),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill J_{\left[\mathrm{O}\right]}^{\mathrm{sm}}& =\frac{1}{A^{\mathrm{sm}}}\frac{\mathrm{d}{n}_{\left[\mathrm{O}\right]}^{\mathrm{sm}}}{\mathrm{d}t}={\beta }_{\left[\mathrm{O}\right]}(c_{\left[\mathrm{O}\right]}^{*\mathrm{sm}}-c_{\left[\mathrm{O}\right]}),\hfill \end{array}$$

(15)

where $\frac{\mathrm{d}{n}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\mathrm{d}t}$ is the mol change rate of $\left(\mathrm{FeO}\right)$ at the slag–metal interface and ${\beta }_{\left(\mathrm{FeO}\right)}$ is the mass transfer coefficient of $\left(\mathrm{FeO}\right)$. At high temperatures, the chemical reaction (13) is carried out rapidly and can be considered to be in equilibrium [20]. The equilibrium constant is

$$K_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}=\frac{c_{\left[\mathrm{O}\right]}^{*\mathrm{sm}}}{c_{\left(\mathrm{FeO}\right)}^{*\mathrm{sm}}}.$$

(16)

In stable state, the $\left(\mathrm{FeO}\right)$ diffusing to the interface is entirely used for the oxidation reaction (3)–(6) and decomposition reaction (13); that is,

$$J_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}=\frac{3}{2}{J}_{\left[\mathrm{V}\right]}^{\mathrm{sm}}+2J_{\left[\mathrm{Ti}\right]}^{\mathrm{sm}}+2J_{\left[\mathrm{Si}\right]}^{\mathrm{sm}}+J_{\left[\mathrm{Mn}\right]}^{\mathrm{sm}}+J_{\left[\mathrm{O}\right]}^{\mathrm{sm}}.$$

(17)

Slag plays an important role in the converter blowing process. The slag layer is located between the molten steel and the emulsion system, which is related to the slag–metal interface and emulsion system. On one hand, the slag–metal interface is formed through the interaction of slag and molten steel; on the other hand, the emulsion system is formed by slag, molten steel droplets, and bubbles. In many articles [17,20,25], the contact area of reactions has been taken as a constant in the empirical formula; even the mass of the molten steel and slag are considered to be constant, as well. Obviously, this treatment does not provide a representative approximation of the actual process, as the contact area and the masses of the molten steel and slag change over time. Generally, the contact area increases with the mass of slag. This paper assumes that the contact area at the slag–metal interface is proportional to the slag mass:

$$A^{\mathrm{sm}}=k^{\mathrm{sm}}{W}_{\mathrm{s}},$$

(18)

where $W_{\mathrm{s}}$ is the total mass of slag and the proportionality coefficient $k^{\mathrm{sm}}$ is a positive constant.

By (7)–(12), (14)–(18), we can obtain the chemical reaction rate equation of each element present at the slag–metal interface:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{V}\right]}^{\mathrm{sm}}}{\mathrm{d}t}& =-M_{\mathrm{V}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{\Delta G_{\left[\mathrm{V}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Ti}\right]}^{\mathrm{sm}}}{\mathrm{d}t}& =-M_{\mathrm{Ti}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Si}\right]}^{\mathrm{sm}}}{\mathrm{d}t}& =-M_{\mathrm{Si}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{\Delta G_{\left[\mathrm{Si}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Mn}\right]}^{\mathrm{sm}}}{\mathrm{d}t}& =-M_{\mathrm{Mn}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}^{\mathrm{sm}}}{\mathrm{d}t}& =M_{\mathrm{Fe}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}\left(c_{\left(\mathrm{FeO}\right)}-\frac{c_{\left[\mathrm{O}\right]}}{K_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}\right)\hfill \\ \hfill & +M_{\mathrm{Fe}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}\left(\frac{3}{2}\frac{\Delta G_{\left[\mathrm{V}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]}+2{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]}\right.\hfill \\ \hfill & \left.+2\frac{\Delta G_{\left[\mathrm{Si}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]}+\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]}\right),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}^{\mathrm{sm}}}{\mathrm{d}t}& =M_{\mathrm{O}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}\left(c_{\left(\mathrm{FeO}\right)}-\frac{c_{\left[\mathrm{O}\right]}}{K_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}\right)\hfill \\ \hfill & -M_{\mathrm{O}}{k}^{\mathrm{sm}}{W}_{\mathrm{s}}\frac{{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}\left(\frac{3}{2}\frac{\Delta G_{\left[\mathrm{V}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]}+2{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]}\right.\hfill \\ \hfill & \left.+2\frac{\Delta G_{\left[\mathrm{Si}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]}+\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]}\right),\hfill \end{array}$$

(24)

where $\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{sm}}}{\mathrm{d}t}$ is the mass change rate of $\left[\mathrm{M}\right]$ at the slag–metal interface.

2.3. Emulsion System

During the converter blowing process, the interaction of the supersonic oxygen jet and the gas generated in the converter will break the oxygen jet, molten metal, and slag into droplets and bubbles, generating the metal–slag-bubble emulsion system. The contact area of the chemical reaction in the emulsion system increases rapidly and the oxidation reaction becomes more intense, which is the fundamental reason behind the high reaction speed and high productivity of oxygen converter blowing. Then, $\left(\mathrm{FeO}\right)$ films are rapidly formed on the surfaces of the metal droplets which are incorporated into the jet. These droplets are the basic carrier, transferring oxygen into the molten pool. With the rapid motion of the jet, the oxygen-containing droplets participate in the circulation of the molten pool, becoming scattered in the slag and forming an emulsified state.

In the emulsion system, the major oxygen source and product of the decarburizing reaction are $\left(\mathrm{FeO}\right)$ and $\left\{\mathrm{CO}\right\}$. The corresponding chemical reaction equation is

$$\left[\mathrm{C}\right]+\left(\mathrm{FeO}\right)=\left\{\mathrm{CO}\right\}+\left[\mathrm{Fe}\right].$$

(25)

In order to establish the rate equation of the chemical reaction (25), the rate limiting steps of (25) are analyzed in the two following aspects:

• Interface Chemical Reaction: The interface chemical reaction is carried out rapidly at high temperature and, so, the chemical reaction process does not become the rate limiting step.
• Mass Transfer of Reactant and Resultant: Generally, the concentration of the reactant $\left(\mathrm{FeO}\right)$ is high and the mass transfer process of $\left(\mathrm{FeO}\right)$ will not be the rate limiting step. The concentration of the resultant $\left[\mathrm{Fe}\right]$ is also very high and the mass transfer resistance of $\left[\mathrm{Fe}\right]$ can be ignored. The resultant $\left\{\mathrm{CO}\right\}$ is a gas; the mass transfer process of a gas will not be the rate limiting step, either.

Therefore, in this paper, we assume that the main influencing factor of the decarbonization reaction is the mass transfer process of $\left[\mathrm{C}\right]$. By Fick’s law

$$J_{\left[\mathrm{C}\right]}^{\mathrm{eg}}=-\frac{1}{A^{\mathrm{eg}}}\frac{\mathrm{d}{n}_{\left[\mathrm{C}\right]}^{\mathrm{eg}}}{\mathrm{d}t}={\beta }_{\left[\mathrm{C}\right]}(c_{\left[\mathrm{C}\right]}-c_{\left[\mathrm{C}\right]}^{*\mathrm{eg}}),$$

(26)

where $A^{\mathrm{eg}}$ is the contact area of the decarbonization reaction in the emulsion system, $\frac{\mathrm{d}{n}_{\left[\mathrm{C}\right]}^{\mathrm{eg}}}{\mathrm{d}t}$ is the mol change rate of $\left[\mathrm{C}\right]$ in the emulsion system where the decarbonization occurs, $c_{\left[\mathrm{C}\right]}^{*\mathrm{eg}}$ is the concentration of $\left[\mathrm{C}\right]$ at the interface of the decarbonization reaction. According to (26), the rate change equation of $\left[\mathrm{C}\right]$ can be derived, as long as $c_{\left[\mathrm{C}\right]}^{*\mathrm{eg}}$ can be determined.

Generally, as the chemical reactions in the emulsion system are complex and coupled, it is difficult to determine $c_{\left[\mathrm{C}\right]}^{*\mathrm{em}}$ exactly; hence, we give an estimate of $c_{\left[\mathrm{C}\right]}^{*\mathrm{em}}$ to establish the rate equation of decarbonization. Note that [22]

$$c_{\left[\mathrm{C}\right]}^{*\mathrm{eg}}\ll c_{\left[\mathrm{C}\right]}$$

(27)

is the case in the process of vanadium extraction. For convenience, let

$$c_{\left[\mathrm{C}\right]}^{*\mathrm{eg}}=0$$

(28)

be our estimate of the interface concentration.

By (26), (28), and chemical reaction (25), we have

$$\begin{array}{c}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{C}\right]}^{\mathrm{eg}}}{\mathrm{d}t}=-M_{\mathrm{C}}{A}^{\mathrm{eg}}{\beta }_{\left[\mathrm{C}\right]}{c}_{\left[\mathrm{C}\right]},\end{array}$$

(29)

$$\begin{array}{c}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}^{\mathrm{eg}}}{\mathrm{d}t}=M_{\mathrm{Fe}}{A}^{\mathrm{eg}}{\beta }_{\left[\mathrm{C}\right]}{c}_{\left[\mathrm{C}\right]}.\end{array}$$

(30)

In the emulsion system, $\left(\mathrm{FeO}\right)$ passes $\left[\mathrm{O}\right]$ to the system by

$$\left(\mathrm{FeO}\right)=\left[\mathrm{Fe}\right]+\left[\mathrm{O}\right]$$

(31)

and oxidizes $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$ by

$$\begin{array}{cc}\hfill \left[\mathrm{V}\right]+\frac{3}{2}\left[\mathrm{O}\right]& =\frac{1}{2}\left({\mathrm{V}}_2{\mathrm{O}}_3\right),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \left[\mathrm{Ti}\right]+2\left[\mathrm{O}\right]& =\left(\mathrm{Ti}{\mathrm{O}}_2\right),\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill \left[\mathrm{Si}\right]+2\left[\mathrm{O}\right]& =\left(\mathrm{Si}{\mathrm{O}}_2\right),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill \left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]& =\left(\mathrm{MnO}\right).\hfill \end{array}$$

(35)

Similar to the analysis and assumption used for the slag–metal interface, we obtain

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{V}\right]}^{\mathrm{es}}}{\mathrm{d}t}& =-M_{\mathrm{V}}{A}^{\mathrm{es}}\frac{\Delta G_{\left[\mathrm{V}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]},\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Ti}\right]}^{\mathrm{es}}}{\mathrm{d}t}& =-M_{\mathrm{Ti}}{A}^{\mathrm{es}}{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Si}\right]}^{\mathrm{es}}}{\mathrm{d}t}& =-M_{\mathrm{Si}}{A}^{\mathrm{es}}\frac{\Delta G_{\left[\mathrm{Si}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]},\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Mn}\right]}^{\mathrm{es}}}{\mathrm{d}t}& =-M_{\mathrm{Mn}}{A}^{\mathrm{es}}\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]},\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}^{\mathrm{es}}}{\mathrm{d}t}& =M_{\mathrm{Fe}}{A}^{\mathrm{es}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(c_{\left(\mathrm{FeO}\right)}-\frac{c_{\left[\mathrm{O}\right]}}{K_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\right)\hfill \\ \hfill & +M_{\mathrm{Fe}}{A}^{\mathrm{es}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(\frac{3}{2}\frac{\Delta G_{\left[\mathrm{V}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]}+2{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]}\right.\hfill \\ \hfill & \left.+2\frac{\Delta G_{\left[\mathrm{Si}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]}+\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]}\right),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}^{\mathrm{es}}}{\mathrm{d}t}& =M_{\mathrm{O}}{A}^{\mathrm{es}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(c_{\left(\mathrm{FeO}\right)}-\frac{c_{\left[\mathrm{O}\right]}}{K_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\right)\hfill \\ \hfill & -M_{\mathrm{O}}{A}^{\mathrm{es}}\frac{{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(\frac{3}{2}\frac{\Delta G_{\left[\mathrm{V}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]}+2{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]}\right.\hfill \\ \hfill & \left.+2\frac{\Delta G_{\left[\mathrm{Si}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]}+\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]}\right),\hfill \end{array}$$

(41)

where $\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{es}}}{\mathrm{d}t}$ is the mass change rate of $\left[\mathrm{M}\right]$ in the region of the oxidation and decomposition reactions in the emulsion system, $A^{\mathrm{es}}$ is the contact area of the oxidation and decomposition reactions in the emulsion system, $K_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}$ is the equilibrium constant of the chemical reaction (31), and $\Delta G_{\left[\mathrm{M}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}$ is the Gibbs free energy of the oxidation reactions (32)–(35) in the emulsion system.

The mass of the substance $\left[\mathrm{M}\right]$ in the emulsion system is equal to the sum of the masses in the region of the decarburizing reaction and the region of the oxidation and decomposition reactions; that is,

$$m_{\left[\mathrm{M}\right]}^{\mathrm{em}}=m_{\left[\mathrm{M}\right]}^{\mathrm{eg}}+m_{\left[\mathrm{M}\right]}^{\mathrm{es}}.$$

(42)

Taking the derivative of (42) with respect to t, we get

$$\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{em}}}{\mathrm{d}t}=\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{eg}}}{\mathrm{d}t}+\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{es}}}{\mathrm{d}t},$$

(43)

where $\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{em}}}{\mathrm{d}t}$ is the mass change rate of $\left[\mathrm{M}\right]$ in the emulsion system.

Similar to (18), we assume that the total contact area of the emulsion system is proportional to the slag mass

$$A^{\mathrm{em}}=k^{\mathrm{em}}{W}_{\mathrm{s}},$$

(44)

where $A^{\mathrm{em}}$ is the total contact area of the emulsion system and the proportionality coefficient $k^{\mathrm{em}}$ is a positive constant. The total contact area of the emulsion system is the sum of the contact area of the decarbonization reaction and the contact area of the oxidation and decomposition reactions; that is,

$$A^{\mathrm{em}}=A^{\mathrm{eg}}+A^{\mathrm{es}}.$$

(45)

When the external conditions (e.g., oxygen lance position, oxygen flow, and so on) are left basically unchanged, we assume that $A^{\mathrm{eg}}$ and $A^{\mathrm{es}}$ are basically stable at a certain percentage:

$$\frac{A^{\mathrm{eg}}}{r^{\mathrm{eg}}}=\frac{A^{\mathrm{es}}}{r^{\mathrm{es}}},$$

(46)

where the proportionality coefficients $r^{\mathrm{eg}}$ and $r^{\mathrm{es}}$ are positive constants. By (44)–(46), we have

$$\begin{array}{cc}\hfill A^{\mathrm{eg}}& =\frac{r^{\mathrm{eg}}}{r^{\mathrm{eg}}+r^{\mathrm{es}}}{k}^{\mathrm{em}}{W}_{\mathrm{s}}\stackrel{def}{=}{k}^{\mathrm{eg}}{W}_{\mathrm{s}},\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill A^{\mathrm{es}}& =\frac{r^{\mathrm{es}}}{r^{\mathrm{eg}}+r^{\mathrm{es}}}{k}^{\mathrm{em}}{W}_{\mathrm{s}}\stackrel{def}{=}{k}^{\mathrm{es}}{W}_{\mathrm{s}},\hfill \end{array}$$

(48)

where $k^{\mathrm{eg}}$ and $k^{\mathrm{es}}$ are positive constants.

By (29)–(30), (36)–(41), (43), and (47)–(48), we obtain the chemical reaction rate equation of each element in the emulsion system as

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{C}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =-M_{\mathrm{C}}{k}^{\mathrm{eg}}{W}_{\mathrm{s}}{\beta }_{\left[\mathrm{C}\right]}{c}_{\left[\mathrm{C}\right]},\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{V}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =-M_{\mathrm{V}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{\Delta G_{\left[\mathrm{V}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]},\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Ti}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =-M_{\mathrm{Ti}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]},\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Si}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =-M_{\mathrm{Si}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{\Delta G_{\left[\mathrm{Si}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]},\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Mn}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =-M_{\mathrm{Mn}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]},\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =M_{\mathrm{Fe}}{k}^{\mathrm{eg}}{W}_{\mathrm{s}}{\beta }_{\left[\mathrm{C}\right]}{c}_{\left[\mathrm{C}\right]}+M_{\mathrm{Fe}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(c_{\left(\mathrm{FeO}\right)}-\frac{c_{\left[\mathrm{O}\right]}}{K_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\right)\hfill \\ \hfill & +M_{\mathrm{Fe}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(\frac{3}{2}\frac{\Delta G_{\left[\mathrm{V}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]}+2{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]}\right.\hfill \\ \hfill & \left.+2\frac{\Delta G_{\left[\mathrm{Si}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]}+\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]}\right),\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}^{\mathrm{em}}}{\mathrm{d}t}& =M_{\mathrm{O}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{{\beta }_{\left(\mathrm{FeO}\right)}{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(c_{\left(\mathrm{FeO}\right)}-\frac{c_{\left[\mathrm{O}\right]}}{K_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\right)\hfill \\ \hfill & -M_{\mathrm{O}}{k}^{\mathrm{es}}{W}_{\mathrm{s}}\frac{{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{{\beta }_{\left(\mathrm{FeO}\right)}+{\beta }_{\left[\mathrm{O}\right]}{K}_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}\left(\frac{3}{2}\frac{\Delta G_{\left[\mathrm{V}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{V}\right]}{c}_{\left[\mathrm{V}\right]}+2{\beta }_{\left[\mathrm{Ti}\right]}{c}_{\left[\mathrm{Ti}\right]}\right.\hfill \\ \hfill & \left.+2\frac{\Delta G_{\left[\mathrm{Si}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Si}\right]}{c}_{\left[\mathrm{Si}\right]}+\frac{\Delta G_{\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\Delta G_{\left[\mathrm{Ti}\right]+\left[\mathrm{O}\right]}^{\mathrm{es}}}{\beta }_{\left[\mathrm{Mn}\right]}{c}_{\left[\mathrm{Mn}\right]}\right).\hfill \end{array}$$

(55)

At this point, the reaction rate equations at the gas–liquid interface, the slag–metal interface, and in the emulsion system have been established. Next, the rate equations for the different interfaces need to be combined to form a closed system.

2.4. Dynamic Model of Vanadium Extraction

The mass of substance $\left[\mathrm{M}\right]$ is equal to the sum of the mass in the molten steel $m_{\left[\mathrm{M}\right]}^{\mathrm{b}}$, at the gas–liquid interface of the impact pit $m_{\left[\mathrm{M}\right]}^{\mathrm{cav}}$, at the slag–metal interface $m_{\left[\mathrm{M}\right]}^{\mathrm{sm}}$, and in the emulsion system $m_{\left[\mathrm{M}\right]}^{\mathrm{em}}$; that is,

$$m_{\left[\mathrm{M}\right]}=m_{\left[\mathrm{M}\right]}^{\mathrm{b}}+m_{\left[\mathrm{M}\right]}^{\mathrm{cav}}+m_{\left[\mathrm{M}\right]}^{\mathrm{sm}}+m_{\left[\mathrm{M}\right]}^{\mathrm{em}}.$$

(56)

Taking the derivative of (56) with respect to t, we have

$$\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}}{\mathrm{d}t}=\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{b}}}{\mathrm{d}t}+\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{cav}}}{\mathrm{d}t}+\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{sm}}}{\mathrm{d}t}+\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{em}}}{\mathrm{d}t}.$$

(57)

Note that the chemical reaction of the substance $\left[\mathrm{M}\right]$ mainly occurs at the gas–liquid interface of impact pit, at the slag–metal interface, and in the emulsion system; it is almost unchanged in the molten steel. Thus,

$$\frac{\mathrm{d}{m}_{\left[\mathrm{M}\right]}^{\mathrm{b}}}{\mathrm{d}t}=0.$$

(58)

The concentration of $\left[\mathrm{M}\right]$ in the model satisfies

$$c_{\left[\mathrm{M}\right]}=\frac{{\rho }_{\mathrm{m}}}{M_{\mathrm{M}}}\frac{m_{\left[\mathrm{M}\right]}}{W_{\mathrm{m}}},$$

(59)

where ${\rho }_{\mathrm{m}}$ is the density of molten steel and $W_{\mathrm{m}}$ is the mass of the molten steel. The mass of the molten steel is equal to the total mass of each element:

$$W_{\mathrm{m}}=m_{\left[\mathrm{C}\right]}+m_{\left[\mathrm{V}\right]}+m_{\left[\mathrm{Ti}\right]}+m_{\left[\mathrm{Si}\right]}+m_{\left[\mathrm{Mn}\right]}+m_{\left[\mathrm{Fe}\right]}+m_{\left[\mathrm{O}\right]}.$$

(60)

The concentration of $\left(\mathrm{FeO}\right)$ in the model satisfies

$$c_{\left(\mathrm{FeO}\right)}=\frac{{\rho }_{\mathrm{s}}}{M_{\mathrm{FeO}}}\frac{{\tilde{m}}_{\left(\mathrm{FeO}\right)}}{W_{\mathrm{s}}},$$

(61)

where ${\rho }_{\mathrm{s}}$ is the density of the slag and ${\tilde{m}}_{\left(\mathrm{FeO}\right)}$ is the mass of free $\left(\mathrm{FeO}\right)$. The $\left(\mathrm{FeO}\right)$ in the slag is not only in the form of simple molecules, but is also combined with other oxides and present in the form of complex oxides (such as vanadium–iron spinel ${\mathrm{V}}_2{\mathrm{O}}_3·\mathrm{FeO}$) in the slag. Only free $\left(\mathrm{FeO}\right)$ can react with the material $\left[\mathrm{M}\right]$ in the molten steel. We assume that the mass of free $\left(\mathrm{FeO}\right)$ is proportional to the total mass of the $\left(\mathrm{FeO}\right)$:

$${\tilde{m}}_{\left(\mathrm{FeO}\right)}=k_{\left(\mathrm{FeO}\right)}{m}_{\left(\mathrm{FeO}\right)}$$

(62)

where the proportionality coefficient $k_{\left(\mathrm{FeO}\right)}$ is a positive constant.

The oxidized $\left[\mathrm{Fe}\right]$ is present as oxides $\left(\mathrm{FeO}\right)$ in the slag. By the law of conservation of mass, we have

$$\frac{m_{\left(\mathrm{FeO}\right)}-m_{\left(\mathrm{FeO}\right)}^0}{M_{\mathrm{FeO}}}=\frac{m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]}}{M_{\mathrm{Fe}}},$$

(63)

where $m_{\left[\mathrm{M}\right]}^0$ and $m_{\left(\mathrm{S}\right)}^0$ are the initial values of $\left[\mathrm{M}\right]$ and $m_{\left(\mathrm{S}\right)}$, respectively. Note that

$$m_{\left(\mathrm{S}\right)}^0=0.$$

(64)

Substituting (64) into (63), we have

$$m_{\left(\mathrm{FeO}\right)}=\frac{M_{\mathrm{FeO}}}{M_{\mathrm{Fe}}}(m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]}).$$

(65)

The slag mass is equal to the sum of the mass of each substance of slag; that is,

$$\begin{array}{cc}\hfill W_{\mathrm{s}}& =\frac{M_{{\mathrm{V}}_2{\mathrm{O}}_3}}{2M_{\mathrm{V}}}(m_{\left[\mathrm{V}\right]}^0-m_{\left[\mathrm{V}\right]})+\frac{M_{\mathrm{Ti}{\mathrm{O}}_2}}{M_{\mathrm{Ti}}}(m_{\left[\mathrm{Ti}\right]}^0-m_{\left[\mathrm{Ti}\right]})+\frac{M_{\mathrm{Si}{\mathrm{O}}_2}}{M_{\mathrm{Si}}}(m_{\left[\mathrm{Si}\right]}^0-m_{\left[\mathrm{Si}\right]})\hfill \\ \hfill & +\frac{M_{\mathrm{MnO}}}{M_{\mathrm{Mn}}}(m_{\left[\mathrm{Mn}\right]}^0-m_{\left[\mathrm{Mn}\right]})+\frac{M_{\mathrm{FeO}}}{M_{\mathrm{Fe}}}(m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]}).\hfill \end{array}$$

(66)

Substituting (62) and (65) into (61), we have

$$c_{\left(\mathrm{FeO}\right)}=\frac{{\rho }_{\mathrm{s}}}{M_{\mathrm{Fe}}}{k}_{\left(\mathrm{FeO}\right)}\frac{m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]}}{W_{\mathrm{s}}}.$$

(67)

By (2), (19)–(24), (49)–(55), (57), (58), and (67), and letting the corresponding constants be marked as $r_{\mathrm{C}}$, $r_{\mathrm{V}}$, $r_{\mathrm{Ti}}$, $r_{\mathrm{Si}}$, $r_{\mathrm{Mn}}$, $r_{\mathrm{Fe}}$, $r_{\mathrm{O}}$, $r_{\mathrm{Fe}}^{\mathrm{V}}$, $r_{\mathrm{Fe}}^{\mathrm{Ti}}$, $r_{\mathrm{Fe}}^{\mathrm{Si}}$, $r_{\mathrm{Fe}}^{\mathrm{Mn}}$, $r_{\mathrm{O}}^{\mathrm{V}}$, $r_{\mathrm{O}}^{\mathrm{Ti}}$, $r_{\mathrm{O}}^{\mathrm{Si}}$, and $r_{\mathrm{O}}^{\mathrm{Mn}}$, we obtain the dynamic model of vanadium extraction as follows:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{C}\right]}}{\mathrm{d}t}& =-r_{\mathrm{C}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{C}\right]},\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{V}\right]}}{\mathrm{d}t}& =-r_{\mathrm{V}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{V}\right]},\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Ti}\right]}}{\mathrm{d}t}& =-r_{\mathrm{Ti}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Ti}\right]},\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Si}\right]}}{\mathrm{d}t}& =-r_{\mathrm{Si}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Si}\right]},\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Mn}\right]}}{\mathrm{d}t}& =-r_{\mathrm{Mn}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Mn}\right]},\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}}{\mathrm{d}t}& =-M_{\mathrm{Fe}}\frac{2{\eta }_{{\mathrm{O}}_2}{Q}_{{\mathrm{O}}_2}}{V_{\mathrm{mol}}}+r_{\mathrm{Fe}}(m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]})-\frac{M_{\mathrm{Fe}}}{M_{\mathrm{O}}}{r}_{\mathrm{O}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{O}\right]}\hfill \\ \hfill & +\frac{M_{\mathrm{Fe}}}{M_{\mathrm{C}}}{r}_{\mathrm{C}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{C}\right]}+\frac{3}{2}\frac{M_{\mathrm{Fe}}}{M_{\mathrm{V}}}{r}_{\mathrm{Fe}}^{\mathrm{V}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{V}\right]}+2\frac{M_{\mathrm{Fe}}}{M_{\mathrm{Ti}}}{r}_{\mathrm{Fe}}^{\mathrm{Ti}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Ti}\right]}\hfill \\ \hfill & +2\frac{M_{\mathrm{Fe}}}{M_{\mathrm{Si}}}{r}_{\mathrm{Fe}}^{\mathrm{Si}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Si}\right]}+\frac{M_{\mathrm{Fe}}}{M_{\mathrm{Mn}}}{r}_{\mathrm{Fe}}^{\mathrm{Mn}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Mn}\right]},\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}}{\mathrm{d}t}& =\frac{M_{\mathrm{O}}}{M_{\mathrm{Fe}}}{r}_{\mathrm{Fe}}(m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]})-r_{\mathrm{O}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{O}\right]}-\frac{3}{2}\frac{M_{\mathrm{O}}}{M_{\mathrm{V}}}{r}_{\mathrm{O}}^{\mathrm{V}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{V}\right]}\hfill \\ \hfill & -2\frac{M_{\mathrm{O}}}{M_{\mathrm{Ti}}}{r}_{\mathrm{O}}^{\mathrm{Ti}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Ti}\right]}-2\frac{M_{\mathrm{O}}}{M_{\mathrm{Si}}}{r}_{\mathrm{O}}^{\mathrm{Si}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Si}\right]}-\frac{M_{\mathrm{O}}}{M_{\mathrm{Mn}}}{r}_{\mathrm{O}}^{\mathrm{Mn}}\frac{W_{\mathrm{s}}}{W_{\mathrm{m}}}{m}_{\left[\mathrm{Mn}\right]},\hfill \end{array}$$

(74)

where

$$\begin{array}{cc}\hfill W_{\mathrm{m}}& =m_{\left[\mathrm{C}\right]}+m_{\left[\mathrm{V}\right]}+m_{\left[\mathrm{Ti}\right]}+m_{\left[\mathrm{Si}\right]}+m_{\left[\mathrm{Mn}\right]}+m_{\left[\mathrm{Fe}\right]}+m_{\left[\mathrm{O}\right]},\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill W_{\mathrm{s}}& =\frac{M_{{\mathrm{V}}_2{\mathrm{O}}_3}}{2M_{\mathrm{V}}}(m_{\left[\mathrm{V}\right]}^0-m_{\left[\mathrm{V}\right]})+\frac{M_{\mathrm{Ti}{\mathrm{O}}_2}}{M_{\mathrm{Ti}}}(m_{\left[\mathrm{Ti}\right]}^0-m_{\left[\mathrm{Ti}\right]})+\frac{M_{\mathrm{Si}{\mathrm{O}}_2}}{M_{\mathrm{Si}}}(m_{\left[\mathrm{Si}\right]}^0-m_{\left[\mathrm{Si}\right]})\hfill \\ \hfill & +\frac{M_{\mathrm{MnO}}}{M_{\mathrm{Mn}}}(m_{\left[\mathrm{Mn}\right]}^0-m_{\left[\mathrm{Mn}\right]})+\frac{M_{\mathrm{FeO}}}{M_{\mathrm{Fe}}}(m_{\left[\mathrm{Fe}\right]}^0-m_{\left[\mathrm{Fe}\right]}).\hfill \end{array}$$

(76)

3. Numerical Simulation and Discussion

The values of the mass transfer coefficients of each element in the model are given in

Table 1. Mass transfer coefficients [20] ($\mathrm{m}·{\mathrm{s}}^{-1}$).

Parameters	${\beta }_{\left[\mathrm{Fe}\right]}$	${\beta }_{\left[\mathrm{C}\right]}$	${\beta }_{\left[\mathrm{V}\right]}$	${\beta }_{\left[\mathrm{Ti}\right]}$	${\beta }_{\left[\mathrm{Si}\right]}$	${\beta }_{\left[\mathrm{Mn}\right]}$
Value	$1\times {10}^{-3}$	$3\times {10}^{-6}$	$3.5\times {10}^{-5}$	$2.4\times {10}^{-5}$	$1.9\times {10}^{-5}$	$2.65\times {10}^{-5}$
Parameters	${\beta }_{\left(\mathrm{FeO}\right)}$	${\beta }_{\left[\mathrm{O}\right]}$	${\beta }_{\left({\mathrm{V}}_2{\mathrm{O}}_3\right)}$	${\beta }_{\left({\mathrm{TiO}}_2\right)}$	${\beta }_{\left({\mathrm{SiO}}_2\right)}$	${\beta }_{\left(\mathrm{MnO}\right)}$
Value	$3.4\times {10}^{-6}$	$5\times {10}^{-6}$	$3.2\times {10}^{-8}$	$7\times {10}^{-8}$	$5\times {10}^{-8}$	$3.4\times {10}^{-8}$

[20]. The values of the standard Gibbs free energy of each element in the model are given in

Table 2. Standard Gibbs Free Energies [22] ($\Delta G=A+B·T$ $/\mathrm{J}·\mathrm{mo}{\mathrm{l}}^{-1}$).

Chemical Reaction	$\mathit{A}/\mathbf{J}·\mathbf{mo}{\mathbf{l}}^{-1}$	$\mathit{B}/\mathbf{J}·{(\mathbf{mol}·\mathbf{K})}^{-1}$
$\left(\mathrm{FeO}\right)=\left[\mathrm{Fe}\right]+\left[\mathrm{O}\right]$	121,009	−52.35
$\left[\mathrm{V}\right]+\frac{3}{2}\left(\mathrm{FeO}\right)=\frac{1}{2}\left({\mathrm{V}}_2{\mathrm{O}}_3\right)+\frac{3}{2}\left[\mathrm{Fe}\right]$	−452,710	137.55
$\left[\mathrm{Ti}\right]+2\left(\mathrm{FeO}\right)=\left(\mathrm{Ti}{\mathrm{O}}_2\right)+2\left[\mathrm{Fe}\right]$	−835,421	125.87
$\left[\mathrm{Si}\right]+2\left(\mathrm{FeO}\right)=\left(\mathrm{Si}{\mathrm{O}}_2\right)+2\left[\mathrm{Fe}\right]$	−386,769	202.3
$\left[\mathrm{Mn}\right]+\left(\mathrm{FeO}\right)=\left(\mathrm{MnO}\right)+\left[\mathrm{Mn}\right]$	−123,307	56.48
$\left[\mathrm{V}\right]+\frac{3}{2}\left[\mathrm{O}\right]=\frac{1}{2}\left({\mathrm{V}}_2{\mathrm{O}}_3\right)$	−428,826	168.11
$\left[\mathrm{Ti}\right]+2\left[\mathrm{O}\right]=\left(\mathrm{Ti}{\mathrm{O}}_2\right)$	−932,145	167.84
$\left[\mathrm{Si}\right]+2\left[\mathrm{O}\right]=\left(\mathrm{Si}{\mathrm{O}}_2\right)$	−594,285	229.76
$\left[\mathrm{Mn}\right]+\left[\mathrm{O}\right]=\left(\mathrm{MnO}\right)$	−244,316	106.84

[22]. The equilibrium constant of the chemical reactions (13) and (31) are

$$\begin{array}{cc}\hfill K_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}& =exp\left(-\frac{\Delta G_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}}{R{T}^{\mathrm{sm}}}\right),\hfill \\ \hfill K_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}& =exp\left(-\frac{\Delta G_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}}{R{T}^{\mathrm{es}}}\right),\hfill \end{array}$$

where $\Delta G_{\left(\mathrm{FeO}\right)}^{\mathrm{sm}}$ and $\Delta G_{\left(\mathrm{FeO}\right)}^{\mathrm{es}}$ are the Gibbs free energies of the chemical reactions (13) and (31) in Table 2, $R=8.134\mathrm{J}/(\mathrm{mol}·\mathrm{K})$ is the ideal gas constant, and $T^{\mathrm{sm}}$ and $T^{\mathrm{es}}$ are the average temperatures of the slag–metal interface and the emulsion system, respectively. According to [1], $T^{\mathrm{sm}}$ and $T^{\mathrm{es}}$ can be taken as

$$\begin{array}{cc}\hfill T^{\mathrm{sm}}& =1573\mathrm{K},\hfill \\ \hfill T^{\mathrm{es}}& =1673\mathrm{K}.\hfill \end{array}$$

The values of the initial conditions of each element in the model are given in

Table 3. Initial conditions of each element in the model [20,22] ($\mathrm{kg}$).

Parameter	${\mathit{m}}_{\left[\mathbf{C}\right]}^0$	${\mathit{m}}_{\left[\mathbf{V}\right]}^0$	${\mathit{m}}_{\left[\mathbf{Ti}\right]}^0$	${\mathit{m}}_{\left[\mathbf{Si}\right]}^0$	${\mathit{m}}_{\left[\mathbf{Mn}\right]}^0$	${\mathit{m}}_{\left[\mathbf{Fe}\right]}^0$	${\mathit{m}}_{\left[\mathbf{O}\right]}^0$	${\mathit{W}}_{\mathit{m}}^0$	${\mathit{W}}_{\mathit{s}}^0$
Value	3014.2	210.7	113.4	205.8	210.7	66,210	14	70,000	0

[20,22]. The proportionality coefficients in the model are given in

Table 4. Proportionality coefficient [1,22].

Parameter	${\mathit{k}}^{\mathbf{sm}}$	${\mathit{k}}^{\mathbf{eg}}$	${\mathit{k}}^{\mathbf{es}}$	${\mathit{k}}_{\left(\mathbf{FeO}\right)}$
Value	2.20	1.35	7.65	0.15

[1,22]. In addition, the oxygen flow $Q_{{\mathrm{O}}_2}$ can be taken as [20]

$$Q_{{\mathrm{O}}_2}=\frac{8}{3}{\mathrm{m}}^3/\mathrm{s}.$$

Furthermore, the densities of molten steel (${\rho }_{\mathrm{m}}$) and of slag (${\rho }_{\mathrm{s}}$) can be taken as [22]

$$\begin{array}{cc}\hfill {\rho }_{\mathrm{m}}& =7\times {10}^3\mathrm{kg}/{\mathrm{m}}^3,\hfill \\ \hfill {\rho }_{\mathrm{s}}& =3\times {10}^3\mathrm{kg}/{\mathrm{m}}^3.\hfill \end{array}$$

According to the parameters and initial conditions above, the MATLAB [26] numerical simulation results and discussion are as follows.

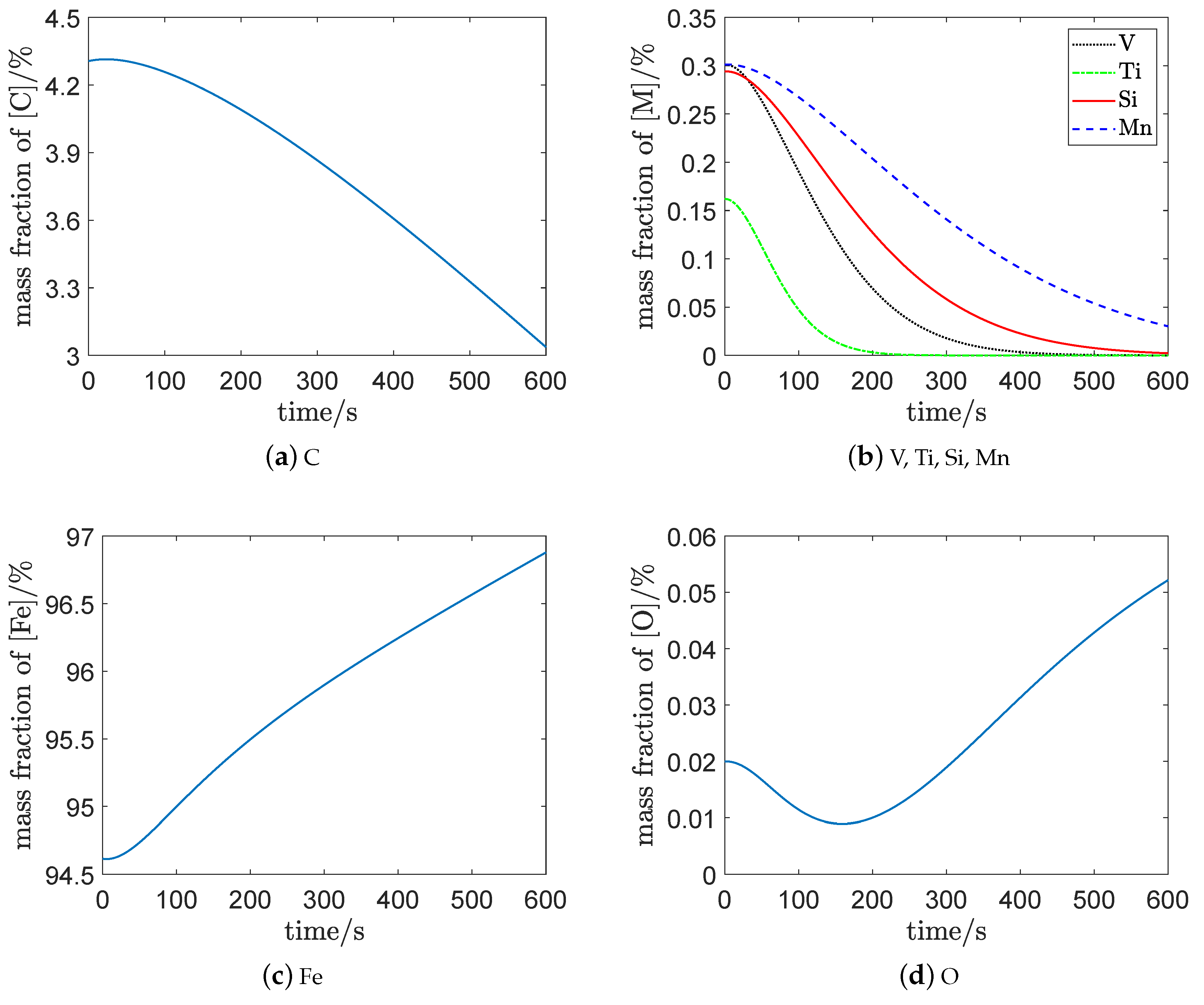
The composition of the molten steel is shown in Figure 3. From about 0–0.5 min (at the beginning), the slope of each curve is fairly flat, which indicates that the mass fraction remained almost unchanged. The reason for this is that the slag–metal interface and the emulsion system gradually formed at the beginning and, so, the contact area of each reaction was not large enough to visually change the content of each element. As the contact area of the slag–metal interface and the emulsion system are considered to be non-constant, the model in this paper can capture this characteristic.

Figure 3a shows that the carbon content changed slightly at the beginning, with the decarburization rate increasing later. The reason for this is that the emulsion system was present at the beginning of generation and the contact area of the decarbonizing reaction limited the decarbonization rate.

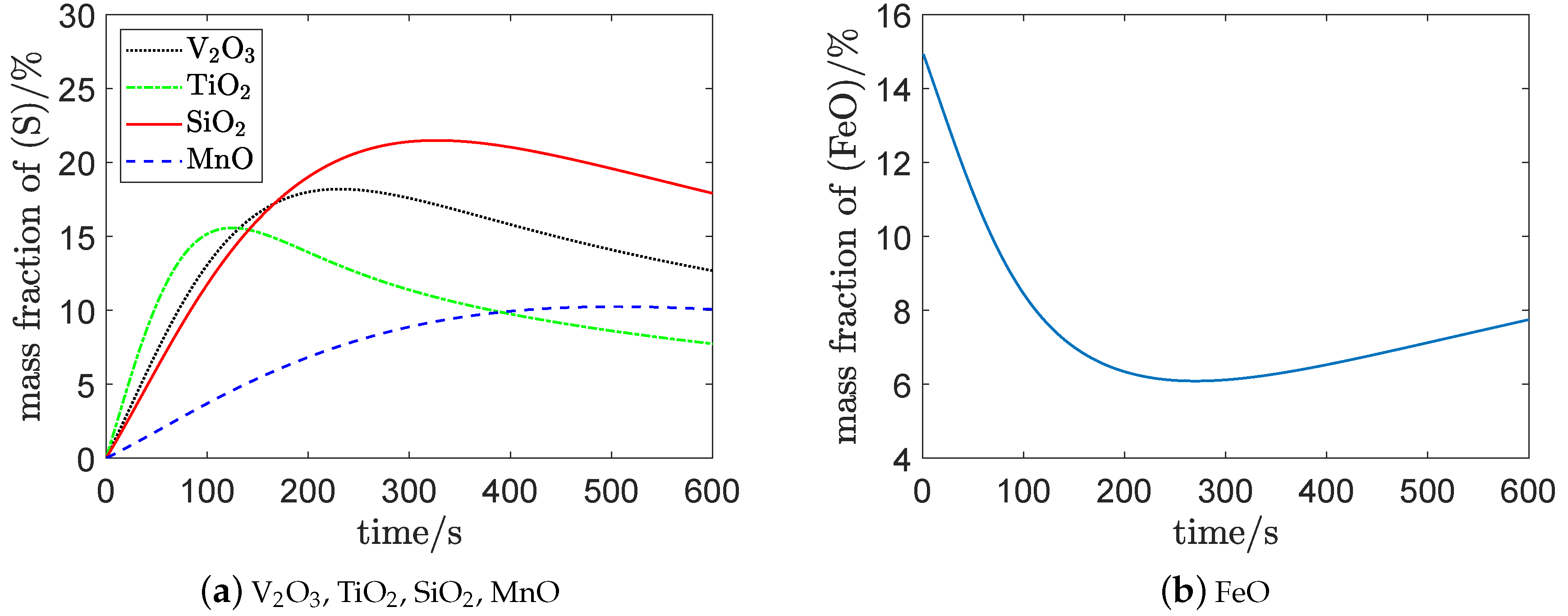
Figure 3a,b show that the mass fraction of $\left[\mathrm{C}\right]$ was about $4.02\%$. Meanwhile, the mass fraction of $\left[\mathrm{V}\right]$ reached the endpoint control target of the vanadium extraction process [1]:

$$\begin{array}{cc}\hfill {\omega }_{\left[\mathrm{C}\right]}& \ge 3.2\%,\hfill \\ \hfill {\omega }_{\left[\mathrm{V}\right]}& \le 0.05\%,\hfill \end{array}$$

where ${\omega }_{\left[\mathrm{M}\right]}$ is the mass fraction of $\left[\mathrm{M}\right]$.

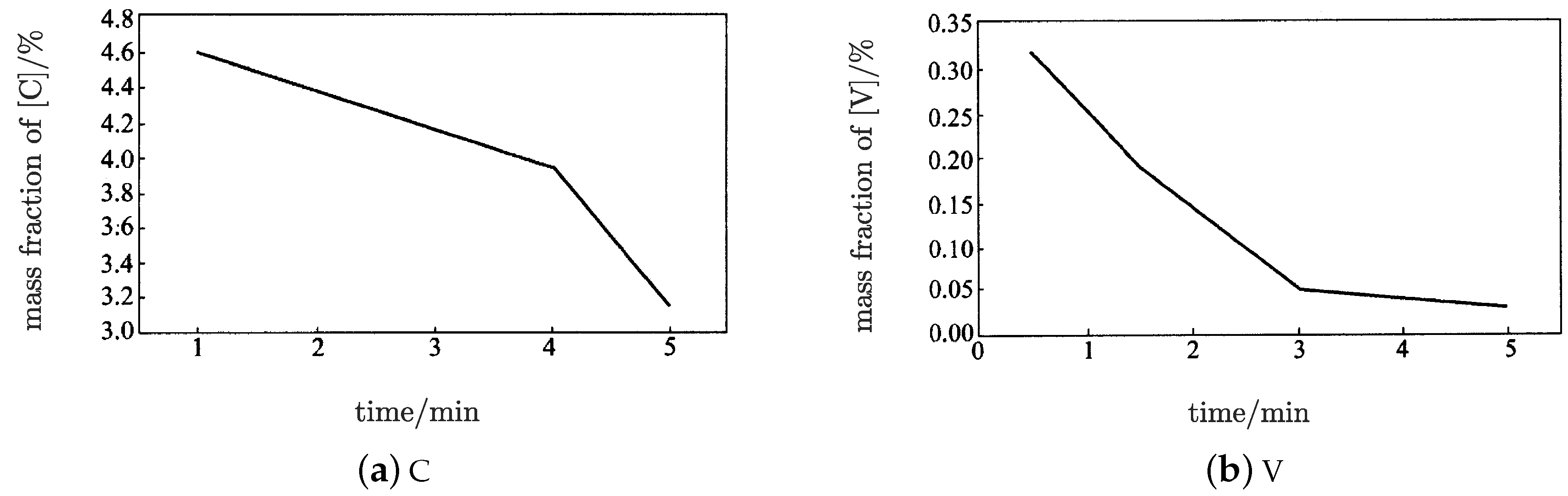
The mass fractions of $\left[\mathrm{C}\right]$ and $\left[\mathrm{V}\right]$ were about $4.02\%$ and $0.05\%$, respectively, when the endpoint control target was reached; which is consistent with Figure 4 [1]. In Figure 4, the mass fraction of $\left[\mathrm{C}\right]$ was about $4.1\%$ when the mass fraction of $\left[\mathrm{V}\right]$ reached $0.05\%$.

The mass fractions of $\left[\mathrm{C}\right]$ and $\left[\mathrm{V}\right]$ were about $3.5\%$ and 0 when the curve of $\left[\mathrm{V}\right]$ became approximately parallel to the horizontal axis. In Figure 4, the mass fraction of $\left[\mathrm{C}\right]$ was about $3.5\%$ when the mass fraction of $\left[\mathrm{V}\right]$ reached $0.025\%$.

According to (68) and (69), we have

$$\frac{1}{r_{\mathrm{C}}}\frac{1}{m_{\left[\mathrm{C}\right]}}\mathrm{d}{m}_{\left[\mathrm{C}\right]}=\frac{1}{r_{\mathrm{V}}}\frac{1}{m_{\left[\mathrm{V}\right]}}\mathrm{d}{m}_{\left[\mathrm{V}\right]}.$$

Integrating both sides of the equation above and substituting the initial conditions, we can obtain the first integrals of $m_{\left[\mathrm{C}\right]}$ and $m_{\left[\mathrm{V}\right]}$:

$$\frac{1}{r_{\mathrm{C}}}ln\frac{m_{\left[\mathrm{C}\right]}}{m_{\left[\mathrm{C}\right]}^0}=\frac{1}{r_{\mathrm{V}}}ln\frac{m_{\left[\mathrm{V}\right]}}{m_{\left[\mathrm{V}\right]}^0}.$$

(77)

The Equation (77) shows that $m_{\left[\mathrm{C}\right]}$ and $m_{\left[\mathrm{V}\right]}$ changed uniformly. When $m_{\left[\mathrm{V}\right]}$ was reduced, the mass of $m_{\left[\mathrm{C}\right]}$ was reduced accordingly. Equation (77) implies a contradiction between “vanadium extraction” and “carbon protection”. It is impossible to oxidize all the $\left[\mathrm{V}\right]$ into the slag and keep enough $\left[\mathrm{C}\right]$ in the molten steel simultaneously. In fact,

$$m_{\left[\mathrm{C}\right]}\to 0$$

as $m_{\left[\mathrm{V}\right]}\to 0$. That is to say, in order to keep enough carbon, there must be a certain amount of $\left[\mathrm{V}\right]$ left.

Similarly to (77), we obtain a series of the first integrals by (69)–(72):

$$\frac{1}{r_{\mathrm{C}}}ln\frac{m_{\left[\mathrm{C}\right]}}{m_{\left[\mathrm{C}\right]}^0}=\frac{1}{r_{\mathrm{V}}}ln\frac{m_{\left[\mathrm{V}\right]}}{m_{\left[\mathrm{V}\right]}^0}=\frac{1}{r_{\mathrm{Ti}}}ln\frac{m_{\left[\mathrm{Ti}\right]}}{m_{\left[\mathrm{Ti}\right]}^0}=\frac{1}{r_{\mathrm{Si}}}ln\frac{m_{\left[\mathrm{Si}\right]}}{m_{\left[\mathrm{Si}\right]}^0}=\frac{1}{r_{\mathrm{Mn}}}ln\frac{m_{\left[\mathrm{Mn}\right]}}{m_{\left[\mathrm{Mn}\right]}^0}.$$

(78)

The equation (78) shows that the competitive oxidation between each element is mainly related to their initial value $m_{\left[\mathrm{M}\right]}^0$ and parameter $r_{\mathrm{M}}$. The parameter $r_{\mathrm{M}}$ is related to the mass transfer coefficient of each element and the Gibbs free energy of each reaction. Thus, the initial value and the mass transfer coefficient of each element and the Gibbs free energy of each reaction work together to control their oxidation rate and oxygen consumption ratio, which affects the competitive oxidation between elements. Equation (78) can be used to estimate the content of each element at the end of vanadium extraction process. For example, it is generally used to measure the carbon content of the iron water after the vanadium extraction process. Then, the other element’s contents can be estimated by using (78).

At the end of vanadium extraction, the mass fraction of $\left[\mathrm{V}\right]$ and $\left[\mathrm{Ti}\right]$ were approximately parallel to the horizontal axis, which implies that the oxidation of $\left[\mathrm{V}\right]$ and $\left[\mathrm{Ti}\right]$ had been approximately completed. The remaining $\left[\mathrm{Si}\right]$ and $\left[\mathrm{Mn}\right]$ in the molten pool are continuously oxidized in the steelmaking process.

Figure 3c shows that the mass fraction of $\left[\mathrm{Fe}\right]$ kept increasing with the oxidation of $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$. The reason for this is that a lot of $\left[\mathrm{Fe}\right]$ is generated constantly with the consumption of $\left(\mathrm{FeO}\right)$, which is then fed back to the molten steel.

Figure 3d shows that the mass fraction of $\left[\mathrm{O}\right]$ decreased first, then gradually rose to a higher level. This implies that some $\left[\mathrm{O}\right]$ and $\left[\mathrm{Fe}\right]$ combined to supply the oxidants $\left(\mathrm{FeO}\right)$ at the beginning of vanadium extraction process. With the increase of $\left(\mathrm{FeO}\right)$ generated by the top-blown oxygen, the $\left(\mathrm{FeO}\right)$ decomposed to improve $\left[\mathrm{O}\right]$; that is, the mass fraction of $\left[\mathrm{O}\right]$ consequently increased.

The composition of the slag is shown in Figure 5. Figure 5a shows that the curves of $\left(\mathrm{Ti}{\mathrm{O}}_2\right)$, $\left(\mathrm{Si}{\mathrm{O}}_2\right)$, and $\left({\mathrm{V}}_2{\mathrm{O}}_3\right)$ quickly reached their respective maxima, then decreased gradually. However, the curve of $\left(\mathrm{MnO}\right)$ was relatively flat, indicating that $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{V}\right]$ were more easily oxidized than $\left[\mathrm{Mn}\right]$.

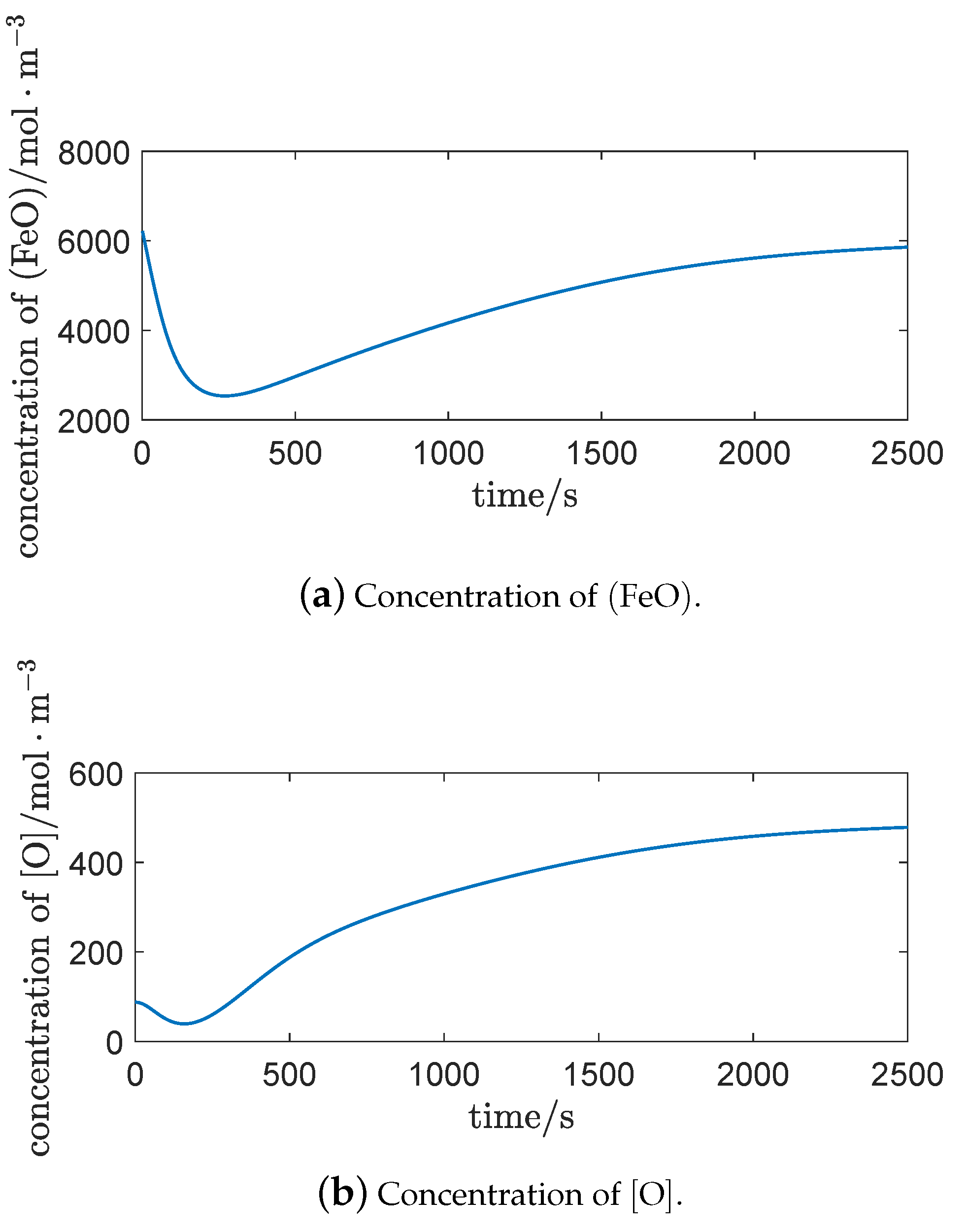
Figure 5b shows that the content of $\left(\mathrm{FeO}\right)$ was higher at first, reached its lowest level in the intermediate stage, and gradually recovered in the latter period. The reasons for this are that:

• At the beginning of vanadium extraction process, with the rapid formation of the gas–liquid interface of the impact pit, plenty of $\left(\mathrm{FeO}\right)$ were generated through the oxidation reaction (1). Then, the $\left(\mathrm{FeO}\right)$ took part in the oxidation reaction at the slag–metal interface and in the emulsion system as an oxidant. At that time, the slag–metal interface and the emulsion system were at the beginning of generation, and the contact areas of the corresponding oxidation reactions were small. So, the consumption of $\left(\mathrm{FeO}\right)$ was not large.
• During the vanadium extraction process, with the formation of the slag–metal interface and the emulsion system, the oxidation rates of $\left[\mathrm{C}\right]$, $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$ continually increased. As $\left(\mathrm{FeO}\right)$ was largely consumed as an oxidant, the content of $\left(\mathrm{FeO}\right)$ reduced significantly.
• At the end of vanadium extraction process, with a decrease of $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$, the consumption of $\left(\mathrm{FeO}\right)$ also decreased. As $\left(\mathrm{FeO}\right)$ was generated continually at the gas–liquid interface of the impact pit, the content of $\left(\mathrm{FeO}\right)$ then recovered.

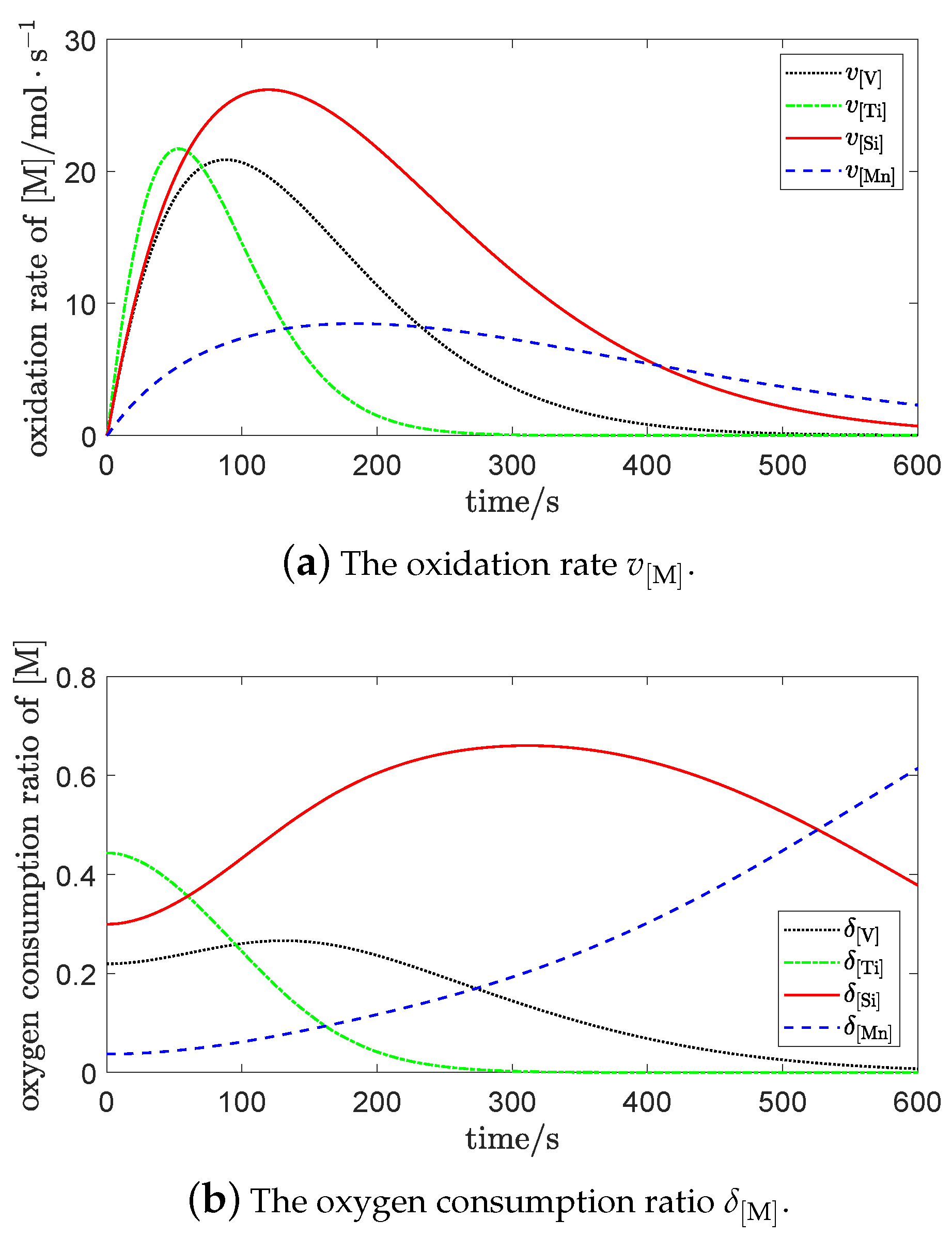
The oxidation rates of each element were

$$v_{\left[\mathrm{M}\right]}=-\frac{\mathrm{d}{n}_{\left[\mathrm{M}\right]}}{\mathrm{d}t}(\mathrm{M}=\mathrm{V},\mathrm{Ti},\mathrm{Si},\mathrm{Mn})$$

and the oxygen consumption ratios of each element were

$$\begin{array}{cc}\hfill {\delta }_{\left[\mathrm{V}\right]}& =\frac{3}{2\delta }\frac{\mathrm{d}{n}_{\left[\mathrm{V}\right]}}{\mathrm{d}t},\hfill \\ \hfill {\delta }_{\left[\mathrm{Ti}\right]}& =\frac{2}{\delta }\frac{\mathrm{d}{n}_{\left[\mathrm{Ti}\right]}}{\mathrm{d}t},\hfill \\ \hfill {\delta }_{\left[\mathrm{Si}\right]}& =\frac{2}{\delta }\frac{\mathrm{d}{n}_{\left[\mathrm{Si}\right]}}{\mathrm{d}t},\hfill \\ \hfill {\delta }_{\left[\mathrm{Mn}\right]}& =\frac{1}{\delta }\frac{\mathrm{d}{n}_{\left[\mathrm{Mn}\right]}}{\mathrm{d}t},\hfill \end{array}$$

where

$$\delta =\frac{3}{2}\frac{\mathrm{d}{n}_{\left[\mathrm{V}\right]}}{\mathrm{d}t}+2\frac{\mathrm{d}{n}_{\left[\mathrm{Ti}\right]}}{\mathrm{d}t}+2\frac{\mathrm{d}{n}_{\left[\mathrm{Si}\right]}}{\mathrm{d}t}+\frac{\mathrm{d}{n}_{\left[\mathrm{Mn}\right]}}{\mathrm{d}t}.$$

Figure 6 shows that:

• At the beginning of vanadium extraction process, the order of oxidation rates of each element was $v_{\left[\mathrm{Ti}\right]}>v_{\left[\mathrm{Si}\right]}>v_{\left[\mathrm{V}\right]}>v_{\left[\mathrm{Mn}\right]}$. This indicates that the oxygen was mainly used to oxidize $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{V}\right]$ in the early stage; only a small amount of oxidant was used to oxidize $\left[\mathrm{Mn}\right]$. As the Gibbs free energy of $\left[\mathrm{Ti}\right]$ can be large, its oxygen consumption ratio decreased gradually. The reason for this is that its concentration decreased rapidly, making its oxidation reaction most violent in the beginning.
• During the vanadium extraction process, the oxidation rate and the oxygen consumption ratio of $\left[\mathrm{Si}\right]$ became the strongest, following the consumption of $\left[\mathrm{Ti}\right]$. In the whole process of blowing, the oxidation rate and the oxygen consumption ratio of $\left[\mathrm{Si}\right]$ was bigger than that of $\left[\mathrm{V}\right]$.
• At the end of vanadium extraction process, the oxygen consumption ratio of $\left[\mathrm{Mn}\right]$ basically monotonically increased, following the consumption of $\left[\mathrm{Ti}\right]$, $\left[\mathrm{V}\right]$, and $\left[\mathrm{Si}\right]$. The oxidation rate and the oxygen consumption ratio of $\left[\mathrm{Mn}\right]$ exceeded that of $\left[\mathrm{Si}\right]$ in the later stage, which indicates that more $\left[\mathrm{Mn}\right]$ was oxidized in middle and later stages.

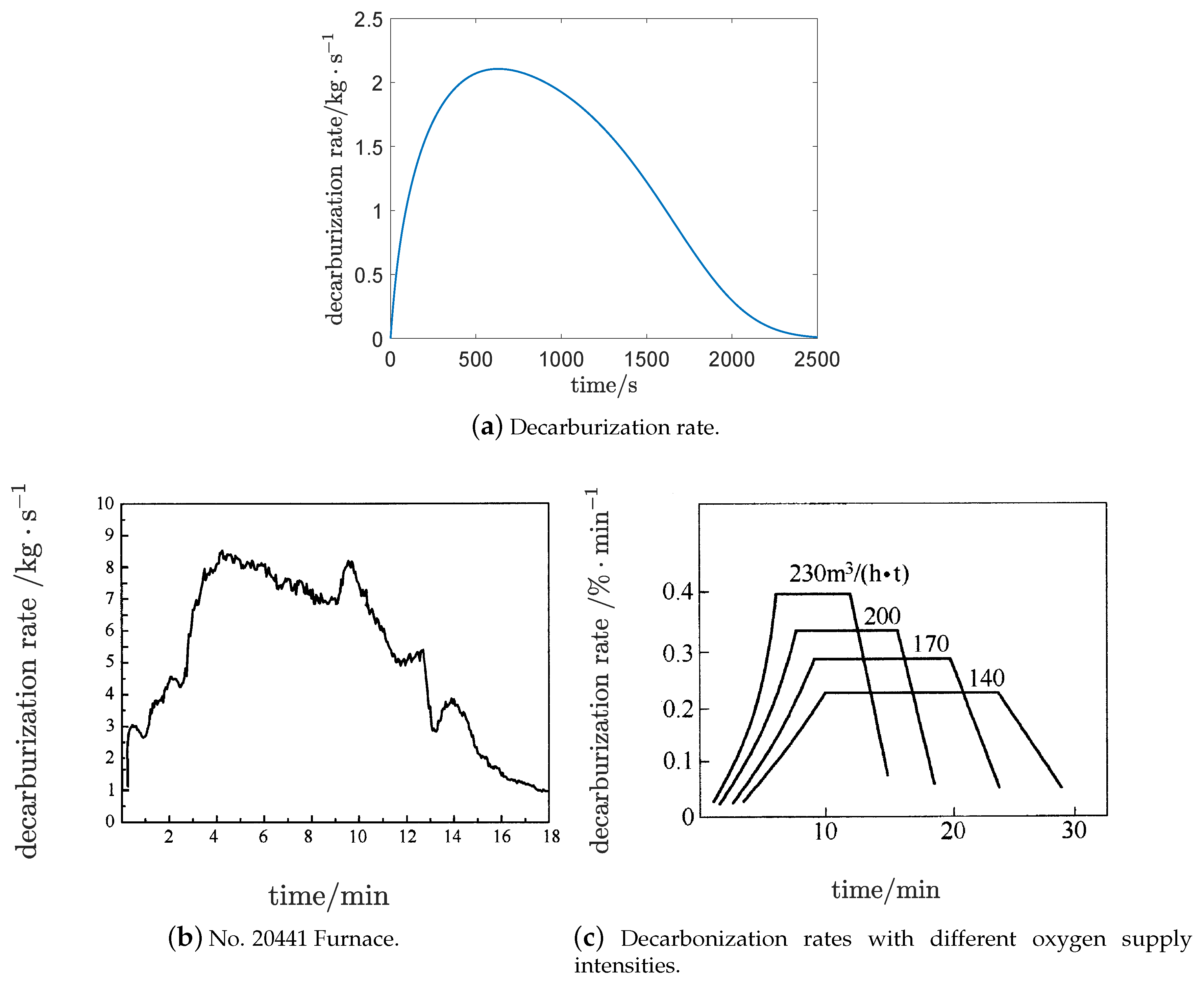
Figure 7a shows that the decarburization rate gradually accelerated, increasing almost linearly at the beginning. The decarbonization rate reached its maximum and remained almost unchanged for some time. Finally, the decarbonization rate decreased with an approximate exponential decay, along with the decrease of $\left[\mathrm{C}\right]$. According to (47), (59), and the equations of model (68), we have

$$\frac{\mathrm{d}{m}_{\left[\mathrm{C}\right]}}{\mathrm{d}t}=-M_{\mathrm{C}}{\beta }_{\left[\mathrm{C}\right]}{A}^{\mathrm{eg}}{c}_{\left[\mathrm{C}\right]}.$$

(79)

Obviously, the decarburization rate is determined by the contact area $A^{\mathrm{eg}}$ and concentration $c_{\left[\mathrm{C}\right]}$. The probable causes for the “trapezoid” structure of the decarburization rate are:

• At the beginning of vanadium extraction process, the contact area of the decarbonization reaction was small, with little consumption of $\left[\mathrm{C}\right]$. At this time, the effect of $A^{\mathrm{eg}}$ was greater than that of $c_{\left[\mathrm{C}\right]}$. The main reason for the linear growth of the decarburization rate was that the contact area $A^{\mathrm{eg}}$ increased almost linearly.
• During the vanadium extraction process, with the formation of the emulsion system, the effects of $A^{\mathrm{eg}}$ and $c_{\left[\mathrm{C}\right]}$ reached a balance, ausing the decarburization rate to remain almost unchanged.
• At the end of vanadium extraction process, the effect of $c_{\left[\mathrm{C}\right]}$ was greater than that of $A^{\mathrm{eg}}$. The decarbonization rate decreased with the decrease of $\left[\mathrm{C}\right]$.

Figure 7b [27] is from the production data of a steel plant. It shows a similar “trapezoid” structure of the decarburization rate to Figure 7a. Figure 7c [22] is the decarbonization rates for different oxygen supply intensities. The decarburization rate curves show a similar “trapezoid” structure for converters with different oxygen blowing strengths and capacities.

Figure 8 shows that $c_{\left[\mathrm{O}\right]}$ and $c_{\left(\mathrm{FeO}\right)}$ changed consistently, which is in agreement with the distribution law of the solution.

Note that

$$\begin{array}{cc}\hfill r_{\mathrm{V}}& =r_{\mathrm{Fe}}^{\mathrm{V}}+r_{\mathrm{O}}^{\mathrm{V}}\hfill \\ \hfill r_{\mathrm{Ti}}& =r_{\mathrm{Fe}}^{\mathrm{Ti}}+r_{\mathrm{O}}^{\mathrm{Ti}}\hfill \\ \hfill r_{\mathrm{Si}}& =r_{\mathrm{Fe}}^{\mathrm{Si}}+r_{\mathrm{O}}^{\mathrm{Si}}\hfill \\ \hfill r_{\mathrm{Mn}}& =r_{\mathrm{Fe}}^{\mathrm{Mn}}+r_{\mathrm{O}}^{\mathrm{Mn}}\hfill \end{array}$$

By (68)–(74), we obtain the first integral as follows

$$\begin{array}{cc}\hfill \frac{2{\eta }_{{\mathrm{O}}_2}{Q}_{{\mathrm{O}}_2}}{V_{\mathrm{mol}}}& =-\frac{1}{M_{\mathrm{Fe}}}\frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}}{\mathrm{d}t}-\frac{1}{M_{\mathrm{C}}}\frac{\mathrm{d}{m}_{\left[\mathrm{C}\right]}}{\mathrm{d}t}-\frac{3}{2}\frac{1}{M_{\mathrm{V}}}\frac{\mathrm{d}{m}_{\left[\mathrm{V}\right]}}{\mathrm{d}t}-2\frac{1}{M_{\mathrm{Ti}}}\frac{\mathrm{d}{m}_{\left[\mathrm{Ti}\right]}}{\mathrm{d}t}\hfill \\ \hfill & -2\frac{1}{M_{\mathrm{Si}}}\frac{\mathrm{d}{m}_{\left[\mathrm{Si}\right]}}{\mathrm{d}t}-\frac{1}{M_{\mathrm{Mn}}}\frac{\mathrm{d}{m}_{\left[\mathrm{Mn}\right]}}{\mathrm{d}t}+\frac{1}{M_{\mathrm{O}}}\frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}}{\mathrm{d}t}.\hfill \end{array}$$

(80)

Equation (80) shows the conservation of the oxygen in the system. The left side of the Equation (80) shows the oxygen sources of the system, and the right side shows where the oxygen goes to. In the middle and later stages, the oxidation rates of $\left[\mathrm{V}\right]$, $\left[\mathrm{Ti}\right]$, $\left[\mathrm{Si}\right]$, and $\left[\mathrm{Mn}\right]$ were very small, and the top-blown oxygen was almost entirely used for decarbonization; that is,

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}{m}_{\left[\mathrm{V}\right]}}{\mathrm{d}t},\frac{\mathrm{d}{m}_{\left[\mathrm{Ti}\right]}}{\mathrm{d}t},\frac{\mathrm{d}{m}_{\left[\mathrm{Si}\right]}}{\mathrm{d}t},\frac{\mathrm{d}{m}_{\left[\mathrm{Mn}\right]}}{\mathrm{d}t}=0,\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill & -\frac{1}{M_{\mathrm{C}}}\frac{\mathrm{d}{m}_{\left[\mathrm{C}\right]}}{\mathrm{d}t}=\frac{2{\eta }_{{\mathrm{O}}_2}{Q}_{{\mathrm{O}}_2}}{V_{\mathrm{mol}}}.\hfill \end{array}$$

(82)

Substituting (81) and (82) into (80), we have

$$\frac{1}{M_{\mathrm{Fe}}}\frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}}{\mathrm{d}t}=\frac{1}{M_{\mathrm{O}}}\frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}}{\mathrm{d}t}.$$

(83)

Taking the derivative of (65) with respect to t, we have

$$\frac{\mathrm{d}{m}_{\left(\mathrm{FeO}\right)}}{\mathrm{d}t}=-\frac{M_{\mathrm{FeO}}}{M_{\mathrm{Fe}}}\frac{\mathrm{d}{m}_{\left[\mathrm{Fe}\right]}}{\mathrm{d}t}.$$

(84)

Substituting (83) into (84), we have

$$\frac{\mathrm{d}{m}_{\left(\mathrm{FeO}\right)}}{\mathrm{d}t}=\frac{M_{\mathrm{FeO}}}{M_{\mathrm{O}}}\frac{\mathrm{d}{m}_{\left[\mathrm{O}\right]}}{\mathrm{d}t}.$$

(85)

Equation (85) implies that the masses of $\left(\mathrm{FeO}\right)$ and $\left[\mathrm{O}\right]$ change consistently.

4. Conclusions

A numerical simulation showed that the vanadium extraction process was approximately completed after about 4 min of blowing, providing an important reference for production control. The model in this paper demonstrates the characteristic that the mass fraction of each element remained almost unchanged at the beginning of the process, as the contact area of the slag–metal interface and the emulsion system were considered to be non-constant. Through analysis, the model exemplified a contradiction between “vanadium extraction” and “carbon protection”. This means that it is impossible to oxidize all of the $\left[\mathrm{V}\right]$ in the slag while simultaneously keeping enough $\left[\mathrm{C}\right]$ in the molten steel. The model also shows the competitive oxidation between each element, along with their factors. In fact, the initial value and the mass transfer coefficient of each element and the Gibbs free energy of each reaction work together to control the oxidation rates and oxygen consumption ratios, which affect the competitive oxidation between the elements. At the beginning of the vanadium extraction process, the decarburization rate increased almost linearly. Then, the decarburization rate remained almost unchanged, for some time. The model presents the “trapezoid” structure of the decarburization rate; there are few such results in the present literature. During the vanadium extraction process, the $c_{\left[\mathrm{O}\right]}$ and $c_{\left(\mathrm{FeO}\right)}$ values change consistently, which is in agreement with the distribution law of the solution. At the end of the vanadium extraction process, oxidation of $\left[\mathrm{V}\right]$ and $\left[\mathrm{Ti}\right]$ were approximately complete. The remaining $\left[\mathrm{Si}\right]$, $\left[\mathrm{Mn}\right]$, and $\left[\mathrm{C}\right]$ will, then, take part in the oxidation reaction of the steelmaking process.