Application of Duration Measure in Quantifying the Sensitivity of Project Returns to Changes in Discount Rates
Abstract
:1. Introduction
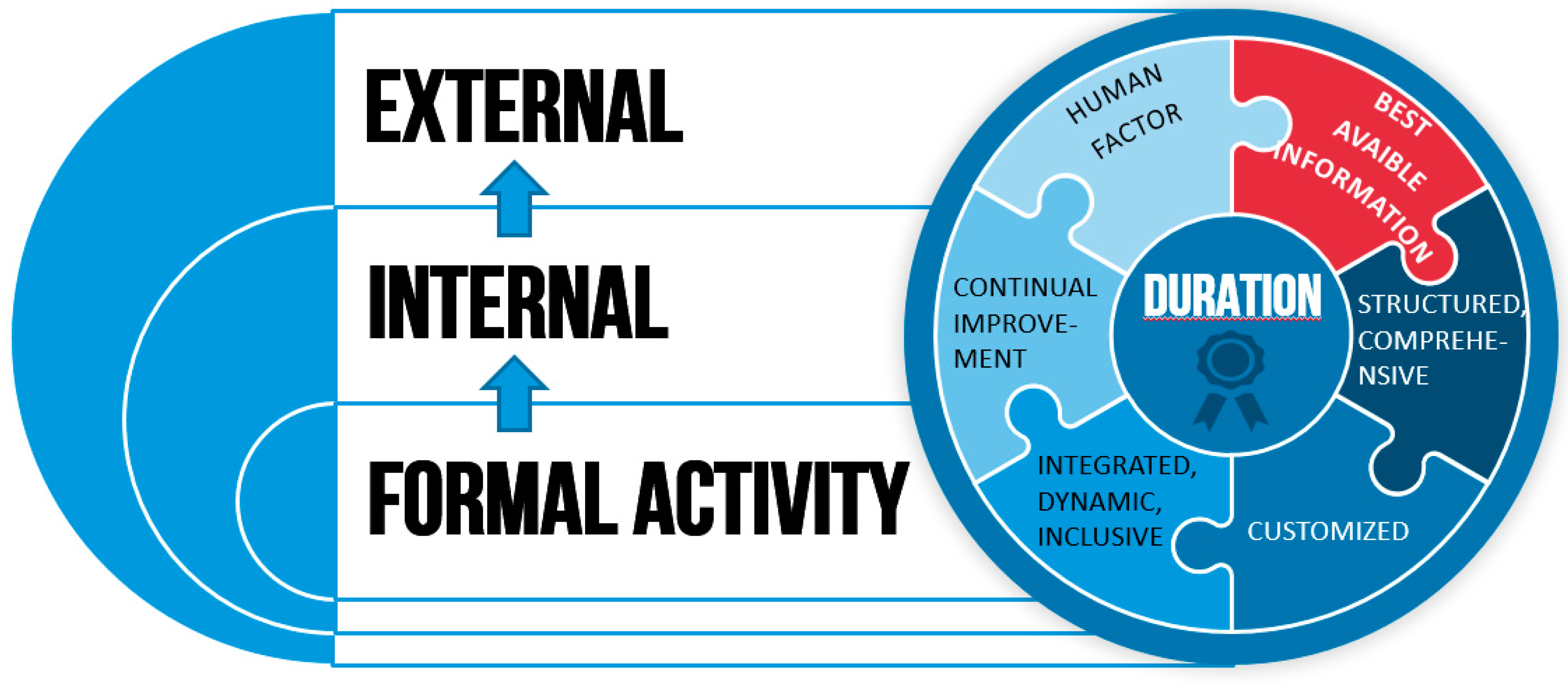
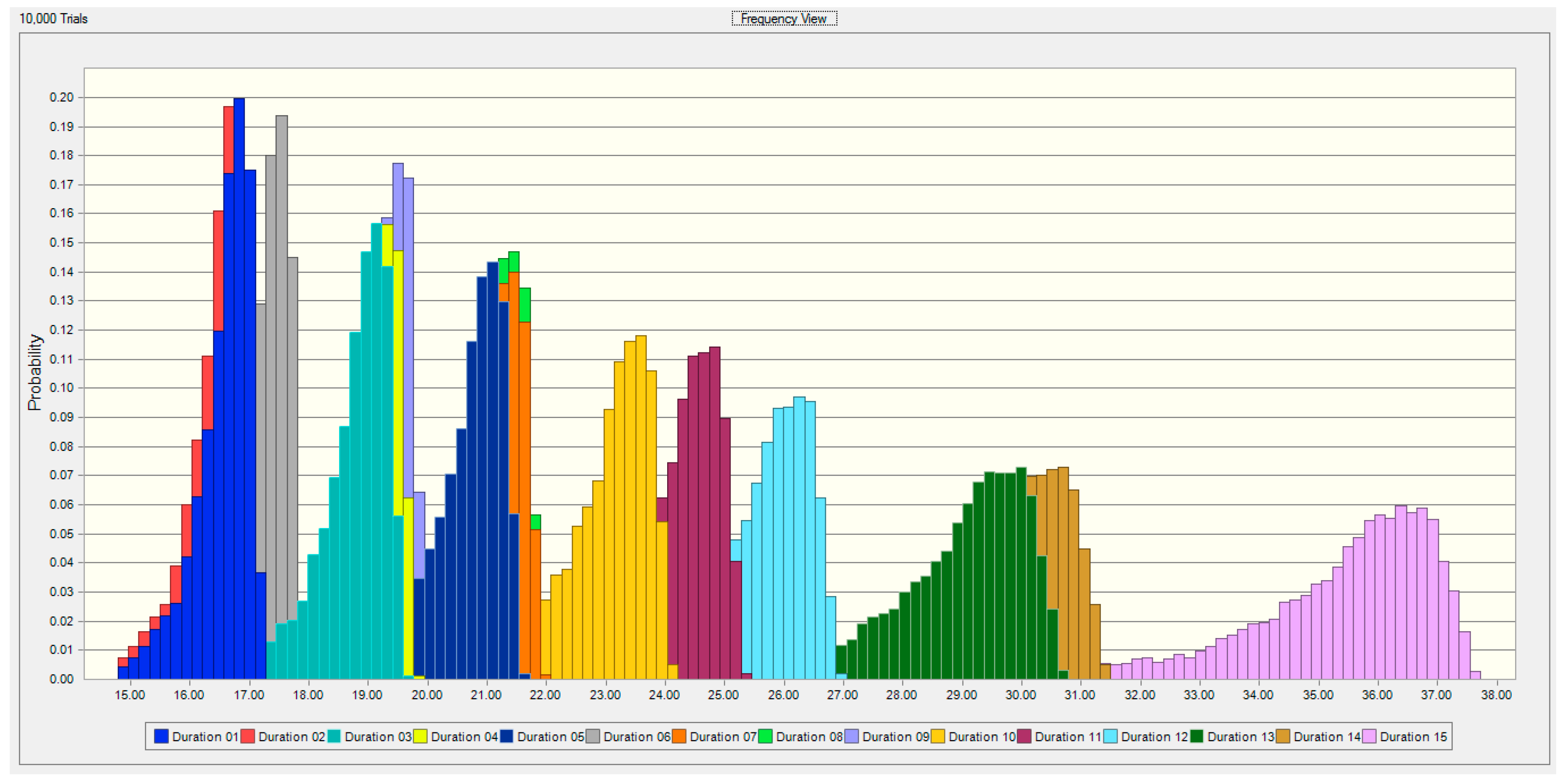
2. Project Duration
3. Duration and Sensitivity of the Project Returns to Changes in Discount Rates
4. Convexity
5. Discount Rate Risk and Reinvestment Risk
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Acebes, Fernando, María Pereda, David Poza, Javier Pajares, and José Manuel Galán. 2015. Stochastic earned value analysis using Monte Carlo simulation and statistical learning techniques. International Journal of Project Management 33: 1597–609. [Google Scholar] [CrossRef]
- Asadi, Pezhman, Javad Rezaeian Zeidi, Toraj Mojibi, Abdolreza Yazdani-Chamzini, and Jolanta Tamošaitienė. 2018. Project risk evaluation by using a new fuzzy model based on Elena guideline. Journal of Civil Engineering and Management 24: 284–300. [Google Scholar] [CrossRef]
- Bejaoui, Azza, and Adel Karaa. 2016. Revisiting the bull and bear markets notions in the Tunisian stock market: New evidence from multi-state duration-dependence Markov-switching models. Economic Modelling 59: 529–45. [Google Scholar] [CrossRef]
- Bessler, Wolfgang, and Dominik Wolff. 2014. Hedging European government bond portfolios during the recent sovereign debt crisis. Journal of International Financial Markets, Institutions and Money 33: 379–99. [Google Scholar] [CrossRef]
- Boquist, John A., George A. Racette, and Gary G. Schlarbaum. 1975. Duration and risk assessment for bonds and common stocks. The Journal of Finance 30: 1360–65. [Google Scholar] [CrossRef]
- Brandt, Michael W., Amit Goyal, Pedro Santa-Clara, and Jonathan R. Stroud. 2005. A Simulation Approach to Dynamic Portfolio Choice with an Application to Learning About Return Predictability. Review of Financial Studies 18: 831–73. [Google Scholar] [CrossRef]
- Buchner, Axel. 2015. Equilibrium option pricing: A Monte Carlo approach. Finance Research Letters 15: 138–45. [Google Scholar] [CrossRef]
- Cesari, Riccardo, and David Cremonini. 2003. Benchmarking, portfolio insurance and technical analysis: A Monte Carlo comparison of dynamic strategies of asset allocation. Journal of Economic Dynamics and Control 27: 987–1011. [Google Scholar] [CrossRef]
- Chatterjee, Kajal, Edmundas Kazimieras Zavadskas, Jolanta Tamošaitienė, Krishnendu Adhikary, and Samarjit Kar. 2018. A hybrid MCDM technique for risk management in construction projects. Symmetry 10: 46. [Google Scholar] [CrossRef]
- Cong, Fei, and Cornelis W. Oosterlee. 2016. Multi-period mean–variance portfolio optimization based on Monte-Carlo simulation. Journal of Economic Dynamics and Control 64: 23–38. [Google Scholar] [CrossRef]
- de Vasconcelos, Ana Brandão, António Cabaço, Manuel Duarte Pinheiro, and Armando Manso. 2016. The impact of building orientation and discount rates on a Portuguese reference building refurbishment decision. Energy Policy 91: 329–40. [Google Scholar] [CrossRef]
- Denault, Michel, and Jean-Guy Simonato. 2017. Dynamic portfolio choices by simulation-and-regression: Revisiting the issue of value function vs portfolio weight recursions. Computers & Operations Research 79: 174–89. [Google Scholar] [CrossRef]
- Dierkes, Thomas, and Karl Michael Ortmann. 2015. On the efficient utilisation of duration. Insurance: Mathematics and Economics 60: 29–37. [Google Scholar] [CrossRef]
- Fricke, Christoph, and Lukas Menkhoff. 2015. Financial conditions, macroeconomic factors and disaggregated bond excess returns. Journal of Banking & Finance 58: 80–94. [Google Scholar] [CrossRef]
- Fukuta, Yuichi, and Akiko Yamane. 2015. Value premium and implied equity duration in the Japanese stock market. Journal of International Financial Markets, Institutions and Money 39: 102–21. [Google Scholar] [CrossRef]
- García-Gusano, Diego, Kari Espegren, Arne Lind, and Martin Kirkengen. 2016. The role of the discount rates in energy systems optimisation models. Renewable and Sustainable Energy Reviews 59: 56–72. [Google Scholar] [CrossRef]
- Ghasemi, Foroogh, Mohammad Hossein Mahmoudi Sari, Vahidreza Yousefi, Reza Falsafi, and Jolanta Tamošaitienė. 2018. Project portfolio risk identification and analysis, considering project risk interactions and using Bayesian networks. Sustainability 10: 1609. [Google Scholar] [CrossRef]
- Grieves, Robin, Alan J. Marcus, and Adrian Woodhams. 2010. Delivery options and convexity in Treasury bond and note futures. Review of Financial Economics 19: 1–7. [Google Scholar] [CrossRef]
- Groom, Ben, Phoebe Koundouri, Ekaterini Panopoulou, and Theologos Pantelidis. 2007. Discounting the distant future: How much does model selection affect the certainty equivalent rate? Journal of Applied Econometrics 22: 641–56. [Google Scholar] [CrossRef]
- Gupta, Anurag, and Marti G. Subrahmanyam. 2000. An empirical examination of the convexity bias in the pricing of interest rate swaps. Journal of Financial Economics 55: 239–79. [Google Scholar] [CrossRef]
- Hanson, Samuel G. 2014. Mortgage convexity. Journal of Financial Economics 113: 270–99. [Google Scholar] [CrossRef]
- Hansson, Sven Ove, Kristin Lilieqvist, Karin Edvardsson Björnberg, and Maria Vredin Johansson. 2016. Time horizons and discount rates in Swedish environmental policy: Who decides and on what grounds? Futures 76: 55–66. [Google Scholar] [CrossRef]
- Hatchondo, Juan Carlos, and Leonardo Martinez. 2009. Long-duration bonds and sovereign defaults. Journal of International Economics 79: 117–25. [Google Scholar] [CrossRef]
- Hatefi, Seyed Morteza, and Jolanta Tamošaitienė. 2018. Construction projects assessment based on the sustainable development criteria by an integrated fuzzy AHP and improved GRA model. Sustainability 10: 991. [Google Scholar] [CrossRef]
- Houweling, Patrick, Albert Mentink, and Ton Vorst. 2005. Comparing possible proxies of corporate bond liquidity. Journal of Banking & Finance 29: 1331–58. [Google Scholar] [CrossRef]
- Hyong-Chol, O., Jong-Jun Jo, and Ji-Sok Kim. 2016. General properties of solutions to inhomogeneous Black–Scholes equations with discontinuous maturity payoffs. Journal of Differential Equations 260: 3151–72. [Google Scholar] [CrossRef]
- Jacoby, Gady, and Gordon S. Roberts. 2003. Default-and call-adjusted duration for corporate bonds. Journal of Banking & Finance 27: 2297–321. [Google Scholar] [CrossRef]
- Jagannathan, Ravi, David A. Matsa, Iwan Meier, and Vefa Tarhan. 2016. Why do firms use high discount rates? Journal of Financial Economics 120: 445–63. [Google Scholar] [CrossRef]
- Jouini, Elyès, and Clotilde Napp. 2014. How to aggregate experts’ discount rates: An equilibrium approach. Economic Modelling 36: 235–43. [Google Scholar] [CrossRef]
- Kazlauskienė, Vilma. 2015. Application of Social Discount Rate for Assessment of Public Investment Projects. Procedia—Social and Behavioral Sciences 213: 461–67. [Google Scholar] [CrossRef]
- Kolb, Robert W., and Raymond Chiang. 1981. Improving hedging performance using interest rate futures. Financial Management 10: 72–79. [Google Scholar] [CrossRef]
- Kolb, Robert W., and Raymond Chiang. 1982. Duration, immunization, and hedging with interest rate futures. Journal of Financial Research 5: 161–70. [Google Scholar] [CrossRef]
- Kossova, Tatiana, and Maria Sheluntcova. 2016. Evaluating performance of public sector projects in Russia: The choice of a social discount rate. International Journal of Project Management 34: 403–11. [Google Scholar] [CrossRef]
- Lee, Chijoo, and Eul-Bum Lee. 2017. Prediction method of real discount rate to improve accuracy of life-cycle cost analysis. Energy and Buildings 135: 225–32. [Google Scholar] [CrossRef]
- Lee, Hei Wai, Yan Alice Xie, and Jot Yau. 2011. The impact of sovereign risk on bond duration: Evidence from Asian sovereign bond markets. International Review of Economics & Finance 20: 441–51. [Google Scholar] [CrossRef]
- Lesseig, Vance P., and Duane Stock. 2000. Impact of correlation of asset value and interest rates upon duration and convexity of risky debt. Journal of Business Research 49: 289–301. [Google Scholar] [CrossRef]
- Lu, Erin P., Gene C. Lai, and Qingzhong Ma. 2017. Organizational structure, risk-based capital requirements, and the sales of downgraded bonds. Journal of Banking & Finance 74: 51–68. [Google Scholar] [CrossRef]
- Macaulay, Frederick R. 1938. Some Theoretical Problems Suggested by the Movements of Interest Rates, Bond Yields and Stock Prices in the United States Since 1856. New York: NBER Books. [Google Scholar]
- Nesticò, Antonio, and Gabriella Maselli. 2019. Intergenerational Discounting in the Economic Evaluation of Projects. In Smart Innovation, Systems and Technologies. Edited by Calabrò Francesco, Della Spina Lucia and Bevilacqua Carmelina. Cham: Springer, vol. 101. [Google Scholar] [CrossRef]
- Osborne, Michael J. 2005. On the computation of a formula for the duration of a bond that yields precise results. The Quarterly Review of Economics and Finance 45: 161–83. [Google Scholar] [CrossRef]
- Pajares, Javier, and Adolfo Lopez-Paredes. 2011. An extension of the EVM analysis for project monitoring: The Cost Control Index and the Schedule Control Index. International Journal of Project Management 29: 615–21. [Google Scholar] [CrossRef]
- Project Management Institute. 2017. A Guide to the Project Management Body of Knowledge (PMBOK Guide), 6th ed. Newtown Square: Project Management Institute, ISBN 978-1-62825-184-5. [Google Scholar]
- Sarkar, Sudipto. 1999. Duration and convexity of zero-coupon convertible bonds. Journal of Economics and Business 51: 175–92. [Google Scholar] [CrossRef]
- Sarkar, Sudipto, and Gwangheon Hong. 2004. Effective duration of callable corporate bonds: Theory and evidence. Journal of Banking & Finance 28: 499–521. [Google Scholar] [CrossRef]
- Shaffer, Sherrill. 2007. Equity duration and convexity when firms can fail or stagnate. Finance Research Letters 4: 233–41. [Google Scholar] [CrossRef]
- Shariati, Shahram, Masoumeh Abedi, Alieh Saedi, Abdolreza Yazdani-Chamzini, Jolanta Tamošaitienė, Jonas Šaparauskas, and Stanislav Stupak. 2017. Critical factors of the application of nanotechnology in construction industry by using ANP technique under fuzzy intuitionistic environment. Journal of Civil Engineering and Management 23: 914–25. [Google Scholar] [CrossRef]
- Valipour, Alireza, Nordin Yahaya, Norhazilan Md Noor, Jurgita Antuchevičienė, and Jolanta Tamošaitienė. 2017. Hybrid SWARA-COPRAS method for risk assessment in deep foundation excavation project: An Iranian case study. Journal of Civil Engineering and Management 23: 524–32. [Google Scholar] [CrossRef]
- Wang, Xiaoyu, Dejun Xie, Jingjing Jiang, Xiaoxia Wu, and Jia He. 2016. Value-at-Risk estimation with stochastic interest rate models for option-bond portfolios. Finance Research Letters. [Google Scholar] [CrossRef]
- Weil, Roman L. 1973. Macaulay’s duration: An appreciation. The Journal of Business 46: 589–92. [Google Scholar] [CrossRef]
- Xie, Yan Alice, Sheen Liu, Chunchi Wu, and Bing Anderson. 2009. The effects of default and call risk on bond duration. Journal of Banking & Finance 33: 1700–8. [Google Scholar] [CrossRef]
- Yousefi, Vahidreza, Siamak Haji Yakhchali, Jonas Šaparauskas, and Sarmad Kiani. 2018. The Impact Made on Project Portfolio Optimisation by the Selection of Various Risk Measures. Engineering Economics 29: 168–75. [Google Scholar] [CrossRef]
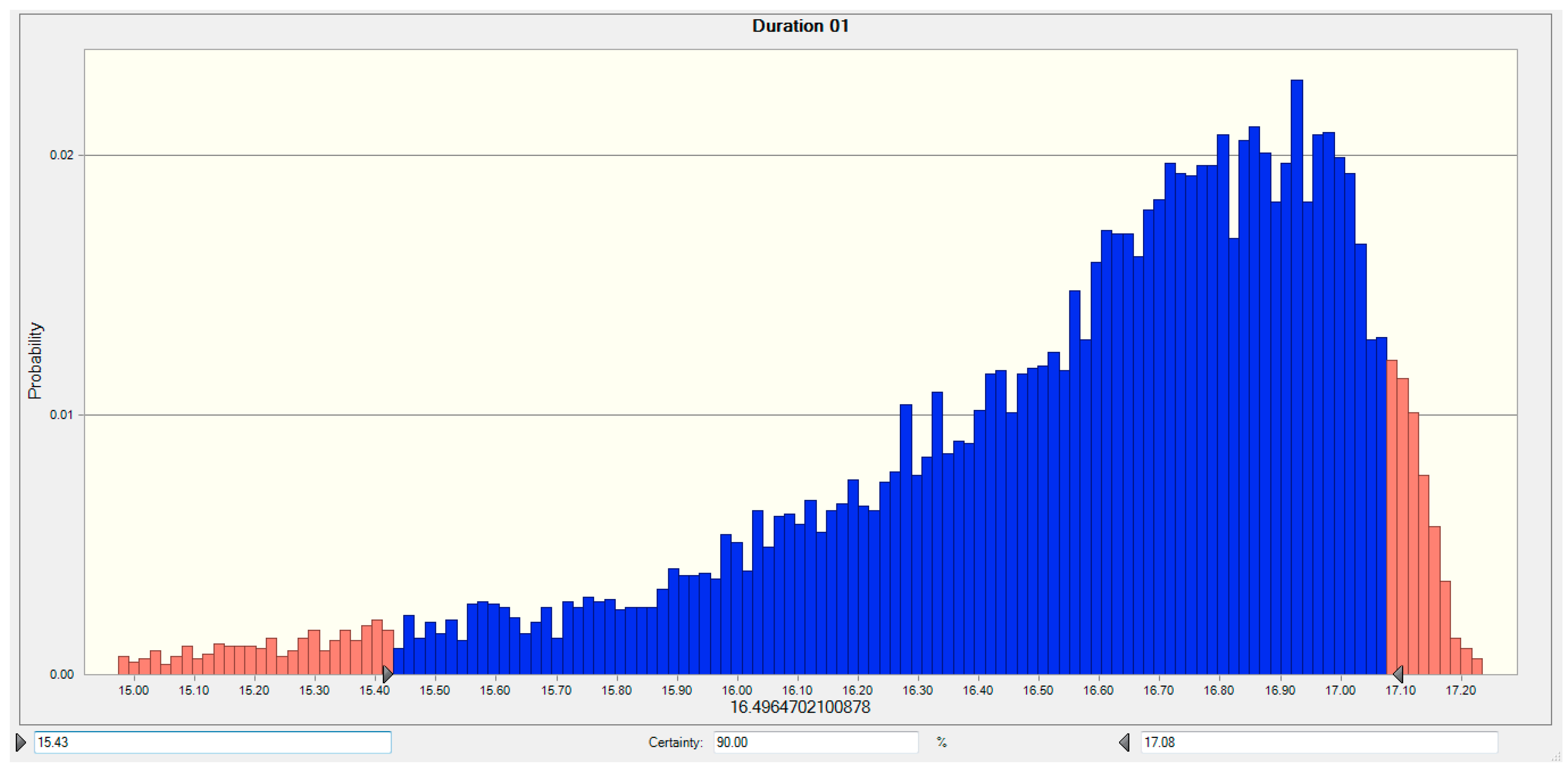
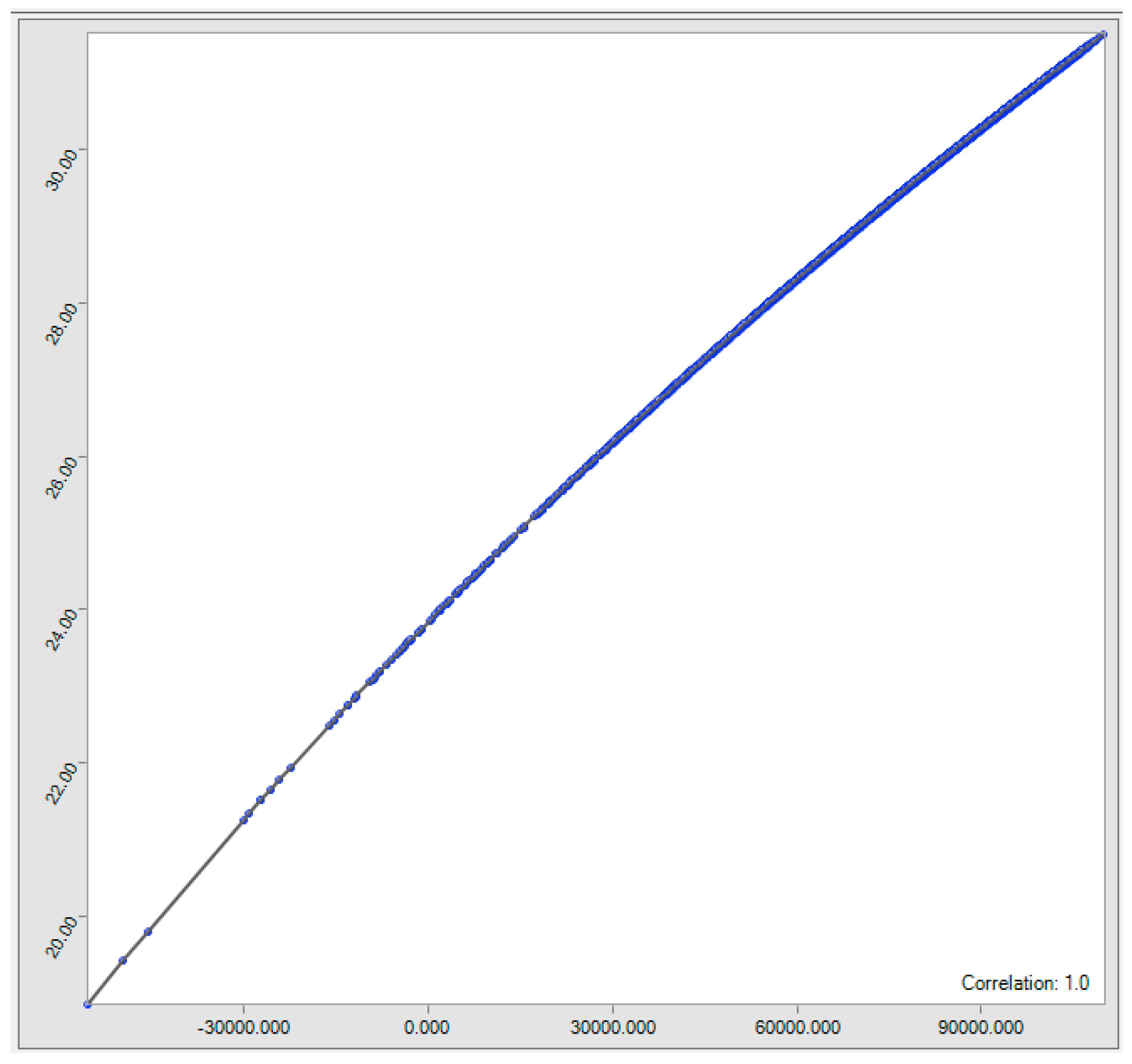
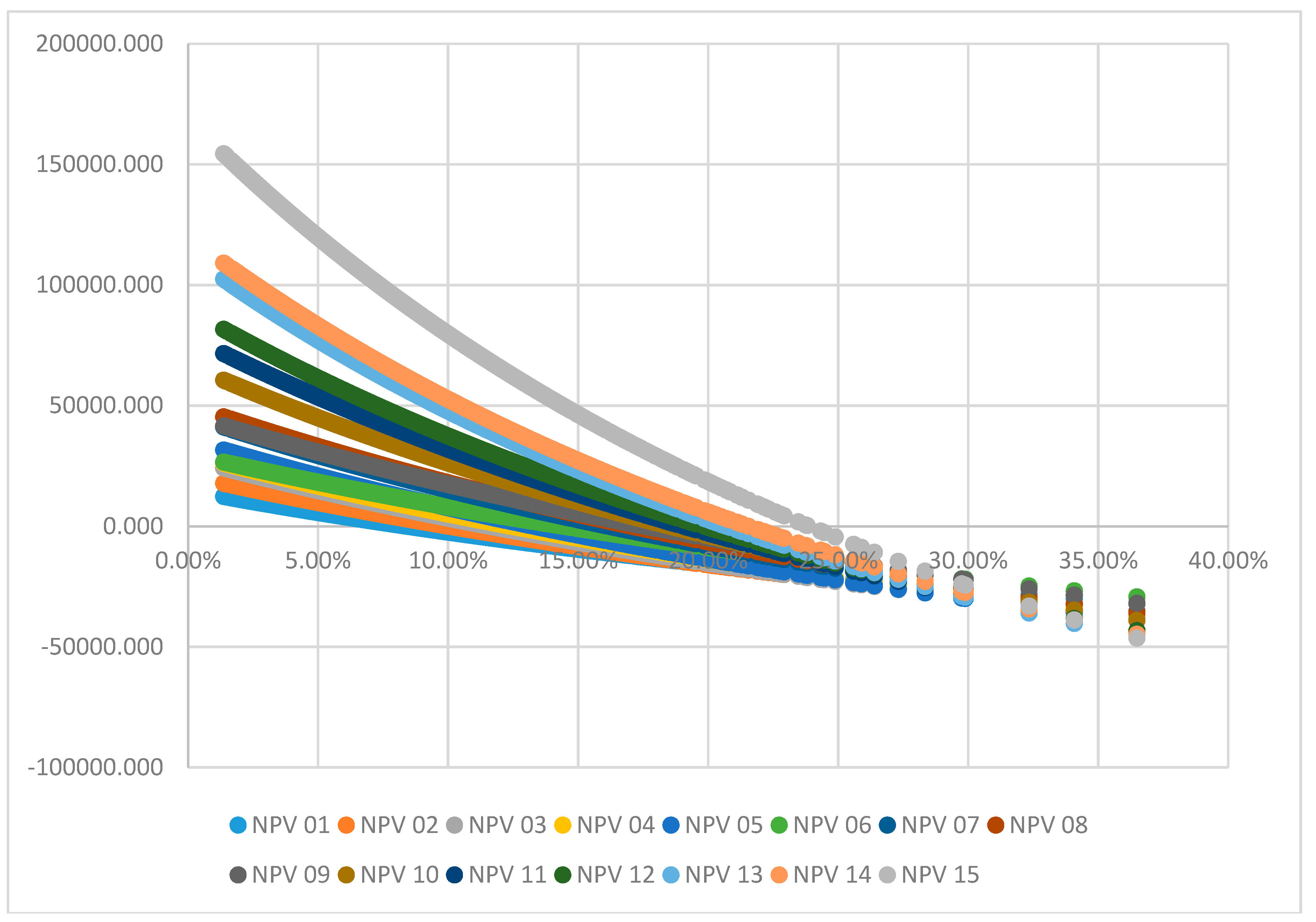
| Discount Rates | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Project | 2.00% | 1 Unit Decrease 1.00% | 1 Unit Increase 3.00% | 5.00% | 1 Unit Decrease 4.00% | 1 Unit Increase 6.00% | ||||
| NPV | NPV | Percentage Change in NPV | NPV | Percentage Change in NPV | NPV | NPV | Percentage Change in NPV | NPV | Percentage Change in NPV | |
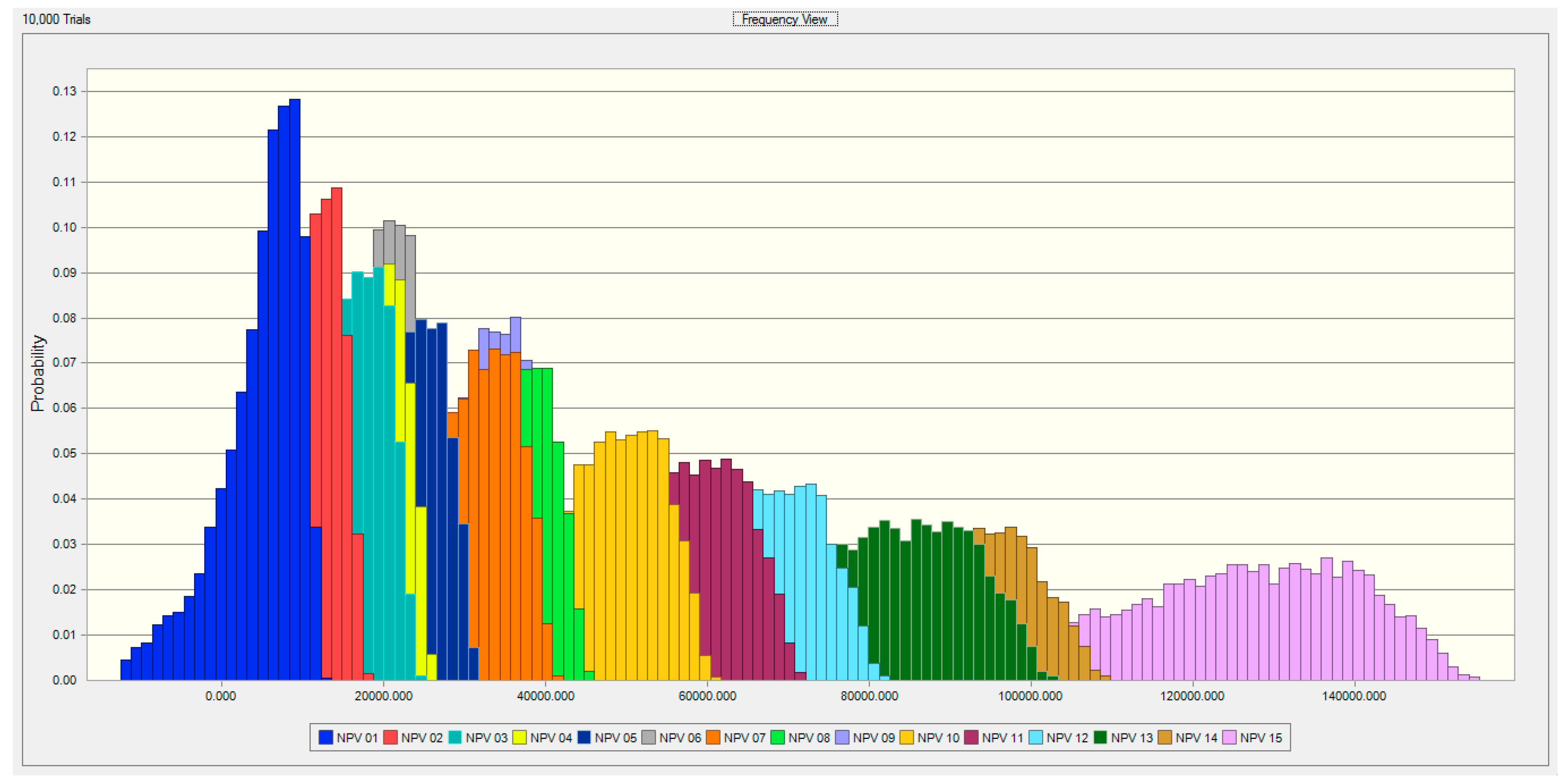
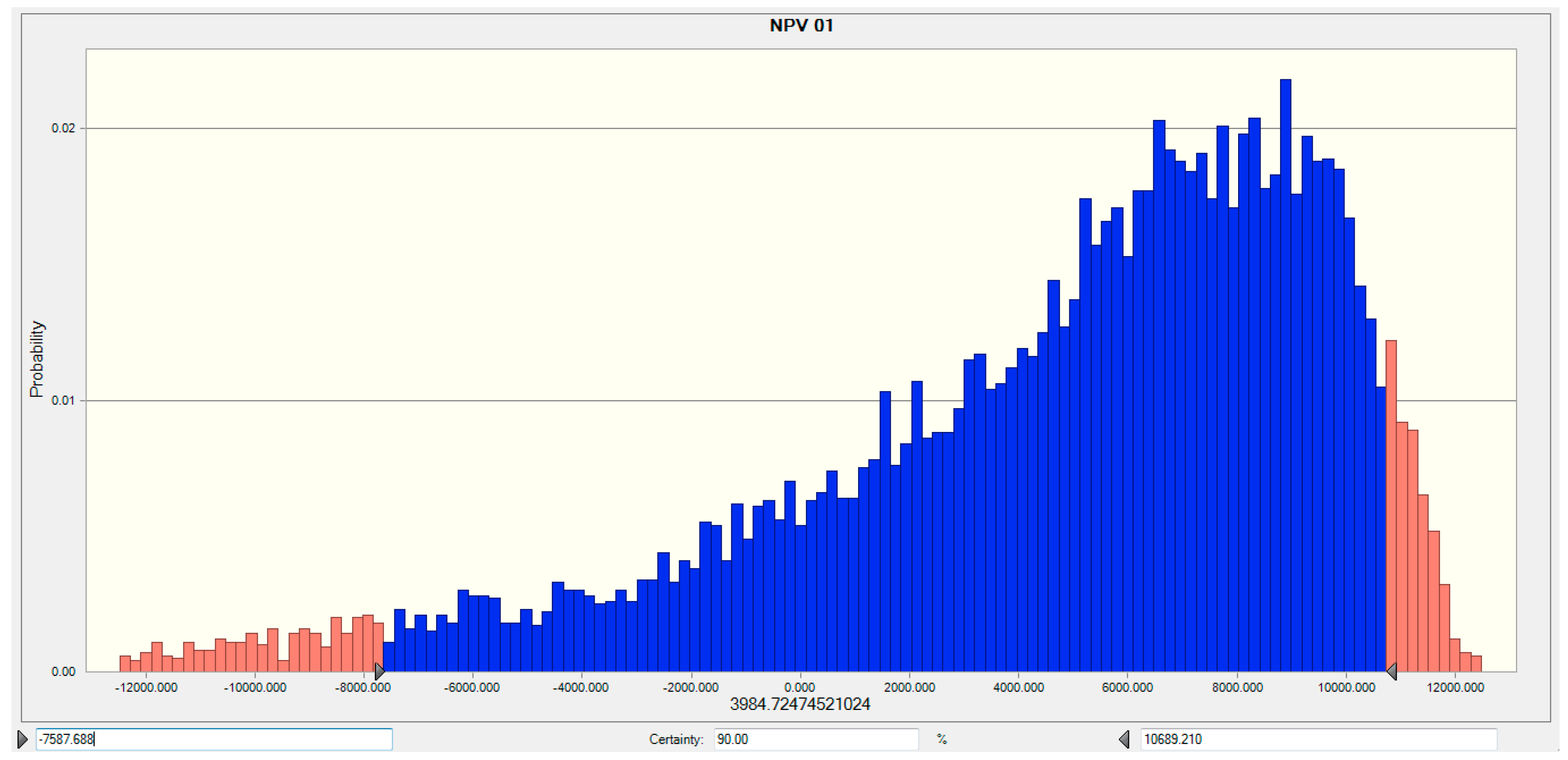
| 1 | 11,122 | 13,034 | 17.19 | 9263 | −16.71 | 5696 | 7455 | 30.88 | 3985 | −30.05 |
| 2 | 16,346 | 18,640 | 14.03 | 14,116 | −13.64 | 9836 | 11,947 | 21.45 | 7783 | −20.88 |
| 3 | 22,481 | 25,199 | 12.09 | 19,842 | −11.74 | 14,791 | 17,280 | 16.83 | 12,373 | −16.35 |
| 4 | 24,433 | 27,175 | 11.22 | 21,770 | −10.90 | 16,670 | 19,183 | 15.08 | 14,227 | −14.65 |
| 5 | 29,650 | 32,776 | 10.54 | 26,617 | −10.23 | 20,817 | 23,674 | 13.72 | 18,043 | −13.32 |
| 6 | 25,089 | 27,509 | 9.64 | 22,739 | −9.37 | 18,235 | 20,455 | 12.18 | 16,076 | −11.84 |
| 7 | 39,033 | 42,462 | 8.78 | 35,710 | −8.51 | 29,364 | 32,489 | 10.64 | 26,333 | −10.32 |
| 8 | 43,137 | 46,713 | 8.29 | 39,668 | −8.04 | 33,029 | 36,300 | 9.90 | 29,853 | −9.62 |
| 9 | 39,613 | 42,761 | 7.95 | 36,552 | −7.73 | 30,679 | 33,575 | 9.44 | 27,860 | −9.19 |
| 10 | 57,766 | 62,306 | 7.86 | 53,373 | −7.60 | 45,002 | 49,121 | 9.15 | 41,013 | −8.86 |
| 11 | 68,355 | 73,589 | 7.66 | 63,288 | −7.41 | 53,630 | 58,382 | 8.86 | 49,026 | −8.58 |
| 12 | 77,966 | 83,874 | 7.58 | 72,264 | −7.31 | 61,443 | 66,759 | 8.65 | 56,307 | −8.36 |
| 13 | 97,834 | 105,263 | 7.59 | 90,696 | −7.30 | 77,239 | 83,836 | 8.54 | 70,893 | −8.22 |
| 14 | 104,350 | 112,017 | 7.35 | 96,983 | −7.06 | 83,088 | 89,900 | 8.20 | 76,533 | −7.89 |
| 15 | 148,149 | 158,358 | 6.89 | 138,350 | −6.61 | 119,903 | 128,941 | 7.54 | 111,217 | −7.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousefi, V.; Yakhchali, S.H.; Tamošaitienė, J. Application of Duration Measure in Quantifying the Sensitivity of Project Returns to Changes in Discount Rates. Adm. Sci. 2019, 9, 13. https://doi.org/10.3390/admsci9010013
Yousefi V, Yakhchali SH, Tamošaitienė J. Application of Duration Measure in Quantifying the Sensitivity of Project Returns to Changes in Discount Rates. Administrative Sciences. 2019; 9(1):13. https://doi.org/10.3390/admsci9010013
Chicago/Turabian StyleYousefi, Vahidreza, Siamak Haji Yakhchali, and Jolanta Tamošaitienė. 2019. "Application of Duration Measure in Quantifying the Sensitivity of Project Returns to Changes in Discount Rates" Administrative Sciences 9, no. 1: 13. https://doi.org/10.3390/admsci9010013
APA StyleYousefi, V., Yakhchali, S. H., & Tamošaitienė, J. (2019). Application of Duration Measure in Quantifying the Sensitivity of Project Returns to Changes in Discount Rates. Administrative Sciences, 9(1), 13. https://doi.org/10.3390/admsci9010013






