1. Introduction
Many public-private partnership (PPP) projects are frequently unsuccessful in achieving quality, meeting deadlines, and respecting budgets, and most of these PPP projects have been exposed to various risks (
Sarvari et al. 2014). According to the World Bank, from 2008 to 2016, there were 327 unsuccessful PPP projects in the world (
World Bank 2016). “Risks in Projects” is defined as an uncertain event, if it occurs, which has a negative or positive result on the project target, such as scope, time, cost, and quality (
PMI 2008). The implementation of PPP projects faces high costs. The occurrence of risks plays a role in increasing those costs. An accurate assessment of risks can reduce the implementation costs associated with risks. According to previous research on risk assessment, it is very important that PPP project stakeholders obtain a risk ranking technique to assess significant risks (
Valipour et al. 2015). An accurate assessment of risks is significant for the public and private sectors as an input for the risk allocation phase and for risk response to ensure successful risk management in PPP projects (
Heravi and Hajihosseini 2011). However, the lack of an accurate risk assessment technique in PPP projects makes the practice of risk prioritization impossible (
Lam et al. 2007). The process of risk assessment acts as a bridge between proper risk assessment and the balanced management of major risks. The purpose of risk assessment is to determine the effects related to risk and to evaluate the influence of risk, using risk assessment (
Zavadskas et al. 2010). Risk assessment methods have included qualitative or quantitative approaches based on the amount of data and time available as well as the necessity of the valuation (
Akintoye et al. 2003). Qualitative assessment is used when there is uncertainty due to a lack of information to manage sources of occurrence and effects. Qualitative assessment is carried out with the help of risk registers and impact–probability tables (
Alfen et al. 2009). Quantitative assessment techniques are best used to obtain the statistical and numerical nature of a project’s risk exposure.
Traditional risk assessment methods in PPP projects based on impact and frequency criteria are too limited (
Iqbal et al. 2015). Hence, in order to obtain meaningful risk assessment results, a comprehensive risk assessment technique must be extended to become better aligned for risk assessment in construction and PPP projects. This research proposes to test a PPP project risk assessment technique that better reflects a broad spectrum of criteria whose impact is to make these projects successful. Based on the literature, there are many multi-criteria decision-making (MCDM) methods for risk assessment in construction and PPP projects. However, there is no well-defined technique that could be followed step-by-step throughout the decision-aiding process (
Yazdani et al. 2011). Methodological selection for the assessment of risk in construction projects is still under study. The main problem is how to estimate and evaluate a set of alternatives in terms of criteria and conflicting targets (
Mulliner et al. 2016). There are different units of measurement for each target and criterion. (
Srinivasa Raju and Kumar 2013). One of the critiques of MCDM methods is that different methods can yield various outcomes when applied to the same issue. Researcher looks for a solution that is closest to the ideal, and alternatives are evaluated to match all determinate criteria (
Chitsaz and Banihabib 2015). It is necessary to compare the MCDM method used for risk assessment purposes with a sensitivity analysis of the input data. It is also important to test the compatibility of various techniques with a specific type of decision problem (
Gan and Hill 2009).
This paper compares several MCDM methods—simple additive weighting (SAW), fuzzy technique for order of preference by similarity to ideal solution (FTOPSIS), and fuzzy analytic hierarchy process (FAHP), as well as hybrid methods including fuzzy analytic network process (FANP), step-wise weight assessment ratio analysis (SWARA), and complex proportional assessment (COPRAS)—applied to the assessment of risks in PPP and construction projects. Alternative rankings and their tolerances for changes in criteria weights were compared against selected MCDM methods to establish the most appropriate and compatible methodology for risk assessment in construction and PPP projects. This comparison evaluated a technique’s capacity to provide significant results and handle uncertainty for a balanced and fair risk allocation of problems. The findings of this study will help project stakeholders to select the best method for risk allocation and project owners to better manage risk, cost, time, and quality for construction and PPP projects.
2. Reviews of Multi-Attribute Decision-Making (MADM) Techniques for the Risk Assessment Problem
This section reviews various perceptions about MADM techniques for the risk assessment problem. Decision-making is a procedure that includes different actors such as individuals, groups, states, and institutions. Decision-making is a difficult and complex task. Risk management is a tool used by the construction industry to reduce cost and time overruns (
Hwang and Chen 2015;
Iqbal et al. 2015). Customers have more requirements due to difficulties with coordination, enhanced project complexity, and uncertainties between diverse stakeholders (
Hwang and Ng 2016).
Many researchers have dedicated their time to developing multi-attribute decision-making techniques (
Yazdani et al. 2011). These investigations on multi-criteria decision-making (MCDM) methods have illustrated that these techniques use conflicting criteria for the ranking of alternatives (
Zavadskas et al. 2014). Recently, many risk assessment techniques have been extended.
Baloi and Price (
2003) developed a fuzzy decision approach to model worldwide risk factors that affect construction costs.
Zhang and Zou (
2007) established a framework for the risk assessment of joint venture projects in Mainland China using the fuzzy analytical hierarchy process. Ng proposed a simulation model for public partners (government) to define the concession period of a public-private partnership scheme, based on predictable investments and tariffs (
Ng and Loosemore 2007).
In recent years, most research studies have focused on the existing risks in PPP projects. A method for risk assessment in PPP projects called “fuzzy AHP” was developed to evaluate risks for an expressway project in China and the researchers discovered that the lack of planning ability, low project residual values (after 30 years of operation), the lack of qualified bidders, weaknesses in design, and long approval durations were the top five risks for the project (
Li and Zou 2011). Xu evaluated risk factors for Chinese PPP projects using a fuzzy synthetic assessment tactic and his results showed that “moderate risk” and “high risk” are two separate risk levels in highway PPP projects. Delphi survey results show that “Government Intervention” is the most critical risk group, with “Government Maturity Risk” being the second and “Economic Viability Risk”, the third. These findings show that government interference and dishonesty, brought about by insufficient regulations and weak management, might be an obstacle for Chinese highway PPP projects (
Xu et al. 2010). Yu and Lee suggested a contrast assessment of risk prototype for an urban renewal project based on fuzzy-based failure mode and effect analysis (fuzzy-FMEA). There is a lack of efficient risk assessment in PPP or other projects (
Yu and Lee 2012).
Ebrahimnejad et al. (
2010) used a fuzzy multi-quality decision-making prototype for the evaluation of risk in a build–operate–transfer (BOT) project. That paper identified common risk factors in BOT projects. A new graded risk structure was reported on the basis of project-oriented opinions and some operative standards for risk ranking. The problem was determined using a fuzzy multi-attribute decision-making (FMADM) technique. The fuzzy linear programming technique for multidimensional analysis of preference (FLINMAP) and the fuzzy technique for order of preference by similarity to ideal solution (FTOPSIS) methods were used to assess risks in BOT projects. That study compared these two techniques using four aspects: separation between alternatives, fuzzy errors in risk response planning, criteria weights, and number of alternatives in relation to criteria. The suggested prototype was used to classify and evaluate risks in a BOT power plant project in Iran.
An analytic network process (ANP) technique to evaluate risk was used by
Tang et al. (
2011) for Chinese urban rail transit projects and by
Alireza et al. (
2013) for a gas refinery engineering–procurement–construction (EPC) project in Iran.
Yu and Lee (
2012) used a conflict–risk assessment technique for an urban renewal project based on the fuzzy failure mode (Fuzzy-FMEA).
Valipour et al. (
2016) developed a hybrid fuzzy cybernetic analytic network process technique to identify shared risks in PPP projects. Fuzzy ANP was used for the risk prioritization of Iranian freeway PPP projects (
Valipour et al. 2015).
Zavadskas et al. (
2010) used the TOPSIS and COPRAS techniques for the assessment of risk in construction projects.
Valipour et al. (
2017) used the SWARA and COPRAS techniques for the assessment of risk in in deep foundation excavation project.
Chatterjee et al. (
2018) presented a hybrid MCDM Technique for risk assessment in construction projects.
Hafeti and Tamošaitienė (
2018) analysed construction projects assessment model based on the Sustainable development criteria including risk aspects by an integrated fuzzy AHP and improved GRA model.
Yazdani et al. (
2011) used fuzzy COPRAS for the risk analysis of critical projects. From a review of previous studies, there is clear need for the development of new ideas for ranking risks in PPP projects, identifying major factors, and identifying related risks. Effective resource development is important because private and public enterprises have restricted resources.
In recent years, most research studies have focused on the comparison of various multi-criteria decision-making.
Mulliner et al. (
2016) compared multi-criteria decision-making methods for the assessment of sustainable housing affordability. They compared the efficiency of the weighted sum model (WSM), the weighted product model (WPM), the revised TOPSIS, COPRAS, and AHP. They found that the COPRAS method was the best method for assessing sustainable housing affordability.
Chitsaz and Banihabib (
2015) compared several multi-criteria decision-making methods to rank flood management alternatives. They compared the results from VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje), TOPSIS, ELECTRE (ELimination Et Choix Traduisant la Realité) I, and ELECTRE III in prioritizing flood management alternatives. The results showed that the ELECTRE III method was the best method for their issue.
Hodgett (
2016) compared multi-criteria decision-making methods for equipment selection. In that study, a new multi-criteria decision-making method was offered for the risk assessment of list items. The proposed technique, called EDAS (evaluation based on distance from average solution), used an average solution for evaluating the alternatives (inventory items).
Ghorabaee et al. (
2015) compared multi-criteria decision-making techniques for ABC classification. They compared the EDAS, COPRAS, SAW, VIKOR, and TOPSIS methods.
Ghorabaee et al. (
2016) extended the EDAS method and used it for supplier selection. The selection of a proper MCDM technique is not a simple task. It has been acknowledged that various techniques are possibly reliable for a specific decision-making situation and that there is not always an overwhelming cause to adopt one method over another (
Hajkowicz and Higgins 2008). They briefly introduced certain factors that must be considered when identifying the right MCDM method to address the research problem. It was also observed that there is a plethora of MCDM methods. However, none can be considered as the “ultimate”’ choice for all decision situations (
Guitouni 2004). This is mainly because of the following:
Diverse decisions fit the broad circumstances of MCDM;
The nature and the amount of data available to support the analysis vary;
The time required to undertake the assessment for a particular decision scenario varies;
The administrative culture and the requirements of the organization vary;
The analytical skills of those participating in the analysis process vary.
Accordingly, identifying the right MCDM method for a particular situation has been acknowledged as an imperative step in an effective multi-criteria analysis process.
Guitouni (
2004) appreciated the multiplicity of multi-criteria decision analysis (MCDA) methods but argued that the purpose of every MCDA method was to assist in making a good recommendation. However, not all MCDA methods produce a good recommendation for all situations. This is because every method’s theoretical and axiomatic development is based on some assumptions and hypotheses.
Guitouni (
2004) noted that in most decision-making situations where MCDA techniques are applied, there is no clear justification as to why a particular method is applied over the other. In spite of these facts, the authors of this article used the FAHP, FANP, fuzzy TOPSIS, SAW, SWARA, COPRAS, and EDAS methods because these methods have received the most academic and researcher interest, they are the latest, and they represent a familiar method in the risk assessment of PPP and construction projects.
3. Review of Used Multi-Attribute Decision-Making Methods
MADM, sometimes referred as multi-criteria decision-making (MCDM), is a well-known topic in decision science, management and operations research (
Kahraman 2008). MADM provides structured, justifiable tools and transparency that permit the quantification and integration of heterogeneous aspects such as economic, political, technical, and social. MADM models facilitate a systematic and effective decision-making process. Therefore, MADM offers a decision-making framework that allows decision-makers to analyze complex decision problems by assessing different competing alternatives with the intention of achieving certain goals. MADM permits the decision-makers to present their subjective judgments about the existing alternatives, which are defined by multiple and usually conflicting features. The outcome of the MADM process is the identification of a single most acceptable alternative or rank of options or a basically distinguished/sorted one taken from unacceptable possibilities (
Linkov et al. 2006). Borrowing a page from
Polatidis et al. (
2006) and
Moffett and Sarkar (
2006), this study has dedicated some effort to identifying the right MADM technique to apply to the research problem. However, it should be noted that an exhaustive evaluation of all MADM methods is impractical, as there are various methods. Thus, based on an extensive literature review, the evaluation has been limited to common methods that are deemed to be more applicable to the research problem. This study instituted some requirements that must be satisfied in order to use the MADM technique to address the study research problem. These requirements are listed in
Table 1.
With the requirements in
Table 1, common MADM methods were evaluated in order to identify the most appropriate technique to address the research problem. A comparison of some of the common MADM methods is provided in
Table 2.
Several MCDA Methods are presented in the review:
• Fuzzy Analytic Hierarchy Process (FAHP)
AHP was developed by Thomas L. Saaty and published in 1980 (
Saaty 1980). In an AHP framework, the decision problem is hierarchically decomposed into a linear top-to-bottom structure, assuming a one-way hierarchy relationship among decision levels. On the other hand, many decision problems cannot be structured hierarchically or there may exist strong interactions and dependencies between decision variables. Due to this assumption, the AHP cannot be efficiently used in complex decisions involving a variety of interactions and dependencies between decision variables (
Yüksel and Dagdeviren 2007). The fuzzy set theory was presented by Zadeh (
Zadeh 1965) to solve problems in which the explanation of activities, judgments, and observations are subjective, imprecise, and vague. A fuzzy set can be defined as a “collection of objects, whose elements have different degrees of belonging to the set.” The extent fuzzy AHP method was introduced by
Chang (
1996).
• Fuzzy Analytic Network Process (FANP)
FANP advances the ANP technique by including the fuzzy set concept in an ANP procedure. ANP on the other hand is an extension of AHP that is a more popular and widely applied method (
Saaty 1996). To overcome the limitation, Saaty proposed the ANP method. ANP decomposes the problem into a network structure which is more flexible and allows interrelationships among decision levels and attributes, replacing the AHP strict hierarchy structure (
Saaty 1996).
• Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (FTOPSIS)
TOPSIS, prepared by Hwang and Yoon in 1981 (
Hwang and Kwangsun 2012), identifies solutions from a limited set of alternatives based on the concept of the simultaneous minimization of distance from a positive ideal solution and maximization of distance from a negative ideal solution (
Jadidi et al. 2008). The rule of the TOPSIS technique is that the best alternative or solution must have the shortest distance from the positive ideal solution and be furthest from the negative ideal solution (
Jahanshahloo et al. 2006). The positive ideal solution is the solution that minimizes cost attributes and maximizes the advantage attributes, whereas the negative ideal situation is one that maximizes the cost attributes and minimizes the benefit attributes. This study applies FTOPSIS with triangular fuzzy numbers.
• Simple Additive Weighting (SAW) method
• Step-Wise Weight Assessment Ratio Analysis (SWARA) method
The SWARA method was used in this study for obtaining the weight of each risk assessment criterion. Experts prioritized and ranked each criterion for risk assessment from the first to the last. Using this technique, the most important criterion created was ranked 1, and the least important criterion was ranked last. The average value of the ranks was used for obtaining the overall ranking from the group of experts (
Keršulienė and Turskis 2011). In recent years, the following researchers have applied the SWARA method:
Turskis et al. (
2016), Multicriteria Evaluation of Building Foundation Alternatives;
Karabasevic et al. (
2015), Selection of candidates in the mining industry based on the application of the SWARA and the MULTIMOORA methods.
• COmplex PRoportional ASsessment (COPRAS) method
The COPRAS method was introduced by Zavadskas and Kaklauskas in 1996. This method can be used in situations where decision-makers have to select among various alternatives by considering a particular set of inconsistent criteria. The COPRAS technique determines a solution with the ratio to the best solution (
Zavadskas and Kaklauskas 1996). The COPRAS method is proportionally dependent on the significance and assumes direct and utility degree of considered versions based on a system of criteria proportionally explaining the alternatives and on weights and values of the criteria. Recent developments of decision-making models based on the COPRAS method are listed as follows:
Kundakcı and Işık (
2016), Integration of MACBETH and COPRAS methods to select air compressor for a textile company;
Mulliner et al. (
2016) presented a comparative analysis of MCDM methods for the assessment of sustainable housing affordability.
• Evaluation Based on Distance from Average Solution (EDAS) method
The EDAS technique was initially prepared by
Ghorabaee et al. (
2015) for multi-criteria inventory classification. The EDAS technique was also found to be an effective technique in handling MCDM problems. With this technique, it is not necessary to calculate the ideal and the nadir solution. This technique uses two measures dealing with the desirability of the alternatives: the first measure is the positive distance from average (PDA), and the second is the negative distance from average (NDA).
4. Results and Discussion
4.1. Data Collection
To identify risk, risk assessment criteria were needed as the primary data for this study. The results of this step were extracted from previous studies on risk assessment (
Zegordi et al. 2012;
Valipour et al. 2015;
Yazdani et al. 2011). The 10 top risks (Limited capital, Improper design, Change in the value of granted lands due to inflation, Termination of concession by the Government, Change in the value of granted lands due to development, Inflation risk, Delay in resolving a contractual dispute, Force majeure, Financial problems due to environmental protection, Inadequate study and insufficient data) in freeway projects were identified. The second step in the risk assessment of PPP projects was to identify risk assessment criteria. To do so, a decision-making group composed of a quality manager, a project manager, a main contractor, a deputy director, a technical director, a sub-contractor, and a PPP project contractor was established. The initial outcome of this step was to create data following interviews with the experts and using previous studies on risk assessment in PPP and construction projects such as
Zegordi et al. (
2012),
Valipour et al. (
2015),
Hong et al. (
2013), and
Sarvari et al. (
2014). From this, 5 risk assessment criteria were selected: Impact of risk, Consequence, Risk predictability, Risk uncertainty, and Detectability. Consequence is defined as the effect of the incident. Risk predictability determines where and when the risk might occur during the project. Risk uncertainty is defined as the shortage of data about the nature of the probability distribution function of risk measures. Detectability means the possibility of eliminating and identifying the weakness. An interview and a questionnaire survey were used as third resources to rank the risks in each MADM method. A team at Delphi built a comprehensive pairwise comparison matrix for the assessment of risks using the FANP and FAHP methods with carefully selected decision-makers. The selected experts had previous experience in construction and knowledge of risk management. The experts included project managers, construction managers, supervisors, owner representatives, and risk management groups. The experts were encouraged to identify the significance of each risk based on the selected criteria.
4.2. Comparative Methods
A MADM method was used to prepare a complete ranking of alternatives. The MADM technique handles qualitative and quantitative positive (benefit) and negative (cost) criteria. The MADM methods (SWARA, COPRAS, FANP, FAHP, FTOPSIS, EDAS, and SAW) were applied to the case study data.
Table 3 shows the initial decision-making applied in the SWARA COPRAS, fuzzy TOPSIS, EDAS, and SAW methods, and
Table 4 shows the initial pairwise comparison matrix used in the FANP and FAHP methods.
These methods differ in their basic principles. The way they combine criteria values, the data normalization process, and their criteria weights are different (
Mulliner et al. 2016). These methods were used to obtain the relative importance of each risk (alternative) and compare their priority orders. The final risk rankings are shown in
Table 5 and
Figure 1.
The priority order for risk types is compared in
Figure 1. All methods concluded that the first rank was R
1 and the second rank was R
2. All methods except FAHP, FANT, and EDAS concluded that R
10 had the lowest rank. R
7 was the 7th rank obtained from SWARA, COPRAS, FANP, and SAW methods. In
Table 6, SWARA, COPRAS, and EDAS had the most similarities with 6 similar ranks (60%). The least similarities were between FAHP–FTOPSIS and FANP–FAHP with two similarities (20%). SWARA and COPRAS had the most similarities with EDAS, FAHP, and FANP with scores of 60%, 50%, and 40%, respectively. The SWARA, COPRAS, and EDAS methods produced contrasting results when compared to all other methods. That result is a reliable topic for future research studies that focus on combining positive and negative criteria.
4.3. Seperman and Kedall Tests
To determine the suitability and applicability of the 7 MADM methods for risk assessment in PPP projects, their relative ranking performance was compared using the following measures:
- (a)
Spearman’s rank correlation coefficient,
- (b)
Kendall’s coefficient of concordance.
Using Spearman’s rank correlation coefficient (r), the similarity between two sets of rankings can be measured. Spearman’s rank correlation coefficient value varies between −1 and +1, with a value of +1 denoting a perfect match between two rank orderings (
Adafin et al. 2016).
Table 7 illustrates the Spearman’s rank correlation coefficients obtained in this study. r
s values ranged from 0.794 to 0.976. The performance of the SWARA, COPRAS, and EDAS methods was satisfactory with respect to r
s values. The MADM techniques also performed well. It was observed that SWARA and COPRAS to EDAS is similar to EDAS to FTOPSIS with respect to their ranking performance of 0.976.
Kendall’s coefficient of concordance was used to demonstrate similarities in the rankings obtained using different methods. The pairwise correlation results from
Table 8 show that the seven MADM methods (SWARA, COPRAS, FANP, FAHP, FTOPSIS, EDAS, and SAW) perform similarly with scores ranging from 0.6 to 0.934. The average correlation coefficient used to obtain the overall similarity for each method is as follows: SWARA (0.772) > SAW (0.761) > EDAS (0.7601) > FTOPSIS (0.7536) > COPRAS (0.748) > FAHP (0.695) > FANP (0.6895). SWARA, COPRAS, and SAW are highly correlated methods. Interestingly, FANP and FAHP differed significantly from other MADM methods.
Zanakis et al. (
1998) concluded that all versions of AHP behave similarly to TOPSIS, whereas
Rao (
2007) found that TOPSIS behaves closer to COPRAS.
The model validation was done using face-to-face interviews. Ten experts with direct hands-on experience with PPP projects were invited to evaluate (C
1) risk comprehensiveness; (C
2) degree of objectivity; (C
3) model clarity; (C
4) overall reliability; and (C
5) model practicality. The experts were asked to complete a validation form with five multiple-choice questions using a five-point Likert scale with 1 denoting “poor” and 5 denoting “excellent.” The average scores of all five criteria were well above 3.50, confirming that the model was comprehensive, clear, reliable, practical, and objective (
Yeung et al. 2009). Validation results are shown in
Table 9. Results confirm that the EDAS, COPRAS, and SWARA methods had the highest scores with values of 4.690, 4.640 and 4.610, respectively, compared to the other methods and were validated as comprehensive, clear, reliable, practical, and objective.
4.4. Sensitivity Analysis
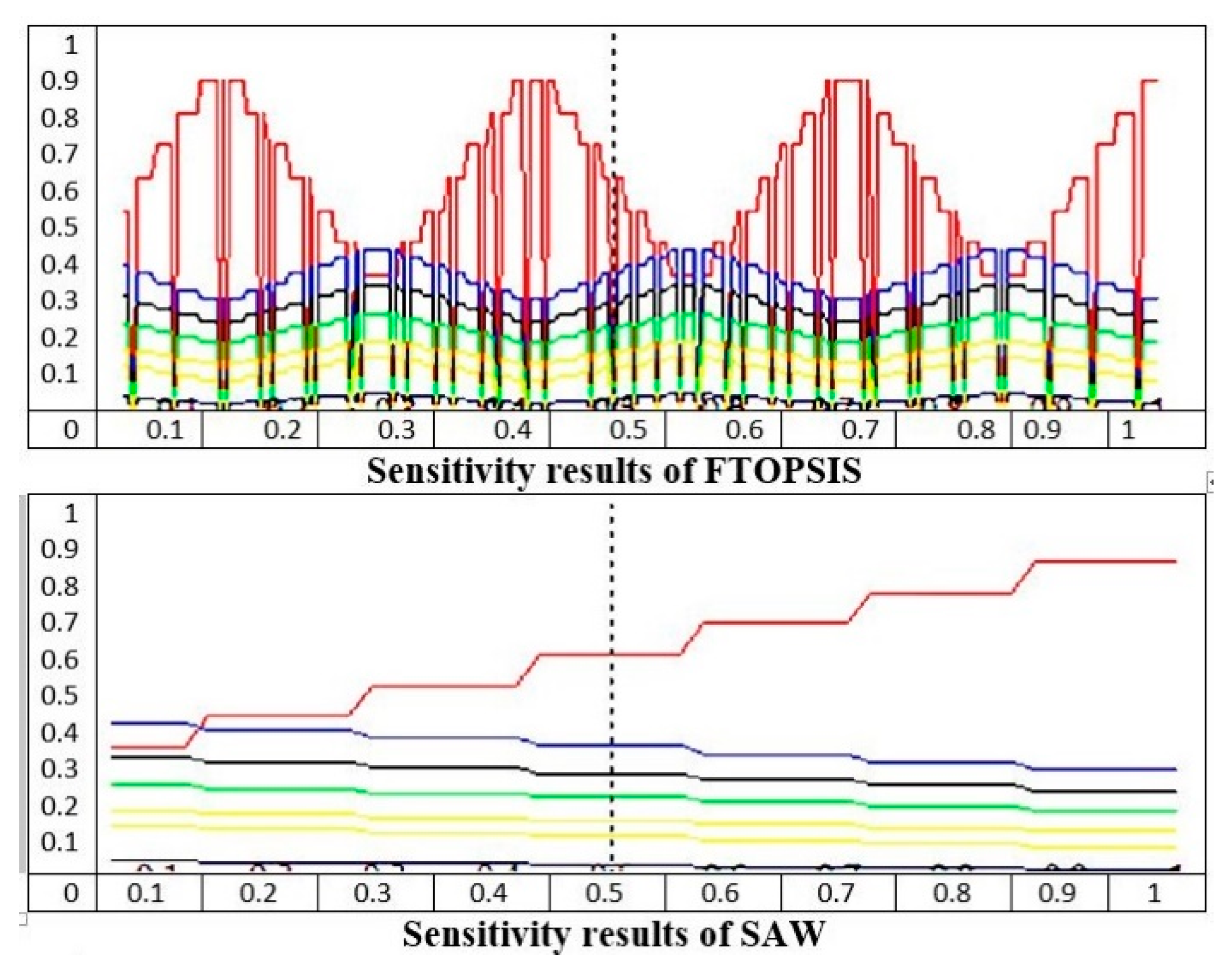
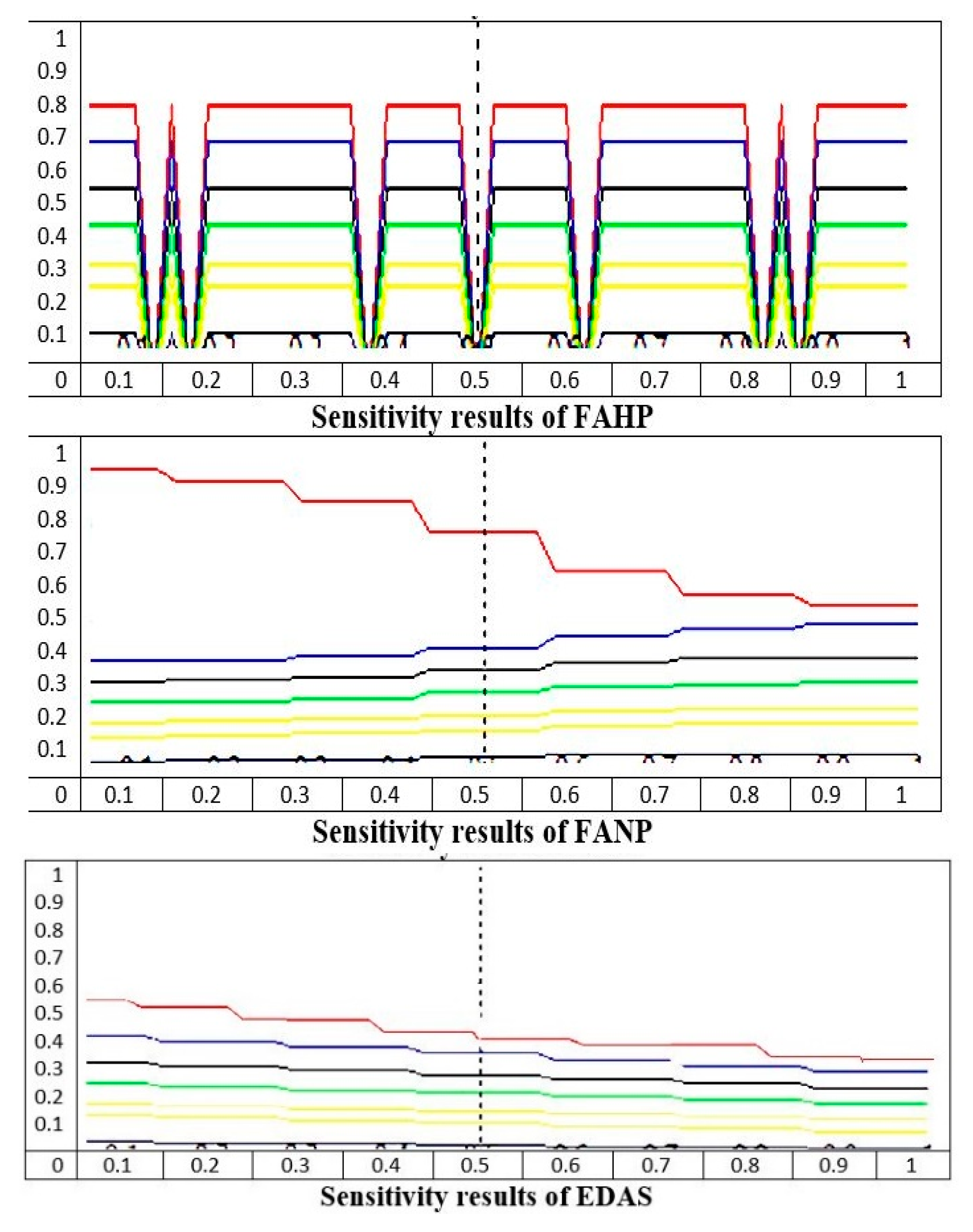
Sensitivity analysis discovers the stability of alternatives after variable changes (
Agha et al. 2013). A sensitivity analysis is needed for determining the validity of solutions for reducing uncertainties. To test the consistency of the ranking outcome of the MADM technique, this study performed a sensitivity analysis. The impact of possible deviations from the weight value was evaluated because the criteria weights were determined on the basis of subjective conception. The ranking results in the MCDM technique depends heavily on the nature of the criteria that are applied in the resolution and most notably on the distribution of the weighting between criteria. The effect of a possible deviation in the weight value must be evaluated. A sensitivity analysis was carried out to quantify the level of cross-talk among the rankings and criteria, in order to reveal how the ranking of alternatives varies due to change in criteria weights. The outcome of the sensitivity analysis for each individual criterion is presented in
Figure 2. The sensitivity analysis illustrated that if criteria weights are subjected to a higher level of variation (50% decrease or increase), the MCDM technique such as FTOPSIS, SAW, FAHP and FANP must be considered as there is some tolerance to criterion variation in certain instances and there is an exceptional tolerance in the SWARA, COPRAS and EDAS methods. In particular, FTOPSIS and FAHP showed some tolerance to the high level of uncertainty in criteria weight.
The final decision regarding risks (Alternatives) based on the sensitivity analysis for SWARA and COPRAS is shown in
Table 10. The alternative rating of risk did not change if the relative importance was decreased from 0.5 and increased from 0.5 in the COPRAS method. This illustrates that the ranking of alternatives does not change if the ideas of the experts as well as the managerial preferences decrease or increase. Accordingly, ensuring that the total criteria weight and remaining criteria weights by adjusting proportionally criteria weights is unification equal. Therefore, at this particular level, the resolution is hardly robust with little variation in the final selection. The sensitivity analysis showed the risk ranking changed for the first and second rankings of the SAW method. It should be noted that there were some changes in criteria weight (decrease or increase), which were reflected in the final rank of each alternative in SAW, FAHP, FANAP and FTOPSIS.
The sensitivity coefficients represented in
Figure 3 were analyzed for each criterion using all seven multi-criteria decision methods. The particular value of the sensitivity coefficients for each criterion, represented as a −5% or 50% decrease or increase of each criteria weight, leads to multiple, double or single changes in the alternative’s rank. The sensitivity ratio results for the seven MCDM techniques allowing for −5%, −50%, +5%, and +50% variations of each criteria weight are shown in multiple bars in
Figure 3. The results in
Figure 3 revealed that criteria C
3 and C
5 were robust for all seven MCDM techniques used in the sensitivity coefficients.
The comparative analysis of the EDAS, SWARA, COPRAS, FANP, FAHP, FTOPSIS, and SAW methods showed that EDAS, SWARA, and COPRAS are relatively simple to use. FANP and FAHP are time-consuming due to a high number of questions and decision matrices; however, the use of zero values within the analysis was problematic. A drawback of the SAW, FAHP and FANP methods was that benefit and cost criteria should not generally be used at the same time within the analysis. In contrast, EDAS, SWARA, COPRAS, and FTOPSIS allowed for the incorporation of both positive and negative criteria. However, the FTOPSIS, SWARA, and COPRAS methods were the more complicated and time-consuming than EDAS. The complexity of many MADM techniques prevents their application. The application of simpler evaluation techniques is often better than more complicated ones. The sensitivity results showed that SWARA, COPRAS, and EDAS had the best tolerance for changes in criteria weight. A correlation analysis revealed that SWARA, COPRAS, and EDAS were the best methods for risk ranking. The SWARA and COPRAS techniques are transparent, simple to use, and quick in comparison with other hybrid MADM techniques, such as the FANP, FAHP, and FTOPSIS in the risk assessment of PPP projects.
5. Conclusions
The selection of a risk assessment method is an important activity for PPP projects because choosing the wrong method can be costly and time-consuming. It has been suggested that an effective and efficient multi-criteria decision-making (MCDM) tool can be applied to risk assessment. Different MCDM methods yield different results when applied to the same decision problem. In this context, this study examined the ranking performance of five familiar MADM methods and one of the newest methods (i.e., EDAS) for risk assessment in PPP projects. Five decision criteria, weighted by experts, were the basis of the risk assessment of construction and PPP projects using 10 types of risks identified by previous researchers. Four widely applied hybrid MADM methods and two single methods—SWARA COPRAS, FANP, FAHP, FTOPSIS, EDAS, and SAW—were assessed to evaluate their similarities and contrasts in the resulting rankings. Four performance tests were used to measure agreement between rankings, suitability, and applicability. The results showed that the SWARA, COPRAS, and EDAS techniques had a slight advantage over the other methods. Minor differences between obtained results were due to differences in their mathematical modelling. Rankings were not significantly impacted by the selection of a MADM method. This study suggests that the SWARA, COPRAS, and EDAS methods exhibit the highest potential for risk assessment in PPP projects. Future studies may compare the relative permanence of newly developed hybrid MADM methods. The results of this study will help stakeholders of construction and PPP projects to select the best method for risk assessment.