Abstract
In this research, the concept of Duration with a new application in project management has been defined. The Duration of each project provides the project manager with a combined measure containing concepts of return, cost and time of the project. Further in this article, the changes in project return, based on different assumptions such as discount rate, have been examined. To examine the effect of the changes in these factors, the Monte Carlo simulation has been used. The relationship between these factors is nonlinear which reflects the great importance of investment on appropriate risk management systems. The data from a set of construction projects have been used in order to verify the results of this study. Similar relationships can be expected to exist in other industries as well.
1. Introduction
The purpose of this study is to introduce a new concept in Project Management. Based on PMI definition, a project is a temporary endeavor undertaken to create a unique product, service, or result. There are various standards for proper management of the projects. PMI’s A Guide to the Project Management Body of Knowledge (PMBOK® Guide) is one of the main project management standards. Based on this standard, Project management is the application of knowledge, skills, tools, and techniques to project activities in order to meet the project requirements. For this purpose, 10 knowledge areas are defined to properly manage the project tasks, which include: Integration, Scope, Scheduling, Cost, Quality, Procurement, Resources, Communications, Risk and Stakeholder management (Project Management Institute 2017). Different areas, such as time, cost, quality, etc. have been defined for efficient management of projects. The definition of these areas is often done separately. However, in practice all of these different areas affect each other and any decision that may have effects on any of them can lead to changes in other relevant areas. Many studies have been conducted on the effect of these areas, on each other. In this study, we have introduced a new concept known as the Duration. This title has sometimes been used, in different studies, for time management and with the purpose of scheduling. The concept addressed in our study has been covered to a great extent in the finance literature. In the discussions regarding bonds, this concept was first defined by Macaulay.
2. Project Duration
Duration is a well-established and practical concept in finance literature. The concept of duration was first introduced by Macaulay (1938). After duration was presented lots of studies were carried out on its usages. Weil (1973) in his research titled, Macaulay’s duration: an appreciation, investigated the various applications of this practical measure. Boquist et al. (1975) used duration as a risk assessment tool. After that much research has been conducted on the concept of duration. Osborne (2005) developed a more precise formula for duration. Dierkes and Ortmann (2015) proposed an estimation model and compared it with approximation methods that were based on duration. Sarkar and Hong (2004) estimated the effective duration for corporate bonds with call provision. Jacoby and Roberts (2003) studied the adjustment of Macaulay duration caused by call and default. Xie et al. (2009) investigated the effect of these two factors on duration. Lee et al. (2011) investigated the effect of sovereign risk on duration. Hatchondo and Martinez (2009) investigated the possibility of government borrowing using long-duration bonds, and its impact on the level and volatility of interest rates. Bejaoui and Karaa (2016) considered duration dependency and tried to realize relevant bull and bear markets notions. Fukuta and Yamane (2015) compared the performance of equity duration with Capital Asset Pricing model and Fama–French model in the Japanese stock market. Project Duration has been defined to be consistent with the following:
where: t—cash flow number in time t; CF—cash flow amount; n—period number; r—discount rate of the project.
Project Duration is in fact a combination of a project’s time, cost, and return measures, which are defined in an index. The unit of this measure is time and therefore this is an index with a time unit. Project Duration is a measure of how long it takes for the present value of the future returns to fully repay the present value of future costs of the project. It should be noted that Duration can be very different from the project’s period or life cycle. It is in fact the time and the amount of costs and returns of the project, as well as the discount rate that determines it. If the earnings of a project start earlier, or a big part of its costs are at the later phases of the project’s life cycle, then the Duration of that project will be less compared to similar projects. The Duration of the project can provide valuable information for portfolio and project managers; which may not available through other measures.
In the model, for project value creation, several elements must be considered which are presented in Figure 1.
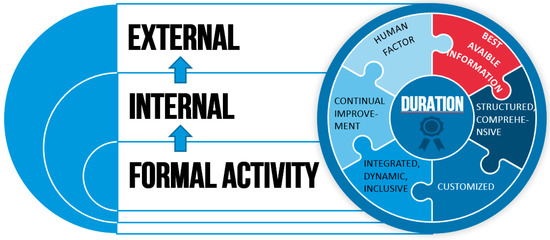
Figure 1.
The elements for the project value creation.
The model for the value creation must include all types of risks. The risk can be assessed with a developed hybrid MCDM technique for risk management (Chatterjee et al. 2018). Ghasemi et al. (2018), Yousefi et al. (2018) presented project portfolio risk identification and analysis, considering project risk interactions and using Bayesian networks. Valipour et al. (2017) developed the hybrid SWARA-COPRAS method for risk assessment. Asadi et al. (2018) presented project risk evaluation by using a new fuzzy model based on the Elena guideline. Shariati et al. (2017) analyzed the critical factors by using the ANP technique under a fuzzy intuitionistic environment. The sustainable development criteria must all be integrated into the project value creation system (Hatefi and Tamošaitienė 2018).
Choosing an appropriate risk measure must be considered as well. Yousefi et al. (2018) investigated the impact made by the selection of various risk measures. In their research, semi-standard deviation was used to differentiate between desirable and undesirable opportunities. Value at Risk and Expected Shortfall were applied to make a better estimate of the tail risks. To explore this concept and its applications on different projects, we have used the Monte Carlo Simulation to compare its changes in different projects. The Monte Carlo approach has been applied a lot to deal with complex project management problems. The Monte-Carlo simulation is a possible solution for dealing with multi-dimensional problems, as indicated by Cong and Oosterlee (2016). Cesari and Cremonini (2003) compared the dynamic strategies of asset allocation by using this approach. Pajares and Lopez-Paredes (2011) used it to acquire the cost and time distribution at the end of the project (Acebes et al. 2015). Denault and Simonato (2017) applied simulations-and-regression for Dynamic portfolio selection. Cong and Oosterlee (2016) applied this method for a Multi-period mean–variance portfolio optimization. Brandt et al. (2005) used it in a dynamic portfolio selection, as did Denault and Simonato (2017). Wang et al. (2016) applied Monte Carlo for calculating the Value at Risk. (Buchner 2015) proposed the Monte Carlo method for Equilibrium option pricing. By assuming the stochastic nature of the projects’ characteristics, Acebes et al. (2015), proposed to apply a statistical learning method and a Monte Carlo simulation. To conduct this research, several different projects of a construction company are grouped in similar categories, based on the experts’ points of view and according to their time, cost, return and risk characteristics. Each of firm’s new projects fall into one of the 15 defined groups, according to their unique characteristics. Then, according to the distributions of each of these projects and Monte Carlo simulation, the data were simulated 10,000 times and the cash flows of each project have been estimated. In the figures below, the overlay charts of Duration and NPV distributions for all groups of projects are illustrated in Figure 2 and Figure 3.
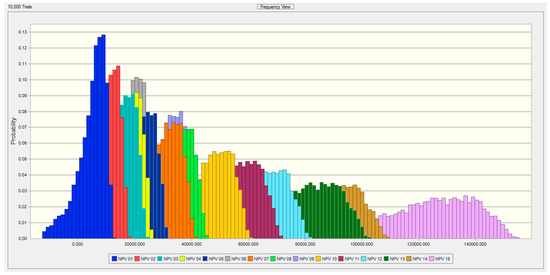
Figure 2.
Overlay charts of NPV distributions.
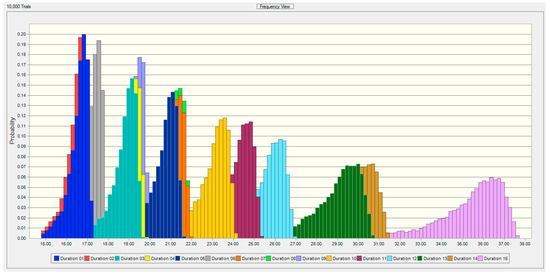
Figure 3.
Overlay charts of Duration distributions.
At the later stages of this study, there has been an attempt to estimate the impact of changes on each of these measures, according to the shift in the discount rate. It should be noted that the minimum amount of possible discount rate is 0%. That is, the negative discount rate is not meaningful for projects. So, in a Monte Carlo simulation, the log-normal distribution has been used for the discount rate. In Figure 4 and Figure 5 below, the effect of changes in NPV and Duration measures have been illustrated alongside the changes in the discount rate are presented.
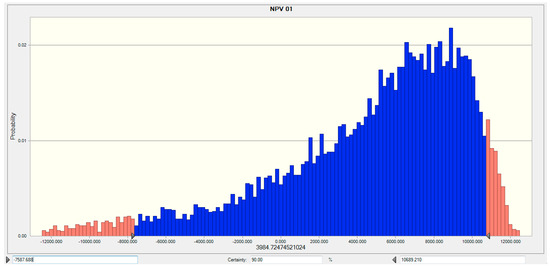
Figure 4.
The NPV distribution with the changes in discount rate.
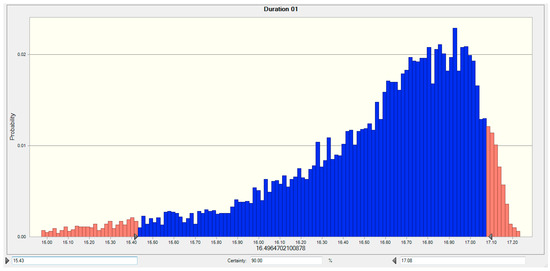
Figure 5.
The Duration distribution with the changes in discount rate.
It is clear from the above figures that the NPV and Duration distributions of projects have negative skewness. Therefore, changes in the discount rate will lead to a non-normal distribution, wherein the possibility of occurrence of bad results (negative NPV) is more than the normal distribution.
3. Duration and Sensitivity of the Project Returns to Changes in Discount Rates
Another issue is the relationship between the changes in NPV and the discount rate. These two have an inverse relationship, meaning that, as expected, an increase in the discount rate will result in a decrease in a project’s NPV. One application of the Duration measure could be the estimation of the NPV changes by changing the discount rate. It should be noted that one of the most important assumptions taken by managers in the feasibility study phase of the project is the assumption of the discount rate. Duration can provide management with an estimate of possible changes in NPV for the changes in the discount rate.
Much research has been conducted for choosing the appropriate discount rate of the projects. Lee and Lee (2017) proposed a method to predict the real discount rate. Jagannathan et al. (2016) concluded that firms use higher discount rates which are approximately twice the firms’ capital cost. Firms apply these higher discount rates to account for idiosyncratic risks. Jouini and Napp (2014) discussed an equilibrium approach for the aggregation of discount rates. de Vasconcelos et al. (2016) examined the impact of various discount rates on refurbishment decisions of construction projects. Groom et al. (2007) in their paper show that the employment of models that account for changes in the interest rate generating mechanism has important implications for operationalizing a theory of DDRs that depends upon uncertainty.
In some research, the liaison of discount rates and time horizons was investigated. Hansson et al. (2016) studied this relationship on a long-term basis. Kossova and Sheluntcova (2016) studied the social discount rate in public sector projects in Russia, Kazlauskienė (2015) surveyed its application for assessment of public investment projects, and García-Gusano et al. (2016) discussed its role on energy systems optimization models. Nesticò and Maselli (2019) in their research considered the Social Discount Rate (SDR) in Cost-Benefit Analysis for making economic evaluations. This measure allows us to make the costs and the benefits that an investment generates over time financially comparable. This rate must reflect the organization and project’s Weighted Average Cost of Capital (WACC), and also be consistent with the project’s risk. Even for an organization with a constant weighted average cost of capital, the discount rate of two different projects must not be the same. The amount of this discount rate should be adjusted consistently with the project’s risk, and of course, the amount of the risk in different phases of a project can change. The amount of an organization’s risk appetite and management’s perception of risk are very effective in the appropriate allocation of discount rate as well. There are numerous assumptions in choosing appropriate discount rates. Thus, it is practical to have a measure that provides the management with a perspective on the influence of the changes in discount rates on the projects. Duration helps the project and portfolio managers to have an estimate of possible changes in NPV. In Figure 6 below, it is clear that there is a strong relationship between the NPV of the project and defined Duration.
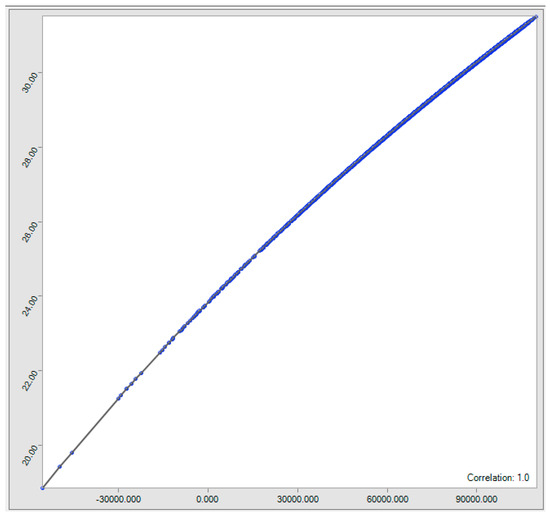
Figure 6.
Correlation between the NPV of the project and defined Duration.
It should be noted that, projects with a higher duration have more risk and the volatility of their NPV is higher. Duration can be considered as a measure to estimate sensitivity of NPV to changes in discount rates. Since NPV is an important measure in selection of proper projects for the firm, and other indices in choosing projects are in some way related to NPV, it can be helpful to have a criterion for its sensitivity. In other words, projects with a higher duration have more sensitivity to changes in the discount rate and higher volatility in their NPV. Since projects’ NPV are calculated according to the assumptions regarding the discount rate, management should not merely focus on the amount of NPV when choosing proper projects for the organization. The Duration measure can provide the manager with an index of NPV sensitivity. Therefore, if the managers are looking for appropriate projects for investment, they must select projects with the maximum NPV and minimum duration, which have less sensitivity with the assumptions of discount rate. A higher duration means more sensitivity and thus indicates projects with more volatility (higher risk). If the manager considers the assumptions regarding the discount rate as being conservative and decides to select projects with more volatility, which may contain proper opportunities, he should select the projects with a higher duration.
As was mentioned, duration reflects NPV’s sensitivity to the assumptions regarding the discount rate, and it can be used to obtain an estimate of the future changes in NPV. As discussed, one of the applications of this new measure is to forecast the changes in the NPV by varying the amount of discount rate. In Figure 7, the difference between forecasted changes with duration and actual NPV changes (error Term) have been illustrated for 1000 trials.
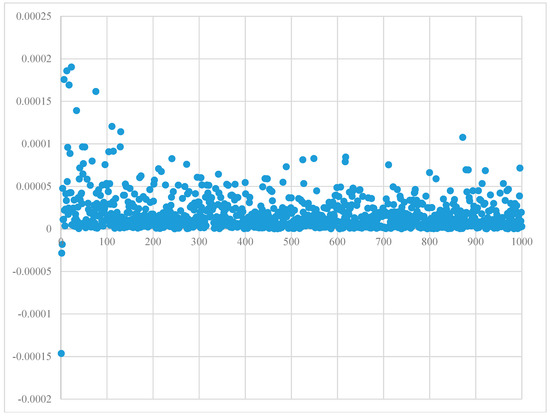
Figure 7.
Error term diagram, difference between forecasted changes with duration and actual NPV changes.
It is necessary to note that the amount of duration may change with project execution. That is, by passing time, and with the payment of costs and receiving of project returns, the duration changes, which necessitates reassessment of it. Clearly, with the passage of time and the project progression, the amount of duration decreases. With every return received from the project, the amount of duration increases immediately and then it further decreases gradually by project progression. Therefore, the overall amount of duration is continually decreasing, with smaller sudden increases at the times of receiving the project returns.
4. Convexity
As is evident from Figure 7, the relationship of NPV with the changes in discount rate is a convex one. This convexity shows that for every one unit change of the discount rate in different rates, the amount of change in NPV can vary. The basic idea of the duration is to use the concepts of the duration and convexity for matching the price sensitivities of future and spot positions (Bessler and Wolff (2014); Kolb and Chiang (1981, 1982)). Osborne (2005) developed a more precise formula compared to adding convexity. Fricke and Menkhoff (2015) used a convexity adjustment term in their model. Shaffer (2007) estimated duration and convexity by considering risks of failure. Lesseig and Stock (2000) examined the duration and convexity of both senior and junior debt, and Sarkar (1999) did the same for zero-coupon convertible bonds. (Hanson 2014) studied the convexity effect in the mortgage backed securities (MBS) which have an embedded prepayment option. Gupta and Subrahmanyam (2000) investigated convexity bias in the pricing of interest rate swaps. Hyong-Chol et al. (2016) considered the convexity of stock price and exercise price relationship in Black–Scholes equations. Houweling et al. (2005), Lu et al. (2017) also considered the positive convexity effect and concluded that the loss of market value of downgraded bonds in a high-interest-rate environment is less than that of a low-interest-rate environment. Grieves et al. (2010) examined and determined whether contract prices display negative convexity. It is clear that the amount of NPV changes by considering various discount rates. As expected, the NPV declines by increasing the expected discount rates. In the following table the amount of change in the NPV is shown for different discount rates and it is clear that this change is not linear. As mentioned, one of the purposes of defining duration is to use it for prediction of this change and if this relationship is not linear the amount of errors of the forecast can be non-negligible. Figure 8 shows the amount of this convexity that we want to estimate.
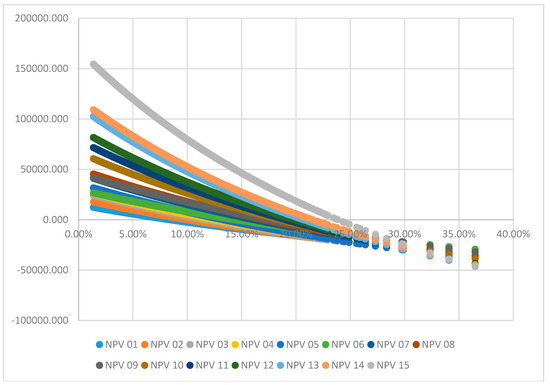
Figure 8.
The amount of NPV changes in different discount rates.
The important intuition from this chart is the difference in the changes of NPV for every unit of increase or decrease in the discount rate. In the table below, the amount of change in NPV has been determined for one percent increase and decrease in the discount rate are presented in the Table 1.

Table 1.
The amount of change in NPV for one percent volatility in the discount rate.
As it is evident from the table and can be perceived from the convexity of the diagram, in every discount rate, the amount of increase in NPV for one percent decrease in discount rate is more than the amount of decrease in NPV for one percent increase in the discount rate. This difference is shown in the table above. Moreover, in higher discount rates, the amount of changes in the NPV of a project is much more than that of low discount rates. It should be noted that the discount rate of any project is determined according to the weighted average cost of capital of the organization/project, as well as the risk. Therefore, it can be concluded that using projects with less risk and also low a duration, will lead to lower volatility of NPV. It also reflects the importance of an organization/project’s financing to be able to lower the weighted average cost of capital. Various financing methods have different capital costs, which, as it is evident, have great impact on the final result of the project and its returns. The importance of this effect is even greater in higher discount rates. That is, the method of financing is more important for high-risk projects, than it is for low-risk ones. As is evident, the importance of this financing is even more influential in high rates than project cost management. That is the case while sometimes all of the efforts of management are put into lowering the costs, even though the focus should be directed towards lowering the risk of the project and its cost of capital. That is because lowering the project risk can substantially help lower its financial costs.
This, once more, shows the importance of risk management for lowering the project risks and the effort to lower the cost of capital. If successful, the benefits of this improvement are greater than a situation in which the said effort has failed and has led into an increase in risk and cost of capital. It can also be useful to consider that, in practice, one percent decrease in the discount rate will be much more feasible in higher rates than it is in lower rates. That is, changes that can be made to lower the risk or cost of capital, at high rates, are more probable. However, the benefits of lowering this rate at high discount rates, are greater. This emphasizes the importance of risk management and proper financing of projects.
5. Discount Rate Risk and Reinvestment Risk
Companies and projects have different financing methods, based on maturity, the type of organization, the type of projects, the country of origin and many other factors. Based on the source of financing (equity, debt and etc.) and their proportions, the company’s capital costs change. This cost of capital affects the discount rate of organization’s projects. The risk of the project affects the discount rate, as well. That is, all of the projects of one firm (which may even have the same cost of capital for all the projects) do not have the same discount rate and the company adjusts the discount rate of each project, based on its unique risks. Projects may have numerous risks. The effects of most of these risks can be considered using the proper discount rate. Since duration displays the NPV’s sensitivity according to the changes in the discount rate, it can represent the discount rate risk. Therefore, projects with higher duration have higher sensitivity to this discount rate risk. The higher the project duration is, the more the firm has to wait to earn back the funds invested in that project. As was mentioned before, the greater duration means more volatility in project return. On the other hand, projects with higher returns (higher NPV and IRR) have a lower duration, because projects with higher return repay their costs sooner. Moreover, shorter time intervals for project earnings result in a lower project duration.
Based on the presented definition of project duration, it is equal to the time it takes to present the value of project costs to be repaid. Therefore, in that time, the organization can start another project. However, if there is no possibility for starting a proper new project or the conditions have changed in a way so that the organization can start a similar project with lower return or higher risk (and therefore a higher discount rate), then reinvestment risk exists. Projects with a lower duration have a higher reinvestment risk. Therefore, the management must select the project with the appropriate duration, according to the current macroeconomic and organizational conditions, and predictions of the future. This selection should have the proper level of both risks based on the situations. It should be noted that an inverse relationship exists between these two risks and with a decrease in the discount rate risk, the reinvestment risk increases. Choosing the proper level of these risks require optimization.
Selection of the appropriate project duration is closely correlated to organization and project’s finance method. If a big part of discount rate of the project is allocated based on the weighted average cost of capital of the organization and the project, then a smaller part of the discount rate will be influenced by the project risk. So, if the finance method of the organization can keep the cost of capital fixed, the marginal change of the discount rate decreases. Therefore, the discount rate volatility, and as a result the return volatility decreases. Under these conditions, if the manager forecasts that the capital costs will increase in the future, he must select projects with a higher duration to minimize the reinvestment risk. That is because execution of a similar project in the future will entail a higher cost of capital and higher discount rate and therefore, a lower expected return. In this situation, selection of a project with a higher duration will improve organizational benefits and gains. Thus, optimization of duration and considering it in selecting projects can lead into an increase in the portfolio and the organization’s value. This can be helpful in selecting appropriate projects for the organization. One of the applications of duration can be the optimization of firm’s project portfolio, with the duration as a constraint. Also, duration can provide management with an estimate of the appropriate starting time for new projects, because in fact, duration is the time it takes to receive present value of project costs. Therefore, the organization will have enough resources to start a similar project.
Another benefit of using duration is the selection of proper investment projects, based on the firm’s balance sheet. A number of investment companies, such as pension funds and endowments have long-term liabilities. These organizations can invest in projects with a higher duration. Even though the discount rate risk in this type of projects is higher, they also have higher returns. Therefore, these companies can gain higher returns, based on their long-term liabilities. Therefore, duration can also be an appropriate criterion for the selection of an organization’s projects. Optimization of this method can be similar to Asset-Liability Management (ALM) in finance and projects must be matched with their corresponding liabilities.
6. Conclusions
In the first step of this study, the projects were grouped according to their unique characteristics. Then, a Monte Carlo Simulation was used to estimate project’s return and risks, with different discount rates. In this research, a new concept in project management literature, Duration, was defined. Duration has a long history and major applications in finance literature. All three concepts of return, cost, and time of the project were considered in the definition of Duration, and thus, the management can possess an index combined of a number of important project factors, using this measure.
Duration reflects the sensitivity of NPV and its volatility to changes in the discount rate. Therefore, the management can have a measure of NPV’s volatility based on the assumptions. If the manager is willing to select projects with lower risk, or if he is uncertain of propriety of the discount rate, projects with a lower duration should be chosen. Furthermore, the duration of each project will provide the management with an estimate of the changes in NPV, if the discount rate is unreliable.
In this research, the convexity effects between NPV and discount rate have been examined. That is, the changes in NPV, with the changes in the assumptions of discount rate, are much higher in lower rates than they are in higher rates. Furthermore, the amount of change in NPV for each unit of increase or decrease in the discount rate also varies. This means that the benefits of the project from a decrease in the discount rate are greater than the losses realized by an increase in the discount rate of the same value. This shows the importance of special attention and investment in proper risk management systems to lower the risk and also appropriate project financing, because it has a great impact on the final result and return of the project.
A decrease in duration means a decrease in the discount rate risk, and an increase in the reinvestment risk. Since by the time respective to the duration of the project, the present value of its construction costs has been repaid, the company can then start another project. In the absence of suitable projects, or a change in the investment criteria, the start of a new appropriate project may not be possible, and the manager faces reinvestment risk.
Duration can be an appropriate criterion for selecting projects by investment companies. To this end, an approach, similar to Asset-Liability Management (ALM) approach in finance, can be used and projects that match the liabilities periods can be selected. The benefits of using this method are much greater than the conservative method of simple cash flow matching.
Author Contributions
V.Y. designed the research, set the objectives, studied the literature, analyzed data, designed and developed the model. J.T. and S.H.Y. gathered and analyzed the data, provided extensive advice throughout the study, revised the manuscript, methodology and findings, and provided extensive advice on the literature review, model development and its evaluation. Conceptualization, V.Y.; Methodology, V.Y.; Software, V.Y.; Validation, V.Y. and J.T.; Formal Analysis, V.Y.; Investigation, V.Y.; Resources, V.Y., S.H.Y. and J.T.; Data Curation, V.Y., S.H.Y. and J.T.; Writing-Original Draft Preparation, V.Y. and J.T.; Writing-Review & Editing, J.T. and S.H.Y.; Visualization, V.Y. and J.T.; Supervision, J.T. and S.H.Y.; Project Administration, V.Y., S.H.Y. and J.T. All authors discussed the model evaluation results and commented on the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Acebes, Fernando, María Pereda, David Poza, Javier Pajares, and José Manuel Galán. 2015. Stochastic earned value analysis using Monte Carlo simulation and statistical learning techniques. International Journal of Project Management 33: 1597–609. [Google Scholar] [CrossRef]
- Asadi, Pezhman, Javad Rezaeian Zeidi, Toraj Mojibi, Abdolreza Yazdani-Chamzini, and Jolanta Tamošaitienė. 2018. Project risk evaluation by using a new fuzzy model based on Elena guideline. Journal of Civil Engineering and Management 24: 284–300. [Google Scholar] [CrossRef]
- Bejaoui, Azza, and Adel Karaa. 2016. Revisiting the bull and bear markets notions in the Tunisian stock market: New evidence from multi-state duration-dependence Markov-switching models. Economic Modelling 59: 529–45. [Google Scholar] [CrossRef]
- Bessler, Wolfgang, and Dominik Wolff. 2014. Hedging European government bond portfolios during the recent sovereign debt crisis. Journal of International Financial Markets, Institutions and Money 33: 379–99. [Google Scholar] [CrossRef]
- Boquist, John A., George A. Racette, and Gary G. Schlarbaum. 1975. Duration and risk assessment for bonds and common stocks. The Journal of Finance 30: 1360–65. [Google Scholar] [CrossRef]
- Brandt, Michael W., Amit Goyal, Pedro Santa-Clara, and Jonathan R. Stroud. 2005. A Simulation Approach to Dynamic Portfolio Choice with an Application to Learning About Return Predictability. Review of Financial Studies 18: 831–73. [Google Scholar] [CrossRef]
- Buchner, Axel. 2015. Equilibrium option pricing: A Monte Carlo approach. Finance Research Letters 15: 138–45. [Google Scholar] [CrossRef]
- Cesari, Riccardo, and David Cremonini. 2003. Benchmarking, portfolio insurance and technical analysis: A Monte Carlo comparison of dynamic strategies of asset allocation. Journal of Economic Dynamics and Control 27: 987–1011. [Google Scholar] [CrossRef]
- Chatterjee, Kajal, Edmundas Kazimieras Zavadskas, Jolanta Tamošaitienė, Krishnendu Adhikary, and Samarjit Kar. 2018. A hybrid MCDM technique for risk management in construction projects. Symmetry 10: 46. [Google Scholar] [CrossRef]
- Cong, Fei, and Cornelis W. Oosterlee. 2016. Multi-period mean–variance portfolio optimization based on Monte-Carlo simulation. Journal of Economic Dynamics and Control 64: 23–38. [Google Scholar] [CrossRef]
- de Vasconcelos, Ana Brandão, António Cabaço, Manuel Duarte Pinheiro, and Armando Manso. 2016. The impact of building orientation and discount rates on a Portuguese reference building refurbishment decision. Energy Policy 91: 329–40. [Google Scholar] [CrossRef]
- Denault, Michel, and Jean-Guy Simonato. 2017. Dynamic portfolio choices by simulation-and-regression: Revisiting the issue of value function vs portfolio weight recursions. Computers & Operations Research 79: 174–89. [Google Scholar] [CrossRef]
- Dierkes, Thomas, and Karl Michael Ortmann. 2015. On the efficient utilisation of duration. Insurance: Mathematics and Economics 60: 29–37. [Google Scholar] [CrossRef]
- Fricke, Christoph, and Lukas Menkhoff. 2015. Financial conditions, macroeconomic factors and disaggregated bond excess returns. Journal of Banking & Finance 58: 80–94. [Google Scholar] [CrossRef]
- Fukuta, Yuichi, and Akiko Yamane. 2015. Value premium and implied equity duration in the Japanese stock market. Journal of International Financial Markets, Institutions and Money 39: 102–21. [Google Scholar] [CrossRef]
- García-Gusano, Diego, Kari Espegren, Arne Lind, and Martin Kirkengen. 2016. The role of the discount rates in energy systems optimisation models. Renewable and Sustainable Energy Reviews 59: 56–72. [Google Scholar] [CrossRef]
- Ghasemi, Foroogh, Mohammad Hossein Mahmoudi Sari, Vahidreza Yousefi, Reza Falsafi, and Jolanta Tamošaitienė. 2018. Project portfolio risk identification and analysis, considering project risk interactions and using Bayesian networks. Sustainability 10: 1609. [Google Scholar] [CrossRef]
- Grieves, Robin, Alan J. Marcus, and Adrian Woodhams. 2010. Delivery options and convexity in Treasury bond and note futures. Review of Financial Economics 19: 1–7. [Google Scholar] [CrossRef]
- Groom, Ben, Phoebe Koundouri, Ekaterini Panopoulou, and Theologos Pantelidis. 2007. Discounting the distant future: How much does model selection affect the certainty equivalent rate? Journal of Applied Econometrics 22: 641–56. [Google Scholar] [CrossRef]
- Gupta, Anurag, and Marti G. Subrahmanyam. 2000. An empirical examination of the convexity bias in the pricing of interest rate swaps. Journal of Financial Economics 55: 239–79. [Google Scholar] [CrossRef]
- Hanson, Samuel G. 2014. Mortgage convexity. Journal of Financial Economics 113: 270–99. [Google Scholar] [CrossRef]
- Hansson, Sven Ove, Kristin Lilieqvist, Karin Edvardsson Björnberg, and Maria Vredin Johansson. 2016. Time horizons and discount rates in Swedish environmental policy: Who decides and on what grounds? Futures 76: 55–66. [Google Scholar] [CrossRef]
- Hatchondo, Juan Carlos, and Leonardo Martinez. 2009. Long-duration bonds and sovereign defaults. Journal of International Economics 79: 117–25. [Google Scholar] [CrossRef]
- Hatefi, Seyed Morteza, and Jolanta Tamošaitienė. 2018. Construction projects assessment based on the sustainable development criteria by an integrated fuzzy AHP and improved GRA model. Sustainability 10: 991. [Google Scholar] [CrossRef]
- Houweling, Patrick, Albert Mentink, and Ton Vorst. 2005. Comparing possible proxies of corporate bond liquidity. Journal of Banking & Finance 29: 1331–58. [Google Scholar] [CrossRef]
- Hyong-Chol, O., Jong-Jun Jo, and Ji-Sok Kim. 2016. General properties of solutions to inhomogeneous Black–Scholes equations with discontinuous maturity payoffs. Journal of Differential Equations 260: 3151–72. [Google Scholar] [CrossRef]
- Jacoby, Gady, and Gordon S. Roberts. 2003. Default-and call-adjusted duration for corporate bonds. Journal of Banking & Finance 27: 2297–321. [Google Scholar] [CrossRef]
- Jagannathan, Ravi, David A. Matsa, Iwan Meier, and Vefa Tarhan. 2016. Why do firms use high discount rates? Journal of Financial Economics 120: 445–63. [Google Scholar] [CrossRef]
- Jouini, Elyès, and Clotilde Napp. 2014. How to aggregate experts’ discount rates: An equilibrium approach. Economic Modelling 36: 235–43. [Google Scholar] [CrossRef]
- Kazlauskienė, Vilma. 2015. Application of Social Discount Rate for Assessment of Public Investment Projects. Procedia—Social and Behavioral Sciences 213: 461–67. [Google Scholar] [CrossRef]
- Kolb, Robert W., and Raymond Chiang. 1981. Improving hedging performance using interest rate futures. Financial Management 10: 72–79. [Google Scholar] [CrossRef]
- Kolb, Robert W., and Raymond Chiang. 1982. Duration, immunization, and hedging with interest rate futures. Journal of Financial Research 5: 161–70. [Google Scholar] [CrossRef]
- Kossova, Tatiana, and Maria Sheluntcova. 2016. Evaluating performance of public sector projects in Russia: The choice of a social discount rate. International Journal of Project Management 34: 403–11. [Google Scholar] [CrossRef]
- Lee, Chijoo, and Eul-Bum Lee. 2017. Prediction method of real discount rate to improve accuracy of life-cycle cost analysis. Energy and Buildings 135: 225–32. [Google Scholar] [CrossRef]
- Lee, Hei Wai, Yan Alice Xie, and Jot Yau. 2011. The impact of sovereign risk on bond duration: Evidence from Asian sovereign bond markets. International Review of Economics & Finance 20: 441–51. [Google Scholar] [CrossRef]
- Lesseig, Vance P., and Duane Stock. 2000. Impact of correlation of asset value and interest rates upon duration and convexity of risky debt. Journal of Business Research 49: 289–301. [Google Scholar] [CrossRef]
- Lu, Erin P., Gene C. Lai, and Qingzhong Ma. 2017. Organizational structure, risk-based capital requirements, and the sales of downgraded bonds. Journal of Banking & Finance 74: 51–68. [Google Scholar] [CrossRef]
- Macaulay, Frederick R. 1938. Some Theoretical Problems Suggested by the Movements of Interest Rates, Bond Yields and Stock Prices in the United States Since 1856. New York: NBER Books. [Google Scholar]
- Nesticò, Antonio, and Gabriella Maselli. 2019. Intergenerational Discounting in the Economic Evaluation of Projects. In Smart Innovation, Systems and Technologies. Edited by Calabrò Francesco, Della Spina Lucia and Bevilacqua Carmelina. Cham: Springer, vol. 101. [Google Scholar] [CrossRef]
- Osborne, Michael J. 2005. On the computation of a formula for the duration of a bond that yields precise results. The Quarterly Review of Economics and Finance 45: 161–83. [Google Scholar] [CrossRef]
- Pajares, Javier, and Adolfo Lopez-Paredes. 2011. An extension of the EVM analysis for project monitoring: The Cost Control Index and the Schedule Control Index. International Journal of Project Management 29: 615–21. [Google Scholar] [CrossRef]
- Project Management Institute. 2017. A Guide to the Project Management Body of Knowledge (PMBOK Guide), 6th ed. Newtown Square: Project Management Institute, ISBN 978-1-62825-184-5. [Google Scholar]
- Sarkar, Sudipto. 1999. Duration and convexity of zero-coupon convertible bonds. Journal of Economics and Business 51: 175–92. [Google Scholar] [CrossRef]
- Sarkar, Sudipto, and Gwangheon Hong. 2004. Effective duration of callable corporate bonds: Theory and evidence. Journal of Banking & Finance 28: 499–521. [Google Scholar] [CrossRef]
- Shaffer, Sherrill. 2007. Equity duration and convexity when firms can fail or stagnate. Finance Research Letters 4: 233–41. [Google Scholar] [CrossRef]
- Shariati, Shahram, Masoumeh Abedi, Alieh Saedi, Abdolreza Yazdani-Chamzini, Jolanta Tamošaitienė, Jonas Šaparauskas, and Stanislav Stupak. 2017. Critical factors of the application of nanotechnology in construction industry by using ANP technique under fuzzy intuitionistic environment. Journal of Civil Engineering and Management 23: 914–25. [Google Scholar] [CrossRef]
- Valipour, Alireza, Nordin Yahaya, Norhazilan Md Noor, Jurgita Antuchevičienė, and Jolanta Tamošaitienė. 2017. Hybrid SWARA-COPRAS method for risk assessment in deep foundation excavation project: An Iranian case study. Journal of Civil Engineering and Management 23: 524–32. [Google Scholar] [CrossRef]
- Wang, Xiaoyu, Dejun Xie, Jingjing Jiang, Xiaoxia Wu, and Jia He. 2016. Value-at-Risk estimation with stochastic interest rate models for option-bond portfolios. Finance Research Letters. [Google Scholar] [CrossRef]
- Weil, Roman L. 1973. Macaulay’s duration: An appreciation. The Journal of Business 46: 589–92. [Google Scholar] [CrossRef]
- Xie, Yan Alice, Sheen Liu, Chunchi Wu, and Bing Anderson. 2009. The effects of default and call risk on bond duration. Journal of Banking & Finance 33: 1700–8. [Google Scholar] [CrossRef]
- Yousefi, Vahidreza, Siamak Haji Yakhchali, Jonas Šaparauskas, and Sarmad Kiani. 2018. The Impact Made on Project Portfolio Optimisation by the Selection of Various Risk Measures. Engineering Economics 29: 168–75. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).