Improved Methods for Predicting the Financial Vulnerability of Nonprofit Organizations
Abstract
1. Introduction
2. Methodology
2.1. Outline of the Hazard Analysis Procedure
2.2. Methods for Time-At-Risk Estimation
2.3. Using the Results for Predicting Financial Vulnerability
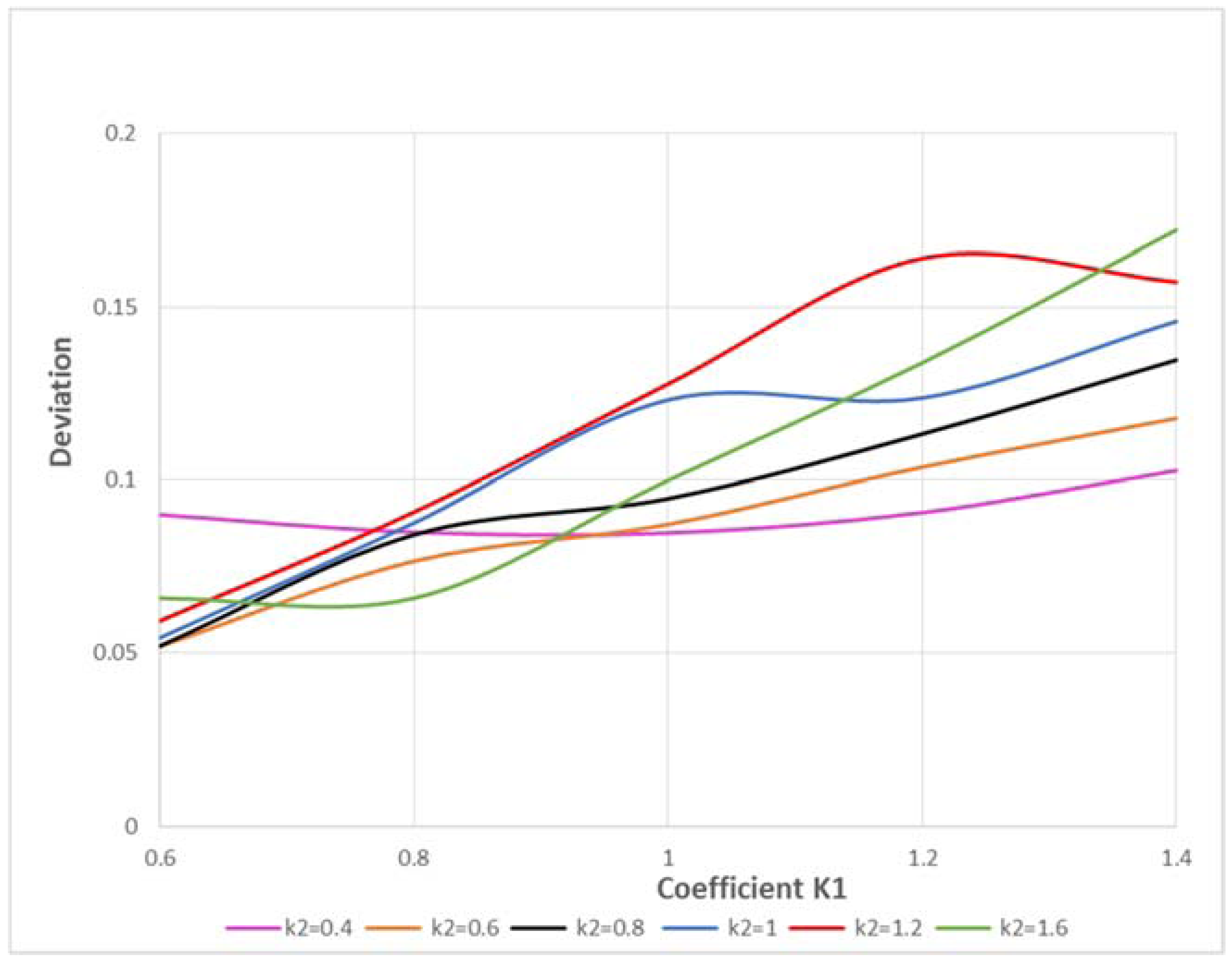
2.4. Testing the Robustness and Optimization Procedure
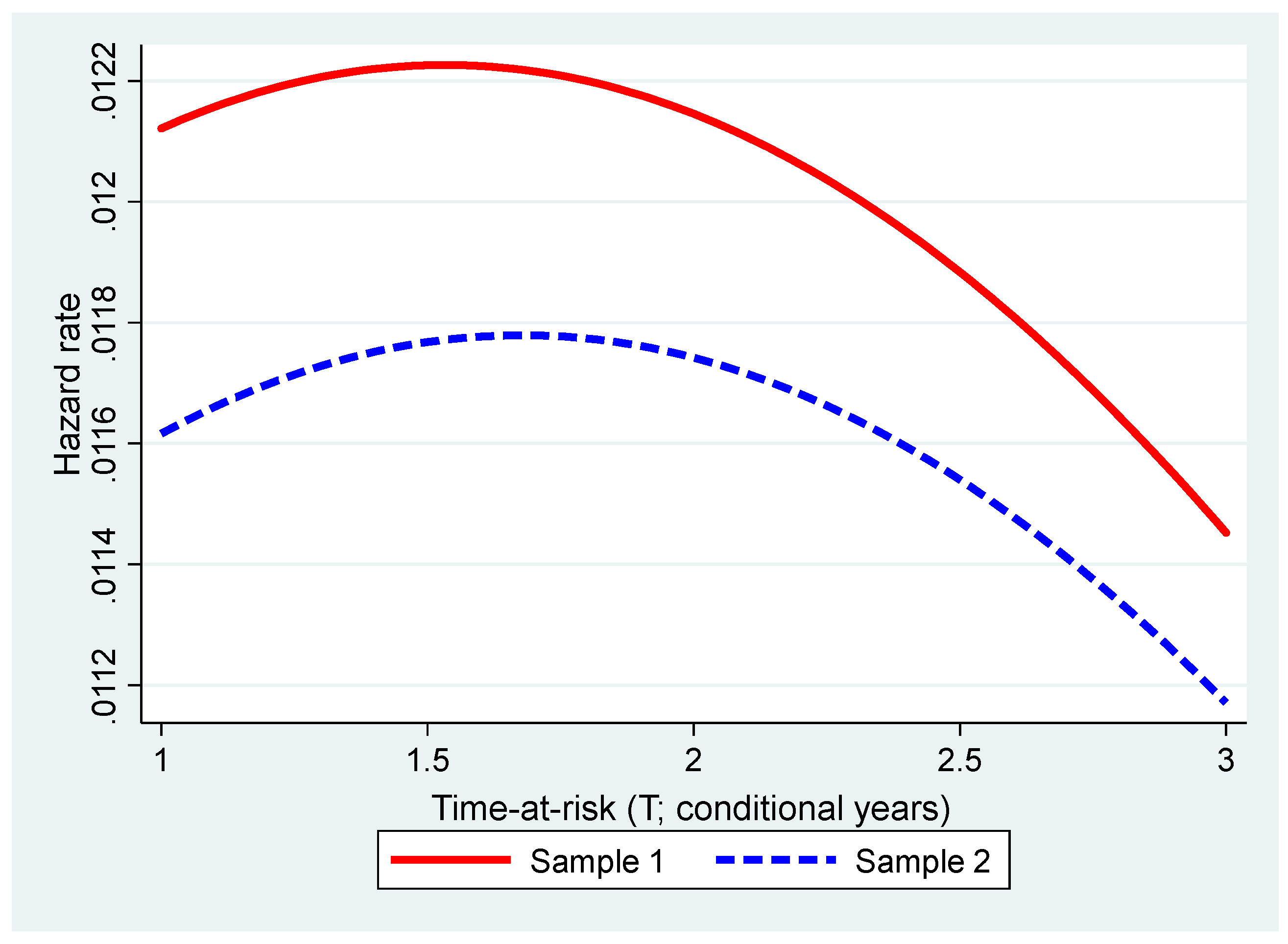
3. Example of Results
4. Conclusions
Acknowledgements
Conflicts of Interest
Appendix A. Definitions of Generalized Time-At-Risk
References
- Allison, Paul D. 2014. Event History and Survival Analysis: Regression for Longitudinal Event Data. Thousand Oaks: SAGE Publications, vol. 46. [Google Scholar]
- Altman, Edward I. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Balcaen, Sofie, and Hubert Ooghe. 2006. 35 years of studies on business failure: An overview of the classic statistical methodologies and their related problems. The British Accounting Review 38: 63–93. [Google Scholar] [CrossRef]
- Bauer, Julian, and Vineet Agarwal. 2014. Are hazard models superior to traditional bankruptcy prediction approaches? A comprehensive test. Journal of Banking & Finance 40: 432–42. [Google Scholar]
- Beaver, William H. 1966. Financial ratios as predictors of failure. Journal of Accounting Research 4: 71–111. [Google Scholar] [CrossRef]
- Beck, Nathaniel, Jonathan N. Katz, and Richard Tucker. 1998. Taking time seriously: Time-series-cross-section analysis with a binary dependent variable. American Journal of Political Science 42: 1260–88. [Google Scholar] [CrossRef]
- Burde, Gila. 2012. Prediction of Financial Vulnerability: The Case of Israeli Nonprofit Organizations. Ph.D. Thesis, Ben-Gurion University of the Negev, Beer-Sheva, Israel. Available online: http://aranne5.bgu.ac.il/others/BurdeGila.pdf (accessed on 21 February 2012).
- Burde, Gila, Ahron Rosenfeld, and Zachary Sheaffer. 2016. Prediction of Financial Vulnerability to Funding Instability. Nonprofit and Voluntary Sector Quarterly 46: 280–304. [Google Scholar] [CrossRef]
- Campbell, John Y., Jens Hilscher, and Jan Szilagyi. 2008. In search of distress risk. The Journal of Finance 63: 2899–939. [Google Scholar] [CrossRef]
- Chava, Sudheer, and Robert A. Jarrow. 2004. Bankruptcy prediction with industry effects. Review of Finance 8: 537–69. [Google Scholar] [CrossRef]
- Cox, David R. 1972. Regression models and life tables. Journal of the Royal Statistical Society 34: 187–220. [Google Scholar]
- Duffie, Darrell, Leandro Saita, and Ke Wang. 2007. Multi-period corporate default prediction with stochastic covariates. Journal of Financial Economics 83: 635–65. [Google Scholar] [CrossRef]
- Gepp, Adrian, and Kuldeep Kumar. 2008. The role of survival analysis in financial distress prediction. International Research Journal of Finance and Economics 16: 13–34. [Google Scholar]
- Gepp, Adrian, and Kuldeep Kumar. 2015. Predicting financial distress: A comparison of survival analysis and decision tree techniques. Procedia Computer Science 54: 396–404. [Google Scholar]
- Greenlee, Janet S., and John M. Trussel. 2000. Predicting the financial vulnerability of charitable organizations. Nonprofit Management and Leadership 11: 199–210. [Google Scholar] [CrossRef]
- Gupta, Jairaj, Andros Gregoriou, and Jerome Healy. 2015. Forecasting bankruptcy for SMEs using hazard function: To what extent does size matter? Review of Quantitative Finance and Accounting 45: 845–69. [Google Scholar] [CrossRef]
- Gupta, Jairaj, Andros Gregoriou, and Tahera Ebrahimi. 2017. Empirical comparison of hazard models in predicting SMEs failure. Quantitative Finance 18: 1–30. [Google Scholar] [CrossRef]
- Hager, Mark A. 2001. Financial vulnerability among art organization: A test of the Tuckman-Chang measures. Nonprofit and Voluntary Sector Quarterly 30: 376–92. [Google Scholar] [CrossRef]
- Hager, Mark A., Joseph Galaskiewicz, and Jeff A. Larson. 2004. Structural embeddedness and the liability of newness among nonprofit organization. Public Management Review 6: 159–88. [Google Scholar] [CrossRef]
- Klein, John P., and Melvin L. Moeschberger. 2003. Survival Analysis: Techniques for Censored and Truncated Data, 2nd ed. New York: Springer. [Google Scholar]
- Ohlson, James A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef]
- Shumway, Tyler. 2001. Forecasting bankruptcy more accurately: A simple hazard model. Journal of Business 74: 101–24. [Google Scholar] [CrossRef]
- Trussel, John M. 2002. Revisiting the prediction of financial vulnerability. Nonprofit Management and Leadership 13: 17–31. [Google Scholar] [CrossRef]
- Trussel, John, and Janet Greenlee. 2004. A financial rating system for charitable nonprofit organization. In Research in Governmental and Nonprofit Accounting. Edited by Pual A. Copley. Bingley: Emerald, vol. 11. [Google Scholar]
- Tuckman, Howard P., and Cyril F. Chang. 1991. A methodology for measuring the financial vulnerability of charitable nonprofit organization. Nonprofit and Voluntary Sector Quarterly 20: 445–60. [Google Scholar] [CrossRef]
- Wang, Jane-Ling. 2005. Smoothing hazard rates. In Encyclopedia of Biostatistics. Edited by Peter Armitage and Theodore Colton. New York: John Wiley, pp. 4986–97. [Google Scholar]
- Yeager, Valerie A., Nir Menachemi, Grant T. Savage, Peter M. Ginter, Bisakha P. Sen, and Leslie M. Beitsch. 2014. Using Resource-Dependency Theory to measure the environment in health-care organizational studies: A systematic review of the literature. Healthcare Management Review 39: 50–65. [Google Scholar] [CrossRef] [PubMed]
- Zmijewski, Mark E. 1984. Methodological issues related to the estimation of financial distress prediction models. Journal of Accounting Research 22 Supplement: 59–86. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burde, G. Improved Methods for Predicting the Financial Vulnerability of Nonprofit Organizations. Adm. Sci. 2018, 8, 3. https://doi.org/10.3390/admsci8010003
Burde G. Improved Methods for Predicting the Financial Vulnerability of Nonprofit Organizations. Administrative Sciences. 2018; 8(1):3. https://doi.org/10.3390/admsci8010003
Chicago/Turabian StyleBurde, Gila. 2018. "Improved Methods for Predicting the Financial Vulnerability of Nonprofit Organizations" Administrative Sciences 8, no. 1: 3. https://doi.org/10.3390/admsci8010003
APA StyleBurde, G. (2018). Improved Methods for Predicting the Financial Vulnerability of Nonprofit Organizations. Administrative Sciences, 8(1), 3. https://doi.org/10.3390/admsci8010003




