Factor Structure of Almutairi’s Critical Cultural Competence Scale

Abstract

This paper reports on a psychometric study conducted to explore the factor structure and refine the Critical Cultural Competence Scale (CCCS). Critical Cultural Competence (CCC) functions to promote the safety, equity, and well-being of patients, their families, and health care professionals. The development process of this measurement scale was systematic and iterative, and included generating a pool of potential items based on the theoretical definitions of CCC. In this study, conducted with a sample of 170 registered nurses from British Columbia, Canada, we used Principal Component Analysis (PCA) to explore the factor structure of the initial set of 84 items as a final step in developing the CCCS. The final version of the measure consists of 43 items, and the PCA results supported a four-factor solution consistent with the theoretical underpinnings of the scale. Future research is recommended to further assess the construct validity of this newly created scale.

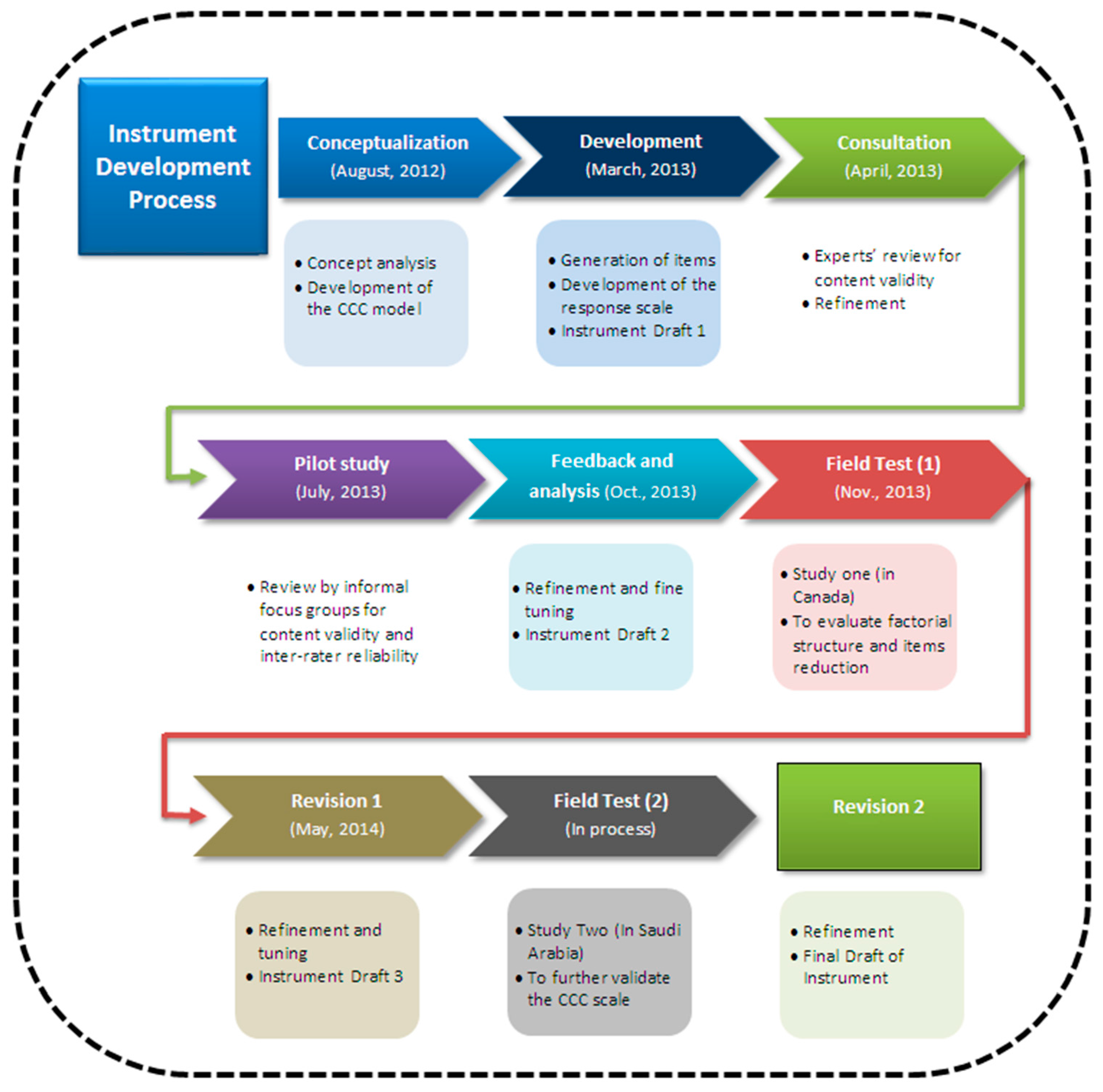
1. Introduction

This paper reports on a psychometric study conducted to investigate the factor structure and refine the Critical Cultural Competence Scale (CCCS). The CCCS was developed to measure healthcare providers’ perceptions of their critical cultural competence in a multicultural healthcare context. A number of frameworks and instruments have been developed to measure cultural competence, including the Cultural Self-Efficacy Scale [1,2], the Cultural Attitude Survey-Modified [3], the Cultural Awareness Survey [4], the Multicultural Sensitivity Scale [5], and the Multicultural Counseling Inventory (adopted scale) [6].

Despite evidence of reliability and validity, a review of these instruments has revealed several limitations at both the conceptual and structural level. Most of these frameworks were developed in the United States and represent unique socio-cultural issues related to American contexts and/or testing of knowledge related to specific cultural groups. The latter is a fundamental issue that has been widely criticized in the literature due to the reduction of the complex nature of the concept of culture into a set of measurable variables [7,8]. This approach runs the risk of fostering stereotypes and could provide a fertile climate for racism and discrimination [9,10]. Another limitation at the conceptual level is that these frameworks do not take into account power-difference factors such as race, class, gender, etc. that can influence interactions and health-related outcomes. Further limitations are that many of these frameworks fail to address the culture of Western biomedicine and institutional oppression [7,11].

One of the widely used instruments to measure cultural competence, particularly in the nursing discipline, is the Inventory for Assessing the Process of Cultural Competence among Health Care Professionals (IAPCC) [12]. This instrument has a number of problematic structural issues. First, the items are written at an advanced reading level that can pose difficulties for a multidisciplinary healthcare team where members have varying levels of fluency in the language of the questionnaire and varying levels of education, such as with the items that ask about “ethnic pharmacology” and “anatomical and physiological variations.” The second limitation pertains to the multiple response formats used for the 20-item instrument, which can pose difficulties when transitioning from one response format to another [13]. The CCCS was developed to overcome these aforementioned limitations.

One particular strength of CCCS is its strong theoretical base—the Critical Cultural Competence (CCC) model—which was developed through empirical research and subsequent theoretical refinement. The development work originated with an investigation of the cultural competence of a multicultural nursing workforce in Saudi Arabia [14]. The study was informed by Campinha-Bacote’s cultural competence framework [15], which was useful, but failed to explain all the nurses’ experiences. In follow-up work, the first author drew on other theories in the field, such as culture theory, cultural safety, and postcolonial theoretical perspectives, with the aim of finding other factors that operate in either subtle or unsubtle ways to influence and affect health-related outcomes within a multicultural context [10,16,17,18,19,20]. Thus, Almutairi’s empirical and theoretical work led to an explicit conceptual framework for the CCCS.

Critical cultural competence is a comprehensive process that aims to manage the difficulties that arise during cross-cultural interactions. Critical cultural competence also aims to promote the safety, equity, and well-being of patients, their families, and healthcare providers, which ultimately results in a safe and peaceful environment. Almutairi and Rodney conceptualized CCC as a process composed of four components with 14 facets as essential requirements for healthcare professionals to become critically culturally competent [9]. The four components represent three conceptual domains: the cognitive, behavioural, and affective domains [21].

There are two components that fall within the cognitive domain: critical awareness and critical knowledge. Critical awareness refers to recognition of socio-cultural differences, individual attitudes, and biases, as well as the resultant consequences of cross-cultural interactions. It also includes the recognition of power relation determinants, such as class, racialization, gender, geographic location, and poverty. Critical knowledge refers to conceptualizations of culture (including the culture of Western biomedicine) as well as communication challenges that arise during cross-cultural interactions. The third component, critical skills, fall within the behavioural domain. Critical skills are “comprised of an individual’s agency to enact the aspects of critical awareness and knowledge when interacting with people from other cultures in the context as a whole” [22] (p. 322). They include the ability to negotiate cultural meaning and ethical decisions during clinical encounters to meet the cultural needs of the patients and their families, and to use intercultural communication skills and appropriate body language. Critical empowerment is the fourth component, which falls within the affective domain. Critical empowerment “encompasses the perception of healthcare providers about their own empowerment within their context, particularly in terms of whether they have experienced racialization, or been disempowered due to their gender, economic situation, culture, geographic location or institutional or individual racism” [22]. The CCC model, with its four components, is explained in more detail in the Almutairi et al. paper [22].

After establishing the theoretical framework for CCC, we began a systematic and iterative process to develop a measure of CCC. This process included generating a pool of potential items, obtaining expert review of the items, conducting focus group interviews, and testing the instrument with the target population. Figure 1 illustrates the process that we followed with the aim of developing a reliable and valid measure of CCC consistent with the CCC theoretical model. We began by generating a pool of items for potential inclusion in the CCCS by deconstructing the theoretical components of the CCC model into a number of representative items. The first draft of the instrument contained 81 items; between four and 14 items were generated for each component. Content validity of the items was then assessed by three faculty experts (with expertise in quantitative measurement, ethics, and critical cultural perspectives), and suggestions were made to improve the clarity of the item or its relevance to the particular component it was intended to reflect. This was followed by informal pilot testing with three graduate nursing students in Canada and four practising nurses from diverse cultural backgrounds in Saudi Arabia. The purpose was to assess the intra- and inter-rater reliability and content validity of the CCCS and enhance clarity and content relevance of the pool of items. Based on the advisory interviews, we eliminated, split, added, and revised items, yielding an 84-item CCCS for psychometric testing. The items pertaining to various components were distributed in a mixed order throughout the questionnaire. The response scale for the CCCS was a seven-point Likert scale, anchored from 1 (“strongly disagree”) to 7 (“strongly agree”) for most of the items, and from 1 (“never”) to 7 (“always”) for the items that measure how often certain events have happened.

The purpose of the current study was to further refine and reduce the number of items in the CCCS, and to assess its factor structure through the use of Principal Component Analysis (PCA). We hypothesized that the empirical factor structure would reflect the four theoretical components of the CCC model, and that the observed factors would be weakly to moderately correlated. Demonstrating an observed factor structure that is theoretically meaningful and reflective of the underlying theory is the first step in providing evidence of construct validity [23,24,25].

2. Methods

2.1. Study Participants and Recruitment and Data Collection Procedures

After obtaining ethical approval from the Behavioural Research Ethics Board of the University of British Columbia, eligible nurses were invited to participate in the study. A random sample of 1000 nurses was computer generated through the College of Registered Nurses of British Columbia (CRNBC). The target sample consisted of registered nurses who (a) were registered with the CRNBC as practising nurses, (b) had agreed to be contacted for research purposes, (c) were currently working in a hospital in British Columbia, and (d) were working either full-time or part-time. The researcher provided CRNBC with stamped recruitment and data collection packages; CRNBC affixed address labels and mailed the packages to the potential participants. As an incentive for participation, participants who completed the instrument were eligible to enter a draw to win $200 cash by completing a coupon with their contact information. Participants were assured that this coupon would be separated from the envelope immediately upon receipt to maintain their anonymity.

Nurses in the target sample received a recruitment and data collection package containing an invitation letter, a cover sheet explaining the study’s purpose and procedure, a paper questionnaire containing the 84-item CCCS and a set of 9 demographic questions, and a self-addressed and stamped envelope for returning the completed instrument. Participants were asked to complete the questionnaire and return it to the researcher within three weeks of receiving the package. Completing and returning the questionnaire signified consent. The total time required to complete the questionnaire was estimated to be 30 to 45 min. One hundred and seventy nurses completed the questionnaire.

2.2. Data Analysis

The data were analyzed using the Statistics Package for the Social Sciences (SPSS) for Windows Version 21. Out of 1000, the 170 completed questionnaires were scanned and entered directly into the SPSS database. The recorded data were screened for accuracy by using two common methods. First, approximately 10% of the returned questionnaires were randomly selected and checked for correct entry. Second, frequencies were computed for each variable and checked for invalid codes (codes that fell outside of the specified range of values for the response scale) [26]. Negatively worded items were then reverse scored so that higher scores on CCCS items represented higher levels of critical cultural competence. Seventy of the 84 items showed use of the full range of responses across the study sample. Missing data was found to be minimal (i.e., less than 10% per item). A series of PCAs were conducted to assess the factor structure of the CCCS and refine the scale.

3. Results

3.1. Respondent Characteristics

Table 1. Demographic characteristics of respondents.

Variable	Frequency	%	Mean (SD)
	(N = 170)
Age (years)			43.6 ± 11.7
Experience in the profession (years)			16.6 ± 12.1
Experience in the organization (years)			11.1 ± 9.4
Gender
Male	14	8.8
Female	146	91.3
Nursing Education
Diploma	55	3.4
BSN	96	60
MSN	9	5.6
Job Position
Staff nurse	141	88.1
Clinical nurse specialist	4	2.5
Nurse educator	2	1.3
Nurse leader	6	3.8
Nurse manager	1	0.6
Other	6	3.8
Nursing Specialty
Medical unit	45	28.1
Emergency department	30	18.8
Outpatient clinic	29	18.1
Surgical unit	26	16.3
Intensive care units	12	7.5
Oncology units	4	2.5
Pediatric unit	3	1.9
Other	11	6.9
Ethnicity
Caucasian	118	74.2
South Asian	20	12.6
Chinese	9	5.7
Far East Asian	3	1.9
Other Asian	2	1.3
First nation	1	0.6
Other	6	3.8
Cultural Training
Yes	64	40.5
No	94	59.5

presents the demographic characteristics of respondents. The majority of respondents were female (91.3%), had a bachelor degree in nursing (60.0%), and were in staff nurse positions (88.1%). Their ages ranged from 23 to 67 years (M = 43.6, SD = 11.7). The mean length of experience in the profession and in the organization was 16.6 years (SD = 12.1) and 11.1 years (SD = 9.4), respectively. Respondents worked in a variety of specialty areas, where the greater proportion of them worked in medical units (28.1%), followed by the emergency departments (18.8%) and outpatient clinics (18.1%). Almost half of the respondents (40.5%) reported having received some cultural training.

Ethnicity is an important variable in this study because of its focus on cultural difference and competence. The majority of respondents identified themselves as Caucasian (74.2%) with the two next largest groups being South Asian (12.6%) and Chinese (5.7%). Other ethnic identities included Far East Asian (1.9%), other Asian (1.3%), and First Nation (0.6%). Respondents identified 24 nations as their country of birth, including Canada, the Philippines, Taiwan, Hong Kong, South Korea, Slovakia, China, Ireland, Germany, Netherlands, Paraguay, Hungary, the United Kingdom, India, Russia, the United States, Zimbabwe, South Africa, Ukraine, Australia, Japan, Iran, and Jamaica. These countries were grouped into three major categories: Anglo-Saxon countries, European countries, and Asian countries so that the sub-sample size would be sufficient to support correlation analysis.

3.2. Principal Component Analysis Results

Exploratory factor analysis is used to explore and identify the factor structure of a large set of variables (items), in contrast to confirmatory factor analysis in which the researcher tests specific hypotheses about factor structure. Exploratory factor analysis, PCA in particular, is appropriate during the early stages of instrument development and testing, especially in situations where the goal is to develop a shorter scale [27,28,29].

Prior to performing PCA on the 84 items (N = 170), we assessed the suitability of the data set for this procedure. The issue of sample size in PCA has been studied and debated for several years. Some authors have argued for a cases-to-variables ratio, but others have demonstrated that overall sample size matters more, in combination with the size of factor loadings and communalities [30]. For example, one study [31] showed that sample size was irrelevant as long as there were at least four loadings greater than 0.60 on each factor, or 10 loadings greater than 0.40 with a minimum sample size of 150. Another study [32] suggested that even a small sample of less than 100 can be reliable if all communalities are 0.60 or greater. Thus, the adequacy of our sample of 170 could only be fully assessed after completing the PCA. Another means of assessing the suitability of the data is through visual inspection of the correlational matrix with the ideal range for correlation coefficients being between 0.30 and 0.70 [30]. Finally, the Kaiser-Meyer-Olkin Measure of Sampling Adequacy (0.66) and Bartlett’s Test of Sphericity (p < 0.001) both supported the factorability of the data and suggested that PCA was an appropriate method for performing factor extraction.

Factor extraction refers to the process of grouping a large number of items into a fewer number of factors in order to identify the underlying dimensions. The most commonly used methods are PCA and principal axis factor analysis (PAF). PCA estimates linear components within the data and contributions of a particular item to that component, whereas PAF estimate the items to be linear combination of the unique factors [30]. Although these two methods differ slightly, they often lead to a similar result in terms of the underlying dimensions [29]. In this study, we used PCA as the simpler method for variable/item reduction [28,33].

Three techniques were used in determining the number of factors to be extracted: Kaiser’s criterion, a scree test, and parallel analysis. Kaiser’s criterion calls for retaining factors that have eigenvalues equal to or greater than 1.0 for further investigation. Although this technique is commonly used, it can be problematic and has been widely criticized in the literature for retaining a large number of factors. This technique is also most appropriate when the case-to-item ratio is 10 to 1 [34]. Using Kaiser’s criterion in this study yielded 24 factors with eigenvalues of 1.0 or greater; thus, we also used Catell’s scree test, which plots the eigenvalues against factor numbers. We were looking for a sharp break in the slopes and a levelling off, which would indicate “the number of meaningful factors, different from random error” [35]. Inspection of the scree plot indicated that there was a break after the fourth component with the curve changing direction; however, it was not a clear and sharp elbow-like break which posed some uncertainty about the number of factors that should be retained. Therefore, although the number of factors (4) was congruent with the theoretical foundation of the CCCS, the data were subjected to further investigation using a parallel analysis technique.

In parallel analysis, we used the eigenvalue Monte Carlo simulation technique, in which the size of the observed eigenvalues are compared with those “obtained from a randomly generated data set of the same size” [36] (p. 183). The number of factors with observed eigenvalues greater than that obtained in the simulated data set determines the number of factors that should be retained. However, critics have noted that a problem with this technique is the possibility of retaining factors that may poorly defined [37]. The use of parallel analysis in this study suggested a nine-factor solution.

Given the wide range in the number of factors that might best describe the dimensionality of the data, we conducted a series of PCA with a forced number of factors ranging between 4 and 9, comparing the eigenvalues, factor loadings, and communalities of the factor structure. The best solution was obtained with a four-factor solution that accounted for 33% of variance of the full set of 84 items, with the first two factors accounting for 14% and 9% of the variance, respectively. We then employed an orthogonal rotation method (Varimax) that assumes that underlying factors are only weakly correlated, consistent with recommendations in the literature for initial investigations of factor structure [38].

The next step was to refine the CCCS by deleting 22 items with low factors loadings (i.e., less than 0.40) and low communalities (i.e., less than 0.30) [35,39]. There were 12 other items with communalities less than 0.30 but we retained these due to their theoretical relevance and factor loadings of greater than 0.40. After re-running the PCA with the reduced set of items (k = 62), we found that most (but not all) of the items showed a moderate to strong loading on a theoretically appropriate factor. We then deleted an additional 11 items because they were irrelevant to the factor (three items), cross-loaded on two factors (two items), or cross-loaded on two factors and were irrelevant to the dominant factor (six items). The remaining items were further evaluated for redundancy (i.e., items that were worded similarly or tapped closely into the same idea) and we retained the item with the higher factor loading. For example, we kept the first of two items (“I feel safe in expressing my concerns to management” and “I feel supported in expressing my concerns to management”) because of its higher loading. The deleted items came from across the four factors. The final solution consisted of 43 items that loaded cleanly across four factors explaining 42.3% of the variance. The final analysis yielded a scree plot that indicated the clear presence of four factors.

Table 2. Final principal component analysis results for the critical cultural competence scale.

	Item	Rotated Factor Loadings					Communalities
		1 Critical Empowerment	2 Critical Awareness	3 Critical Skills	4 Critical Knowledge
1.	CCC 49: I feel disrespected because of my culture. [R]	0.796					0.715
2.	CCC48: I face biased remarks and racism. [R]	0.776					0.628
3.	CCC 51: I feel alienated in my workplace because of my cultural background. [R]	0.761					0.608
4.	CCC 56: I am treated differently to my counterparts by management because of my cultural background. [R]	0.700					0.561
5.	CCC50: I feel disrespected because of my gender.	0.689					0.500
6.	CCC 61: In this organization, people are treated differently according to their country of origin. [R]	0.684					0.520
7.	CCC 60: I have an equal opportunity in terms of professional development compared to colleagues in my organization.	0.643					0.439
8.	CCC 83: My colleagues from other cultures look down on me. [R]	0.643					0.492
9.	CCC 64: I feel that my colleagues from other cultures are more powerful. [R]	0.626					0.513
10.	CCC47: I feel that my skin colour determines how people relate to me in this context. [R]	0.622					0.411
11.	CCC 59: I have an equal opportunity in terms of promotion compared to colleagues in my organization.	0.606					0.417
12.	CCC 62: I worry about losing my job if I speak out about my concerns of discrimination.. [R]	0.606					0.450
13.	CCC44: I feel reluctant to speak out about my conditions of work0. [R]	0.587					0.372
14.	CCC46: My nursing competence is frequently challenged by my colleagues compared to that of my counterparts. [R]	0.536					0.421
15.	CCC 57: I feel safe in expressing my concerns to management.	0.528					0.322
16.	CCC45: My nursing competence is frequently challenged by my patients compared to that of my counterparts. [R]	0.524					0.393
17.	CCC 66: Social norms limit my ability to advocate for my patients. [R]	0.502					0.351
18.	CCC15: Gender can determine the way people relate to others.		0.729				0.581
19.	CCC14: Social class is an important factor in determining the way people relate to others.		0.713				0.509
20.	CCC 16: Gender roles, positions or activities can empower some people over others.		0.667				0.481
21.	CCC23: Cultural differences between people can generate conflicts and tensions during interactions.		0.608				0.404
22.	CCC 24: Cultural differences influence how we interact and relate to others from other cultures.		0.564				0.387
23.	CCC 19: An interpersonal power imbalance could compromise a healthcare provider’s well-being.		0.530				0.327
24.	CCC 73: When I interact with people from other cultures, I feel my cultural values and norms are better.		−0.503				0.285
25.	CCC 74: I find it annoying when time is not important for some people from other cultures.		−0.502				0.295
26.	CCC 75: The large number of visitors for patients from other cultures is a nuisance.		−0.490				0.259
27.	CCC 18: Cultural and linguistic differences could compromise healthcare provider’s well-being.		0.470				0.275
28.	CCC13: In a multicultural environment, ‘race’ can determine the way people relate to others.		0.463				0.279
29.	CCC 20: Cultural and linguistic differences between the healthcare provider and patient could compromise patient’s safety.		0.447				0.288
30.	CCC 34: There are no cultural variations between different cultural groups. [R]			0.763			0.619
31.	CCC33: There are no cultural variations within a cultural group of people. [R]			0.705			0.509
32.	CCC 36: It is not important to assess a patient’s preferences in terms of healthcare services if I am knowledgeable about their culture. [R]			0.550			0.361
33.	CCC 9: People from the same culture have the same religion.			0.533			0.291
34.	CCC37: Western biomedicine is always attentive to diverse cultural meanings.			0.521			0.309
35.	CCC31: Cultural norms that people adhere to are largely fixed and unvarying. [R]			0.505			0.324
36.	CCC 35: It is easy to anticipate behaviors and practices of people if I know their culture. [R]			0.457			0.274
37.	CCC 80: I use some of my patients’ languages during my care if I know a little.					0.733	0.555
38.	CCC 81: I use culturally congruent body language when interacting with people from other cultures.					0.730	0.536
39.	CCC 79: I am able to change healthcare practices to meet my patients’ cultural and religious needs and expectations.					720	0.529
40.	CCC 76: I discuss the different cultural meanings in terms of health and illness with my patients from other cultures in order to provide them with optimal care0.					0.621	0.460
41.	CCC 82: I use simple language when I speak with people from other cultures and I consider their potential language limitations.					0.568	0.332
42.	CCC 78: I discuss ethically sensitive issues with my patients/families.					0.515	0.299
43.	CCC 39: Assessing the linguistic needs of my patients and their family during care delivery is important					0.440	0.330
	Eigenvalues	8.25	4.29	3.03		2.60
	% of variance explained	19.19	9.98	7.06		6.10

Notes: Extraction Method: Principal Component Analysis. Rotation Method: Varimax with Kaiser Normalization. Factor loadings less than 0.40 are not reported.

presents the factor loadings for each of the items, their communalities, and the percent of variance explained by each factor.

To interpret and label the four factors, we evaluated the theoretical meaning of the set of items that loaded on each factor. The set of items loading on Factor 1 pertained to the individual’s perception of racialization, assessment of their organization, and personal confidence; therefore, this factor was labelled as “Critical Empowerment.” The items that loaded on Factor 2 reflected self-awareness of the respondent’s own attitudes and values, and recognition of the determinants of power and consequences of both power and cultural differences, so this factor was labelled “Critical Awareness.” Factor 3 items were concerned with the skills needed for safe and competent cross-cultural interactions, so this factor was labelled as “Critical Skills.” Factor 4, labelled as “Critical Knowledge,” pertained to conceptualizations of culture. Thus, the observed factor structure of the refined CCCS closely reflects the original conceptual model of CCC developed by Almutairi, Dahinten and Rodney [22]. The four components of the CCC model, with associated constituent facets and items, are presented in

Table 3. Components of Almutairi’s critical cultural competence codel and their corresponding CCCS items.

Components	Corresponding Items
Critical Empowerment	The individual’s experience of racialization: 1. I feel disrespected because of my culture. [Reverse coded] 2. I face biased remarks and racism. [Reverse coded] 3. I feel alienated in my workplace because of my cultural background. [Reverse coded] 4. I feel disrespected because of my gender. 5. My colleagues from other cultures look down on me. [Reverse coded] 6. I feel that my skin colour determines how people relate to me in this context. [Reverse coded] The individual’s assessment of their organization 7. I am treated differently to my counterparts by management because of my cultural background. [Reverse coded] 8. I have an equal opportunity in terms of promotion compared to colleagues in my organization. 9. I have an equal opportunity in terms of professional development compared to colleagues in my organization. 10. In this organization, people are treated differently according to their country of origin. [Reverse coded] 11. I worry about losing my job if I speak out about my concerns of discrimination. [Reverse coded] 12. I feel safe in expressing my concerns to management. The individual’s confidence 13. I feel that my colleagues from other cultures are more powerful. [Reverse coded] 14. My nursing competence is frequently challenged by my colleagues compared to that of my counterparts. [Reverse coded] 15. My nursing competence is frequently challenged by my patients compared to that of my counterparts. [Reverse coded] 16. I feel reluctant to speak out about my conditions of work. [Reverse coded] 17. Social norms limit my ability to advocate for my patients. [Reverse coded]
Critical Awareness	Self-awareness of own attitudes and values 18. I find it annoying when time is not important for some people from other cultures. 19. The large number of visitors for patients from other cultures is a nuisance. 20. When I interact with people from other cultures, I feel my cultural values and norms are better. Recognition of power determinants 21. Gender can determine the way people relate to others 22. Social class is an important factor in determining the way people relate to others. 23. Gender roles, positions or activities can empower some people over others. 24. Cultural differences influence how we interact and relate to others from other cultures. 25. In a multicultural environment, ‘race’ can determine the way people relate to others. Awareness of the consequences of cultural and power differences 26. Cultural differences between people can generate conflicts and tensions during interactions. 27. An interpersonal power imbalance could compromise a healthcare provider’s well-being. 28. Cultural and linguistic differences could compromise healthcare provider’s well-being. 29. Cultural and linguistic differences between the healthcare provider and patient could compromise patient’s safety.
Critical Knowledge	30. There are no cultural variations between different cultural groups. [Reverse coded] 31. There are no cultural variations within a cultural group of people. [Reverse coded] 32. Cultural norms that people adhere to are largely fixed and unvarying. [Reverse coded] 33. It is not important to assess a patient’s preferences in terms of healthcare services if I am knowledgeable about their culture. [Reverse coded] 34. Western biomedicine is always attentive to diverse cultural meanings. 35. It is easy to anticipate behaviors and practices of people if I know their culture. [Reverse coded] 36. People from the same culture have the same religion. [Reverse coded]
Critical Skills	37. I use culturally congruent body language when interacting with people from other cultures. 38. I use some of my patients’ languages during my care if I know a little. 39. I am able to change healthcare practices to meet my patients’ cultural and religious needs and expectations. 40. I discuss the different cultural meanings in terms of health and illness with my patients from other cultures in order to provide them with optimal care. 41. I use simple language when I speak with people from other cultures and I consider their potential language limitations. 42. I discuss ethically sensitive issues with my patients/families. 43. Assessing the linguistic needs of my patients and their family during care delivery is important.

.

Finally, to check our assumptions about the appropriateness of orthogonal rotation, we re-ran the PCA using oblique rotation (Oblimin). The resulting component correlation matrix showing correlations ranging between −0.13 and 0.22 supported our assumptions about the independence of the factors, and the use of Varimax rotation.

3.3. Internal Consistency

The internal consistency of the four factors was assessed using Cronbach’s alphas, and results are presented in

Table 4. Internal consistency of the Critical Cultural Competence Scale (CCCS) and subscales.

Scale	No. of Items	Cronbach’s Alpha
Critical Awareness	12	0.60
Critical Knowledge	7	0.70
Critical Skills	7	0.77
Critical Empowerment	17	0.92
Overall score of CCC	43	0.86

. The Cronbach’s alpha statistics for the four subscales ranged from 0.60 (Critical Awareness) to 0.92 (Critical Empowerment). A value of 0.60 is considered the minimum acceptable score by many authors; scores in the 0.70s are considered acceptable, particularly for new instruments; and scores greater than 0.90 are considered excellent [40]. Inspection of the corrected item-total correlation showed that deletion of three items (#73, 74, 75) would increase the alpha for Critical Awareness to 0.64. However, we chose to retain these items because deletion would yield an increase of only 0.04, and because of their theoretical relevance.

4. Discussion and Conclusions

This paper reports on the first field test of the CCCS as part of the instrument development process. The content of the CCCS was conceptually grounded in the experiences of a multicultural nursing workforce in Saudi Arabia, and refined through follow-up theoretical work. The instrument development process was overseen by an expert advisory group and the instrument was informally piloted through focus groups with Canadian nurses prior to this first field test. The objectives of this study were to investigate the factor structure and refine the Critical Cultural Competence Scale (CCCS). The use of EFA also helped to reduce the length of the CCCS from an initial set of 84 items to 43.

In the early process of developing the CCCS, we hypothesized that the empirical factor structure would reflect the theoretical components of the CCC model, and that the resulting factors would be moderately correlated. The results of the PCA supported most of our hypotheses. Findings indicated that a four-factor solution best describes the underlying components of CCC, congruent with the theoretical explanations underpinning the CCC model. Congruency between the observed factor structure and the underlying theory is a beginning step to providing evidence of construct validity, and is sometimes referred to as factorial validity [27,36,41]. Based on their theoretical meanings, these factors were labelled as Critical Awareness, Critical Knowledge, Critical Skills, and Critical Empowerment. Although we had hypothesized each of these factors as multifaceted, some of the facets (or sub-components) did not factor out as distinct factors, or they disappeared completely. However, an inspection of the component correlation matrix supported our assumption about the independence of the observed factors. Internal consistency was found to be adequate for each of the subscales.

The number of items within the CCCS was reduced from 84 to 43, with seven to 17 items in each component. This difference in number of items retained in each component may be related to the depth of the theoretical explanations of these components. Our final scale with 43 items is longer than many of the other published cultural competence scales which contain 20 to 31 items (e.g., see [12,15,42,43,44]). This difference could be related to the richness of theoretical meanings underpinning the CCC model.

Another strength of the CCCS is that it uses a seven-point Likert-type scale in comparison to the four- to six-point response scale used in many of the other cultural competence scales (e.g., [1,12,15,43,44]). Use of a seven-point scale has been recommended by many scholars for more accurately determining the participants’ level of agreement [45,46,47].

A strength of our PCA process was the way in which we determined the optimal number of underlying components. Identifying the factor structure in this study was not a straightforward process, perhaps due to the large set of items. In the course of analysis, we obtained contradictory results from the three techniques used to determine the number of factors: Kaiser’s criterion, a Scree test, and parallel analysis. Therefore, we explored solutions with a different numbers of factors, starting from the highest (nine) to the lowest (four), until a satisfactory and interpretable factor structure was obtained. This strategy is recommended in the literature, as it is generally preferable to overestimate rather than underestimate the number of factors [35].

A potential limitation of the study is the representativeness of the respondents and generalizability of findings. The sample was representative of British Columbia nurses with respect to gender, highest education level, and mean age and experience in the nursing profession [48]. However, the response rate was low, which raises questions about potential bias if the nurses who participated in the study are different than those who did not participate. Therefore, further testing of the scale in varied contexts is recommended.

Cultural awareness, knowledge, skills, and empoawerment are integral to the provision of equitable and safe health care in today’s multicultural environment [9,49,50]. Therefore, our intent in developing the CCCS is to provide a measure of critical cultural competency that can be used by researchers and policy makers to evaluate the cultural competence of healthcare providers and the effectiveness of educational and policy initiatives that aim to promote cultural competence. The outcome of this study was a four-factor, 43-item scale that can measure healthcare providers’ perceptions of their critical cultural competence. Further research is necessary to evaluate the discriminant and convergent validity of the CCCS, and to assess its reliability in a variety of contexts.