COMSOL Modeling of Heat Transfer in SVE Process

Abstract

Non aqueous phase liquid (NAPL) pollution exists in porous media such as soil. SVE technology can be used to remove this pollution in soil. However, few domestic and international studies have paid attention to the changes of soil temperature in the field, which we believe can be useful information to optimize the layout of heating wells. In this research we established partial differential equations of soil heat transfer using the COMSOL multi-field coupling tool to simulate the field distribution of the change in soil internal temperature in the process of SVE to obtain the change of effective heating area with time under certain initial heating conditions. At the same time, we used liquid ethylbenzene to represent NAPL pollutants, and designed a simulation of soil temperature field distribution under the movement of liquid ethylbenzene under external pressure. It was found that under the action of Darcy’s velocity field, the utilization efficiency of the SVE system for the heat source was significantly improved, that is, the temperature distribution of the soil was more uniform. However, the temperature of the heated area increased slowly because the extraction well took away the heat energy. The heat source power should be increased or prolonged to improve the effect of Darcy’s field. Through a coupled simulation, we obtained a variation relationship of the soil temperature field in 1800 min under the action of one extraction well and four heating wells. These data will provide the basis for our next step in designing an algorithm to optimize the distribution of heating wells.

1. Introduction

Soil pollution of industrial land has caused great pressure on the ecosystem. Compared with other pollution, such as water pollution, NAPL pollution can exist in soil for many years, and its soluble components gradually penetrate and diffuse into groundwater along the soil layer, forming deep-seated and more lasting pollution. Many studies have been conducted on the transport and distribution of NAPL. For example, an electrical imaging method and a soil radon deficiency survey have been used to evaluate the pollution degree of NAPL in aeration zones [1,2], and nanotechnology and biotechnology have been used to study the concentration and transfer trend of NAPL [3,4]. In addition, some researchers have also studied the repair process of NAPL pollution with surfactants [5,6,7,8] and the effects of temperature and other factors on the diffusion rate of NAPL in groundwater and other media [9,10,11,12].

Since 1990s, soil vapor extraction (SVE) has been used in industry to remove the pollution caused by NAPLs. In this field, many scholars have established SVE models to simulate mass transfer and other processes in the SVE method [13,14,15,16,17]. Other scholars have focused on the effects of gas flow rate [18], water level fluctuation [19,20] and initial organic concentration [21] on pollutant migration efficiency in gas phase extraction. In addition, some scholars have used SVE combined with bioremediation and other remediation methods to remove NAPLs pollutants in soil [22,23]. However, domestic and international scholars have paid more attention to the influence of conditions and removal results of SVE technology to remove pollutants, while few have paid attention to the energy consumption cost of SVE removal of pollutants, which is the reason why SVE technology has not been used on a large scale in China.

Optimizing heater well distribution is an effective way to reduce the cost of SVE. Considering that heating temperature is an important factor for the removal of volatile organic compounds, and some organic compounds can be oxidized into water and carbon dioxide with SVE technology, we established a heat transfer model for the SVE process, aiming to obtain the soil temperature during the SVE heating process through simulation. This study focuses on changes of the soil temperature field caused by heating wells as important reference information for optimizing the distribution of heating wells.

COMSOL is a powerful multi physical field simulation tool. It integrates many self-developed solution modules and allows users to add control equations to the model according to their needs. Compared with classical mechanical analysis software, such as ANSYS, it can also effectively converge in multi-physics coupling simulation.

In this paper, the COMSOL multi field coupling tool and other calculation tools are used to establish partial differential equations, materialize conceptual units, and simulate the change of the soil temperature field under a multi-field coupling state, based on porous medium heat transfer and Darcy’s law, to provide a reference for removing industrial land pollution by SVE Technology.

The other parts of this paper are as follows. The second part introduces the relevant principles of porous media heat transfer and Darcy’s law, the third part introduces the simulation results of porous media heat transfer, the fourth part introduces the simulation results of the COMSOL model after adding the Darcy velocity field, and the fifth part is the conclusion.

2. Materials and Methods

2.1. Heat Transfer Model of Porous Media

2.1.1. Model Building

In a simulation, time and temperature should be given priority because they have the greatest impact on the removal result of soil pollution, and the impact of exhaust flow from the removal effect of pollutants is less than that of the concentration of pollutants themselves. Therefore, the model can be simplified to focus on analysis of the temperature field distribution of soil with time under a given initial condition.

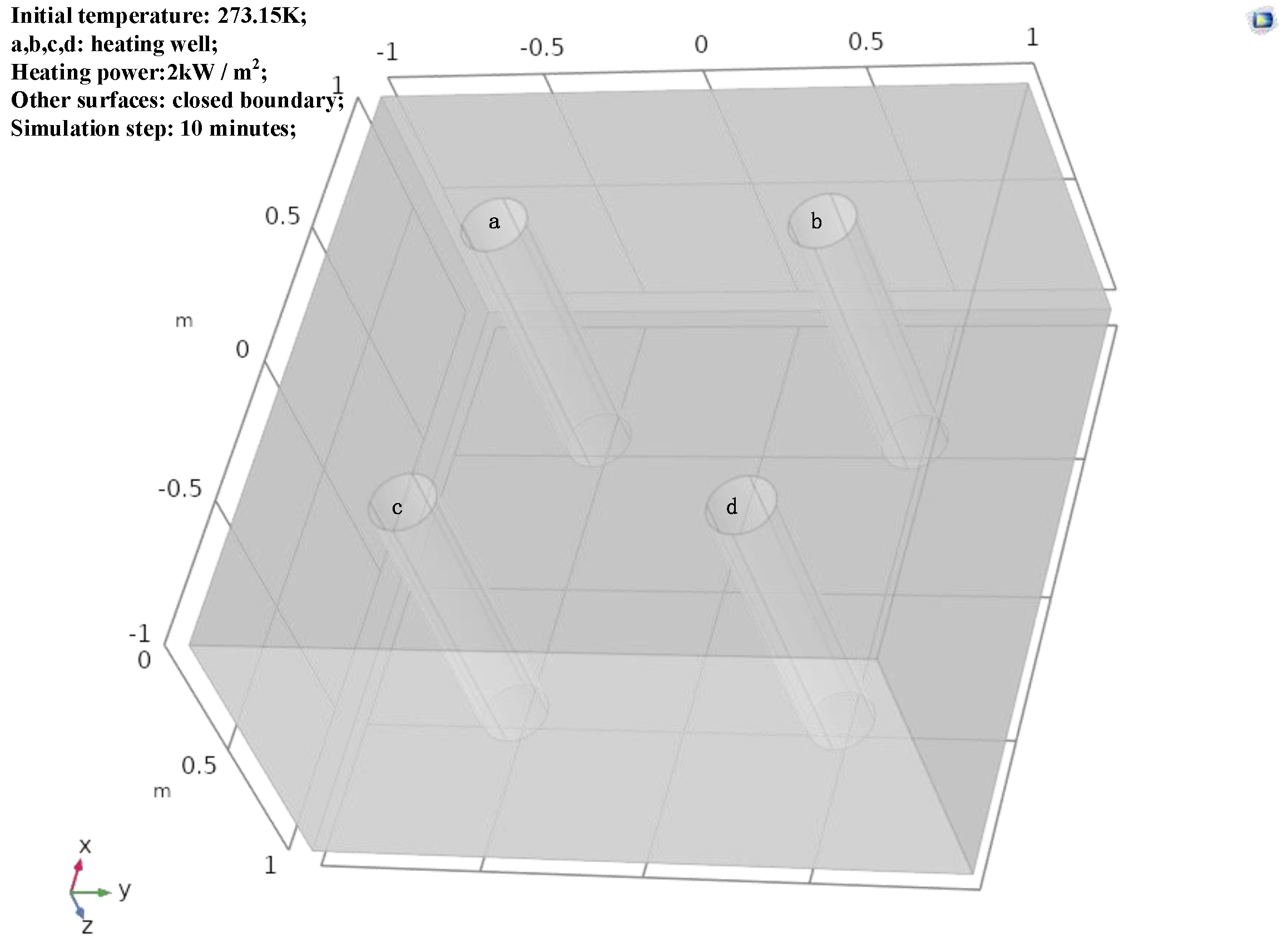
A heat transfer model of porous media is shown in the Figure 1 below:

As showed in the figure, the model is a rectangle of (2 × 2 × 1) m³. Assuming that the upper boundary of the model is the ground, four heat source areas with a diameter of 1dm and a depth of 1m are symmetrically distributed with four positions {(0.5, 0.5), (0.5, −0.5), (−0.5, 0.5), (−0.5, −0.5)} on the xoy plane of the model as the center. The heat source is a boundary heat source, the constant heating power is 2 kW/m², and the heat distribution in the heat source area is uniform. Therefore, the heat source medium does not need to be considered. The main solid medium in porous media is soil and the fluid medium is ethylbenzene. The specific properties are introduced later in this paper. The grid division is controlled by the physical field, and the division result is as follows.

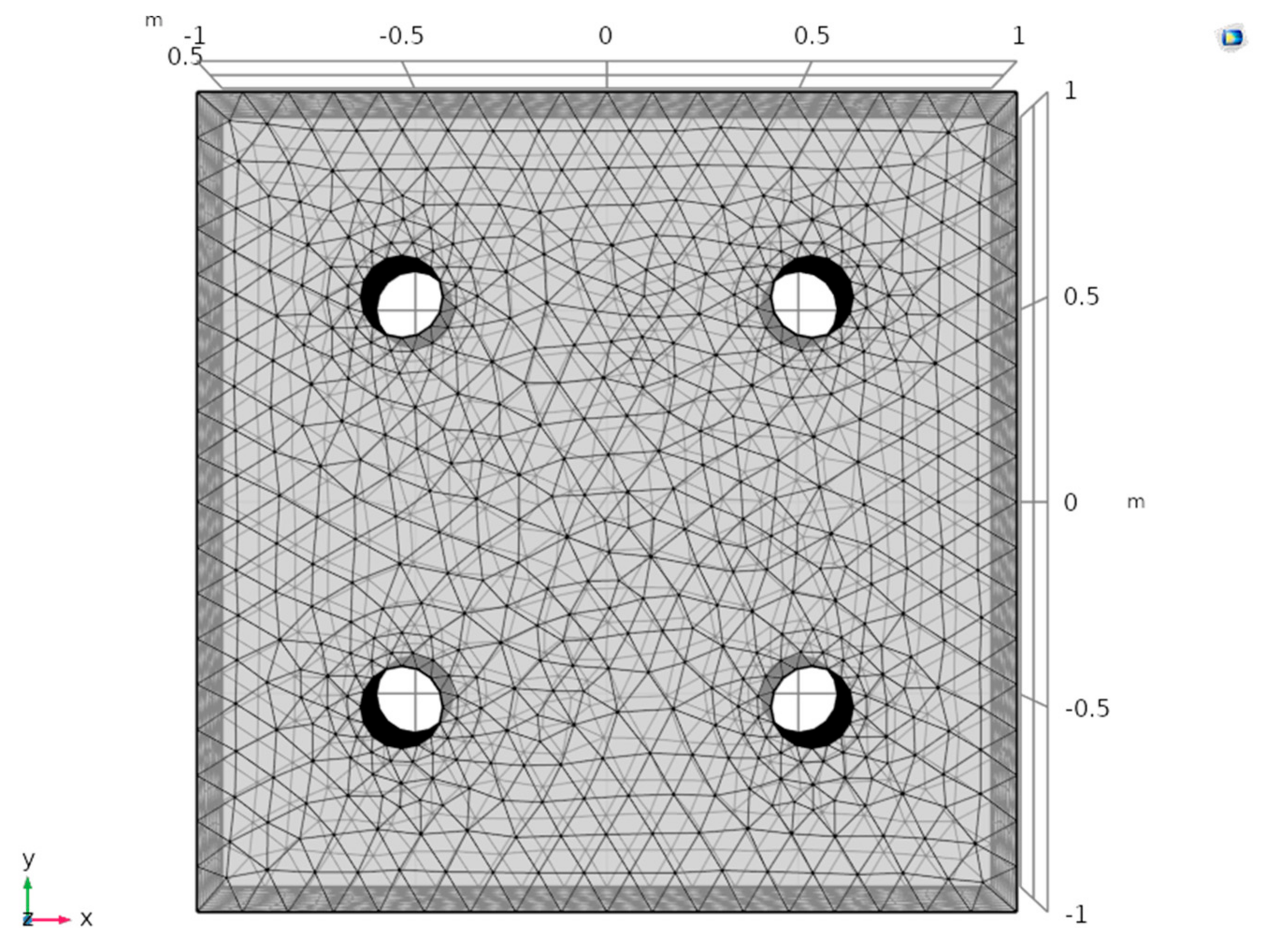
As shown in Figure 2, the model is divided into a group of unstructured tetrahedrons with a maximum cell size of 0.11 m, a minimum cell size of 0.008 m, a maximum growth rate of adjacent elements of 1.4, and a ratio of boundary cell size to radius of curvature of 0.4. The mesh is automatically generated by COMSOL according to the corresponding parameters.

2.1.2. Theoretical Derivation

Transient thermodynamic modeling was carried out and the corresponding ordinary differential control equation is:

$${\left(\rho c_p\right)}_{eff}\frac{\partial T}{\partial t}+\rho c_{p}u\cdot \nabla T+\nabla \cdot q=Q$$

(1)

$$q=-k_{eff}\nabla T$$

(2)

$${\left(\rho c_p\right)}_{eff}={\displaystyle \sum _i{\theta }_{pi}{\rho }_{pi}{c}_{p,pi}}+\left(1-{\displaystyle \sum _i{\theta }_{pi}}\right)\rho c_p$$

(3)

$$k_{eff}={\displaystyle \sum {\theta }_{pi}{k}_{pi}+\left(1-{\displaystyle \sum _i{\theta }_{pi}}\right)}k$$

(4)

where: T (SI unit: k) is the temperature; t (SI unit: s) is the time; ρ (SI unit: kg/m³) is the soil density; c_p (SI unit: J/(kg K)) is the constant pressure heat capacity; c_p,pi (SI unit: J/(kg K)) is the specific heat capacity of the medium under pressure pi; k_eff, k_pi and k are effective thermal conductivity, medium thermal conductivity and pollutant thermal conductivity, respectively; θ_pi is the volume fraction of solid material, and u (SI unit: M/s) is the velocity field of fluid in the model, which can be in the form of analytical expression or the velocity field of fluid flow interface; Q is heat sources of the system.

The first term on the left of Equation (1) represents the change of temperature with time, and its coefficient is given by Equation (3), which is the effective volume heat capacity considering the properties of solid and fluid. The second term is the convection term, which is the change of heat under the action of reaction velocity field. The third term is the heat conduction term, which represents the heat change in heat conduction. Equation (2) is Fourier’s law of thermal conductivity, that is, the change of heat under the action of effective thermal conductivity. Equation (4) is the calculation formula of effective thermal conductivity, which characterizes the relationship between effective thermal conductivity and the volume fraction of solid material.

2.1.3. Simulation Conditions and Basic Assumptions

Related assumptions are as follows. (1) Assume that the soil is a uniform porous medium and ignore the thermal conductivity of other phase components. (2) The porous medium is in local thermal equilibrium and the effective thermal conductivity satisfies the volume average. The effective thermal conductivity is the same in all directions. (3) The heat source is an ideal heat source, the temperature is the same everywhere on the heat source surface, and there is no contact resistance and no heat transfer loss. (4) The heat diffusion from the soil to the surface air above the soil and the power loss during heating are ignored. (5) Except for the heating shaft wall, other vertical surfaces are thermally insulated.

The corresponding initial simulation conditions are as follows. The initial soil temperature is 273.15 K, and the four heating well walls are distributed with a heat source of 2000 W/m². The simulation step size is 10 min, and the simulation time is 900 min. In the simulation, the relative tolerance is set to 0.01 and the tolerance factor set to 0.1. The absolute tolerance is the product of the relative tolerance and the tolerance factor, and also applies to scaled variables.

The simulation step size and mesh generation meet the accuracy requirements of repairing polluted soil with SVE technology in industry. The radius of influence (ROI) of the SVE system is usually more than 1 m, and the minimum heating well spacing used in the experiment is 1, which is within the ROI.

The thermodynamic parameters of porous media and pollutants are shown in

Table 1. Heat transfer simulation parameters of porous media.

Material	Thermal Conductivity k/[W/(m·K)]	Constant Pressure Heat Capacity Cp/[J/(kg·K)]	Density ρ/[kg/m3]	Volume Fraction θpi	Porosity ε	Permeability κ/m2	Dynamic Viscosity μ/[Pa·s]
Porous Medium	0.70	1010	2300	0.82	0.3	0.00179
Contam-inants	0.129	1697	870	-	-	-	6.1 × 10−4

:

2.2. Darcy’s Law

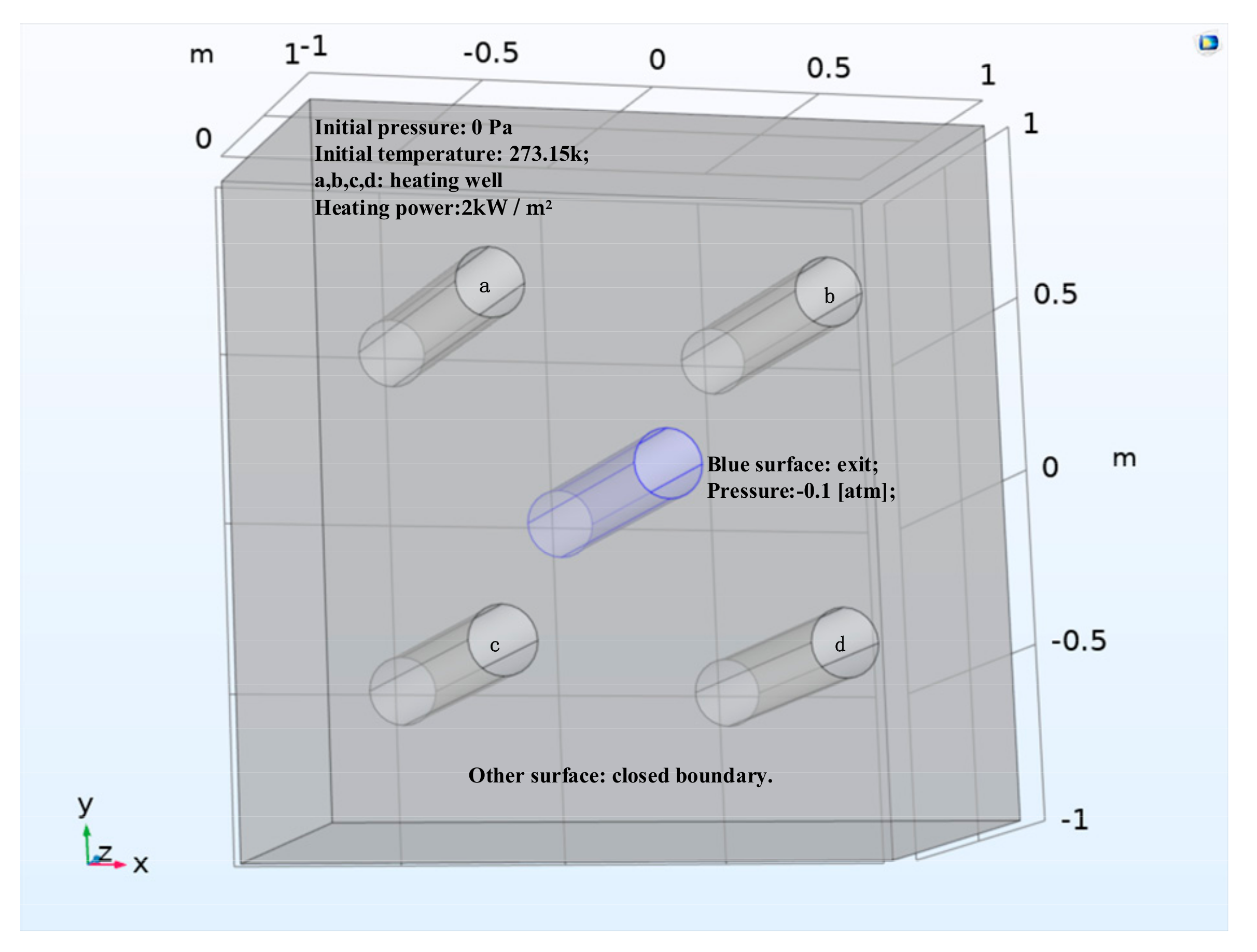
2.2.1. Model Establishment

On the basis of the original model, an air extraction port with a diameter of 1 dm is added in the middle of the square surface. The whole model is shown in Figure 3:

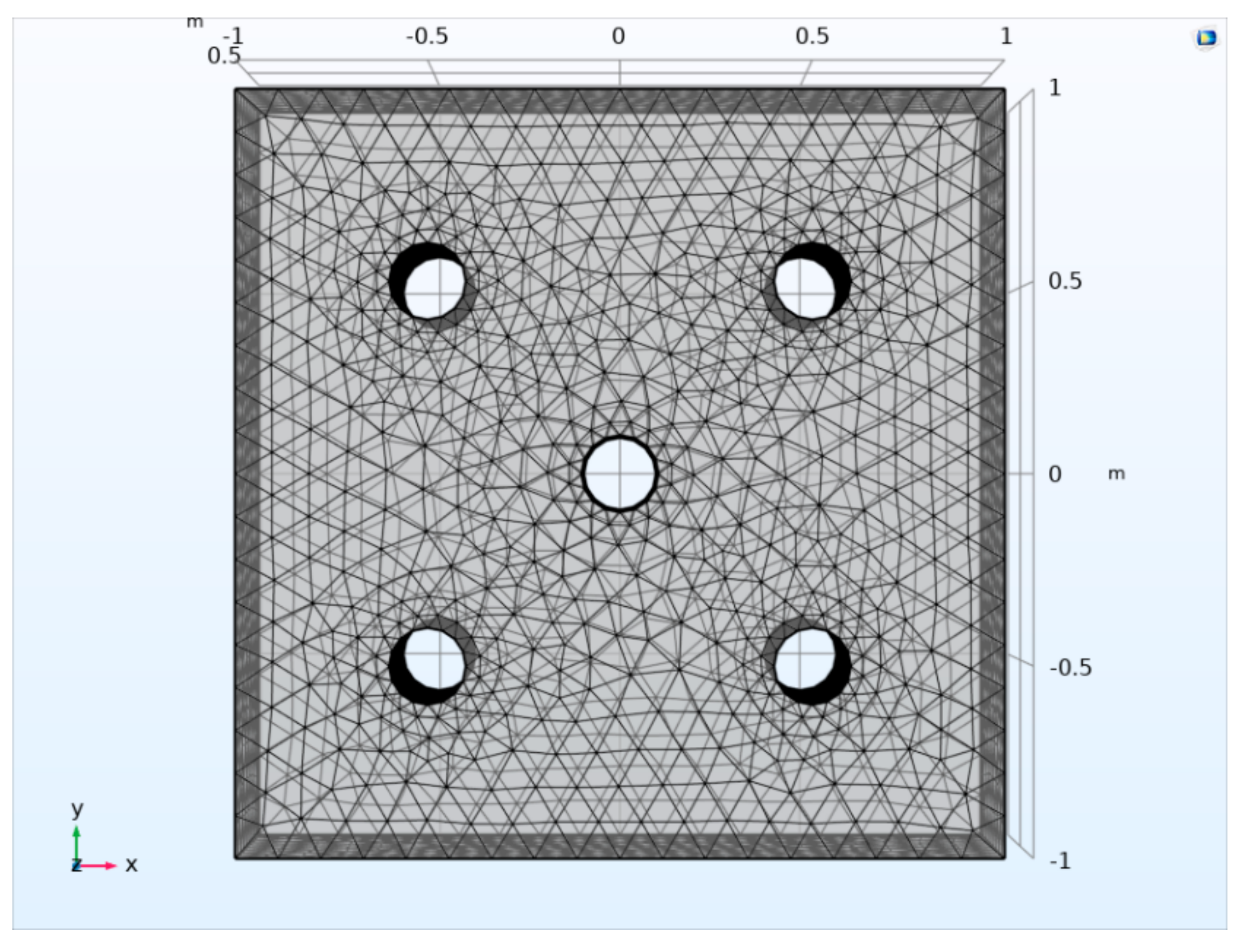
The grid division is still controlled by the physical field. The result of grid division is shown in Figure 4.

2.2.2. Theoretical Basis

Darcy’s law was developed by French engineer Darcy through experiments. It describes the linear relationship between fluid seepage velocity and hydraulic gradient in saturated sand:

$$Q_f=\frac{\kappa A\left(P_b-P_a\right)}{\mu L}$$

(5)

where Q_f is the total flow, k is the inherent permeability of the medium, A is the cross-sectional area of the medium, (P_b − P_a) is the total pressure drop, L is the distance of pressure drop, and µ is the viscosity of the fluid. The formula indicates that the seepage flow Q_f is directly proportional to the upstream and downstream water pressure drop (P_b − P_a) and the cross-sectional area A perpendicular to the flow direction, but inversely proportional to the seepage length L.

Because the porous medium used in the experimental model is soil, not idealized sand, the effects of viscosity and various internal and external pressures should be calculated. Moreover, due to the existence of an air extraction port, complex force field changes occur in the soil in the process of air extraction, such as the effect of various resistances. Because simulating the flow of porous media at the micro level requires a lot of computational resources and time, the detailed structure of porous media is ignored here. Instead, two macro quantities of porosity and permeability are used to describe the properties of porous media at the macro level, which greatly reduce the computational cost. The corresponding governing equation is:

$$\begin{array}{l}\frac{\partial }{\partial t}\left({\epsilon }_p\rho \right)+\nabla ·\left(\rho u\right)=Q_m\\ u=-\frac{\kappa }{\mu }\nabla p\end{array}$$

(6)

where ε_p represents the porosity of the soil, ρ represents the density of soil, u represents the flow velocity field of medium, Q_m represents heat source, κ represents the permeability of the soil, μ is the dynamic viscosity of the soil and P is the fluid pressure. The first equation represents the relationship between soil porosity and heat source distribution, and the second equation represents the relationship between fluid velocity field and soil permeability and pressure drop. The simulation parameters of this experiment are still set according to Table 1.

2.2.3. Basic Assumptions and Simulation Conditions

To add Darcy’s law physical field to the COMSOL simulation model, the following assumptions need to be made for the whole model: (1) the soil medium is homogeneous and the relevant parameters are isotropic; (2) the pores of porous media are uniformly filled with pollutants; (3) the pressure difference of each part of the extraction hole wall is evenly distributed; (4) there is no displacement at each point at the boundary; (5) the effect of gravity on the pressure distribution is ignored.

We used the equation in our previous article [24] to calculate the Reynolds number of the flowing fluid to ensure that the fluid is laminar, so its motion can be described by Darcy’s law.

In the corresponding initial simulation conditions the extraction hole wall pressure is 0.1 [atm] lower than the average pressure inside the soil. Except for the extraction hole wall, there is no gas exchange at other boundaries. The remaining conditions for the coupled field simulation are the same as for the porous media temperature simulation.

During the simulation, the properties of each material are as shown in Table 1.

2.3. Energy Efficiency

Since the boiling point of ethylbenzene is 409.35 K and the critical temperature is 616.25 K, 620 K is taken as the effective removal temperature of ethylbenzene. The area with a temperature of 620 K and above can be regarded as the effective heating area. The optimal heating time interval can be obtained by calculating the relationship between the effective heating area and time. Because the heat source is a generalized source and the model boundary is closed, the total energy input power of the system is constant, and the change relationship between the effective heating area and time is the energy consumption efficiency of the whole system with heating.

3. Results

3.1. Numerical Simulation of Temperature Field Changes in Heat Transfer Process of Porous Media

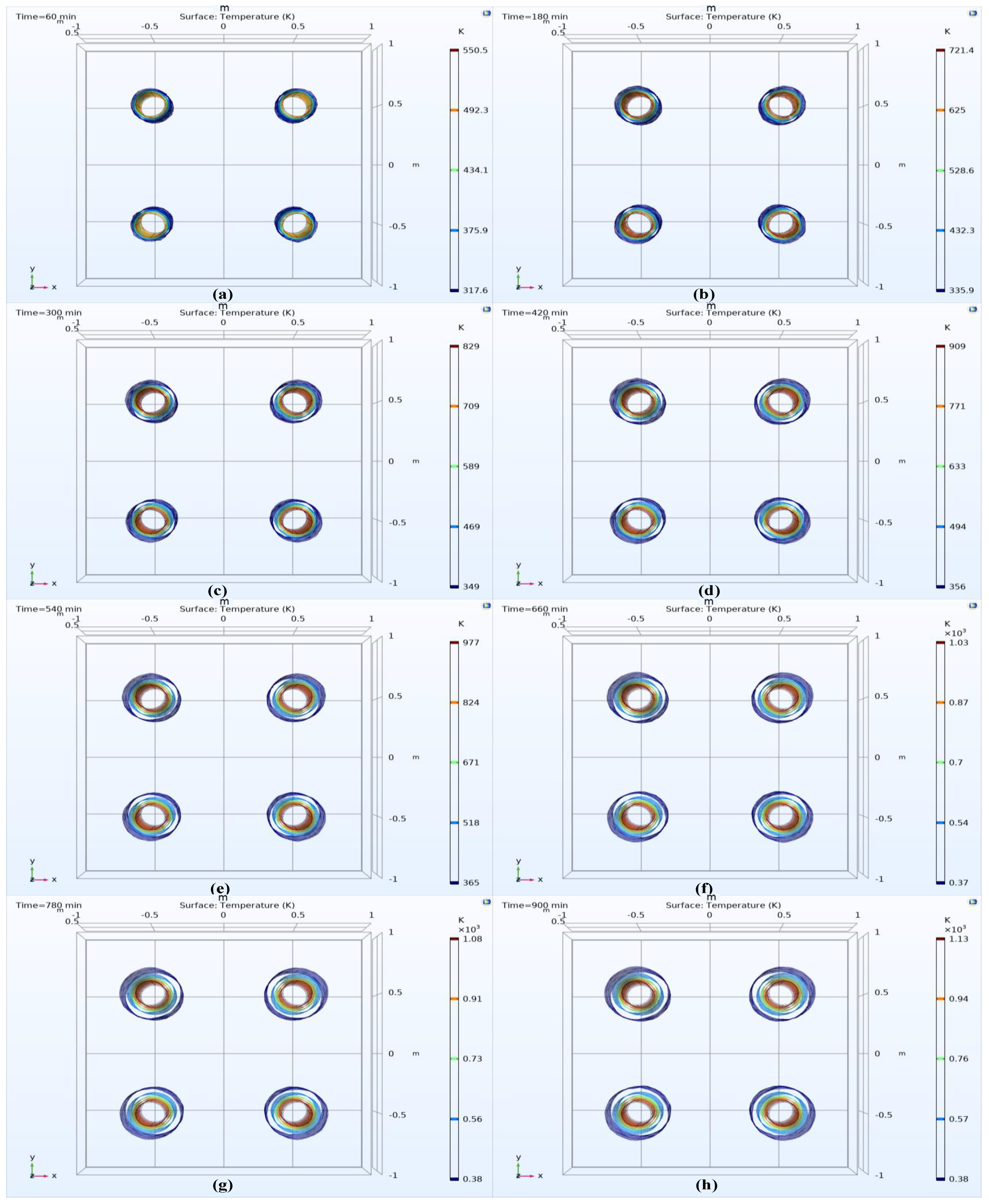
According to the given initial simulation conditions, a transient study was adopted, the time step was 10 min, and the simulation time range was 0–15 h. The temperature field distribution of porous medium heat transfer model in the range of 0–15 h in the process of SVE was simulated. Some results are shown in the figure below. Since the temperature at all positions of the model was 293.15 K at the initial time, the temperature field distribution at the initial time was ignored.

It can be seen from Figure 5 that after heating, the heat begins to transfer from the heat source to the surrounding, and the position of the aperture in the corresponding figure gradually increases. However, according to Fourier’s law, the efficiency of heat conduction is directly proportional to the temperature gradient, that is, the widening speed of the outer ring of the aperture gradually decreases with time, which is reflected in the figure. After 9 h, the change of the position of the outer ring of the aperture is less obvious. This shows that with heating, the whole temperature field distribution tends to be stable, the increment of effective heating area gradually decreases, and the overall energy consumption efficiency of SVE system gradually decreases. In order to see this characteristic, a temperature isosurface distribution was drawn, as shown in Figure 6.

It can be seen from Figure 6 that the central temperature of the heat source rises rapidly at the beginning of heating, and then the increase of the central temperature of the heat source decreases gradually every hour, and the central temperature of the heat source rises steadily after the fifth hour. In the 10th to 15th hour, the temperature of the outermost ring of the medium value surface is the same, the widening speed of the outer ring of the whole figure is slow, and the whole temperature field distribution tends to be stable, indicating that the increment of the effective heating area decreases gradually. This is the same as the conclusion obtained from the previous analysis of the temperature field distribution diagram.

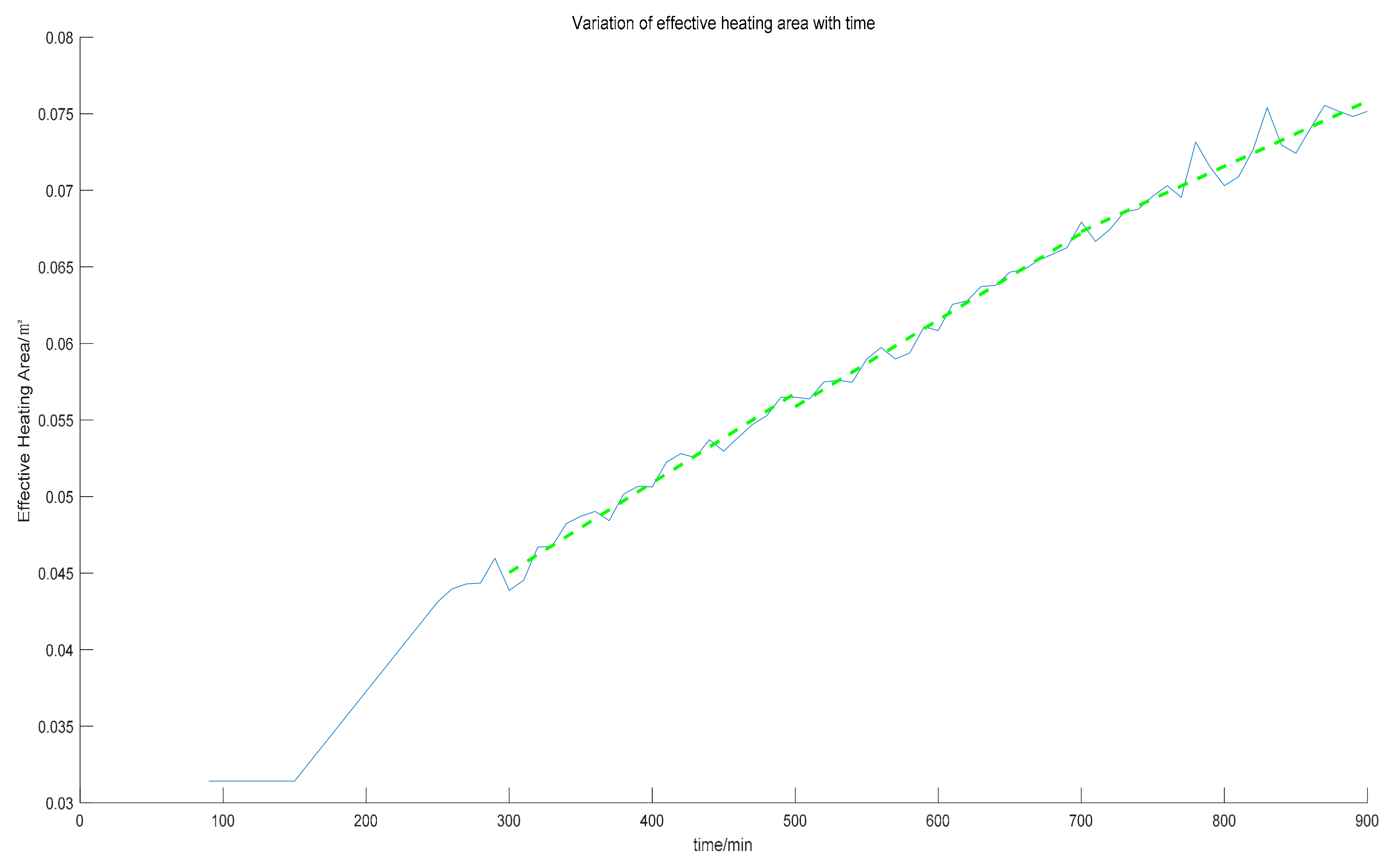
Since the temperature distribution along the vertical direction of the whole model is almost the same, as defined in Section 2.1, the effective heating area can be simplified as the soil area enveloped by the curve of temperature 620 K on the horizontal plane, rather than the volume of soil column. It can be seen from the figure that the effective heating area gradually expands with time. There is an obvious band break after the start time in the figure, because the temperature changes greatly at the beginning of heating, so there is no point with a temperature of about 620 K in this time period. With the increase of heating time, the temperature fluctuation of each point at the boundary of the effective heating area gradually decreases, so more and more points with a temperature of about 620 K are detected.

The effective heating area on the xoy plane was calculated, and its variation with time is shown in Figure 7.

The slope of the curve begins to decrease gradually at the 600th minute, the increment of the effective heating area becomes smaller, and the energy consumption efficiency of the system decreases. The conclusion is the same as that of the numerical simulation.

3.2. Numerical Simulation of Temperature Field Changes under Pollutant Migration

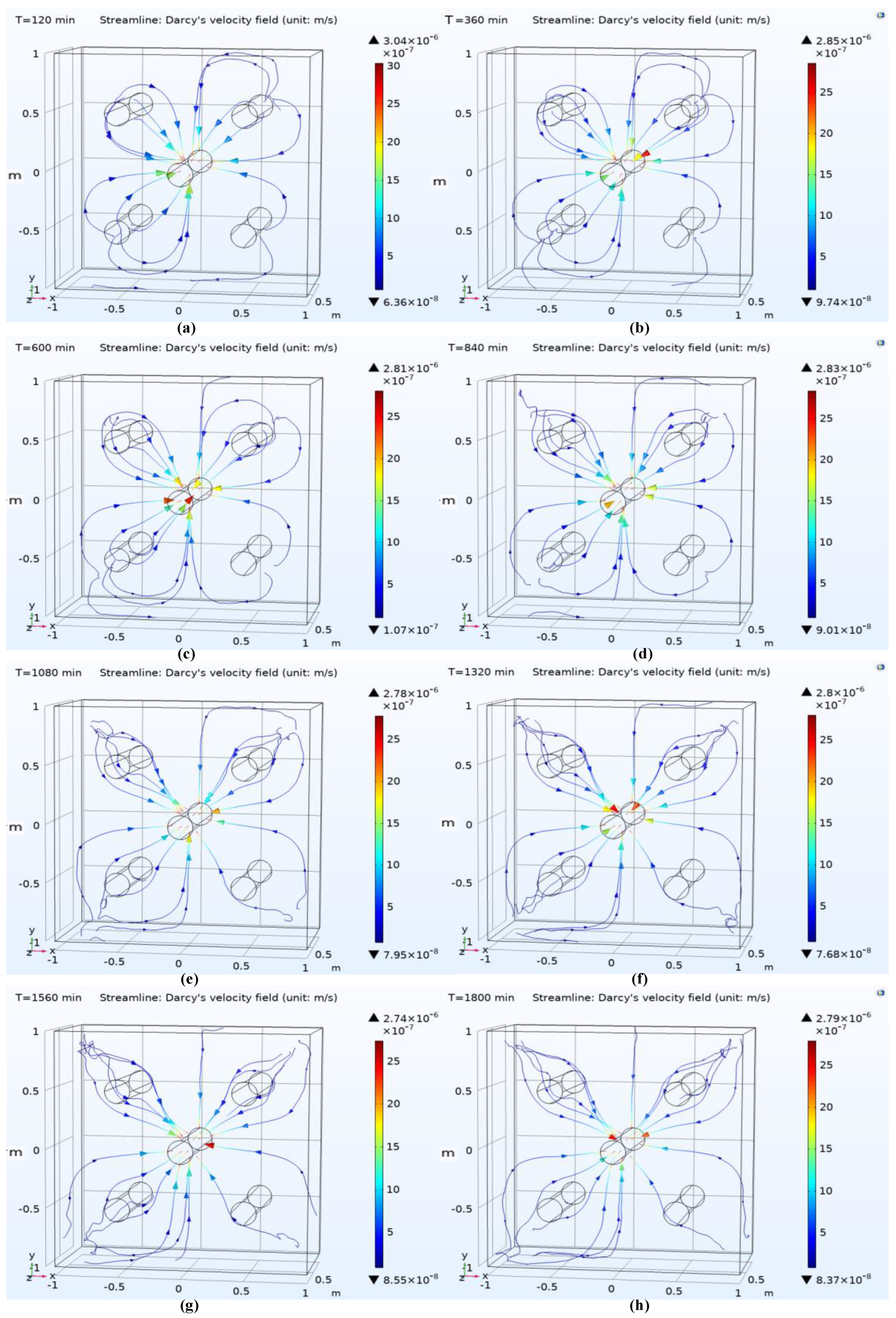
The physical field of Darcy’s law was introduced to simulate the coupling of heat transfer field of porous media and Darcy’s velocity field. The pressure at the extraction port was set to −10132.5 Pa, which is within an easily accessible and relatively safe pressure range. Since the extraction port takes away part of the heat energy, the simulation time was set to 1800 min.

The velocity field distribution of coupling simulation is shown in Figure 8.

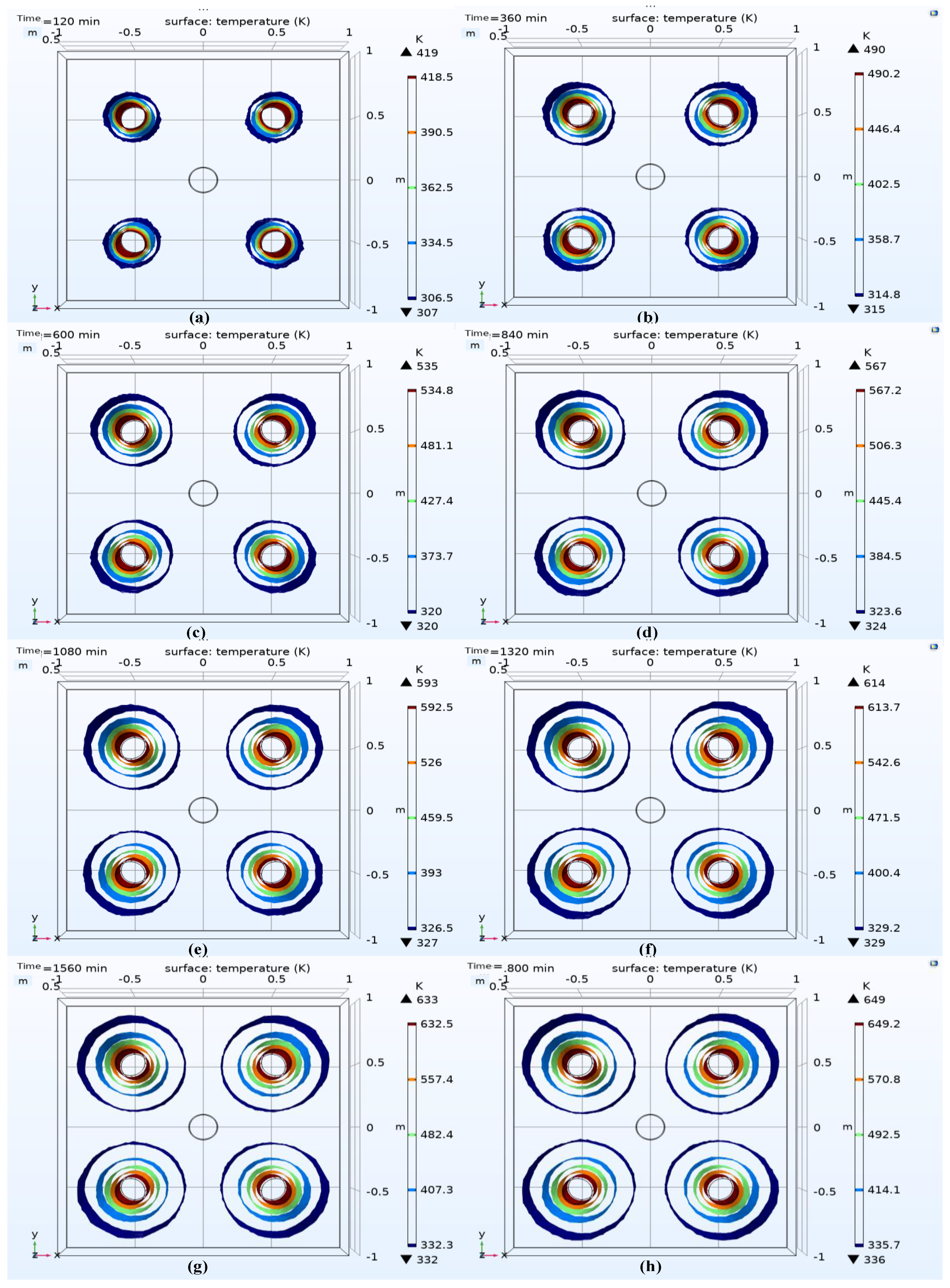
The variation relationship of soil temperature field with time under the action of Darcy’s law physical field is shown in Figure 9.

Comparing images of the same simulation time in Figure 6 and Figure 9, such as the temperature field distribution in 840^th minute, it can be seen that the distance between the two different temperature isosurfaces is almost the same. However, the temperature gradient of the different temperature isosurfaces in Figure 6 is about three times that of the corresponding temperature gradient in Figure 9, indicating that the temperature field distribution in Figure 9 is more uniform. This shows that the Darcy field improves the utilization efficiency of the SVE model for the heat source, and we believe that pollutants can be effectively removed when the temperature is higher than 620 K. However, at the same time, due to decrease of the maximum temperature, some of the original effective heating areas cannot reach the effective heating temperature within the same heating time. Therefore, it is necessary to increase the heat source power or prolong the heating time. In order to more intuitively reflect the change of temperature field distribution, a temperature isosurface of the coupling field was made, as showed in Figure 10.

4. Discussion and Conclusions

The heat transfer simulation of porous media shows that when the soil is heated by a heat source with constant thermal power, the soil heat is rapidly transferred from the heat source to the surroundings, and the effective heating area gradually increases. With the heating time getting longer, the added value of the effective heating area of the soil gradually decreases, and the energy consumption efficiency of the system decreases.

By adding the Darcy field simulation, it was found that after adding the Darcy velocity field outlet, the temperature of the heat source decreases significantly and the heat diffusion area increases significantly. The utilization efficiency of the heat source is significantly improved because, we believe, that when the temperature is higher than 620 K, the pollutants can be effectively removed and temperature has little effect on the pollutant removal efficiency. However, due to the decrease of the heat source temperature, the temperature rise rate in the original heating area is lower than that without Darcy field. To continue to meet a certain effective heating area, the heating time can be extended, or the heat source power can be increased.

Through simulation, we obtained the soil temperature field distribution for the first 1800 min under the specific heating well distribution, and through the analysis of these data we verified that the extraction well could improve the utilization efficiency of the heat source of the SVE system.

However, the transformation between the phases of NAPL was not involved in this model, and the changes in the characteristics of porous media caused by the removal of ethylbenzene were not considered. We think that the ethylbenzene can be successfully removed in the region reaching this temperature. In fact, since the thermal conductivity of air is lower than that of ethylbenzene, the actual temperature of the peripheral area is lower than the simulated temperature, which means that a longer heating time is required to achieve the same removal effect.

In future research we will continue to improve our model, define NAPL materials, add a transformation simulation between different phases of NAPL, and optimize the distribution of the heating wells.