Riverine Water Quality Response to Precipitation and Its Change
Abstract
1. Introduction
2. Materials and Methods
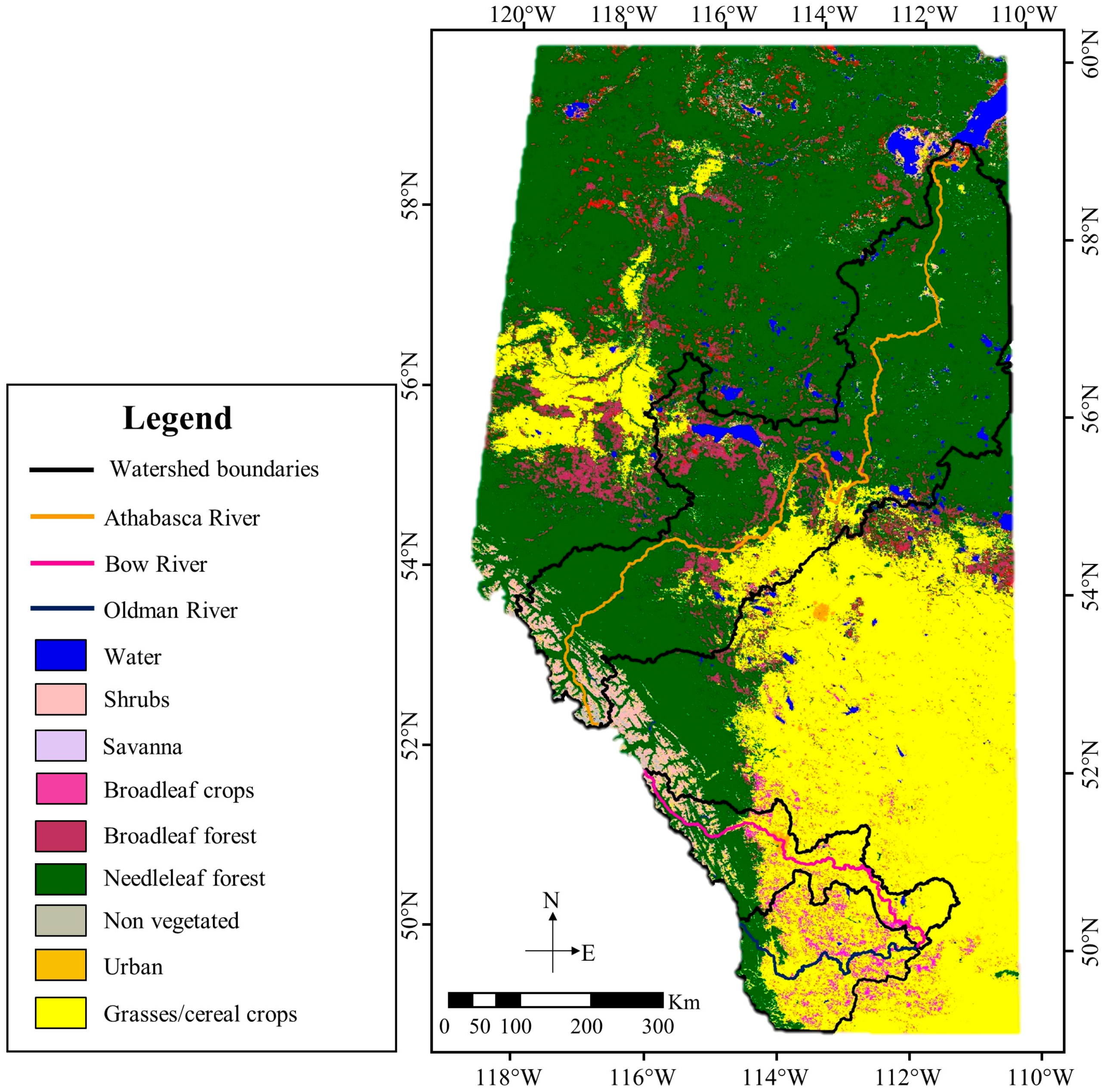
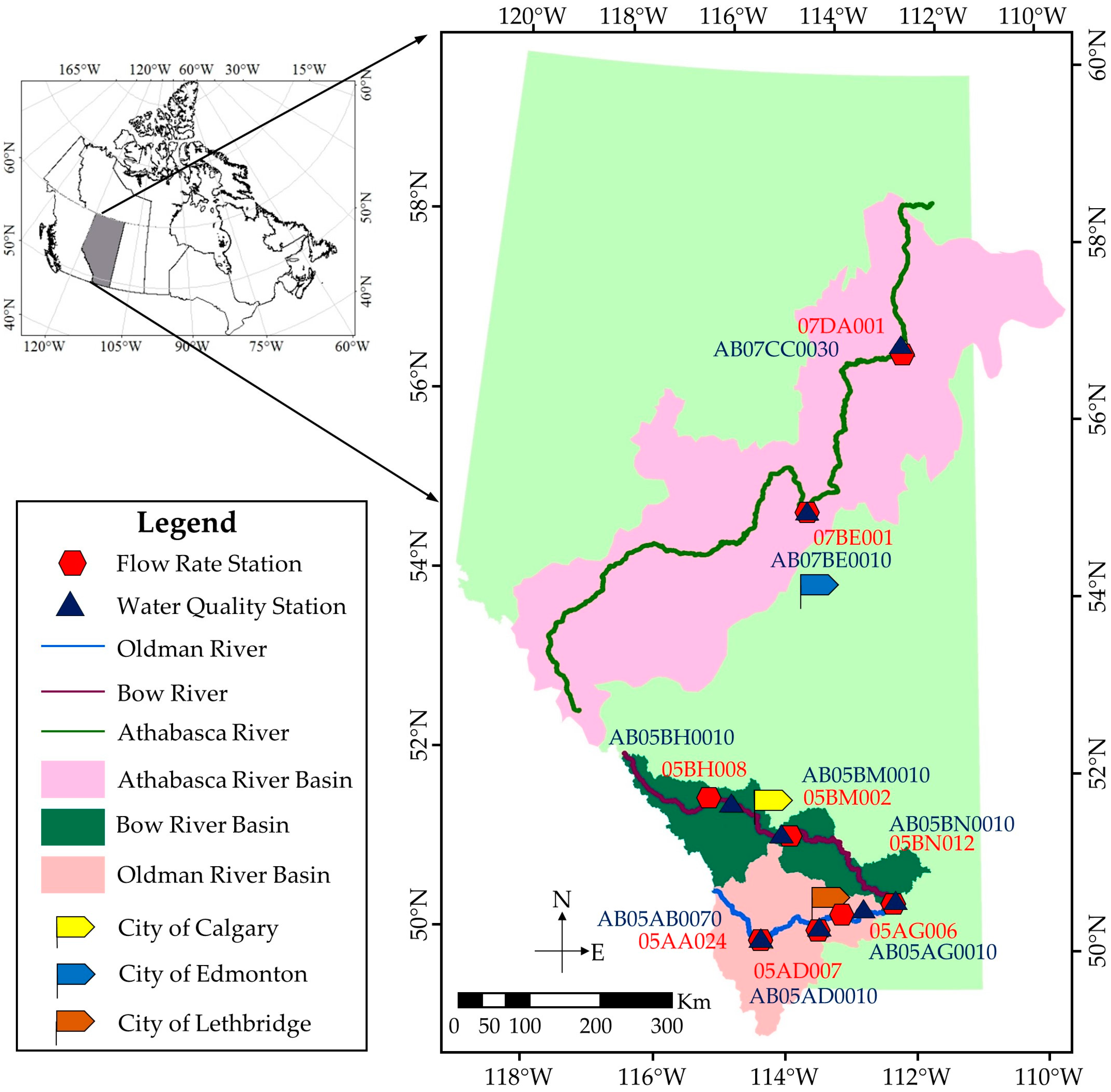
2.1. Study Area
2.2. Water Quality, Flow, and Precipitation Data
2.3. Analysis Methods
3. Results and Discussions
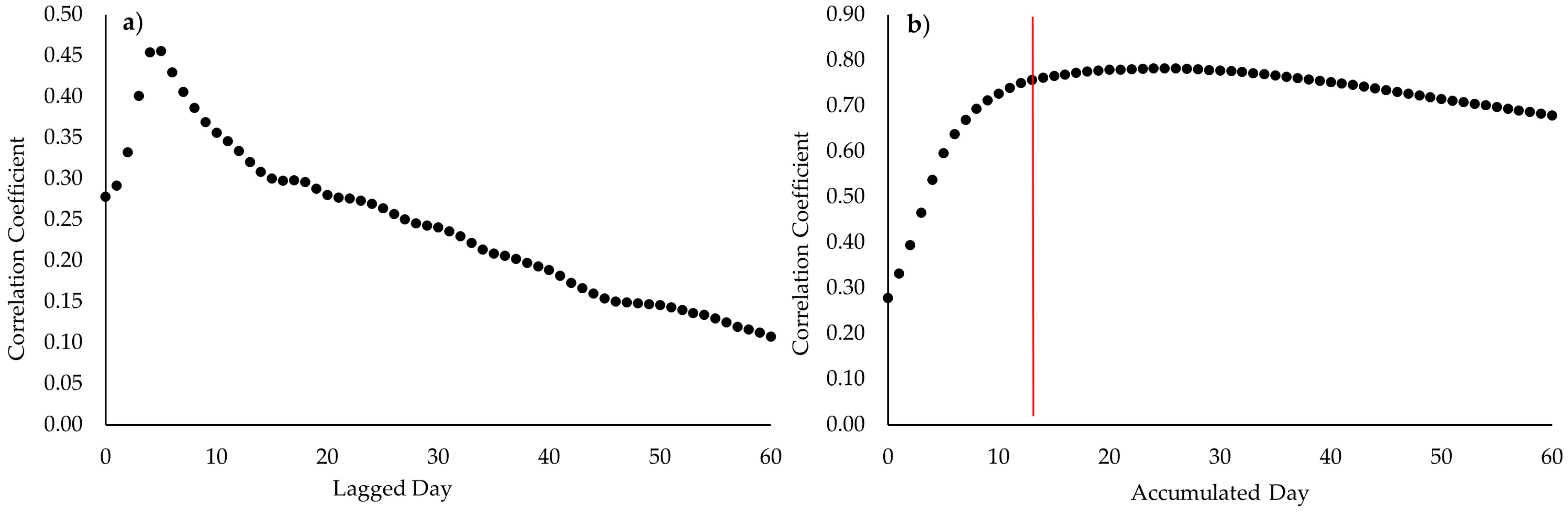
3.1. The Dependence of Flow on Precipitation
3.2. The Dependence of Water Quality on Precipitation
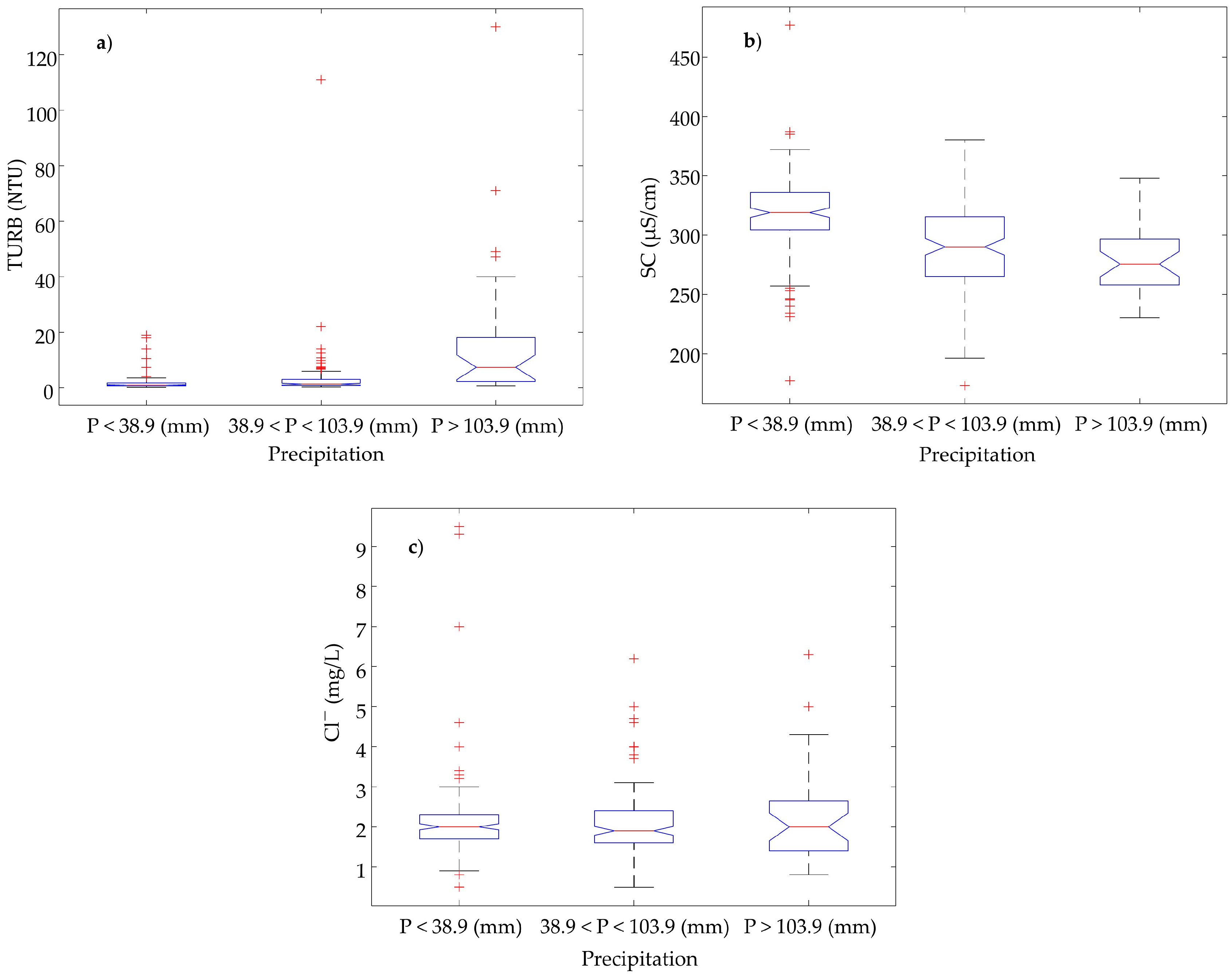
3.3. Water Quality Variation under Different Precipitation Magnitudes
3.4. Changes in Water Quality under a Changing Climate
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Jarvie, H.P.; Neal, C.; Withers, P.J. Sewage-effluent phosphorus: A greater risk to river eutrophication than agricultural phosphorus? Sci. Total Environ. 2006, 360, 246–253. [Google Scholar] [CrossRef] [PubMed]
- Bowes, M.J.; Smith, J.T.; Neal, C.; Leach, D.V.; Scarlett, P.M.; Wickham, H.D.; Harman, S.A.; Armstrong, L.K.; Davy-Bowker, J.; Haft, M.; et al. Changes in water quality of the River Frome (UK) from 1965 to 2009: Is phosphorus mitigation finally working? Sci. Total Environ. 2011, 409, 3418–3430. [Google Scholar] [CrossRef] [PubMed]
- Bowes, M.J.; Jarvie, H.P.; Naden, P.S.; Old, G.H.; Scarlett, P.M.; Roberts, C.; Armstrong, L.K.; Harman, S.A.; Wickham, H.D.; Collins, A.L. Identifying priorities for nutrient mitigation using river concentration–flow relationships: The Thames basin, UK. J. Hydrol. 2014, 517, 1–12. [Google Scholar] [CrossRef]
- Xia, X.H.; Wu, Q.; Mou, X.L.; Lai, Y.J. Potential Impacts of Climate Change on the Water Quality of Different Water Bodies. J. Environ. Inform. 2015, 25, 85–98. [Google Scholar] [CrossRef]
- Tu, J. Combined impact of climate and land use changes on streamflow and water quality in eastern Massachusetts, USA. J. Hydrol. 2009, 379, 268–283. [Google Scholar] [CrossRef]
- Fan, M.; Shibata, H. Simulation of watershed hydrology and stream water quality under land use and climate change scenarios in Teshio River watershed, northern Japan. Ecol. Indic. 2015, 50, 79–89. [Google Scholar] [CrossRef]
- Whitehead, P.G.; Wilby, R.L.; Battarbee, R.W.; Kernan, M.; Wade, A.J. A review of the potential impacts of climate change on surface water quality. Hydrol. Sci. J. 2009, 54, 101–123. [Google Scholar] [CrossRef]
- Benítez-Gilabert, M.; Alvarez-Cobelas, M.; Angeler, D.G. Effects of climatic change on stream water quality in Spain. Clim. Chang. 2010, 103, 339–352. [Google Scholar] [CrossRef]
- Fukushima, T.; Ozaki, N.; Kaminishi, H.; Harasawa, H.; Matsushige, K. Forecasting the changes in lake water quality in response to climate changes, using past relationships between meteorological conditions and water quality. Hydrol. Process. 2000, 14, 593–604. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, X.J. Advances and prospects for nonpoint source pollution studies. Adv. Water Sci. 2002, 13, 105–110. [Google Scholar]
- Kalkhoff, S.J.; Hubbard, L.E.; Tomer, M.D.; James, D. Effect of variable annual precipitation and nutrient input on nitrogen and phosphorus transport from two Midwestern agricultural watersheds. Sci. Total Environ. 2016, 559, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Göransson, G.; Larson, M.; Bendz, D. Variation in turbidity with precipitation and flow in a regulated river system. Hydrol. Earth Syst. Sci. 2013, 17, 2529–2542. [Google Scholar] [CrossRef]
- McCarthy, D.; Hathaway, J.; Hunt, W.; Deletic, A. Intra-event variability of Escherichia coli and total suspended solids in urban stormwater runoff. Water Res. 2012, 46, 6661–6670. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chang, H. Response of discharge, TSS, and E. coli to rainfall events in urban, suburban, and rural watersheds. Environ. Sci. 2014, 16, 2313–2324. [Google Scholar] [CrossRef] [PubMed]
- Bae, H.-K. Changes of River’s Water Quality Responded to Rainfall Events. Environ. Ecol. Res. 2013, 1, 21–25. [Google Scholar]
- Hamilton, J.L.; Luffman, I. Precipitation, pathogens, and turbidity trends in the Little River, Tennessee. Phys. Geogr. 2009, 30, 236–248. [Google Scholar] [CrossRef]
- Rueda, F.J.; Fleenor, W.E.; De Vicente, I. Pathways of river nutrients towards the euphotic zone in a deep-reservoir of small size: Uncertainty analysis. Ecol. Model. 2007, 202, 345–361. [Google Scholar] [CrossRef]
- Chorus, I.; Bartram, J. Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management; Chorus, I., Bertram, J., Eds.; World Health Organization: Geneva, Switzerland, 1999. [Google Scholar]
- Clark, J.M.; Lane, S.N.; Chapman, P.J.; Adamson, J.K. Export of dissolved organic carbon from an upland peatland during storm events: Implications for flux estimates. J. Hydrol. 2007, 347, 438–447. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Krysanova, V. Climate change and stream water quality in the multi-factor context. Clim. Chang. 2010, 103, 353–362. [Google Scholar] [CrossRef]
- Eghball, B.; Gilley, J.E.; Baltensperger, D.D.; Blumenthal, J. Long-term manure and fertilizer application effects on phosphorus and nitrogen in runoff. Trans. ASAE 2002, 45, 687–694. [Google Scholar] [CrossRef]
- Dyer, F.; ElSawah, S.; Croke, B.; Griffiths, R.; Harrison, E.; Lucena-Moya, P.; Jakeman, A. The effects of climate change on ecologically-relevant flow regime and water quality attributes. Stoch. Environ. Res. Risk Assess. 2014, 28, 67–82. [Google Scholar] [CrossRef]
- Kienzle, S.W.; Nemeth, M.W.; Byrne, J.M.; McDonald, R.J. Simulating the hydrological impacts of climate change in the upper North Saskatchewan River basin, Alberta, Canada. J. Hydrol. 2012, 412–413, 76–89. [Google Scholar] [CrossRef]
- Forbes, K.A.; Kienzle, S.W.; Coburn, C.A.; Byrne, J.M.; Rasmussen, J. Simulating the hydrological response to predicted climate change on a watershed in southern Alberta, Canada. Clim. Chang. 2011, 105, 555–576. [Google Scholar] [CrossRef]
- Tanzeeba, S.; Gan, T.Y. Potential impact of climate change on the water availability of South Saskatchewan River Basin. Clim. Chang. 2012, 112, 355–386. [Google Scholar] [CrossRef]
- MacDonald, R.J.; Byrne, J.M.; Boon, S.; Kienzle, S.W. Modelling the Potential Impacts of Climate Change on Snowpack in the North Saskatchewan River Watershed, Alberta. Water Resour. Manag. 2012, 26, 3053–3076. [Google Scholar] [CrossRef]
- Delpla, I.; Baurres, E.; Jung, A.V.; Thomas, O. Impacts of rainfall events on runoff water quality in an agricultural environment in temperate areas. Sci. Total Environ. 2011, 409, 1683–1688. [Google Scholar] [CrossRef] [PubMed]
- St Laurent, J.; Mazumder, A. Influence of seasonal and inter-annual hydro-meteorological variability on surface water fecal coliform concentration under varying land-use composition. Water Res. 2014, 48, 170–178. [Google Scholar] [CrossRef] [PubMed]
- Hongve, D.; Riise, G.; Kristiansen, J.F. Increased colour and organic acid concentrations in Norwegian forest lakes and drinking water—A result of increased precipitation? Aquat. Sci. 2004, 66, 231–238. [Google Scholar] [CrossRef]
- Downing, D.J.; Pettapiece, W.W. Natural Regions and Subregions of Alberta; Natural Region Committee: Edmonton, Alberta, Canada, 2006. [Google Scholar]
- Barrow, E.; Yu, G. Climate Scenarios for Alberta, Prairie Adaptation. Available online: http://www.parc.ca/pdf/research_publications/summary_docs/SD2006-02.pdf (accessed on 24 November 2017).
- Hay, L.E.; Wilby, R.L.; Leavesketm, G.H. A comparison of delta change and downscaled GCM scenarios for three mountainous basins in the United States. J. Am. Water Resour. Assoc. 2000, 36, 387–397. [Google Scholar] [CrossRef]
- Diaz-Nieto, J.; Wilby, R.L. A comparison of statistical downscaling and climate change factor methods: Impacts on low flows in the River Thames, United Kingdom. Clim. Chang. 2005, 69, 245–268. [Google Scholar] [CrossRef]
- Nilsson, C.; Renöfält, B. Linking flow regime and water quality in rivers: A challenge to adaptive catchment management. Ecol. Soc. 2008, 13, 18. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Ahmadi, M. Long-term variations of water quality parameters in the Maroon River, Iran. Environ. Monit. Assess. 2011, 177, 273–287. [Google Scholar] [CrossRef] [PubMed]
- Prathumratana, L.; Sthiannopkao, S.; Kim, K.W. The relationship of climatic and hydrological parameters to surface water quality in the lower Mekong River. Environ. Int. 2008, 34, 860–866. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Su, B.; Hartmann, H. Temporal and spatial trends of precipitation and river flow in the Yangtze River Basin 1961–2000. Geomorphology 2007, 45, 143–154. [Google Scholar] [CrossRef]
- Interlandi, S.J.; Crockett, C.S. Recent water quality trends in the Schuylkill River, Pennsylvania, USA: A preliminary assessment of the relative influences of climate, river discharge and suburban development. Water Res. 2003, 37, 1737–1748. [Google Scholar] [CrossRef]
- Budai, P.; Clement, A. Estimation of nutrient load from urban diffuse sources: Experiments with runoff sampling at pilot catchments of Lake Balaton, Hungary. Water Sci. Technol. 2007, 56, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Akbar, T.A.; Hassan, Q.K.; Achari, G. Clusterization of surface water quality and its relation to climate and land use/cover. J. Environ. Prot. 2013, 4, 333–343. [Google Scholar] [CrossRef]
- Akbar, T.A.; Hassan, Q.K.; Achari, G. Development of remote sensing based models for surface water quality. CLEAN–Soil Air Water 2014, 42, 1044–1051. [Google Scholar] [CrossRef]
| Watershed | Baseline (1961–1990) | Baseline (1988–2014) | ||
|---|---|---|---|---|
| 2050s | 2080s | 2050s | 2080s | |
| Athabasca River | +7.2% | +10.2% | +4.7% | +7.6% |
| Bow River | +3.3% | +9.8% | +2.2% | +7.3% |
| Oldman River | +4.7% | +15.7% | +3.1% | +11.7% |
| River | Flow Station | Flow and Antecedent AAP | Flow and Cumulative Antecedent AAP | ||
|---|---|---|---|---|---|
| Optimal Lagged Day (Day) | Correlation Coefficient (r) | Optimal Cumulative Day (Day) | Correlation Coefficient (r) | ||
| Athabasca River | 07BE001 (midstream) | 5 | 0.456 | 14 | 0.762 |
| 07DA001 (downstream) | 6 | 0.441 | 15 | 0.746 | |
| Bow River | 05BH008 (upstream) | 2 | 0.278 | 28 | 0.692 |
| 05BM002 (midstream) | 2 | 0.464 | 13 | 0.681 | |
| 05BN012 (downstream) | 4 | 0.413 | 15 | 0.639 | |
| Oldman River | 05AA024 (upstream) | 2 | 0.302 | 12 | 0.532 |
| 05AD007 (midstream) | 2 | 0.388 | 12 | 0.604 | |
| 05AG006 (downstream) | 3 | 0.395 | 13 | 0.612 | |
| Station | Midstream Station (AB07BE0010) | Downstream Station (AB07CC0030) | ||
|---|---|---|---|---|
| Optimal Antecedent AAP | Optimal Cumulative AAP | Optimal Antecedent AAP | Optimal Cumulative AAP | |
| Chl-a | 0.220 | 0.325 | 0.238 | 0.454 |
| WT | 0.257 | 0.597 | 0.367 | 0.589 |
| DO | −0.164 | −0.441 | −0.258 | −0.577 |
| TURB | 0.285 | 0.526 | 0.272 | 0.528 |
| DOC | 0.020 | 0.014 | 0.099 | 0.214 |
| TP | 0.218 | 0.403 | 0.220 | 0.462 |
| TN | 0.103 | 0.044 | 0.027 | 0.125 |
| pH | 0.027 | 0.119 | 0.207 | 0.278 |
| Cl− | −0.199 | −0.511 | −0.337 | −0.570 |
| −0.251 | −0.573 | −0.302 | −0.580 | |
| SC | −0.313 | −0.603 | −0.340 | −0.586 |
| Station | Upstream Station (AB05BH0010) | Midstream Station (AB05BM0010) | Downstream Station (AB05BN0010) | |||
|---|---|---|---|---|---|---|
| Optimal Antecedent AAP | Optimal Cumulative AAP | Optimal Antecedent AAP | Optimal Cumulative AAP | Optimal Antecedent AAP | Optimal Cumulative AAP | |
| Chl-a | 0.038 | −0.073 | 0.083 | 0.078 | 0.163 | 0.320 |
| WT | 0.126 | 0.579 | 0.098 | 0.434 | 0.142 | 0.519 |
| DO | −0.128 | −0.544 | −0.093 | −0.386 | −0.128 | −0.530 |
| TURB | 0.224 | 0.389 | 0.231 | 0.316 | 0.151 | 0.402 |
| DOC | 0.124 | 0.332 | 0.129 | 0.362 | 0.115 | 0.388 |
| TP | 0.069 | 0.169 | 0.059 | 0.044 | 0.065 | 0.331 |
| TN | 0.108 | 0.136 | −0.151 | −0.358 | −0.095 | −0.341 |
| pH | −0.008 | 0.144 | 0.069 | 0.202 | 0.105 | 0.276 |
| Cl− | 0.022 | −0.027 | −0.070 | −0.310 | −0.144 | −0.370 |
| −0.122 | −0.575 | −0.136 | −0.377 | −0.012 | −0.197 | |
| SC | −0.096 | −0.423 | −0.056 | −0.307 | −0.050 | −0.291 |
| Station | Upstream Station (AB05AB0070) | Midstream Station (AB05AD0010) | Downstream Station (AB05AG0010) | |||
|---|---|---|---|---|---|---|
| Optimal Antecedent AAP | Optimal Cumulative AAP | Optimal Antecedent AAP | Optimal Cumulative AAP | Optimal Antecedent AAP | Optimal Cumulative AAP | |
| Chl-a | 0.032 | 0.077 | 0.100 | 0.338 | 0.164 | 0.302 |
| WT | −0.098 | −0.010 | −0.077 | 0.138 | 0.047 | 0.223 |
| DO | 0.107 | 0.022 | 0.061 | −0.221 | −0.097 | −0.310 |
| TURB | 0.042 | 0.227 | 0.196 | 0.385 | 0.269 | 0.386 |
| DOC | 0.048 | 0.167 | 0.063 | 0.290 | 0.121 | 0.233 |
| TP | 0.134 | 0.234 | 0.189 | 0.388 | 0.138 | 0.279 |
| TN | 0.077 | 0.160 | 0.173 | 0.165 | 0.141 | 0.069 |
| pH | 0.049 | 0.105 | −0.111 | 0.019 | −0.085 | 0.050 |
| Cl− | 0.031 | 0.062 | 0.034 | 0.073 | −0.160 | −0.278 |
| 0.100 | −0.003 | −0.009 | −0.054 | −0.080 | −0.133 | |
| SC | 0.005 | −0.039 | −0.021 | −0.021 | −0.096 | −0.147 |
| Quality | Upstream Station | Midstream Station | Downstream Station |
|---|---|---|---|
| Athabasca River | |||
| Chl-a | -- | y = 0.68x0.33 | y = 0.35x0.57 |
| WT | -- | y = −0.0041x2 + 0.55x − 0.41 | y = −0.003x2 + 0.51x − 1.44 |
| DO | -- | y = 0.0005x2 − 0.076x + 11.48 | y = 12.84e−0.006x |
| TURB | -- | y = 3.54e0.054x | y = 3.56e0.054x |
| DOC | -- | -- | y = 0.0007x2 + 0.0061x + 7.60 |
| TP | -- | y = 0.017e0.031x | y = 0.00002x2 + 0.0011x + 0.024 |
| TN | -- | -- | -- |
| pH | -- | y = −0.0001x2 + 0.01x + 7.77 | y = −0.0002x2 + 0.016x + 7.69 |
| Cl− | -- | y = 4.97x−0.30 | y = 5.4679e−0.02x |
| -- | y = 42.70e−0.016x | y = 49.78e−0.016x | |
| SC | -- | y = 0.039x2 − 5.53x + 393.25 | y = 0.035x2 − 5.57x + 430.83 |
| Bow River | |||
| Chl-a | -- | -- | y = 1.34x0.24 |
| WT | y = −0.0004x2 + 0.15x + 0.60 | y = −0.0011x2 + 0.22x + 3.20 | y = −0.0028x2 + 0.41x + 2.36 |
| DO | y = 0.001x2 − 0.038x + 13.11 | y = 0.0002x2 − 0.046x + 12.09 | y = 0.0006x2 − 0.099x + 13.01 |
| TURB | y = 0.74e0.014x | y = 0.0217x2 − 0.66x + 10.28 | y = 0.024x2 − 0.58x + 15.45 |
| DOC | y = 0.61e0.0054x | y = 0.00004x2 + 0.019x + 1.59 | y = 1.96e0.0083x |
| TP | y = 0.0037e0.0051x | -- | y = 0.00002x2 − 0.0003x + 0.032 |
| TN | y = 0.16e0.0031x | y =0.00008x2 − 0.014x + 1.56 | y = 1.44x−0.16 |
| pH | y = −0.00001x2 + 0.003x + 8.03 | y = −0.00003x2 + 0.0056x + 7.85 | y = −0.0002x2 + 0.017x + 7.90 |
| Cl− | -- | y = 11.06e−0.008x | y = 11.68e−0.01x |
| y = 0.0004x2 − 0.16x + 43.09 | y = 48.71e−0.004x | y = 64.09e−0.003x | |
| SC | y = 0.0019x2 − 0.68x + 326.88 | y = 386.62e−0.002x | y = 420.93e−0.002x |
| Oldman River | |||
| Chl-a | -- | y = 1.00e0.011x | y = 1.76e0.011x |
| WT | -- | y = −0.0005x2 + 0.11x + 7.02 | y = −0.0009x2 + 0.19x + 6.54 |
| DO | -- | y = 0.0001x2 − 0.033x + 11.57 | y = 0.0002x2 − 0.053x + 12.20 |
| TURB | y = 0.0022x2 + 0.11x + 2.96 | y = 0.048x2 − 1.26x + 28.24 | y = 0.036x2 + 0.18x + 7.97 |
| DOC | y = 1.83e0.0024x | y = 0.00005x2 + 0.019x + 2.05 | y = 0.00008x2 + 0.011x + 2.56 |
| TP | y = 0.000001x2 + 0.0001x + 0.0048 | y = 0.00005x2 − 0.0002x + 0.017 | y = 0.00006x2 − 0.0012x + 0.054 |
| TN | y = 0.19e0.0041x | y = 0.0001x2 − 0.0039x + 0.42 | -- |
| pH | -- | -- | -- |
| Cl− | -- | -- | y = 4.77e−0.008x |
| -- | -- | y = 51.88e−0.003x | |
| SC | -- | -- | y = 0.0013x2 − 0.85x + 398.74 |
| Station | Midstream Station (AB07BE0010) | Downstream Station (AB07CC0030) | ||
|---|---|---|---|---|
| 2050s | 2080s | 2050s | 2080s | |
| Chl-a | 1.51% | 2.42% | 2.65% | 4.26% |
| WT | 3.03% | 4.81% | 3.98% | 6.35% |
| DO | −0.32% | −0.52% | −0.56% | −0.90% |
| TURB | 17.20% | 29.68% | 16.51% | 28.42% |
| DOC | - | - | 0.73% | 1.20% |
| TP | 5.55% | 9.23% | 4.19% | 6.84% |
| TN | - | - | - | - |
| pH | 0.04% | 0.07% | 0.01% | 0.02% |
| Cl− | −1.37% | −2.17% | −1.53% | −2.45% |
| −1.11% | −1.78% | −1.23% | −2.07% | |
| SC | −0.74% | −1.17% | −0.87% | −1.39% |
| Station | Upstream Station (AB05BH0010) | Midstream Station (AB05BM0010) | Downstream Station (AB05BN0010) | |||
|---|---|---|---|---|---|---|
| 2050s | 2080s | 2050s | 2080s | 2050s | 2080s | |
| Chl-a | - | - | - | - | 0.53% | 1.71% |
| WT | 1.41% | 4.57% | 0.83% | 2.71% | 0.95% | 3.06% |
| DO | −0.19% | −0.63% | −0.12% | −0.39% | −0.20% | −0.65% |
| TURB | 3.99% | 14.40% | 3.81% | 13.10% | 2.73% | 9.40% |
| DOC | 0.74% | 2.51% | 0.55% | 1.84% | 0.47% | 1.57% |
| TP | 0.69% | 2.33% | - | - | 1.49% | 5.11% |
| TN | 0.38% | 1.28% | −0.25% | −0.82% | −0.34% | −1.10% |
| pH | 0.02% | 0.06% | 0.02% | 0.06% | 0.00% | 0.01% |
| Cl− | - | - | −0.34% | −1.11% | −0.39% | −1.28% |
| −0.28% | −0.93% | −0.18% | −0.61% | −0.13% | −0.44% | |
| SC | −0.13% | −0.42% | −0.10% | −0.32% | −0.09% | −0.30% |
| Station | Upstream Station (AB05AB0070) | Midstream Station (AB05AD0010) | Downstream Station (AB05AG0010) | |||
|---|---|---|---|---|---|---|
| 2050s | 2080s | 2050s | 2080s | 2050s | 2080s | |
| Chl-a | - | - | 1.19% | 4.71% | 0.96% | 3.74% |
| WT | - | - | 0.42% | 1.51% | 0.68% | 2.50% |
| DO | - | - | −0.13% | −0.49% | −0.19% | 0.70% |
| TURB | 3.15% | 12.24% | 4.51% | 17.98% | 4.93% | 19.37% |
| DOC | 0.20% | 0.77% | 0.62% | 2.38% | 0.40% | 1.53% |
| TP | 1.89% | 7.29% | 4.83% | 19.03% | 3.25% | 12.93% |
| TN | 0.37% | 1.41% | 0.92% | 3.70% | - | - |
| pH | - | - | - | - | - | - |
| Cl− | - | - | - | - | −0.42% | −1.55% |
| - | - | - | - | −0.17% | −0.65% | |
| SC | - | -- | - | - | −0.09% | −0.32% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rostami, S.; He, J.; Hassan, Q.K. Riverine Water Quality Response to Precipitation and Its Change. Environments 2018, 5, 8. https://doi.org/10.3390/environments5010008
Rostami S, He J, Hassan QK. Riverine Water Quality Response to Precipitation and Its Change. Environments. 2018; 5(1):8. https://doi.org/10.3390/environments5010008
Chicago/Turabian StyleRostami, Sajjad, Jianxun He, and Quazi K. Hassan. 2018. "Riverine Water Quality Response to Precipitation and Its Change" Environments 5, no. 1: 8. https://doi.org/10.3390/environments5010008
APA StyleRostami, S., He, J., & Hassan, Q. K. (2018). Riverine Water Quality Response to Precipitation and Its Change. Environments, 5(1), 8. https://doi.org/10.3390/environments5010008







