Investigating the Cosmic and Solar Drivers of Stratospheric 7Be Variability
Abstract
1. Introduction
2. Materials and Methods
2.1. Stratospheric 7Be Production, Deposition and Measurement in Casaccia Research Center
2.2. Datasets and Data Analysis
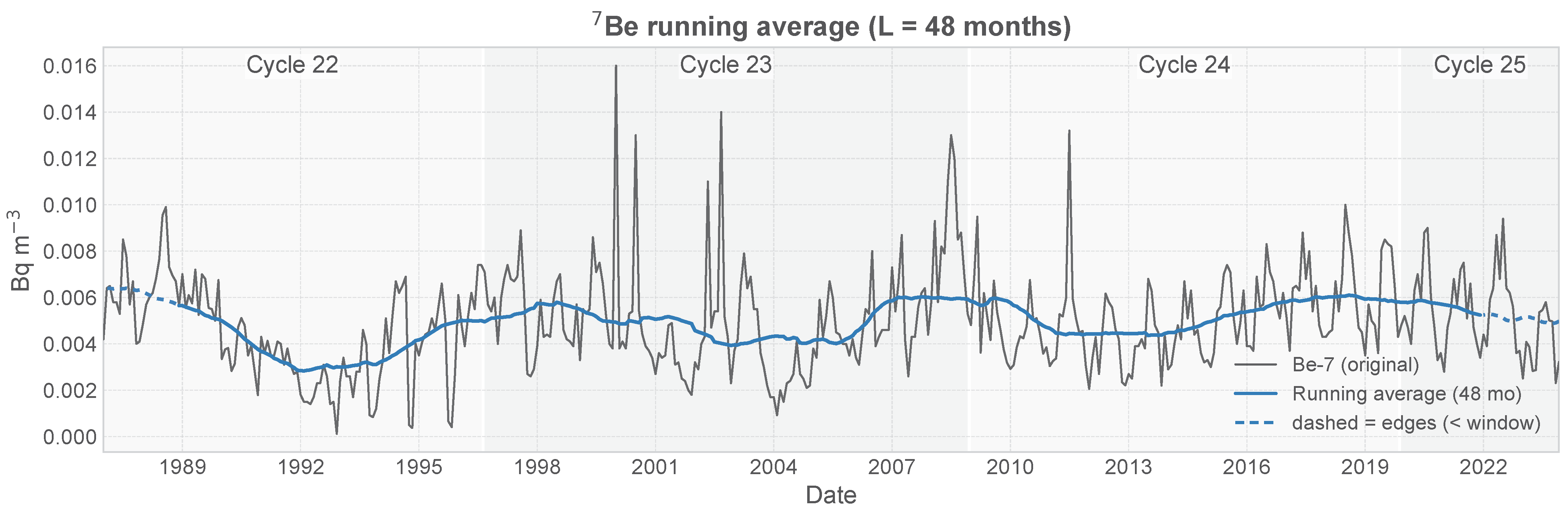
2.3. Detrending of 7Be Time Series
2.4. Correlation Metrics and Confidence Intervals Evaluation
2.4.1. Correlation Metrics
- Pearson’s correlation coefficient r—the metric measures the strength and direction of a linear relationship between two variables. According to [38], it is defined as:where denotes the covariance between X and Y, and and are the standard deviations of X and Y, respectively.
- Spearman’s rank correlation coefficient [40]—the metric measures the strength and direction of a monotonic relationship by computing the Pearson correlation between the ranked values of the variables:where and have the same meaning as in the Pearson case, but are applied to the ranked variables. Spearman’s is particularly effective in detecting relationships that are nonlinear but still consistently increasing or decreasing.
- Kendall’s rank correlation coefficient [41,42]—the metric is based on counting the number of concordant and discordant pairs among all possible pairs of observations:where and are the numbers of concordant and discordant pairs of observations respectively, and n represents the sample size. Two observations are concordant if the ordering of their ranks for both variables is consistent, and discordant otherwise.
2.4.2. Confidence Intervals Evaluation
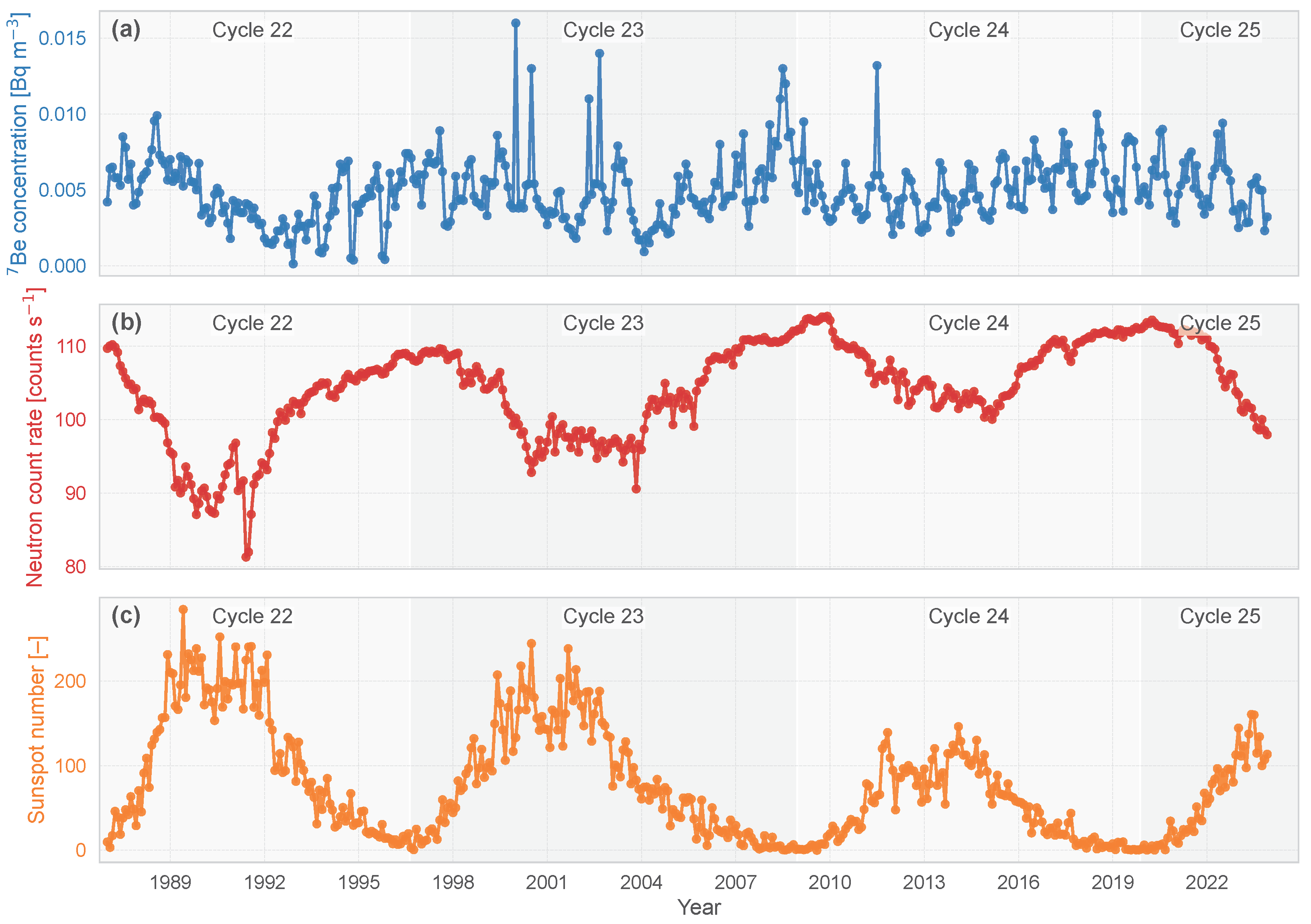
3. Results
3.1. Correlation on the Raw Data
3.2. Running Average Results
3.3. Correlation Metrics Results
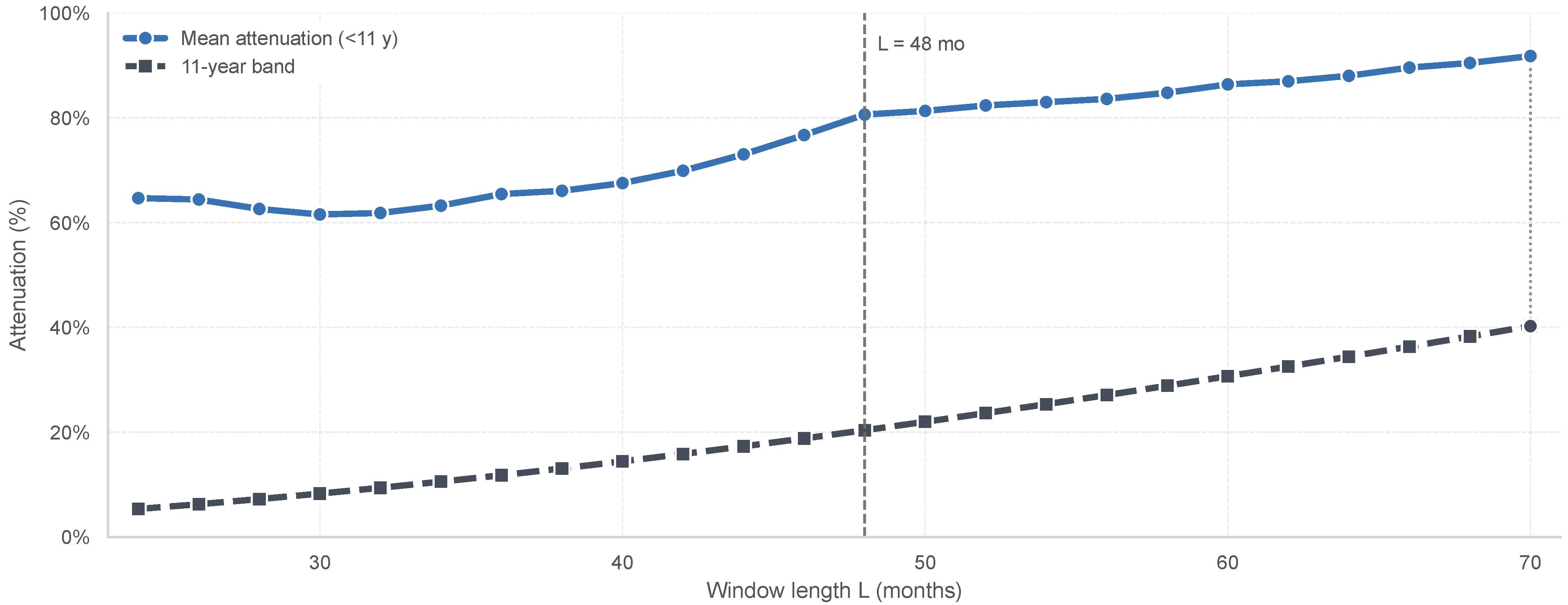
3.3.1. Sensitivity to the Smoothing Window Length
3.3.2. Sensitivity of Confidence Intervals to Block Length b
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CI | Confidence Interval |
| ENSO | El Niño–Southern Oscillation |
| GCR | Galactic Cosmic Rays |
| HPGe | High-Purity Germanium (detector) |
| IACT | Integrated Auto-Correlation Time |
| MDA | Minimum Detectable Activity |
| OLS | Ordinary Least Squares |
| QBO | Quasi-Biennial Oscillation |
| SEP | Solar Energetic Particles |
| r | Pearson’s correlation coefficient |
| Spearman’s rank correlation coefficient | |
| Kendall’s rank correlation coefficient |
References
- Libby, W.F. Atmospheric Helium Three and Radiocarbon from Cosmic Radiation. Phys. Rev. 1946, 69, 671. [Google Scholar] [CrossRef]
- Arnold, J.R.; Al-Salih, H.A. Beryllium-7 produced by cosmic rays. Science 1955, 121, 451–453. [Google Scholar] [CrossRef]
- Young, J.A.; Silker, W.B. Aerosol deposition velocities on the Pacific and Atlantic Oceans calculated from 7Be measurements. Earth Planet. Sci. Lett. 1980, 50, 92–104. [Google Scholar] [CrossRef]
- Sanak, J.; Lambert, G.; Ardouin, B. Measurement of stratosphere-to-troposphere exchange in Antarctica by using short-lived cosmonuclides. Tellus B 1985, 37, 109–115. [Google Scholar] [CrossRef][Green Version]
- Mohan, M.P.; D’Souza, R.S.; Nayak, S.R.; Kamath, S.S.; Shetty, T.; Kumara, K.S.; Mayya, Y.S.; Karunakara, N. Influence of rainfall on atmospheric deposition fluxes of 7Be and 210Pb in Mangaluru (Mangalore) at the Southwest Coast of India. Atmos. Environ. 2019, 202, 281–295. [Google Scholar] [CrossRef]
- Liu, H.; Considine, D.B.; Horowitz, L.W.; Crawford, J.H.; Rodriguez, J.M.; Strahan, S.E.; Damon, M.R.; Steenrod, S.D.; Xu, X.; Kouatchou, J.; et al. Using beryllium-7 to assess cross-tropopause transport in global models. Atmos. Chem. Phys. 2016, 16, 4641–4659. [Google Scholar] [CrossRef]
- Liu, J.; Starovoitova, V.N.; Wells, D.P. Long-term variations in the surface air 7Be concentration and climatic changes. J. Environ. Radioact. 2013, 116, 42–47. [Google Scholar] [CrossRef] [PubMed]
- Schaar, K.; Spiegl, T.; Sato, T.; Langematz, U. The impact of ENSO on near-surface Beryllium-7. J. Environ. Radioact. 2025, 282, 107592. [Google Scholar] [CrossRef]
- Papastefanou, C.; Ioannidou, A.; Stoulos, S.; Manolopoulou, M. Atmospheric deposition of cosmogenic 7Be and 137Cs from fallout of the Chernobyl accident. Sci. Total Environ. 1995, 170, 151–156. [Google Scholar] [CrossRef]
- Todorović, D.; Popović, D.; Đurić, G. Concentration measurements of 7Be and 137Cs in ground level air in the Belgrade city area. Environ. Int. 1999, 25, 59–66. [Google Scholar] [CrossRef]
- Phillips, G.W.; King, S.E.; August, R.A.; Ritter, J.C.; Cutchin, J.H.; Haskins, P.S.; McKisson, J.E.; Ely, D.W.; Weisenberger, A.G.; Piercey, R.B.; et al. Discovery of Be-7 Accretion in Low Earth Orbit. In Proceedings of the 14th Annual AAS Guidance and Control Conference, Keystone, CO, USA, 2–6 February 1991; DTIC Report AD-A236 614. Available online: https://apps.dtic.mil/sti/pdfs/ADA236614.pdf (accessed on 25 August 2025).
- Mewaldt, R.A.; Stone, E.C.; Tylka, A.J. Enhanced beryllium-7 concentrations in the upper atmosphere following solar proton events. Geophys. Res. Lett. 2001, 28, 2585–2588. [Google Scholar] [CrossRef]
- Chen, D.L.; Zell, S.E.; Paulikas, G.A. Observations of cosmogenic beryllium-7 in the mesosphere and lower thermosphere. J. Atmos. Sol.-Terr. Phys. 1993, 55, 707–714. [Google Scholar]
- Golubenko, K.; Rozanov, E.; Kovaltsov, G.; Leppänen, A.-P.; Sukhodolov, T.; Usoskin, I. Chemistry-climate model SOCOL-AERv2-BEv1 with the cosmogenic Beryllium-7 isotope cycle. Geosci. Model Dev. Discuss. 2021, 14, 7605–7620. [Google Scholar] [CrossRef]
- Nelson, G.A. Space Radiation and Human Exposures, A Primer. Radiat. Res. 2016, 185, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, A.; Borra, E.M.; Ciciani, L.; Di Fino, L.; Romoli, G.; Santi Amantini, G.; Sperandio, L.; Vilardi, I.; Narici, L. Foundations of radiological protection in space: The integrated multidisciplinary approach for next manned missions in deep space. Eur. Phys. J. Plus 2023, 138, 1001. [Google Scholar] [CrossRef]
- Papastefanou, C.; Ioannidou, A. Beryllium-7 and solar activity. Appl. Radiat. Isot. 2004, 61, 1493–1495. [Google Scholar] [CrossRef] [PubMed]
- Rajacic, M.M.; Todorovic, D.J.; Krneta Nikolic, J.D.; Puzovic, J.M. The impact of the Solar magnetic field on 7Be activity concentration in aerosols. Appl. Radiat. Isot. 2017, 125, 27–29. [Google Scholar] [CrossRef]
- Aldahan, A.; Hedfors, J.; Possnert, G.; Kulan, A.; Berggren, A.-M.; Söderström, C. Atmospheric impact on beryllium isotopes as solar activity proxy. Geophys. Res. Lett. 2008, 35, L21812. [Google Scholar] [CrossRef]
- Kremenchutskii, D.A.; Konovalov, S.K. Beryllium-7 and its variability in the near-surface atmosphere of Crimea, the Black Sea region. Atmos. Pollut. Res. 2022, 13, 101406. [Google Scholar] [CrossRef]
- Brattich, E.; Liu, H.; Tositti, L.; Considine, D.B.; Crawford, J.H. Processes controlling the seasonal variations in 210Pb and 7Be at the Mt. Cimone WMO-GAW global station, Italy: A model analysis. Atmos. Chem. Phys. 2017, 17, 1061–1080. [Google Scholar] [CrossRef]
- Kulan, A.; Aldahan, A.; Possnert, G.; Vintersved, I. Distribution of 7Be in surface air of Europe. Atmos. Environ. 2006, 40, 3855–3868. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Gray, L.J.; Dunkerton, T.J.; Hamilton, K.; Haynes, P.H.; Randel, W.J.; Holton, J.R.; Alexander, M.J.; Hirota, I.; Horinouchi, T.; et al. The quasi-biennial oscillation. Rev. Geophys. 2001, 39, 179–229. [Google Scholar] [CrossRef]
- Casselman, J.W.; Lübbecke, J.F.; Bayr, T.; Huo, W.; Wahl, S.; Domeisen, D.I.V. The teleconnection of extreme El Niño–Southern Oscillation (ENSO) events to the tropical North Atlantic in coupled climate models. Weather Clim. Dyn. 2023, 4, 471–487. [Google Scholar] [CrossRef]
- Yu, N.; Chen, G.; Ray, J.; Chen, W.; Chao, N. Semi-decadal and decadal signals in atmospheric excitation of length-of-day. Earth Space Sci. 2019, 6, 1205–1216. [Google Scholar] [CrossRef]
- Lal, D.; Peters, B. Cosmic Ray Produced Radioactivity on the Earth. In Kosmische Strahlung II/Cosmic Rays II; Sitte, K., Ed.; Handbuch der Physik/Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 1967; Volume 9, pp. 551–612. ISBN 3540038558. [Google Scholar]
- Talpos, S.; Cuculeanu, V. A Study of the Vertical Diffusion of 7Be in the Atmosphere. J. Environ. Radioact. 1997, 36, 93–106. [Google Scholar] [CrossRef]
- Sitte, K.; Stierwalt, D.L.; Kofsky, I.L. Development of Air Showers in the Atmosphere. Phys. Rev. 1954, 94, 988–993. [Google Scholar] [CrossRef]
- Papastefanou, C.; Ioannidou, A. Beryllium-7 Aerosols in Ambient Air. Environ. Int. 1996, 22, S125–S130. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, H.; Adolphi, F.; Muscheler, R.; Lu, Z.; Wu, M.; Prisle, N.L. Simulations of 7Be and 10Be with the GEOS-Chem global model v14.0.2 using state-of-the-art production rates. Geosci. Model Dev. 2023, 16, 7037–7057. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, J.; Baskaran, M.; Zhong, Q.; Wang, Y.; Paatero, J.; Du, J. A global dataset of atmospheric 7Be and 210Pb measurements: Annual air concentration and depositional flux. Earth Syst. Sci. Data 2021, 13, 2963–2994. [Google Scholar] [CrossRef]
- Yoshimori, M. Beryllium 7 radionuclide as a tracer of vertical air mass transport in the troposphere. Adv. Space Res. 2005, 36, 828–832. [Google Scholar] [CrossRef]
- Koch, D.M.; Jacob, D.J.; Graustein, W.C. Vertical transport of tropospheric aerosols as indicated by 7Be and 210Pb in a chemical tracer model. J. Geophys. Res. Atmos. 1996, 101, 18651–18666. [Google Scholar] [CrossRef]
- Długosz-Lisiecka, M.; Bem, H. Seasonal fluctuation of activity size distribution of 7Be, 210Pb, and 210Po radionuclides in urban aerosols. J. Aerosol Sci. 2020, 144, 105544. [Google Scholar] [CrossRef]
- NMDB Event Search Tool (NEST). Available online: https://www.nmdb.eu/nest/ (accessed on 25 October 2024).
- WDC-SILSO. Royal Observatory of Belgium, Brussels. Available online: https://www.sidc.be/SILSO/datafiles (accessed on 25 October 2024).
- von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 1999; ISBN 0521450713/0521012309. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; International Geophysics Series; Academic Press: San Diego, CA, USA, 2011; Volume 100, ISBN 978-0123850225. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2010; p. 47. ISBN 978-0131988422. [Google Scholar]
- Spearman, C. The Proof and Measurement of Association Between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999; ISBN 978-0471160687. [Google Scholar]
- Künsch, H.R. The jackknife and the bootstrap for general stationary observations. Ann. Statist. 1989, 17, 1217–1241. [Google Scholar] [CrossRef]
- Lahiri, S.N. Resampling Methods for Dependent Data; Springer Series in Statistics; Springer: New York, NY, USA, 2003; ISBN 978-0387954417. [Google Scholar]
- Seber, G.A.F.; Lee, A.J. Linear Regression Analysis, 2nd ed.; Wiley Series in Probability and Statistics; Wiley-Interscience: Hoboken, NJ, USA, 2003; ISBN 978-0471415404. [Google Scholar]
- Sokal, A.D. Monte Carlo methods in statistical mechanics: Foundations and new algorithms. In Functional Integration: Basics and Applications; DeWitt-Morette, C., Cartier, P., Folacci, A., Eds.; NATO ASI Series B: Physics; Springer: Boston, MA, USA, 1997; Volume 361, pp. 131–192. ISBN 978-0306456577. [Google Scholar] [CrossRef]
- Bartlett, M.S. On the Theoretical Specification and Sampling Properties of Autocorrelated Time-Series. J. R. Stat. Soc. Suppl. 1946, 8, 27–41. [Google Scholar] [CrossRef]
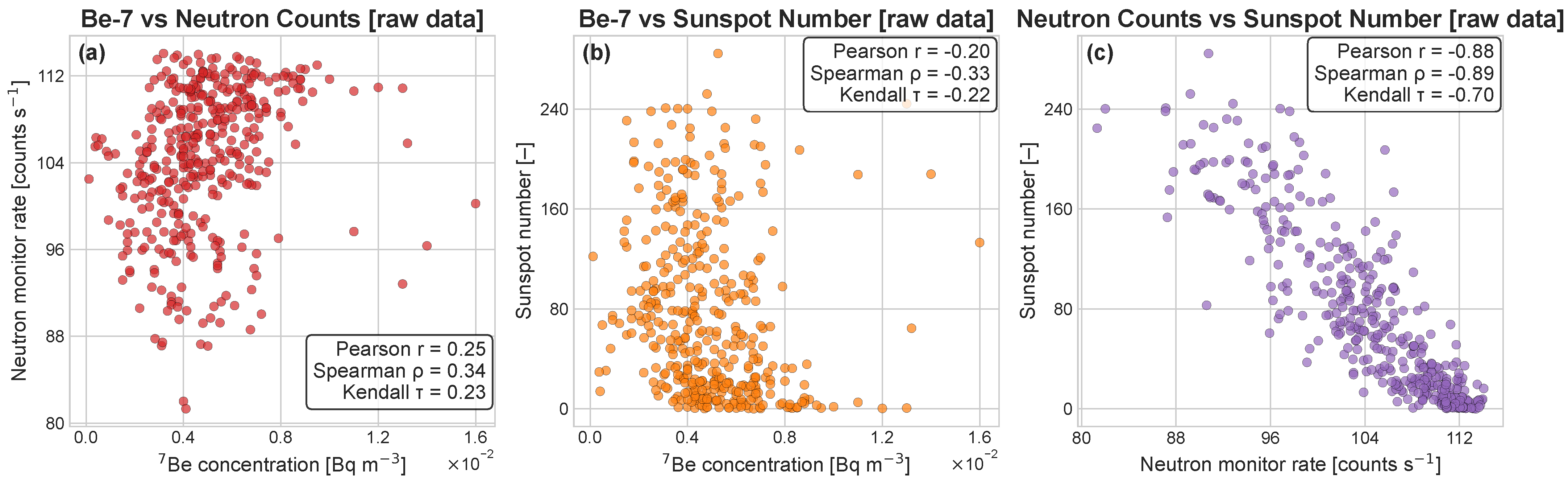

| Pair | r | 95% CI (r) | 95% CI () | 95% CI () | ||
|---|---|---|---|---|---|---|
| Be-7 vs. Neutron Count | 0.25 | [0.11, 0.42] | 0.34 | [0.20, 0.51] | 0.23 | [0.14, 0.34] |
| Be-7 vs. Sunspot Number | −0.20 | [−0.38, −0.03] | −0.33 | [−0.50, −0.17] | −0.22 | [−0.34, −0.11] |
| Neutron Count vs. Sunspot Number | −0.88 | [−0.92, −0.81] | −0.89 | [−0.92, −0.81] | −0.70 | [−0.75, −0.61] |
| Metric | ||||
|---|---|---|---|---|
| Be-7 vs. Neutron | ||||
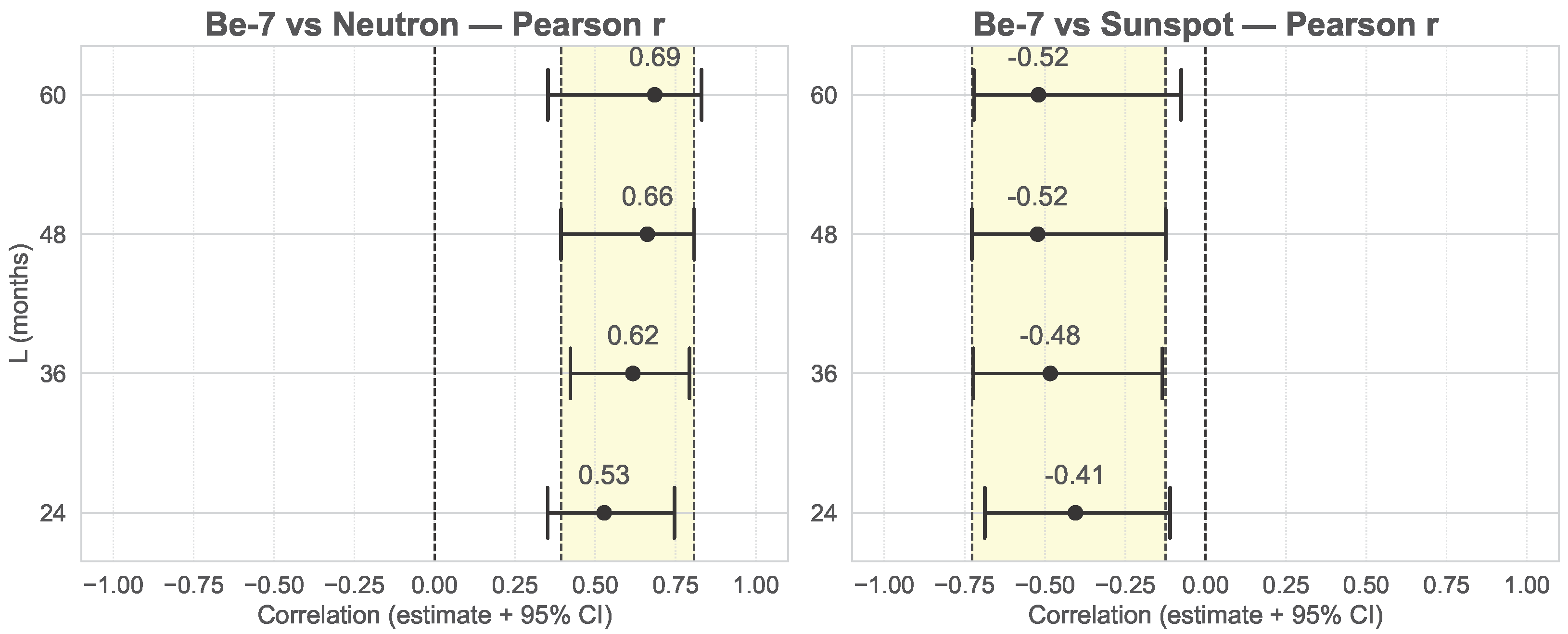
| Pearson | 0.66 | 0.53 | 0.62 | 0.69 |
| Spearman | 0.75 | 0.62 | 0.73 | 0.77 |
| Kendall | 0.54 | 0.43 | 0.51 | 0.57 |
| Be-7 vs. Sunspot | ||||
| Pearson | ||||
| Spearman | ||||
| Kendall | ||||
| Metric | BL = 36 (Ref) | BL = 24 | BL = 48 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Low | High | Width | Low | High | Width% | Low | High | Width% | |
| Be-7 vs. Neutron | |||||||||
| Pearson | 0.40 | 0.81 | 0.41 | 0.44 | 0.83 | 0.37 | 0.81 | ||
| Spearman | 0.41 | 0.85 | 0.44 | 0.41 | 0.86 | 0.38 | 0.85 | ||
| Kendall | 0.29 | 0.65 | 0.37 | 0.32 | 0.65 | 0.27 | 0.65 | ||
| Be-7 vs. Sunspot | |||||||||
| Pearson | −0.72 | −0.12 | 0.60 | −0.74 | −0.17 | −5.7 | −0.72 | −0.09 | |
| Spearman | −0.78 | −0.16 | 0.63 | −0.79 | −0.20 | −5.3 | −0.78 | −0.12 | |
| Kendall | −0.57 | −0.12 | 0.45 | −0.58 | -0.16 | −0.57 | −0.09 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizzo, A.; Antonacci, G.; Astarita, M.; Borra, E.M.; Ciciani, L.; di Marco, N.; la Notte, G.; Ripesi, P.; Sperandio, L.; Vilardi, I.; et al. Investigating the Cosmic and Solar Drivers of Stratospheric 7Be Variability. Environments 2025, 12, 312. https://doi.org/10.3390/environments12090312
Rizzo A, Antonacci G, Astarita M, Borra EM, Ciciani L, di Marco N, la Notte G, Ripesi P, Sperandio L, Vilardi I, et al. Investigating the Cosmic and Solar Drivers of Stratospheric 7Be Variability. Environments. 2025; 12(9):312. https://doi.org/10.3390/environments12090312
Chicago/Turabian StyleRizzo, Alessandro, Giuseppe Antonacci, Massimo Astarita, Enrico Maria Borra, Luca Ciciani, Nadia di Marco, Giovanna la Notte, Patrizio Ripesi, Luciano Sperandio, Ignazio Vilardi, and et al. 2025. "Investigating the Cosmic and Solar Drivers of Stratospheric 7Be Variability" Environments 12, no. 9: 312. https://doi.org/10.3390/environments12090312
APA StyleRizzo, A., Antonacci, G., Astarita, M., Borra, E. M., Ciciani, L., di Marco, N., la Notte, G., Ripesi, P., Sperandio, L., Vilardi, I., & Zazzaron, F. (2025). Investigating the Cosmic and Solar Drivers of Stratospheric 7Be Variability. Environments, 12(9), 312. https://doi.org/10.3390/environments12090312








