Multivariate and Machine Learning-Based Assessment of Soil Elemental Composition and Pollution Analysis
Abstract
1. Introduction
2. Materials and Methods
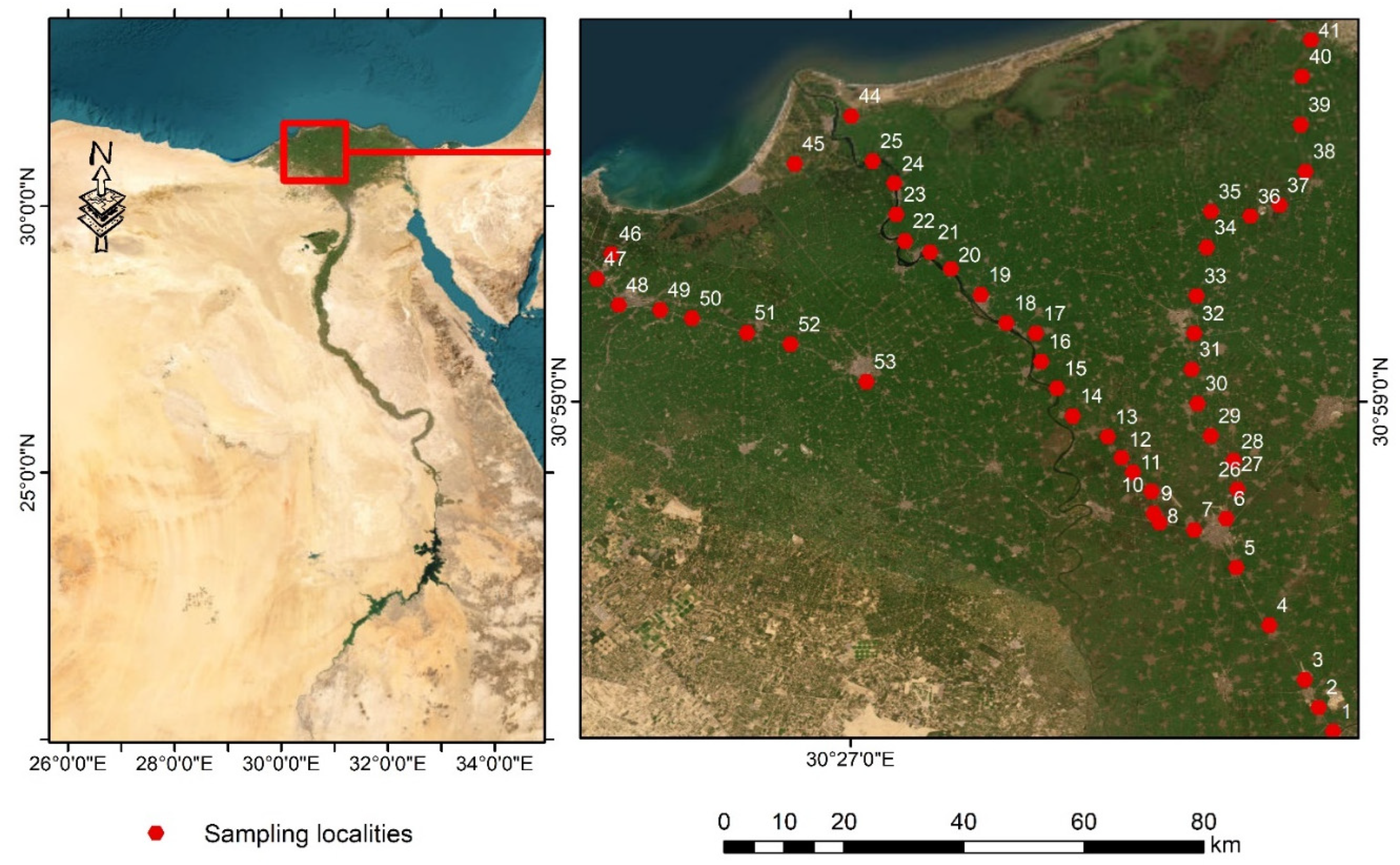
2.1. Sampling Strategy
2.2. Sample Preparation for Analysis Using ICP-MS and ICP-AES
2.3. Quality Control of (ICP-MS and ICP-AES)
3. Statistical Data Analysis
4. Background and Pollution Analysis
4.1. Single Pollution Index (SPI)
4.2. Enrichment Factor (EF)
4.3. Pollution Load Index (PLI)
4.4. Total Pollution Index TPI (Zc)
5. Results and Discussion
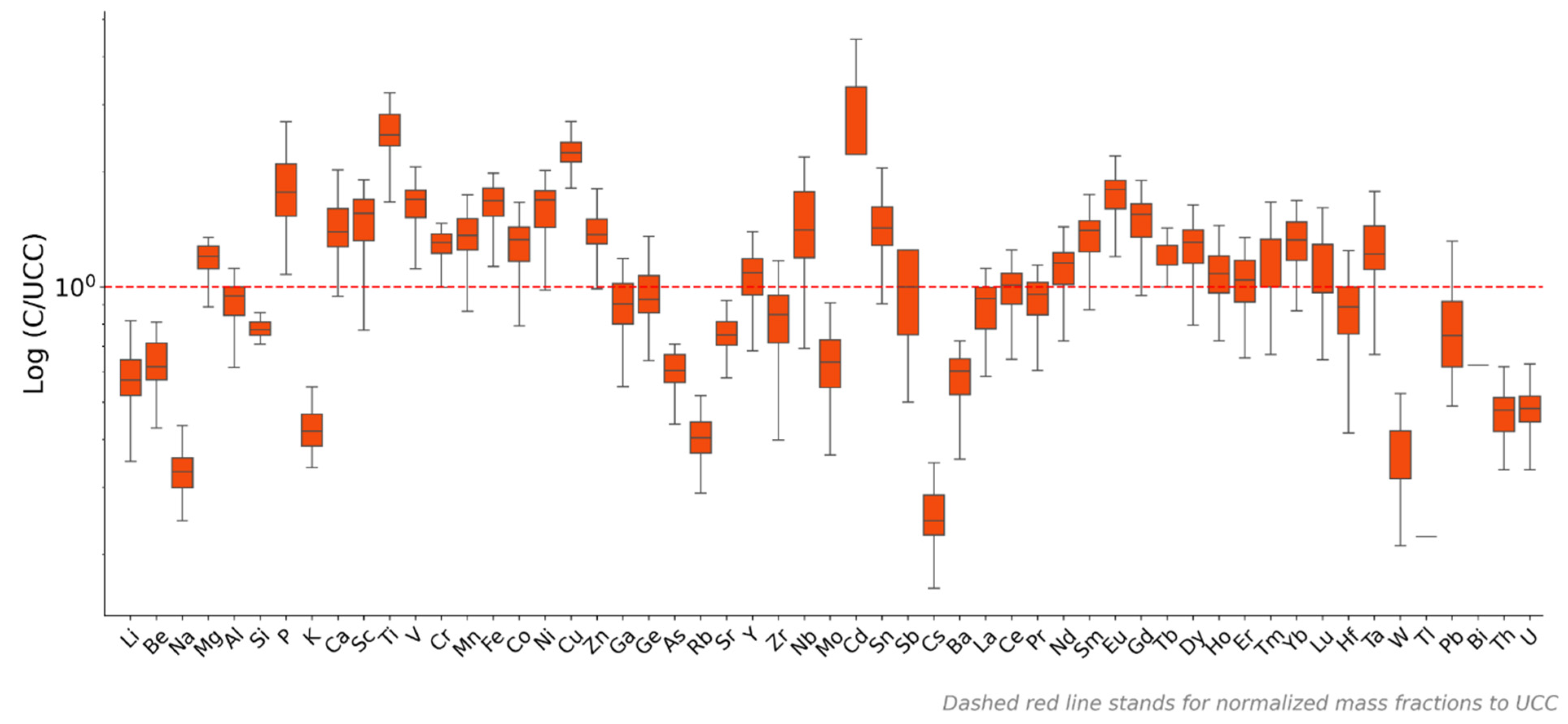
5.1. Elemental Abundances
5.2. Normality Test and Intercorrelation
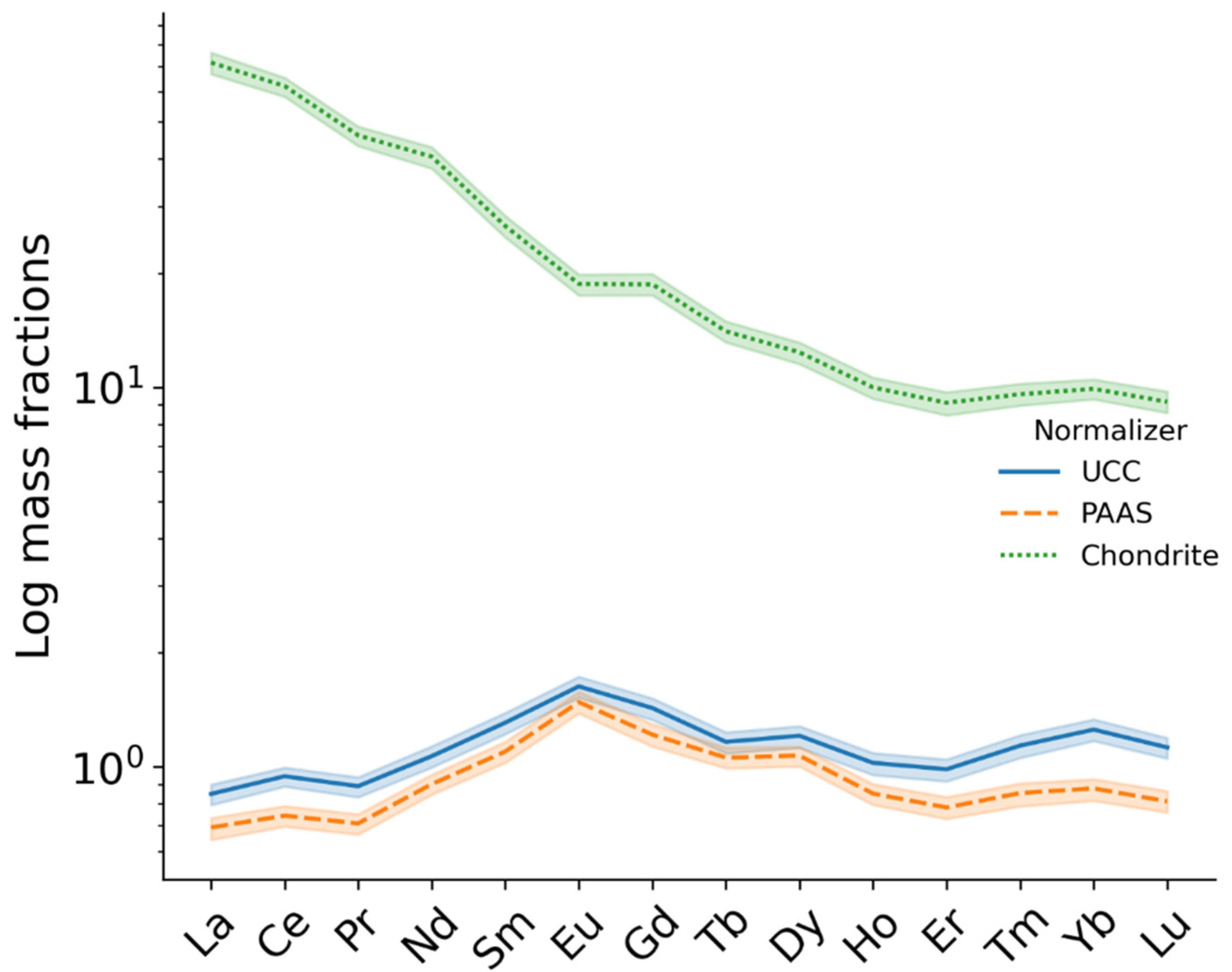
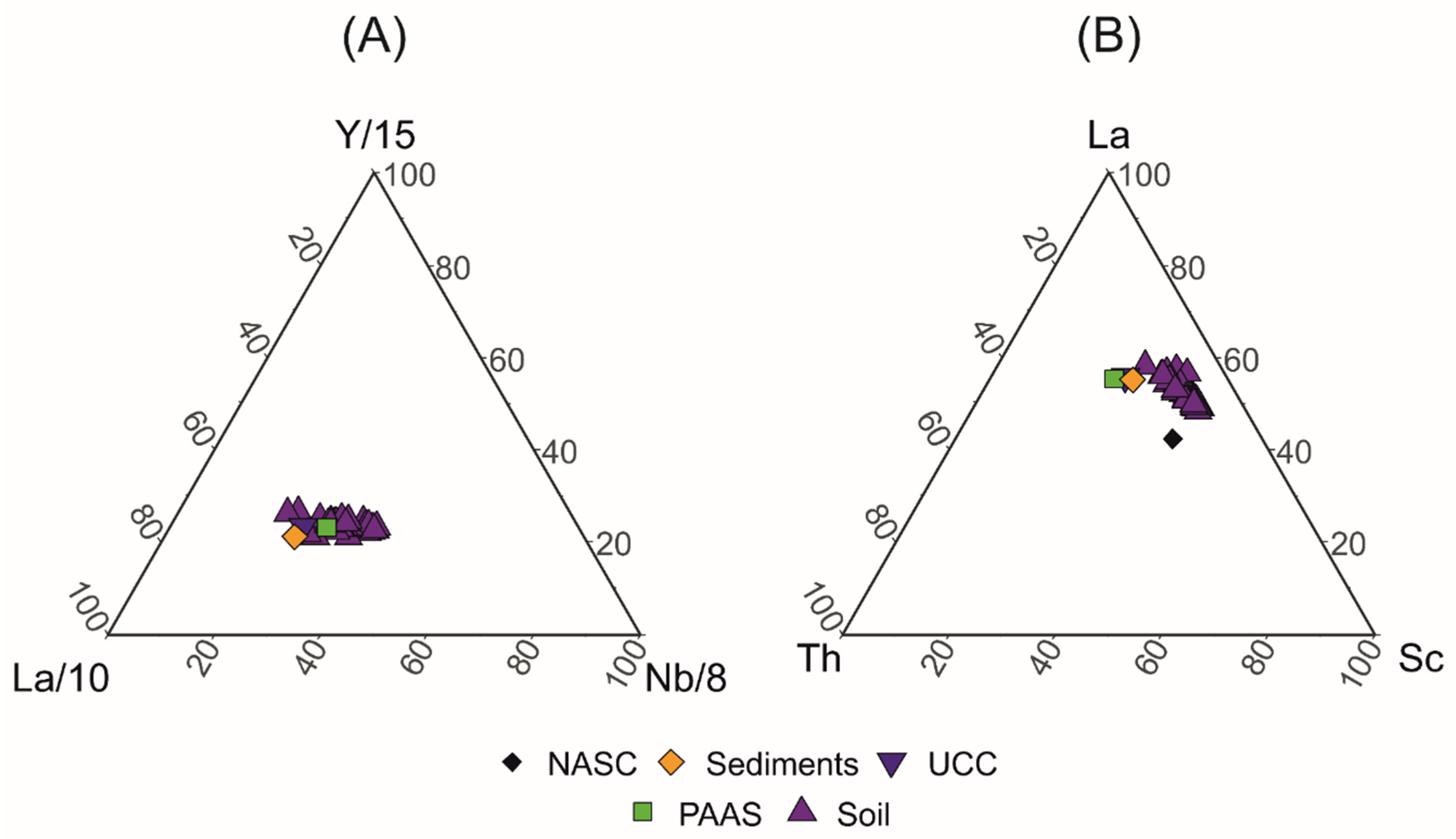
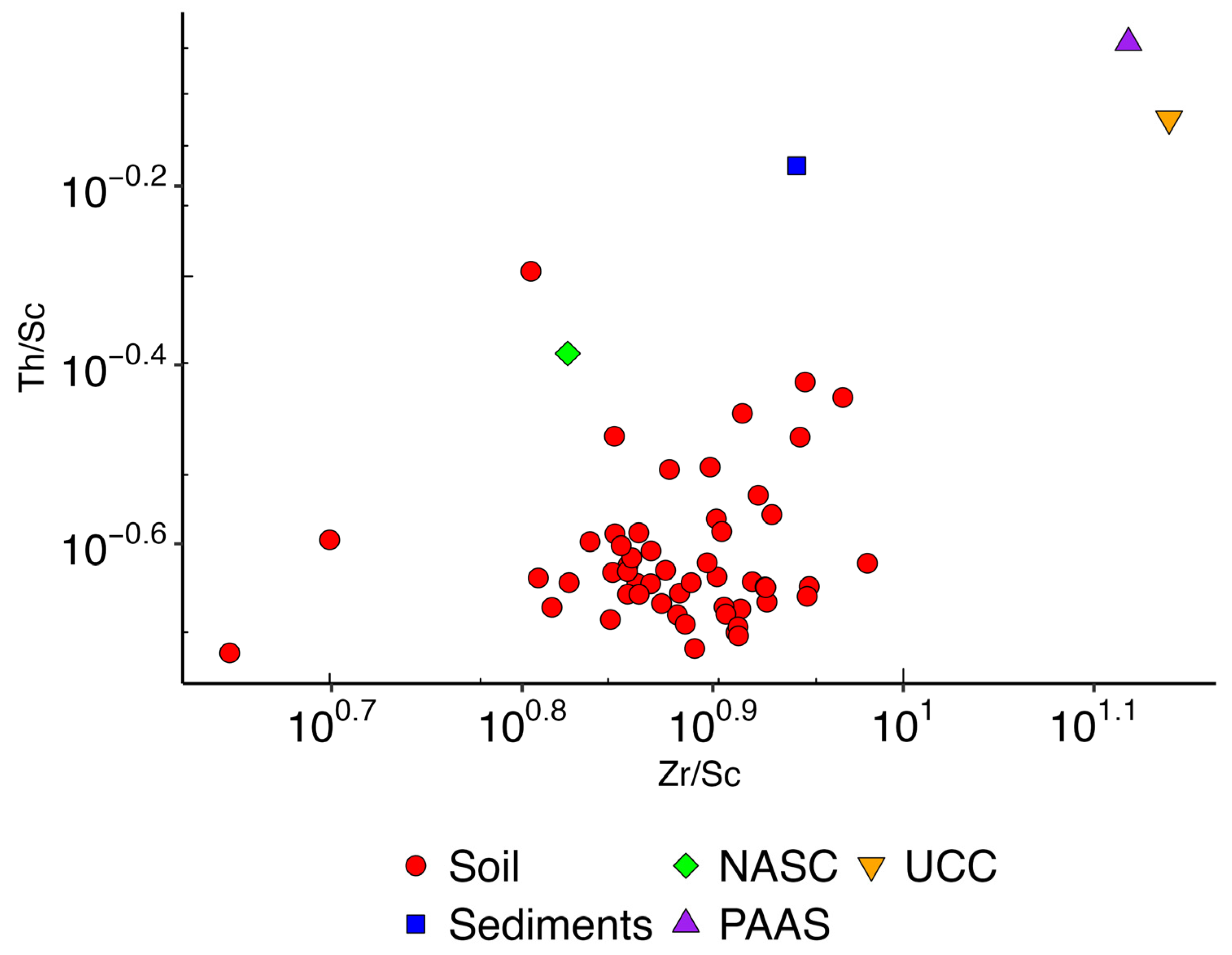
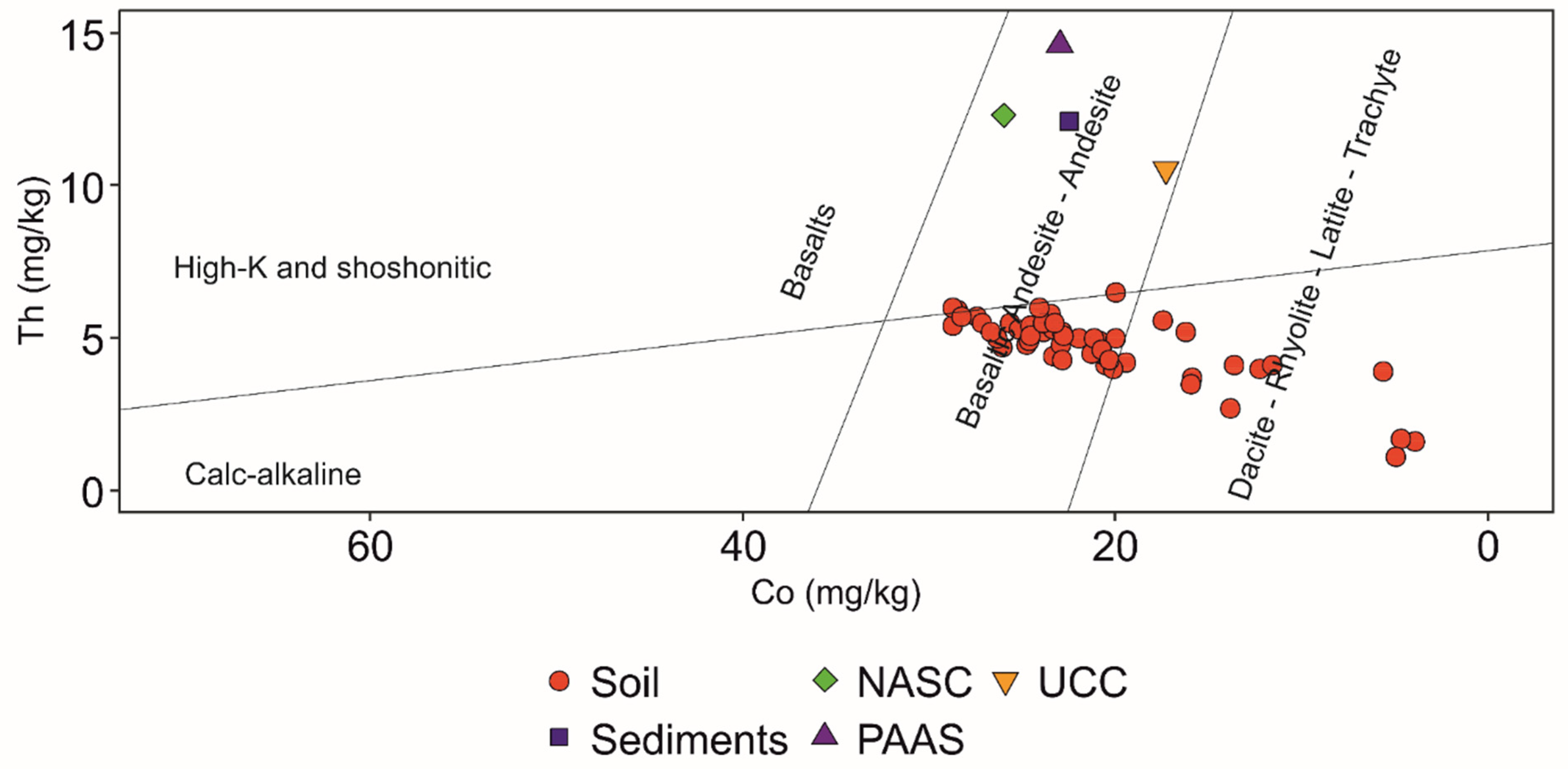
5.3. Geochemical Provenance of Elements in Soil
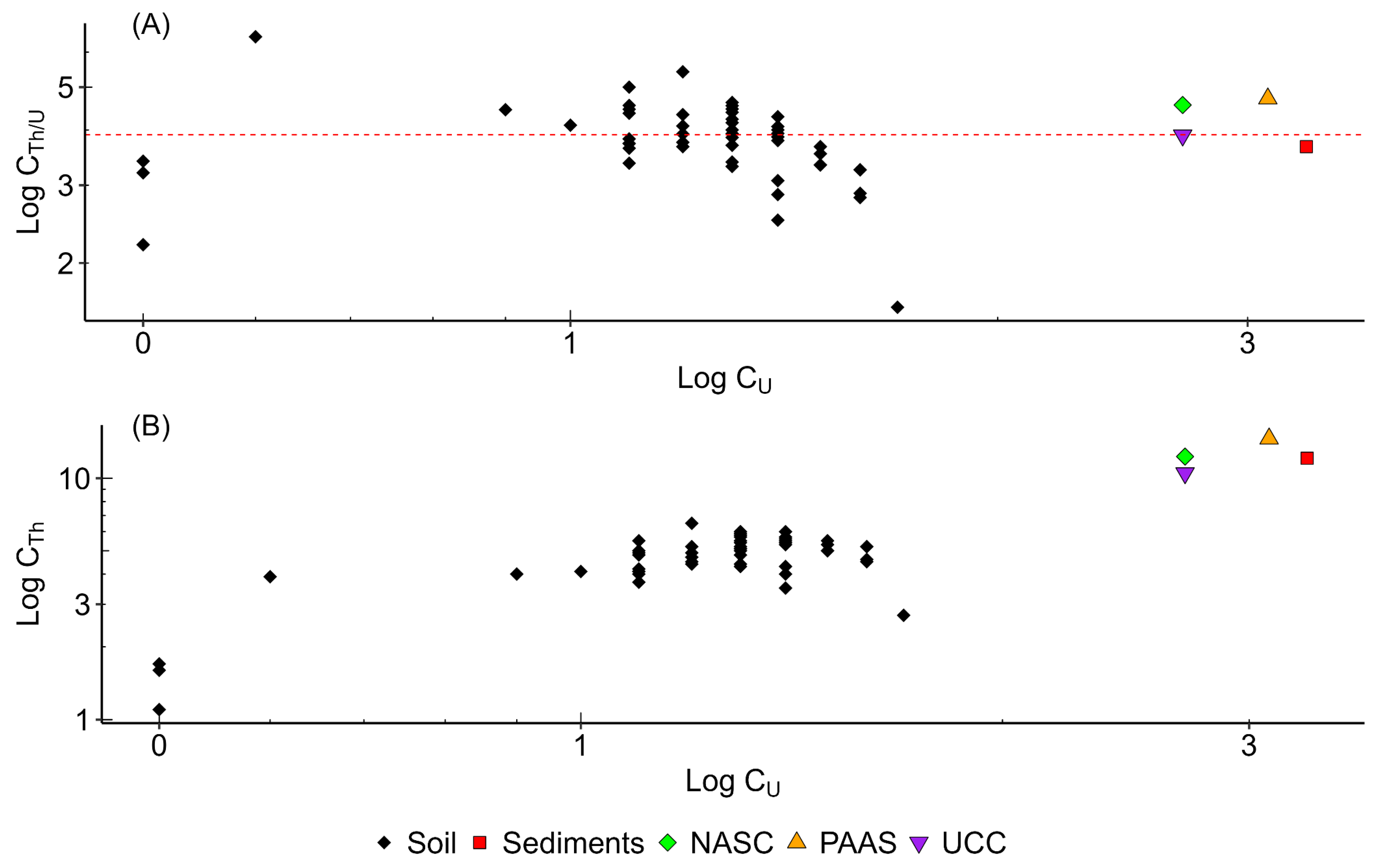
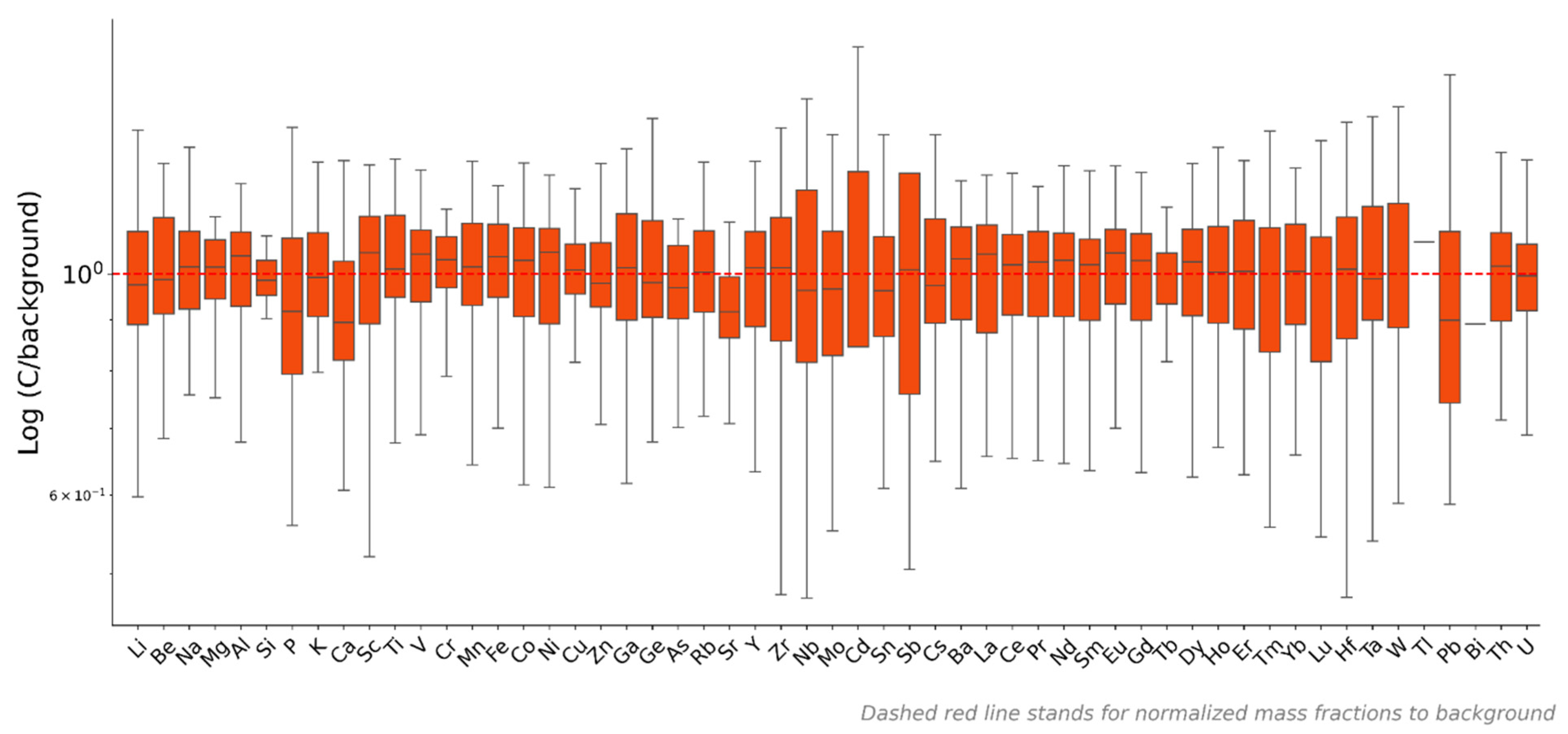
5.4. Findings of the Background and Pollution Analysis
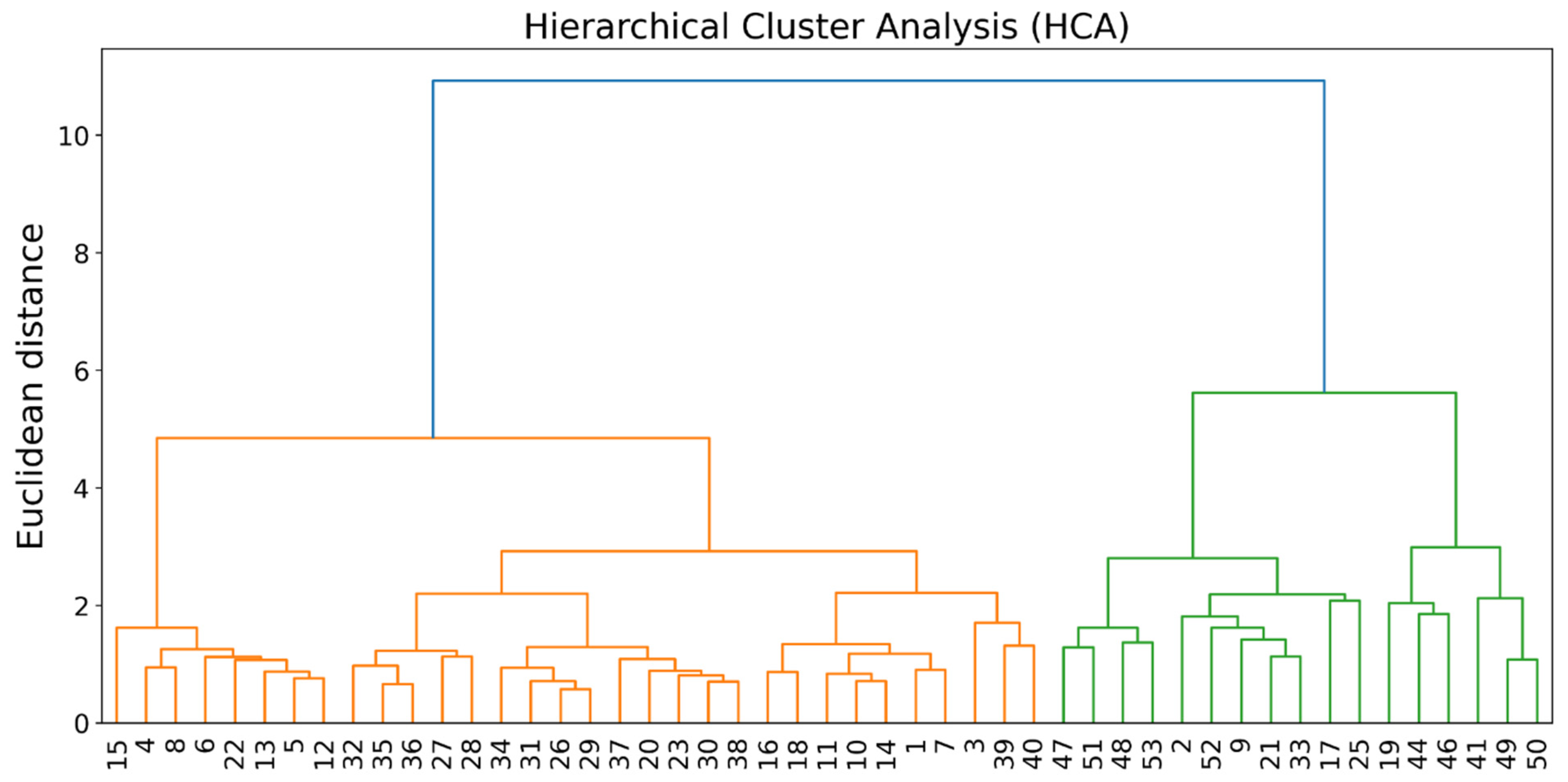
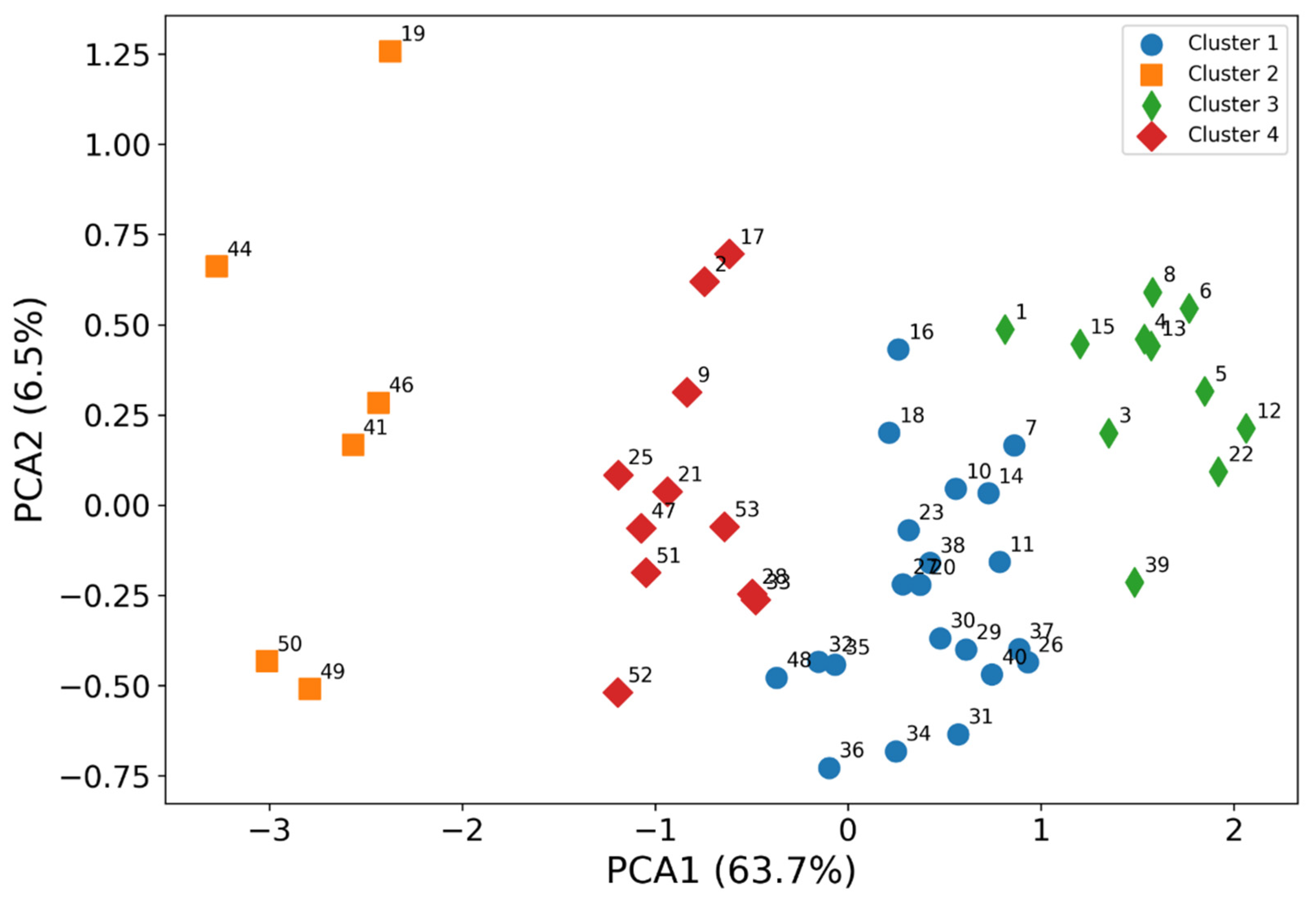
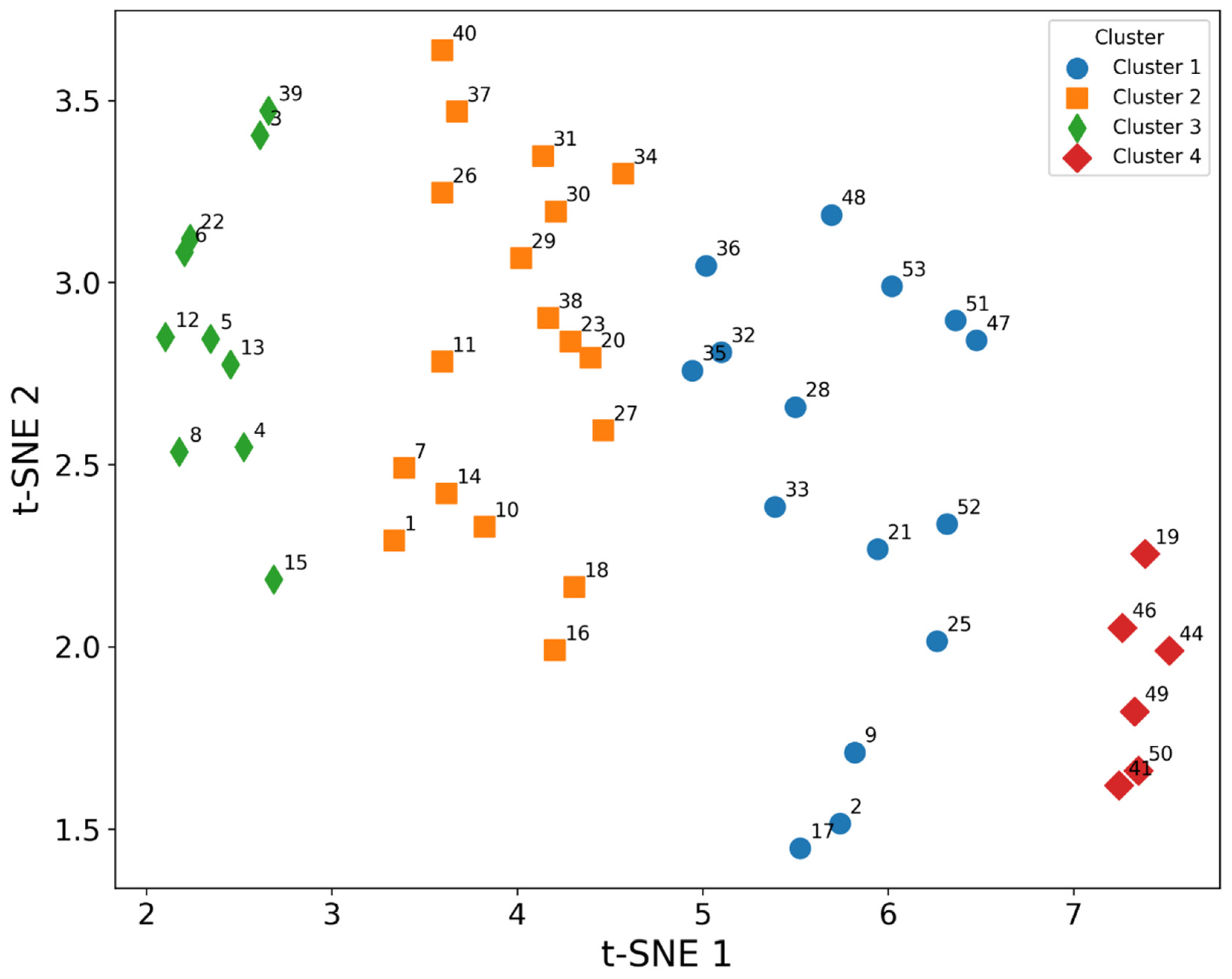
5.5. Findings of the Unsupervised Learning HCA, PCA, t–SNE, and HAC
- Cluster 1 includes the highest number of locations, namely 7, 10, 11, 14, 16, 18, 23, 26, 27, 29, 30, 31, 32, 34, 35, 36, 37, 38, 40, and 48.
- Cluster 2 has a minor number of samples, and they are locations 19, 41, 44, 46, 49, and 50.
- Cluster 3 contains 11 locations: 1, 3, 4, 5, 6, 8, 12, 13, 15, 22, 39.
- Cluster 4 includes the locations 2, 9, 17, 21, 25, 28, 33, 47, 51, 52, 53.
- Cluster 1 includes the soil samples labeled as 2, 9, 17, 21, 25, 28, 32, 33, 35, 36, 47, 48, 51, 52, and 53. Despite the fact that the samples were collected at different locations in the Nile Delta, they are grouped in a cluster, which is due to the fact that the samples were collected in agricultural areas close to the highways. Therefore, it can be assumed that the crustal association from the dust along the highways is the common source of these elements.
- Cluster 2 contains 1, 7, 10, 11, 14, 16, 18, 20, 26, 27, 29, 30, 31, 34, 37, 38, and 40. The samples were taken from agricultural land near rural areas, and most likely the influences and pressures from these areas affect the amount of elemental mass fractions in the adjacent soil. It is good evidence that the analysis of the samples was accurate and that the statistical treatment and hypotheses are precise.
- Cluster 3 has 10 samples, namely 3, 4, 5, 6, 8, 12, 12, 13, 15, 22, and 39. The samples were taken near large cities and industries. For example, some samples were collected near Tanta and Banha. It is, therefore, hypothesized that the common geochemical features that cluster these samples together are due to domestic activities and industry.
- Cluster 4 has the minimum number of soil samples 19, 41, 44, 46, 49, and 50. These samples come from different places, but are collected in one group. This can be explained by the excessive use of fertilizers and the proximity to Lake Burullus [31].
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamza, W. The Nile Delta. In The Nile; Dumont, H.J., Ed.; Monographiae Biologicae; Springer: Dordrecht, The Netherlands, 2009; pp. 75–94. [Google Scholar]
- Fishar, M.R. Nile Delta (Egypt). In The Wetland Book: II: Distribution, Description and Conservation; Finlayson, C.M., Milton, G.R., Prentice, R.C., Davidson, N.C., Eds.; Springer: Dordrecht, The Netherlands, 2016; pp. 1–10. [Google Scholar]
- Arafa, W.M.; Badawy, W.M.; Fahmi, N.M.; Ali, K.; Gad, M.S.; Duliu, O.G.; Frontasyeva, M.V.; Steinnes, E. Geochemistry of sediments and surface soils from the Nile Delta and lower Nile valley studied by epithermal neutron activation analysis. J. Afr. Earth Sci. 2015, 107, 57–64. [Google Scholar] [CrossRef]
- Bratley, K.H.; Woodcock, C.E. Estimating the expansion and reduction of agricultural extent in Egypt using Landsat time series. Int. J. Appl. Earth Obs. 2024, 133, 104141. [Google Scholar] [CrossRef]
- Fritz, S.; See, L.; McCallum, I.; You, L.; Bun, A.; Moltchanova, E.; Duerauer, M.; Albrecht, F.; Schill, C.; Perger, C.; et al. Mapping global cropland and field size. Glob. Change Biol. 2015, 21, 1980–1992. [Google Scholar] [CrossRef] [PubMed]
- Badawy, W.; Frontasyeva, M.V.; Ibrahim, M. Vertical Distribution of Major and Trace Elements in a Soil Profile from the Nile Delta, Egypt. Ecol. Chem. Eng. S 2020, 27, 281–294. [Google Scholar] [CrossRef]
- Stanley, D.J. Nile delta: Extreme case of sediment entrapment on a delta plain and consequent coastal land loss. Mar. Geol. 1996, 129, 189–195. [Google Scholar] [CrossRef]
- Badawy, W.M.; Ghanim, E.H.; Duliu, O.G.; El Samman, H.; Frontasyeva, M.V. Major and trace element distribution in soil and sediments from the Egyptian central Nile Valley. J. Afr. Earth Sci. 2017, 131, 53–61. [Google Scholar] [CrossRef]
- Puthusseri, R.M.; Nair, H.P.; Johny, T.K.; Bhat, S.G. Insights into the response of mangrove sediment microbiomes to heavy metal pollution: Ecological risk assessment and metagenomics perspectives. J. Environ. Manag. 2021, 298, 113492. [Google Scholar] [CrossRef] [PubMed]
- Arbuzov, S.I.; Chekryzhov, I.Y.; Verkhoturov, A.A.; Spears, D.A.; Melkiy, V.A.; Zarubina, N.V.; Blokhin, M.G. Geochemistry and rare-metal potential of coals of the Sakhalin coal basin, Sakhalin island, Russia. Int. J. Coal Geol. 2023, 268, 104197. [Google Scholar] [CrossRef]
- IAEA. Soil Sampling for Environmental Contaminants; International Atomic Energy Agency: Vienna, Austria, 2004. [Google Scholar]
- EGSMA. Geologic Map of Um Safi Area; EGSMA: Cairo, Egypt, 1989. [Google Scholar]
- NSAM, N.-A.M. Determination of Element Composition of Rocks, Soils, Grounds, and Sediments by ICP-AE and ICP-MS Methods. All-Russian Scientific-Research Institute Of Mineral Resources named after N.M. Fedorovsky: Moscow, Russia, 2015. [Google Scholar]
- Badawy, W.M.; Dmitriev, A.Y.; El Samman, H.; El-Taher, A.; Blokhin, M.G.; Rammah, Y.S.; Madkour, H.A.; Salama, S.; Budnitskiy, S.Y. Elemental composition and metal pollution in Egyptian Red Sea mangrove sediments: Characterization and origin. Mar. Pollut. Bull. 2024, 198, 115830. [Google Scholar] [CrossRef]
- Josso, P.; Rushton, J.; Lusty, P.; Matthews, A.; Chenery, S.; Holwell, D.; Kemp, S.J.; Murton, B. Late Cretaceous and Cenozoic paleoceanography from north-east Atlantic ferromanganese crust microstratigraphy. Mar. Geol. 2020, 422, 106122. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing, 4.2.1; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- van Rossum, G. Python Tutorial, Technical Report CS-R9526, Centrum voor Wiskunde en Informatica (CWI), 3.10; Python Software Foundation: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Filzmoser, P.; Hron, K. Outlier Detection for Compositional Data Using Robust Methods. Math. Geosci. 2008, 40, 233–248. [Google Scholar] [CrossRef]
- Filzmoser, P.; Hron, K.; Reimann, C. Principal component analysis for compositional data with outliers. Environmetrics 2009, 20, 621–632. [Google Scholar] [CrossRef]
- Lê, S.; Josse, J.; Husson, F. FactoMineR: An R package for multivariate analysis. J. Stat. Softw. 2008, 25, 18. [Google Scholar] [CrossRef]
- Van Der Maaten, L. Accelerating t-SNE using Tree-Based Algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- Keim, D.A.; Kohlhammer, J.; Ellis, G.P.; Mansmann, F. Mastering the Information Age—Solving Problems with Visual Analytics; Eurographics Association: Eindhoven, The Netherlands, 2010. [Google Scholar]
- Badawy, W.; Silachyov, I.; Dmitriev, A.; Lennik, S.; Saleh, G.; Mitwalli, M.; El-Farrash, A.; Sallah, M. Elemental distribution patterns in rock samples from Egypt using neutron activation and complementary X-ray fluorescence analyses. Appl. Radiat. Isot. 2023, 202, 111063. [Google Scholar] [CrossRef]
- Hinton, G.; Roweis, S. Stochastic Neighbor Embedding. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2003; Volume 15, pp. 857–864. [Google Scholar]
- Baxter, M.J. Exploratory Multivariate Analysis in Archaeology; Percheron Press, a division of Eliot Werner Publications, Inc.: Clinton Corners, NY, USA, 2015. [Google Scholar]
- Carlson, D.L. Quantitative Methods in Archaeology Using R; University of Cambridge: Cambridge, UK, 2017. [Google Scholar]
- Badawy, W.M.; Dmitriev, A.Y.; Koval, V.Y.; Smirnova, V.S.; Chepurchenko, O.E.; Lobachev, V.V.; Belova, M.O.; Galushko, A.M. Formation of reference groups for archaeological pottery using neutron activation and multivariate statistical analyses. Archaeometry 2022, 64, 1377–1393. [Google Scholar] [CrossRef]
- Müllner, D. Modern hierarchical, agglomerative clustering algorithms. arXiv 2011. [CrossRef]
- Bar-Joseph, Z.; Gifford, D.K.; Jaakkola, T.S. Fast optimal leaf ordering for hierarchical clustering. Bioinformatics 2001, 17, S22–S29. [Google Scholar] [CrossRef] [PubMed]
- Badawy, W.; Elsenbawy, A.; Dmitriev, A.; El Samman, H.; Shcheglov, A.; El-Gamal, A.; Kamel, N.H.M.; Mekewi, M. Characterization of major and trace elements in coastal sediments along the Egyptian Mediterranean Sea. Mar. Pollut. Bull. 2022, 177, 113526. [Google Scholar] [CrossRef] [PubMed]
- Badawy, W.M.; Duliu, O.G.; El Samman, H.; El-Taher, A.; Frontasyeva, M.V. A review of major and trace elements in Nile River and Western Red Sea sediments: An approach of geochemistry, pollution, and associated hazards. Appl. Radiat. Isot. 2021, 170, 109595. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Lunn, D.J.; Spiegelhalter, D.J.; Thomas, A.; Best, N. The BUGS project: Evolution, critique and future directions. Stat. Med. 2009, 28, 3049–3067. [Google Scholar] [CrossRef]
- Plummer, M. JAGS: A Program for Analysis of Bayesian Graphical Models Using Gibbs Sampling. In Proceedings of the Third International Workshop on ‘Distributed Statistical Computing’ (DSC 2003), Vienna, Austria, 20–22 March 2003; Technische Universität Wien: Vienna, Austria, 2003. [Google Scholar]
- Kruschke, J.K. Bayesian estimation supersedes the t test. J. Exp. Psychol. Gen. 2013, 142, 573–603. [Google Scholar] [CrossRef]
- Park, J.H.; Quinn, K.; Martin, A. MCMCpack: Markov chain Monte Carlo in R. J. Stat. Softw. 2011, 42, 1–21. [Google Scholar] [CrossRef]
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. Output Analysis and Diagnostics for MCMC (CODA). R News 2006, 6, 7–11. [Google Scholar]
- Kamanina, I.Z.; Badawy, W.M.; Kaplina, S.P.; Makarov, O.A.; Mamikhin, S.V. Assessment of Soil Potentially Toxic Metal Pollution in Kolchugino Town, Russia: Characteristics and Pollution. Land 2023, 12, 439. [Google Scholar] [CrossRef]
- Abrahim, G.M.S.; Parker, R.J. Assessment of heavy metal enrichment factors and the degree of contamination in marine sediments from Tamaki Estuary, Auckland, New Zealand. Environ. Monit. Assess. 2008, 136, 227–238. [Google Scholar] [CrossRef]
- Lv, J.; Liu, Y.; Zhang, Z.; Zhou, R.; Zhu, Y. Distinguishing anthropogenic and natural sources of trace elements in soils undergoing recent 10-year rapid urbanization: A case of Donggang, Eastern China. Environ. Sci. Pollut. Res. 2015, 22, 10539–10550. [Google Scholar] [CrossRef] [PubMed]
- Reimann, C.; de Caritat, P. Distinguishing between natural and anthropogenic sources for elements in the environment: Regional geochemical surveys versus enrichment factors. Sci. Total Environ. 2005, 337, 91–107. [Google Scholar] [CrossRef] [PubMed]
- Ergin, M.; Saydam, C.; Baştürk, Ö.; Erdem, E.; Yörük, R. Heavy metal concentrations in surface sediments from the two coastal inlets (Golden Horn Estuary and İzmit Bay) of the northeastern Sea of Marmara. Chem. Geol. 1991, 91, 269–285. [Google Scholar] [CrossRef]
- Chen, C.W.; Kao, C.M.; Chen, C.F.; Di Dong, C. Distribution and accumulation of heavy metals in the sediments of Kaohsiung Harbor, Taiwan. Chemosphere 2007, 66, 1431–1440. [Google Scholar] [CrossRef]
- Varol, M. Assessment of heavy metal contamination in sediments of the Tigris River (Turkey) using pollution indices and multivariate statistical techniques. J. Hazard. Mater. 2011, 195, 355–364. [Google Scholar] [CrossRef]
- Andreev, D.N.; Dzyuba, E.A. Total soil heavy metal contamination in various biotops at the territory of Vishersky reserve. Gen. Biol. 2016, 64, 5. [Google Scholar]
- Shaykhutdinova, A.N. Assessment of the degree of contamination agricultural soils Kuzbass mobile forms of heavy metals. In Proceedings of the V International Scientific Conference Dedicated to the 85th Anniversary of the Department of Soil Science and Soil Ecology of TSU, Tomsk, Russia, 10 August 2015; p. 5. [Google Scholar]
- Saet, Y.E.; Revich, B.A.; Yanin, E.P.; Smirnova, R.S.; Basharkevich, I.L.; Onishchenko, T.L.; Pavlova, L.N.; Trefilova, N.Y.; Achkasov, A.I.; Sarkisyan, S.S. Geochemistry of the Environment; Nedra: Moscow, Russia, 1990. [Google Scholar]
- Rudnick, R.L.; Gao, S. Composition of the Continental Crust. In Treatise on Geochemistry; Turekian, K.K., Ed.; Elsevier: Oxford, UK, 2014; pp. 1–51. [Google Scholar]
- Hair, J.F.; Sarstedt, M.; Pieper, T.M.; Ringle, C.M. The use of partial least squares structural equation modeling in strategic management research: A review of past practices and recommendations for future applications. Long Range Plan. 2012, 45, 320–340. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, Q.; Liu, C.; Fang, Y. Using moss to assess airborne heavy metal pollution in Taizhou, China. Int. J. Environ. Res. Public Health 2017, 14, 430. [Google Scholar] [CrossRef] [PubMed]
- Taylor, S.R.; McLennan, S.M. The Continental Crust: Its Composition and Evolution; Blackwell Scientific Publications: Oxford, UK, 1985; p. 312. [Google Scholar]
- Fowler, A.D.; Doig, R. The significance of europium anomalies in the REE spectra of granites and pegmatites, Mont Laurier, Quebec. Geochim. Cosmochim. Acta 1983, 47, 1131–1137. [Google Scholar] [CrossRef]
- Rudnick, R.L.; Gao, S. Composition of the continental crust. Treatise Geochem. 2003, 3, 1–64. [Google Scholar] [CrossRef]
- Viers, J.; Dupre, B.; Gaillardet, G. Chemical composition of suspended sediments in World Rivers: New insights from a new database. Sci. Total Environ. 2009, 407, 853–868. [Google Scholar] [CrossRef]
- Gromet, L.P.; Haskin, L.A.; Korotev, R.L.; Dymek, R.F. The “North American shale composite”: Its compilation, major and trace element characteristics. Geochim. Cosmochim. Acta 1984, 48, 2469–2482. [Google Scholar] [CrossRef]
- Bhatia, M.R.; Crook, K.A.W. Trace element characteristics of graywackes and tectonic setting discrimination of sedimentary basins. Contrib. Mineral. Petrol. 1986, 92, 181–193. [Google Scholar] [CrossRef]
- Kowalska, J.B.; Mazurek, R.; Gąsiorek, M.; Zaleski, T. Pollution indices as useful tools for the comprehensive evaluation of the degree of soil contamination–A review. Environ. Geochem. Health 2018, 40, 2395–2420. [Google Scholar] [CrossRef] [PubMed]
- Ranjbarzadeh, R.; Caputo, A.; Tirkolaee, E.B.; Jafarzadeh Ghoushchi, S.; Bendechache, M. Brain tumor segmentation of MRI images: A comprehensive review on the application of artificial intelligence tools. Comput. Biol. Med. 2023, 152, 106405. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, F. Hierarchical Clustering. In Introduction to HPC with MPI for Data Science; Nielsen, F., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 195–211. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
| Element | Mean ± SE | Median ± MAD * | Min–Max | CV% | Skewness | Kurtosis | W-Static | p-Value | UCC | Element | Mean ± SE | Median ± MAD * | Min–Max | CV% | Skewness | Kurtosis | W-Static | p-Value | UCC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Li | 14.1 ± 0.407 | 13.7 ± 1.6 | 7–23.8 | 20.3 | 0.527 | 1.91 | 0.961 | 0.101 | 24 | Cd | 0.237 ± 0.008 | 0.2 ± 0 | 0.2–0.4 | 22.3 | 0.974 | −0.197 | 0.645 | 0.000 | 0.09 |
| Be | 1.32 ± 0.033 | 1.3 ± 0.1 | 0.7–1.7 | 17.4 | −0.516 | −0.054 | 0.957 | 0.074 | 2.1 | Sn | 3.12 ± 0.132 | 3 ± 0.4 | 1.5–7.2 | 29.7 | 2.28 | 7.82 | 0.787 | 0.000 | 2.1 |
| Na | 7850 ± 172 | 7980 ± 707 | 4260–10,500 | 15.4 | −0.504 | 0.817 | 0.973 | 0.317 | 24,258.57 | Sb | 0.396 ± 0.021 | 0.4 ± 0.1 | 0.2–1 | 37.5 | 2 | 6.07 | 0.775 | 0.000 | 0.4 |
| Mg | 17,700 ± 291 | 18,000 ± 1280 | 13,300–24,100 | 11.5 | −0.007 | 0.923 | 0.95 | 0.036 | 14,953.85 | Cs | 1.23 ± 0.031 | 1.2 ± 0.1 | 0.6–1.7 | 17.9 | −0.374 | 0.451 | 0.969 | 0.222 | 4.9 |
| Al | 74,100 ± 1650 | 77,200 ± 5610 | 38,000–91,200 | 15.6 | −1.14 | 0.852 | 0.902 | 0.001 | 81,510.71 | Ba | 365 ± 8.11 | 379 ± 37.7 | 223–453 | 15.5 | −0.644 | −0.119 | 0.957 | 0.070 | 628 |
| Si | 245,000 ± 2640 | 241,000 ± 10,100 | 221,000–309,000 | 7.56 | 1.61 | 3.11 | 0.857 | 0.000 | 311,405.14 | La | 27.6 ± 0.635 | 28.9 ± 3 | 18.1–34.7 | 16.1 | −0.452 | −0.765 | 0.949 | 0.034 | 31 |
| P | 1260 ± 61 | 1160 ± 169 | 707–3280 | 33.8 | 2.42 | 8.58 | 0.795 | 0.000 | 654.57 | Ce | 62.4 ± 1.29 | 63.8 ± 5.5 | 40.8–78.8 | 14.4 | −0.399 | −0.393 | 0.971 | 0.262 | 63 |
| K | 9840 ± 177 | 9760 ± 888 | 7840–12,700 | 12.6 | 0.46 | −0.455 | 0.968 | 0.195 | 23,244.16 | Pr | 6.62 ± 0.138 | 6.8 ± 0.6 | 4.3–8.1 | 14.6 | −0.495 | −0.349 | 0.958 | 0.077 | 7.1 |
| Ca | 40,000 ± 1860 | 35,700 ± 4020 | 24,200–80,100 | 32.7 | 1.75 | 2.45 | 0.781 | 0.000 | 25,657.49 | Nd | 30.2 ± 0.677 | 31.2 ± 3.3 | 19.5–38.8 | 15.7 | −0.372 | −0.371 | 0.97 | 0.240 | 27 |
| Sc | 20.7 ± 0.572 | 21.8 ± 2.2 | 10.8–26.7 | 19.3 | −0.926 | 0.235 | 0.915 | 0.002 | 14 | Sm | 6.46 ± 0.149 | 6.6 ± 0.6 | 4.1–8.2 | 16.2 | −0.427 | −0.303 | 0.961 | 0.101 | 4.7 |
| Ti | 9460 ± 273 | 9570 ± 1160 | 4390–12,300 | 20.2 | −0.812 | 0.272 | 0.935 | 0.009 | 3835.79 | Eu | 1.71 ± 0.04 | 1.8 ± 0.2 | 1.1–2.2 | 16.5 | −0.445 | −0.278 | 0.956 | 0.063 | 1 |
| V | 157 ± 3.72 | 164 ± 11.8 | 83.9–200 | 16.6 | −1.16 | 0.772 | 0.89 | 0.000 | 97 | Gd | 6.01 ± 0.137 | 6.2 ± 0.6 | 3.8–7.6 | 16 | −0.426 | −0.408 | 0.964 | 0.132 | 4 |
| Cr | 116 ± 2.11 | 120 ± 7 | 70.7–135 | 12.7 | −1.34 | 1.39 | 0.867 | 0.000 | 92 | Tb | 0.857 ± 0.02 | 0.9 ± 0.1 | 0.6–1.1 | 16 | −0.372 | −0.433 | 0.917 | 0.002 | 0.7 |
| Mn | 1040 ± 26.4 | 1060 ± 112 | 536–1500 | 17.8 | −0.351 | 0.343 | 0.979 | 0.538 | 774.46 | Dy | 4.96 ± 0.117 | 5.1 ± 0.5 | 3.1–6.4 | 16.5 | −0.434 | −0.371 | 0.962 | 0.111 | 3.9 |
| Fe | 63,300 ± 1490 | 65,900 ± 5850 | 36,300–77,700 | 16.4 | −0.987 | 0.255 | 0.908 | 0.001 | 39,175.06 | Ho | 0.896 ± 0.02 | 0.9 ± 0.1 | 0.6–1.2 | 15.6 | −0.342 | −0.057 | 0.935 | 0.009 | 0.83 |
| Co | 22.3 ± 0.619 | 23 ± 2.6 | 11.6–28.8 | 19.4 | −0.638 | −0.024 | 0.949 | 0.032 | 17.3 | Er | 2.39 ± 0.059 | 2.4 ± 0.3 | 1.5–3.1 | 17.2 | −0.392 | −0.457 | 0.965 | 0.154 | 2.3 |
| Ni | 75.5 ± 2.16 | 79.4 ± 5.9 | 39.1–116 | 20 | −0.602 | 0.836 | 0.921 | 0.003 | 47 | Tm | 0.359 ± 0.01 | 0.4 ± 0 | 0.2–0.5 | 18.8 | −0.956 | 0.296 | 0.732 | 0.000 | 0.3 |
| Cu | 62.3 ± 1.48 | 62.9 ± 3.7 | 32.3–82.5 | 16.6 | −0.851 | 1.37 | 0.916 | 0.002 | 28 | Yb | 2.58 ± 0.059 | 2.6 ± 0.3 | 1.7–3.3 | 16 | −0.313 | −0.468 | 0.959 | 0.082 | 1.96 |
| Zn | 93.8 ± 2.08 | 91.8 ± 6.3 | 53.1–123 | 15.5 | −0.259 | 0.622 | 0.958 | 0.077 | 67 | Lu | 0.367 ± 0.008 | 0.4 ± 0 | 0.2–0.5 | 16.1 | −1 | 0.801 | 0.701 | 0.000 | 0.31 |
| Ga | 15.6 ± 0.439 | 15.8 ± 2.1 | 7.4–20.8 | 19.7 | −0.548 | −0.069 | 0.967 | 0.184 | 17.5 | Hf | 4.65 ± 0.144 | 4.7 ± 0.7 | 2.2–6.6 | 21.6 | −0.175 | −0.452 | 0.984 | 0.751 | 5.3 |
| Ge | 1.33 ± 0.032 | 1.3 ± 0.1 | 0.7–1.9 | 17.1 | 0.023 | 0.589 | 0.965 | 0.155 | 1.4 | Ta | 1.11 ± 0.036 | 1.1 ± 0.2 | 0.6–1.6 | 22.4 | −0.108 | −0.685 | 0.966 | 0.170 | 0.9 |
| As | 2.99 ± 0.103 | 2.9 ± 0.3 | 2.1–7.1 | 24.2 | 3.75 | 19.4 | 0.651 | 0.000 | 4.8 | W | 0.68 ± 0.025 | 0.6 ± 0.1 | 0.4–1.3 | 25.5 | 0.975 | 1.95 | 0.911 | 0.001 | 1.9 |
| Rb | 33.7 ± 0.7 | 33.9 ± 3.4 | 20.5–43.7 | 14.5 | −0.188 | −0.009 | 0.99 | 0.955 | 84 | Tl | 0.186 ± 0.005 | 0.2 ± 0 | 0.1–0.2 | 19 | −2.04 | 2.17 | 0.417 | 0.000 | 0.9 |
| Sr | 261 ± 10.9 | 240 ± 16.8 | 171–594 | 29.2 | 2.57 | 7.18 | 0.695 | 0.000 | 320 | Pb | 14.1 ± 0.766 | 12.7 ± 2.6 | 8.3–35.6 | 37.9 | 1.86 | 4.1 | 0.822 | 0.000 | 17 |
| Y | 22.6 ± 0.565 | 22.9 ± 2.8 | 14.3–29.3 | 17.5 | −0.296 | −0.581 | 0.965 | 0.151 | 21 | Bi | 0.112 ± 0.006 | 0.1 ± 0 | 0.1–0.3 | 34.7 | 3.3 | 10.7 | 0.354 | 0.000 | 0.16 |
| Zr | 161 ± 4.99 | 164 ± 21.3 | 76.8–226 | 21.7 | −0.112 | −0.488 | 0.978 | 0.466 | 193 | Th | 4.91 ± 0.106 | 5 ± 0.5 | 2.7–6.5 | 15.1 | −0.484 | 0.29 | 0.978 | 0.468 | 10.5 |
| Nb | 17.5 ± 0.669 | 16.9 ± 3.3 | 8.3–26.3 | 26.7 | 0.095 | −0.848 | 0.972 | 0.290 | 12 | U | 1.31 ± 0.025 | 1.3 ± 0.1 | 0.9–1.7 | 13.3 | 0.074 | −0.352 | 0.962 | 0.113 | 2.7 |
| Mo | 0.724 ± 0.024 | 0.7 ± 0.1 | 0.4–1 | 22.8 | −0.089 | −0.68 | 0.95 | 0.036 | 1.1 |
| Element | µ ± σ with Outliers | µ ± σ Without Outliers | UCC | Element | µ ± σ with Outliers | µ ± σ Without Outliers | UCC |
|---|---|---|---|---|---|---|---|
| Li | 13.3 ± 4 | 14.1 ± 2.9 | 24 | Cd | 0.2 ± 0.1 | 0.2 ± 0.1 | 0.09 |
| Be | 1.2 ± 0.3 | 1.3 ± 0.2 | 2.1 | Sn | 2.9 ± 1.1 | 3.1 ± 1 | 2.1 |
| Na | 7664.5 ± 1607.7 | 7851.2 ± 1237.4 | 24,258.57 | Sb | 0.4 ± 0.2 | 0.4 ± 0.2 | 0.4 |
| Mg | 16,807.2 ± 3785.8 | 17,679.9 ± 2094.1 | 14,953.85 | Cs | 1.2 ± 0.3 | 1.2 ± 0.2 | 4.9 |
| Al | 70,235.1 ± 17,993.7 | 74,059.1 ± 11,849.1 | 81,510.71 | Ba | 353.4 ± 74.5 | 365.5 ± 58.3 | 628 |
| Si | 25,5903.7 ± 44,770.4 | 244,630 ± 18,993.4 | 311,405.14 | La | 26.3 ± 6.4 | 27.6 ± 4.6 | 31 |
| P | 1211.5 ± 462.7 | 1263.4 ± 438.8 | 654.57 | Ce | 59.5 ± 14 | 62.4 ± 9.3 | 63 |
| K | 9561.1 ± 1754.8 | 9837.9 ± 1276.5 | 23,244.16 | Pr | 6.3 ± 1.5 | 6.6 ± 1 | 7.1 |
| Ca | 38,189 ± 14,395.4 | 39,952.4 ± 13,406.1 | 25,657.49 | Nd | 28.8 ± 6.9 | 30.2 ± 4.9 | 27 |
| Sc | 19.6 ± 5.6 | 20.7 ± 4.1 | 14 | Sm | 6.1 ± 1.5 | 6.5 ± 1.1 | 4.7 |
| Ti | 8998.2 ± 2561 | 9463.1 ± 1960.8 | 3835.79 | Eu | 1.6 ± 0.4 | 1.7 ± 0.3 | 1 |
| V | 148.2 ± 41.1 | 157 ± 26.8 | 97 | Gd | 5.7 ± 1.4 | 6 ± 1 | 4 |
| Cr | 111.6 ± 22.9 | 116.2 ± 15.1 | 92 | Tb | 0.8 ± 0.2 | 0.9 ± 0.1 | 0.7 |
| Mn | 988.3 ± 262.2 | 1039.9 ± 190 | 774.46 | Dy | 4.7 ± 1.2 | 5 ± 0.8 | 3.9 |
| Fe | 59,670.8 ± 16,718.8 | 63,318.3 ± 10,687.5 | 39,175.06 | Ho | 0.9 ± 0.2 | 0.9 ± 0.1 | 0.83 |
| Co | 21 ± 6.4 | 22.3 ± 4.5 | 17.3 | Er | 2.3 ± 0.6 | 2.4 ± 0.4 | 2.3 |
| Ni | 71 ± 22.2 | 75.5 ± 15.5 | 47 | Tm | 0.3 ± 0.1 | 0.4 ± 0.1 | 0.3 |
| Cu | 59.1 ± 15.8 | 62.3 ± 10.7 | 28 | Yb | 2.5 ± 0.6 | 2.6 ± 0.4 | 1.96 |
| Zn | 88.8 ± 23 | 93.8 ± 15 | 67 | Lu | 0.3 ± 0.1 | 0.4 ± 0.1 | 0.31 |
| Ga | 14.7 ± 4.4 | 15.6 ± 3.2 | 17.5 | Hf | 4.4 ± 1.4 | 4.6 ± 1 | 5.3 |
| Ge | 1.3 ± 0.3 | 1.3 ± 0.2 | 1.4 | Ta | 1.1 ± 0.3 | 1.1 ± 0.3 | 0.9 |
| As | 2.8 ± 0.9 | 3 ± 0.7 | 4.8 | W | 0.6 ± 0.2 | 0.7 ± 0.2 | 1.9 |
| Rb | 32.1 ± 7.7 | 33.7 ± 5 | 84 | Tl | 0.2 ± 0 | 0.2 ± 0 | 0.9 |
| Sr | 251.6 ± 84.2 | 261.4 ± 78.5 | 320 | Pb | 13.5 ± 5.8 | 14.1 ± 5.5 | 17 |
| Y | 21.5 ± 5.7 | 22.6 ± 4.1 | 21 | Bi | 0.1 ± 0 | 0.1 ± 0 | 0.16 |
| Zr | 151.8 ± 48.5 | 161.2 ± 35.8 | 193 | Th | 4.7 ± 1.1 | 4.9 ± 0.8 | 10.5 |
| Nb | 16.5 ± 5.9 | 17.5 ± 4.8 | 12 | U | 1.2 ± 0.3 | 1.3 ± 0.2 | 2.7 |
| Mo | 0.7 ± 0.2 | 0.7 ± 0.2 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badawy, W.M.; El-Agawany, F.I.; Blokhin, M.G.; Mohamed, E.S.; Uzhinskiy, A.; Morsi, T.M. Multivariate and Machine Learning-Based Assessment of Soil Elemental Composition and Pollution Analysis. Environments 2025, 12, 289. https://doi.org/10.3390/environments12080289
Badawy WM, El-Agawany FI, Blokhin MG, Mohamed ES, Uzhinskiy A, Morsi TM. Multivariate and Machine Learning-Based Assessment of Soil Elemental Composition and Pollution Analysis. Environments. 2025; 12(8):289. https://doi.org/10.3390/environments12080289
Chicago/Turabian StyleBadawy, Wael M., Fouad I. El-Agawany, Maksim G. Blokhin, Elsayed S. Mohamed, Alexander Uzhinskiy, and Tarek M. Morsi. 2025. "Multivariate and Machine Learning-Based Assessment of Soil Elemental Composition and Pollution Analysis" Environments 12, no. 8: 289. https://doi.org/10.3390/environments12080289
APA StyleBadawy, W. M., El-Agawany, F. I., Blokhin, M. G., Mohamed, E. S., Uzhinskiy, A., & Morsi, T. M. (2025). Multivariate and Machine Learning-Based Assessment of Soil Elemental Composition and Pollution Analysis. Environments, 12(8), 289. https://doi.org/10.3390/environments12080289








