Integrating Wastewater-Based Epidemiology and Mobility Data to Predict SARS-CoV-2 Cases
Abstract
1. Introduction
2. Methods
2.1. Case Study Selection
2.2. Epidemiological Data
2.3. Viral Wastewater Data
2.4. Mobility Data
2.5. Statistical Analysis
2.6. Rolling Forecast Cross-Validation
2.7. Modeling Strategy
3. Time Series Preprocessing
4. Results
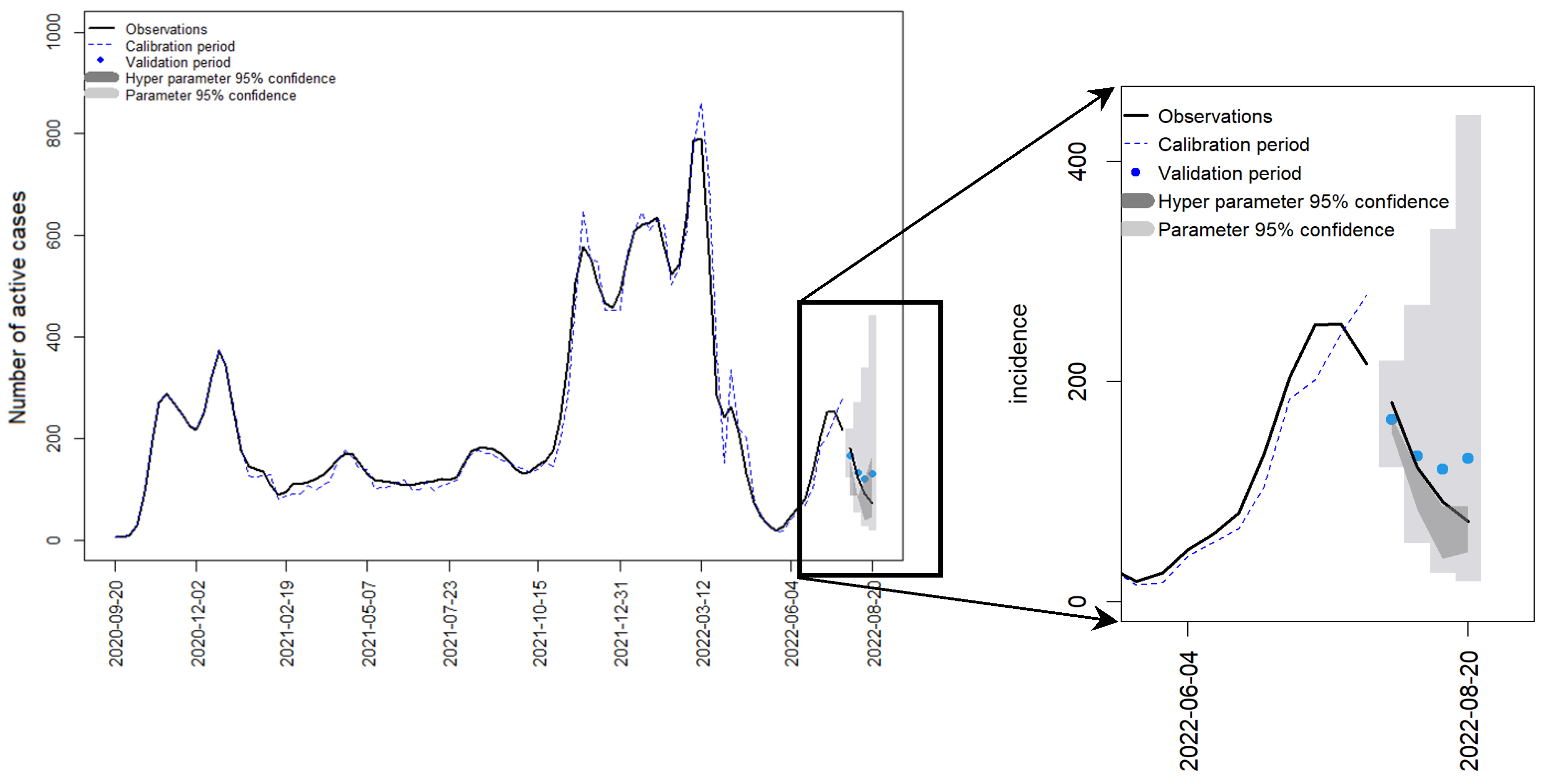
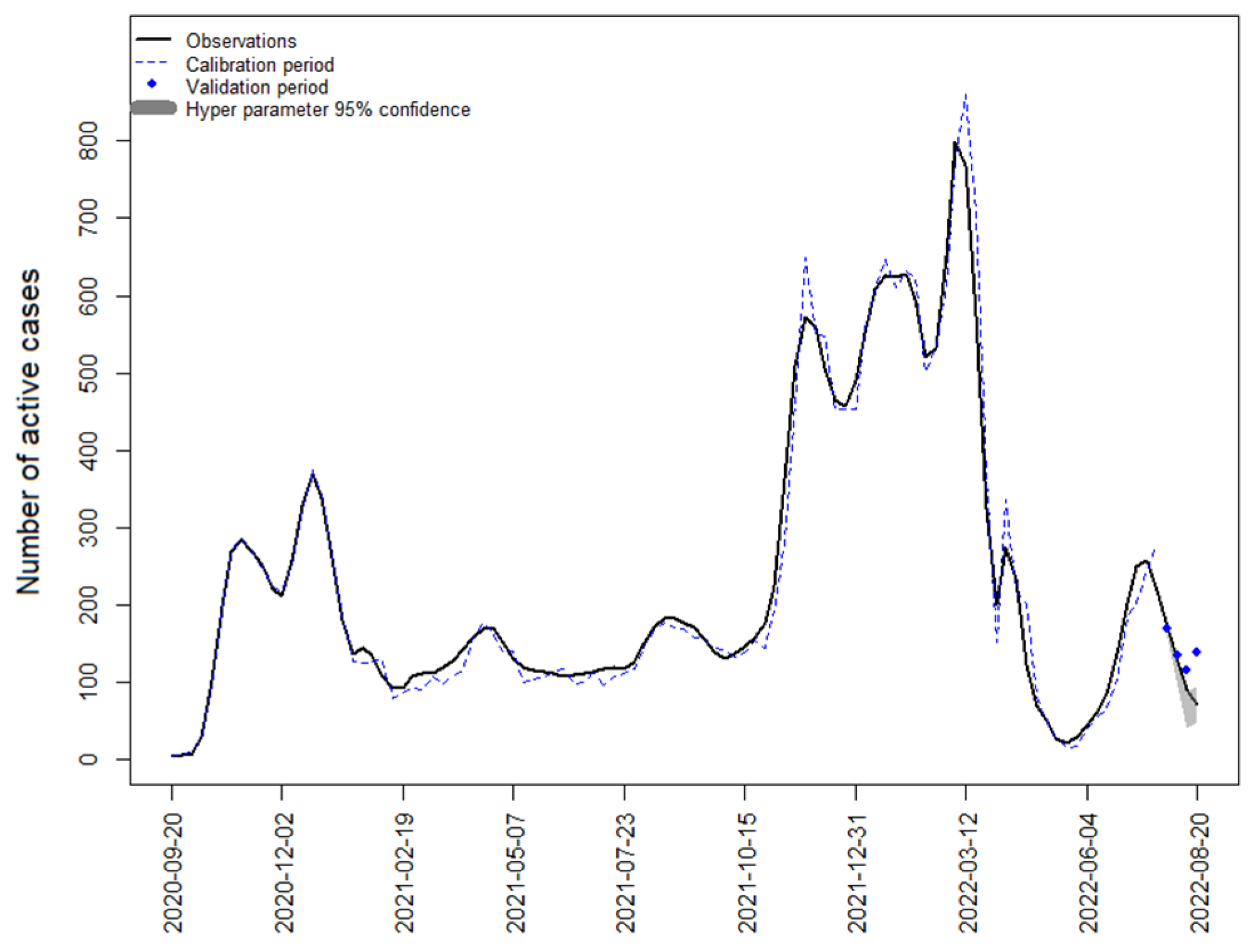
4.1. Strategy 1: SARIMA Model with Active Cases
4.2. Strategy 2: SARIMAX Model with WBE Data
4.3. Strategy 3: SARIMAX Model with Mobility Data
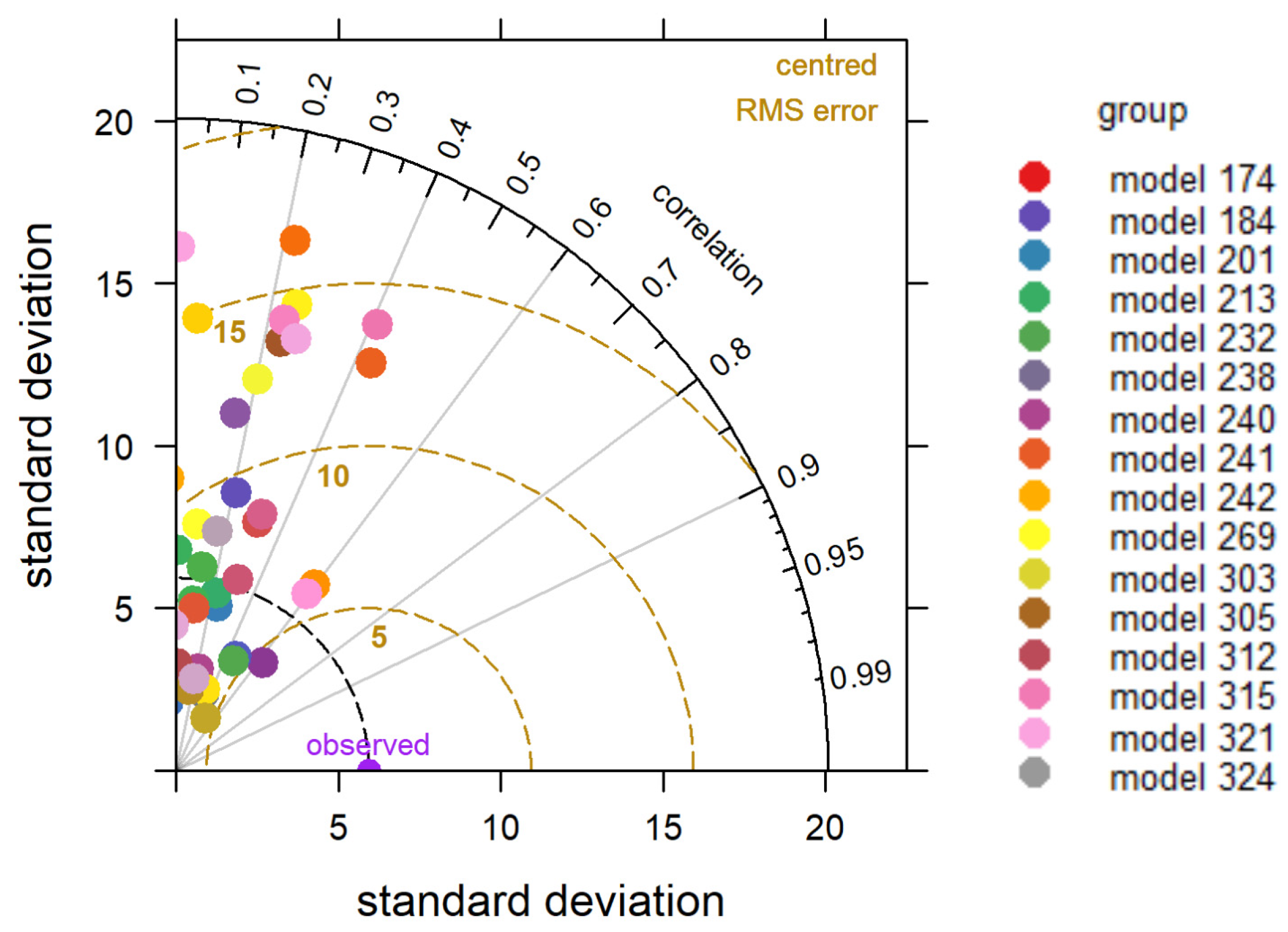
4.4. Sensitivity Analysis of WBE and Mobility Data
4.5. Austrian Data
5. Conclusions
- The optimal model fitness for predicting the number of COVID-19 cases was reached by employing SARIMAX models with either WBE or Google mobility data as exogenous factors, forecasting up to four weeks.
- Transit mobility data and WBE data demonstrated similar capabilities in predicting active cases.
- When the WBE data and mobility data were integrated into forecast models, they served as supplementary information to aid decision makers taking significant and appropriate restriction policies. The forecast accuracy was a function of finetuning the model parameters and the choice of exogenous variables.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shimko, K.M.; Piatkowski, T.; Thomas, K.V.; Speers, N.; Brooker, L.; Tscharke, B.J.; O’brien, J.W. Performance- and image-enhancing drug use in the community: Use prevalence, user demographics and the potential role of wastewater-based epidemiology. J. Hazard. Mater. 2021, 419, 126340. [Google Scholar] [CrossRef] [PubMed]
- Olesen, S.W.; Imakaev, M.; Duvallet, C. Making waves: Defining the lead time of wastewater-based epidemiology for COVID-19. Water Res. 2021, 202, 117433. [Google Scholar] [CrossRef] [PubMed]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [PubMed]
- Polo, D.; Quintela-Baluja, M.; Corbishley, A.; Jones, D.L.; Singer, A.C.; Graham, D.W.; Romalde, J.L. Making waves: Wastewater-based epidemiology for COVID-19—Approaches and challenges for surveillance and prediction. Water Res. 2020, 186, 116404. [Google Scholar] [CrossRef] [PubMed]
- Rauch, W.; Schenk, H.; Insam, H.; Markt, R.; Kreuzinger, N. Data modelling recipes for SARS-CoV-2 wastewater-based epidemiology. Environ. Res. 2022, 214 Pt 1, 113809. [Google Scholar] [CrossRef]
- Fenz, G.; Stix, H.; Vondra, K. Austrian tourism sector badly hit by COVID-19 pandemic. Monet. Policy Econ. 2021, 41–63. [Google Scholar]
- Kuitunen, I.; Artama, M.; Haapanen, M.; Renko, M. Rhinovirus spread in children during the COVID-19 pandemic despite social restrictions—A nationwide register study in Finland. J. Med Virol. 2021, 93, 6063–6067. [Google Scholar] [CrossRef] [PubMed]
- Aberi, P.; Arabzadeh, R.; Insam, H.; Markt, R.; Mayr, M.; Kreuzinger, N.; Rauch, W. Quest for Optimal Regression Models in SARS-CoV-2 Wastewater Based Epidemiology. Int. J. Environ. Res. Public Health 2021, 18, 10778. [Google Scholar] [CrossRef] [PubMed]
- Betancourt, W.Q.; Schmitz, B.W.; Innes, G.K.; Prasek, S.M.; Brown, K.M.P.; Stark, E.R.; Foster, A.R.; Sprissler, R.S.; Harris, D.T.; Sherchan, S.P.; et al. COVID-19 containment on a college campus via wastewater-based epidemiology, targeted clinical testing and an intervention. Sci. Total Environ. 2021, 779, 146408. [Google Scholar] [CrossRef]
- Kumar, M.; Jiang, G.; Thakur, A.K.; Chatterjee, S.; Bhattacharya, T.; Mohapatra, S.; Chaminda, T.; Tyagi, V.K.; Vithanage, M.; Bhattacharya, P.; et al. Lead time of early warning by wastewater surveillance for COVID-19: Geographical variations and impacting factors. Chem. Eng. J. 2022, 441, 135936. [Google Scholar] [CrossRef]
- Cao, Y.; Francis, R. On forecasting the community-level COVID-19 cases from the concentration of SARS-CoV-2 in wastewater. Sci. Total Environ. 2021, 786, 147451. [Google Scholar] [CrossRef] [PubMed]
- Schenk, H.; Heidinger, P.; Insam, H.; Kreuzinger, N.; Markt, R.; Nägele, F.; Oberacher, H.; Scheffknecht, C.; Steinlechner, M.; Vogl, G.; et al. Prediction of hospitalisations based on wastewater-based SARS-CoV-2 epidemiology. Sci. Total Environ. 2023, 873, 162149. [Google Scholar] [CrossRef]
- Vannoni, M.; McKee, M.; Semenza, J.C.; Bonell, C.; Stuckler, D. Using volunteered geographic information to assess mobility in the early phases of the COVID-19 pandemic: A cross-city time series analysis of 41 cities in 22 countries from March 2nd to 26th 2020. Glob. Health 2020, 16, 85. [Google Scholar] [CrossRef]
- Google, COVID-19 Community Mobility Reports. Available online: https://www.google.com/covid19/mobility/ (accessed on 15 January 2024).
- Ribeiro-Dantas, M.d.C.; Alves, G.; Gomes, R.B.; Bezerra, L.C.; Lima, L.; Silva, I. Dataset for country profile and mobility analysis in the assessment of COVID-19 pandemic. Data Brief 2020, 31, 105698. [Google Scholar] [CrossRef] [PubMed]
- Markt, R.; Endler, L.; Amman, F.; Schedl, A.; Penz, T.; Büchel-Marxer, M.; Grünbacher, D.; Mayr, M.; Peer, E.; Pedrazzini, M.; et al. Detection and abundance of SARS-CoV-2 in wastewater in Liechtenstein, and the estimation of prevalence and impact of the B.1.1.7 variant. J. Water Health 2021, 20, 114–125. [Google Scholar] [CrossRef]
- Land Tirol, Coronavirus COVID-19 Informationen. Available online: https://www.tirol.gv.at/gesundheit-vorsorge/infekt/coronavirus/ (accessed on 15 January 2024).
- Landesverwaltung Fürstentum Liechtenstein, Bevölkerung. Available online: https://www.statistikportal.li/de/themen/bevoelkerung (accessed on 16 January 2024).
- Statistics Austria, Independent Statistics for Evidence-Based Decision Making. Available online: https://www.statistik.at/en/statistics/population-and-society/population/population-stock/annual-average-population (accessed on 23 January 2024).
- Kneuer, M.; Wallaschek, S. Framing COVID-19: Public Leadership and Crisis Communication By Chancellor Angela Merkel During the Pandemic in 2020. Ger. Politics 2023, 32, 686–709. [Google Scholar] [CrossRef]
- Daleiden, B.; Niederstätter, H.; Steinlechner, M.; Wildt, S.; Kaiser, M.; Lass-Flörl, C.; Posch, W.; Fuchs, S.; Pfeifer, B.; Huber, A.; et al. Wastewater surveillance of SARS-CoV-2 in Austria: Development, implementation, and operation of the Tyrolean wastewater monitoring program. J. Water Health 2022, 20, 314–328. [Google Scholar] [CrossRef] [PubMed]
- Rasero, F.J.R.; Ruano, L.A.M.; Del Real, P.R.; Gómez, L.C.; Lorusso, N. Associations between SARS-CoV-2 RNA concentrations in wastewater and COVID-19 rates in days after sampling in small urban areas of Seville: A time series study. Sci. Total Environ. 2022, 806 Pt 1, 150573. [Google Scholar] [CrossRef]
- Cheshmehzangi, A.; Sedrez, M.; Ren, J.; Kong, D.; Shen, Y.; Bao, S.; Xu, J.; Su, Z.; Dawodu, A. The Effect of Mobility on the Spread of COVID-19 in Light of Regional Differences in the European Union. Sustainability 2021, 13, 5395. [Google Scholar] [CrossRef]
- Wellenius, G.A.; Vispute, S.; Espinosa, V.; Fabrikant, A.; Tsai, T.C.; Hennessy, J.; Dai, A.; Williams, B.; Gadepalli, K.; Boulanger, A.; et al. Impacts of social distancing policies on mobility and COVID-19 case growth in the US. Nat. Commun. 2021, 12, 3118. [Google Scholar] [CrossRef]
- Box, G.E.P. Time Series Analysis: Forecasting and Control, 5th ed.; Wiley: Hoboken, NJ, USA, 2015; Available online: https://ebookcentral.proquest.com/lib/kxp/detail.action?docID=2064681 (accessed on 23 January 2024).
- Wei, W.; Jiang, J.; Liang, H.; Gao, L.; Liang, B.; Huang, J.; Zang, N.; Liao, Y.; Yu, J.; Lai, J.; et al. Application of a Combined Model with Autoregressive Integrated Moving Average (ARIMA) and Generalized Regression Neural Network (GRNN) in Forecasting Hepatitis Incidence in Heng County, China. PLoS ONE 2016, 11, e0156768. [Google Scholar] [CrossRef] [PubMed]
- Fattah, J.; Ezzine, L.; Aman, Z.; El Moussami, H.; Lachhab, A. Forecasting of demand using ARIMA model. Int. J. Eng. Bus. Manag. 2018, 10, 1847979018808673. [Google Scholar] [CrossRef]
- Sah, S.; Surendiran, B.; Dhanalakshmi, R.; Yamin, M. Covid-19 cases prediction using SARIMAX Model by tuning hyperparameter through grid search cross-validation approach. Expert Syst. 2022, 40, e13086. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice. Available online: https://otexts.com/fpp2/ (accessed on 6 August 2020).
- Katrakazas, C.; Michelaraki, E.; Sekadakis, M.; Ziakopoulos, A.; Kontaxi, A.; Yannis, G. Identifying the impact of the COVID-19 pandemic on driving behavior using naturalistic driving data and time series forecasting. J. Saf. Res. 2021, 78, 189–202. [Google Scholar] [CrossRef] [PubMed]
- Khatun, N. Applications of Normality Test in Statistical Analysis. Open J. Stat. 2021, 11, 113–122. [Google Scholar] [CrossRef]
- Mishra, P.; Pandey, C.M.; Singh, U.; Gupta, A.; Sahu, C.; Keshri, A. Descriptive statistics and normality tests for statistical data. Ann. Card. Anaesth. 2019, 22, 67–72. [Google Scholar] [CrossRef]
- Cawood, P.; van Zyl, T. Feature-Weighted Stacking for Nonseasonal Time Series Forecasts: A Case Study of the COVID-19 Epidemic Curves: Arxiv. Available online: https://europepmc.org/article/PPR/PPR454047 (accessed on 17 January 2024).
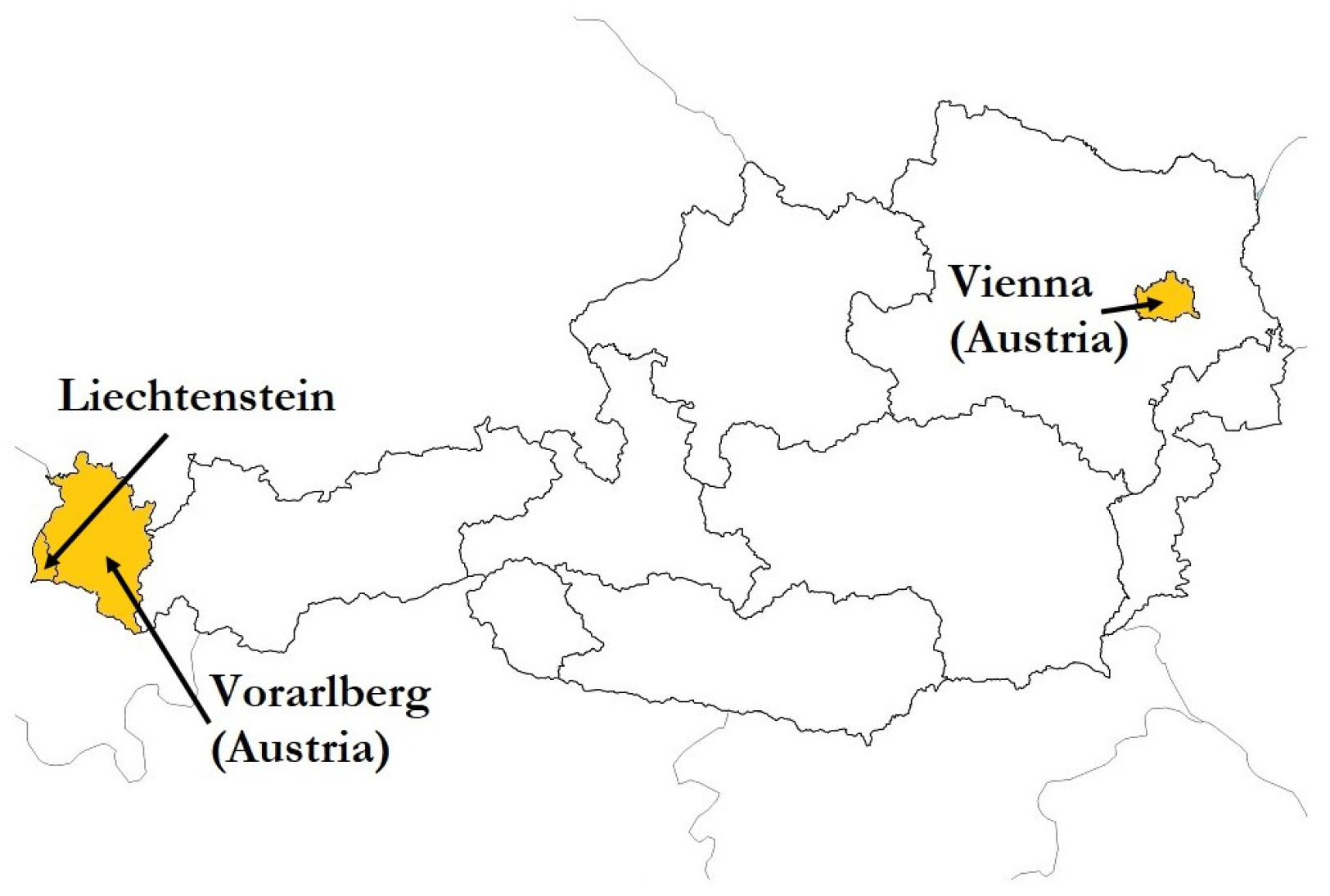




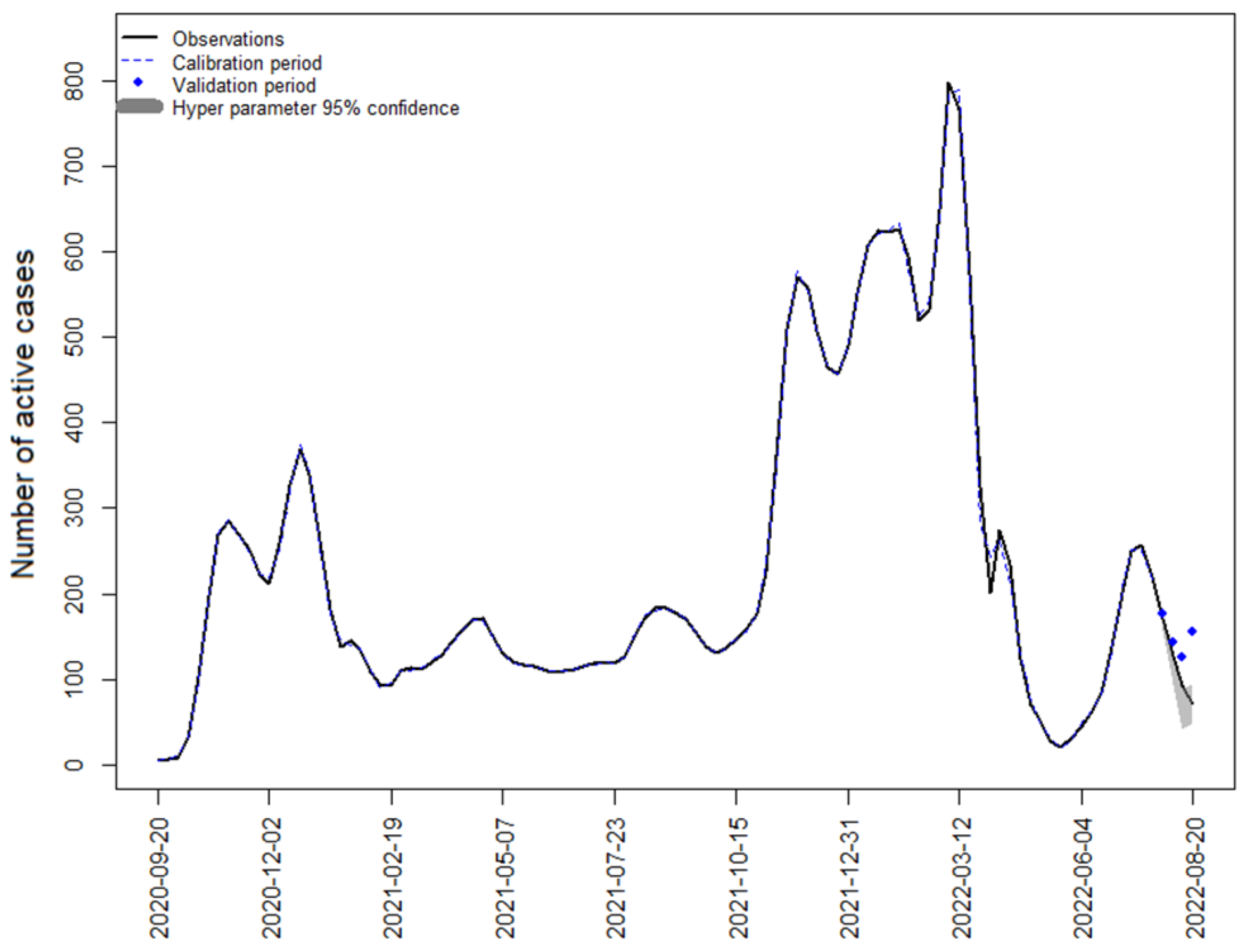
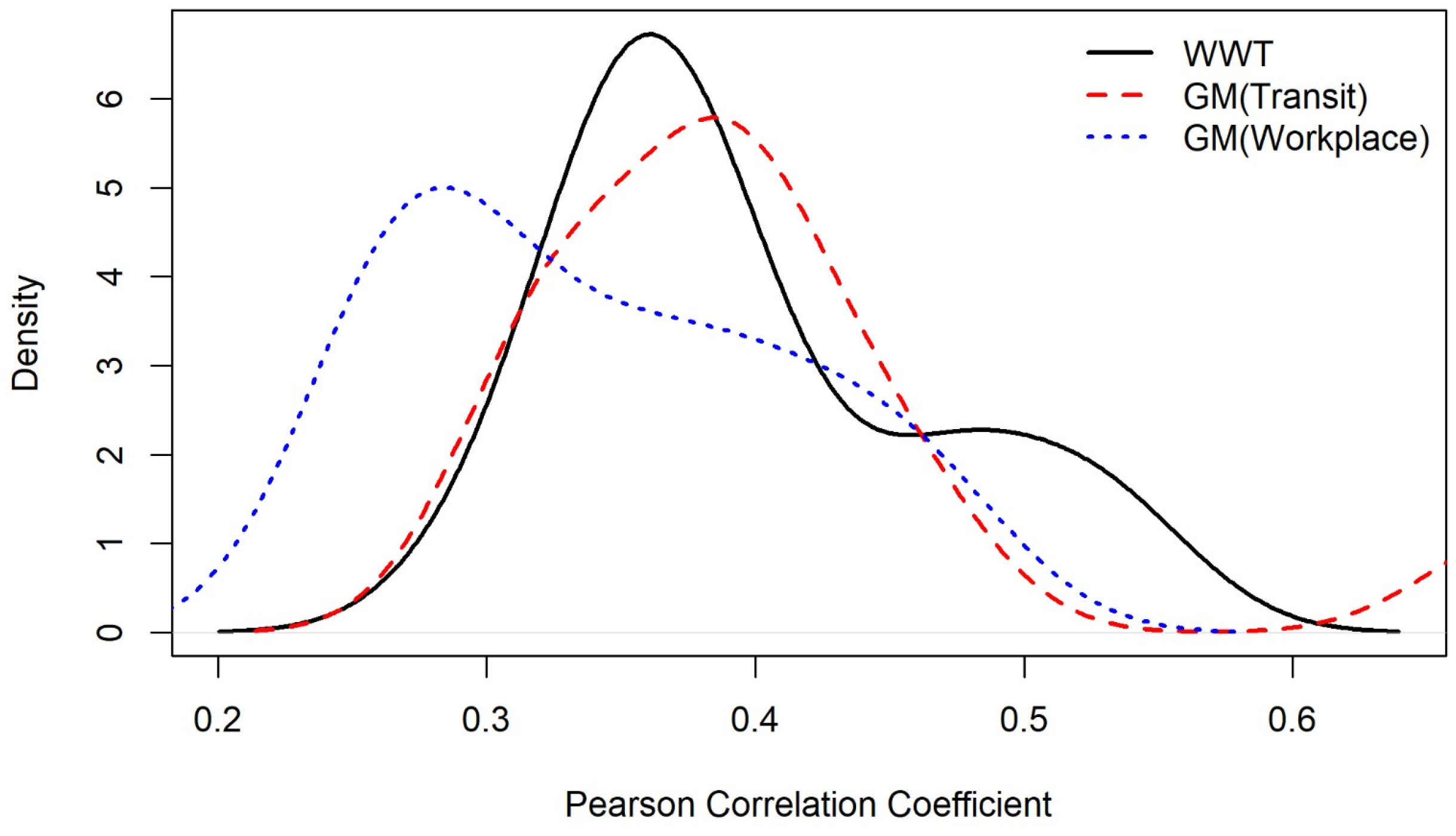
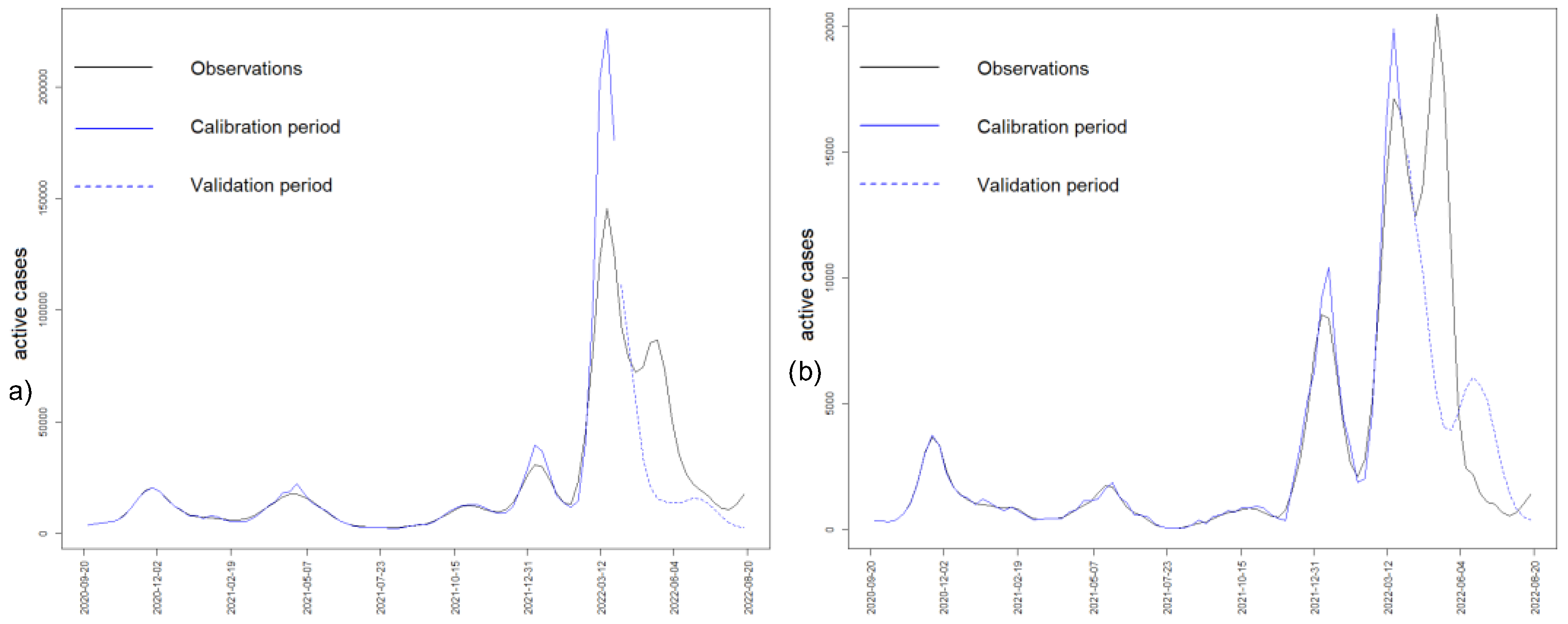
| Country | Region | Population | Area (km2) |
|---|---|---|---|
| Liechtenstein | 39,055 | 160 | |
| Austria | Vienna | 1,923,825 | 414 |
| Vorarlberg | 400,469 | 2601 |
| Strategy No. | Model | Response Variable | Exogenous Variable |
|---|---|---|---|
| 1 | SARIMA | Active cases | - |
| 2 | SARIMAX | Wastewater data | |
| 3 | Google mobility data | ||
| 4 | Sensitivity analysis * | Wastewater and Google mobility data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schenk, H.; Arabzadeh, R.; Dabiri, S.; Insam, H.; Kreuzinger, N.; Büchel-Marxer, M.; Markt, R.; Nägele, F.; Rauch, W. Integrating Wastewater-Based Epidemiology and Mobility Data to Predict SARS-CoV-2 Cases. Environments 2024, 11, 100. https://doi.org/10.3390/environments11050100
Schenk H, Arabzadeh R, Dabiri S, Insam H, Kreuzinger N, Büchel-Marxer M, Markt R, Nägele F, Rauch W. Integrating Wastewater-Based Epidemiology and Mobility Data to Predict SARS-CoV-2 Cases. Environments. 2024; 11(5):100. https://doi.org/10.3390/environments11050100
Chicago/Turabian StyleSchenk, Hannes, Rezgar Arabzadeh, Soroush Dabiri, Heribert Insam, Norbert Kreuzinger, Monika Büchel-Marxer, Rudolf Markt, Fabiana Nägele, and Wolfgang Rauch. 2024. "Integrating Wastewater-Based Epidemiology and Mobility Data to Predict SARS-CoV-2 Cases" Environments 11, no. 5: 100. https://doi.org/10.3390/environments11050100
APA StyleSchenk, H., Arabzadeh, R., Dabiri, S., Insam, H., Kreuzinger, N., Büchel-Marxer, M., Markt, R., Nägele, F., & Rauch, W. (2024). Integrating Wastewater-Based Epidemiology and Mobility Data to Predict SARS-CoV-2 Cases. Environments, 11(5), 100. https://doi.org/10.3390/environments11050100








