Simulating Agricultural Water Recycling Using the APEX Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reservoir Component Update
2.2. Irrigation Reservoir Update
2.3. Study Sites
2.4. Field Data Acquisition
2.5. Simulation Setting
- (1)
- The volume of water entering and leaving the reservoir.
- (2)
- The time the water remains in the reservoir.
- (3)
- The depth of groundwater.
| Variable | Description | Value |
|---|---|---|
| RSEE | Elevation at emergency spillway (m) | 4.5 |
| RSAE | Surface area at emergency spillway elevation (ha) | 1.0 |
| RSVE | Rainfall equivalent depth (or volume) over the surface area at emergency spillway elevation (mm) | 150 |
| RSEP | Elevation at principal spillway (m) | 4.0 |
| RSAP | Surface area at principal spillway elevation (ha) | 0.95 |
| RSVP | Rainfall equivalent depth (or volume) over the surface area at principal spillway elevation (mm) | 140 |
| RSV0 | Initial volume (mm) | 140 |
| RSRR | Average principal spillway release rate in days | 20 |
| RSYS | Initial sediment concentration (ppm) | 300 |
| RSYN | Normal sediment concentration (ppm) | 300 |
| RSHC | Bottom hydraulic conductivity (mm h−1) | 0.00001 |
| RSDP | Time required to return to normal sediment concentration after runoff event (days) | 20 |
| RSBD | Bulk density of sediment in the reservoir (Mg m−3) | 1.2 |
- No Reservoir (Baseline): Each point is simulated without the reservoir.
- No Irrigation Reservoir (noIrr-Res): The reservoir is included in the configuration, but the water in the reservoir is not used for irrigation.
- Irrigation Reservoir (Irr-Res): Adopting an irrigation reservoir is simulated.
2.6. Model Calibration and Validation
3. Results
3.1. Crop Yield
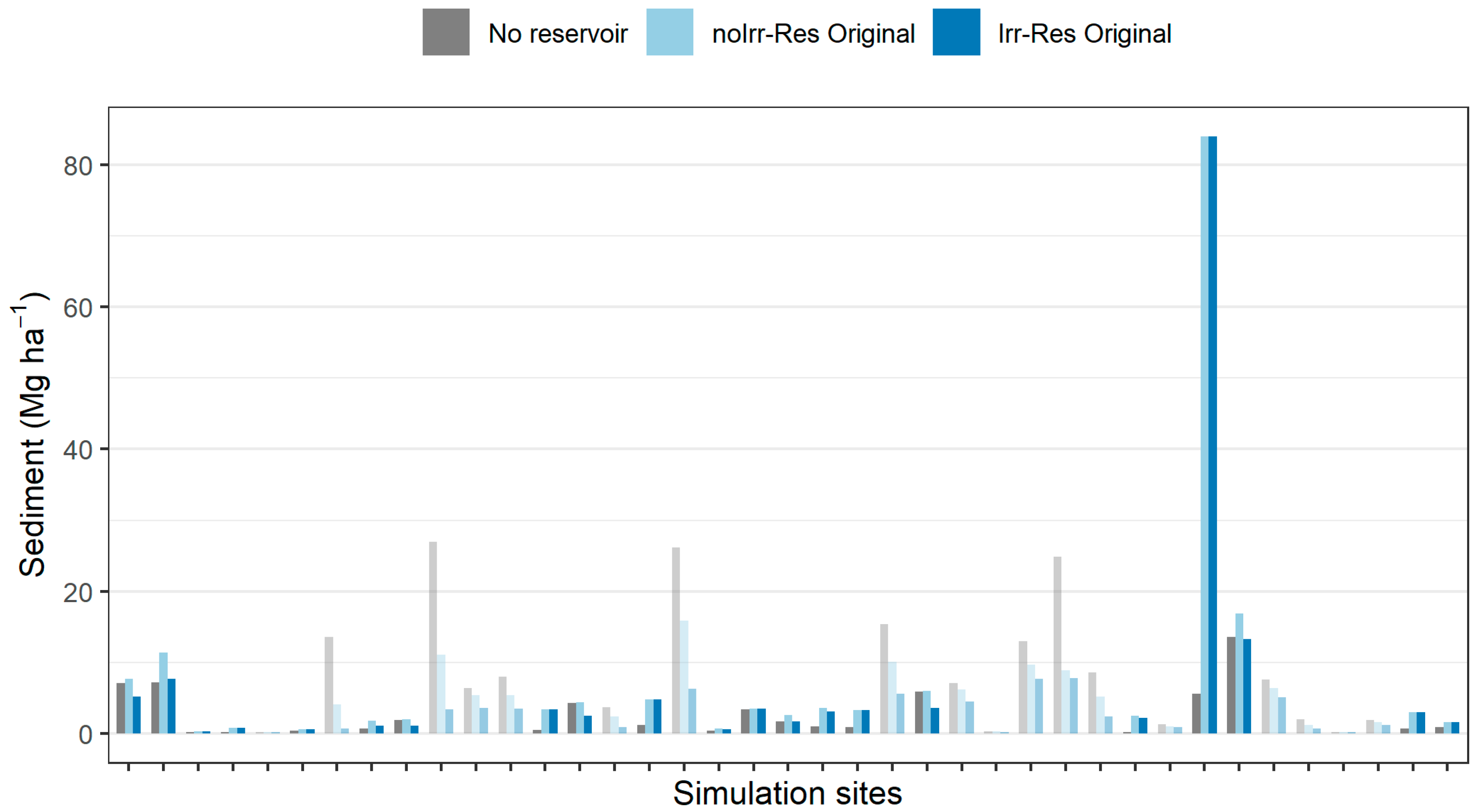
3.2. Sediment and Nutrient Losses with the Original APEX Model
3.3. Reused Water from Cropland
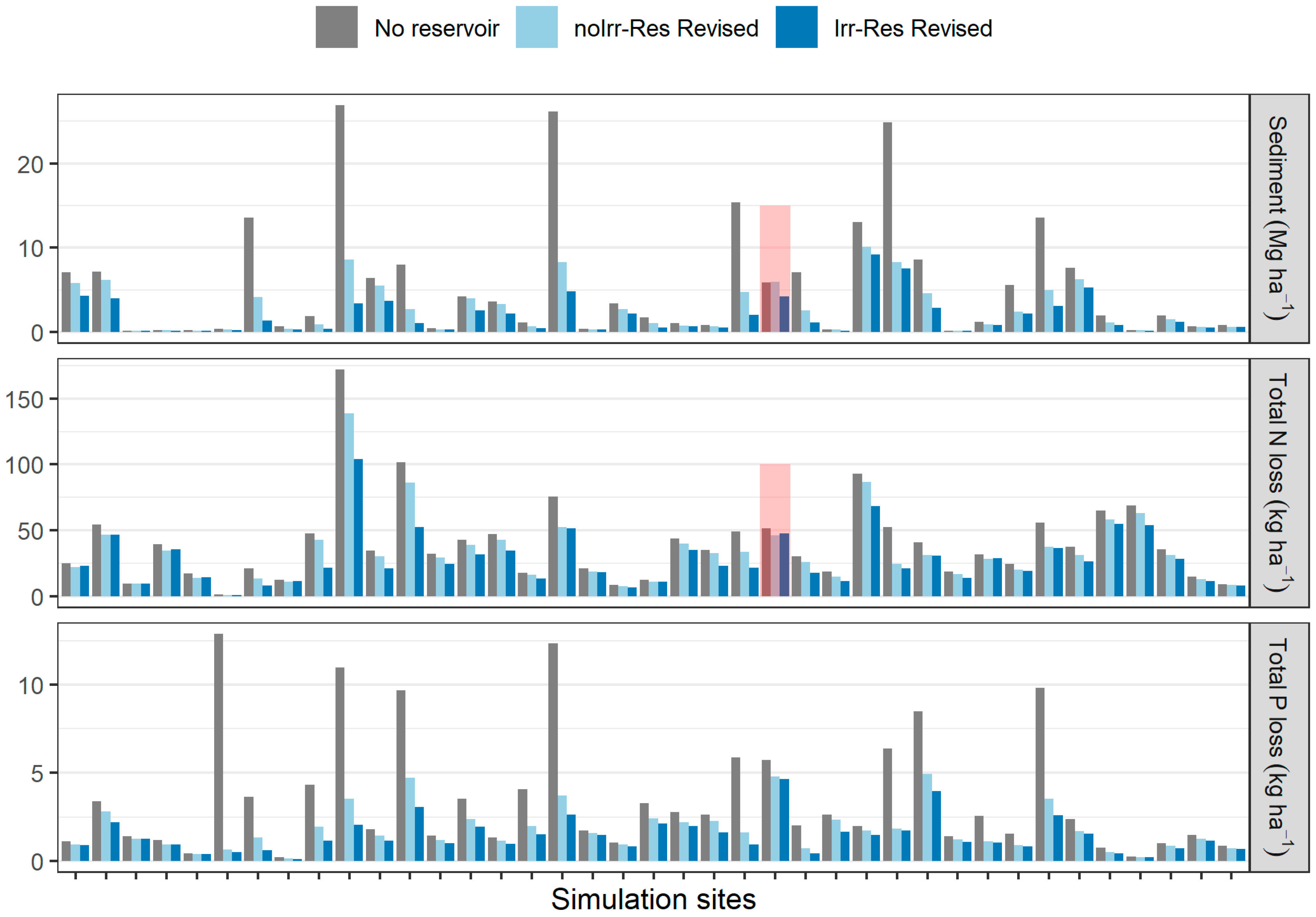
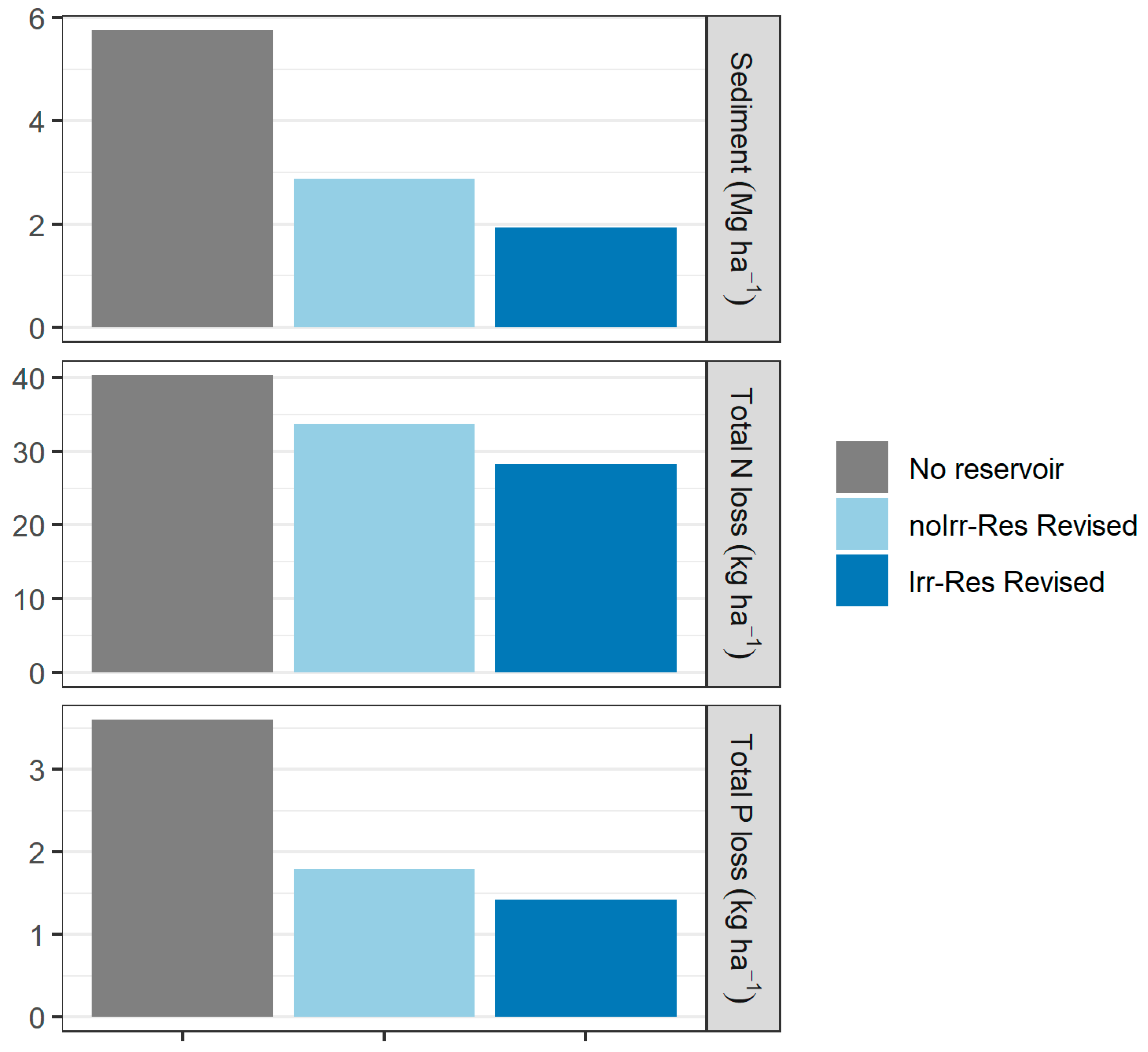
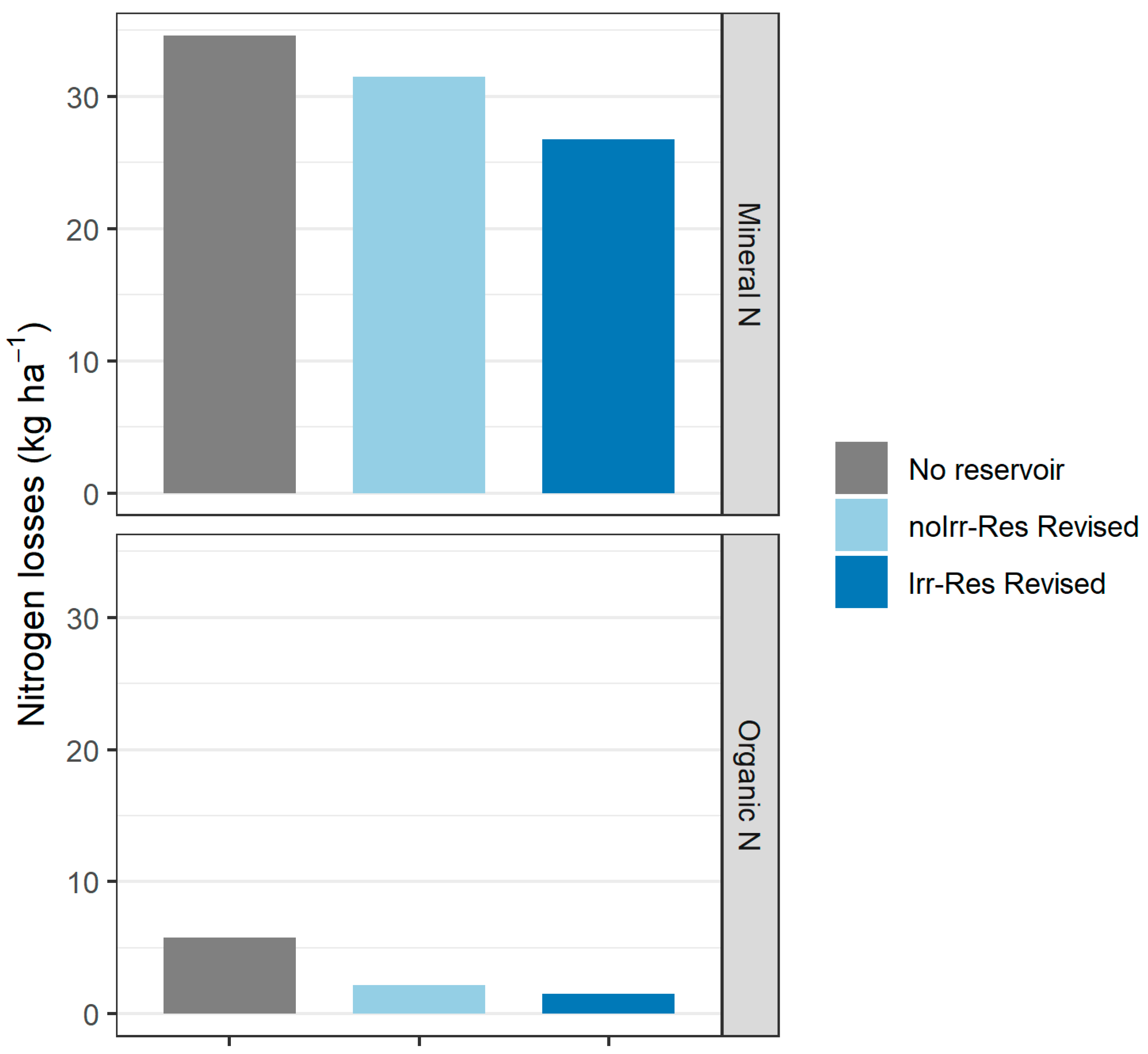
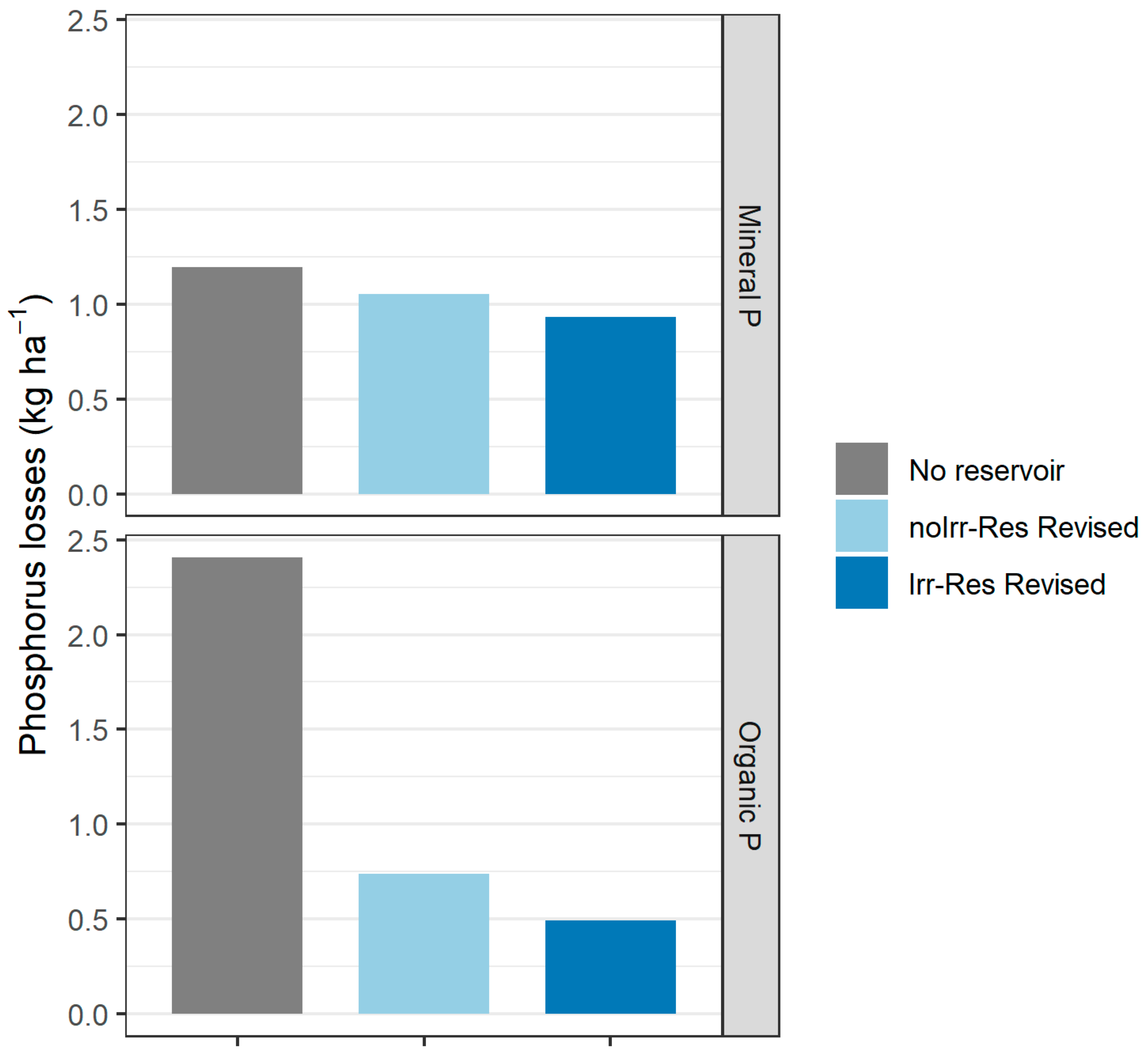
3.4. Sediment and Nutrient Losses
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shiklomanov, I.A. World Water Resources: A New Appraisal and Assessment for the 21st Century: A Summary of the Monograph World Water Resources; UNESCO: Paris, France, 1998. [Google Scholar]
- FAO. The State of Food and Agriculture 2020. In The State of Food and Agriculture (SOFA), 1st ed.; FAO: Rome, Italy, 2020; ISBN 978-92-5-133441-6. [Google Scholar]
- United Nations. (Ed.) Groundwater: Making the Invisible Visible; The United Nations World Water Development Report 2022; UNESCO: Paris, France, 2022; ISBN 978-92-3-100507-7. [Google Scholar]
- Johnson, M.-V.V.; Norfleet, M.L.; Atwood, J.D.; Behrman, K.D.; Kiniry, J.R.; Arnold, J.G.; White, M.J.; Williams, J. The Conservation Effects Assessment Project (CEAP): A National Scale Natural Resources and Conservation Needs Assessment and Decision Support Tool. IOP Conf. Ser. Earth Environ. Sci. 2015, 25, 012012. [Google Scholar] [CrossRef]
- Durincik, L.F.; Bucks, D.; Dobrowolski, J.P.; Drewes, T.; Eckles, S.D.; Jolley, L.; Kellogg, R.L.; Lund, D.; Makuch, J.R.; O’Neill, M.P.; et al. The First Five Years of the Conservation Effects Assessment Project. J. Soil. Water Conserv. 2008, 63, 185A–197A. [Google Scholar] [CrossRef]
- USDA-NRCS Conservation Practices on Cultivated Cropland: A Comparison of CEAP I and CEAP II Survey Data and Modeling; Natural Resources Conservation Service, U.S. Department of Agriculture: Washington, DC, USA, 2022.
- Hay, C.H.; Reinhart, B.D.; Frankenberger, J.R.; Helmers, M.J.; Jia, X.; Nelson, K.A.; Youssef, M.A. Frontier: Drainage Water Recycling in the Humid Regions of the U.S.: Challenges and Opportunities. Trans. ASABE 2021, 64, 1095–1102. [Google Scholar] [CrossRef]
- Moursi, H.; Youssef, M.A.; Chescheir, G.M. Development and Application of DRAINMOD Model for Simulating Crop Yield and Water Conservation Benefits of Drainage Water Recycling. Agric. Water Manag. 2022, 266, 107592. [Google Scholar] [CrossRef]
- Prince Czarnecki, J.M.; Omer, A.R.; Dyer, J.L. Quantifying Capture and Use of Tailwater Recovery Systems. J. Irrig. Drain. Eng. 2017, 143, 05016010. [Google Scholar] [CrossRef]
- Moursi, H.; Youssef, M.A.; Poole, C.A.; Castro-Bolinaga, C.F.; Chescheir, G.M.; Richardson, R.J. Drainage Water Recycling Reduced Nitrogen, Phosphorus, and Sediment Losses from a Drained Agricultural Field in Eastern North Carolina, U.S.A. Agric. Water Manag. 2023, 279, 108179. [Google Scholar] [CrossRef]
- Omer, A.R.; Moore, M.T.; Krutz, L.J.; Kröger, R.; Prince Czarnecki, J.M.; Baker, B.H.; Allen, P.J. Potential for Recycling of Suspended Solids and Nutrients by Irrigation of Tailwater from Tailwater Recovery Systems. Water Supply 2018, 18, 1396–1405. [Google Scholar] [CrossRef]
- Robinson, W.A. Climate Change and Extreme Weather: A Review Focusing on the Continental United States. J. Air Waste Manag. 2021, 71, 1186–1209. [Google Scholar] [CrossRef]
- Gassman, P.W.; Williams, J.R.; Wang, X.; Saleh, A.; Osei, E.; Hauck, L.M.; Izaurralde, R.C.; Flowers, J.D. The Agricultural Policy/Environmental eXtender (APEX) Model: An Emerging Tool for Landscape and Watershed Environmental Analyses. Trans. ASABE 2010, 53, 711–740. [Google Scholar] [CrossRef]
- Williams, J.R.; Izaurralde, R.C. The APEX Model. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2010; pp. 437–482. [Google Scholar]
- Williams, J.R.; Arnold, J.G.; Kiniry, J.R.; Gassman, P.W.; Green, C.H. History of Model Development at Temple, Texas. Hydrol. Sci. J. 2008, 53, 948–960. [Google Scholar] [CrossRef]
- Wang, X.; Hoffman, D.W.; Wolfe, J.E.; Williams, J.R.; Fox, W.E. Modeling the Effectiveness of Conservation Practices at Shoal Creek Watershed, Texas, Using APEX. Trans. ASABE 2009, 52, 1181–1192. [Google Scholar] [CrossRef]
- Williams, J.R.; Potter, S.; Wang, X.; Atwood, J.; Norfleet, M.L.; Gerik, T.; Lemunyon, J.; King, A.; Steglich, E.M.; Wang, C.; et al. APEX Model Validation for CEAP. 2010; pp. 1–13. Available online: https://www.nrcs.usda.gov/sites/default/files/2023-04/ceap-crop-2010-APEX-Model-Validation.pdf (accessed on 1 July 2024).
- Sharifi, A.; Lee, S.; McCarty, G.; Lang, M.; Jeong, J.; Sadeghi, A.; Rabenhorst, M. Enhancement of Agricultural Policy/Environment eXtender (APEX) Model to Assess Effectiveness of WetlandWater Quality Functions. Water 2019, 11, 606. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, H. Modeling the Impacts of Agricultural Management Strategies on Crop Yields and Sediment Yields Using APEX in Guizhou Plateau, Southwest China. Agric. Water Manag. 2019, 216, 325–338. [Google Scholar] [CrossRef]
- Wang, X.; Williams, J.R.; Gassman, P.W.; Baffaut, C.; Izaurralde, R.C.; Jeong, J.; Kiniry, J.R. EPIC and APEX: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1447–1462. [Google Scholar] [CrossRef]
- Steglich, E.M.; Osorio Leyton, J.M.; Doro, L.; Jeong, J.; Williams, J.R. Agricultural Policy/Environmental Extender Model User’s Manual—Version 1501; Blackland Research and Extension Center: Temple, TX, USA, 2019.
- Choi, S.-K.; Jeong, J.; Kim, M.-K. Simulating the Effects of Agricultural Management on Water Quality Dynamics in Rice Paddies for Sustainable Rice Production—Model Development and Validation. Water 2017, 9, 869. [Google Scholar] [CrossRef]
- Hantush, M.M.; Kalin, L.; Isik, S.; Yucekaya, A. Nutrient Dynamics in Flooded Wetlands. I: Model Development. J. Hydrol. Eng. 2013, 18, 1709–1723. [Google Scholar] [CrossRef]
- USDA-NRCS Hydrologic Soil Groups. In Part 630 Hydrology National Engineering Handbook; USDA-NRCS: Washington, DC, USA, 2007; Volume 210-VI-NEH.
- USDA-NRCS Chapter 2, Soils. In National Engineering Handbook. Irrigation Guide, Part 652; National Enginereeng Handbook; USDA-NRCS: Washington, DC, USA, 1997.
- USDA-NASS USDA—National Agricultural Statistics Service—Quick Stats Lite. Available online: https://www.nass.usda.gov/Quick_Stats/Lite/index.php (accessed on 15 October 2024).
- Woodward Donald, E. A Look Back at the Watershed Protection and Flood Prevention Act of 1954 (Pl-566). In Proceedings of the Watershed Management 2015, Reston, VA, USA, 5–7 August 2015; American Society of Civil Engineers: Reston, VA, USA, 2015; pp. 160–168. [Google Scholar]
- USDA-NRCS Articulated Concrete Block Armored Spillways. In National Engineering Handbook. NEH Part 628 Dams; USDA-NRCS: Washington, DC, USA, 2019.
- United States. Bureau of Reclamation Design of Small Dams; Water Resources Technical Publication; U.S. Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987.
- Stephens, T. Manual on Small Earth Dams: A Guide to Siting, Design and Construction; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 2010; ISBN 978-92-5-106547-1. [Google Scholar]
- Sahoo, D.; Yazdi, M.N.; Owen, J.S., Jr.; White, S.A. The Basics of Irrigation Reservoirs for Agriculture; Clemson Cooperative Extension, Land-Grant Press by Clemson Extension: Clemson, SC, USA, 2021; LGP 1121. [Google Scholar]
- MANAGE Measured Annual Nutrient Loads from AGricultural Environments (MANAGE) Database. Available online: https://agdatacommons.nal.usda.gov/articles/dataset/Measured_Annual_Nutrient_loads_from_AGricultural_Environments_MANAGE_database/24660720 (accessed on 15 October 2024).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Correndo, A.A.; Rosso, L.H.M.; Hernandez, C.H.; Bastos, L.M.; Nieto, L.; Holzworth, D.; Ciampitti, I.A. Metrica: An R Package to Evaluate Predictionperformance of Regression and Classification Point-Forecastmodels. J. Open Source Softw. 2022, 7, 4655. [Google Scholar] [CrossRef]
- McDowell, R.W.; Biggs, B.J.F.; Sharpley, A.N.; Nguyen, L. Connecting Phosphorus Loss from Agricultural Landscapes to Surface Water Quality. Chem. Ecol. 2004, 20, 1–40. [Google Scholar] [CrossRef]
- Iseyemi, O.O.; Farris, J.L.; Moore, M.T.; Locke, M.A.; Choi, S. Phosphorus Dynamics in Agricultural Drainage Ditches: An Influence of Landscape Properties. J. Soil Water Conserv. 2018, 73, 558–566. [Google Scholar] [CrossRef]
- Iseyemi, O.; Reba, M.L.; Haas, L.; Leonard, E.; Farris, J. Water Quality Characteristics of Tailwater Recovery Systems Associated with Agriculture Production in the Mid-Southern US. Agric. Water Manag. 2021, 249, 106775. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable Sediment Management in Reservoirs and Regulated Rivers: Experiences from Five Continents. Earths Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Tan, C.S.; Zhang, T.Q.; Drury, C.F.; Reynolds, W.D.; Oloya, T.; Gaynor, J.D. Water Quality and Crop Production Improvement Using a Wetland-Reservoir and Draining/Subsurface Irrigation System. Can. Water Resour. J. 2007, 32, 129–136. [Google Scholar] [CrossRef]
- Tan, C.S.; Zhang, T.Q. Surface Runoff and Sub-Surface Drainage Phosphorus Losses under Regular Free Drainage and Controlled Drainage with Sub-Irrigation Systems in Southern Ontario. Can. J. Soil Sci. 2011, 91, 349–359. [Google Scholar] [CrossRef]
- Drury, C.F.; Tan, C.S.; Gaynor, J.D.; Oloya, T.O.; Welacky, T.W. Influence of Controlled Drainage-Subirrigation on Surface and Tile Drainage Nitrate Loss. J. Environ. Qual. 1996, 25, 317–324. [Google Scholar] [CrossRef]
- Drury, C.F.; Tan, C.S.; Reynolds, W.D.; Welacky, T.W.; Oloya, T.O.; Gaynor, J.D. Managing Tile Drainage, Subirrigation, and Nitrogen Fertilization to Enhance Crop Yields and Reduce Nitrate Loss. J. Environ. Qual. 2009, 38, 1193–1204. [Google Scholar] [CrossRef]





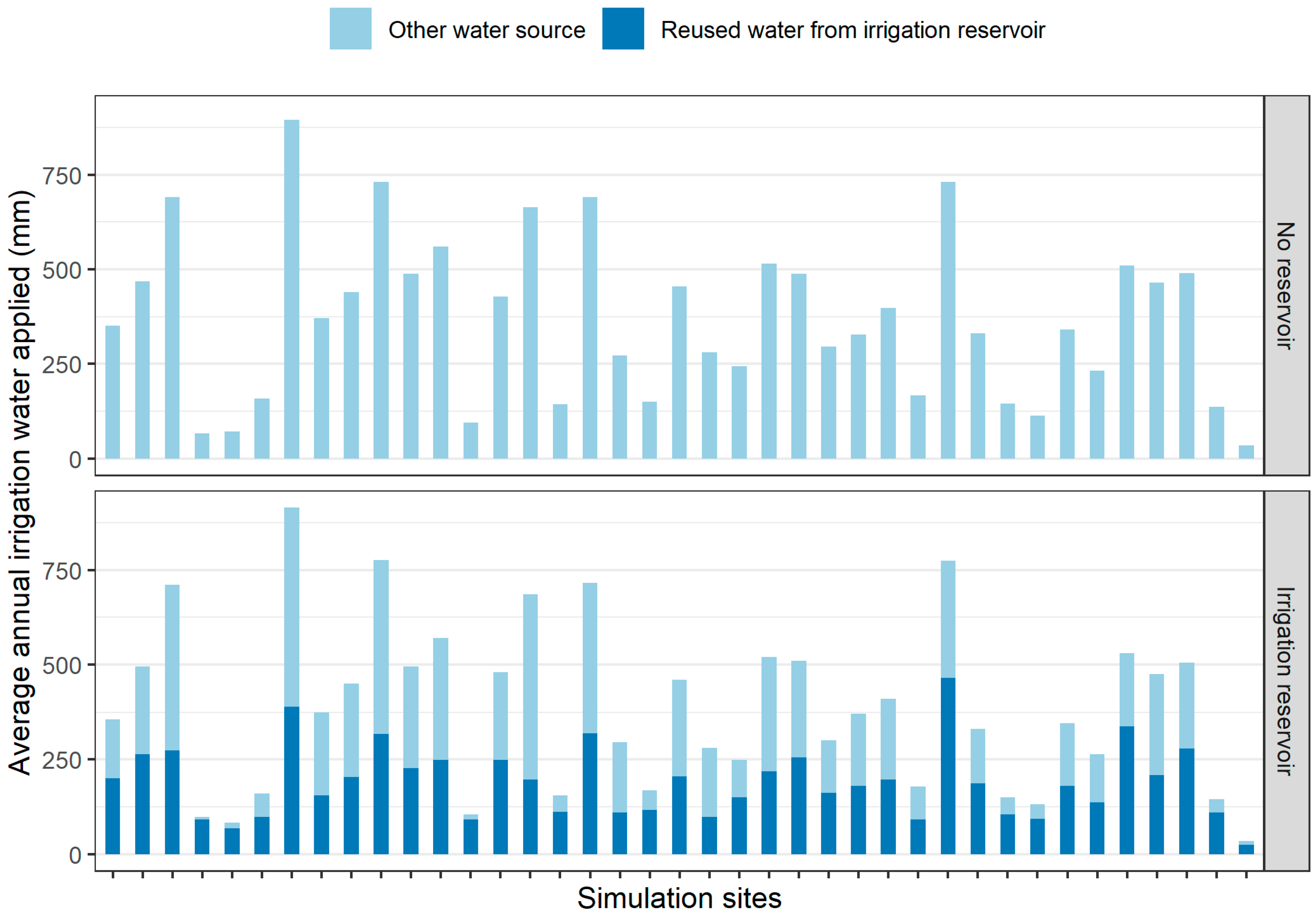
| Supplemental Source Only | Reservoir + Supplemental Source | |||
|---|---|---|---|---|
| Total Irrigation (mm yr−1) | Total Irrigation (mm yr−1) | Reused Water from Percolation (mm yr−1) | Irrigation from Supplemental Source (mm yr−1) | |
| Minimum | 35.0 | 35.0 | 24.5 | 6.8 |
| Maximum | 895.0 | 915.0 | 464.2 | 526.3 |
| Average | 370.0 | 380.1 | 189.8 | 196.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doro, L.; Wang, X.; Jeong, J. Simulating Agricultural Water Recycling Using the APEX Model. Environments 2024, 11, 244. https://doi.org/10.3390/environments11110244
Doro L, Wang X, Jeong J. Simulating Agricultural Water Recycling Using the APEX Model. Environments. 2024; 11(11):244. https://doi.org/10.3390/environments11110244
Chicago/Turabian StyleDoro, Luca, Xiuying Wang, and Jaehak Jeong. 2024. "Simulating Agricultural Water Recycling Using the APEX Model" Environments 11, no. 11: 244. https://doi.org/10.3390/environments11110244
APA StyleDoro, L., Wang, X., & Jeong, J. (2024). Simulating Agricultural Water Recycling Using the APEX Model. Environments, 11(11), 244. https://doi.org/10.3390/environments11110244








