Reaction Time Improvements by Neural Bistability
Abstract
:1. Introduction
2. Sensorimotor Tasks Induce Reaction Delays
3. Materials and Methods
3.1. Participants of the Experiment
3.2. Measurements
3.3. Computational Equipment
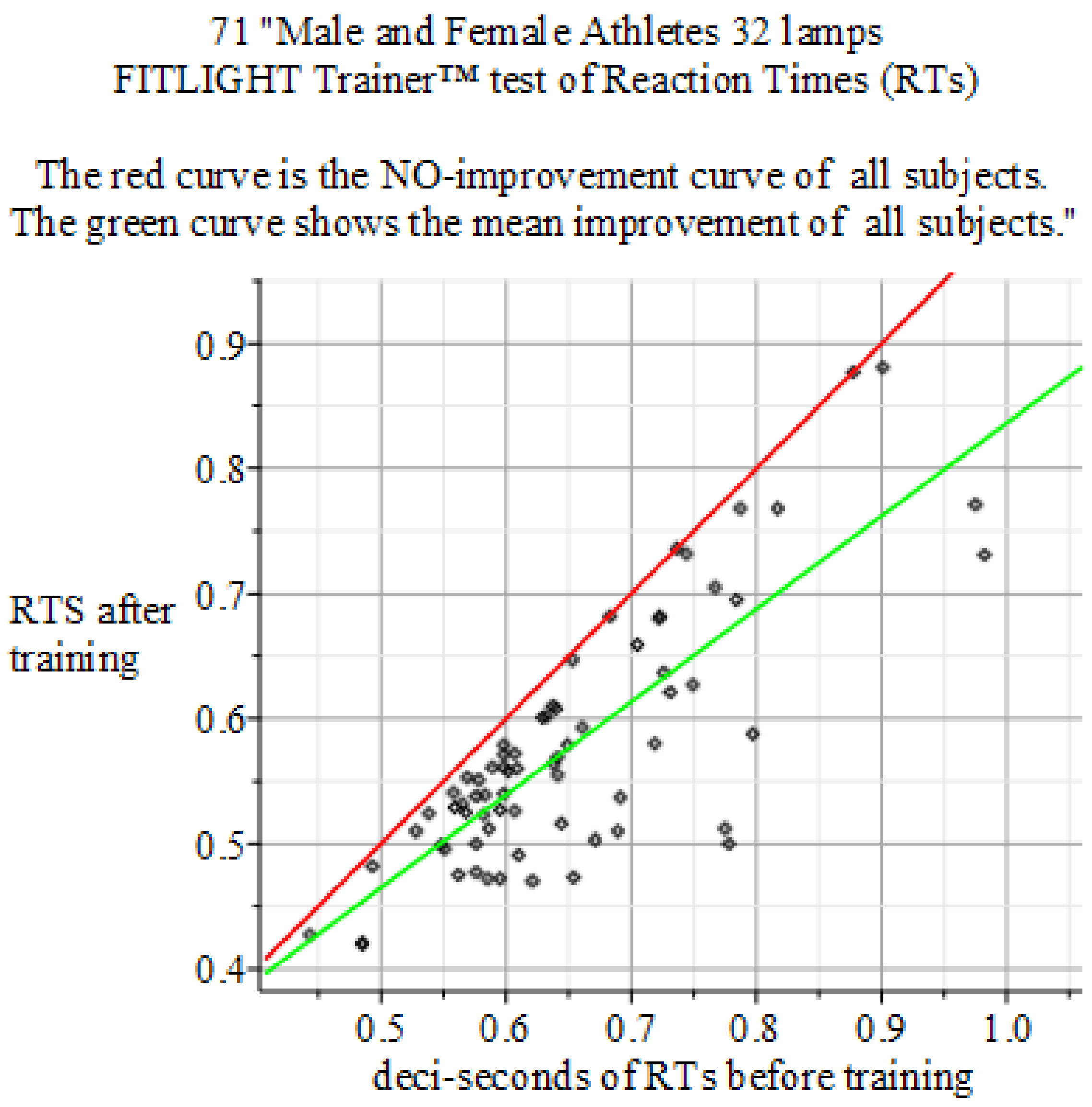
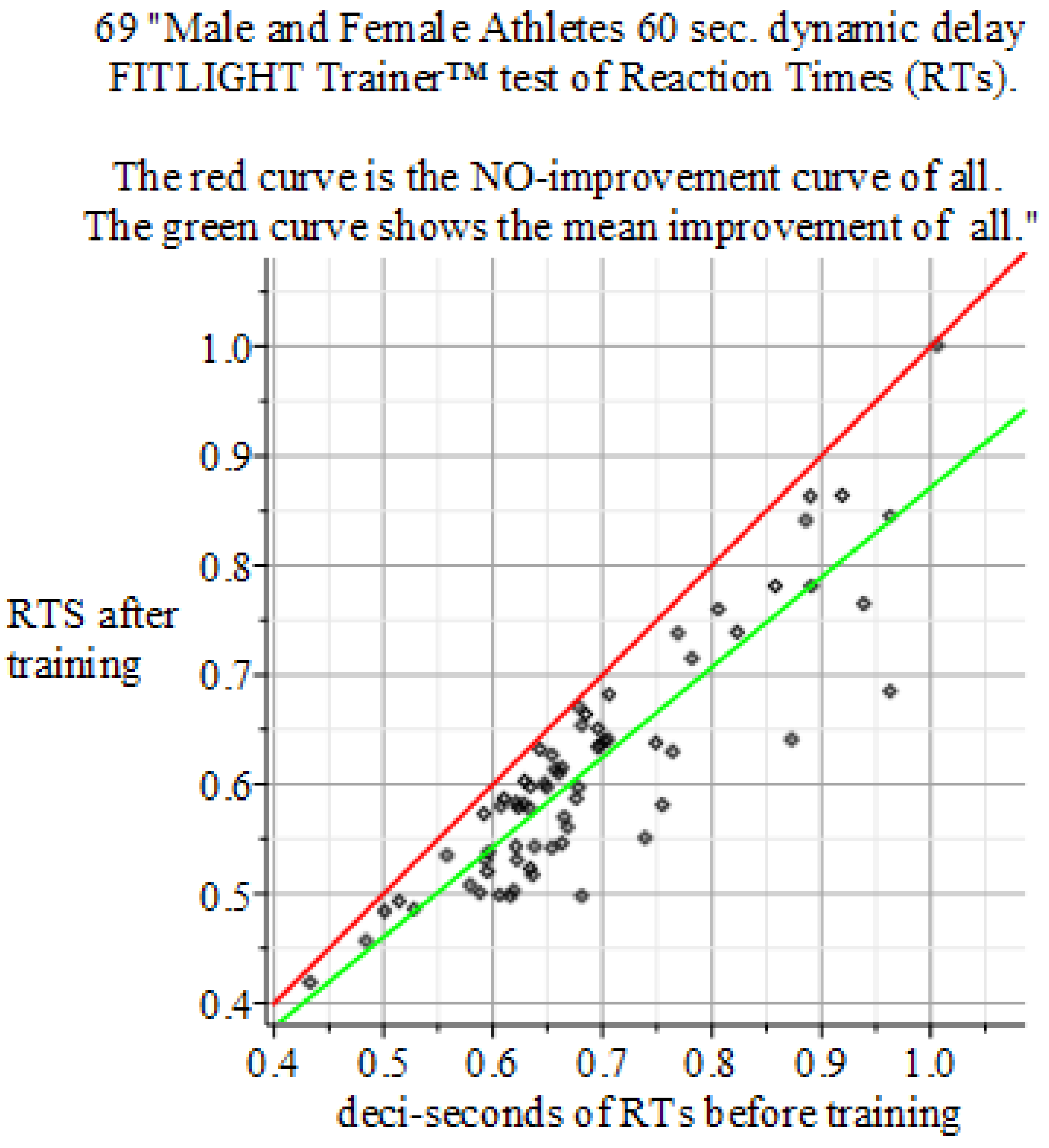
4. Results
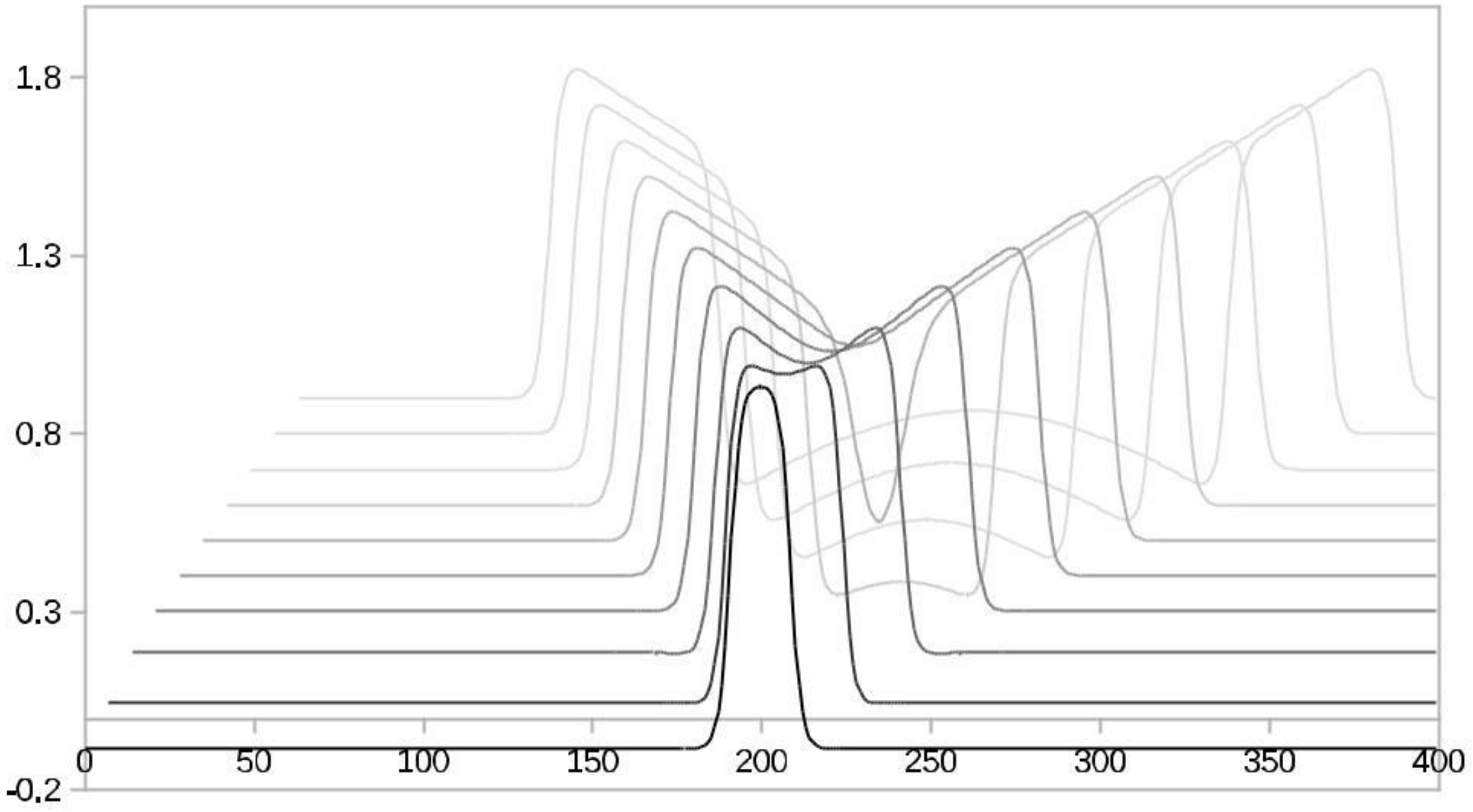
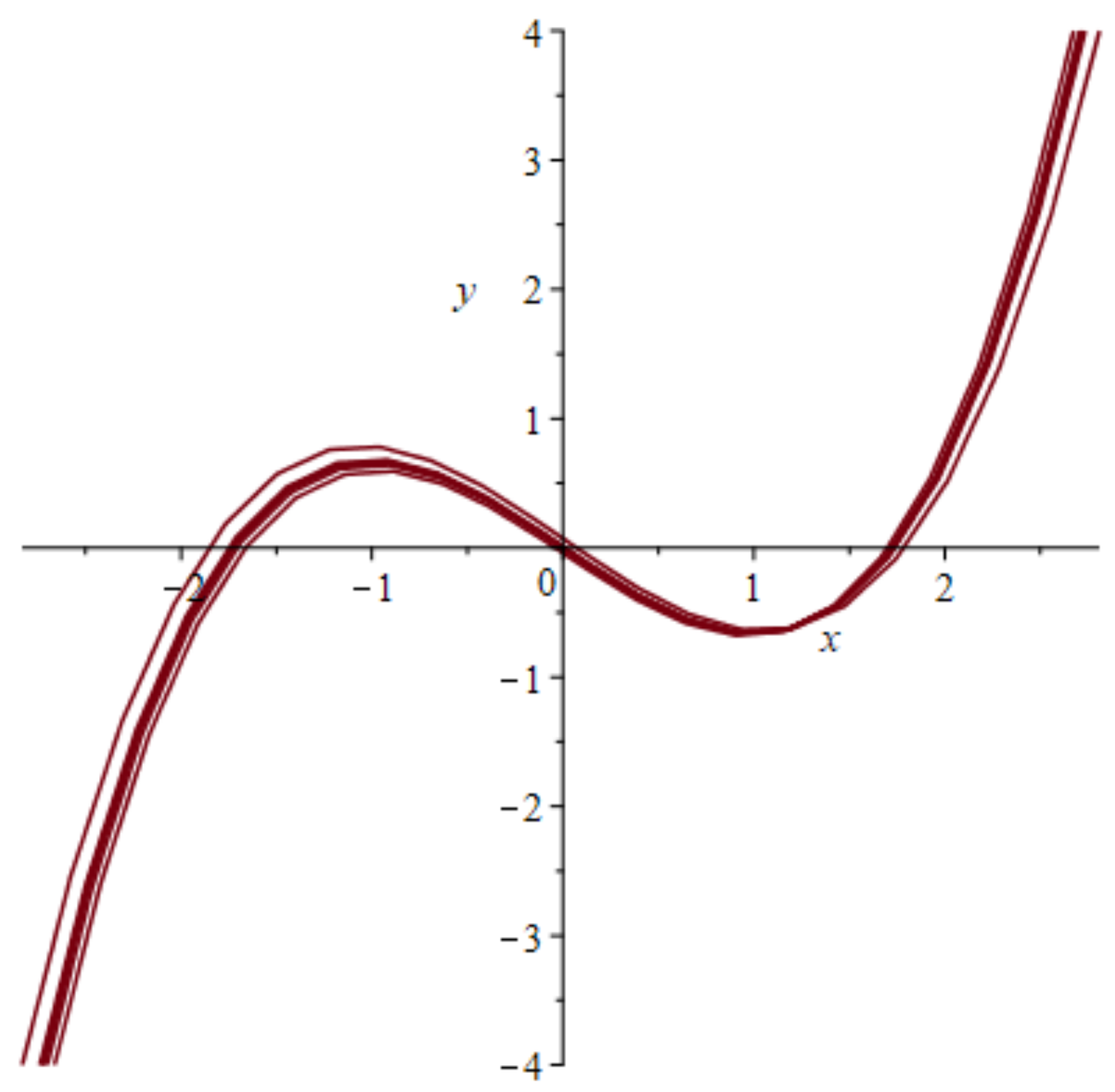
4.1. Models with at Least Two Stable States Depict Learning
4.2. Complimentary Work
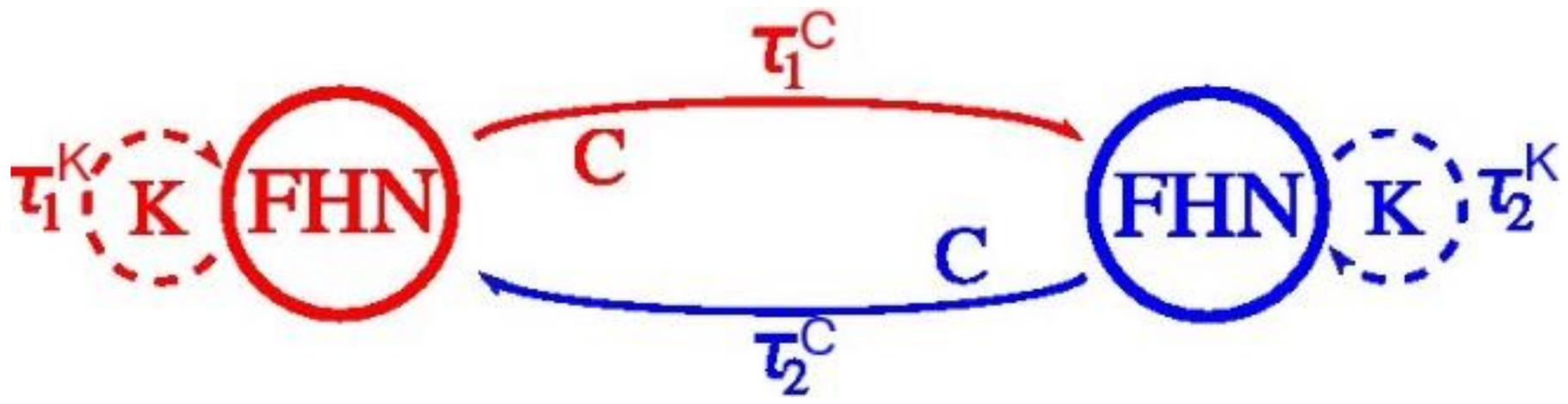
4.3. The FitzHugh-Nagumo (FHN) Model
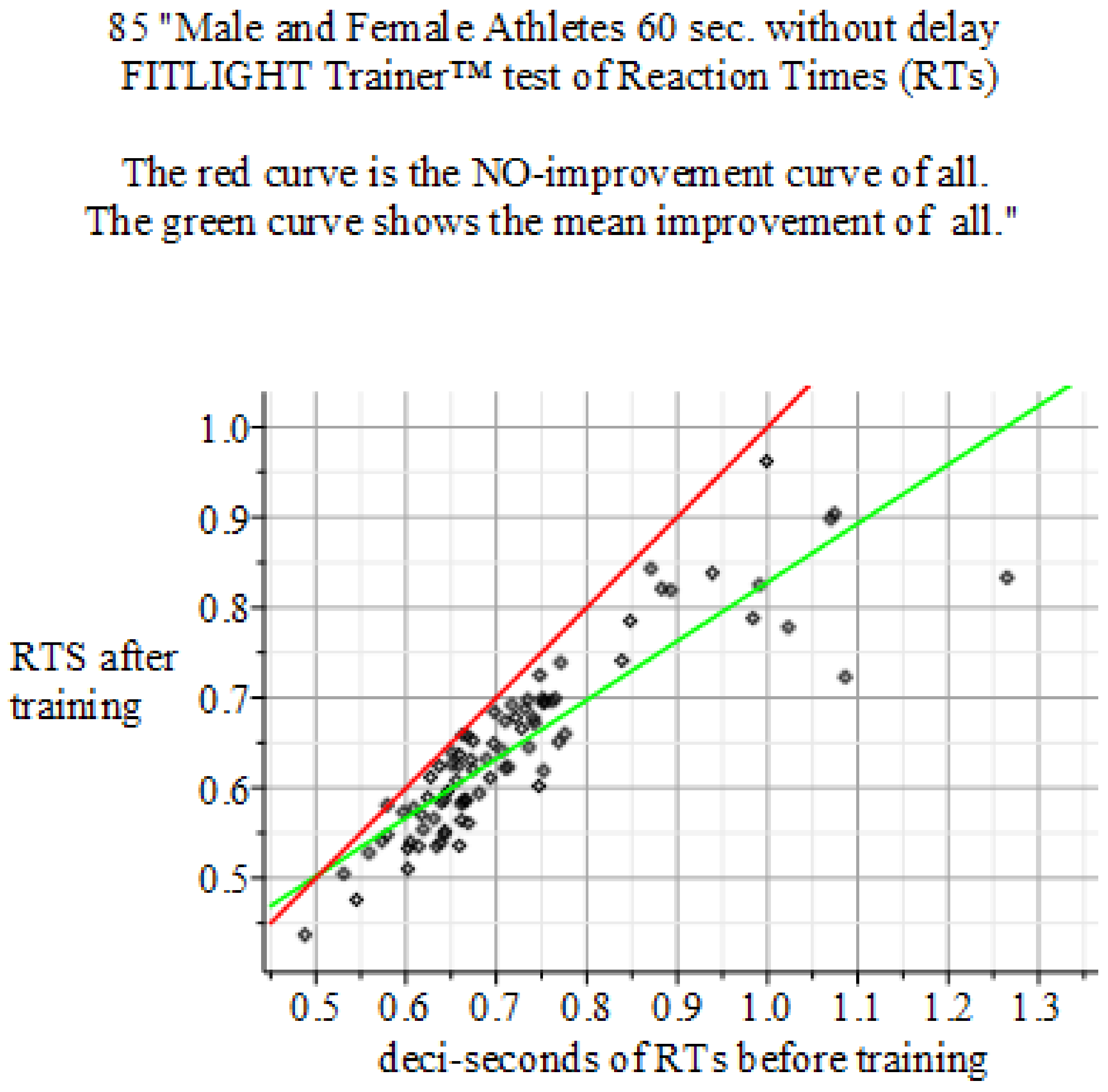
4.4. Results of the Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Ethics Approval
Conflicts of Interest
Appendix A
References
- Abernethy, B. Training the Visual-Perceptual Skills of Athletes: Insights From the Study of Motor Expertise. Am. J. Sports Med. 1996, 24, 89–92. [Google Scholar] [CrossRef]
- Burris, K.; Vittetoe, K.; Ramger, B.; Suresh, S.; Tokdar, S.T.; Reiter, J.P.; Appelbaum, L.G. Sensorimotor abilities predict on-field performance in professional baseball. Sci. Rep. 2018, 8, 1–9. [Google Scholar]
- Rathelot, J.; Dum, R.P.; Strick, P.L. Posterior parietal cortex contains a command apparatus for hand movements. Proc. Natl. Acad. Sci. USA 2017, 114, 4255–4260. [Google Scholar] [CrossRef]
- Scott, S.H. The computational and neural basis of voluntary motor control and planning. Trends Cogn. Sci. 2012, 16, 541–549. [Google Scholar] [CrossRef] [PubMed]
- Jana, S.; Gopal, A.; Murthy, A. A Computational Framework for Understanding Eye-Hand Coordination. J. Indian Inst. Sci. 2017, 97, 543–554. [Google Scholar] [CrossRef]
- Jana, S.; Gopal, A.; Murthy, A. Evidence of common and separate eye and hand accumulators underlying flexible eye-hand coordination. J. Neurophysiol. 2017, 117, 348–364. [Google Scholar] [CrossRef] [PubMed]
- Gopal, A.; Jana, S.; Murthy, A. Contrasting speed accuracy trade-offs for eye and hand movements reveal the optimal nature of saccade kinematics. J. Neurophysiol. 2017, 118, 1664–1667. [Google Scholar] [CrossRef] [PubMed]
- Weiler, J.; Gribble, P.L.; Pruszynski, J.A. Spinal stretch reflexes support efficient hand control. Nat. Neurosci. 2019, 1–11. [Google Scholar] [CrossRef]
- Appelbaum, L.G.; Schroeder, J.E.; Cain, M.S.; Mitroff, S.R. Improved visual cognition through stroboscopic training. Front. Psychol. 2011, 2, 1–13. [Google Scholar] [CrossRef]
- Savazzi, S.; Marzi, C.A. Speeding Up Reaction Time with Invisible Stimuli. Curr. Biol. 2002, 12, 403–407. [Google Scholar] [PubMed]
- Curtis, C.E.; Connolly, J.D. Saccade Preparation Signals in the Human Frontal and Parietal Cortices. J. Neurophysiol. 2007, 99, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Britten, K.H.; Shadlen, M.N.; Newsome, W.T.; Movshon, J.A. The Analysis of Visual Motion: A Comparison of Neuronal and Psychophysical Performance. J. Neurosci. 1992, 12, 4745–4765. [Google Scholar] [CrossRef]
- Smith, T.Q.; Mitroff, S.R. Stroboscopic Training Enhances Anticipatory Timing. Int. J. Exerc. Sci. 2012, 5, 344–353. [Google Scholar] [PubMed]
- Appelbaum, L.G.; Cain, M.S.; Schroeder, J.E.; Darling, E.F.; Mitroff, S.R. Stroboscopic visual training improves information encoding in short-term memory. Atten. Percept. Psychophys. 2012, 74, 1681–1691. [Google Scholar] [CrossRef]
- Mitroff, S.R.; Friesen, P.; Bennett, D.; Yoo, H.; Reichow, A.W. Enhancing Ice Hockey Skills Through Stroboscopic Visual Training: A Pilot Study. Athl. Train. Sport. Health Care 2013, 5, 261–264. [Google Scholar] [CrossRef]
- Smith, P.L.; Lilburn, S.D.; Corbett, E.A.; Sewell, D.K. The attention-weighted sample-size model of visual short-term memory: Attention capture predicts resource allocation and memory load. Cogn. Psychol. 2016, 89, 71–105. [Google Scholar] [CrossRef] [PubMed]
- Brazier, M.A.B. Studies of the EEG activity of limbic structures in man. Electroencephalogr. Clin. Neurophysiol. 1968, 25, 309–318. [Google Scholar] [CrossRef]
- Melnik, A.; Hairston, W.D.; Ferris, D.P.; König, P. EEG correlates of sensorimotor processing: Independent components involved in sensory and motor processing. Sci. Rep. 2017, 7, 4461. [Google Scholar] [CrossRef] [PubMed]
- Samoilenko, A.; Petryshyn, R. Multifrequency Oscillations of Nonlinear Systems; KluwerAcademic Publishers: New York, NY, USA, 2004; ISBN 1402020317. [Google Scholar]
- Schmidt, H.; Avitabile, D.; Montbrio, E.; Roxin, A. Network mechanisms underlying the role of oscillations in cognitive tasks. PLoS Comput. Biol. 2018, 14, e1006430. [Google Scholar]
- Ahissar, M. Perceptual training: A tool for both modifying the brain and exploring it. Proc. Natl. Acad. Sci. USA 2001, 98, 11842–11843. [Google Scholar] [CrossRef]
- Wright, B.A.; Fitzgerald, M.B. Different patterns of human discrimination learning for two interaural cues to sound-source location. Proc. Natl. Acad. Sci. USA 2001, 98, 12307–12312. [Google Scholar] [CrossRef] [PubMed]
- Ho, H.T.; Leung, J.; Burr, D.C.; Alais, D.; Ho, H.T.; Leung, J.; Burr, D.C.; Alais, D.; Morrone, M.C. Auditory Sensitivity and Decision Criteria Oscillate at Different Frequencies Separately for the Two Ears. Curr. Biol. 2017, 27, 3643–3649. [Google Scholar] [CrossRef] [PubMed]
- Marek, S.; Tervo-Clemmens, B.; Klein, N.; Foran, W.; Ghuman, A.S.; Luna, B. Adolescent development of cortical oscillations: Power, phase, and support of cognitive maturation. PLoS Biol. 2018, 16, e2004188. [Google Scholar] [CrossRef] [PubMed]
- Kriegeskorte, N.; Douglas, P.K. Cognitive computational neuroscience. Nat. Neurosci. 2018, 21, 1148–1160. [Google Scholar] [CrossRef]
- Güllich, A. International medallists’ and non-medallists’ developmental sport activities—A matched-pairs analysis. J. Sports Sci. 2017, 35, 2281–2288. [Google Scholar] [CrossRef]
- Cecchi, G.A.; Sigman, M.; Alonso, J.-M.; Martinez, L.; Chialvo, D.R.; Magnasco, M.O. Noise in neurons is message-dependent. Proc. Natl. Acad. Sci. USA 2000, 97, 5557–5561. [Google Scholar] [CrossRef]
- Vidoni, E.D.; McCarley, J.S.; Edwards, J.D.; Boyd, L.A. Manual and oculomotor performance develop contemporaneously but independently during continuous tracking. Exp. Brain Res. 2009, 195, 611–620. [Google Scholar] [CrossRef]
- Dean, H.L.; Martí, D.; Tsui, E.; Rinzel, J.; Pesaran, B. Reaction Time Correlations during Eye–Hand Coordination: Behavior and Modeling. J. Neurosci. 2011, 31, 2399–2412. [Google Scholar] [CrossRef] [PubMed]
- Haak, K.V.; Beckmann, C.F. Objective analysis of the topological organization of the human cortical visual connectome suggests three visual pathways. Cortex 2018, 98, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Ambrosio, B.; Aziz-Alaoui, M.A. Synchronization and control of coupled reaction-diffusion systems of the FitzHugh-Nagumo type. Comput. Math. Appl. 2012, 64, 934–943. [Google Scholar] [CrossRef]
- Ebsch, C.; Rosenbaum, R. Imbalanced amplification: A mechanism of amplification and suppression from local imbalance of excitation and inhibition in cortical circuits. PLoS Comput. Biol. 2018, 14, e1006048. [Google Scholar] [CrossRef]
- Graham, N.V. Beyond multiple pattern analyzers modeled as linear filters (as classical V1 simple cells): Useful additions of the last 25 years. Vis. Res. 2011, 51, 1397–1430. [Google Scholar] [CrossRef]
- Alexik, M. Modelling and identification of eye-hand dynamics. Simul. Pract. Theory 2000, 8, 25–38. [Google Scholar] [CrossRef]
- Schmidt-Hieber, C.; Nolan, M.F. Synaptic integrative mechanisms for spatial cognition. Nat. Neurosci. 2017, 20, 1483–1492. [Google Scholar] [CrossRef] [PubMed]
- Kaminski, M.; Ding, M.; Truccolo, W.A.; Bressler, S.L. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern. 2001, 85, 145–157. [Google Scholar] [CrossRef] [PubMed]
- Stefanescu, R.A.; Jirsa, V.K. A low dimensional description of globally coupled heterogeneous neural networks of excitatory and inhibitory neurons. PLoS Comput. Biol. 2008, 4, e1000219. [Google Scholar] [CrossRef] [PubMed]
- Senk, J.; Schuecker, J.; Hagen, E.; Diesmann, M.; Helias, M. Conditions for traveling waves in spiking neural networks. arXiv, 2018; arXiv:1801.06046. [Google Scholar]
- Bastin, J.; Lebranchu, P.; Jerbi, K.; Kahane, P.; Orban, G.; Lachaux, J.; Berthoz, A. NeuroImage Direct recordings in human cortex reveal the dynamics of gamma-band [50–150 Hz] activity during pursuit eye movement control. Neuroimage 2012, 63, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Hafed, Z.M. Alteration of Visual Perception prior to Microsaccades. Neuron 2013, 77, 775–786. [Google Scholar] [CrossRef]
- Irwin, D.E. Where does attention go when you blink? Attent. Percept. Psychophys. 2011, 73, 1374–1384. [Google Scholar] [CrossRef] [PubMed]
- Terhune, D.B.; Sullivan, J.G.; Simola, J.M. Time dilates after spontaneous blinking. Curr. Biol. 2016, 26, R459–R460. [Google Scholar] [CrossRef]
- Hoppe, D.; Helfmann, S.; Rothkopf, C.A. Humans quickly learn to blink strategically in response to environmental task demands. Proc. Natl. Acad. Sci. USA 2018, 115, 2246–2251. [Google Scholar] [CrossRef] [PubMed]
- Donner, T.H.; Siegel, M.; Oostenveld, R.; Fries, P.; Bauer, M.; Engel, A.K. Population Activity in the Human Dorsal Pathway Predicts the Accuracy of Visual Motion Detection. J. Neurosci. 2007, 98, 345–359. [Google Scholar] [CrossRef]
- Panchuk, A.; Rosin, D.P.; Hoevel, P.; Schoell, E. Synchronization of coupled neural oscillators with heterogeneous delays. Int. J. Bifurc. Chaos 2012, 23, 1330039. [Google Scholar] [CrossRef]
- Toit, P.J.; Krüger, P.E.; Mahomed, A.F.; Kleynhans, M.; Jay-du Preez, T.; Govender, C.; Mercier, J. The effect of ports vision exercises on the visual skills of university students. Afr. J. Phys. Health Educ. Recreat. Dance 2011, 17, 429–440. [Google Scholar]
- Clark, J.F.; Ellis, J.K.; Bench, J.; Khoury, J.; Graman, P. High-performance vision training improves batting statistics for University of Cincinnati baseball players. PLoS ONE 2012, 7, e29109. [Google Scholar] [CrossRef] [PubMed]
- Melstrom, A.J. Effectiveness of a Low-Budget Sports Vision Training Program for Improving Statistics of an NCAA Division I Baseball Team; South Dakota State University: Brookings, SD, USA, 2018. [Google Scholar]
- Kioumourtzoglou, E.; Kourtessis, T.; Michalopoulou, M.; Derri, V. Differences in Several Perceptual Abilities between Experts and Novices in Basketball, Volleyball and Water-Polo. Percept. Mot. Skills 1998, 86, 899–912. [Google Scholar] [CrossRef] [PubMed]
- Ghuntla, T.P.; Mehta, H.B.; Gokhale, P.A.; Shah, C.J. A comparative study of visual reaction time in basketball players and healthy controls. Indian J. Physiol. Pharmacol. 2012, 3, 49–51. [Google Scholar]
- Ghasemi, A.; Momeni, M.; Rezaee, M.; Gholami, A. The Difference in Visual Skills Between Expert Versus Novice Soccer Referees. J. Hum. Kinet. 2009, 22, 15–20. [Google Scholar] [CrossRef]
- Wilkins, L.; Nelson, C.; Tweddle, S. Stroboscopic Visual Training: A Pilot Study with Three Elite Youth Football Goalkeepers. J. Cogn. Enhanc. 2017, 2, 3–11. [Google Scholar] [CrossRef]
- Ellison, P.H. Eye-Hand Coordination: An Exploration of Measurement and Different Training methods using the SVT; Edge Hill University: Ormskirk, UK, 2015. [Google Scholar]
- Du Toit, P.J.; Van Vuuren, P.J.; Le Roux, S.; Henning, E.; Kleynhans, M.; Terblanche, H.C.; Crafford, D.; Grobbelaar, C.; Wood, P.S.; Grant, C.C.; et al. The effect of sport specific exercises on the visual skills of rugby players. Conf. Proc. IEEE Int. Conf. Syst. Man Cybern. 2012, 6, 1158–1161. [Google Scholar]
- Tseng, C.H.; Gobell, J.L.; Lu, Z.-L.L.; Sperling, G. When motion appears stopped: Stereo motion standstill. Proc. Natl. Acad. Sci. USA 2006, 103, 14953–14958. [Google Scholar] [CrossRef]
- Appelbaum, L.G.; Lu, Y.; Khanna, R.; Detwiler, K.R. The Effects of Sports Vision Training on Sensorimotor Abilities in Collegiate Softball Athletes. Athl. Train. Sport. Health Care 2016, 8, 154–163. [Google Scholar] [CrossRef]
- Hughes, P.K.; Bhundell, N.L.; Waken, J.M. Visual and psychomotor performance of elite, intermediate and novice table tennis competitors. Clin. Exp. Optom. 1993, 76, 51–60. [Google Scholar] [CrossRef]
- Reschke, M.F.; Somers, J.T.; Ford, G. Stroboscopic Vision as a Treatment forMotion Sickness: Strobe Lightning vs. Shutter Glasses. Aviat. Space Environ. Med. 2006, 77, 2–7. [Google Scholar] [PubMed]
- Berry, A.S.; Zanto, T.P.; Clapp, W.C.; Hardy, J.L.; Delahunt, P.B.; Mahncke, H.W.; Gazzaley, A. The Influence of Perceptual Training on Working Memory in Older Adults. PLoS ONE 2010, 5, e11537. [Google Scholar] [CrossRef] [PubMed]
- Nyquist, J.B.; Lappin, J.S.; Zhang, R.; Tadin, D. Perceptual training yields rapid improvements in visually impaired youth. Sci. Rep. 2016, 6, 37431. [Google Scholar] [CrossRef]
- Schmidt, J.T.; Buzzard, M. Activity-driven sharpening of the retinotectal projection in goldfish: Development under stroboscopic illumination prevents sharpening. J. Neurobiol. 1993, 24, 384–399. [Google Scholar] [CrossRef] [PubMed]
- Erickson, G. Sports Vision; Butterworth-Heinemann Elsevier Ltd.: Oxford, UK, 2007; ISBN 978-7506-7577-2. [Google Scholar]
- Singhal, A.; Culham, J.C.; Chinellato, E.; Goodale, M.A. Dual-task interference is greater in delayed grasping than in visually guided grasping. J. Vis. 2007, 7, 1–12. [Google Scholar] [PubMed]
- Vidnyanszky, Z.; Sohn, W. Learning to suppress task-irrelevant visual stimuli with attention. Vis. Res. 2005, 45, 677–685. [Google Scholar] [CrossRef]
- Paradiso, M.A.; Meshi, D.; Pisarcik, J.; Levine, S. Eye movements reset visual perception. J. Vis. 2012, 12, 11. [Google Scholar] [CrossRef] [PubMed]
- Appelbaum, L.G.; Erickson, G. Sports vision training: A review of the state-of-the-art in digital training techniques. Int. Rev. Sport Exerc. Psychol. 2016, 11, 160–189. [Google Scholar] [CrossRef]
- FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961, 1, 445–446. [Google Scholar] [CrossRef]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. Inst. Radio Eng. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Dmochowski, J.P.; Norcia, A.M. Cortical Components of Reaction-Time during Perceptual Decisions in Humans. PLoS ONE 2015, 10, e0143339. [Google Scholar]
- Marino, B.; Borghi, A.M.; Gemmi, L.; Cacciari, C.; Riggio, L. Neural Adaptation Effects in Conceptual Processing. Behav. Sci. 2015, 5, 353–371. [Google Scholar] [PubMed]
- Mamassian, P.; Goutcher, R. Temporal dynamics in bistable perception. J. Vis. 2005, 5, 361–375. [Google Scholar] [CrossRef]
- Noest, A.J.; van Ee, R.; Nijs, M.M.; van Wezel, R.J.A. Percept-choice sequences driven by interrupted ambiguous stimuli: A low-level neural model. J. Vis. 2007, 7, 10. [Google Scholar] [CrossRef]
- Fürstenau, N. Computational nonlinear dynamics model of percept switching with ambiguous stimuli. In Proceedings of the Second International Conference on Digital Human Modeling, San Diego, CA, USA, 19–24 July 2009. [Google Scholar]
- Kloosterman, N.A. Brain state and changes of mind: Probing the neural bases of multi-stable perceptual dynamics. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2015. [Google Scholar]
- Pisarchik, A.N.; Bashkirtseva, I.A.; Ryashko, L.B. Controlling bistability in a stochastic perception model. Eur. Phys. J. Spec. Top. 2015, 224, 1477–1484. [Google Scholar]
- Safaai, H.; Neves, R.; Eschenko, O.; Logothetis, N.K.; Panzeri, S. Modeling the effect of locus coeruleus firing on cortical state dynamics and single-trial sensory processing. Proc. Natl. Acad. Sci. USA 2015, 112, 12834–12839. [Google Scholar] [CrossRef]
- Montbrió, E.; Pazó, D.; Roxin, A. Macroscopic description for networks of spiking neurons. Phys. Rev. X 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Jia, J.; Liu, H.; Xu, C.; Yan, F. Dynamic effects of time delay on a coupled FitzHugh-Nagumo neural system. Alexandria Eng. J. 2015, 54, 241–250. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerves. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Loffing, F. Left-handedness and time pressure in elite interactive ball games. Biol. Lett. 2017, 13, 10–13. [Google Scholar] [CrossRef]
- Chen, N.; Majda, A.J. Beating the curse of dimension with accurate statistics for the Fokker–Planck equation in complex turbulent systems. Proc. Natl. Acad. Sci. USA 2017, 114, 12864–12869. [Google Scholar] [CrossRef] [PubMed]
- Dahlem, M.A.; Hiller, G.; Panchuk, A.; Schoell, E. Dynamics of delay-coupled excitable neural systems. Int. J. Bifurc. Chaos 2008, 19, 745–753. [Google Scholar] [CrossRef]
- Caksan, C.; Lehnert, J.; Schoell, E. Heterogeneous delays in neural networks. Eur. Phys. J. B 2014, 87, 54. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, W.; Li, X.; Small, M.; Lu, J. Identifying the Topology of a Coupled FitzHugh–Nagumo Neurobiological Network via a Pinning Mechanism. IEEE Trans. Neural Netw. 2009, 20, 1679–1684. [Google Scholar] [CrossRef]
- Zeng, C.; Zeng, C.; Gong, A.; Nie, L. Effect of time delay in FitzHugh–Nagumo neural model with correlations between multiplicative and additive noises. Physica A 2010, 389, 5117–5127. [Google Scholar] [CrossRef]
- Marquie, P.; Comte, J.C.; Morfu, S. Analog simulation of neural information propagation using an electrical FitzHugh – Nagumo lattice. Chaos Solitons Fractals 2004, 19, 27–30. [Google Scholar] [CrossRef]
- FitzHugh, R. An electronic model of the nerve membrane for demonstration purposes. J. Appl. Physiol. 1966, 21, 305–308. [Google Scholar] [CrossRef] [PubMed]
- Panchuk, A.; Dahlem, M.; Schoell, E. Regular spiking in asymmetrically delay-coupled FitzHugh-Nagumo systems. arXiv, 2009; arXiv:0911.2071. [Google Scholar]
- Yanchuk, S.; Perlikowski, P.; Popovych, O.V.; Tass, P.A. Variability of spatio-temporal patterns in non-homogeneous rings of spiking neurons. Chaos 2011, 21, 047511. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Shamshin, D.V.; Strelkova, G.I.; Vadivasova, T.E. Bifurcations of spatiotemporal structures in a medium of FitzHugh–Nagumo neurons with diffusive coupling. Chaos Solit. Fract. 2017, 104, 153–160. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Vadivasova, T.E.; Bukh, A.V.; Strelkova, G.I.; Anishchenko, V.S. New type of chimera structures in a ring of bistable FitzHugh–Nagumo oscillators with nonlocal interaction. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2017, 381, 1398–1404. [Google Scholar] [CrossRef]
- Churchland, M.M.; Yu, B.M.; Cunningham, J.P.; Sugrue, L.P.; Cohen, M.R.; Corrado, G.S.; Newsome, W.T.; Clark, A.M.; Hosseini, P.; Scott, B.B.; et al. Stimulus onset quenches neural variability: A widespread cortical phenomenon. Nat. Neurosci. 2010, 13, 369–378. [Google Scholar] [CrossRef] [PubMed]
- Chang, J. Flipping Biological Switches: Solving for Optimal Control. Ph.D. Thesis, University of Massachesetts, Worcester, MA, USA, 2015. [Google Scholar]
- Kwon, O.-S.; Tadin, D.; Knill, D.C. Unifying account of visual motion and position perception. Proc. Natl. Acad. Sci. USA 2015, 112, 8142–8147. [Google Scholar] [CrossRef]
- Plotnikov, S.A.; Lehnert, J.; Fradkov, A.L.; Schöll, E. Synchronization in heterogeneous FitzHugh-Nagumo networks with hierarchical architecture. Int. J. Bifurc. Chaos 2016, 94, 012203. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M. New Improvement of the Expansion Methods for Solving the Generalized Fitzhugh-Nagumo Equation with Time-Dependent Coefficients. Int. J. Eng. Math. 2015, 2015, 107978. [Google Scholar] [CrossRef]
- Singh, B.K.; Arora, G.; Singh, M.K. A numerical scheme for the generalized Burgers-Huxley equation. J. Egypt. Math. Soc. 2016, 24, 629–637. [Google Scholar] [CrossRef]
- Chang, C.-J.; Jazayeri, M. Integration of speed and time for estimating time to contact. Proc. Natl. Acad. Sci. USA 2018, 115, E2879–E2887. [Google Scholar] [CrossRef] [PubMed]
- Johns, M.; Crowley, K.; Chapman, R.; Tucker, A.; Hocking, C. The effect of blinks and saccadic eye movements on visual reaction times. Atten. Percept. Psychophys. 2009, 71, 783–788. [Google Scholar] [CrossRef]
- Van Vugt, B.; Dagnino, B.; Vartak, D.; Safaai, H.; Panzeri, S.; Dehaene, S. The threshold for conscious report: Signal loss and response bias in visual and frontal cortex. Science 2018, 360, 537–542. [Google Scholar] [CrossRef]
- Ghadirzadeh, A.; Maki, A.; Bjorkman, M. A sensorimotor approach for self-learning of hand-eye coordination. IEEE Int. Conf. Intell. Robot. Syst. 2015, 4969–4975. [Google Scholar]
- Rao, H.M.; Khanna, R.; Zielinski, D.J.; Lu, Y.; Clements, J.M.; Potter, N.D.; Sommer, M.A.; Kopper, R. Sensorimotor Learning during a Marksmanship Task in Immersive Virtual Reality. Front. Psychol. 2018, 9, 58. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.T.; Khan, K.; Akbar, M.A. Study of Nonlinear Evolution Equations to Construct Traveling Wave Solutions via Modified Simple Equation Method. Phys. Rev. Res. Int. 2013, 3, 490–503. [Google Scholar]
- Khan, K.; Akbar, M.A.; Koppelaar, H. Study of coupled nonlinear partial differential equations for finding exact analytical solutions. R. Soc. Open Sci. 2015, 2, 140406. [Google Scholar] [CrossRef]
- Khan, K.; Koppelaar, H.; Akbar, M.A. Exact and numerical soliton solutions to nonlinear wave equations. Casp. J. Comput. Math. Eng. 2016, 2, 5–22. [Google Scholar]
- Vasiev, B.N. Classification of patterns in excitable systems with lateral inhibition. Phys. Lett. A 2004, 323, 194–203. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koppelaar, H.; Kordestani Moghadam, P.; Khan, K.; Kouhkani, S.; Segers, G.; van Warmerdam, M. Reaction Time Improvements by Neural Bistability. Behav. Sci. 2019, 9, 28. https://doi.org/10.3390/bs9030028
Koppelaar H, Kordestani Moghadam P, Khan K, Kouhkani S, Segers G, van Warmerdam M. Reaction Time Improvements by Neural Bistability. Behavioral Sciences. 2019; 9(3):28. https://doi.org/10.3390/bs9030028
Chicago/Turabian StyleKoppelaar, Henk, Parastou Kordestani Moghadam, Kamruzzaman Khan, Sareh Kouhkani, Gijs Segers, and Martin van Warmerdam. 2019. "Reaction Time Improvements by Neural Bistability" Behavioral Sciences 9, no. 3: 28. https://doi.org/10.3390/bs9030028
APA StyleKoppelaar, H., Kordestani Moghadam, P., Khan, K., Kouhkani, S., Segers, G., & van Warmerdam, M. (2019). Reaction Time Improvements by Neural Bistability. Behavioral Sciences, 9(3), 28. https://doi.org/10.3390/bs9030028




