A Machine Learning Approach for Studying the Comorbidities of Complex Diagnoses
Abstract
1. Introduction
2. Materials and Methods
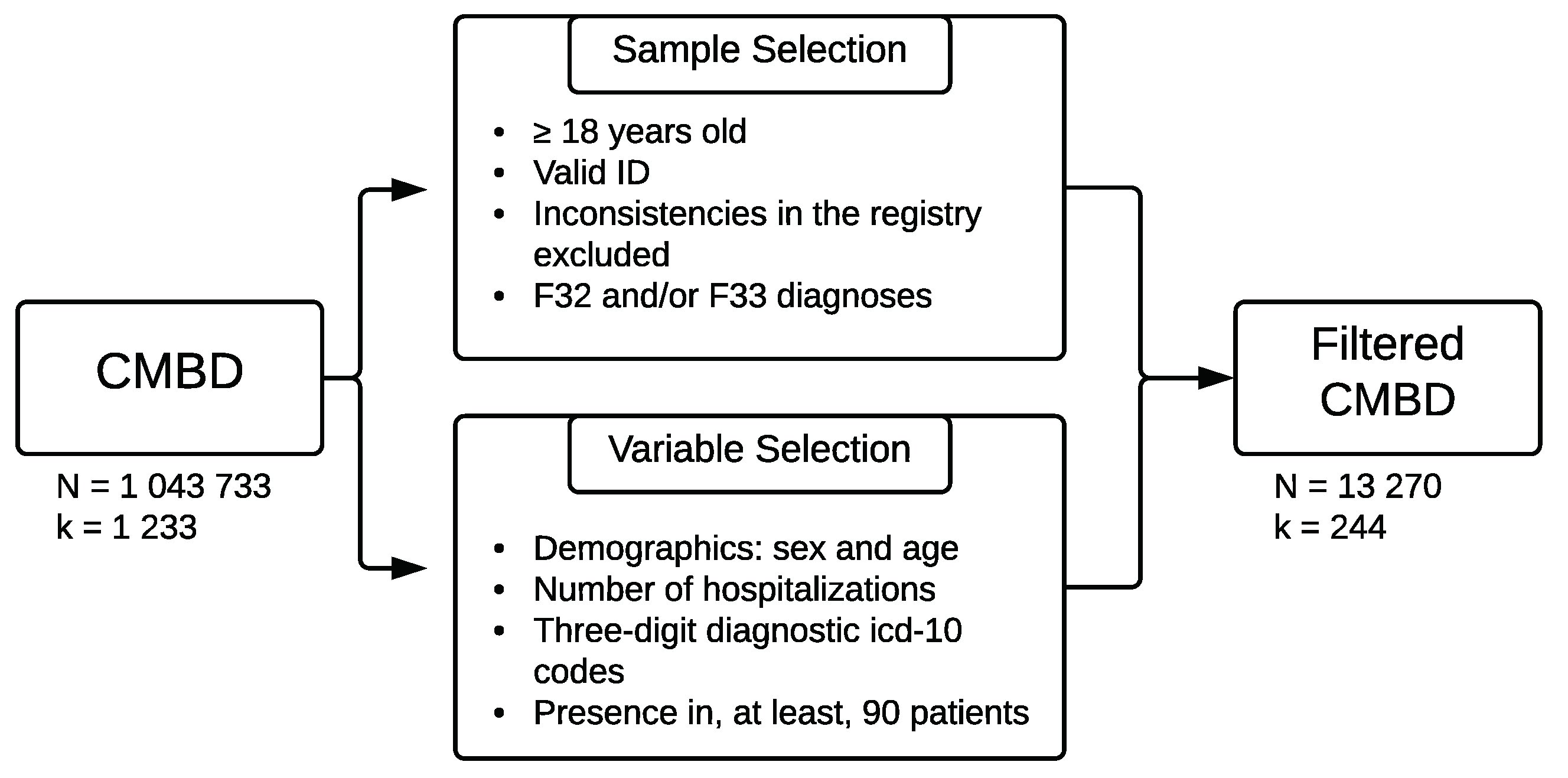
2.1. Data Source
2.2. Statistical Procedure
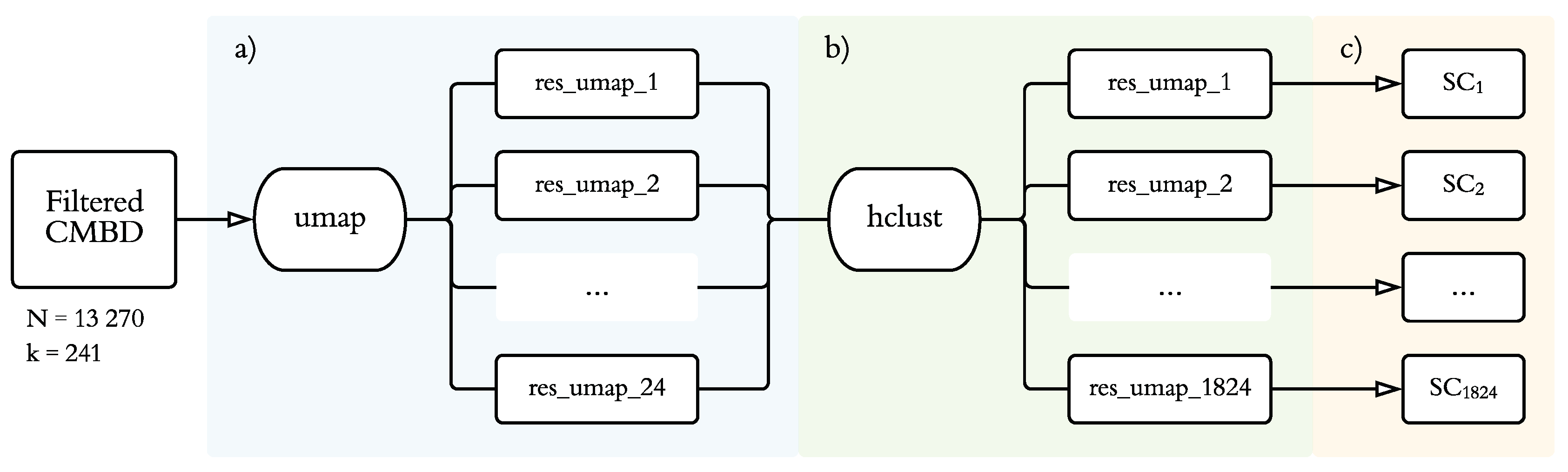
2.2.1. Dimensionality Reduction
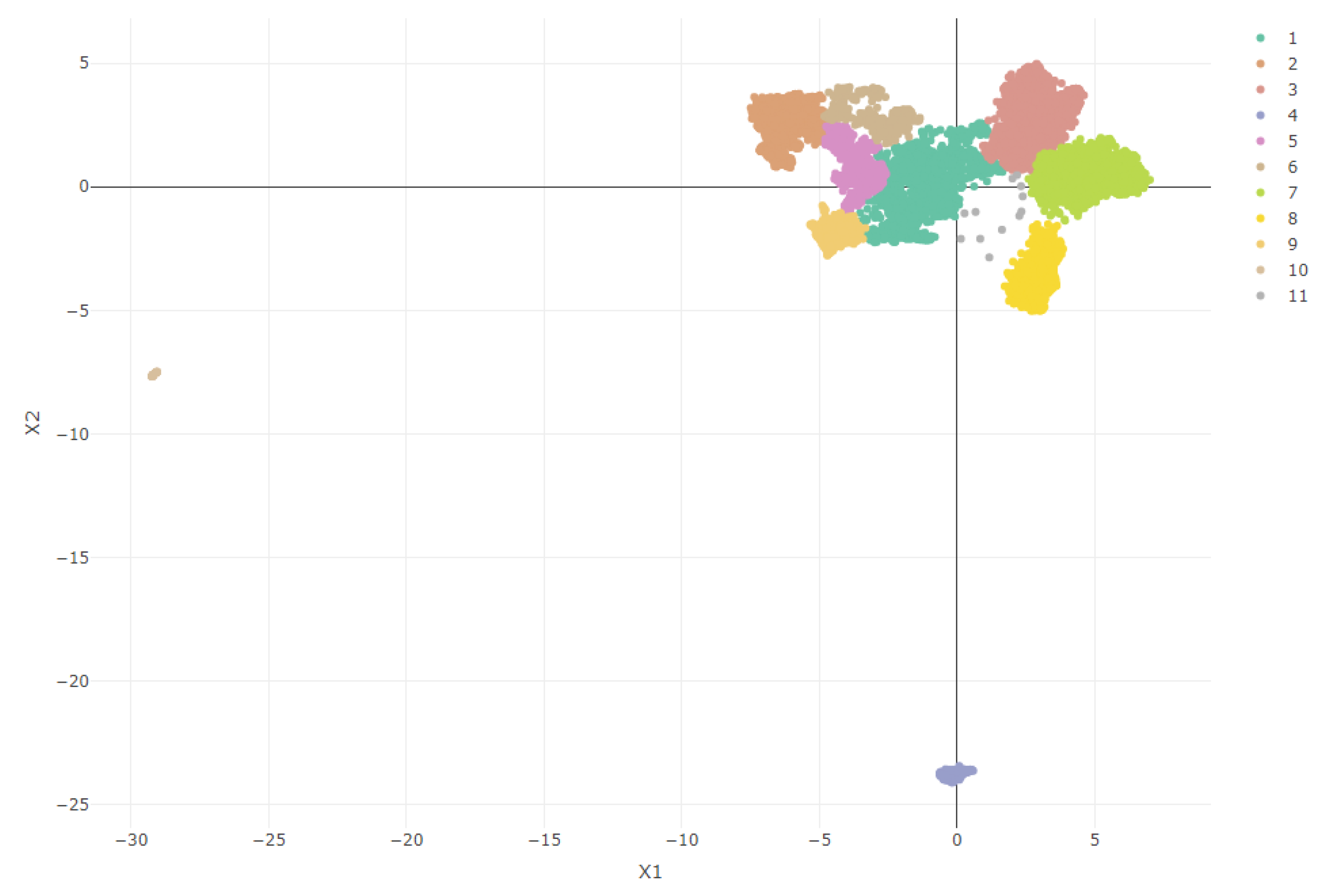
2.2.2. Clustering Analysis
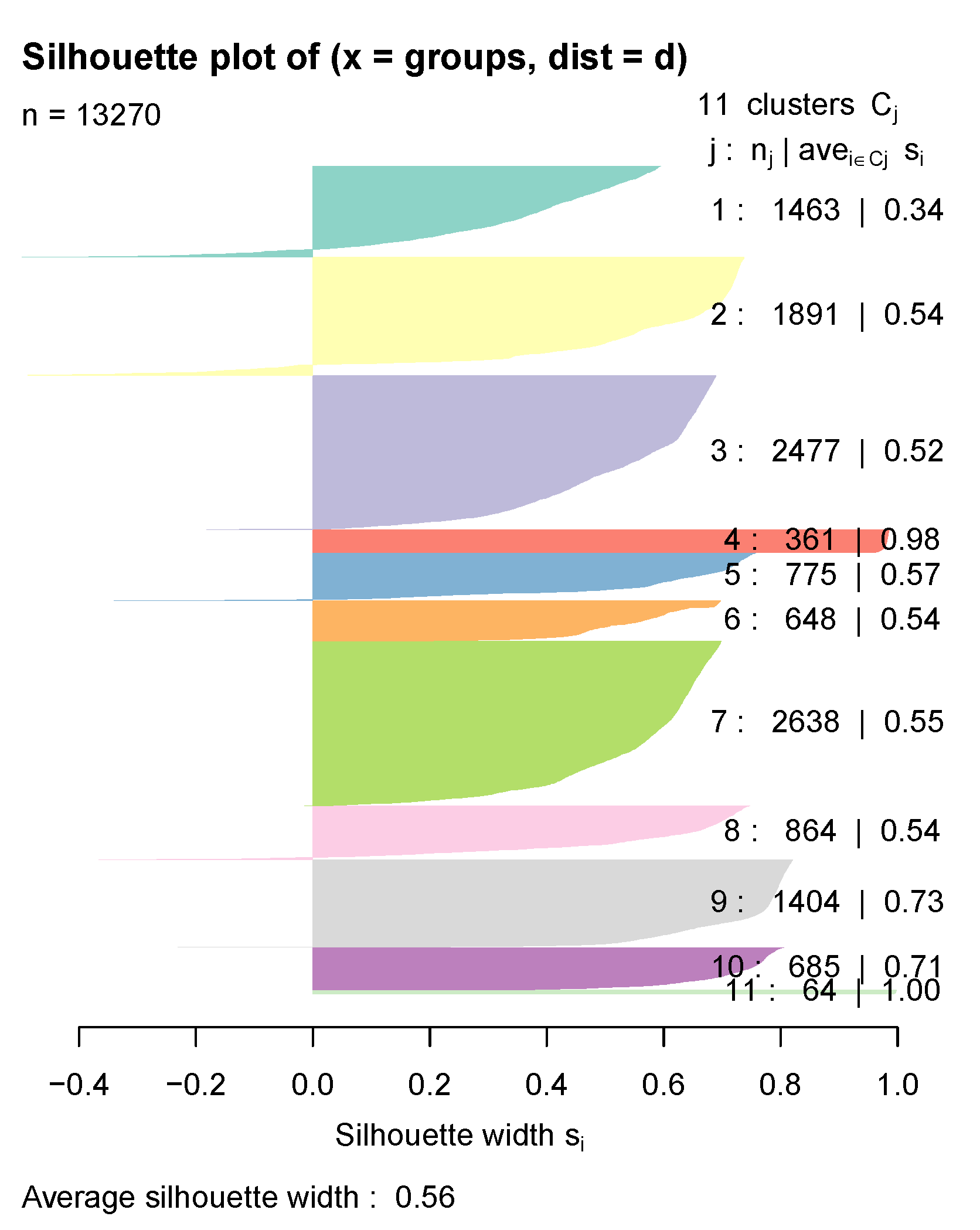
2.2.3. Model Evaluation
3. Results
3.1. Sample Characteristics
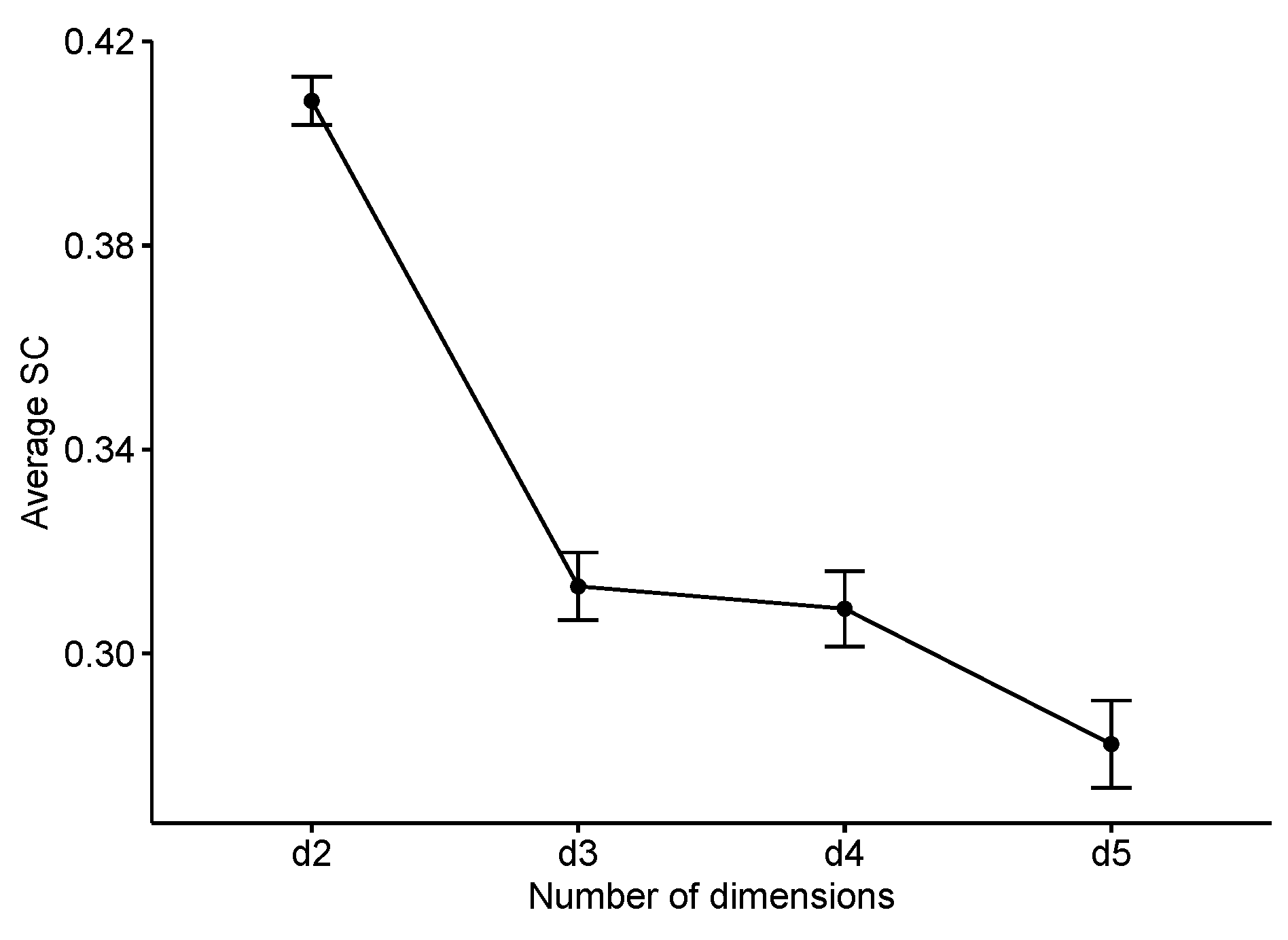
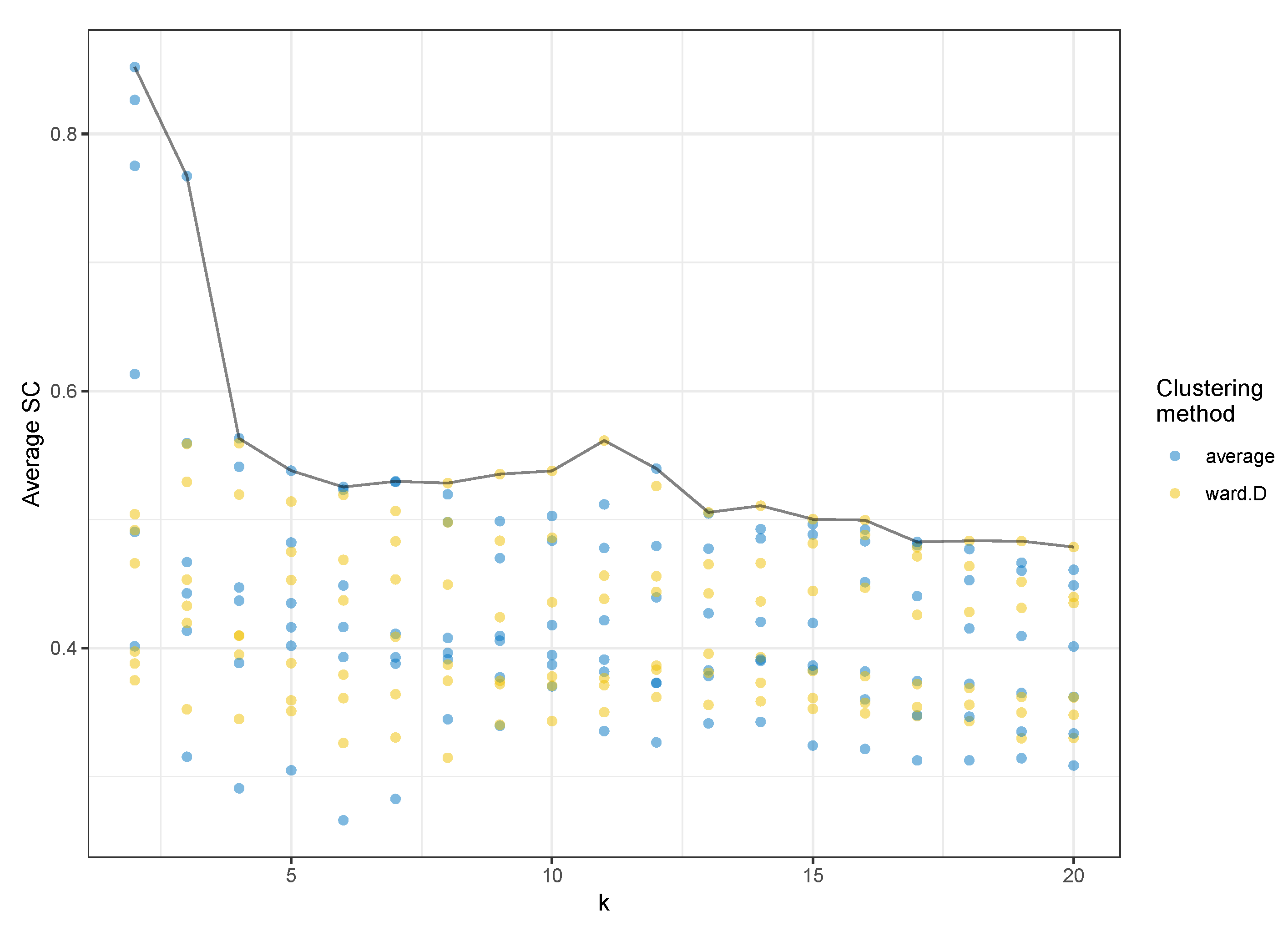
3.2. Model Selection
3.3. Cluster Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EHR | Electronic health record |
| CMBD | Minimum and basic data at hospital discharge (Conjunto Mínimo Básico de Datos al alta hospitalaria) |
| UMAP | Uniform manifold approximation and projection |
| MCA | Multiple correspondence analysis |
| PCA | Principal component analysis |
| t-SNE | t-Stochastic neighbor embedding |
| SC | Silhouette coefficient |
| COPD | Chronic obstructive pulmonary disease |
References
- Ngiam, K.Y.; Khor, I.W. Big data and machine learning algorithms for health-care delivery. Lancet Oncol. 2019, 20, e262–e273. [Google Scholar] [CrossRef]
- Rumsfeld, J.S.; Joynt, K.E.; Maddox, T.M. Big data analytics to improve cardiovascular care: Promise and challenges. Nat. Rev. Cardiol. 2016, 13, 350–359. [Google Scholar] [CrossRef] [PubMed]
- Burgel, P.R.; Paillasseur, J.L.; Roche, N. Identification of Clinical Phenotypes Using Cluster Analyses in COPD Patients with Multiple Comorbidities. BioMed Res. Int. 2014, 2014, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zumel, N.; Mount, J. Practical Data Science with R; Manning Publications Co.: Shelter Island, NY, USA, 2014. [Google Scholar]
- Pikoula, M.; Quint, J.K.; Nissen, F.; Hemingway, H.; Smeeth, L.; Denaxas, S. Identifying clinically important COPD sub-types using data-driven approaches in primary care population based electronic health records. BMC Med. Inform. Decis. Mak. 2019, 19, 86. [Google Scholar] [CrossRef] [PubMed]
- Raherison, C.; Ouaalaya, E.H.; Bernady, A.; Casteigt, J.; Nocent-Eijnani, C.; Falque, L.; Le Guillou, F.; Nguyen, L.; Ozier, A.; Molimard, M. Comorbidities and COPD severity in a clinic-based cohort. BMC Pulm. Med. 2018, 18, 117. [Google Scholar] [CrossRef] [PubMed]
- Castaldi, P.J.; Benet, M.; Petersen, H.; Rafaels, N.; Finigan, J.; Paoletti, M.; Marike Boezen, H.; Vonk, J.M.; Bowler, R.; Pistolesi, M.; et al. Do COPD subtypes really exist? COPD heterogeneity and clustering in 10 independent cohorts. Thorax 2017, 72, 998–1006. [Google Scholar] [CrossRef]
- Burgel, P.R.; Paillasseur, J.L.; Janssens, W.; Piquet, J.; ter Riet, G.; Garcia-Aymerich, J.; Cosio, B.; Bakke, P.; Puhan, M.A.; Langhammer, A.; et al. A simple algorithm for the identification of clinical COPD phenotypes. Eur. Respir. J. 2017, 50, 1701034. [Google Scholar] [CrossRef]
- Dipnall, J.F.; Pasco, J.A.; Berk, M.; Williams, L.J.; Dodd, S.; Jacka, F.N.; Meyer, D. Into the Bowels of Depression: Unravelling Medical Symptoms Associated with Depression by Applying Machine-Learning Techniques to a Community Based Population Sample. PLoS ONE 2016, 11, e0167055. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Mori, Y.; Kuroda, M.; Makino, N. Joint Dimension Reduction and Clustering. In Nonlineal PCA and Its Applications; Springer: Singapore, 2016; pp. 57–64. [Google Scholar]
- Saeys, Y.; Van Gassen, S.; Lambrecht, B.N. Computational flow cytometry: Helping to make sense of high-dimensional immunology data. Nat. Rev. Immunol. 2016, 16, 449–462. [Google Scholar] [CrossRef]
- Lugli, E.; Pinti, M.; Nasi, M.; Troiano, L.; Ferraresi, R.; Mussi, C.; Salvioli, G.; Patsekin, V.; Robinson, J.P.; Durante, C.; et al. Subject classification obtained by cluster analysis and principal component analysis applied to flow cytometric data. Cytom. Part A 2007, 71A, 334–344. [Google Scholar] [CrossRef] [PubMed]
- Castaldi, P.J.; Dy, J.; Ross, J.; Chang, Y.; Washko, G.R.; Curran-Everett, D.; Williams, A.; Lynch, D.A.; Make, B.J.; Crapo, J.D.; et al. Cluster analysis in the COPDGene study identifies subtypes of smokers with distinct patterns of airway disease and emphysema. Thorax 2014, 69, 416–423. [Google Scholar] [CrossRef] [PubMed]
- Yeung, K.Y.; Ruzzo, W.L. An Empirical Study on Principal Component Analysis for Clustering Gene Expression Data; Department of Computer Science & Engineering, University of Washington: Seattle, WA, USA, 2000; p. 29. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Hurley, N.C.; Haimovich, A.D.; Taylor, R.A.; Mortazavi, B.J. Visualization of Emergency Department Clinical Data for Interpretable Patient Phenotyping. arXiv 2019, arXiv:1907.11039. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2018, 37, 38. [Google Scholar] [CrossRef]
- Dorrity, M.W.; Saunders, L.M.; Queitsch, C.; Fields, S.; Trapnell, C. Dimensionality reduction by UMAP to visualize physical and genetic interactions. bioRxiv 2019, 681726. [Google Scholar] [CrossRef]
- Ali, M.; Jones, M.W.; Xie, X.; Williams, M. TimeCluster: Dimension reduction applied to temporal data for visual analytics. Vis. Comput. 2019, 35, 1013–1026. [Google Scholar] [CrossRef]
- Salud Madrid. Public Dataset CMBD. 2018 needs to be changed to: Salud Madrid. Public dataset CMBD. 2018. Available online: http://canalcamtv.com/cs/Satellite?cid=1354690911679&language=es&pagename=PortalSalud1%5C%2FPage%5C%2FPTSA_pintarContenidoFinal&vest=1354690911679 (accessed on 30 May 2018).
- ICD-10 Data Codes. 2018. Available online: https://www.icd10data.com/ICD10CM/Codes (accessed on 30 March 2019).
- Choi, S.S.; Cha, S.H.; Tappert, C.C. A Survey of Binary Similarity and Distance Measures; Department of Computer Science, Pace University New York: New York, NY, USA, 2010; p. 6. [Google Scholar]
- Kassambara, A. Practical Guide to Cluster Analysis in R. STHDA. 2017. Available online: https://www.twirpx.com/file/2239131/ (accessed on 20 November 2019).
- Pols, A.D.; van Dijk, S.E.; Bosmans, J.E.; Hoekstra, T.; van Marwijk, H.W.J.; van Tulder, M.W.; Adriaanse, M.C. Effectiveness of a stepped-care intervention to prevent major depression in patients with type 2 diabetes mellitus and/or coronary heart disease and subthreshold depression: A pragmatic cluster randomized controlled trial. PLoS ONE 2017, 12, e0181023. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.L.; Han, K.; Tao, Z.Q.; Wu, Z.M. Biological interaction between sleep quality and depression in type 2 diabetes. Eur. Rev. Med. Pharmacol. Sci. 2016, 20, 3087–3091. [Google Scholar] [PubMed]
- Simning, A.; Seplaki, C.L.; Conwell, Y. The association of a heart attack or stroke with depressive symptoms stratified by the presence of a close social contact: Findings from the National Health and Aging Trends Study Cohort: NHATS social support and depressive symptoms. Int. J. Geriatr. Psychiatry 2018, 33, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Hwang, S.; Jayadevappa, R.; Zee, J.; Zivin, K.; Bogner, H.R.; Raue, P.J.; Bruce, M.L.; Reynolds, C.F.; Gallo, J.J. Concordance Between Clinical Diagnosis and Medicare Claims of Depression Among Older Primary Care Patients. Am. J. Geriatr. Psychiatry 2015, 23, 726–734. [Google Scholar] [CrossRef] [PubMed]
- Ayerbe, L.; Ayis, S.; Wolfe, C.D.A.; Rudd, A.G. Natural history, predictors and outcomes of depression after stroke: systematic review and meta-analysis. Br. J. Psychiatry 2013, 202, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Skala, J.A.; Freedland, K.E.; Carney, R.M. Coronary Heart Disease and Depression: A Review of Recent Mechanistic Research. Can. J. Psychiatry 2006, 51, 738–745. [Google Scholar] [CrossRef]
- Thakur, E.R.; Quigley, B.M.; El-Serag, H.B.; Gudleski, G.D.; Lackner, J.M. Medical comorbidity and distress in patients with irritable bowel syndrome: The moderating role of age. J. Psychosom. Res. 2016, 88, 48–53. [Google Scholar] [CrossRef]
- Han, K.M.; Kim, M.S.; Kim, A.; Paik, J.W.; Lee, J.; Ham, B.J. Chronic medical conditions and metabolic syndrome as risk factors for incidence of major depressive disorder: A longitudinal study based on 4.7 million adults in South Korea. J. Affect. Disord. 2019, 257, 486–494. [Google Scholar] [CrossRef]
- Scalco, A.Z.; Scalco, M.Z.; Azul, J.B.S.; Lotufo Neto, F. Hypertension and depression. Clinics 2005, 60, 241–250. [Google Scholar] [CrossRef]
- Blumenthal, K.G.; Li, Y.; Acker, W.W.; Chang, Y.; Banerji, A.; Ghaznavi, S.; Camargo, C.A.; Zhou, L. Multiple drug intolerance syndrome and multiple drug allergy syndrome: Epidemiology and associations with anxiety and depression. Allergy 2018, 73, 2012–2023. [Google Scholar] [CrossRef]
- Wu, L.T.; Zhu, H.; Ghitza, U.E. Multicomorbidity of chronic diseases and substance use disorders and their association with hospitalization: Results from electronic health records data. Drug Alcohol Depend. 2018, 192, 316–323. [Google Scholar] [CrossRef]
- Eichler, J.; Schmidt, R.; Hiemisch, A.; Kiess, W.; Hilbert, A. Gestational weight gain, physical activity, sleep problems, substance use, and food intake as proximal risk factors of stress and depressive symptoms during pregnancy. BMC Pregnancy Childbirth 2019, 19, 175. [Google Scholar] [CrossRef] [PubMed]
- Altazan, A.D.; Redman, L.M.; Burton, J.H.; Beyl, R.A.; Cain, L.E.; Sutton, E.F.; Martin, C.K. Mood and quality of life changes in pregnancy and postpartum and the effect of a behavioral intervention targeting excess gestational weight gain in women with overweight and obesity: A parallel-arm randomized controlled pilot trial. BMC Pregnancy Childbirth 2019, 19, 50. [Google Scholar] [CrossRef] [PubMed]
- Rejnö, G.; Lundholm, C.; Öberg, S.; Lichtenstein, P.; Larsson, H.; D’Onofrio, B.; Larsson, K.; Saltvedt, S.; Brew, B.K.; Almqvist, C. Maternal anxiety, depression and asthma and adverse pregnancy outcomes—A population based study. Sci. Rep. 2019, 9, 13101. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: All samples used in this study are available from the authors. |
| Chapter Name | 3D Code | 3D Name | Cl 1 | Cl 2 | Cl 3 | Cl 4 | Cl 5 | Cl 6 | Cl 7 | Cl 8 | Cl 9 | Cl 10 | Cl 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Endocrine, Nutritional | |||||||||||||
| and Metabolic Diseases | E03 | Other hypothyroidism | 31.3 | ||||||||||
| E11 | Type 2 diabetes mellitus | 39.2 | 39.7 | ||||||||||
| E78 | Disorders of lipoprotein | ||||||||||||
| metabolism and lipidemias | 42.0 | 33.8 | 96.5 | 95.5 | 39.1 | ||||||||
| E87 | Other disorders of fluid, | ||||||||||||
| electrolyte and acid-base | 30.0 | ||||||||||||
| Mental, Behavioral and | |||||||||||||
| Neurodevelopmental disorders | F10 | Alcohol related disorders | 35.5 | ||||||||||
| F17 | Nicotine dependence | 99.3 | |||||||||||
| F32 | Major depressive disorder, | ||||||||||||
| single episode | 99.5 | 99.9 | 99.4 | 100 | 99.8 | 99.6 | 99.9 | 99.0 | 99.6 | 100 | |||
| F33 | Major depressive disorder, | ||||||||||||
| recurrent | 100 | ||||||||||||
| Diseases of the | |||||||||||||
| Circulatory System | I10 | Primary hypertension | 99.2 | 31.3 | 98.0 | 49.1 | |||||||
| I12 | Hypertensive chronic | ||||||||||||
| kidney disease | 55.5 | ||||||||||||
| I48 | Atrial fibrillation flutter | 37.9 | |||||||||||
| I50 | Heart faliure | 43.5 | |||||||||||
| Diseases of the | |||||||||||||
| Respiratory System | J96 | Respiratory failure, | |||||||||||
| not elsewhere classified | 46.1 | ||||||||||||
| Diseases of the | |||||||||||||
| Genitourinary System | N17 | Acute kidney failure | 39.8 | ||||||||||
| N18 | Chronic Kidney Disease | 66.2 | |||||||||||
| Pregnancy, Childbirth and | |||||||||||||
| the Puerperium | O99 | Other maternal diseases | |||||||||||
| classifiable elsewhere (...) | 100 | ||||||||||||
| Symptoms, signs and abnormal | |||||||||||||
| clinical and laboratory findings | R05 | Cough | 55.4 | 32.1 | 38.4 | 99.9 | 100 | ||||||
| Factors influencing health status | |||||||||||||
| and contact with health services | Z85 | Personal history of | |||||||||||
| malignant neoplasm | 58.3 | ||||||||||||
| Z88 | Allergy status to drugs, | ||||||||||||
| medicaments (...) | 98.6 | ||||||||||||
| Z90 | Acquired absence of organs, | ||||||||||||
| not elsewhere classified | 32.3 | ||||||||||||
| Z92 | Personal history of medical | ||||||||||||
| treatment | 28.7 | ||||||||||||
| Z99 | Dependence on enabling | ||||||||||||
| machines and devices (...) | 31.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Rico, M.; Alvarado, J.M. A Machine Learning Approach for Studying the Comorbidities of Complex Diagnoses. Behav. Sci. 2019, 9, 122. https://doi.org/10.3390/bs9120122
Sánchez-Rico M, Alvarado JM. A Machine Learning Approach for Studying the Comorbidities of Complex Diagnoses. Behavioral Sciences. 2019; 9(12):122. https://doi.org/10.3390/bs9120122
Chicago/Turabian StyleSánchez-Rico, Marina, and Jesús M. Alvarado. 2019. "A Machine Learning Approach for Studying the Comorbidities of Complex Diagnoses" Behavioral Sciences 9, no. 12: 122. https://doi.org/10.3390/bs9120122
APA StyleSánchez-Rico, M., & Alvarado, J. M. (2019). A Machine Learning Approach for Studying the Comorbidities of Complex Diagnoses. Behavioral Sciences, 9(12), 122. https://doi.org/10.3390/bs9120122






