Aberrant Responding in Hypothesis Testing: A Threat to Validity or Source of Insight?
Abstract
1. Framework for Aberrant Responding in Measurement
2. Studying Student–Teacher Relations and School Safety
3. Importance of the Present Study
- Aberrant responding (measured by U3 and the number of Guttman errors) acts as a bifurcation parameter, leading to discontinuous and unpredictable changes in school safety perceptions when present in large amounts.
- The cusp model will provide a better fit to the data compared to traditional linear and logistic models, demonstrating the need for nonlinear modeling in studying measurement artifacts.
- The relationship between student–teacher relations and school safety will be significantly moderated by aberrant responding, leading to differential effects depending on the level of aberrance in the data.
4. Major Research Hypothesis and Analytical Model
5. Goal of the Present Study
6. Method
6.1. Participants and Procedures
6.2. Measures
6.2.1. Student–Teacher Relations
6.2.2. Feelings of Safety
6.2.3. Aberrant Responding
6.3. Data Analyses
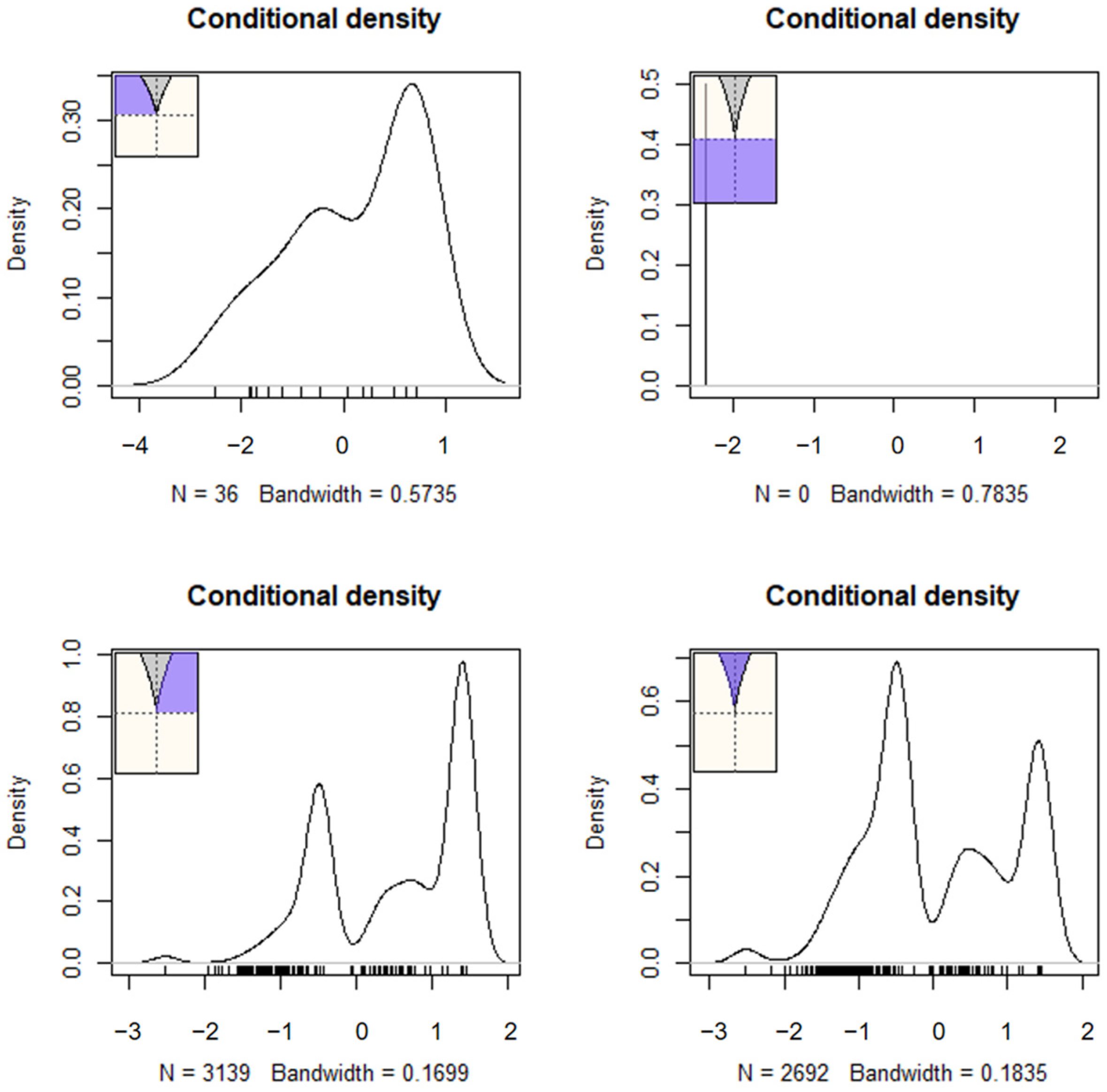
6.3.1. Evaluating Person Aberrance Levels
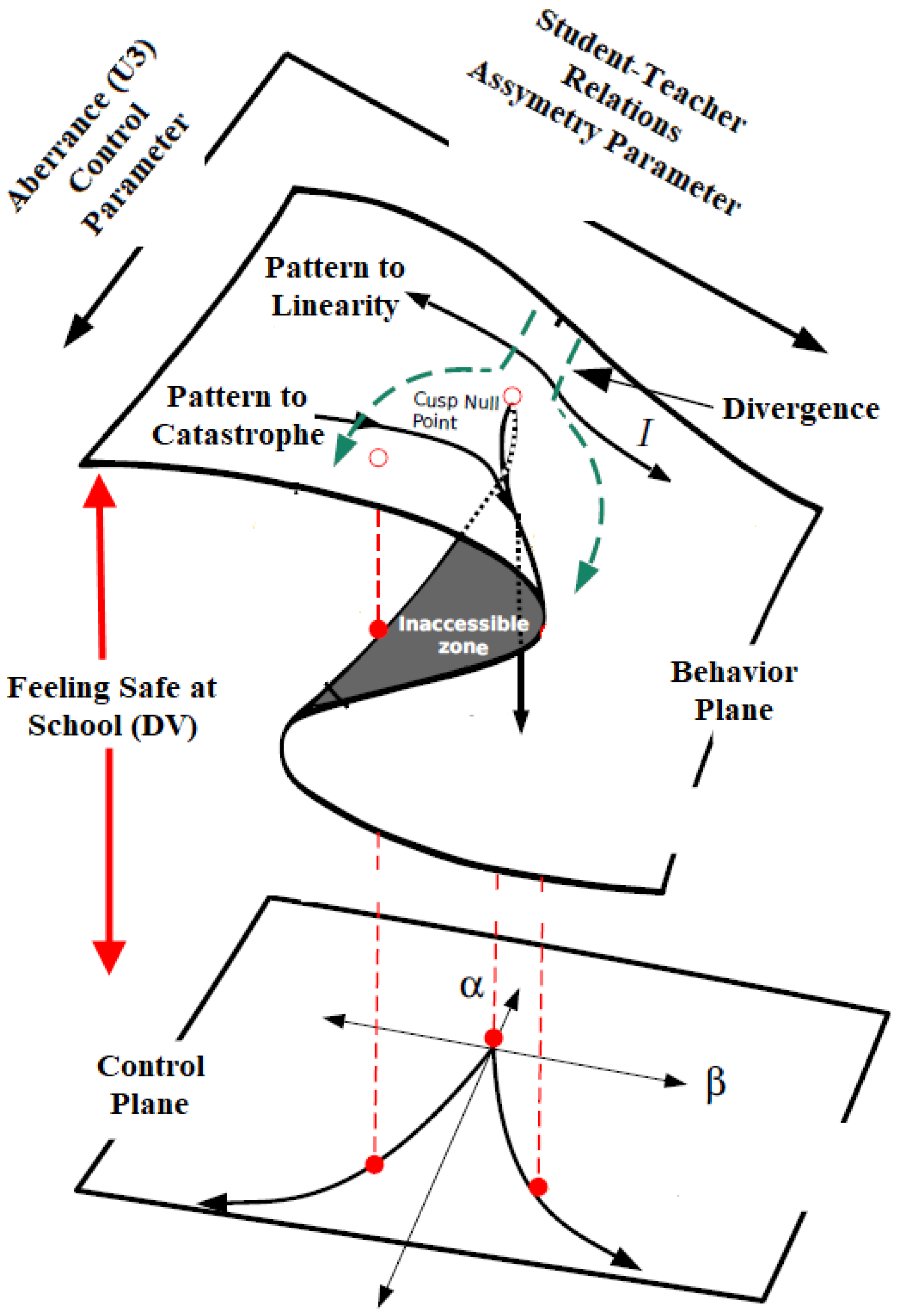
6.3.2. Cusp Catastrophe Model: Description
7. Results
7.1. Prerequisite Analyses of the Cusp Catastrophe Model
7.2. Examining the Role of Aberrant Responding to the Prediction of School Safety from Student–Teacher Relations
8. Discussion
8.1. Limitations
8.2. Implications of the Findings for Educational Policy
8.3. Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Abulela, M. A. A., & Rios, J. A. (2022). Comparing the robustness of three nonparametric DIF procedures to differential rapid guessing. Applied Measurement in Education, 35(2), 81–94. [Google Scholar] [CrossRef]
- Ameijeiras-Alonso, J., Crujeiras, R. M., & Rodriguez-Casal, A. (2021). multimode: An R package for mode assessment. Journal of Statistical Software, 97(9), 1–32. [Google Scholar] [CrossRef]
- Astor, R. A., Benbenishty, R., & Estrada, J. N. (2009). School violence and theoretical perspectives: Where should we go next? Educational Researcher, 38(1), 27–36. [Google Scholar]
- Bolt, D. M., & Newton, J. R. (2011). Multiscale measurement of extreme response style. Educational and Psychological Measurement, 71(5), 814–833. [Google Scholar] [CrossRef]
- Chen, D.-G., & Chen, X. (2017). Cusp catastrophe regression and its application in public health and behavioral research. International Journal of Environmental Research and Public Health, 14(10), 1220. [Google Scholar] [CrossRef] [PubMed]
- Chen, X., Wang, K., & Chen, D. G. (2020). Cusp catastrophe regression analysis of testosterone in bifurcating the age-related changes in PSA, a biomarker for prostate cancer. In X. Chen, & D. G. Chen (Eds.), Statistical methods for global health and epidemiology: Principles, methods and applications (pp. 353–372). Springer. [Google Scholar]
- Cobb, L. (1998). An Introduction to cusp surface analysis. Technical Report. Aetheling Consultants. Available online: http://www.aetheling.com/models/cusp/Intro.htm (accessed on 2 February 2025).
- Cornell, D., & Mayer, M. J. (2010). Why do school order and safety matter? Educational Researcher, 39(1), 7–15. [Google Scholar] [CrossRef]
- Emons, W. H. M., Meijer, R. R., & Sijtsma, K. (2002). Comparing simulated and theoretical sampling distributions of the U3 person-fit statistic. Applied Psychological Measurement, 26(1), 88–108. [Google Scholar] [CrossRef]
- Ferrando, P. J. (2015). Assessing person fit in typical-response measures. In S. P. Reise, & D. A. Revicki (Eds.), Handbook of item response theory modeling: Applications to typical performance assessment (pp. 128–155). Routledge/Taylor & Francis Group. [Google Scholar]
- Grasman, R. P., van der Maas, H. L. J., & Wagenmakers, E. J. (2009). Fitting the cusp catastrophe in R: A cusp package primer. Journal of Statistical Software, 32, 1–27. [Google Scholar] [CrossRef]
- Gregory, A., Cornell, D., Fan, X., Sheras, P., Shih, T.-H., & Huang, F. (2010). Authoritative school discipline: High school practices associated with lower bullying and victimization. Journal of Educational Psychology, 102(2), 483–496. [Google Scholar] [CrossRef]
- Guastello, S. J. (2001). Nonlinear dynamics in psychology. Discrete Dynamics in Nature and Society, 6, 11–29. [Google Scholar] [CrossRef]
- Guastello, S. J. (2002). Managing emergent phenomena: Non-linear dynamics in work organizations. Lawrence. [Google Scholar]
- Hartelman, A. I. (1997). Stochastic catastrophe theory. University of Amsterdam. [Google Scholar]
- Hartelman, P. A. I., van der Maas, H. L. J., & Molenaar, P. C. M. (1998). Detecting and modelling developmental transitions. British Journal of Developmental Psychology, 16(1), 97–122. [Google Scholar] [CrossRef]
- Hartigan, J. A., & Hartigan, P. M. (1985). The Dip Test of Unimodality. The Annals of Statistics, 13(1), 70–84. [Google Scholar] [CrossRef]
- Jia, B., Zhang, X., & Zhu, Z. (2019). A short note on aberrant responses bias in item response theory. Frontiers in Psychology, 10, 43. [Google Scholar] [CrossRef] [PubMed]
- Karabatsos, G. (2003). Comparing the aberrant response detection performance of thirty-six person-fit statistics. Applied Measurement in Education, 16(4), 277–298. [Google Scholar] [CrossRef]
- Meijer, R. R. (1996). Person-Fit research: An introduction. Applied Measurement in Education, 9, 3–8. [Google Scholar] [CrossRef]
- Meijer, R. R., & Sijtsma, K. (2001). Methodology review: Evaluating person fit. Applied Psychological Measurement, 25(2), 107–135. [Google Scholar]
- Minnotte, M. C., & Scott, D. W. (1993). The mode tree: A tool for visualization of nonparametric density features. Journal of Computational and Graphical Statistics, 2(1), 51–68. [Google Scholar] [CrossRef]
- Mokken, R. J. (1971). A theory and procedure of scale analysis: With applications in political research. Mouton. [Google Scholar]
- Mokkan, R. J., & Lewis, C. (1982). A nonparametric approach to the analysis of dichotomous item responses. Applied Psychological Measurement, 6(4), 417–430. [Google Scholar] [CrossRef]
- Nicolis, G., & Nicolis, C. (2007). Foundations of complex systems. World Scientific. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). (2019). PISA 2018 assessment and analytical framework. OECD Publishing. [Google Scholar] [CrossRef]
- R Core Team. (2023). R: A language and environment for statistical computing (Version 4.3.0). [R Foundation for Statistical Computing]. Available online: https://www.R-project.org/ (accessed on 2 February 2025).
- Rutkowski, L., & Rutkowski, D. (2009). Trends in TIMSS responses over time: Evidence of global forces in education? Educational Research & Evaluation, 15(2), 137–152. [Google Scholar]
- Sijtsma, K., & Meijer, R. R. (2001). The person-response function in personality testing and assessment. Applied Psychological Measurement, 25(3), 192–210. [Google Scholar]
- Stewart, I. N., & Peregoy, P. L. (1983). Catastrophe theory modeling in psychology. Psychological Bulletin, 94, 336–362. [Google Scholar] [CrossRef]
- Tendeiro, J. N., Meijer, R. R., & Niessen, A. S. M. (2016). PerFit: An R package for person-fit analysis in IRT. Journal of Statistical Software, 74(5), 1–27. [Google Scholar] [CrossRef]
- Thapa, A., Cohen, J., Guffey, S., & Higgins-D’Alessandro, A. (2013). A review of school climate research. Review of Educational Research, 83(3), 357–385. [Google Scholar] [CrossRef]
- Thissen-Roe, A., & Thissen, D. (2013). A two-decision model for responses to likert-type items. Journal of Educational and Behavioral Statistics, 38(5), 522–547. [Google Scholar] [CrossRef]
- Thom, R. (1975). Structural stability and morphogenesis. W.A. Benjamin. [Google Scholar]
- Ulitzsch, E., Shin, H. J., & Lüdtke, O. (2023). Accounting for careless and insufficient effort responding in large-scale survey data—Development, evaluation, and application of a screen-time-based weighting procedure. Behavior Research Methods, 56, 804–825. [Google Scholar] [CrossRef]
- van der Flier, H. (1982). Deviant response patterns and comparison groups: The use of the person-fit measure. Applied Psychological Measurement, 6(3), 327–339. [Google Scholar]
- Van der Maas, H. L. J., & Molennar, P. C. (1992). Stagewise cognitive development: An application of catastrophe theory. Psychological Review, 3, 395–417. [Google Scholar] [CrossRef]
- Van der Maas, H. L. J., Molenaar, P. C. M., & van der Pligt, J. (2003). Sudden transitions in attitudes. Sociological Methods and Research, 23(2), 125–152. [Google Scholar] [CrossRef]
- Wang, M. T., & Degol, J. L. (2016). School climate: A review of the definitions, measures, and impact on student outcomes. Educational Psychology Review, 28, 315–352. [Google Scholar] [CrossRef]
- Wind, S. A., & Ge, Y. (2023). Identifying response styles using person fit analysis and response-styles models. Measurement: Interdisciplinary Research and Perspectives, 21(3), 147–166. [Google Scholar] [CrossRef]
- Wise, S., & Demars, C. (2005). Low examinee effort in low-stakes assessment: Problems and potential solutions. Educational Assessment, 10(1), 1–17. [Google Scholar] [CrossRef]
- Wise, S. L., Kuhfeld, M. R., & Soland, J. (2019). The effects of effort monitoring with proctor notification on test-taking engagement, test performance, and validity. Applied Measurement in Education, 32(2), 183–192. [Google Scholar] [CrossRef]

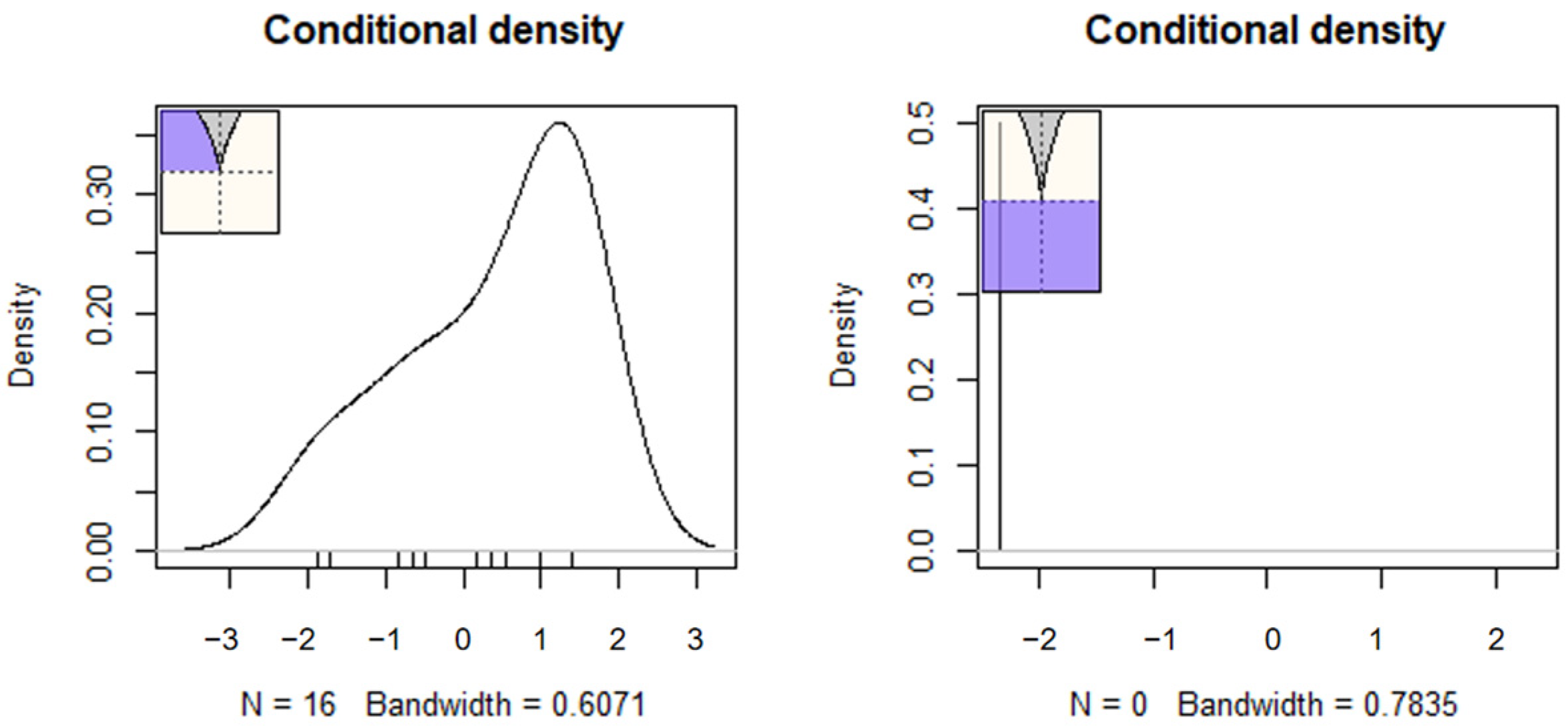
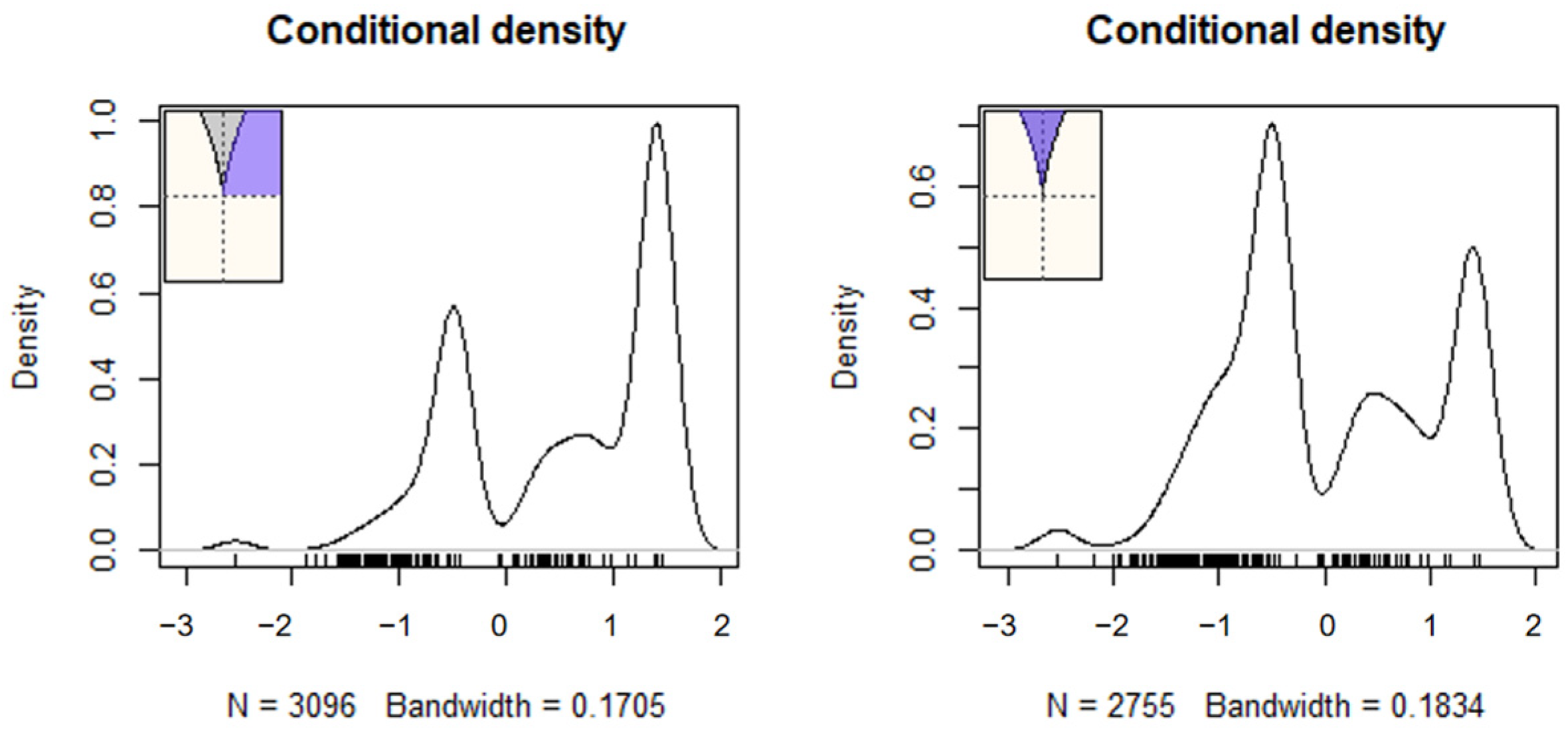


| Goal | U3 | Guttman Errors |
|---|---|---|
| Target | Local inconsistencies | Global response misfit |
| Aberrance Detected | Erratic responses to specific items | Systematic patterns or biases |
| Estimation Method | Residual-based | Likelihood-based |
| Sensitivity in Detecting | Inattention/fatigue/contextual factors | Systematic biases/carelessness/guessing/extreme response style |
| Model | R-Squared | logLik | Npar | AIC | AICc | BIC |
|---|---|---|---|---|---|---|
| U3 | ||||||
| Linear | 0.079 | −8020.634 | 4 | 16,049.270 | 16,049.270 | 16,075.980 |
| Logistic | 0.095 | −7970.330 | 5 | 15,950.660 | 15,950.670 | 15,984.050 |
| Cusp | 0.319 | −7497.490 | 6 | 15,006.980 | 15,006.990 | 15,047.040 |
| Guttman Errors | ||||||
| Linear | 0.080 | −8018.734 | 4 | 16,045.470 | 16,045.470 | 16,072.180 |
| Logistic | 0.095 | −7970.781 | 5 | 15,951.560 | 15,951.570 | 15,984.950 |
| Cusp | 0.291 | −7512.091 | 6 | 15,036.180 | 15,036.200 | 15,076.240 |
| Coefficients: | Estimate | S.E. | z-Value | p-Value | LCI0.025 | UCI0.975 |
|---|---|---|---|---|---|---|
| U3 Bifurcation Term Model | ||||||
| a[(Intercept)] | 0.285 *** | 0.020 | 14.010 | <0.001 | 0.245 | 0.324 |
| a[RELATST] | 0.274 *** | 0.013 | 20.360 | <0.001 | 0.248 | 0.301 |
| b[(Intercept)] | 0.714 *** | 0.050 | 14.360 | <0.001 | 0.616 | 0.811 |
| b[U3poly] | 1.696 *** | 0.169 | 10.050 | <0.001 | 1.365 | 2.027 |
| w[(Intercept)] | 0.280 *** | 0.012 | 22.980 | <0.001 | 0.256 | 0.304 |
| w[FEELSAFE] | 1.009 *** | 0.010 | 102.320 | <0.001 | 0.990 | 1.028 |
| Guttman Errors Bifurcation Term Model | ||||||
| a[(Intercept)] | 0.289 *** | 0.020 | 14.707 | <0.001 | 0.250 | 0.327 |
| a[RELATST] | 0.279 *** | 0.014 | 20.542 | <0.001 | 0.252 | 0.306 |
| b[(Intercept)] | 0.691 *** | 0.056 | 12.249 | <0.001 | 0.580 | 0.801 |
| b[Gpoly] | 0.019 *** | 0.002 | 7.479 | <0.001 | 0.014 | 0.023 |
| w[(Intercept)] | 0.287 *** | 0.012 | 23.254 | <0.001 | 0.263 | 0.311 |
| w[FEELSAFE] | 1.004 *** | 0.010 | 101.744 | <0.001 | 0.985 | 1.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sideridis, G.; Alghamdi, M.H. Aberrant Responding in Hypothesis Testing: A Threat to Validity or Source of Insight? Behav. Sci. 2025, 15, 319. https://doi.org/10.3390/bs15030319
Sideridis G, Alghamdi MH. Aberrant Responding in Hypothesis Testing: A Threat to Validity or Source of Insight? Behavioral Sciences. 2025; 15(3):319. https://doi.org/10.3390/bs15030319
Chicago/Turabian StyleSideridis, Georgios, and Mohammed H. Alghamdi. 2025. "Aberrant Responding in Hypothesis Testing: A Threat to Validity or Source of Insight?" Behavioral Sciences 15, no. 3: 319. https://doi.org/10.3390/bs15030319
APA StyleSideridis, G., & Alghamdi, M. H. (2025). Aberrant Responding in Hypothesis Testing: A Threat to Validity or Source of Insight? Behavioral Sciences, 15(3), 319. https://doi.org/10.3390/bs15030319





