The Effectiveness of Professional Development in the Self-Efficacy of In-Service Teachers in STEM Education: A Meta-Analysis
Abstract
1. Introduction
1.1. Professional Development and Features of Effective PD
1.2. Content of Effective Professional Development
1.3. Format of Professional Development
1.4. Training Time
1.5. Self-Efficacy and Measurement of Self-Efficacy
1.6. Professional Development on Teacher Self-Efficacy
1.7. The Educational Stage, Area, and PD’s Impact on Teachers’ Self-Efficacy
1.8. Research Questions
- (1)
- What is the overall effect size of PD on STEM teachers’ self-efficacy?
- (2)
- Which moderators of the characteristics of PD have an impact on the improvement of STEM teachers’ self-efficacy? In the present study, the moderators consisted of publication type, area, educational stage, PD format, PD content, participant size, duration, and training hour.
- (3)
- Are there any differences in the effectiveness of PD with different scales of self-efficacy on STEM teachers’ self-efficacy?
2. Methods
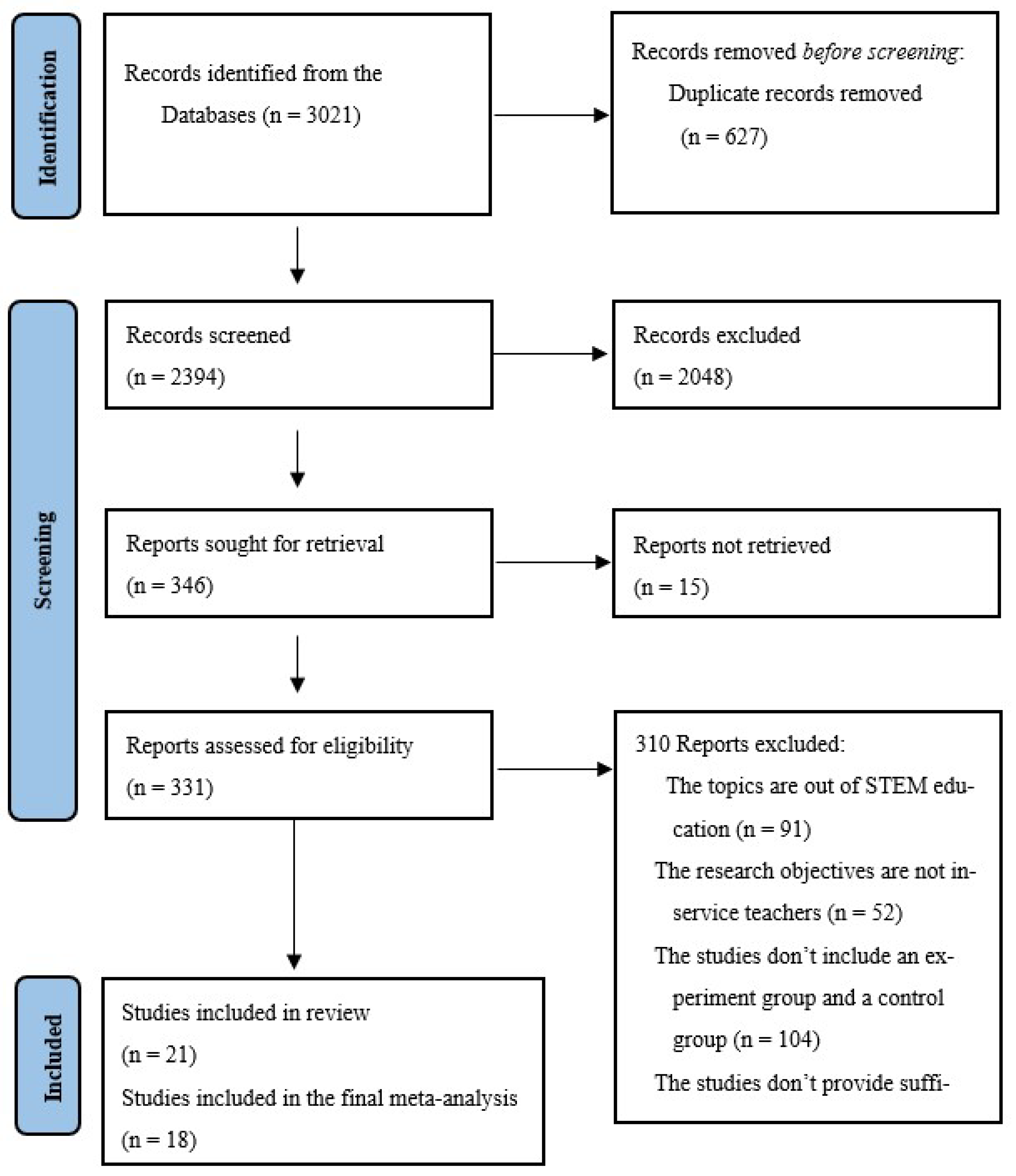
2.1. Study Inclusion and Exclusion Criteria
2.2. Study Search
2.3. Study Coding
2.4. Effect Size Calculation
2.5. Modeling Strategy
2.6. Outlier Control
2.7. Publication Bias
2.8. Moderator Analysis
3. Results
3.1. Selected Studies
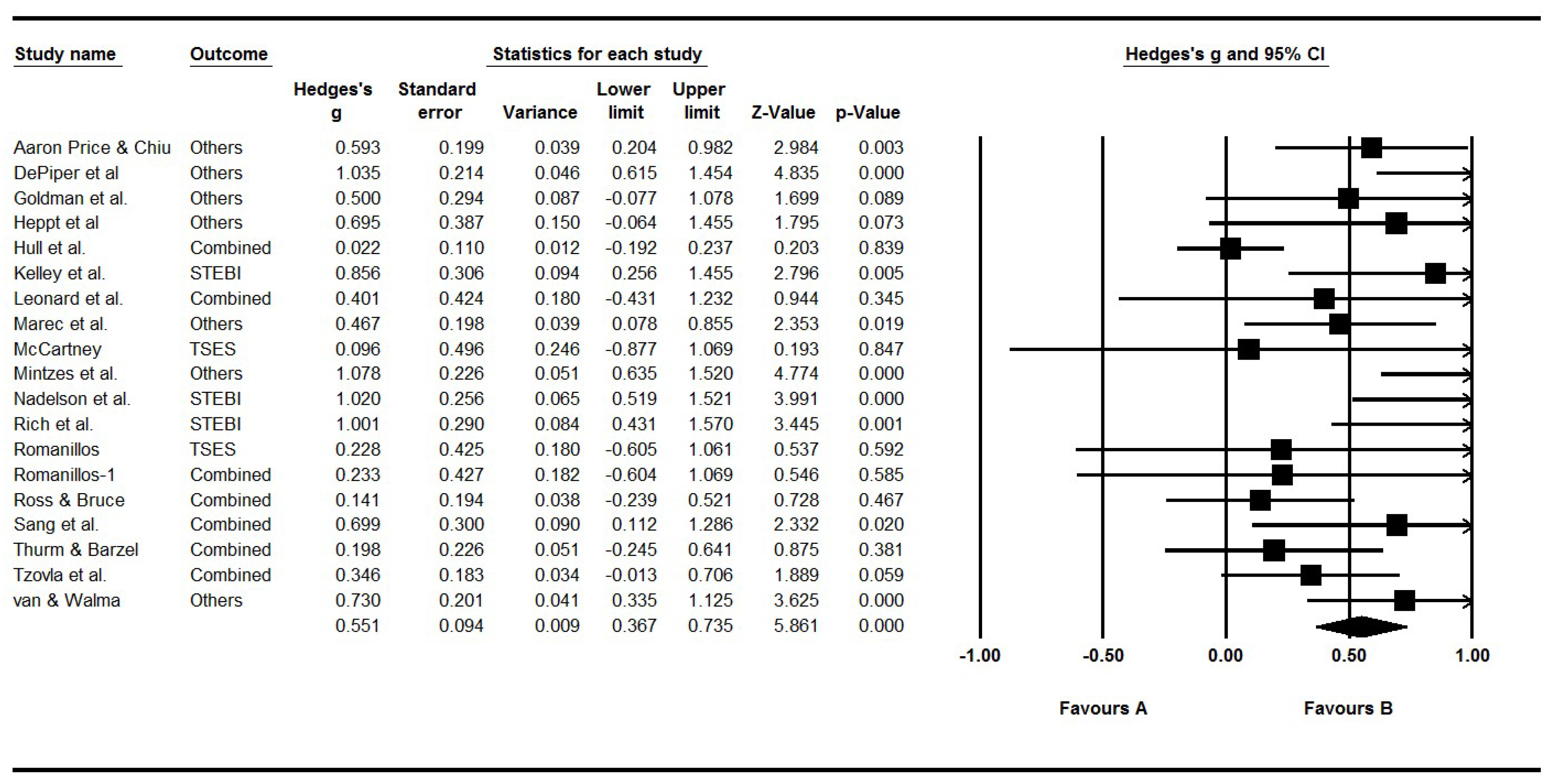
3.2. Overall Effectiveness of PD on STEM Teacher Self-Efficacy
3.3. Heterogeneity
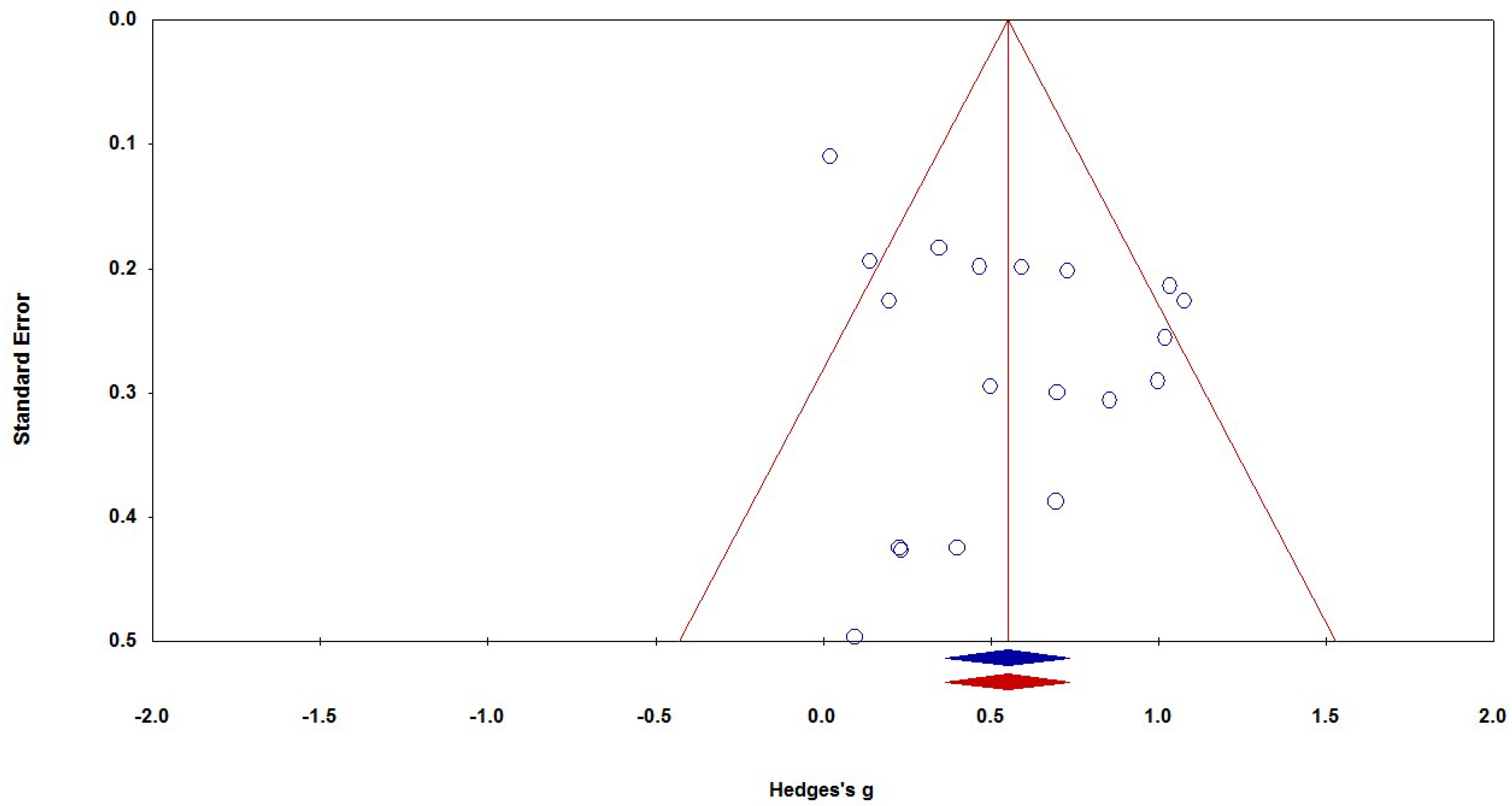
3.4. Examining Publication Bias
3.5. Moderator Analysis on the Overall Effect Sizes
4. Discussion
4.1. Overall Effects of PD
4.2. Effect Moderator of PD’s Format and Content
4.3. Effect Moderators of PD’s Participant Size, Training Hours, and Duration
4.4. Effect Moderator of Educational Stages and Areas
4.5. Diversity of Self-Efficacy Tools
4.6. Limitations and Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aaron Price, C., & Chiu, A. (2018). An experimental study of a museum-based, science PD programme’s impact on teachers and their students. International Journal of Science Education, 40(9), 941–960. [Google Scholar] [CrossRef]
- Ainley, J., & Carstens, R. (2018). Teaching and learning international survey (TALIS) 2018 conceptual framework. (OECD Education Working Papers No. 187). OECD Publishing. [Google Scholar] [CrossRef]
- Aloe, A. M., Amo, L. C., & Shanahan, M. E. (2014). Classroom management self-efficacy and burnout: A multivariate meta-analysis. Educational Psychology Review, 26(1), 101–126. [Google Scholar] [CrossRef]
- Ashton, P. T., & Webb, R. B. (1986). Making a difference: Teacher’s sense of efficacy and student achievement. Longman. [Google Scholar]
- Avery, Z. K. (2010). Effects of professional development on infusing engineering design into high school science, technology, engineering and math (STEM) curricula [Doctoral dissertation, Utah State University]. Available online: http://digitalcommons.usu.edu/etd/548/ (accessed on 12 December 2023).
- Bandura, A. (1994). Social cognitive theory and exercise of control over HIV infection. In Preventing AIDS (pp. 25–59). Springer. [Google Scholar]
- Bandura, A. (1997). Self-efficacy: The exercise of control. W. H. Freeman and Company. [Google Scholar]
- Basma, B., & Savage, R. (2018). Teacher professional development and student literacy growth: A systematic review and meta-analysis. Educational Psychology Review, 30(2), 457–481. [Google Scholar] [CrossRef]
- Berlin, J. A., & Antman, E. M. (1994). Advantages and limitations of metanalytic regressions of clinical trials data. The Online Journal of Current Clinical Trials, 13(5), 422. [Google Scholar] [CrossRef]
- Berman, P., McLaughlin, M., Bass, G., Pauly, E., & Zellman, G. (1977). Federal programs supporting educational change. Vol. VII: Factors affecting implementation and continuation. (Report No. R-1589/7-HEW. ERIC Document Reproduction Service No. 140 432). The Rand Corporation. [Google Scholar]
- Birman, B. F., Desimone, L., Porter, A. C., & Garet, M. S. (2000). Designing professional development that works. Educational Leadership, 57(8), 28–33. [Google Scholar]
- Blank, R. K., de las Alas, N., & Smith, C. (2008). Does teacher professional development have effects on teaching and learning? Analysis of evaluation findings from programs for mathematics and science teachers in 14 states. Council of Chief State School Officers. [Google Scholar]
- Borenstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2011). Introduction to meta-analysis. John Wiley & Sons. [Google Scholar]
- Borko, H. (2004). Professional development and teacher learning: Mapping the terrain. Educational Researcher, 33(8), 3–15. [Google Scholar] [CrossRef]
- Burla, L., Knierim, B., Barth, J., Liewald, K., Duetz, M., & Abel, T. (2008). From text to codings: Intercoder reliability assessment in qualitative content analysis. Nursing Research, 57(2), 113–117. [Google Scholar] [CrossRef]
- Buysse, V., Winton, P. J., & Rous, B. (2009). Reaching consensus on a definition of professional development for the early childhood field. Topics in Early Childhood Special Education, 28(4), 235–243. [Google Scholar] [CrossRef]
- Carney, M. B., Brendefur, J. L., Thiede, K., Hughes, G., & Sutton, J. (2016). Statewide mathematics professional development: Teacher knowledge, self-Efficacy, and beliefs. Educational Policy, 30(4), 539–572. [Google Scholar] [CrossRef]
- Chen, P., Yang, D., Metwally, A. H. S., Lavonen, J., & Wang, X. (2023). Fostering computational thinking through unplugged activities: A systematic literature review and meta-analysis. International Journal of STEM Education, 10, 47. [Google Scholar] [CrossRef]
- Chesnut, S. R., & Burley, H. (2015). Self-efficacy as a predictor of commitment to the teaching profession: A meta-analysis. Educational Research Review, 15, 1–16. [Google Scholar] [CrossRef]
- Cohen, J. (1988). The effect size index: D. In Statistical power analysis for the behavioral sciences (2nd ed., pp. 20–26). Lawrence Erlbaum Associates. [Google Scholar]
- Cooper, H. (2010). Research synthesis and meta-analysis (4th ed., Vol. 2). Applied Social Research Methods Series. Sage. [Google Scholar]
- Cooper, H., Hedges, L. V., & Valentine, J. C. (Eds.). (2019). The handbook of research synthesis and meta-analysis. Russell Sage Foundation. [Google Scholar]
- Darling-Hammond, L., Hyler, M. E., & Gardner, M. (2017). Effective teacher professional development. Learning Policy Institute. [Google Scholar]
- Darling-Hammond, L., Wei, R. C., & Johnson, C. M. (2009). Teacher preparation and teacher learning: A changing policy landscape. In G. Sykes, B. L. Schneider, & D. N. Plank (Eds.), Handbook on education policy research (pp. 613–636). Routledge. [Google Scholar]
- DePiper, J. N., Louie, J., Nikula, J., Buffington, P., Tierney-Fife, P., & Driscoll, M. (2021). Promoting teacher self-efficacy for supporting English learners in mathematics: Effects of the visual access to Mathematics professional development. ZDM–Mathematics Education, 53(2), 489–502. [Google Scholar] [CrossRef]
- Desimone, L. M. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educational Researcher, 38(3), 181–199. [Google Scholar] [CrossRef]
- Duval, S., & Tweedie, R. (2000). Trim and fill: A simple funnel-plot-based method of testing and adjusting for publication bias in meta-analysis. Biometrics, 56(2), 455–463. [Google Scholar] [CrossRef] [PubMed]
- Education Council. (2015). National STEM school education strategy, 2016—2026. Available online: https://files.eric.ed.gov/fulltext/ED581690.pdf (accessed on 9 October 2023).
- Egert, F., Fukkink, R. G., & Eckhardt, A. G. (2018). Impact of in-service professional development programs for early childhood teachers on quality ratings and child outcomes: A meta-analysis. Review of Educational Research, 88(3), 401–433. [Google Scholar] [CrossRef]
- Egger, M., Smith, G. D., Schneider, M., & Minder, C. (1997). Bias in meta-analysis detected by a simple, graphical test. BMJ, 315(7109), 629–634. [Google Scholar] [CrossRef]
- Elmore, R. F. (2004). School reform from the inside out: Policy, practice, and performance. Harvard Education Press. [Google Scholar]
- English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3, 3. [Google Scholar] [CrossRef]
- Enochs, L., Smith, P., & Huinker, D. (2000). Establishing factorial validity of the mathematics teaching efficacy beliefs instrument. School Science and Mathematics, 100(4), 194–202. [Google Scholar] [CrossRef]
- Fullan, M. G., & Miles, M. B. (1992). Getting reform right: What works and what doesn’t. Phi Delta Kappan, 73(10), 745–752. [Google Scholar]
- Garet, M. S., Porter, A. C., Desimone, L., Birman, B. F., & Yoon, K. S. (2001). What makes professional development effective? Results from a national sample of teachers. American Educational Research Journal, 38(4), 915–945. [Google Scholar] [CrossRef]
- Gaudin, C., & Chalies, S. (2015). Video viewing in teacher education and professional development: A literature review. Educational Research Review, 16, 41–67. [Google Scholar] [CrossRef]
- Gesel, S. A., LeJeune, L. M., Chow, J. C., Sinclair, A. C., & Lemons, C. J. (2020). A meta-analysis of the impact of professional development on teachers’ knowledge, skill, and self-efficacy in data-based decision-making. Journal of Learning Disabilities, 54(4), 269–283. [Google Scholar] [CrossRef]
- Glass, G. V., McGaw, B., & Smith, M. L. (1981). Meta-analysis in social research. Sage. [Google Scholar]
- Goldman, S. R., Greenleaf, C., Yukhymenko-Lescroart, M., Brown, W., Ko, M. L. M., Emig, J. M., George, M., Wallace, P., Blaum, D., & Britt, M. A. (2019). Explanatory modeling in science through text-based investigation: Testing the efficacy of the Project READI intervention approach. American Educational Research Journal, 56(4), 1148–1216. [Google Scholar] [CrossRef]
- Guskey, T. R. (1994). Professional development in education: In search of the optimal mix. American Educational Research Association. Available online: http://files.eric.ed.gov/fulltext/ED369181.pdf (accessed on 15 November 2023).
- Guskey, T. R. (2003). What makes professional development effective? Phi Delta Kappan, 84(10), 748–750. [Google Scholar] [CrossRef]
- Gümüş, E., & Bellibaş, M. Ş. (2023). The relationship between the types of professional development activities teachers participate in and their self-efficacy: A multi-country analysis. European Journal of Teacher Education, 46(1), 67–94. [Google Scholar] [CrossRef]
- Hamond, K. M. K. (2018). Effect of professional learning program on mathematics teachers’ self-efficacy (UMI No. 10809548; ProQuest Dissertations & Theses Global). [Doctoral dissertation, New England College]. [Google Scholar]
- Hamre, B. K., & Hatfield, B. E. (2012). Moving evidenced-based professional development into the field: Recommendations for policy and research. In C. Howes, B. Hamre, & R. Pianta (Eds.), Effective early childhood professional development. Improving teacher practice and child outcomes (pp. 213–228). Brookes. [Google Scholar]
- Hartshorne, R., Baumgartner, E., Kaplan-Rakowski, R., Mouza, C., & Ferdig, R. E. (2020). Special issue editorial: Preservice and inservice professional development during the COVID-19 pandemic. Journal of Technology and Teacher Education, 28(2), 137–147. [Google Scholar] [CrossRef]
- Hedges, L. V. (2007). Effect sizes in cluster-randomized designs. Journal of Educational and Behavioral Statistics, 32(4), 341–370. [Google Scholar] [CrossRef]
- Heppt, B., Henschel, S., Hardy, I., Hettmannsperger-Lippolt, R., Gabler, K., Sontag, C., Mannel, S., & Stanat, P. (2022). Professional development for language support in science classrooms: Evaluating effects for elementary school teachers. Teaching and Teacher Education, 109, 103518. [Google Scholar] [CrossRef]
- Higgins, J. P., Thompson, S. G., Deeks, J. J., & Altman, D. G. (2003). Measuring inconsistency in meta-analyses. BMJ, 327(7414), 557–560. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, C. L. (2018). Examining the impact of professional development on science teachers’ knowledge and self-efficacy: A causal-comparative inquiry(ProQuest No. 10785306; ProQuest Dissertations & Theses Global). [Doctoral dissertation, Texas A&M University-Corpus Christi]. [Google Scholar]
- Horvitz, B. S., Beach, A. L., Anderson, M. L., & Xia, J. (2015). Examination of faculty self-efficacy related to online teaching. Innovative Higher Education, 40(4), 305–316. [Google Scholar] [CrossRef]
- Hull, D. M., Booker, D. D., & Näslund-Hadley, E. I. (2016). Teachers’ self-efficacy in Belize and experimentation with teacher-led math inquiry. Teaching and Teacher Education, 56, 14–24. [Google Scholar] [CrossRef]
- Jeanpierre, B., Oberhauser, K., & Freeman, C. (2005). Characteristics of professional development that effect change in secondary science teachers’ classroom practices. Journal of Research in Science Teaching, 42(6), 668–690. [Google Scholar] [CrossRef]
- Johnson, C. C., & Fargo, J. D. (2010). Urban school reform enabled by transformative professional development: Impact on teacher change and student learning of science. Urban Education, 45(1), 4–29. [Google Scholar] [CrossRef]
- Kalinowski, E., Egert, F., Gronostaj, A., & Vock, M. (2020). Professional development on fostering students’ academic language proficiency across the curriculum—A meta-analysis of its impact on teachers’ cognition and teaching practices. Teaching and Teacher Education, 88, 102971. [Google Scholar] [CrossRef]
- Kanter, D. E., & Konstantopoulos, S. (2010). The impact of a project-based science curriculum on minority student achievement, attitudes, and careers: The effects of teacher content and pedagogical content knowledge and inquiry-based practices. Science Education, 94(5), 855–887. [Google Scholar] [CrossRef]
- Kaschalk-Woods, E., Fly, A. D., Foland, E. B., Dickinson, S. L., & Chen, X. (2021). Nutrition curriculum training and implementation improves teachers’ self-efficacy, knowledge, and outcome expectations. Journal of Nutrition Education and Behavior, 53(2), 142–150. [Google Scholar] [CrossRef]
- Kelani, R. R. E. D. (2009). A professional development study of technology education in secondary science teaching in Benin: Issues of teacher change and self-efficacy beliefs (UMI No. 3351073; ProQuest Dissertations & Theses Global). [Doctoral dissertation, Kent State University]. [Google Scholar]
- Kelley, T. R., Knowles, J. G., Holland, J. D., & Han, J. (2020). Increasing high school teachers self-efficacy for integrated STEM instruction through a collaborative community of practice. International Journal of STEM Education, 7, 14. [Google Scholar] [CrossRef]
- Kennedy, M. (1998). Form and substance in inservice teacher education. Research Monograph No. 13. National Institute for Science Education, University of Wisconsin-Madison. [Google Scholar]
- Knight, P. (2002). A systemic approach to professional development: Learning as practice. Teaching and Teacher Education, 18(3), 229–241. [Google Scholar] [CrossRef]
- Kraft, M. A., Blazar, D., & Hogan, D. (2018). The effect of teacher coaching on instruction and achievement: A meta-analysis of the causal evidence. Review of Educational Research, 88(4), 547–588. [Google Scholar] [CrossRef]
- Lee, B., Cawthon, S., & Dawson, K. (2013). Elementary and secondary teacher self-efficacy for teaching and pedagogical conceptual change in a drama-based professional development program. Teaching and Teacher Education, 30, 84–98. [Google Scholar] [CrossRef]
- Leonard, J., Mitchell, M., Barnes-Johnson, J., Unertl, A., Outka-Hill, J., Robinson, R., & Hester-Croff, C. (2018). Preparing teachers to engage rural students in computational thinking through robotics, game design, and culturally responsive teaching. Journal of Teacher Education, 69(4), 386–407. [Google Scholar] [CrossRef]
- Li, X., Dusseldorp, E., Su, X., & Meulman, J. J. (2020). Multiple moderator meta-analysis using the R-package Meta-CART. Behavior Research Methods, 52(6), 2657–2673. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. (2018). Journal for STEM education research–Promoting the development of interdisciplinary research in STEM education. Journal for STEM Education Research, 1(1), 1–6. [Google Scholar] [CrossRef]
- Li, Y., Wang, K., Xiao, Y., & Froyd, J. E. (2020). Research and trends in STEM education: A systematic review of journal publications. International Journal of STEM Education, 7(1), 11. [Google Scholar] [CrossRef]
- Little, C. A., & Paul, K. A. (2009). WEIGHING the WORKSHOP. The Learning Professional, 30(5), 26–30. [Google Scholar]
- Lohman, L. (2019). Collaborative engagement in the work of teaching mathematics and its impacts on teacher efficacy (UMI No. 13885215; ProQuest Dissertations & Theses Global). [Doctoral dissertation, ST. John’s University]. [Google Scholar]
- Loucks-Horsley, S., & Bybee, R. (1998). Implementing the national science education standards: How we will know when we get there. The Science Teacher, 65(6), 22–26. [Google Scholar]
- Lumpe, A., Czerniak, C., Haney, J., & Beltyukova, S. (2012). Beliefs about Teaching Science: The relationship between elementary teachers’ participation in professional development and student achievement. International Journal of Science Education, 34(2), 153–166. [Google Scholar] [CrossRef]
- Lynch, K., Hill, H. C., Gonzalez, K. E., & Pollard, C. (2019). Strengthening the research base that informs STEM instructional improvement efforts: A meta-analysis. Educational Evaluation and Policy Analysis, 41(3), 260–293. [Google Scholar] [CrossRef]
- Ma, K., Chutiyami, M., Zhang, Y., & Nicoll, S. (2021). Online teaching self-efficacy during COVID-19: Changes, its associated factors and moderators. Education and Information Technologies, 26, 6675–6697. [Google Scholar] [CrossRef]
- Marec, C. É., Tessier, C., Langlois, S., & Potvin, P. (2021). Change in elementary school teacher’s attitude toward teaching science following a pairing program. Journal of Science Teacher Education, 32(5), 500–517. [Google Scholar] [CrossRef]
- McCartney, K. P. (2013). The effects of professional development on the knowledge, attitudes, & anxiety of intermediate teachers of mathematics (UMI No. 3565668; ProQuest Dissertations & Theses Global). [Doctoral dissertation, Trevecca Nazarene University]. [Google Scholar]
- Mintzes, J. J., Marcum, B., Messerschmidt-Yates, C., & Mark, A. (2013). Enhancing self-efficacy in elementary science teaching with professional learning communities. Journal of Science Teacher Education, 24(7), 1201–1218. [Google Scholar] [CrossRef]
- Morris, S. B. (2008). Estimating effect sizes from pretest-posttest-control group designs. Organizational Research Methods, 11(2), 364–386. [Google Scholar] [CrossRef]
- Nadelson, L. S., Callahan, J., Pyke, P., Hay, A., Dance, M., & Pfiester, J. (2013). Teacher STEM perception and preparation: Inquiry-based STEM professional development for elementary teachers. The Journal of Educational Research, 106(2), 157–168. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. (2015). Science teachers’ learning: Enhancing opportunities, creating supportive contexts. The National Academies Press. [Google Scholar] [CrossRef]
- Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ, 372, n71. [Google Scholar] [CrossRef]
- Pinner, P. C. (2012). Efficacy development in science: Investigating the effects of the Teacher-to-Teacher (T2T) professional development model in Hilo elementary schools (UMI No. 3573453; ProQuest Dissertations & Theses Global). [Doctoral dissertation, Concordia University]. [Google Scholar]
- Pressley, T., & Ha, C. (2021). Returning to teaching during COVID-19: An empirical study on teacher self-efficacy. Teaching and Teacher Education, 106, 103465. [Google Scholar] [CrossRef]
- Ribeiro, J. J. (2009). How does a co-learner delivery model in professional development affect teachers’ self-efficacy in teaching mathematics and specialized mathematics knowledge for teaching? (UMI No. 3387318; ProQuest Dissertations & Theses Global). [Doctoral dissertation, Johnson & Wales University]. [Google Scholar]
- Rich, P. J., Jones, B., Belikov, O., Yoshikawa, E., & Perkins, M. (2017). Computing and engineering in elementary school: The effect of year-long training on elementary teacher self-efficacy and beliefs about teaching computing and engineering. International Journal of Computer Science Education in Schools, 1(1), 1–20. [Google Scholar] [CrossRef]
- Riggs, I., & Enochs, L. (1990). Toward the development of an elementary teacher’s science teaching efficacy belief instrument. Science Education, 74, 625–638. [Google Scholar] [CrossRef]
- Romanillos, R. (2017). Improving science teachers’ self-efficacy for science practices with diverse students(ProQuest No. 3704976; ProQuest Dissertations & Theses Global). [Doctoral dissertation, Johns Hopkins University]. [Google Scholar]
- Ross, J., & Bruce, C. (2007). Professional development effects on teacher efficacy: Results of randomized field trial. Journal of Educational Research, 101(1), 50–60. [Google Scholar] [CrossRef]
- Sang, G., Valcke, M., Van Braak, J., Zhu, C., Tondeur, J., & Yu, K. (2012). Challenging science teachers’ beliefs and practices through a video-case-based intervention in China’s primary schools. Asia-Pacific Journal of Teacher Education, 40(4), 363–378. [Google Scholar] [CrossRef]
- Shields, P. M., Marsh, J. A., & Adelman, N. E. (1998). Evaluation of NSF’s Statewide Systemic Initiatives (SSI) program: The SSIs impact on classroom practice. SRI. [Google Scholar]
- Shoji, K., Cieslak, R., Smoktunowicz, E., Rogala, A., Benight, C. C., & Luszczynska, A. (2016). Associations between job burnout and self-efficacy: A meta-analysis. Anxiety, Stress, & Coping, 29(4), 367–386. [Google Scholar] [CrossRef]
- Supovitz, J. A., & Turner, H. M. (2000). The effects of professional development on science teaching practices and classroom culture. Journal of Research in Science Teaching, 37(9), 963–980. [Google Scholar] [CrossRef]
- The Committee on STEM Education. (2018). Charting a course for success: America’s strategy for STEM education. Available online: https://trumpwhitehouse.archives.gov/wp-content/uploads/2018/12/STEM-Education-Strategic-Plan-2018.pdf (accessed on 2 December 2023).
- Thurm, D., & Barzel, B. (2020). Effects of a professional development program for teaching mathematics with technology on teachers’ beliefs, self-efficacy and practices. ZDM, 52(7), 1411–1422. [Google Scholar] [CrossRef]
- Trikoilis, D., & Papanastasiou, E. C. (2020). The potential of research for professional development in isolated settings during the COVID-19 crisis and beyond. Journal of Technology and Teacher Education, 28(2), 295–300. [Google Scholar] [CrossRef]
- Trimmell, M. D. (2015). The effects of stem-rich clinical professional development on elementary teachers’ sense of self-efficacy in teaching science (UMI No. 3704976; ProQuest Dissertations & Theses Global). [Doctoral dissertation, California State University]. [Google Scholar]
- Tschannen-Moran, M., & Hoy, A. W. (2001). Teacher efficacy: Capturing an elusive construct. Teaching and Teacher Education, 17(7), 783–805. [Google Scholar] [CrossRef]
- Tzovla, E., Kedraka, K., Karalis, T., Kougiourouki, M., & Lavidas, K. (2021). Effectiveness of in-service elementary school teacher professional development MOOC: An experimental research. Contemporary Educational Technology, 13(4), ep324. [Google Scholar] [CrossRef]
- van Aalderen-Smeets, S. I., & Walma van der Molen, J. H. (2015). Improving primary teachers’ attitudes toward science by attitude-focused professional development. Journal of Research in Science Teaching, 52(5), 710–734. [Google Scholar] [CrossRef]
- Viechtbauer, W., & Cheung, M. W. L. (2010). Outlier and influence diagnostics for meta-analysis. Research Synthesis Methods, 1(2), 112–125. [Google Scholar] [CrossRef]
- Villegas-Reimers, E. (2003). Teacher professional development: An international review of the literature. International Institute for Educational Planning, UNESCO. Available online: http://unesdoc.unesco.org/images/0013/001330/133010e.pdf (accessed on 2 December 2024).
- Wayne, A. J., Yoon, K. S., Zhu, P., Cronen, S., & Garet, M. S. (2008). Experimenting with teacher professional development: Motives and methods. Educational Researcher, 37(8), 469–479. [Google Scholar] [CrossRef]
- Werner, C. D., Linting, M., Vermeer, H. J., & van Ijzendoorn, M. H. (2016). Do intervention programs in childcare promote the quality of caregiver-child interactions? A meta-analysis of randomized controlled trials. Prevention Science, 17, 259–273. [Google Scholar] [CrossRef]
- Wilson, D. B., & Lipsey, M. W. (2001). The role of method in treatment effectiveness research: Evidence from meta-analysis. Psychological Methods, 6(4), 413–429. [Google Scholar] [CrossRef]
- Woolfolk, A. E., & Hoy, W. K. (1990). Prospective teachers’ sense of efficacy and beliefs about control. Journal of Educational Psychology, 82, 81–91. [Google Scholar] [CrossRef]
- Wu, X. N., Liao, H. Y., & Guan, L. X. (2024). Examining the influencing factors of elementary and high school STEM teachers’ self-efficacy: A meta-analysis. Current Psychology, 43(31), 25743–25759. [Google Scholar] [CrossRef]
- Yoon, K. S., Duncan, T., Lee, S. W.-Y., Scarloss, B., & Shapley, K. L. (2007). Reviewing the evidence on how teacher professional development affects student achievement. Issues & Answers. REL 2007-No. 033. Regional Educational Laboratory Southwest (NJ1). Available online: http://eric.ed.gov/?id=ED498548 (accessed on 2 December 2023).
- Yoon, S. Y., Evans, M. G., & Strobel, J. (2014). Validation of the teaching engineering self-efficacy scale for K-12 teachers: A structural equation modeling approach. Journal of Engineering Education, 103(3), 463–485. [Google Scholar] [CrossRef]
- You, H., Park, S., Hong, M., & Warren, A. (2025). Unveiling effectiveness: A meta-analysis of professional development programs in science education. Journal of Research in Science Teaching, 62(4), 971–1005. [Google Scholar] [CrossRef]
- Yu, S., Yuan, K., Zhou, N., & Wang, C. (2023). The development and validation of a scale for measuring EFL secondary teachers’ self-efficacy for English writing and writing instruction. Language Teaching Research. [Google Scholar] [CrossRef]
- Zhou, X., Shu, L., Xu, Z., & Padrón, Y. (2023). The effect of professional development on in-service STEM teachers’ self-efficacy: A meta-analysis of experimental studies. International Journal of STEM Education, 10(1), 37. [Google Scholar] [CrossRef]
| Code | Description |
|---|---|
| Study | |
| Publication type | (1) Peer-reviewed journal, (2) non-journal (chapter, conference, dissertation or thesis, report, other). |
| Area | (1) USA, (2) other countries. |
| Educational stage | (1) Elementary (K-5), (2) secondary (G 6–12), (3) mixed (K-12). |
| Instruments | The scale of teacher self-efficacy * (1) Science Teaching Efficacy Belief Instrument (STEBI), (2) Teacher’s Efficacy Beliefs Inventory (TSES), (3) others. |
| Participant size | Number of teachers participating in the study. |
| Intervention | |
| Format | Delivery format(s) employed. (1) Tradition (include workshops, courses, and conferences); (2) non-tradition (include tradition and study group, or mentoring, or coaching). |
| Content | (1) Mathematics, (2) science, (3), technology, (4) engineering, (5) multidiscipline. |
| Duration time | Total duration in months that the PD lasts. If a study did not include the information about duration in months, we calculated it in terms of months. For example, one school year equals nine months. |
| Training hour | Training of PD in hours. If a study did not show PD training time in hours, we calculated the training time by using eight hours instead of one full day. |
| Effect size level | |
| Statistical data | Outcome data for meta-analysis. We used sample sizes, means, standard deviations, pre-post correlations, t, p, F, d to calculate effect size. |
| Study | Instruments | PD Format | PD Content | Duration (Week) | Training Hour | Education Stage | Publication Type | Area | Participant Size | ES (g) |
|---|---|---|---|---|---|---|---|---|---|---|
| Aaron Price and Chiu (2018) | DAS-TE (3) | tradition | S | 36 | 56 | mixed | journal | USA | 78 | 0.593 |
| DePiper et al. (2021) | Author Modified (3) | tradition | M | 40 | 50 | secondary | journal | USA | 52 | 1.035 |
| Goldman et al. (2019) | Author Modified (3) | tradition | S | 36 | 88 | secondary | journal | USA | 23 | 0.500 |
| Heppt et al. (2022) | Author Modified (3) | tradition | S | 80 | 76 | primary | journal | Germany | 10 | 0.695 |
| Hopkins (2018) | STEBI-PSTE/STOE (1) | tradition | S | 36 | 100 | mixed | non-journal | USA | 60 | −0.121 |
| Hull et al. (2016) | TSES-CM/IS/SE (2) | tradition | M | 36 | 34 | primary | journal | Belize | 166 | 0.022 |
| Kaschalk-Woods et al. (2021) | STEBI PSTE/STOE (1) | tradition | S | 20 | 5 | secondary | journal | USA | 22 | 3.679 |
| Kelley et al. (2020) | T-STEM (1) | tradition | STEM | 2 | 70 | secondary | journal | USA | 30 | 0.856 |
| Leonard et al. (2018) | CRTSE/CRTOE (3) | tradition | STEM | 8 | 24 | mixed | journal | USA | 10 | 0.401 |
| Marec et al. (2021) | DAS-TE (3) | non-tradition | STEM | 36 | 36 | primary | journal | Canada | 69 | 0.467 |
| McCartney (2013) | MSES (2) | tradition | M | 4 | 8 | primary | non-journal | USA | 6 | 0.096 |
| Mintzes et al. (2013) | TSI (3) | non-tradition | S | 108 | 170 | primary | journal | USA | 48 | 1.078 |
| Nadelson et al. (2013) | STEBI (1) | tradition | STEM | 1 | 24 | primary | journal | USA | 36 | 1.020 |
| Rich et al. (2017) | T-STEM (1) | tradition | T | 36 | 27 | primary | journal | USA | 27 | 1.001 |
| Rich et al. (2017) (1) | T-STEM (1) | tradition | E | 36 | 27 | primary | journal | USA | 27 | 1.607 |
| Romanillos (2017) | TSES (2) | tradition | S | 1 | 40 | secondary | non-journal | USA | 12 | 0.228 |
| Romanillos (2017) (1) | STEBI-PSTE/STOE (1) | tradition | S | 1 | 40 | secondary | non-journal | USA | 12 | 0.233 |
| Ross and Bruce (2007) | TSES-CM/IS/SE (2) | tradition | M | 2 | 14 | secondary | journal | Canada | 57 | 0.141 |
| Sang et al. (2012) | STEBI-PSTE/STOE (1) | non-tradition | STEM | 10 | 10 | primary | journal | China | 23 | 0.699 |
| Thurm and Barzel (2020) | Author Modified (3) | tradition | M | 24 | 24 | secondary | journal | Germany | 39 | 0.198 |
| Trimmell (2015) | STEBI (1) | tradition | STEM | 72 | 50 | primary | non-journal | USA | 25 | 2.504 |
| Tzovla et al. (2021) | STEBI (1) | tradition | STEM | 5 | 48 | primary | Journal | Greece | 127 | 0.346 |
| van Aalderen-Smeets and Walma van der Molen (2015) | DAS-TE (3) | tradition | S | 24 | 18 | primary | journal | Netherlands | 61 | 0.730 |
| Model | K | Effect Size | 95% CI | Test of Null | Heterogeneity | ||
|---|---|---|---|---|---|---|---|
| g (SE) | Z(p) | Q (df) | p | I2 | |||
| Random | 19 | 0.551(0.094) | [0.367, 0.735] | 5.860 (0.000) | 49.46 (18) | 0.000 | 63.61% |
| Variable | k | g | SE | 95% CI | Z | p | Qb | df | pb |
|---|---|---|---|---|---|---|---|---|---|
| Publication type | 1.433 | 1 | 0.231 | ||||||
| Journal | 16 | 0.586 | 0.162 | [0.392, 0.780] | 5.925 | 0.000 | |||
| Non-journal | 3 | 0.192 | 0.315 | [−0.425, 0.808] | 0.609 | 0.543 | |||
| Area | 7.657 | 1 | 0.006 | ||||||
| USA | 11 | 0.750 | 0.106 | [0.542, 0.958] | 7.060 | 0.000 | |||
| Other | 8 | 0.347 | 0.100 | [0.151, 0.542] | 3.471 | 0.001 | |||
| Educational Stage | 0.392 | 2 | 0.822 | ||||||
| Primary | 10 | 0.607 | 0.135 | [0.342, 0.873] | 4.485 | 0.000 | |||
| Secondary | 7 | 0.473 | 0.170 | [0.140, 0.805] | 2.785 | 0.005 | |||
| Mixed | 2 | 0.526 | 0.321 | [−0.103, 1.156] | 1.639 | 0.101 | |||
| Format | 3.250 | 1 | 0.071 | ||||||
| Tradition | 15 | 0.462 | 0.097 | [0.272, 0.652] | 4.762 | 0.000 | |||
| Non-tradition | 4 | 0.820 | 0.173 | [0.480, 1.160] | 4.726 | 0.000 | |||
| Content | 4.714 | 2 | 0.094 | ||||||
| M | 5 | 0.296 | 0.144 | [0.013, 0.578] | 2.053 | 0.040 | |||
| S | 5 | 0.731 | 0.154 | [0.430, 1.032] | 4.754 | 0.000 | |||
| Multidiscipline | 9 | 0.608 | 0.125 | [0.362, 0.854] | 4.848 | 0.000 | |||
| Instruments | 15.505 | 2 | 0.000 | ||||||
| STEBI | 6 | 0.684 | 0.125 | [0.440, 0.928] | 5.489 | 0.000 | |||
| TSES | 4 | 0.080 | 0.129 | [−0.173, 0.332] | 0.618 | 0.537 | |||
| Others | 9 | 0.654 | 0.092 | [0.473, 0.835] | 7.076 | 0.000 | |||
| Instruments 1 | 17.175 | 1 | 0.000 | ||||||
| STEBI | 6 | 0.667 | 0.110 | [0.451, 0.883] | 6.047 | 0.000 | |||
| TSES | 4 | 0.063 | 0.095 | [−0.230, 0.954] | 1.200 | 0.230 | |||
| Instruments 2 | 16.215 | 1 | 0.000 | ||||||
| TSES | 4 | 0.073 | 0.115 | [−0.153, 0.300] | 0.637 | 0.524 | |||
| Others | 7 | 0.655 | 0.087 | [0.485, 0.825] | 7.536 | 0.000 |
| K | B | SE | 95% CI | p | R2 Analog | |
|---|---|---|---|---|---|---|
| Model 1 | 19 | 0.55 | ||||
| Intercept | 0.7666 | 0.1199 | [0.5316, 1.0017] | 0.0000 | ||
| Participant size | −0.0037 | 0.0015 | [−0.0066, −0.0007] | 0.0157 | ||
| Model 2 | 0.28 | |||||
| Intercept | 0.3576 | 0.1226 | [0.1173, 0.5980] | 0.0035 | ||
| Training hour | 0.0042 | 0.0021 | [0.0001, 0.0083] | 0.0471 | ||
| Model 3 | 0.17 | |||||
| Intercept | 0.4069 | 0.1177 | [0.1761, 0.6376] | 0.0005 | ||
| Duration | 0.0050 | 0.0030 | [−0.0010, 0.0109] | 0.1001 | ||
| Model 4 | 0.89 | |||||
| Intercept | 0.6029 | 0.1293 | [0.3495, 0.8563] | 0.0000 | ||
| Participant size | −0.0038 | 0.0012 | [−0.0061, −0.0015] | 0.0010 | ||
| Training hour | 0.0039 | 0.0016 | [0.0008, 0.0071] | 0.0154 | ||
| Model 5 | 0.27 | |||||
| Intercept | 0.3563 | 0.1232 | [0.1148, 0.5978] | 0.0038 | ||
| Duration | 0.0007 | 0.0050 | [−0.0091, 0.0106] | 0.8847 | ||
| Training hour | 0.0037 | 0.0036 | [−0.0033, 0.0108] | 0.2988 | ||
| Model 6 | 0.80 | |||||
| Intercept | 0.6478 | 0.1248 | [0.4032, 0.8924] | 0.0000 | ||
| Participant size | −0.0041 | 0.0013 | [−0.0065, −0.0016] | 0.0012 | ||
| Duration | 0.0051 | 0.0024 | [0.0005, 0.0098] | 0.0305 | ||
| Model 7 | 0.88 | |||||
| Intercept | 0.6057 | 0.1297 | [0.3515, 0.8600] | 0.0000 | ||
| Participant size | −0.0039 | 0.0012 | [−0.0063, −0.0016] | 0.0010 | ||
| Training hour | 0.0028 | 0.0046 | [−0.0027, 0.0084] | 0.3187 | ||
| Duration | 0.0018 | 0.0040 | [−0.0060, 0.0097] | 0.6429 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, K.; Pan, Z. The Effectiveness of Professional Development in the Self-Efficacy of In-Service Teachers in STEM Education: A Meta-Analysis. Behav. Sci. 2025, 15, 1364. https://doi.org/10.3390/bs15101364
Liu J, Wang K, Pan Z. The Effectiveness of Professional Development in the Self-Efficacy of In-Service Teachers in STEM Education: A Meta-Analysis. Behavioral Sciences. 2025; 15(10):1364. https://doi.org/10.3390/bs15101364
Chicago/Turabian StyleLiu, Jiao, Ke Wang, and Zilong Pan. 2025. "The Effectiveness of Professional Development in the Self-Efficacy of In-Service Teachers in STEM Education: A Meta-Analysis" Behavioral Sciences 15, no. 10: 1364. https://doi.org/10.3390/bs15101364
APA StyleLiu, J., Wang, K., & Pan, Z. (2025). The Effectiveness of Professional Development in the Self-Efficacy of In-Service Teachers in STEM Education: A Meta-Analysis. Behavioral Sciences, 15(10), 1364. https://doi.org/10.3390/bs15101364






