Prototype or Exemplar Representations in the 5/5 Category Learning Task
Abstract
1. Introduction
1.1. The 5/4 and 5/5 Category Learning Tasks
1.2. Factors Influencing Reliance on Prototype and Exemplar Representations
1.3. Computational Modeling
1.4. Current Study
2. Methods
2.1. Participants
2.2. Design
2.3. Materials
2.4. Procedure
2.5. Computational Modelling
2.5.1. The GCM
2.5.2. The MPM
3. Results
3.1. Learning to Criterion
3.2. Representations: Diagnostic Stimulus Classification Evidence
3.3. Representation: MPM and GCM Model Fitting Evidence
3.4. Dimensional Weighting
4. Discussion
4.1. Representational Change across the Process of Category Learning
4.2. Between Task Structure and Representations: Implications for Strategy Use in Category Learning
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shepard, R.N.; Hovland, C.I.; Jenkins, H.M. Learning and memorization of classifications. Psychol. Monogr. Gen. Appl. 1961, 75, 1. [Google Scholar] [CrossRef]
- Medin, D.L.; Wattenmaker, W.D.; Hampson, S.E. Family resemblance, conceptual cohesiveness, and category construction. Cogn. Psychol. 1987, 19, 242–279. [Google Scholar] [CrossRef] [PubMed]
- Medin, D.L.; Schaffer, M.M. Context theory of classification learning. Psychol. Rev. 1978, 85, 207–238. [Google Scholar] [CrossRef] [PubMed]
- Minda, J.P.; Smith, J.D. Prototypes in category learning: The effects of category size, category structure, and stimulus complexity. J. Exp. Psychol. Learn. Mem. Cogn. 2001, 27, 775–799. [Google Scholar] [CrossRef] [PubMed]
- Minda, J.P.; Smith, J.D. Comparing prototype-based and exemplar-based accounts of category learning and attentional allocation. J. Exp. Psychol. Learn. Mem. Cogn. 2002, 28, 275–292. [Google Scholar] [CrossRef] [PubMed]
- Rosch, E.; Mervis, C.B. Family resemblances: Studies in the internal structure of categories. Cogn. Psychol. 1975, 7, 573–605. [Google Scholar] [CrossRef]
- Kruschke, J.K. ALCOVE: An exemplar-based connectionist model of category learning. Psychol. Rev. 1992, 99, 22–44. [Google Scholar] [CrossRef] [PubMed]
- Nosofsky, R.M. Choice, similarity, and the context theory of classification. J. Exp. Psychol. Learn. Mem. Cogn. 1984, 10, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Nosofsky, R.M. Exemplars, prototypes, and similarity rules. In From Learning Theory to Connectionist Theory: Essays in honor of William K. Estes; Healy, A.F., Kosslyn, S.M., Shiffrin, R.M., Eds.; Erlbaum: Hillsdale, NJ, USA, 1992; pp. 149–167. [Google Scholar]
- Nosofsky, R.M.; Sanders, C.A.; McDaniel, M.A. Tests of an Exemplar-Memory model of classification learning in a High-Dimensional Natural-Science category domain. J. Exp. Psychol. Gen. 2018, 147, 328–353. [Google Scholar] [CrossRef]
- Braunlich, K.; Love, B.C. Occipitotemporal representations reflect individual differences in conceptual knowledge. J. Exp. Psychol. Gen. 2019, 148, 1192–1203. [Google Scholar] [CrossRef]
- Johansen, M.K.; Palmeri, T.J. Are there representational shifts during category learning? Cogn. Psychol. 2002, 45, 482–553. [Google Scholar] [CrossRef] [PubMed]
- Rehder, B.; Hoffman, A. Thirty-something categorization results explained: Attention, eyetracking, and models of category learning. J. Exp. Psychology. Learn. Mem. Cogn. 2005, 31, 811–829. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.D.; Minda, J.P. Thirty categorization results in search of a model. J. Exp. Psychol. Learn. Mem. Cogn. 2000, 26, 3–27. [Google Scholar] [CrossRef] [PubMed]
- Zaki, S.R.; Nosofsky, R.M.; Stanton, R.D.; Cohen, A.L. Prototype and exemplar accounts of category learning and attentional allocation: A reassessment. J. Exp. Psychol. Learn. Mem. Cogn. 2003, 29, 1160–1173. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Huang, Y.L.; Seger, A.C. The expectation effect of the sample size in category learning. Acta Psychol. Sin. 2012, 44, 754–765. (In Chinese) [Google Scholar] [CrossRef]
- Ashby, F.G.; Alfonso-Reese, L.A.; Turken, A.U.; Waldron, E.M. A neuropsychological theory of multiple systems in category learning. Psychol. Rev. 1998, 105, 442–481. [Google Scholar] [CrossRef] [PubMed]
- Ashby, F.G.; Maddox, W.T. Human category learning. Annu. Rev. Psychol. 2005, 56, 149–178. [Google Scholar] [CrossRef] [PubMed]
- Seger, C.A.; Miller, E.K. Category learning in the brain. Annu. Rev. Neurosci. 2010, 33, 203–219. [Google Scholar] [CrossRef] [PubMed]
- Mack, M.; Preston, A.; Love, B. Decoding the brain’s algorithm for categorization from its neural implementation. Curr. Biol. 2013, 20, 2023–2027. [Google Scholar] [CrossRef]
- Bowman, C.R.; Iwashita, T.; Zeithamova, D. Tracking prototype and exemplar representations in the brain across learning. eLife 2020, 9, e59360. [Google Scholar] [CrossRef]
- Xing, Q.; Sun, H.; Che, J. Effect of feedback value on family resemble category learning: An ERPs study. Stud. Psychol. Behav. 2018, 16, 300–307. (In Chinese) [Google Scholar]
- Bowman, C.R.; Zeithamova, D. Training set coherence and set size effects on concept generalization and recognition. J. Exp. Psychol. Learn. Mem. Cogn. 2020, 46, 1442–1464. [Google Scholar] [CrossRef] [PubMed]
- Mack, M.L.; Love, B.C.; Preston, A.R. Dynamic updating of hippocampal object representations reflects new conceptual knowledge. Proc. Natl. Acad. Sci. USA 2016, 113, 13203–13208. [Google Scholar] [CrossRef] [PubMed]
- Mack, M.L.; Preston, A.R.; Love, B.C. Ventromedial prefrontal cortex compression during concept learning. Nat. Commun. 2020, 11, 46. [Google Scholar] [CrossRef] [PubMed]
- Mok, R.; Love, B.C. A non-spatial account of place and grid cells based on clustering models of concept learning. Nat. Commun. 2019, 10, 5685. [Google Scholar] [CrossRef] [PubMed]
- Rosedahl, L.; Eckstein, M.; Ashby, F. Retinal-specific category learning. Nat. Hum. Behav. 2018, 2, 500–506. [Google Scholar] [CrossRef] [PubMed]
- McKinley, S.C.; Nosofsky, R.M. Investigations of exemplar and decision bound models in large, ill-defined category structures. J. Exp. Psychol. Hum. Percept. Perform. 1995, 21, 128–148. [Google Scholar] [CrossRef] [PubMed]
- Nosofsky, R.M.; Zaki, S.R. Exemplar and prototype models revisited: Response strategies, selective attention, and stimulus generalization. J. Exp. Psychol. Learn. Mem. Cogn. 2002, 28, 924–940. [Google Scholar] [CrossRef]
- Ashby, F.G. State-trace analysis misinterpreted and misapplied: Reply to Stephens, Matzke, and Hayes (2019). J. Math. Psychol. 2019, 91, 195–200. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Song, X.H.; Seger, C.A. Six-year-old children’s ability on category learning: Category representation, attention and learning strategy. Acta Psychol. Sin. 2012, 44, 634–646. (In Chinese) [Google Scholar] [CrossRef]
- Sweller, J.; Ayres, P.; Kalyuga, S. Cognitive Load Theory in Perspective; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Davis, T.; Love, B.C.; Preston, A.R. Learning the exception to the rule: Model-based FMRI reveals specialized representations for surprising category members. Cereb. Cortex 2011, 22, 260–273. [Google Scholar] [CrossRef] [PubMed]
- Ashby, F.G.; Paul, E.J.; Maddox, W.T. COVIS. In Formal Approaches in Categorization; Pothos, E.M., Wills, A.J., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 65–87. [Google Scholar] [CrossRef]
- Ashby, F.G.; Rosedahl, L. A neural interpretation of exemplar theory. Psychol. Rev. 2017, 124, 472–482. [Google Scholar] [CrossRef] [PubMed]
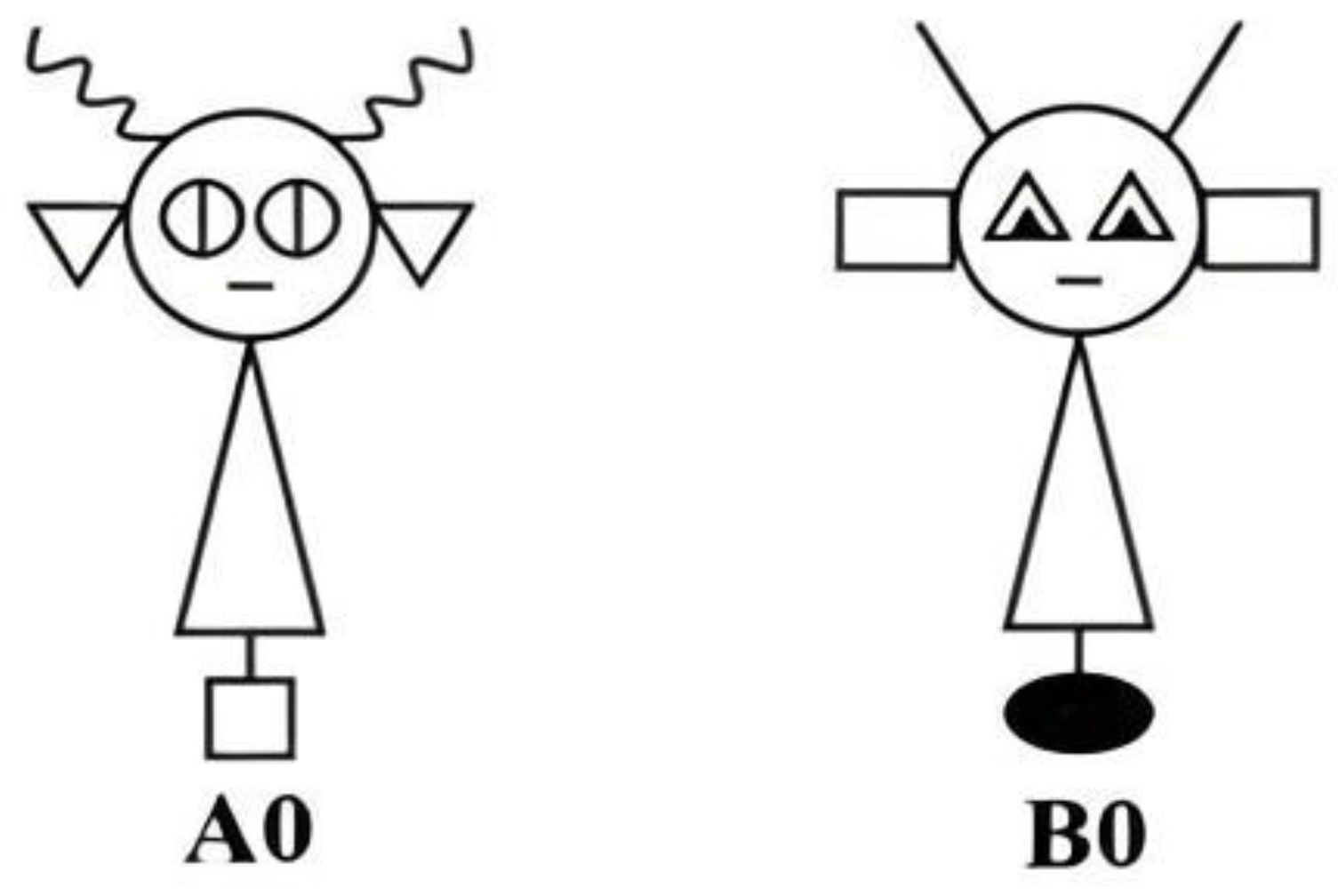

| A | B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D1 | D2 | D3 | D4 | ||
| A1 | 1 | 1 | 1 | 0 | B1 | 1 | 1 | 0 | 0 |
| A2 | 1 | 0 | 1 | 0 | B2 | 0 | 1 | 1 | 0 |
| A3 | 1 | 0 | 1 | 1 | B3 | 0 | 0 | 0 | 1 |
| A4 | 1 | 1 | 0 | 1 | B4 | 0 | 0 | 0 | 0 |
| A5 | 0 | 1 | 1 | 1 | B5 | 1 | 0 | 0 | 1 |
| A0 | 1 | 1 | 1 | 1 | B0 | 0 | 0 | 0 | 0 |
| Whole | First Half | Second Half | Good Learner (N = 18) | Poor Learner (N = 26) | |
|---|---|---|---|---|---|
| A1 | 0.71(0.17) | 0.64(0.20) | 0.85(0.18) | 0.77(0.16) | 0.67(0.17) |
| A2 | 0.70(0.15) | 0.66(0.18) | 0.77(0.24) | 0.72(0.16) | 0.68(0.14) |
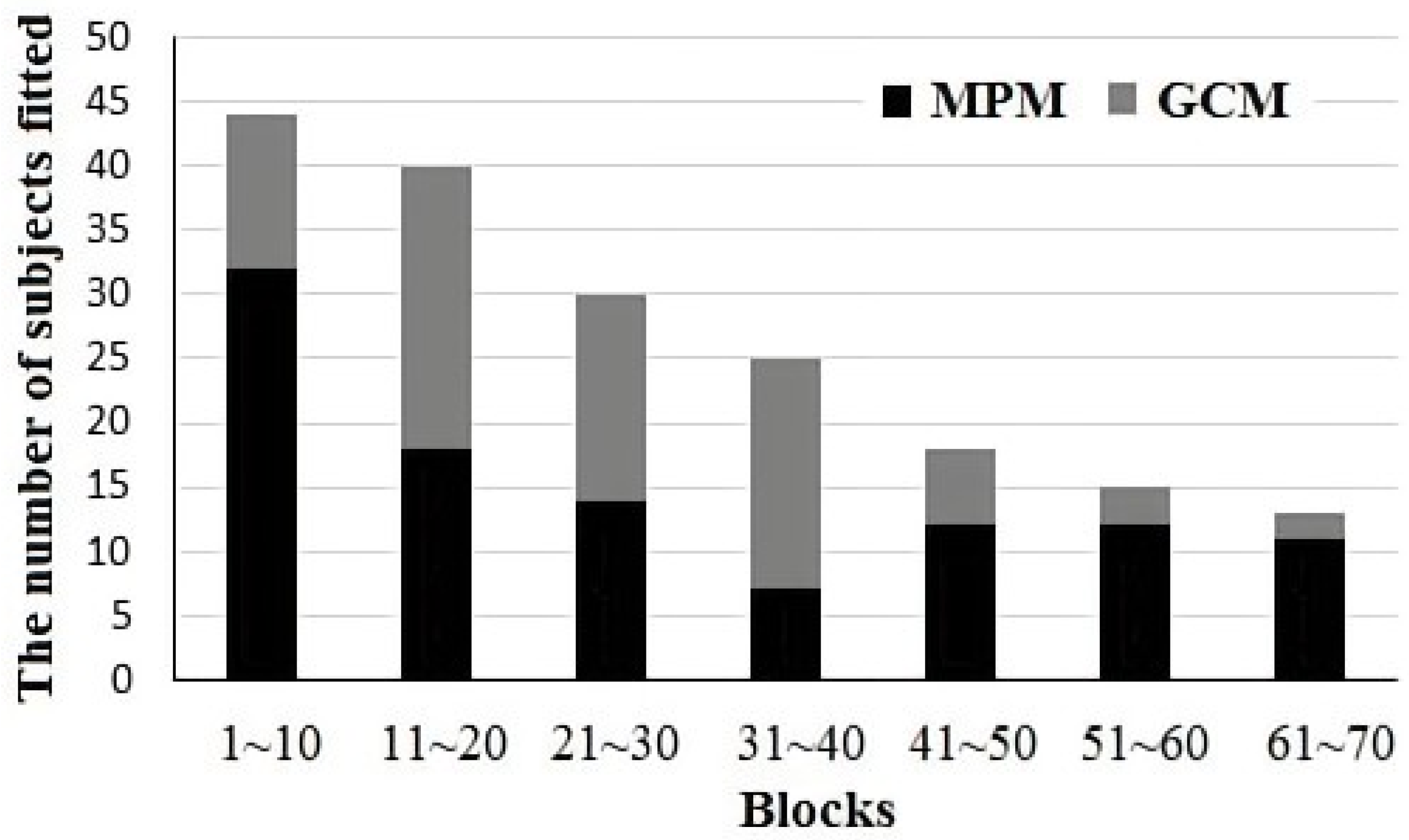
| Blocks | 1~10 | 11~20 | 21~30 | 31~40 | 41~50 | 51~60 | 61~70 | |
|---|---|---|---|---|---|---|---|---|
| N | 44 | 40 | 30 | 25 | 18 | 15 | 13 | |
| MPM | SSD | 0.217 | 0.256 | 0.253 | 0.329 | 0.222 | 0.274 | 0.133 |
| Fitness | 0.73 | 0.45 | 0.47 | 0.28 | 0.66 | 0.80 | 0.85 | |
| GCM | SSD | 0.237 | 0.241 | 0.240 | 0.299 | 0.282 | 0.323 | 0.234 |
| Fitness | 0.27 | 0.55 | 0.53 | 0.72 | 0.33 | 0.20 | 0.15 |
| Model | Fitness | D1 | D2 | D3 | D4 | C | |
|---|---|---|---|---|---|---|---|
| MPM | 1st half | 0.535 | 0.311 | 0.055 | 0.331 | 0.303 | 0.230 |
| 2nd half | 0.973 | 0.201 | 0.079 | 0.532 | 0.188 | 0.395 | |
| Total | 0.103 | 0.233 | 0.103 | 0.521 | 0.144 | 1.242 | |
| GCM | 1st half | 1.430 | 0.223 | 0.088 | 0.477 | 0.212 | 0.477 |
| 2nd half | 0.978 | 0.394 | 0.098 | 0.351 | 0.158 | 2.228 | |
| Total | 0.106 | 0.226 | 0.158 | 0.403 | 0.214 | 4.125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Li, P.; Chen, H.; Seger, C.A.; Liu, Z. Prototype or Exemplar Representations in the 5/5 Category Learning Task. Behav. Sci. 2024, 14, 470. https://doi.org/10.3390/bs14060470
Chen F, Li P, Chen H, Seger CA, Liu Z. Prototype or Exemplar Representations in the 5/5 Category Learning Task. Behavioral Sciences. 2024; 14(6):470. https://doi.org/10.3390/bs14060470
Chicago/Turabian StyleChen, Fang, Peijuan Li, Hao Chen, Carol A. Seger, and Zhiya Liu. 2024. "Prototype or Exemplar Representations in the 5/5 Category Learning Task" Behavioral Sciences 14, no. 6: 470. https://doi.org/10.3390/bs14060470
APA StyleChen, F., Li, P., Chen, H., Seger, C. A., & Liu, Z. (2024). Prototype or Exemplar Representations in the 5/5 Category Learning Task. Behavioral Sciences, 14(6), 470. https://doi.org/10.3390/bs14060470






