Abstract
Traffic–induced vibrations may constitute a considerable load to buildings. In this paper, vibrations transmitted through the ground caused by wheeled vehicles are considered. This phenomenon may cause cracking of plaster, cracks in load-bearing elements or even, in extreme cases, collapse of the whole structure. Measurements of vibrations of real structures are costly and laborious. Therefore, the aim of the present paper is to propose a method of using Bayesian networks combined with implementation of geoscience for assessment of impact of traffic–induced vibrations on residential buildings. Firstly, the experimental tests were performed on different buildings using specialized equipment taking into account five factors: Distance from the building to the edge of the road, condition of road surface, condition of the building, the absorption of soil and the type of vehicle. Then, probabilistic analyses applying Bayesian networks were conducted and two methods of assessing the information value (EVSI method and entropy method) were compared. Finally, the developed diagnostic–decision support model was tested, so as to verify the most important parameter, affecting the possibility of structural vibrations to occur. The results of the study clearly showed that the use of Bayesian networks was a very effective approach to assess the impact of traffic-induced vibrations. The developed algorithm could be successfully applied both to existing and planned buildings, for which the source of vibration is already present or may appear in the future.
1. Introduction
Vibrations of buildings may be induced by different types of dynamic excitations. The most common reasons of such vibrations are related to wind, earthquakes (see, for example, [1,2,3,4]), piling works, large mechanical vibrating entities, jumping of people or vibrations resulting from passing of vehicles and trains [5,6]. The last reason may lead to traffic-induced vibrations of geological structures generating negative effects, both for buildings and residents of buildings subjected to these dynamic excitations [7]. Vibrations caused by road traffic causes also noise troublesome for residents. Fortunately, modern, constantly developing technology brings many possibilities to solve such problems. One of them is the use of effective methods of forecasting the impact of traffic-induced vibrations on residential buildings [8]. Experts are very important in the process and their experience and knowledge can be used to provide information that forms the basis for calculation programs and systems.
There are many methods of forecasting various types of phenomena, starting from decision trees and risk analysis (see [9]) through statistics and random algorithms (e.g., [10,11]) to artificial intelligence and machine learning. The problem is therefore to find solutions that are both useful and not expensive. That is why the approximate methods are often used. These methods allow us to solve the engineering problem with satisfactory results, even if they are still approximate. The use of Bayesian networks (BN) is an example of such applications. Definitions and detailed rules related to the application of BNs in buildings can be found in [12]. An interesting example of the practical application of the method, by using the conventional regularized learning approach, as a particular approximation of the Bayesian framework, was described in [13]. The example concerns the two-step strategy for the assessment of the integrity of a long-suspension bridge under ambient vibrations. In the first step of the proposed strategy, the occurrence of damage was detected and the damaged portion of the bridge was identified. In the second step, the specific damaged element was recognized and the intensity of damage was evaluated. The Bayesian framework was applied in both steps and the improvements in the results were discussed. Another application of BNs was presented in [14] and it demonstrates how Bayesian belief networks (BBNs) can be used as a diagnostic–decision support model (D-DSM) during the implementation phase of a large construction project. The example concerns a road tunnel and demonstrates how the D-DSM can combine expert knowledge with the monitoring information. The model is able to use evidence from various sources in a mathematically rigorous manner. Attention should also be paid to the use of Bayes networks for building the model of cross passages between tunnel tubes in soft soils [15]. To ameliorate the problem related to the scarcity of risks information, often encountered in construction projects, the authors used BBNs and expert knowledge to augment available information. The paper describes proposed modifications to the standard methods used to develop BBNs in order to deal with divergent information originated from epistemic uncertainty of risks.
2. Motivation and the Study Objective
Traffic–induced vibrations may be caused by wheeled vehicles, trams and trains. Meanwhile, many structures are located near roads (tracks) with significant traffic. They are exposed to continuous vibrations, which often affect not only people, but also buildings themselves. As a consequence, structures may be subjected to considerable damages. When assessing the technical condition of a building, an expert should also pay the attention to the reasons of structural degradation. That would allow us to prevent the occurrence of cracks, or even major damages, in buildings in the future.
In this paper, the analysis is focused on vibrations transmitted through the ground caused by wheeled vehicles, which may affect the technical condition of the building. Measurements of vibrations of real structures are costly and laborious. Therefore, the aim of the present paper is to propose a method of using Bayesian networks combined with the implementation of geoscience for assessment of impact of traffic–induced vibrations on residential buildings. In this way, we can create an expert system, which is able to predict, with a certain probability, the threat of negative dynamic impact on the building considered, without performing costly and labor-intensive field measurements.
The need of field data for the development and calibration of numerical models should also be emphasized [16,17,18].
A literature review shows that Bayesian networks can be successfully used in various fields, and the implementation of the method can positively affect the development of technology and reduce costs while minimizing the risk of adverse effects. However, according to the authors’ knowledge, Bayesian networks have not been considered so far to predict the influence of traffic-induces vibrations on buildings in relation to standard regulations [19,20,21,22,23,24]. That is why the aim of the present paper is conduct such an attempt and to verify the effectiveness of the method analyzed.
3. Materials and Methods
Traffic-induced vibrations are becoming very common not only in urban areas but also in the suburbs. The problem may occur everywhere in the cases of buildings located near roads or railways. Vibrations are caused by various types of vehicles (columns of cars, trucks of different weights), trams, trains and subway (see [25]). Polish standard [19] indicates that the distance of impact of vibrations on buildings is usually equal to about 25 m from the tram track axis or the outer road lane and about 50 m from the axis of the railroad track. The size of impact and the possible effects may be different. Vibrations may cause cracking of plaster and damage to load-bearing elements. In the extreme cases, they may also lead to the collapse of the whole structure [19]. Traffic-induced vibrations results in degradation of a building reducing its durability and resistance to shocks [7,25].
The isolation of endangered buildings can be easily carried out due to the use of geomap, which enables the construction of land information collections, their updating and analysis. The user of the GEO PLUS module for geodetic calculations and data transmission from field recorders receives the necessary data for the construction of expert systems.
Some formal regulations (e.g., [19,20,21,22,23,24]) describe the impact of vibrations on residential buildings and people as well as measurement principles. The standard analysis in a number of countries, including Poland, starts with performing measurements of accelerations in time using specialized equipment. Then filtration in one-third bands in the range of 1–100 Hz takes place (see [20] for example). The peak amplitude values are marked on the special scale, known as the dynamic influence scale (DIS). The result may be located in one of five zones (see [19]). The first zone means no impact of vibrations on building. The second zone shows that vibrations are noticeable but do not pose a threat to the structure. The third zone means that the overall load bearing capacity of building may be weakened. The next zone indicates that vibrations may have a major influence on building, the amplitudes for the specific frequencies are high enough to cause various objects in the apartments to tremble and there is also a negative impact on the health of inhabitants. The last zone means that the load bearing capacity is dysfunctional and vibrations may lead to major malfunction or even total collapse of the structure.
The residential buildings should be analyzed so as to exclude dangerous impact of passing vehicles. Laborious and costly measurements are often performed in such cases. It is believed that Bayesian networks can be used not only to support the decisions concerning the necessity of in situ measurements, but also to validate the probabilistic method (see [26] for example).
The Bayesian networks, based on the correlation between variables, allowed us to calculate the probability of events. For variables Xi (i = 1, …, n) given П(Xi), Xi is conditionally independent on all non-parents nodes, a joint distribution probability of n variables can be decomposed according to a chain rule as [27]:
where π(Xi) = ØP(Xi|π(Xi)) is a marginal probability of Xi, P(Xi). In order to conduct the Bayesian inference, prior probabilities and posterior probabilities are required (see Figure 1) [27].
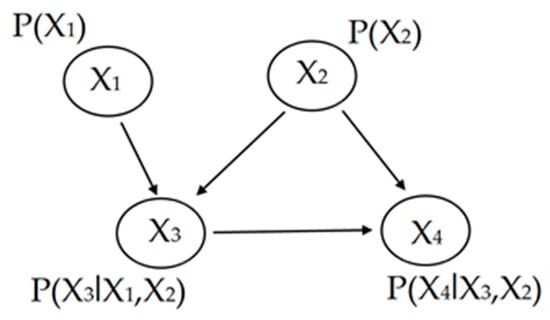
Figure 1.
Example model of a Bayesian network.
Let X and Y be two stochastic variables, and suppose that X = x and Y = y. Before considering the evidence Y = y, the prior probability of the event X = x or P (X = x) should be estimated first. After taking into account the evidence Y = y, according to Bayes theorem, the posterior probability P (X = x|Y = y) can be calculated as [27]:
where P (X = x|Y = y) is the probability of the joint event P (X = x ^ Y = y). If X, Y are independent, then P (X = x|Y = y) = P (X = x).
In practice, information is usually introduced into the available and current network by updating the distribution of probabilities for the next random variable (see also [28]). The algorithms defining the probability are very complex, but still time to upgrade the network is very short. The principle of operation of the Bayesian network is based on modeling the knowledge about the analyzed object by assigning the probability P(Xi) to each of its state Xi. Subsequently, we obtained new information I about the analyzed object, whereby we knew the probability for each object state, P(Xi/I) to obtain this particular information, if the object was in the state Xi. By applying the Bayesian formula, the probability P(Xi/I) was calculated taking into account new information I [27].
Bayesian networks can be provided by an expert and/or learnt from the data. The data was treated as a set of m vectors (x1 (i), ..., xn (i)), i = 1, ..., m, generated independently of each of them from the probability distribution represented by a real Bayesian network (X, S, P), S—structure, P—parameters. Based on the data, a Bayesian network (X’, S’, P’) is created to bring (X, S, P) as close as possible [29].
Eliciting Bayesian networks from experts can be a laborious and difficult procedure, especially in the case of large networks. Therefore, a number of methods for learning the structure of the network and parameters from the data have been developed [30]. There are two, the most popular algorithms that allow the automatic construction of the structural part and the parametric learning Bayesian network to be created. These algorithms are:
- The PC algorithm (see [30] for details). It relies on minimizing the amount of necessary d-separation tests, which means quick and effective execution of lower-order tests. In the first phase of the algorithm’s operation, the structure of the network is determined, and then some of the edges are oriented as far as possible. Thus, a partially oriented structure is generated representing the whole class of potential Bayesian networks. Algorithms take two input parameters. The first one is the confidence level for the independence test. The lower the confidence level, the more attributes are considered to be independent and the smaller edge has the resulting network. The second parameter is the strategy of selecting pairs for the d-separation test. The d-separation test is performed for all attribute pairs in the sample. The complexity of the test for each pair depends on the number of edges eliminated in previous tests.
- The expectation–maximization (EM) algorithm (see [31] for details). It is an iterative algorithm to find the maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.
4. Results
4.1. Experimental Study
The experimental study was firstly conducted, so as to collect the real data to be used in the Bayesian network created to study the impact of traffic-induced vibrations on residential buildings. In order to create a network, it was necessary to collect an input database of our own measurements, data measured by other researchers (described in detail in [32], standard [19] and data specified by the geographic information system [33]. Our own measurements for 11 buildings were carried out (see Table 1). A number of different factors were considered in the study. The first factor was the distance from the building to the edge of the road. In the cases analyzed, the distance was between one and 23 m, and all the cases were divided into two sets: The first one for distances from one to 11 m and the second set with distances from 11 to 23 m. Type and condition of road surface was also taken into account. We could distinguish: Very good road condition (smooth surface, no damages, no breaks, no manholes), average road condition (homogeneous surface, few damages) and bad condition (patchy surface, a lot of damages, undulations, holes, cracks). Next factor considered in the study was related to the building condition: Good condition (no damage of structural elements and plaster coatings), average condition (no damage of structural elements, few damages of plaster coatings) and bad condition (a lot of damages, wall cracks). A very important factor to consider is the type of soil in which vibrations are transmitted. Since each soil absorbs the waves differently, the correlation between the type of soil and vibration absorption can be approximated using the three-step criterion according to [34]. The soil type, determined based on the geographic information system [33], was classified for vibration absorption. For this purpose, the absorption coefficient was used. It is an approximate parameter based on many field studies (see [35,36] for example) that can be used for approximate, predictive methods. Taking into account the absorption coefficient, the soil type was divided into three classes: Good (in the case of condensed sand, dry clay, cohesive soils, compact and half-compact), average (in the case of medium and fine moistened clayey sand and hard-plastic cohesive soils) and bad (in the case of wet, loose silty sand, fine clay sand and fine plastic cohesive soils) [35,36].

Table 1.
Characteristics of the buildings studied and the result of measurements.
The type of vehicle is also important. In the analysis, this factor was classified for three different types of vehicles: Type 1 (passenger car up to 3.5 t of total weight), type 2 (bus, truck up to 10 t of total weight) and type 3 (truck from 10 t to 40 t of total weight). It should also be added that a number of studies indicate (see [7,17] for example) that also the type of suspension system used in vehicles may influence the resulting vibrations. This aspect, however, was not considered in the present study.
Field measurements for different types of vehicles were conducted for each residential building (see Table 1). The data were analyzed and filtered in one-third octave bands within the 1–100 Hz range [20]. The results were marked on the DIS scale (see [19]) and impact of traffic-induced vibrations on each of the structure was determined (see last column of Table 1). The results of the experimental study shown in Table 1 indicate that seven buildings belong to zone II of the DIS scale, meaning that some kind of damage could be initiated due to vibrations. On the other hand, in the case of remaining four structures, no impact of vibrations on these structures was expected (zone I of the DIS scale).
4.2. Problem Model
In the second stage of the study, a model, supporting the decision-making process, was created based on the learning Bayesian networks. Sixty-three different experimental measurements were used. All analyzed factors, including distance from the building to the edge of the road, type and condition of road surface, condition of the building, absorption of soil and type of passing vehicles, were considered as variables in the model. Probabilistic relationships between them were created and represented by the conditional probabilities (see the conditional probabilities tables, CPT, on Figure 2). Model of network describing the problem of operational decisions related to impact of traffic-induced vibrations on residential buildings is shown on Figure 3.
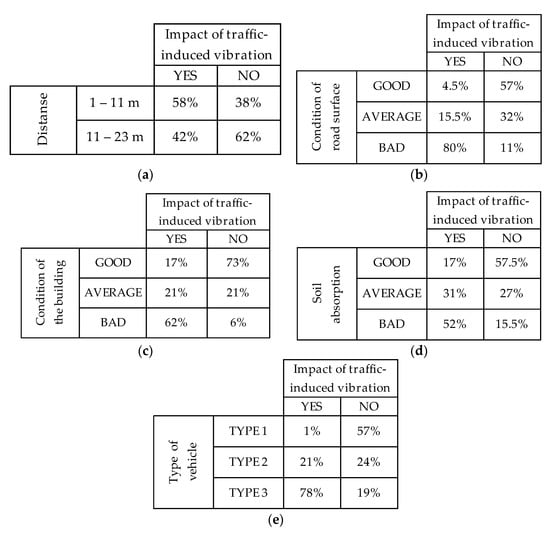
Figure 2.
Tables of conditional probabilities for different variables: (a) Distance; (b) condition of the road; (c) condition of the building; (d) absorption of soil and (e) type of passing vehicle.
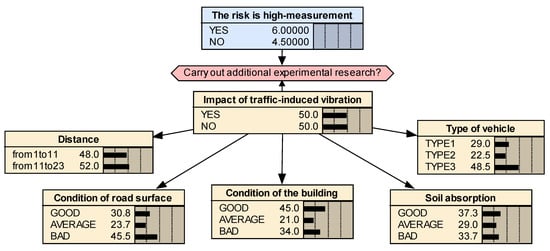
Figure 3.
Model of a Bayesian network (BN) for impact of traffic-induced vibrations on residential buildings.
All 63 experimental measurements were treated as samples and randomly divided into two sets. The networks were subjected to learning from available data, but also to verify using interactive learning. 45 samples were randomly allocated to the training set (71.43% of all samples) and 18 cases were assigned to the verification set (28.57% of all cases). The field results obtained by the network were compared with the results from the experimental study obtained for the verification set (verification phase). The details of the verification of the constructed model are presented in Table 2. It can be observed from the table that the probability of prediction was larger than 50% for all the cases and the average probability of prediction was equal to 84.27%. That confirms the accuracy of the model created.

Table 2.
Characteristics of the input predictors and results of measurements.
4.3. Rating the Value of Information
The decision making process is often defined in order to select one of the available actions: a1, a2, …, an included in the space of action A, and its graphical representation is the dendrite decision [37]. The logical basis for the choice between alternative observations of variable diagnostic symptoms is known as the expected value of sample information (EVSI) and defined as [38]:
where:
- EMV—expected decision value without any additional testing;
- EV|SI—expected decision value as a result of an additional testing, which can be determined as:
- p(z|e)—a priori conditional probability from a result of experiment (e) and observed state (z);
- u(e, z)—value of the most preferred decision from a result of experiment (e) and observed state (z).
Based on the initial Bayes grid shown in Figure 3, the risk of the impact of vibrations on the building was fifty to fifty percent. Taking into account possible decisions, the decision about conducting field measurements should be made. The value of such a decision was EMV = 6.00. The value of new information regarding the condition of the building was:
- EV|SI1 = 0.45 × 7.30 + 0.21 × 6.00 + 0.34 × 9.29 = 7.705,
- EVSI1 = 7.705 – 6 = 1.705.
The monitoring network quality could also be assessed in terms of criteria that would allow us to measure how information obtained from the monitoring network reduces uncertainty regarding the decision/diagnostic variable.
It happens that, in spite of the extensive set of the data and high costs of maintaining the network, a small amount of useful information is obtained [39]. It is often proposed (see, for example, [40]) to use monitoring methods derived from information theory developed by Shannon [41] so as to assess the quality of the network. The basic concept of this theory is the information entropy, which is a measure of the information contained in the data. By treating the monitoring network as a signal communication system, having the ability to transfer operational information, evaluation criteria using the entropy of information could be applied to this system. It allows us (in a quantitative way) to describe the uncertainty associated with the occurrence of the random phenomenon or, in other words, to assess the amount of information that carries the observation of this phenomenon’s symptoms. If X is a discrete random variable taking the value of x1, x2, …, xn with the probability p(xn), where n = 1, 2, …, N, the marginal entropy, H(X), can be calculated as [41]:
where:
- k—base of logarithm,
- N—number of possible states.
The unit of H(X) is:
- Napier—if the natural logarithm is used in formula (5);
- Decibel—if decimal logarithm is applied in formula (5);
- Bit—if log with base 2 is used in formula (5).
The marginal entropy value is in the range from 0 to log N [42]. If we assume that the variable X represents a decision variable in the monitoring network, thus the marginal entropy H(X) defines the uncertainty associated with this variable. It should be noted that, in the case of the centered distribution, the entropy is small. In particular, in an event in which there is no uncertainty (the condition has only one value with probability 1), the entropy value is equal to 0. Alternatively, when a high scatter distributions are concerned, for which there are various observation results with a suitably low probability, the entropy is large. In the extreme case, when each from N observations xn (n = 1, 2, …, N) is equally likely to take place with a probability of pn = 1/N, the entropy reaches its maximum value equal to log N [42].
If two random variables X and Y are correlated (e.g., a diagnostic variable X and its symptom Y), then for the evaluation of the data from an observation of symptom, the conditional entropy, H(X/Y), is used. It is expressed as [41]:
where:
- M—number of symptom Y variable states;
- p(ym)—probability of the a priori state ym;
- H(X|ym)—entropy of the diagnostic variable at the given state ym of the symptom variable.
At this point, we could define the reduction of entropy as a result of observation of a variable symptom Y [41]:
Using Equation (5), the initial entropy for a state from the Bayes example network (Figure 2) was calculated as:
- H(X) = – (0.5 × log20.5 + 0.5 × log20.5) = 1.
Moreover, using Equations (6) and (7), the entropy for observations regarding checking the condition of a building was calculated as:
- H(X|’Condition of the building’ = GOOD) = – (0.189 × log20.189 + 0.811 × log20.811) = 0.6993,
- H(X|’Condition of the building’ = AVERAGE) = – (0.5 × log20.5 + 0.5 × log20.5) = 1,
- H(X|’Condition of the building’ = BAD) = – (0.912 × log20.912 + 0.088 × log20.088) = 0.4298,
- H(X|’Condition of the building’) = 0.45 × 0.6996 + 0.21 × 1 + 0.34 × 0.4298 = 0.671,
- δH(X|’Condition of the building’) = 1 – 0.671 = 0.329.
It should be underlined that the symptom that gives the largest reduction in entropy is more efficient from the standpoint of minimizing the diagnostic variable uncertainty [42].
By using two methods, the influence of different parameters, affecting the possibility of impact of traffic-induced vibrations on the building, was assessed. A summary of the results of the reliability of network is presented in Table 3.

Table 3.
A summary of the reliability of the network.
It can be seen from Table 3 that the most important parameter, affecting the possibility of impact of traffic-induced vibrations, was the ‘Type of vehicle’ for the EVSI method. By contrast, using the method of entropy, the largest influence had the ‘Condition of road surface’. In the case of both methods, the ‘Distance from the building’ was the least important. Special attention should be paid to the parameter relating to soil absorption. Both methods were shown that this was also an important factor. The forecast of phenomena in the substrate related to the dynamic response of road pavements, as well as the interaction of the structure with the ground, was not the subject of this study; however, it is a very important aspect of geotechnical research [43,44,45,46].
5. Conclusions
Impact of traffic-induced vibrations on residential buildings located near roads was experimentally and probabilistically studied in this paper. Firstly, the experimental tests were performed on different buildings using specialized equipment. Then, probabilistic analyses using Bayesian networks were conducted and two methods of assessing the information value (EVSI method and entropy method) were compared. Finally, the developed diagnostic–decision support model was tested, so as to verify the most important parameter, affecting the possibility of structural vibrations to occur.
The results of the study presented in this paper clearly show that the application of Bayesian networks is a very effective approach for assessing the impact of traffic-induced vibrations on residential buildings. An important aspect is that an author’s algorithm based on Bayesian networks allows the forecast of the impact of vibration without labor-intensive measurements. In addition, it could be determined whether soil cross-section studies were justified. These are, of course, probabilistic methods, but in today’s engineering they are very much needed to make economic decisions.
It allowed us to predict the threat exposed to structures with relatively large probability. The major advantage of the proposed method lied in the fact that a created risk of the model works as an integrating tool in which both past and current information about the building operation and the surrounding conditions was used to assess the risk problems’ probabilities at any time. This effect was obtained mainly due to the combination of the expert knowledge of the risk problem elements and the cause–effect relationships among them (expressed by conditional probabilities) with new evidence (monitoring observations). The results of the study also showed that the parameter with the largest influence on structural vibrations was the type of vehicle (due to the EVSI method) and the condition of road surface (due to the entropy method). On the other hand, the distance from the building was found to be the least important parameter in the analysis, apart from the method applied.
The developed algorithm could be successfully applied both to existing and planned buildings, for which the source of vibration is already present or may appear in the future. The algorithm presented in this paper met the requirements to be helpful when making a decision on the location of the planned investment; and in the case of existing buildings, it provides the basis for performing specialized vibration measurements in the case of any doubts.
Author Contributions
Conceptualization, A.S. and A.J.-G.; methodology, A.S.; software, A.S.; validation, A.S., A.J.-G. and R.J.; formal analysis, A.S. and A.J.-G.; investigation, R.J.; resources, A.J.-G.; data curation, A.S.; writing—original draft preparation, A.S. and A.J.-G.; writing—review and editing, R.J.; visualization, A.S.; supervision, R.J.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R. Polymeric bearings — A new base isolation system to reduce structural damage during earthquakes. In Key Engineering Materials; Trans Tech Publications: Zürich, Switzerland, 2013; Volume 569–570, pp. 143–150. [Google Scholar] [CrossRef]
- Elwardany, H.; Seleemah, A.; Jankowski, R. Seismic pounding behavior of multi-story buildings in series considering the effect of infill panels. Eng. Struct. 2017, 144, 139–150. [Google Scholar] [CrossRef]
- Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Appl. Sci. 2019, 9, 1201. [Google Scholar] [CrossRef]
- Mezeh, R.; Sadek, M.; Hage Chehade, F.; Mroueh, H. Adaptive meshing scheme for prediction of high-speed moving loads induced ground vibrations. Comput. Geotech. 2018, 100, 188–202. [Google Scholar] [CrossRef]
- Mezeh, R.; Sadek, M.; Hage Chehade, F.; Shahrour, I. Adaptive analysis of infinite beams dynamics problems using the periodic configuration update method in the time domain. Int. J. Numer. Anal. Methods Geomech. 2017, 42, 618–635. [Google Scholar] [CrossRef]
- Hunaidi, O. Traffic vibrations in buildings. Constr. Tech. Update 2000, 39, 1–6. [Google Scholar]
- Jakubczyk–Gałczyńska, A.; Jankowski, R. Traffic–induced vibrations. The impact on buildings and people. In Environmental Engineering, Proceedings of the International Conference on Environmental Engineering, Vilnius, Lithuania, 22–23 May 2014; Vilnius Gediminas Technical University Press Technika: Vilnius, Lithuania, 2014. [Google Scholar] [CrossRef]
- Goetz, T. The Decision Tree: How to Make Better Choices and Take Control of Your Health; Rodale: Emmaus, PA, USA, 2010. [Google Scholar]
- Schmidt, V. Stochastic Geometry, spatial Statistics and Random Fields: Models and Algorithms; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Jankowski, R.; Walukiewicz, H. Modeling of two-dimensional random fields. Probab. Eng. Mech. 1997, 12, 115–121. [Google Scholar] [CrossRef]
- Neapolitan, R.E. Learning Bayesian Networks; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Arangio, S.; Beck, J.L. Bayesian neural networks for bridge integrity assessment. Struct. Control. Health Monit. 2012, 19, 3–21. [Google Scholar] [CrossRef]
- Kembłowski, M.W.; Grzyl, B.; Kristowski, A.; Siemaszko, A. Risk modelling with Bayesian Networks - case study: construction of tunnel under the Dead Vistula River in Gdansk. Procedia Eng. 2017, 196, 585–591. [Google Scholar] [CrossRef]
- Cárdenas, I.C.; Al-Jibouri, S.; Halman, J.I. A Bayesian belief networks approach to risk control in construction projects. In Proceedings of the 14th International Conference on Computing and Civil Engineering, Moscow, Russia, 27–29 June 2012. [Google Scholar]
- Lombaert, G.; Degrande, G. The experimental validation of a numerical model for the prediction of the vibrations in the free field produced by road traffic. J. Sound Vib. 2003, 262, 309–331. [Google Scholar] [CrossRef]
- Mhanna, M.; Shahrour, I.; Sadek, M.; Dunez, P. Efficiency of heavy mass technology in traffic vibration reduction: Experimental and numerical investigation. Comput. Geotech. 2014, 55, 141–149. [Google Scholar] [CrossRef]
- Mezeh, R.; Mroueh, H.; Sadek, M.; Hosseingholian, M. New approach for the assessment of train/track/ground dynamics using in-situ measurements of high-speed train induced vibrations. Soil Dyn. Earthq. Eng. 2019, 116, 50–59. [Google Scholar] [CrossRef]
- PN-B-02170:2016–12. Ocena szkodliwości drgań przekazywanych przez podłoże na budynki: Evaluation of the harmfulness of building vibrations due to ground motion; Polish Committee for Standardization of Measurement and Quality: Warszawa, Poland, 2016. (In Polish) [Google Scholar]
- ISO 2631-5:2018. Mechanical Vibration and Shock. Evaluation of Human Exposure to Whole-Body Vibration Part 5: Method for Evaluation of Vibration Containing Multiple Shocks; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- BS 6472–1:2008. Guide to Evaluation of Human Exposure to Vibration in Buildings. Part 1: Vibration Sources Other Than Blasting; BSI: Plano, TX, USA, 2008. [Google Scholar]
- ISO 10137:2007. Bases for Design Of Structures – Serviceability of Buildings and Walkways against Vibrations; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- DIN 4150–2. Structural Vibration, Part 2: Human Exposure to Vibration in Buildings; Deutsches Institut für Normung e.V.: Berlin, Germany, 1999. [Google Scholar]
- European Commission. Directive 2002/49/EC of the European parliament and the Council of 25 June 2002 relating to the assessment and management of environmental noise. Off. J. Eur. Communities 2002, 189, 12–25. [Google Scholar]
- Kawecki, J.; Stypula, K. Designing roads near the buildings providing the necessary vibrational comfort for the residents. Procedia Eng. 2013, 57, 549–556. [Google Scholar] [CrossRef][Green Version]
- Fenton, N.; Neil, M. Risk Assessment and Decision Analysis with Bayesian Networks; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Kjaerulff, U.; Madsen, A. Bayesian networks and influence diagrams. Springer Sci. Bus. Media 2008, 200, 114. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Friedman, N.; Goldszmidt, M. Learning Bayesian networks with local structure. Learn. Graph. Model. 1998, 89, 421–459. [Google Scholar] [CrossRef]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian networks: The combination of knowledge and statistical data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1997, 39, 1–38. [Google Scholar] [CrossRef]
- Jakubczyk-Gałczyńska, A. Predicting the impact of traffic–induced vibrations on buildings using artificial neural networks. In Proceedings of the 2nd Baltic Conference for Students and Young Researchers, Gdynia, Poland, 20–23 April 2018; p. 219. [Google Scholar] [CrossRef][Green Version]
- Central Geological Database. Available online: http://baza.pgi.gov.pl (accessed on 27 December 2016).
- Hanson, C.E.; Towers, D.A.; Meister, L.D. Transit Noise And Vibration Impact Assessment; Report FTA-VA-90-1003-06; U.S. Department of Transportation, Federal Transit Administration, Office Planning and Environment: Washington, DC, USA, 2006.
- Ciesielski, R. Podstawy i nowości naukowe w inżynierii parasejsmicznej. Zesz. Naukowe Politech. Rzeszowskiej Mech. 2002, 60, 85–115. (In Polish) [Google Scholar]
- Dulińska, J.; Kawecki, J.; Kozioł, K.; Stypuła, K.; Tatara, T. Oddziaływania Parasejsmiczne Przekazywane na Obiekty Budowlane; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2014. (In Polish) [Google Scholar]
- Singpurwalla, N.D. Reliability and Risk: A Bayesian Perspective; John Wiley & Sons: Austin, TX, USA, 2016. [Google Scholar]
- Apollo, M.; Kembłowski, M.W. Observation value analysis – integral part of Bayesian diagnostics. Procedia Eng. 2015, 123, 24–31. [Google Scholar] [CrossRef]
- Xiang, Y.; Wong, S.K.M.; Cercone, N.A. Microscopic study of minimum entropy search in learning decomposable markov networks. Mach. Learn. 1997, 26, 65–92. [Google Scholar] [CrossRef]
- Mays, D.C.; Faybishenko, B.A.; Finsterle, S. Information entropy to measure temporal and spatial complexity of unsaturated flow in heterogeneous media. Water Resour. Res. 2002, 38, 1313. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kucharek, M.; Treichel, W. Assessment of groundwater quality monitoring network based on information theory. In Recent Advances in Stochastic Modeling and Data Analysis; World Scientific: Singapore, 2007; pp. 636–644. [Google Scholar] [CrossRef]
- Beskou, N.D.; Theodorakopoulos, D.D. Dynamic effects of moving loads on road pavements: A review. Soil Dyn. Earthq. Eng. 2011, 31, 547–567. [Google Scholar] [CrossRef]
- Grundmann, H.; Lieb, M.; Trommer, E. The response of a layered half-space to traffic loads moving along its surface. Arch. Appl. Mech. 1999, 69, 55–67. [Google Scholar] [CrossRef]
- Paneiro, G.; Durão, F.O.; Costa e Silva, M.; Falcão Neves, P. Artificial neural network model for ground vibration amplitudes prediction due to light railway traffic in urban areas. Neural Comput. Appl. 2016, 29, 1045–1057. [Google Scholar] [CrossRef]
- Watts, G.R.; Krylov, V.V. Ground-borne vibration generated by vehicles crossing road humps and speed control cushions. Appl. Acoust. 2000, 59, 221–236. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).










