How Well can Spaceborne Digital Elevation Models Represent a Man-Made Structure: A Runway Case Study
Abstract
:1. Introduction
- Calculating the statistical indicators of the differences between the surveyed runway surface and the corresponding surface extracted from the investigated DEMs.
- Analyzing the statistics of the differences, and drawing conclusions and recommendations for engineering structure surveyors and operators on the suitability of the freely available or reasonably priced spaceborne DEMs for monitoring anthropogenic or natural features.
2. Materials and Methods
2.1. Area of Interest
2.2. Digital Elevation Data
2.2.1. ASTER
2.2.2. AW3D30
2.2.3. Aerial Photogrammetry (AP)
2.2.4. Leveling
2.2.5. SRTM-1” and SRTM-3”
2.2.6. SRTM-X
2.2.7. TanDEM-3” (TanDEM)
2.2.8. WorldDEMTM
2.2.9. Aeronautical Data on the Runway
2.3. Data Processing
- Using a bilinear interpolation method, the elevation for the locations corresponding to 475 control points were calculated for each investigated DEM;
- The discrepancies between the interpolated elevation and the control point elevation were calculated for each investigated DEM;
- The mean (D) and standard deviation (σ) of the differences were calculated for each DEM;
- The root mean square error (RMSE) of the differences for each DEM was calculated using the following formula:
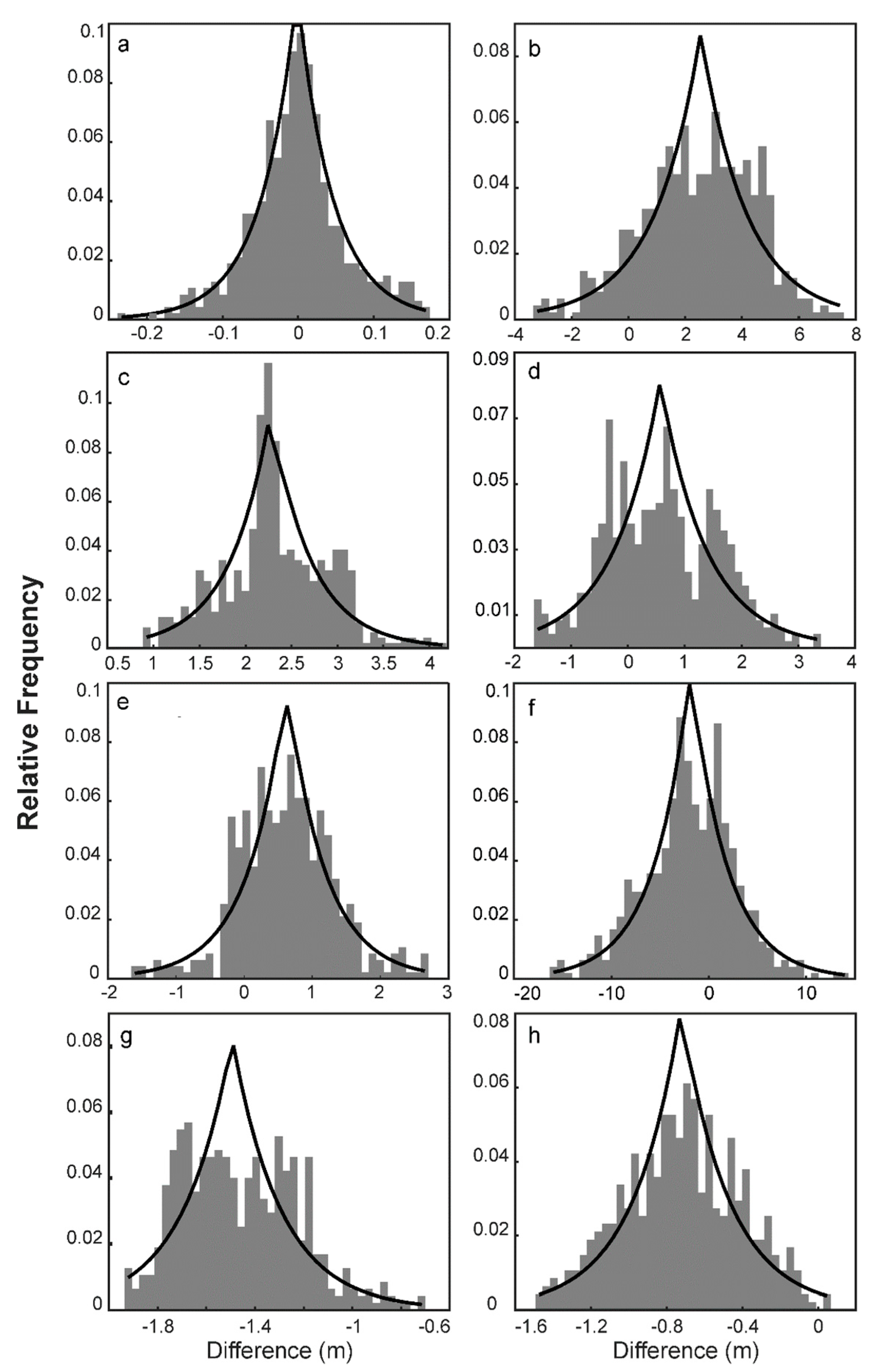
- A histogram of differences was calculated for each DEM; and
- The Laplace probability density function (pdf) was calculated according to Equation (4):
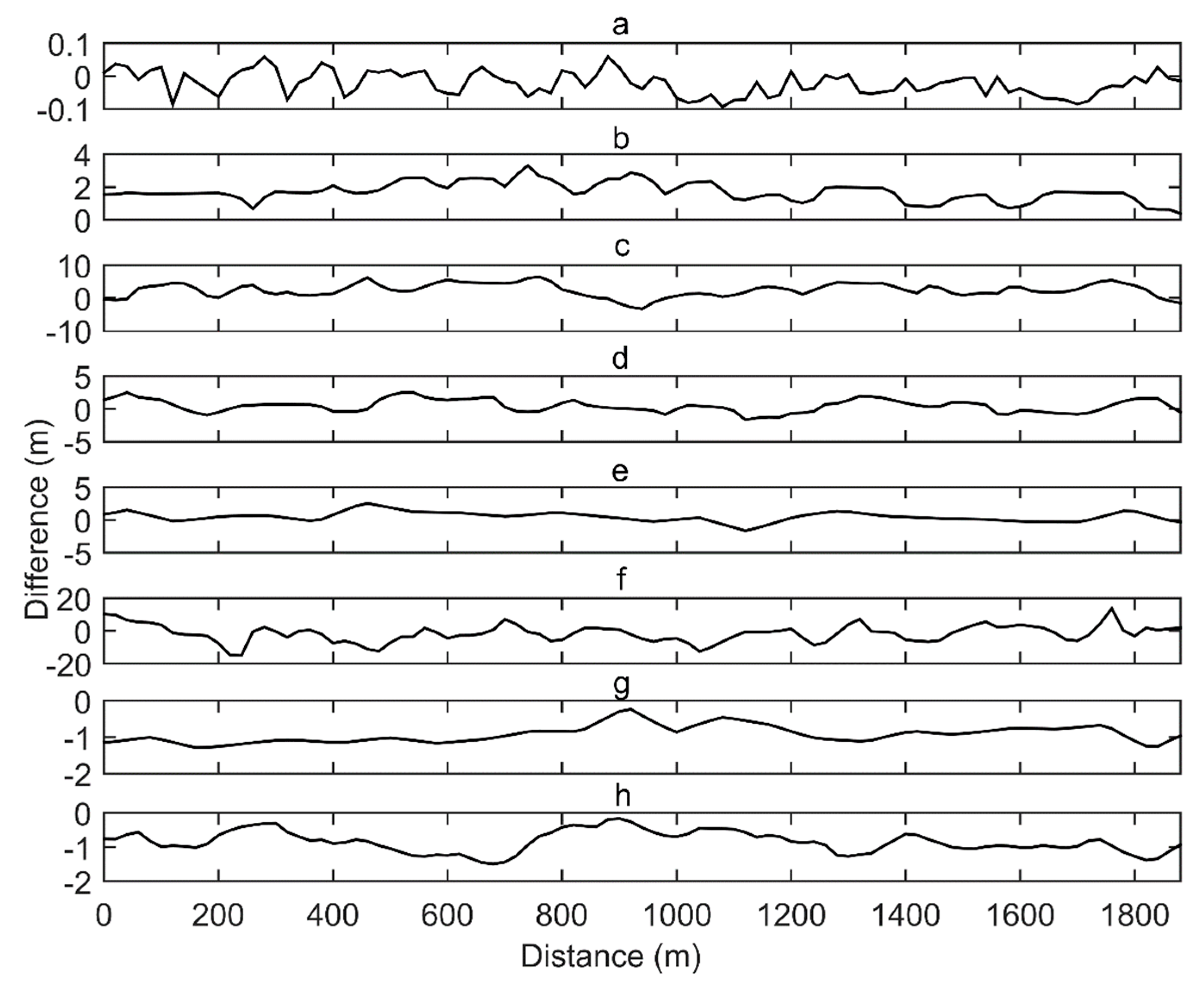
3. Results
4. Discussion
5. Conclusions
- It appears that the spaceborne InSAR technology is more accurate than the traditional photogrammetry based on the satellite imagery for DEM production. The limiting factor is the cloud cover that restricts the number of stereopairs used to develop DEMs (e.g., [2]).
- The TanDEM dataset is slated to replace the SRTM model as a global DEM due to its higher vertical accuracy and the fact that it is more current than the almost 20-year-old SRTM dataset.
- All the investigated DEMs, except the AP one, exhibited a vertical bias. The reason for the bias is probably related to the DEMs’ vertical calibration. A separate study of the effect is being considered.
- The vertical bias can be locally determined and subtracted from the DEM. This operation will increase the TanDEM’s absolute accuracy to a level of approximately 0.5 m and the AW3D30 to 0.6 m (one sigma RMSE).
- Both the TanDEM and AW3D30 spaceborne elevation data are good enough to perform at least preliminary studies on a variety of engineering projects.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The Shuttle Radar Topography Mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Becek, K. Assessing global digital elevation models using the runway method: The Advanced Spaceborne Thermal Emission and Reflection Radiometer versus the Shuttle Radar Topography Mission Case. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4823–4831. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.J.; Danielson, J.J.; Meyer, D. Validation of the ASTER Global Digital Elevation Model version 3 over the conterminous United States. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 143–148. [Google Scholar] [CrossRef]
- Girod, L.; Nuth, C.; Kääb, A.; McNabb, R.; Galland, O. MMASTER: Improved ASTER DEMs for Elevation Change Monitoring. Remote Sens. 2017, 7, 704. [Google Scholar] [CrossRef]
- JPL. ASTER Global Digital Elevation Map. Available online: https://asterweb.jpl.nasa.gov/gdem.asp (accessed on 19 June 2019).
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the global TanDEM-X Digital Elevation Model with GPS data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- Tadono, T.; Takaku, J.; Tsutsui, K.; Oda, F.; Nagai, H. Status of ALOS World 3D (AW3D) global DSM generation. In Proceedings of the IEEE International. Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar] [CrossRef]
- JAXA. ALOS Global Digital Surface Model ALOS World 3D–30m (AW3D30). Available online: http://www.eorc.jaxa.jp/ALOS/en/aw3d30/ (accessed on 1 August 2019).
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Generation of the 30 m-Mesh Global Digital Surface Model by ALOS Prism. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B41, 157–162. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Tsutsui, K. Generation of High Resolution Global DSM from ALOS PRISM. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-4, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Santillana, J.; Makinano-Santillana, M. Vertical Accuracy Assessment of 30-m Resolution ALOS, ASTER, and SRTM Global DEMs Over Northeastern Mindanao, Philippines. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 149–156. [Google Scholar] [CrossRef]
- EUROCONTROL. The European Organisation for the Safety of Air Navigation. Available online: https://www.ead.eurocontrol.int/eadcms/eadsite/index.php.html (accessed on 19 June 2019).
- Becek, K.; Koppe, W.; Kutoğlu, Ş.H. Evaluation of Vertical Accuracy of the WorldDEM™ Using the Runway Method. Remote Sens. 2016, 8, 934. [Google Scholar] [CrossRef]
- Becek, K.; Akgül, V.; Inyurt, S.; Mekik, Ç.; Pochwatka, P. Spaceborne Digital Elevation Data of Runway at Zonguldak Airport, Turkey. Mendeley Data 2019, V2. [Google Scholar] [CrossRef]
- Fujisada, H.; Urai, M.; Iwasaki, A. Advanced methodology for ASTER DEM generation. IEEE Trans. Geosci. Remote Sens. 2011, 9, 5080–5091. [Google Scholar] [CrossRef]
- Becek, K. Investigating error structure of shuttle radar topography mission elevation data product. Geophys. Res. Lett. 2008, 35, L15403. [Google Scholar] [CrossRef]
- Huber, M.; Gruber, A.; Wendleder, A.; Wessel, B.; Roth, A.; Schmitt, A. The Global Tandem-X DEM: Production Status and First Validation Results. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2012, XXXIX-B7, 45–50. [Google Scholar] [CrossRef]
- Norton, R.M. The Double Exponential Distribution: Using Calculus to Find a Maximum Likelihood Estimator. Amer. Stat. 1984, 38, 135–136. [Google Scholar] [CrossRef]
- Bayik, C.; Becek, K.; Mekik, C.; Ozendi, M. On the vertical accuracy of the ALOS world 3D-30m digital elevation model. Remote Sens. Lett. 2018, 9, 607–615. [Google Scholar] [CrossRef]
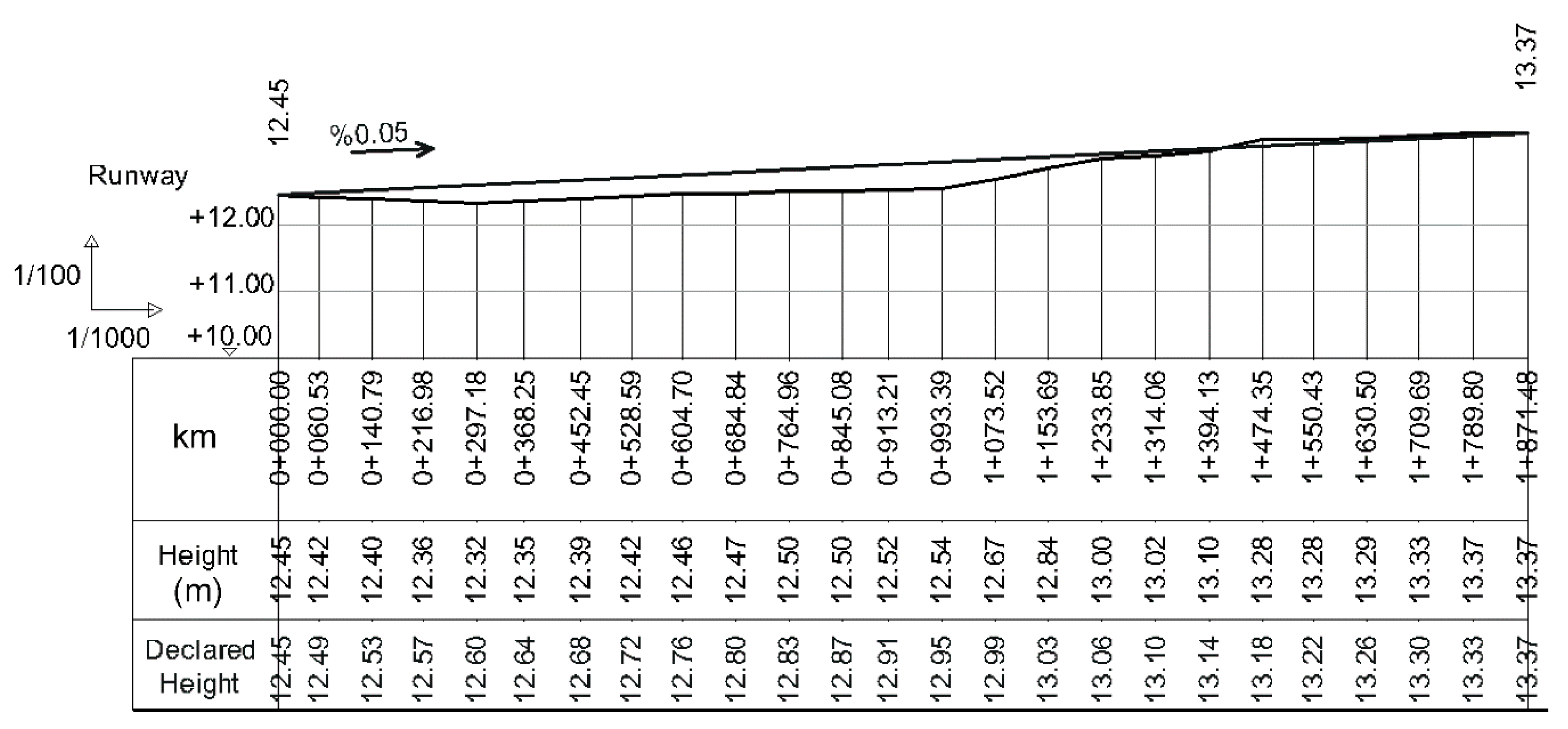

| Parameter | Value |
|---|---|
| Length (m) | 1881 |
| Width (m) | 30 |
| Threshold elevation a.m.s.l. (18/36) (m) | 12.45/13.3 |
| Surface | Concrete |
| Slope (centerline) | 0.05% |
| Cross-slope (left/right from centerline) | 1.0% |
| Local geoid undulation (m) | 34.14 |
| DEM Brand | Horizontal Reference System | Vertical Reference System |
|---|---|---|
| ASTER | WGS84 | EGM96 |
| AW3D30 | GRS80 (ITRF97) | EGM96 |
| AP | WGS94/UTM36T | Local geoid |
| SRTM-1”, SRTM-3” | WGS84 | EGM96 |
| SRTM-X | WGS84 | WGS84 1 |
| TanDEM, WorldDEMTM | WGS84-G1150 | EGM2008 |
| DEM | Mean Diff. (Bias) (m) | STD (m) | RMSE (m) | LE90 (m) | Difference (m) | |
|---|---|---|---|---|---|---|
| Maximum | Minimum | |||||
| AP | ‒0.002 | 0.064 | 0.064 | 0.105 | 0.174 | ‒0.238 |
| ASTER | 2.435 | 1.992 | 3.146 | 5.159 | 7.583 | ‒3.341 |
| AW3D30 | 1.820 | 0.578 | 1.910 | 3.140 | 3.684 | 0.383 |
| SRTM-1” | 0.580 | 0.990 | 1.147 | 1.882 | 3.392 | ‒1.652 |
| SRTM-3” | 0.614 | 0.712 | 0.940 | 1.542 | 2.705 | ‒1.656 |
| SRTM-X | ‒1.570 | 5.209 | 5.440 | 8.922 | 13.631 | ‒14.977 |
| TanDEM | ‒0.923 | 0.231 | 0.951 | 1.560 | ‒0.233 | ‒1.286 |
| WorldDEMTM | ‒0.722 | 0.327 | 0.787 | 1.291 | 0.113 | ‒1.493 |
| DEM | m–Median of Differences (m) | a–Equation (5) (m) |
|---|---|---|
| ASTER | 2.546 | 1.619 |
| AW3D30 | 1.774 | 0.439 |
| AP | ‒0.002 | 0.047 |
| SRTM-1” | 0.568 | 0.813 |
| SRTM-3” | 0.624 | 0.553 |
| SRTM-X | ‒1.875 | 3.694 |
| TanDEM | ‒1.494 | 0.200 |
| WorldDEMTM | ‒0.724 | 0.251 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becek, K.; Akgül, V.; Inyurt, S.; Mekik, Ç.; Pochwatka, P. How Well can Spaceborne Digital Elevation Models Represent a Man-Made Structure: A Runway Case Study. Geosciences 2019, 9, 387. https://doi.org/10.3390/geosciences9090387
Becek K, Akgül V, Inyurt S, Mekik Ç, Pochwatka P. How Well can Spaceborne Digital Elevation Models Represent a Man-Made Structure: A Runway Case Study. Geosciences. 2019; 9(9):387. https://doi.org/10.3390/geosciences9090387
Chicago/Turabian StyleBecek, Kazimierz, Volkan Akgül, Samed Inyurt, Çetin Mekik, and Patrycja Pochwatka. 2019. "How Well can Spaceborne Digital Elevation Models Represent a Man-Made Structure: A Runway Case Study" Geosciences 9, no. 9: 387. https://doi.org/10.3390/geosciences9090387
APA StyleBecek, K., Akgül, V., Inyurt, S., Mekik, Ç., & Pochwatka, P. (2019). How Well can Spaceborne Digital Elevation Models Represent a Man-Made Structure: A Runway Case Study. Geosciences, 9(9), 387. https://doi.org/10.3390/geosciences9090387






