Sequential Earthquake Damage Assessment Incorporating Optimized sUAV Remote Sensing at Pescara del Tronto
Abstract
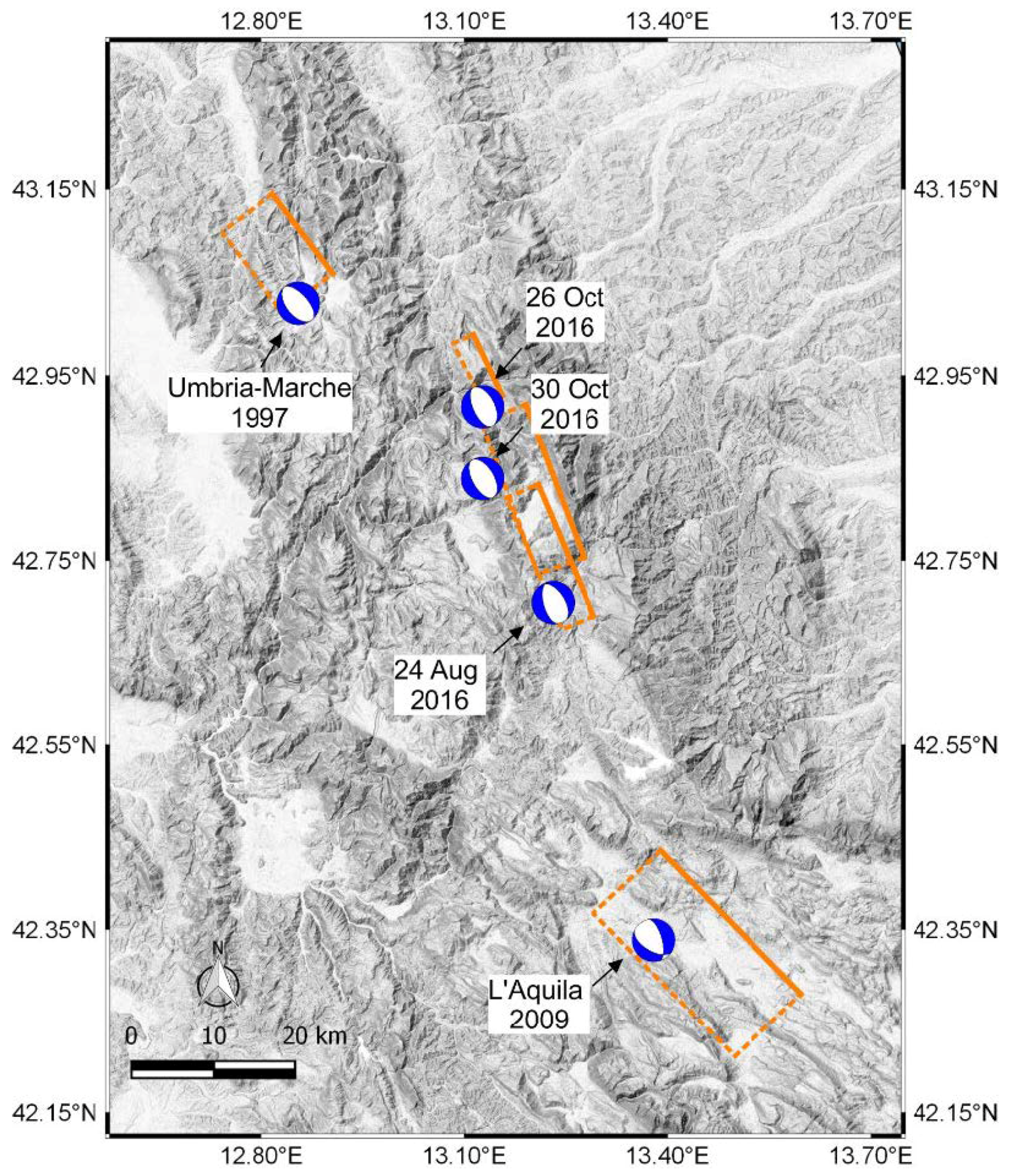
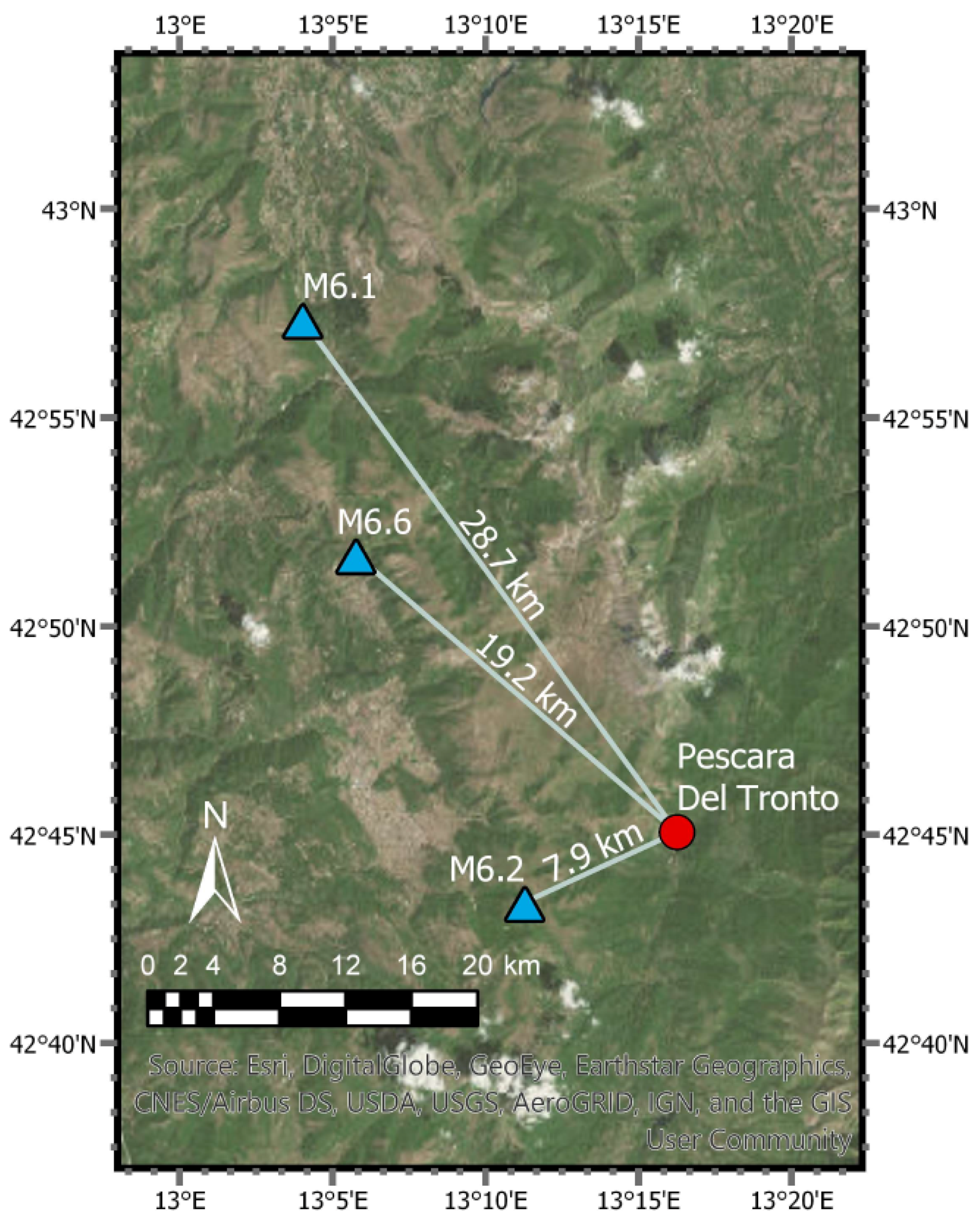
1. Introduction
2. Method of Preliminary sUAV Reconnaissance and Modeling in 2016
3. Explanation of the Algorithms Implemented in 2018
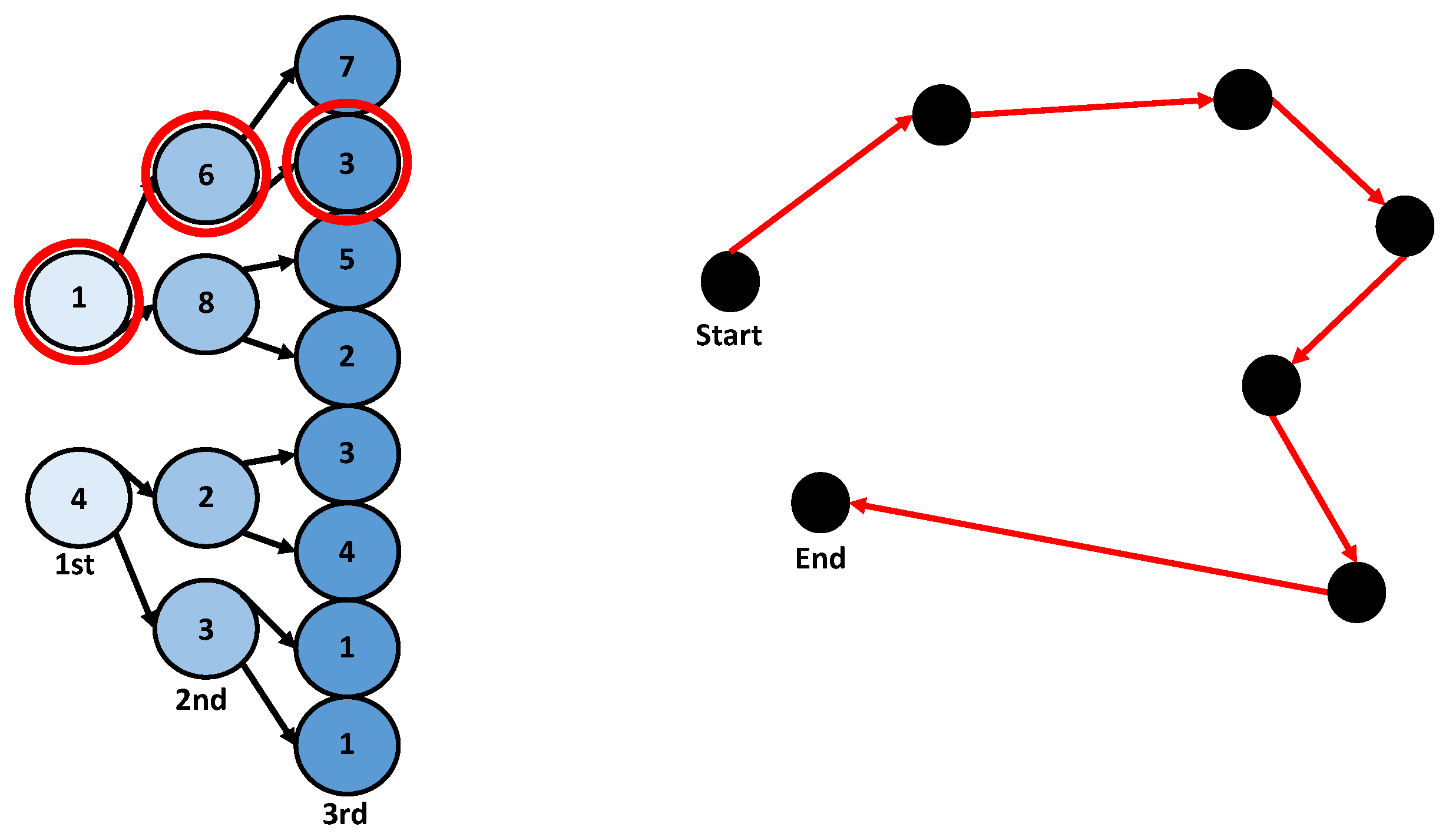
3.1. Optimized View and Path Planning Algorithms
3.2. Evolutionary View-Planning
3.2.1. A Priori Terrain Data
3.2.2. Fitness Function
3.2.3. Inheritance
3.2.4. Diversity and Elitism
3.2.5. Convergence
3.2.6. Why Evolutionary View-Planning Matters
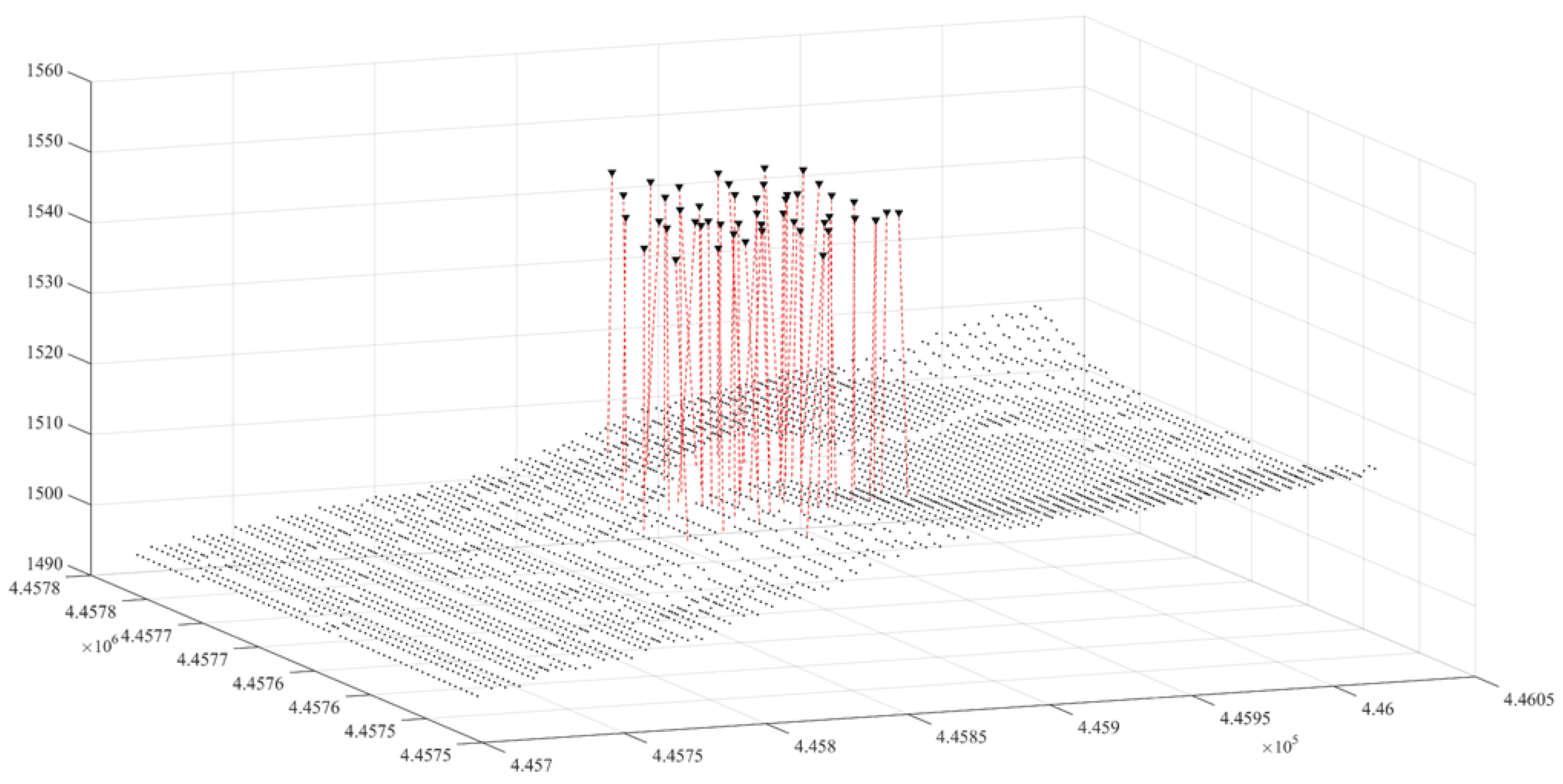
4. Application of the Algorithm to Pescara del Tronto in 2018
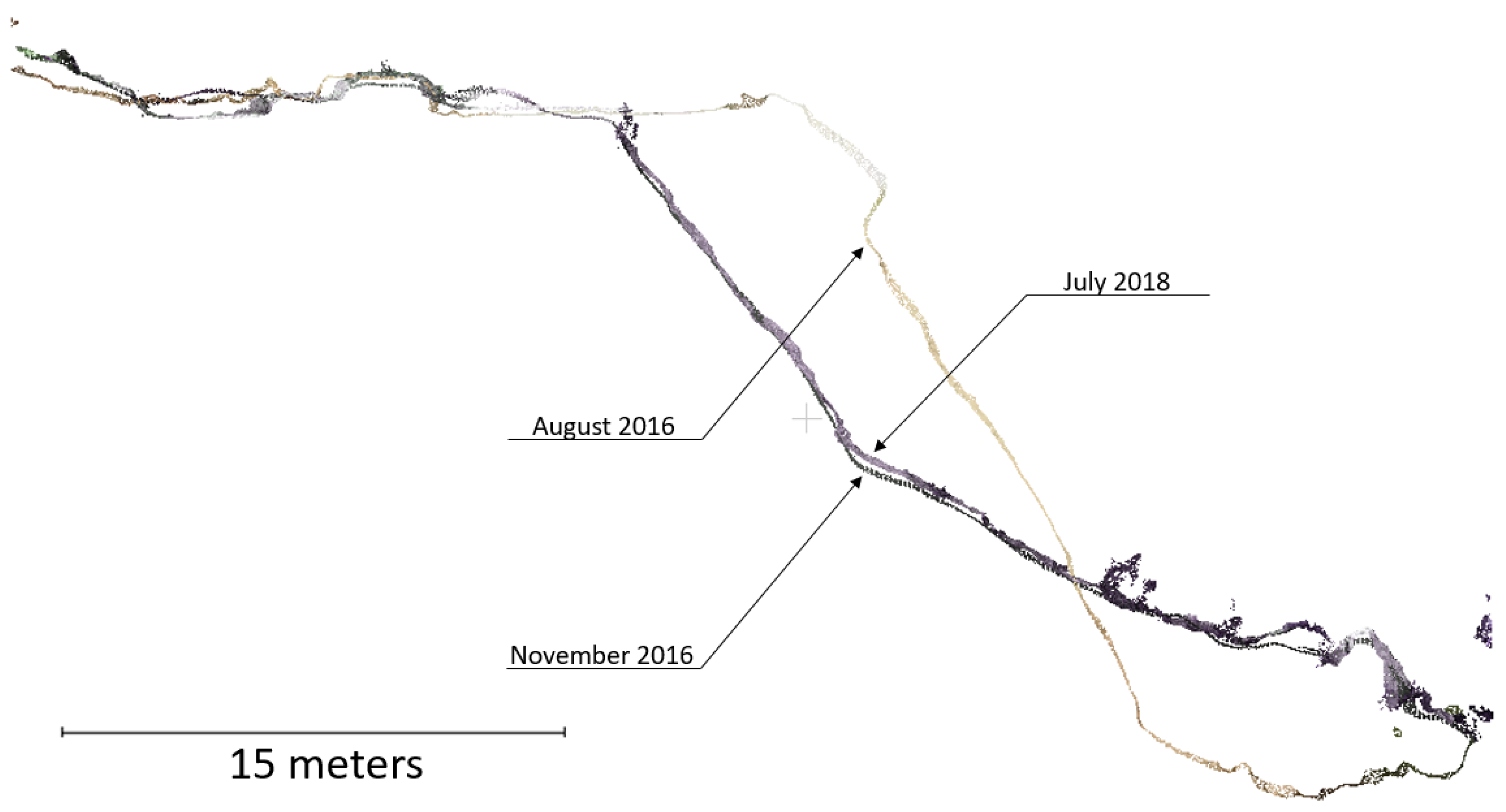
5. Model Observations of Temporal Changes Two Years after the Earthquake
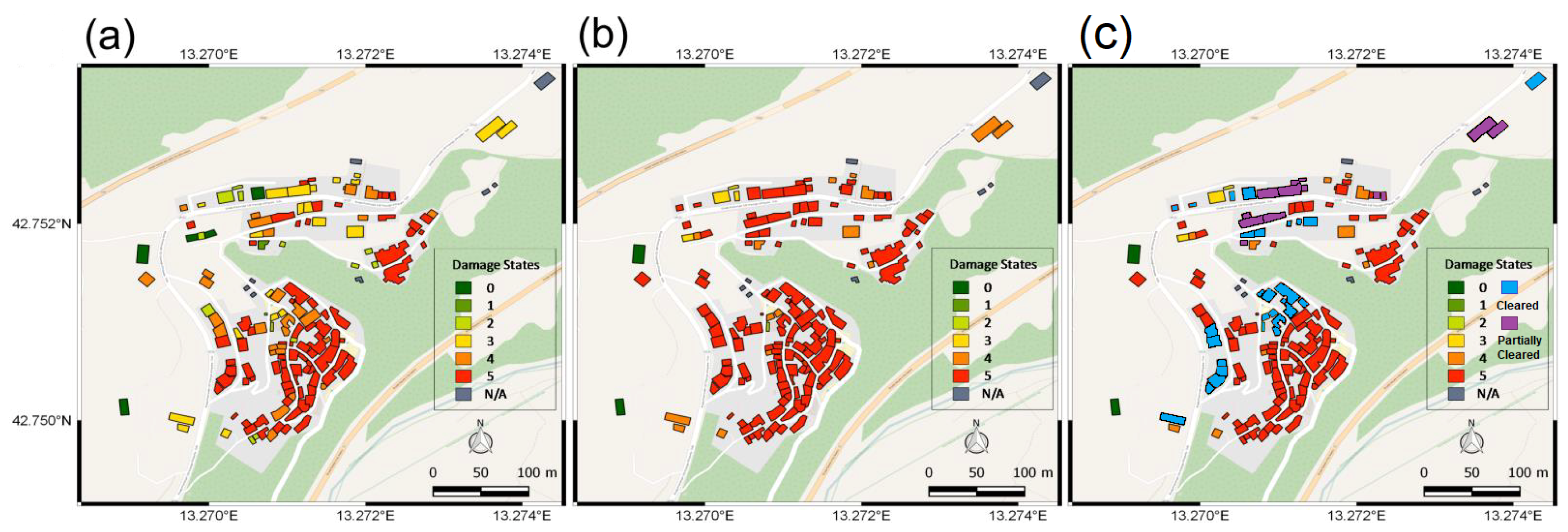
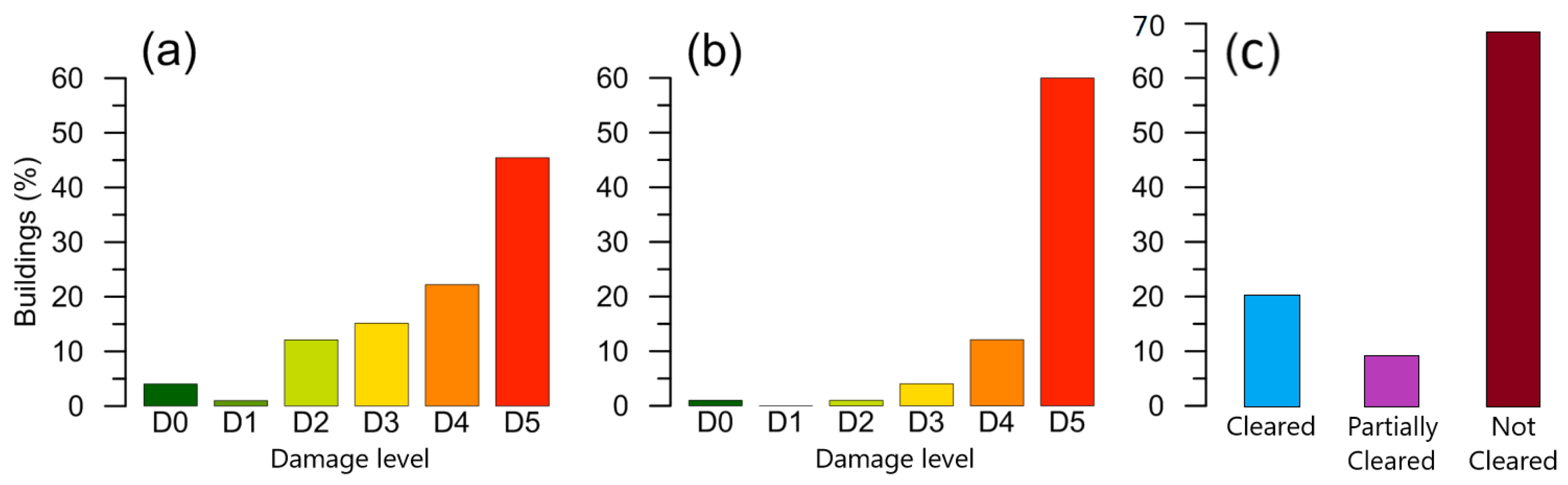
6. Results of Observed Damage over Time
6.1. Damage Observations between the August and October 2016 Events and the July 2018 Follow-Up Visit
6.1.1. Structural Damage Area (Location 1)
6.1.2. Landslides Impacting Strada Statale (Location 2)
6.1.3. Failed Retaining Wall Surrounding Village (Location 3)
6.1.4. Localized Landslides along Gully Wall (Location 4)
6.1.5. Landslide on Northern Slope of Village (Location 5)
6.1.6. Haul Road and Exposed Pipeline near the Gravel Pit (Location 6)
6.1.7. Large Slope Failure North of Village (Location 7)
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BYU | Brigham Young University |
| C-UAS | Center for Unmanned Aircraft Systems |
| DSM | Digital Surface Model |
| GCP | Ground Control Point |
| GSD | Ground-Sampling Distance |
| GEER | Geotechnical Extreme Events Reconnaissance |
| GPS | Global Positioning System |
| INGV | Instituto Nazionale di Geofisica e Vulcanologia |
| I/UCRC | Industry/University Cooperative Research Center |
| PGA | Peak Ground Acceleration |
| PRISM | Process Research and Intelligent Systems Modeling |
| NSF | National Science Foundation |
| ROAM | Research in Optimized Aerial Modeling |
| RMS | Root Mean Square |
| RSN | Rete Sismica Nazionale |
| RTK | Real Time Kinematic |
| SDK | Software Developer Kit |
| SfM | Structure-from-Motion |
| sUAS | Small Unmanned Aerial Systems |
| sUAV | Small Unmanned Aerial Vehicle |
| TSP | Traveling Salesman Problem |
| USGS | United States Geological Survey |
References
- Stewart, J.P. Engineering Reconnaissance Following the 2016 M 6.0 Central Italy Earthquake: Ver 1; GeotechnicalExtreme Events Reconnaissance Association: Berkeley, CA, USA, 2016. [Google Scholar]
- Stewart, J.; Lanzo, G.; Ausilio, E.; Cairo, R.; Bozzoni, F.; Capatti, M.C.; della Pasqua, F.; Dezi, F.; Di Sarno, L.; Durante, M.; et al. Engineering Reconnaissance Following the October 2016 Central Italy Earthquakes; GeotechnicalExtreme Events Reconnaissance Association: Berkeley, CA, USA, 2017. [Google Scholar]
- Stewart, J.; Lanzo, G.; Ausilio, E.; Cairo, R.; Bozzoni, F.; Capatti, M.C.; della Pasqua, F.; Dezi, F.; Di Sarno, L.; Simonelli, A.L.; et al. Engineering Reconnaissance Following the October 2016 Central Italy Earthquakes—Version 2; GeotechnicalExtreme Events Reconnaissance Association: Berkeley, CA, USA, 2017. [Google Scholar]
- Stewart, J.; Lanzo, G.; Aversa, S.; Bozzoni, F.; Dashti, S.; Di Sarno, L.; Durante, M.; Simonelli, A.L.; Penna, A.; Foti, S.; et al. Engineering Reconnaissance of the 24 August 2016 Central Italy Earthquake. Version 2; GeotechnicalExtreme Events Reconnaissance Association: Berkeley, CA, USA, 2016. [Google Scholar]
- Stewart, J.; Zimmaro, P.; Lanzo, G.; Mazzoni, S.; Ausilio, E.; Aversa, S.; Bozzoni, F.; Cairo, R.; Chiara, M.; Castiglia, M.; et al. Reconnaissance of 2016 Central Italy Earthquake Sequence. Earthq. Spectra 2018, 34, 1547–1555. [Google Scholar] [CrossRef]
- Franke, K.W.; Lingwall, B.N.; Zimmaro, P.; Kayen, R.E.; Tommasi, P.; Chiabrando, F.; Santo, A. Phased Reconnaissance Approach to Documenting Landslides Following the 2016 Central Italy Earthquakes. Earthq. Spectra 2018, 34, 1693–1719. [Google Scholar] [CrossRef]
- Lanzo, G.; Tommasi, P.; Ausilio, E.; Aversa, S.; Bozzoni, F.; Cairo, R.; d’Onofrio, A.; Durante, M.G.; Foti, S.; Giallini, S.; et al. Reconnaissance of geotechnical aspects of the 2016 Central Italy earthquakes. Bull. Earthq. Eng. 2018, 1, 1–38. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Feizizadeh, B.; Matsuoka, M. From a GIS-based hybrid site condition map to an earthquake damage assessment in Iran: Methods and trends. Int. J. Disaster Risk Reduct. 2017, 22, 23–36. [Google Scholar] [CrossRef]
- Barone, P.M.; Di Maggio, R.M. Forensic Investigations of Geohazards: The Norcia 2016 Earthquake. Geosciences 2018, 8, 316. [Google Scholar] [CrossRef]
- Valerio, E.; Tizzani, P.; Carminati, E.; Doglioni, C.; Pepe, S.; Petricca, P.; De Luca, C.; Bignami, C.; Solaro, G.; Castaldo, R.; et al. Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated through Seismological Data, DInSAR Measurements, and Numerical Modelling. Remote Sens. 2018, 10, 1901. [Google Scholar] [CrossRef]
- Zhong, S.; Xu, C.; Yi, L.; Li, Y. Focal Mechanisms of the 2016 Central Italy Earthquake Sequence Inferred from High-Rate GPS and Broadband Seismic Waveforms. Remote Sens. 2018, 10, 512. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M. Building Damage Assessment Using Multisensor Dual-Polarized Synthetic Aperture Radar Data for the 2016 M 6.2 Amatrice Earthquake, Italy. Remote Sens. 2017, 9, 330. [Google Scholar] [CrossRef]
- Istituto Nazionale di Geofisica e Vulcanologia. INGV Centro Nazionale Terremoti: Seismic Network IV; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2017. [Google Scholar] [CrossRef]
- INGV Sede Irpinia. RETE Sismica Nazionale. 2019. Available online: http://www.gm.ingv.it/ (accessed on 15 March 2019).
- Copernicus Emergency Management Service. 2019. Available online: https://emergency.copernicus.eu/ (accessed on 2 April 2019).
- Pavelka, K.; Šedina, J.; Matoušková, E. High Resolution Drone Surveying of the Pista Geoglyph in Palpa, Peru. Geosciences 2018, 8, 479. [Google Scholar] [CrossRef]
- Pellicani, R.; Argentiero, I.; Manzari, P.; Spilotro, G.; Marzo, C.; Ermini, R.; Apollonio, C. UAV and Airborne LiDAR Data for Interpreting Kinematic Evolution of Landslide Movements: The Case Study of the Montescaglioso Landslide (Southern Italy). Geosciences 2019, 9, 248. [Google Scholar] [CrossRef]
- DJI. Phantom 4 Pro. 2019. Available online: https://www.dji.com/phantom-4-pro/info (accessed on 20 April 2019).
- Group, P. eMotion. 2019. Available online: https://www.sensefly.com/software/emotion/ (accessed on 20 April 2019).
- Koenderink, J.J.; van Doorn, A.J. Affine structure from motion. J. Opt. Soc. Am. A 1991, 8, 377. [Google Scholar] [CrossRef] [PubMed]
- Barrett, B.J. Field Validation of an Advanced Autonomous Method of Exterior Dam Inspection Using Unmanned Aerial Vehicles. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2018. [Google Scholar]
- Scaioni, M.; Crippa, J.; Corti, M.; Barazzetti, L.; Fugazza, D.; Azzoni, R.; Cernuschi, M.; Diolaiuti, G.A. Technical Aspects Related to the Application of SFM Photogrammetry in High Mountain. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 1029–1036. [Google Scholar] [CrossRef]
- Martin, R.; Rojas, I.; Franke, K.; Hedengren, J. Evolutionary View Planning for Optimized UAV Terrain Modeling in a Simulated Environment. Remote Sens. 2015, 8, 26. [Google Scholar] [CrossRef]
- ASPRS. The Imaging & Geospatial Information Society; ASPRS: Bethesda, MD, USA, 2018. [Google Scholar]
- Jung, D.; Dong, Y.; Frisk, E.; Krysander, M.; Biswas, G. Sensor selection for fault diagnosis in uncertain systems. Int. J. Control 2018, 91, 1–11. [Google Scholar] [CrossRef]
- Henriques, M.; Roque, D. Unmanned Aerial Vehicles (UAV) as a Support to Visual Inspections of Concrete Dams; LNEC: Lisbon, Portugal, 2015. [Google Scholar]
- Zhao, J.; Cheung, S.C. Optimal visual sensor planning. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 165–168. [Google Scholar] [CrossRef]
- Palmer, L.M.; Franke, K.W.; Abraham Martin, R.; Sines, B.E.; Rollins, K.M.; Hedengren, J.D. Application and Accuracy of Structure from Motion Computer Vision Models with Full-Scale Geotechnical Field Tests. In IFCEE 2015; American Society of Civil Engineers: Reston, VA, USA, 2015; pp. 2432–2441. [Google Scholar] [CrossRef]
- Liu, J.; Sridharan, S.; Fookes, C. Recent Advances in Camera Planning for Large Area Surveillance. ACM Comput. Surv. 2016, 49, 6. [Google Scholar] [CrossRef]
- Rahimian, P.; Kearney, J.K. Optimal Camera Placement for Motion Capture Systems. IEEE Trans. Vis. Comput. Graph. 2016, 23, 1209–1221. [Google Scholar] [CrossRef] [PubMed]
- Arabnia, H.R.; Deligiannidis, L. Emerging Trends in Image Processing, Computer Vision and Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1–609. [Google Scholar] [CrossRef]
- Martin, R.; Blackburn, L.; Pulsipher, J.; Franke, K.; Hedengren, J. Potential Benefits of Combining Anomaly Detection with View Planning for UAV Infrastructure Modeling. Remote Sens. 2017, 9, 434. [Google Scholar] [CrossRef]
- Lu, E.H.-C.; Yang, Y.W. A hybrid route planning approach for logistics with pickup and delivery. Expert Syst. Appl. 2019, 118, 482–492. [Google Scholar] [CrossRef]
- Tauer, G.; Date, K.; Nagi, R.; Sudit, M. An incremental graph-partitioning algorithm for entity resolution. Inf. Fusion 2019, 46, 171–183. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009; pp. 357–478. [Google Scholar]
- Gass, S.I.; Fu, M.C. (Eds.) Encyclopedia of Operations Research and Management Science: Traveling Salesman Problem; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Hoppe, C.; Wendel, A.; Zollmann, S.; Pirker, K.; Irschara, A.; Bischof, H.; Kluckner, S. Photogrammetric camera network design for micro aerial vehicles. In Proceedings of the Computer Vision Winter Workshop (CVWW), Mala Nedelja, Slovenia, 1–3 February 2012; Volume 8, pp. 1–3. [Google Scholar]
- Bożejko, W.; Gnatowski, A.; Niżyński, T.; Affenzeller, M.; Beham, A. Local Optima Networks in Solving Algorithm Selection Problem for TSP. In Proceedings of the DepCoS-RELCOMEX 2018, Brunow, Poland, 2–6 July 2018; pp. 83–93. [Google Scholar] [CrossRef]
- Dollison, R. The National Map: New Viewer, Services, and Data Download: U.S. Geological Survey Fact Sheet 2010–3055; United States Geological Survey: Reston, VA, USA, 2016. [CrossRef]
- Whitten, A. Decentralized Planning for Autonomous Agents Cooperating in Complex Missions. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Dobrokhodov, V.N.; Yakimenko, O.A.; Jones, K.D.; Kaminer, I.; Bourakov, E.; Kitsios, I.; Lizarraga, M. New generation of rapid flight test prototyping system for small unmanned air vehicles. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Hilton Head, SC, USA, 20–23 August 2007; pp. 1–26. [Google Scholar]
- Li, R.; Fulp, E.W. Evolutionary Approaches for Resilient Surveillance Management. In Proceedings of the 2017 IEEE Security and Privacy Workshops (SPW), San Jose, CA, USA, 25–25 May 2017. [Google Scholar] [CrossRef]
- Li, R.; Fulp, E. Using Evolutionary Approaches to Manage Surveillance Cameras in Dynamic Environments. In Proceedings of the 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications and 12th IEEE International Conference on Big Data Science and Engineering, New York, NY, USA, 1–3 August 2018; pp. 191–196. [Google Scholar] [CrossRef]
- PRISM, B. BYU PRISM 3D Model Gallery. 2019. Available online: http://prismweb.groups.et.byu.net/gallery2/ (accessed on 18 April 2019).
- DJI. Inspire 2. 2019. Available online: https://www.dji.com/inspire-2/info (accessed on 28 March 2019).
- Bentley Systems. Reality Modeling Software. 2019. Available online: https://www.bentley.com/ (accessed on 18 April 2019).

















| GCP | Total Photos | Surface Area () | GSD (cm/px) | Adjusted GSD (cm/px) | |
|---|---|---|---|---|---|
| Nadir Grid | 22 | 912 | 0.35 | 2.0 | 2.0 |
| Optimized | 12 | 716 | 0.41 | 2.4 | 1.5 |
| Points Tested | Mean | Standard Deviation | Minimum Number | Maximum Number | |
|---|---|---|---|---|---|
| Nadir Grid | 30 | 28.13 | 17.47 | 6 | 67 |
| Optimized | 30 | 23.20 | 6.78 | 10 | 38 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freeman, M.; Vernon, C.; Berrett, B.; Hastings, N.; Derricott, J.; Pace, J.; Horne, B.; Hammond, J.; Janson, J.; Chiabrando, F.; et al. Sequential Earthquake Damage Assessment Incorporating Optimized sUAV Remote Sensing at Pescara del Tronto. Geosciences 2019, 9, 332. https://doi.org/10.3390/geosciences9080332
Freeman M, Vernon C, Berrett B, Hastings N, Derricott J, Pace J, Horne B, Hammond J, Janson J, Chiabrando F, et al. Sequential Earthquake Damage Assessment Incorporating Optimized sUAV Remote Sensing at Pescara del Tronto. Geosciences. 2019; 9(8):332. https://doi.org/10.3390/geosciences9080332
Chicago/Turabian StyleFreeman, Michael, Cory Vernon, Bryce Berrett, Nicole Hastings, Jeff Derricott, Jenessa Pace, Benjamin Horne, Joshua Hammond, Joseph Janson, Filiberto Chiabrando, and et al. 2019. "Sequential Earthquake Damage Assessment Incorporating Optimized sUAV Remote Sensing at Pescara del Tronto" Geosciences 9, no. 8: 332. https://doi.org/10.3390/geosciences9080332
APA StyleFreeman, M., Vernon, C., Berrett, B., Hastings, N., Derricott, J., Pace, J., Horne, B., Hammond, J., Janson, J., Chiabrando, F., Hedengren, J., & Franke, K. (2019). Sequential Earthquake Damage Assessment Incorporating Optimized sUAV Remote Sensing at Pescara del Tronto. Geosciences, 9(8), 332. https://doi.org/10.3390/geosciences9080332








