Frost Resilience of Stabilized Earth Building Materials

Abstract

Earth-based building materials are increasingly valued in green design for their low embodied energy, humidity-buffering ability, and thermal stability. These materials perform well in warm dry climates, but greater understanding of long-term durability is needed for successful adoption in colder and/or wetter climates. The presence of stabilizers dramatically improves resistance to surface erosion from wind and rain, compared to unstabilized adobe and cob counterparts, and the influences of soil composition, fiber type, and diverse binders, on rain and wind surface erosion have been investigated in detail. Frost and freeze-thaw resistance, however, have been less well-studied, despite strong interest in stabilized earth materials in northern North America, Europe, and Asia. In particular, recent studies have relied on a widespread misunderstanding of the mechanism by which frost damage occurs in porous materials that will impede efforts to create valid models for material design and improvement. In addition, the influence of radiative thermal stresses on wall surfaces has been overlooked in favor of focus on ambient air temperatures. Here, we apply contemporary understanding of cracking by segregated ice growth to develop a macroscopic damage index that enables comparison between performance of different materials subject to different weather patterns. An examination of predicted damage patterns for two stabilized earth building materials and two conventional materials in twelve cities over two time periods reveals the dominant factors that govern frost vulnerability. We find that the frost resilience of earth building materials is comparable to that of the conventional materials we examined, and that assessments that neglect expected variations in water content by assuming full saturation are likely to yield misleading results. Over recent years, increased winter temperatures in several cities we examined predict reduced material vulnerability to frost damage, but we also find that accompanying increases in humidity levels have made some cities much more vulnerable.

1. Introduction

Earth and fiber mixtures stabilized with lime, slag, or cement create building materials that require considerably less production energy than concrete or kiln-fired bricks. In part, they require less cement (typically 6–8% by weight, compared to 10–15% for concrete [1,2,3]), which nevertheless remains the principal contributor to embodied energy and greenhouse gas emissions associated with these materials [3]. If local subsoils are used, they also require less transportation energy, and none require heat treatment [4,5]. Efforts to reduce cement use further through substitution with fly ash [6,7], ground granulated blast-furnace slag [8], and/or fibers [9], as well as tailoring of cement content to specific soil mixes [10,11], are also yielding progressively more environmentally benign forms. Stabilized earth materials are also desirable for their abilities to buffer indoor relative humidity, maintaining it within ranges consistent with comfort and respiratory health [12,13], and for their thermal inertia, promoting indoor temperature stability [14,15,16].

The prospect of lowering a building’s life-cycle environmental impact gives earth materials great appeal in green design: as energy codes demand greater heating, cooling, and lighting efficiency, e.g., [17], the energy consumed and emissions associated with material production account for larger proportions of the total [18,19,20], especially if the materials are sufficiently durable to provide long building lifetimes [21]. Indoor environmental health is likewise an area of growing interest, e.g., [22]. Development of earth materials for contemporary buildings has therefore become a subject of intense investigation in diverse climates, including cool, rainy areas in which durability is a significant concern, e.g., [23,24,25,26,27,28,29,30]. Northern European countries, in particular, have aggressive greenhouse gas reduction targets that they hope to meet in part by reducing or replacing concrete and fired clay bricks in buildings, e.g., [31,32,33]. Traditional forms such as adobe, cob, pisé, and mud plasters gradually crack and erode with exposure to wind-driven rain and freezing temperatures; however, compromising their structural integrity and necessitating ongoing maintenance [34,35,36], as well as limiting their acceptance in contemporary building codes, e.g., [36,37,38]. As a result, stabilizing binders are viewed as essential in moist climates, despite the desire to avoid them, for their ability to provide long-term compressive and shear strength, e.g., [2,39] as well as durability to internal wicking of moisture and surface erosion, e.g., [40,41].

The resistance of these stabilized earth materials to repeated cycles of freezing and thawing has not yet been widely explored, however. In cold and cool climates, this is of particular interest because the frost-related deterioration of historic earth buildings is well documented, e.g., [42,43,44], and changing climate patterns are expected to increase future freeze-thaw stresses in some locations by increasing the frequency of thawing and/or of winter rain, e.g., [45,46].

As hygroscopic porous media, earth materials contain networks of partly interconnected pores and capillaries into which water can enter either as vapor, from the atmosphere, or as liquid water from a wet surface. If this water freezes, the resulting ice can exert stresses on pore surfaces that are large enough to propagate cracks and cause frost damage. While the expansion accompanying the initial water-to-ice phase change can generate large stresses [47], several lines of evidence suggest that this intuitive mechanism is of limited importance for frost damage. A central limitation concerns the modest magnitude of the volume change on freezing, since this constraint would imply that initial water saturations greater than 90% would be needed to exert substantial stresses against pore walls (rather than simply compressing residual air pockets). However, frost damage to stone is commonly observed at much lower total water contents, e.g., [48,49], and experiments demonstrate expansion of porous media that are saturated by pore liquids that contract upon freezing [50,51]. Further evidence comes from studies that document an absence of activity near the freezing point followed by significant cracking only once the temperature drops substantially, e.g., [52,53], and material expansion that takes place when porous media below the ice melting temperature are warmed toward that melting temperature, e.g., [54]. All of these observations are consistent with a central role for “cryosuction”, or the attraction of liquid water toward freezing centers, to supply water for continued ice growth that propagates cracks ([53,55]). As a result, both the frequency of fluctuation of a material through a temperature range that alternately facilitates the redistribution of water for “segregated” ice growth and promotes freezing, and the supply of water at the surface through rain or condensation, are risk factors of interest.

The phenomenon of cryosuction-supplied crack propagation is familiar in soils as the ground expansion known as “frost heave”. In cohesive media, detailed theoretical analysis of ice formation in individual, isolated flaws has revealed factors controlling the initial elastic phases of deformation, followed by the unrecoverable crack propagation that constitutes frost damage, e.g., [56,57]. At much larger scales, interest in the long-term impact of frost damage on alpine and polar landscapes, e.g., [58,59,60,61,62] has led to the development of macroscopic frost-cracking indices [63,64,65,66,67]. Although the analogy between frost heave in soils and frost damage in cohesive media like stone and concrete has been recognized, theoretically formulated, and experimentally validated [68], the building materials research literature shows only sporadic awareness of this body of work, e.g., [69,70]. Instead, the stated or implied assumption that material pore spaces must be virtually saturated with water before frost damage can occur, and accordingly that entrained air can protect a material from frost damage by providing space into which ice can expand, persists in both theoretical and experimental work, e.g., [71,72,73,74,75], as well as in standard tests of building materials, e.g., [76,77]. To strengthen the bridge between these fields, we apply the understanding of cryosuction-fed frost damage to the question of frost resilience of stabilized earth building materials in cities with cold, wet, and changing winters where people have ambitious goals for building life-cycle energy reduction, revealing excellent potential for long-term durability in comparison to conventional building materials under realistic field conditions.

2. Methods

2.1. Theoretical Development

Our analysis begins with a brief overview of the micro-mechanics of frost damage by segregated ice growth. To assess the susceptibility to damage of different materials under different climate forcings, we use an index that was developed initially to approximate the freezing-induced porosity changes that accompany cracking under saturated (i.e., air free) conditions [67] and adapt it to address the unsaturated conditions that are expected to be more relevant for buildings. Next, we summarize the controlling parameters and properties that are needed to describe the evolution of pore phase distribution in several building materials and characterize their response to ice growth. 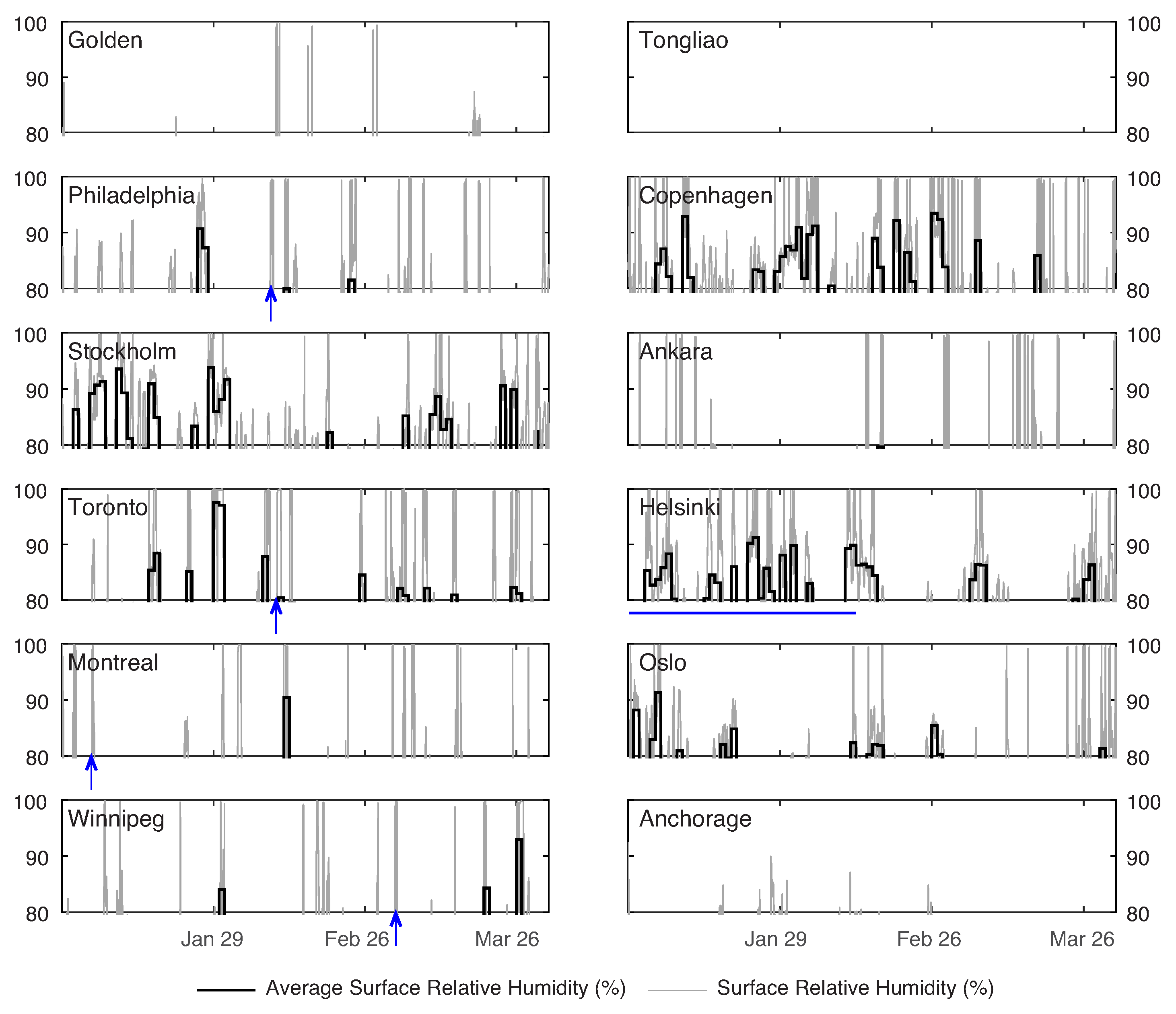Finally, we describe our modeling procedures for assigning environmental forcing in several cities and two time periods, as well as for generating time series of material temperature and moisture contents. A summary of nomenclature is provided in

Table A1. Nomenclature.

Symbol	Description
c	heat capacity—see Table 1
C	water transport parameter—see Table 1 & Equation (2)
$k_0$	permeability under liquid saturated conditions—see Table 1
$K_0$	dry thermal conductivity—see Table 1
L	latent heat of fusion (≈3.3 × 10${}^5$ J/kg)
n	porosity—see Table 1
$\Delta n$	damage index for saturated conditions—see Equation (1)
$\Delta n_u$	damage index for unsaturated conditions—from Equation (1) with $T_{cu}$ in place of $T_c$
$\Delta P$	pressure difference between ice and liquid—see Equation (4)
$R_g$	gas constant ($8.314$ J/(mol K))
$RH$	relative humidity
S	total water content
$S_l$	liquid saturation level
t	time
T	temperature
$T_c$	maximum temperature for saturated frost damage—see Table 1
$T_{cu}$	maximum temperature for unsaturated frost damage—see Equation (7)
$T_{db}$	dry bulb temperature
$T_m$	bulk melting temperature (≈273 K)
$T_f$	temperature of first pore ice formation—see Table 1
$V_m$	partial molar volume of water ($18\times {10}^{-6}$ m${}^3$/mol)
z	depth into wall—measured from exterior surface
$\alpha$	exponent in permeability relation—see Table 1
$\beta$	exponent in freezing curve—see Table 1 & Equation (6)
${\gamma }_{il}$	surface energy of ice-liquid interface (≈0.033 J/m${}^2$)
${\gamma }_{vl}$	surface energy of vapor-liquid interface (≈0.074 J/m${}^2$)
$\mathsf{\Gamma }$	ratio of $\alpha /\beta$—adopted nominal value: 8
${\mu }_0$	vapor diffusion resistance factor—see Table 1
$\rho$	water density (≈10${}^3$ kg/m${}^3$)
${\rho }_{\mathrm{dry}}$	dry material density—see Table 1
$\Psi$	matric potential—see Equation (3)
$\eta$	water viscosity (≈1.8 × 10${}^{-3}$ Pa s)

.

2.1.1. Ice Segregation and Frost Damage

The damage caused by ice formation depends in part upon the influence of pore characteristics on phase equilibria. Figure 1 illustrates the typical pore-scale distribution of phases, with liquid water wetting matrix surfaces and collecting in crevices that are bounded by highly curved interfaces with the non-wetting ice or vapor phase that occupies central pore regions. The surface energy of the phase boundary and the wetting interactions that maintain liquid films give rise to a pressure difference between the ice (or vapor) and the liquid, e.g., [78,79]. This pressure difference increases as the volume of residual liquid is diminished, both by thinning the wetting films, and by further increasing the interfacial curvature bounding crevice reservoirs.

In unsaturated systems, the vapor phase tends to form connections with external air, thereby remaining at atmospheric pressure and resulting in sub-atmospheric liquid pressures (i.e., matric potentials) that cause liquid content to depend on relative humidity, as described by the material’s moisture retention curve, e.g., [80,81,82]. In contrast, when pores are occupied solely by water and ice, fluid connections typically maintain the more mobile liquid phase at a pressure that is reduced only slightly below exterior levels, so that the pressure transmitted by the ice against pore walls must increase dramatically as the liquid saturation is diminished. The generalized Clapeyron equation, e.g.,Wettlaufer, J. et al. [83] describes how the difference between the ice and liquid pressures grows as the temperature T drops further below the normal melting point $T_m$, promoting ongoing freezing at the expense of the shrinking liquid content. In analogy with the moisture retention curve, the partitioning between liquid water and ice can be described by a temperature-dependent freezing curve, e.g., [84,85,86].

Building upon these pore-scale thermodynamic constraints, a central remaining ingredient of frost damage micro-physics can be framed in terms of linear elastic fracture mechanics: the stress intensity factor increases with the ice-matrix pressure and crack growth takes place as a critical value is approached that depends on the strength of mineral bonds. The incipient crack geometry enters the problem, notably with the stress intensity factor increasing roughly with the square root of the longest dimension (labeled $2a$ in Figure 1), e.g., [87]. Finally, hydrogeology also plays a role since significant frost damage requires that crack extension be supplied by liquid transport; this can be described using Darcy’s law with a temperature-dependent permeability that drops monotonically as the temperature is reduced and solid ice clogs an increasing fraction of the pore space, e.g., [56,57,68].

The pore scale behavior just described produces appreciable frost damage on macroscopic scales only when the temperature is cold enough for the ice pressure to wedge open cracks while the permeability to liquid flow remains high enough to supply ice growth. These considerations give rise to the “frost-cracking window” of temperatures (typically $-8{}^{\circ }\mathrm{C}\le T\le -3{}^{\circ }\mathrm{C}$ in rocks [63]) under which most frost damage is observed to take place. Several practical indices have been designed to predict frost damage severity based on weighted integrals of the time spent within such a predefined temperature range [63,64,65,66]. For the present application, an understanding of the controls that material properties exert on how frost damage accumulates requires an assessment that is more closely tied to the micro-mechanics of frost driven crack growth and rooted explicitly in physical parameters that can be measured or inferred. To gauge relative severity under air-free conditions, Rempel et al. [67] reasoned that the degree of frost damage should scale approximately with the predicted change in porosity $\Delta n$ that accompanies changes in water supply with depth z (necessitated by gradients in the temperature-dependent permeability) while the temperature remains below a threshold $T_c$ that is sufficiently cold for ice pressures to propagate cracks that contribute to the additional pore volume. Mechanical considerations imply that $T_c$ should be colder for host materials with higher fracture toughness, and become closer to $T_m$ with increases in the size of the largest ice-occupied pores. Since the hydrodynamic pressure gradients that drive liquid flow are proportional to the temperature gradient, while the ice-bound permeability is a monotonic function of temperature that can be approximated by a power law, the net porosity change over a sequence of time periods with $T\le T_c$ can be written as [67]

$$\Delta n\approx C{\int }_{T\le T_c}{\left(\frac{1}{T_m-T}\right)}^{\alpha +1}{\left(\frac{\partial T}{\partial z}\right)}^2\mathrm{d}t.$$

(1)

Here, in addition to the permeability exponent $\alpha$, and the temperature threshold for crack extension $T_c$, the controlling water transport parameter

$$C=\frac{\alpha \rho L{k}_0{\left(T_m-T_f\right)}^{\alpha }}{T_m\eta }$$

(2)

is defined in terms of the water density $\rho \approx {10}^3$kg/m${}^3$, the latent heat of fusion $L\approx 3.3\times {10}^5$J/kg, the liquid-saturated permeability $k_0$, the absolute melting temperature $T_m\approx 273$K (i.e., $0{}^{\circ }$C), the temperature at which ice first reaches equilibrium in the pore space and begins to restrict liquid flow $T_f$, and the liquid viscosity $\eta \approx 1.8\times {10}^{-3}$Pa s. The dependence of $\Delta n$ on the squared temperature gradient in Equation (1) suggests the likely mechanism behind northern hemisphere observations that frost damage to the built environment is often concentrated near the exterior surfaces of south-facing walls, which are typically subject to the largest magnitude heat fluxes (and hence temperature gradients) as a result of enhanced radiative forcing [42,88]. The inverse dependence on a greater-than-linear power of the temperature offset below melting arises from changes in the permeability to liquid supply, and reflects the observed tendency for frost damage to diminish at very cold temperatures. These restrictions on liquid supply set the effective lower temperature limit of the frost-cracking window.

In the Results and Discussion section below, we interpret the predictions of Equation (1) in terms of the patterns of frost damage that are expected in different building materials and climates. It is important to recognize, however, that the assumption of complete initial water saturation that underlies the derivation of Equation (1) [67] can cause this approach to produce overly pessimistic assessments of frost resistance. When the entire pore space is water filled (a condition that is approximated by many common freeze-thaw testing procedures, e.g., [48,89,90,91]) the cracking threshold $T_c$ marks conditions where the stress intensity factor in the largest pores approaches a critical value. However, in the common case where only limited moisture infiltration takes place, the largest pores tend to contain residual air and fill with water last, so that ice can only grow and exert high pressures on the walls of smaller pores. This reduces the effective cracking threshold $T_{cu}$ to temperatures lower than $T_c$ that enable the higher ice pressures needed to propagate smaller cracks, raising the potential for the frost damage index under unsaturated conditions $\Delta n_u$ to fall well below $\Delta n$.

Previous efforts to assess the propensity for frost damage in the built environment have met with qualitative success by integrating the time spent within the frost cracking window while giving preferential weight to the periods following recent precipitation events, e.g., [92]. A similar approach towards investigating frost damage to alpine rock walls was followed by Rode et al. [93], who tracked near-surface moisture content and evaluated a frost cracking index that was also based on the integrated time spent within the frost cracking window, while including only those periods during which the moisture content exceeded a threshold. The physical balances that determine an approximate moisture content threshold for frost damage must depend on material properties. Here, we model water exchange with exterior surfaces following [94,95] and account for the expected sensitivity to water content of the effective threshold temperature for unsaturated cracking $T_{cu}$, basing our treatment on changes in the sizes of the largest water-filled pores anticipated from the form of the moisture retention curve, as outlined next. The time dependence that changes in moisture content introduce to $T_{cu}$, and hence the integration bounds on Equation (1), constitutes the adaptation to the saturated frost damage index $\Delta n$ needed to define an analogous frost damage index $\Delta n_u$ that is appropriate for unsaturated conditions. To our knowledge, this is the only macroscopic index of unsaturated frost damage that has been developed and expressed solely in terms of physical properties and environmental controls that can be measured or inferred through independent means. It is worth mentioning that in unsaturated subfreezing conditions the relative permeability to liquid flow may be reduced even more drastically than accounted for by the power-law treatment incorporated in Equation (1), thereby further lowering $\Delta n_u$ (i.e., this effect might be approximated in a more elaborate model by increasing the exponent $\alpha$ or decreasing the reference permeability $k_0$); lacking firm empirical constraints, we neglect this complication, effectively producing a conservative assessment of improvements to frost resilience as the water content is reduced.

2.1.2. Frost Cracking Thresholds during Unsaturated Conditions

Figure 2a shows sample moisture retention curves measured for stabilized rammed earth [96], stabilized compressed earth blocks [13], solid brick masonry from the Fraunhofer database [97], and concrete from the Lund LTH database [97] (further material description follows in Section 2.2). Data of this general type are commonly used for studies of moisture uptake by building materials, e.g., [94,95], which can have important implications for modulating energy exchange, e.g., [81,98,99] and interior humidity variations, e.g., [13,100]. The exact form of the moisture retention curve depends on details of the pore size distribution, geometry, and surface chemistry; the data presented here derive from measurements on well-characterized sample materials under experimental conditions that are described in the source references. At low saturations, most liquid is adsorbed to matrix surfaces in films, whereas capillary condensation causes the crevice reservoirs depicted in Figure 1 to dominate the liquid volume at higher saturations. Hysteretic behavior is common, with the saturation at a particular relative humidity generally higher during drying than during liquid uptake. We neglect this complication here and report saturation values derived from measured liquid weights normalized to the weight of water that would saturate the pore space of each material (i.e., the product of water density with the total porosity $\rho n$). Because experimental data acquired during liquid uptake is often affected by trapped air bubbles and does not achieve complete saturation once $RH$ reaches unity, a common approximation in models of moisture suction and redistribution involves interpolation between experimental points and complete liquid saturation at $RH=1.01$, e.g., [95,97]. Though values of relative humidity greater than unity are fictitious, these moisture transport models have been shown to perform well during validation tests. As outlined below, however, for our purposes it is important that $RH$ cannot exceed unity. Accordingly, to construct the moisture retention curves displayed in Figure 2a (from which we approximate total water content S as a function of modeled relative humidity $RH$), we normalized reported experimental water mass values by $\rho n$ and effective relative humidities by 1.01.

Measurements made on building materials to quantify changes in liquid saturation at equilibrium with ice under subfreezing conditions are not well represented in the literature, but moisture retention curves can be used to approximate the expected behavior, as follows. We first note the thermodynamic relationship between the relative humidity $RH$ and the matric potential $\Psi$, which involves the gas constant $R_g=8.314$ J/(mol K), the absolute temperature under the measured conditions $T\approx 293$K, and the partial molar volume of water $V_m=18\times {10}^{-6}$ m${}^3$/mol, so that

$$\Psi =\frac{R_{g}T}{V_m}lnRH.$$

(3)

This gives the magnitude of the pressure difference across vapor-liquid surfaces, such as those illustrated in Figure 1. We expect most frost cracking to take place at relatively high liquid saturations $S_l$ so that liquid mobility remains sufficient to supply ice growth. The liquid content in this regime is dominated volumetrically by crevice reservoirs [78,101], suggesting that the difference between the ice and liquid pressures $\Delta P$ at a particular $S_l$ can be approximated by scaling the matric potential with the ratio of the ice-liquid surface energy ${\gamma }_{il}$ to the vapor-liquid surface energy ${\gamma }_{vl}$ (see [85], for further discussion), leading to

$$\Delta P\approx -\frac{{\gamma }_{il}}{{\gamma }_{vl}}\Psi \approx -0.45\Psi .$$

(4)

The generalized Clapeyron equation is used next to convert this pressure difference to an equivalent offset from the bulk melting temperature, yielding

$$T_m-T\approx \frac{T_m}{\rho L}\Delta P\approx \left(-55\mathrm{K}\right)lnRH,$$

(5)

where the final approximation on the right comes from substitution of Equations (3) and (4). Please note that the condition $RH<1$ must be enforced to ensure that $T_m-T>0$. We used this expression together with the moisture retention curves from Figure 2a to generate the synthetic freezing curve data shown in Figure 2b. As a final step, to estimate the temperature $T_f$ at which ice can first nucleate, to extract further information on the changes in saturation with temperature for assistance with estimating the permeability exponent $\alpha$, and to provide a basis for estimating changes in $T_{cu}$ with variations in total water content, we fit the high liquid-content data fraction (i.e., with $S_l>20$%) to power laws of the form

$$S_l={\left(\frac{T_m-T_f}{T_m-T}\right)}^{\beta },$$

(6)

which are illustrated with the straight lines in Figure 2b using the values of $\Delta T_f=T_m-T_f$ and $\beta$ given in the legend. Observed correlations between measured permeability and $S_l$ in ice-bound porous media suggest that the permeability exponent can be approximated as $\alpha \approx \mathsf{\Gamma }\beta$ [85], with $7\le \mathsf{\Gamma }\le 9$ reflecting details of the residual liquid morphology; we adopt this correlation while assigning $\mathsf{\Gamma }=8$ as a nominal value for the calculations that follow.

To derive a plausible relationship between the unsaturated cracking threshold $T_{cu}$ and the saturated value $T_c$, we first recall that moisture uptake tends to fill the smallest pores first and that the stress intensity factor increases with the square root of the incipient crack size. This suggests that $T_{cu}$ should be sensitive to the dimensions of the largest pores in which liquid water can freeze. The constraints imposed by surface energy imply that the characteristic size of the largest pores in a given medium is inversely proportional to $T_m-T_f$, so with the stress intensity factor approaching a threshold at the onset of cracking we anticipate that $T_m-T_c\propto \sqrt{T_m-T_f}$. When air fills the largest pores so that the total water content is less than unity, the onset of frost cracking is expected to involve smaller water-filled pores that first freeze at some temperature $T<T_f$, suggesting that $T_m-T_{cu}\propto \sqrt{T_m-T}$. The ratio of these expressions is an inverse power of the liquid saturation from Equation (6). Recalling the similarity between the geometry of the residual liquid phase during drying and freezing, depicted schematically in Figure 1, this suggests that the unsaturated cracking threshold temperature should scale as

$$T_m-T_{cu}\approx S^{-1/\left(2\beta \right)}\left(T_m-T_c\right).$$

(7)

Accordingly, to assess frost susceptibility in unsaturated conditions, we track changes in total water content S and revise $T_{cu}$, following Equation (7), as the time-varying lower integration limit for calculating $\Delta n_u$, following Equation (1).

Clearly, it would be preferable to have direct measurements for each building material of the temperature at which frost cracking first begins in the unsaturated regime at several different initial water contents. To our knowledge, no such controlled experiments have been reported upon in the literature. Nevertheless, tying the estimate for $T_{cu}$ in Equation (7) to parameters that are controlled by material microstructure gives some insight into the manner in which differing degrees of partial saturation are likely to affect frost resilience. For example, at a given total water content S, Equation (7) suggests that the reduction in $T_{cu}$ experienced by different materials is likely to be proportionately greater for those with pore size distributions that produce smaller saturation exponents $\beta$, as shown in Figure 3a, whereas the reduced water transport implied by the correlation between $\beta$ and the permeability exponent $\alpha$ is likely a greater factor in limiting damage to unsaturated materials with higher values of $\beta$. Recall that the power-law dependence on the temperature depression in the integrand of Equation (1) suggests that frost-driven porosity changes are most sensitive to conditions very near the onset of cracking. Accordingly, an approximate assessment of the relative sensitivity of $\Delta n_u$, with air saturating all but fraction S of the pore space, in comparison to the fully saturated case $\Delta n$, can be obtained from the scaling

$$\frac{\Delta n_u}{\Delta n}\sim {\left(\frac{T_m-T_c}{T_m-T_{cu}}\right)}^{\alpha +1}\approx S^{(\alpha +1)/\left(2\beta \right)},$$

(8)

where Equation (7) has been substituted to make the final approximation. The plot of the right hand side of Equation (8) in Figure 3b suggests that an order of magnitude reduction in the frost susceptibility of each of our chosen test materials takes place when the initial water content is reduced to the vicinity of 60–65%, in broad agreement with observational reports of a minimum threshold in water content for frost damage, e.g., [48,49]. We emphasize that the scaling in Equation (8) is approximate and that a more thorough assessment of $\Delta n_u$ must still rely on the history of temperatures and their gradients embodied in Equation (1). However, the similarity between predictions for the reduction in frost susceptibility with reduced water content in different materials could be interpreted as a mechanistic justification for simpler time-since-precipitation and moisture-threshold approaches, e.g., [92,93].

Extensive published reports on the results of mechanical tests provide guidance for assigning the saturated cracking threshold temperature $T_c$ for each building material that we consider. It is important to note that as with conventional masonry and concrete, the performance of different earth building materials will be affected by details concerning the particular constituents they incorporate and the preparation methods followed. Accordingly, while the property values adopted here are chosen to be representative, we anticipate considerable variation among similar materials of interest. Absent detailed measurements of incipient crack size populations and fracture toughness, we concentrate on the results of macroscopic tests. Direct measurements of the unconfined compressive strength of stabilized rammed earth tend to cluster around 1–3 MPa [27,102,103,104] though values ranging as high as 15 MPa or greater are also sometimes obtained [8,105]. Reported values for the unconfined compressive strengths of stabilized earth blocks tend to be somewhat higher, around 4–8 MPa [27,106,107,108], and again sometimes exceeding 10 MPa [108,109]. The micro-mechanics of frost cracking are consistent with a tensile failure mechanism, and bulk tensile strengths of these earth building materials are typically measured as approximately 10–20% of unconfined compressive strengths [27,103,110]. However, whereas in bulk testing configurations loads are applied over the entire material cross section, the fractional area over which stresses are applied to the most unfavorably oriented ice-bound cracks are expected to be considerably smaller. This suggests that values somewhat larger than measured bulk tensile failure stresses are likely to be most representative of the ice pressures exerted on pore walls during cracking. Given these considerations, for the calculations that follow we adopt values of $T_c$ based on estimated threshold ice pressures that reach 40% of measured unconfined compressive strengths. Applying the proportionality of $\rho L/T_m\approx 1.1$MPa/K from the generalized Clapeyron Equation (5) to these strength estimates, for stabilized rammed earth we take $T_c=-1{}^{\circ }$C, and for stabilized earth blocks we adopt a nominal value of $T_c=-2{}^{\circ }$C. We view these relatively warm temperature thresholds, combined with the modest values of $\alpha$ assigned following the arguments given above, as conservative estimates in that they should tend to promote assessments for $\Delta n$ that are larger than would be predicted by lower $T_c$ and higher $\alpha$ values. For comparison, experiments provide support for a threshold cracking temperature in the quartz-cemented Berea Sandstone [53] of $-3{}^{\circ }$C, which has comparable mechanical properties to many concretes, e.g., [111]. Pakkala et al. [42] suggest that frost cracking in Finish concrete requires temperatures colder than $-5{}^{\circ }$C, but this should probably be interpreted as an unsaturated value. We adopt a more conservative estimate of $T_c=-3{}^{\circ }$C for concrete, which should facilitate direct comparison with previous work in geomorphology that has adopted this as the upper temperature limit to the frost cracking window, e.g., [63,64,65,66,67,112]. We take $T_c=-2{}^{\circ }$C for solid brick masonry, to better highlight the role of other controlling parameters in comparisons against the modeled behavior of earth blocks.

With $T_c$ and other relevant material properties and physical parameters defined, given a time series of wall temperatures and temperature gradients, calculation of the frost damage index $\Delta n$ relevant for saturated conditions using Equation (1) is straightforward. For unsaturated conditions, a time series of total water content S is needed as well in order to evaluate $T_{cu}$ from Equation (7); this is then used as the time-varying upper temperature limit on the integral in Equation (1) to obtain the frost damage index $\Delta n_u$ that is relevant for unsaturated conditions. In the Results and Discussion section below, all reported values of $\Delta n$ and $\Delta n_u$ represent integrals over the time during each day when the temperature is lower than $T_c$ and $T_{cu}$, respectively.

2.2. Materials

Two well-characterized stabilized earth materials and two conventional materials were chosen to explore the implications of the model described above. The stabilized rammed earth of Allinson and Hall [96] was comprised of well-graded crushed ironstone quarry waste (0–40 mm) combined with more uniform grit sand (2–5 mm), as well as 7% by weight Portland cement. This cement incorporated a non-pore-blocking compound to retain the majority of the desirable vapor permeability while significantly reducing the capillary potential, i.e., the ability to absorb liquid from the surface. Compressed stabilized earth blocks, in turn, consisted of Wealden Clay mixed 1:1 with fine sand to yield a final clay particle content of 10–20%; the final particle-size distribution is shown in McGregor et al. [13]. The moisture retention curve shown in Figure 1 is based on measured values in earth blocks stabilized with 4% lime, which were nearly identical to measured values in earth blocks stabilized with 4% cement [113]. Earth block thermal conductivity was estimated from [114], which showed a close correspondence between bulk density and thermal conductivity, nearly independent of other factors. For comparison, a reference concrete from the LTH Lund database in WUFI Pro 6.3, “Concrete w/c 0,7” (indicating an initial water-to-cement ratio of 0.7) was chosen for its detailed moisture storage function; liquid suction and redistribution functions were then approximated as those of the similar Fraunhofer concrete, “C12/15” [97]. Reference values for solid brick masonry from the Fraunhofer database were used as well [97]. The liquid suction function reported for the solid brick masonry was also adopted for the earth blocks. In all cases, reference permeabilities at compete liquid saturation $k_0$ correspond with peak values extracted from the liquid distribution functions. The hygroscopic properties of these materials, as well as parameters assigned above, are summarized in

Table 1. Material properties used to model frost cracking. Note: the porosity n, dry density ${\rho }_{\mathrm{dry}}$, thermal conductivity $K_0$, heat capacity c, and  vapor diffusion resistance factor ${\mu }_0$ are all inputs to the EnergyPlus [115] calculations used to obtain temperature and moisture time series, as outlined in Section 2.3; a complete list of nomenclature is provided in Table A1.

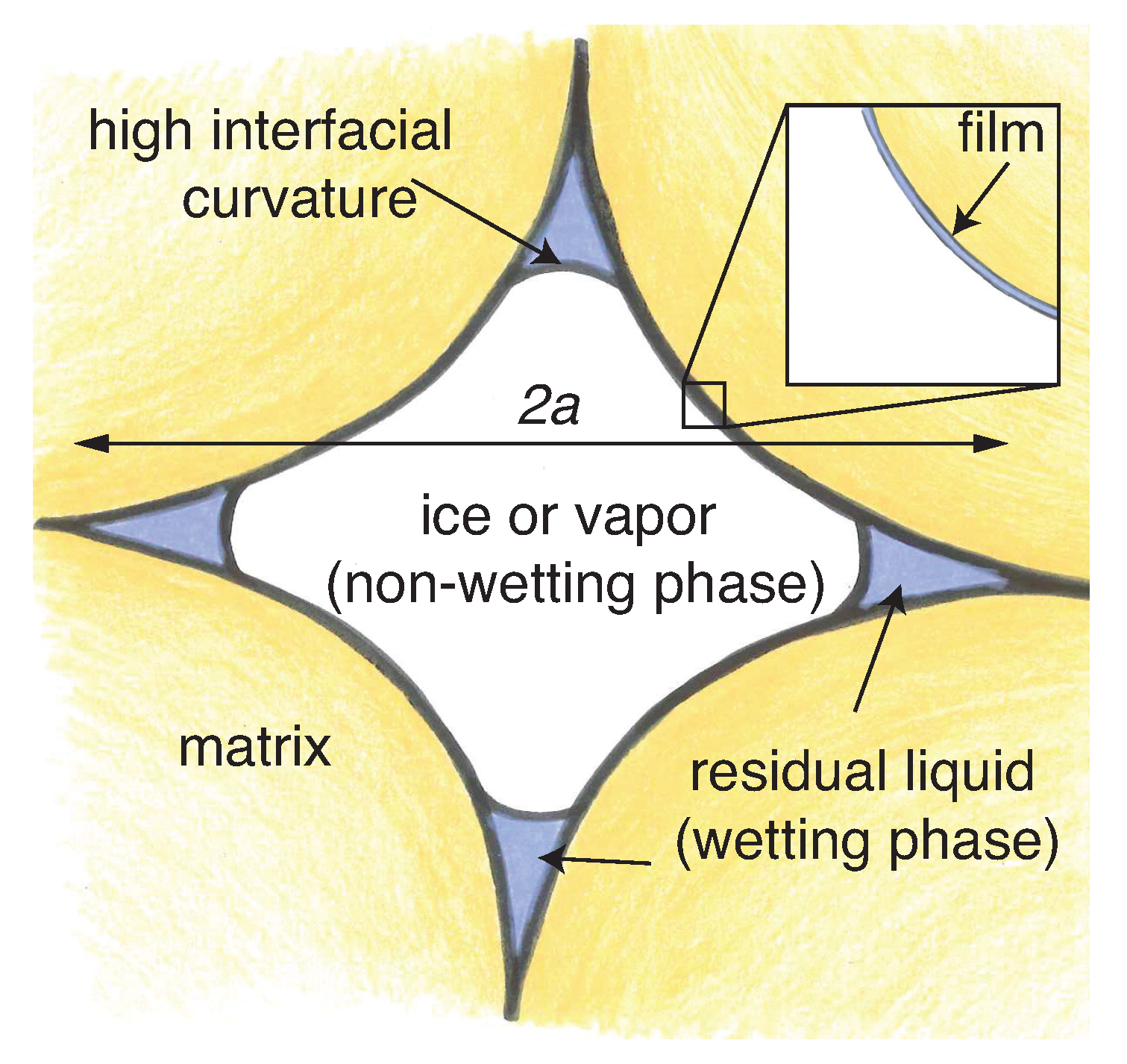
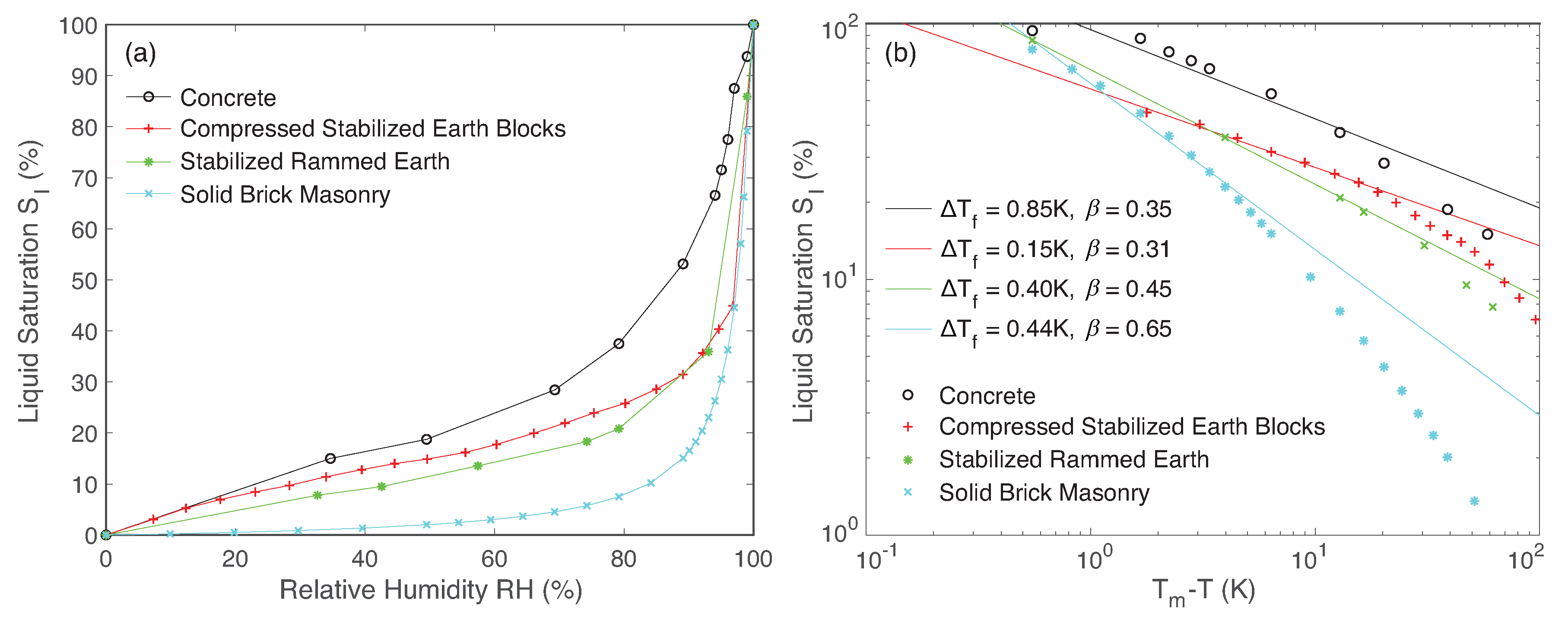
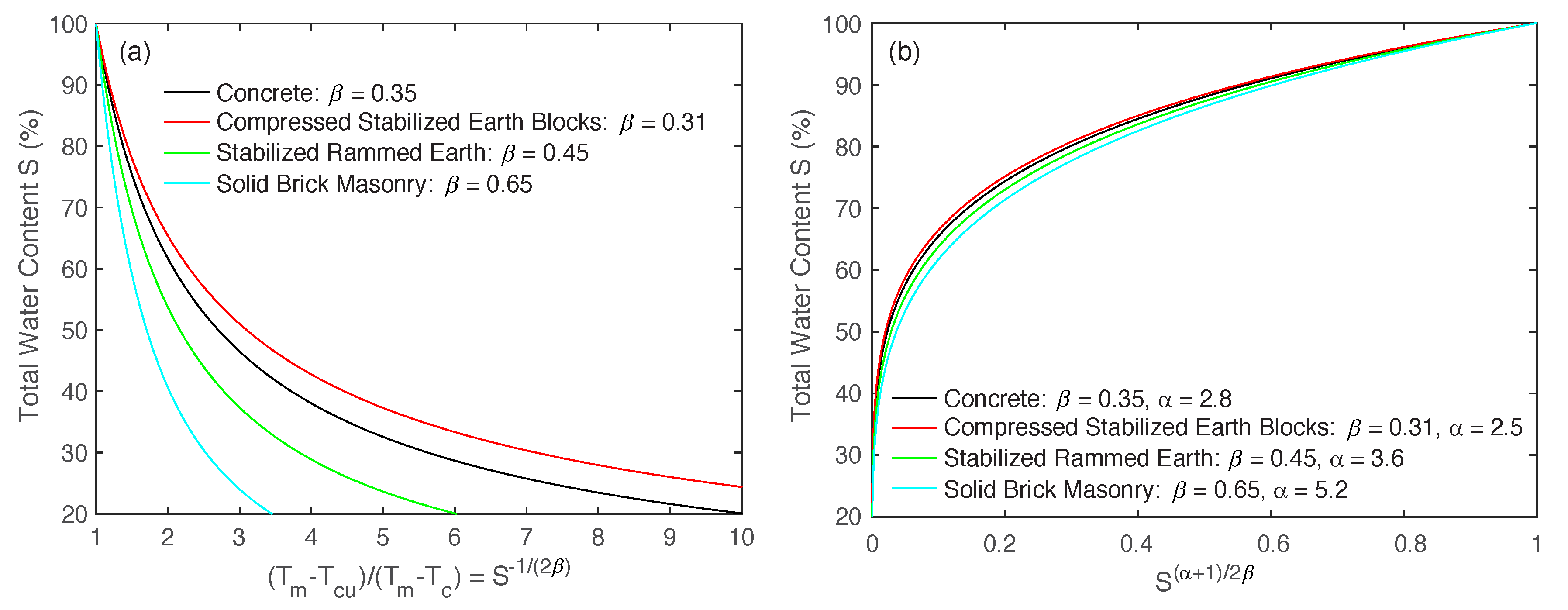
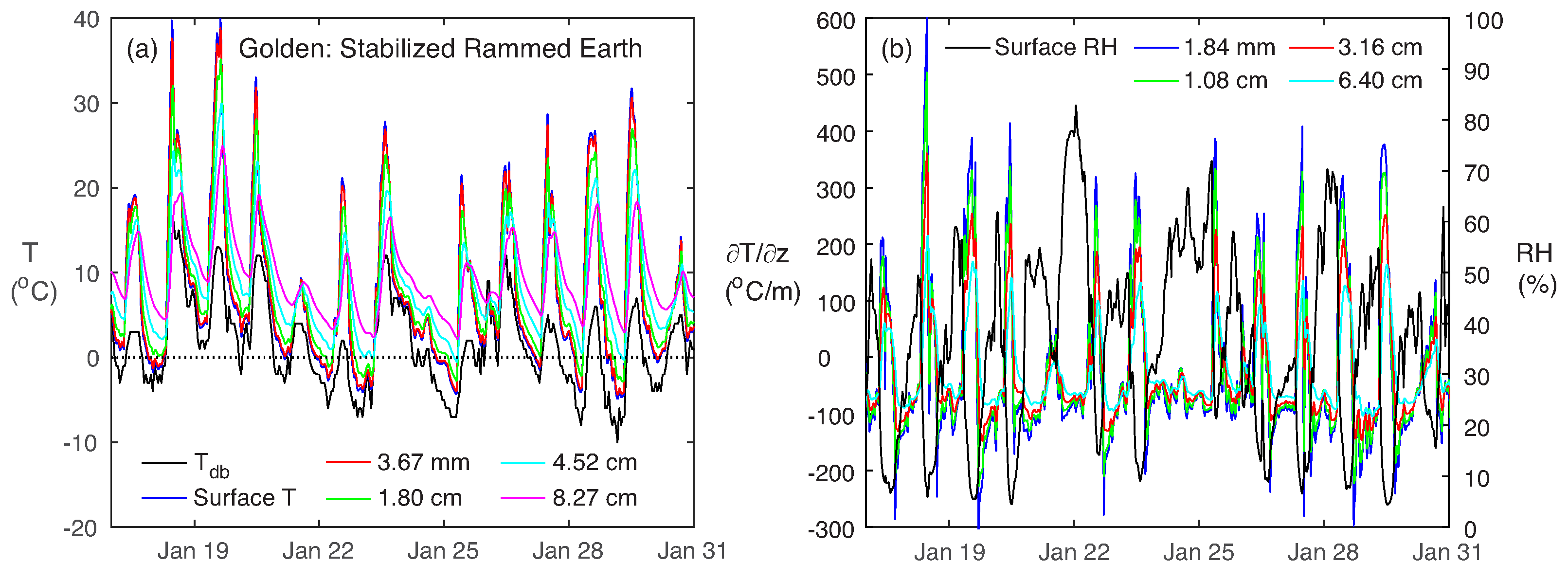
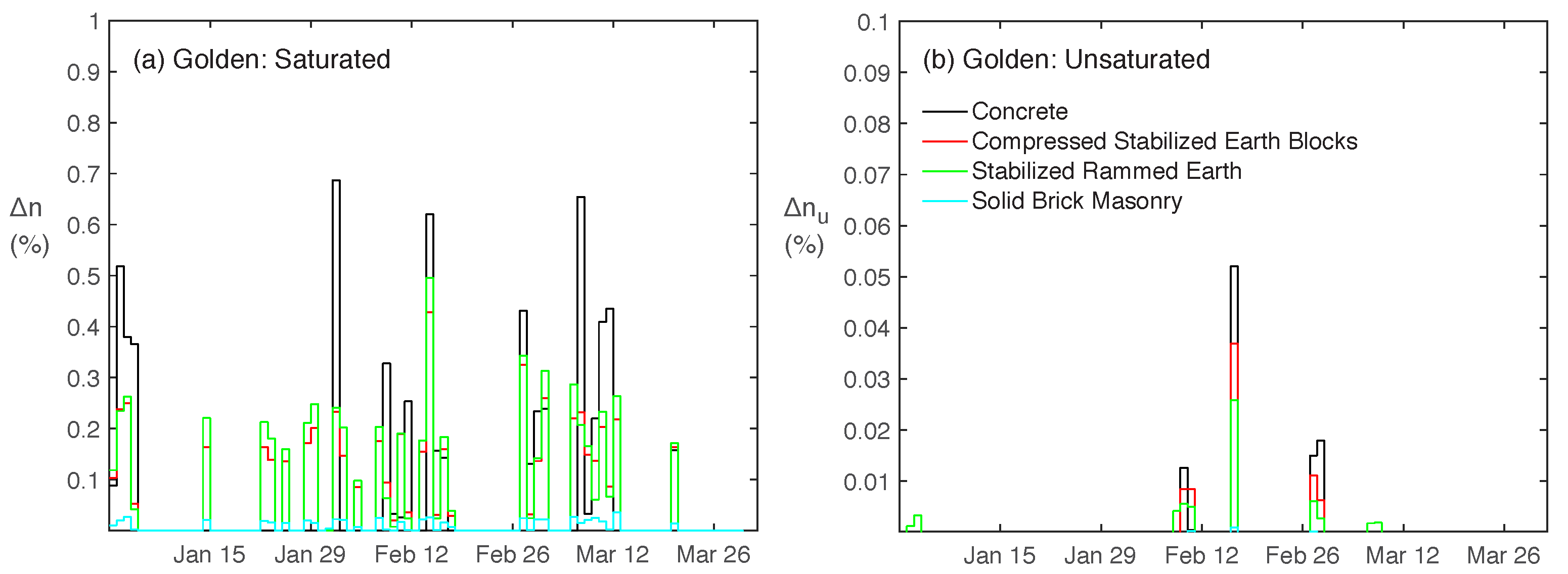
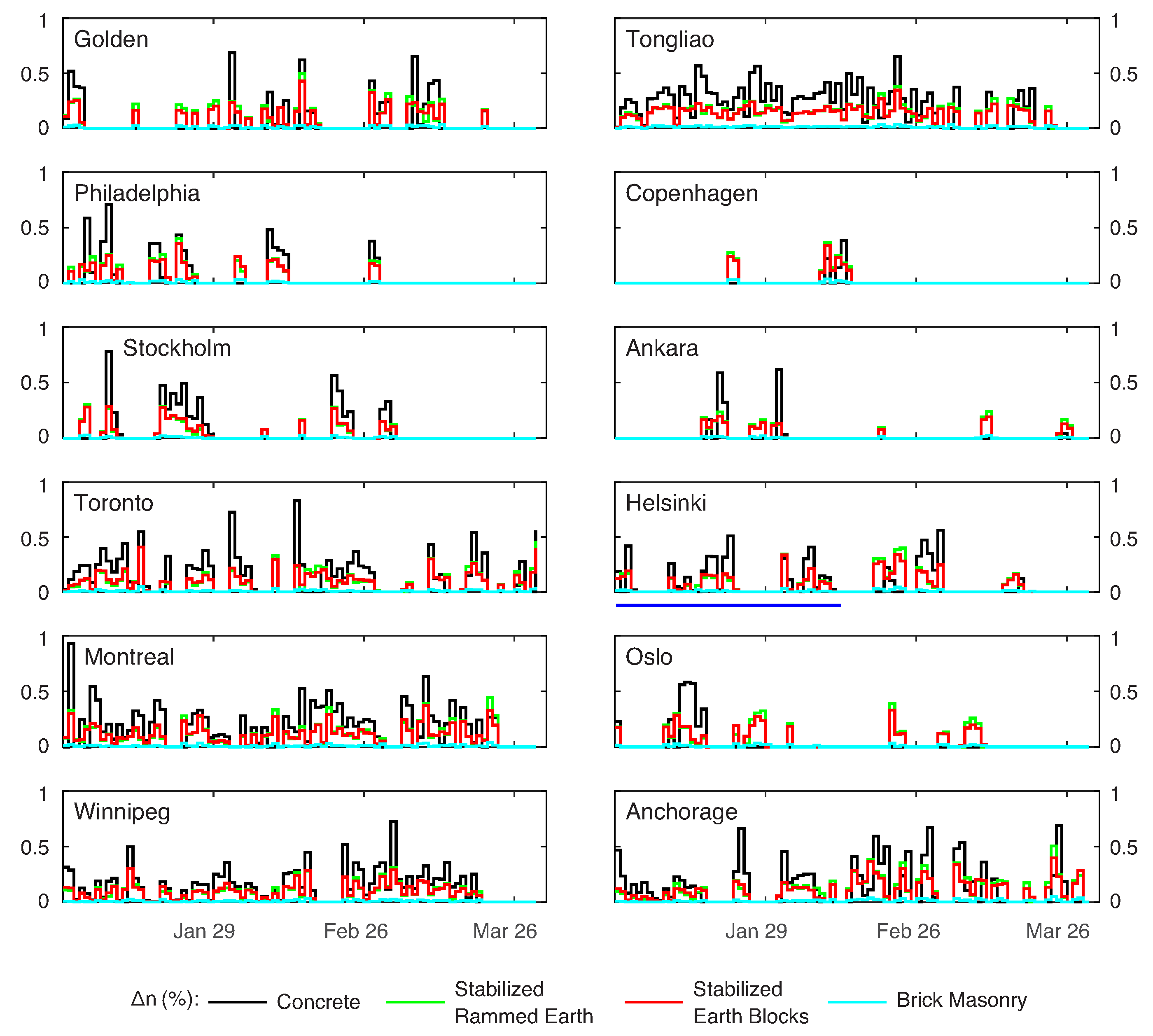
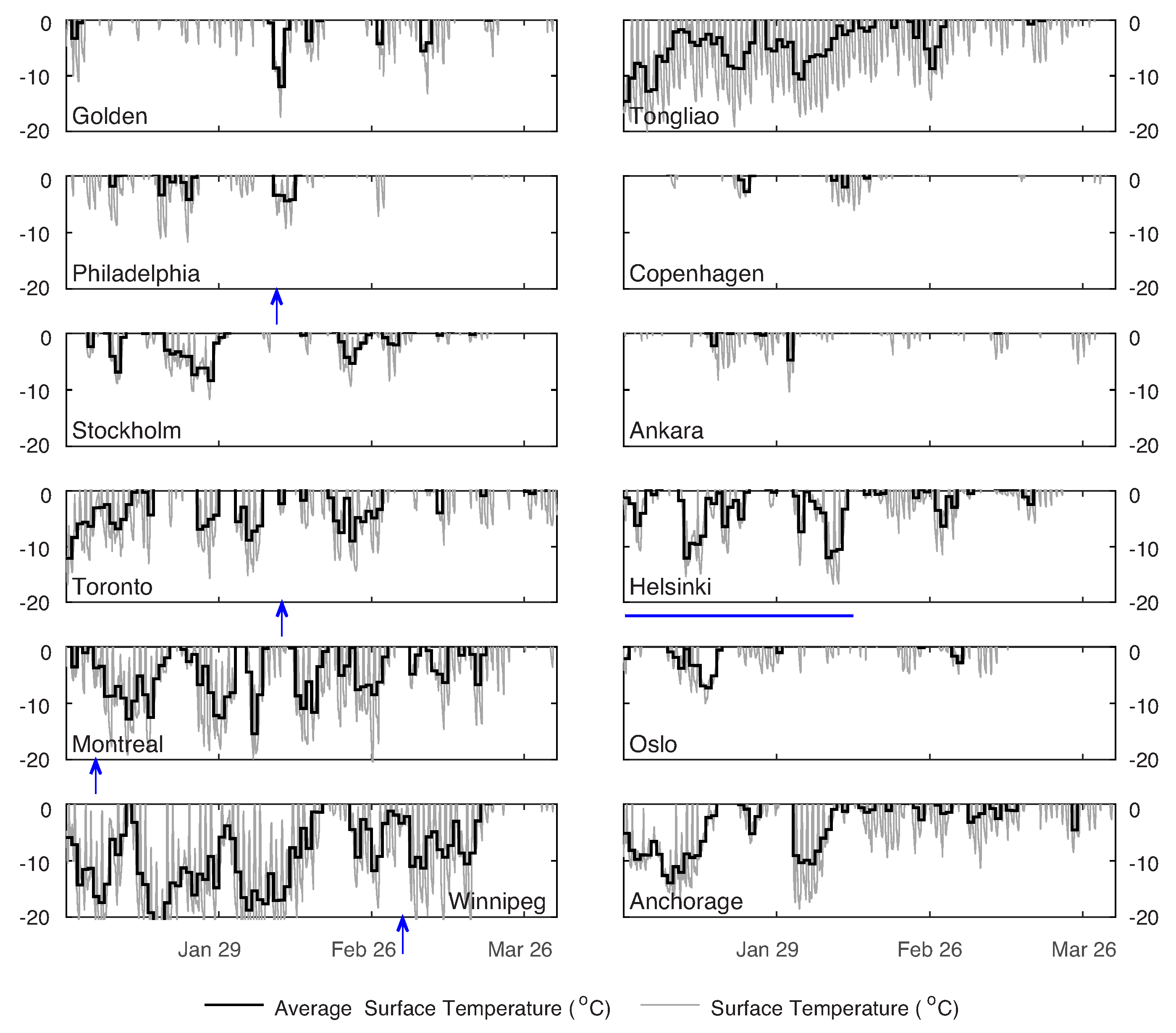
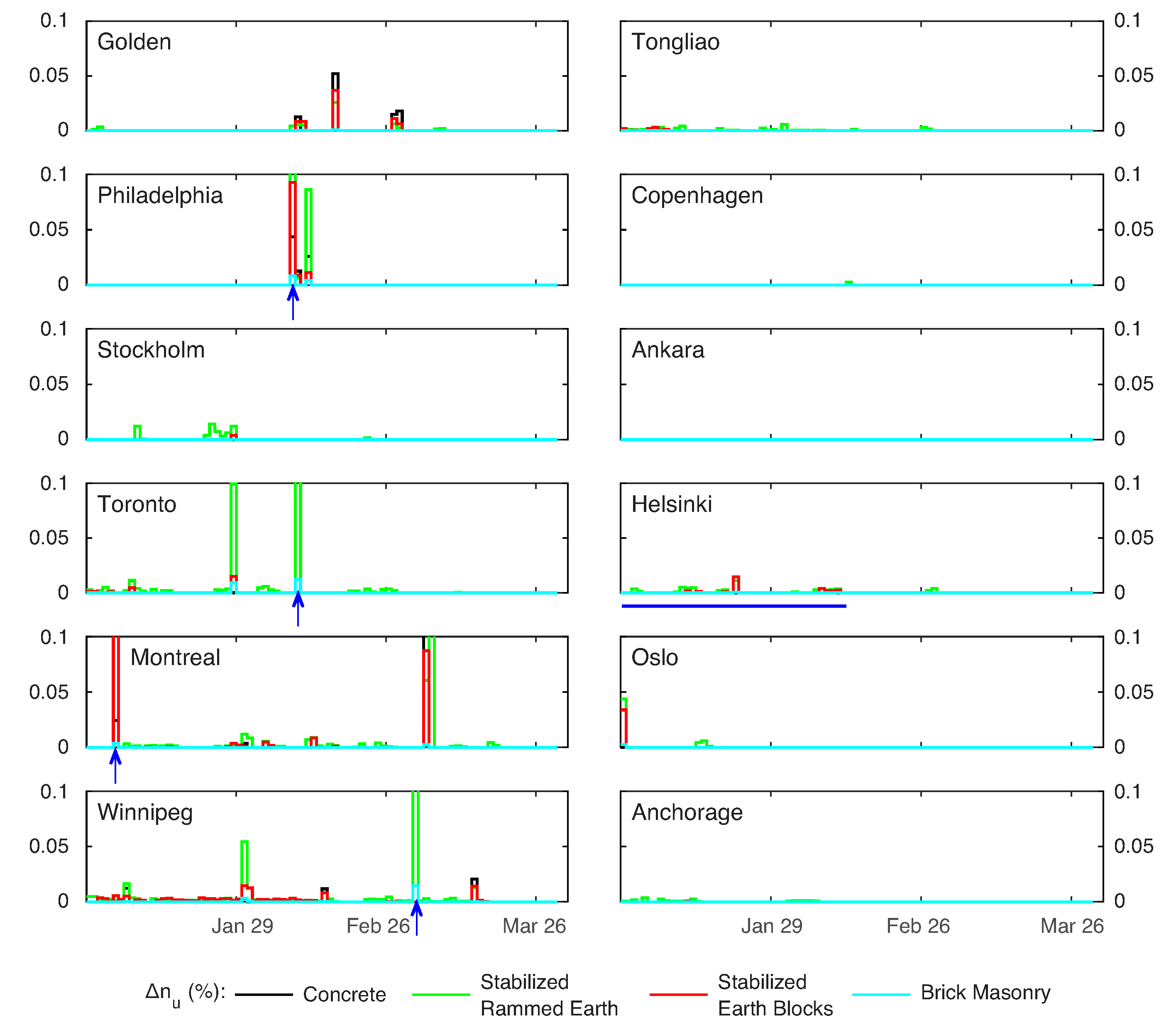
Property	Stabilized Rammed Earth	Compressed Stabilized Earth Blocks	Solid Brick Masonry	Concrete
n	0.295 ${}^a$	0.14 ${}^{c,d}$	0.24 ${}^g$	0.16 ${}^g$
${\rho }_{\mathrm{dry}}$ (kg m${}^{-3}$)	1900 ${}^a$	1735 ${}^c$	1900 ${}^g$	2275 ${}^g$
$K_0$ (W m${}^{-1}$ K${}^{-1}$)	0.643 ${}^a$	0.7 e	0.6 ${}^g$	1.7 ${}^g$
c (J kg${}^{-1}$ K${}^{-1}$)	868 ${}^a$	836 ${}^f$	850 ${}^g$	850 ${}^g$
${\mu }_0$	7.6 ${}^{a,b}$	5.9 ${}^c$	10 ${}^g$	147 ${}^g$
$T_m-T_f$ (K)	0.40	0.15	0.44	0.85
$\beta$	0.45	0.31	0.65	0.35
$\alpha$	3.6	2.5	5.2	2.8
$T_c$ (${}^{\circ }$C)	$-1$	$-2$	$-2$	$-3$
$k_0$ (m${}^2$)	$6.7\times {10}^{-17}$	$8.6\times {10}^{-17}$	$8.6\times {10}^{-17}$	$6.4\times {10}^{-18}$
C (m${}^2$ K${}^{\alpha -1}$ day${}^{-1}$) ${}^h$	$5.0\times {10}^{-4}$	$1.1\times {10}^{-4}$	$3.5\times {10}^{-4}$	$6.7\times {10}^{-4}$

${}^a$ [96], ${}^b$ [81], ${}^c$ [13], ${}^d$ [116], ^e [114], ${}^f$ [117], ${}^g$ [97], ${}^h$ Equation (2).

.

2.3. Temperature and Moisture Time Series

EnergyPlus v8.7, an open-source building energy simulation engine incorporating heat and moisture transfer algorithms [115], was used to estimate pore-space relative humidity and temperature across walls of each material under realistic climate conditions. From these, frost vulnerability estimates were then derived. Supporting thermal zones consisted of 4 m × 4 m × 3 m structures defined with Euclid 0.9.3 [118], an extension for SketchUp Make [119], such that walls faced solar north, east, south, and west. All other objects (e.g., materials, constructions, simulation parameters) were specified directly in the IDF editor. Wall conditions were simulated with the Combined Heat and Moisture Transfer (HAMT) algorithm, based on the work of Kunzel and Kiessl that underlies WUFI Pro [95,97], creating twelve nodes spanning the 30 cm thickness of each wall at which values were reported. We note that the HAMT algorithm was developed initially to describe vapor and liquid transport above the freezing temperature, where it has been validated extensively; performance at subzero temperatures has been less thoroughly examined. In our analysis we focus on conditions nearest the exterior wall surface, where we anticipate that pore saturation predictions should be least vulnerable to any deficiency in the description of interior transport. Roofs and floors were simulated with the Conduction Finite Difference (CFD) algorithm, eliminating consideration of their hygroscopic behavior. Interior air temperatures were held constant at 20 ${}^{\circ }$C; outside air was introduced at 10 ACH to facilitate realistic representation of indoor relative humidity; and Site:Precipitation objects were used to simulate constant light rain or snow, causing surfaces to be wet at all times. To ensure that moisture equilibration was achieved before simulations began, a minimum of 100 warm-up days were used.

Weather files were chosen to represent climates in which earth buildings are of current interest and in which frost damage is a concern; while many of these have cold, moist winters ($Dfa/b$, $Dsc$), drier ($BSk$) and milder ($Cfa/b$) climates are also represented. Rain indicators were removed, where present, to preserve the precipitation uniformity provided by Site:Precipitation objects. Weather files, the years of data represented by each file, and the corresponding Köppen climate types as of 2006 [120], are shown in

Table 2. Climates and weather files used to model environmental forcing.

City	Köppen Climate ${}^{\mathit{a}}$	Description	Weather File ${}^{\mathit{b}}$	Years
Golden	$BSk$	Cold semi-arid	USA_CO_Golden-NREL.724666_TMY3	1991–2005
		grassland	USA_CO_Boulder_HadCM3-A2-2020	2020
Tongliao	$BSk$	Cold semi-arid	CHN_Nei.Mongol.Tongliao.541350_SWERA	1975–1999
		grassland	CHN_NM_Tongliao.541350_TMYx.2003-2017	2003–2017
Philadelphia	$Cfa$	Humid	USA_PA_Philadelphia.Intl.AP.724080_TMY3	1976–2005
		subtropical	USA_PA_Philadelphia_HadCM3-A2-2020	2020
Copenhagen	$Cfb$	Oceanic	DNK_Copenhagen.061800_IWEC	1983–1999
			DNK_HS_Copenhagen-Kastrup.AP.061800_TMYx.2003-2017	2003–2017
Stockholm	$Cfb$	Oceanic	SWE_Stockholm.Arlanda.024600_IWEC	1984–1993
			SWE_ST_Stockholm.Arlanda.AP.024600_TMYx.2003-2017	2003–2017
Ankara	$Csa$	Mediterranean	TUR_Ankara.171280_IWEC	1982–1994
			TUR_AN_Ankara.Central.171300_TMYx.2003-2017	2003–2017
Toronto	$Dfa$	Humid	CAN_ON_Toronto.716240_CWEC	1961–1990
		continental	CAN_ON_Toronto.Pearson.Intl.AP.716240_CWEC2016	2016
Helsinki	$Dfb$	Hemiboreal	FIN_Helsinki.029740_IWEC	1982–1998
			FIN_US_Helsinki-Vantaa.AP.029740_TMYx.2003-2017	2003–2017
Montreal	$Dfb$	Hemiboreal	CAN_PQ_Montreal.Intl.AP.716270_CWEC	1961–1990
			CAN_QC_Montreal-Mirabel.Intl.AP.719050_CWEC2016	2016
Oslo	$Dfb$	Hemiboreal	NOR_Oslo.Fornebu.014880_IWEC	1983–1998
			NOR_OS_Oslo-Fornebu.AP.014881_TMYx.2003-2017	2003–2017
Winnipeg	$Dfb$	Hemiboreal	CAN_MB_Winnipeg.718520_CWEC	1961–1990
			CAN_MB_Winnipeg-Richardson.Intl.AP.718520_CWEC2016	2016
Anchorage	$Dsc$	Subarctic	USA_AK_Anchorage.Intl.AP.702730_TMY3	1975–1999
			USA_AK_ANCHORAGE_HadCM3-A2-2020	2020

${}^a$ [120]; ${}^b$ TMY3, IWEC, CWEC, and SWERA files for time periods of 1991–2005 and earlier were obtained in EPW format from the EnergyPlus weather file database (energyplus.net/weather). TMYx.2003-2017 and CWEC2016 files were obtained from the Climate.OneBuilding.org database (climate.onebuilding.org/default.html), and HadCM3-A2-2020 files were obtained by processing the respective TMY2 files (energyplus.net/weather) with the Climate Change World Weather Generator (www.energy.soton.ac.uk/ccworldweathergen/).

.

Below, we first present results based on earlier weather files, beginning as early as 1961 and extending as late as 2005, but often terminating in the 1990s (Table 2). To highlight potential consequences of climate change, we then show results obtained with later weather files, beginning in 2003 (Table 2). Where time series data for only a single month are shown, January was chosen because it was either the coldest or second-coldest month in all former and near-present weather files. Where data for three months are shown, the January-March interval was chosen because it included the coldest month (February) for Helsinki and Stockholm as well as a greater range of temperatures for all cities than was found in the interval of December-February.

3. Results and Discussion

3.1. Environmental Conditions, Material Properties, and Saturated Damage

Figure 4a shows a two week interval of outdoor air dry-bulb temperature $T_{db}$, surface temperature, and south-facing wall temperatures for a stabilized rammed earth construction in Golden, Colorado, USA at the labeled cell depths; corresponding temperature gradients (left axis) are displayed in Figure 4b, alongside surface relative humidity values (right axis). The effects of radiative heat transfer produce substantial offsets (i.e., often >20 ${}^{\circ }$C) between wall surface and outside air temperatures, particularly during sunny daytime periods, leading to large wall temperature gradients that reach a peak magnitude near the exterior surface exceeding $6{}^{\circ }$C/cm on 18 January. With the stabilized rammed earth threshold cracking temperature set to $T_c=-1{}^{\circ }$C, under water-saturated conditions these modeled time series predict substantial periods during which frost damage would be expected to accumulate. However, as shown in Figure 4b, during this interval the relative humidity at the wall surface reaches a maximum of just over 80%. The moisture retention curve from Figure 2a indicates that liquid saturations peak at around 20% under these conditions, so Figure 3a suggests an estimate for the unsaturated threshold cracking temperature $T_{cu}$ that is never warmer than about $-6{}^{\circ }$C. The combination of high humidity and low temperatures that is necessary for unsaturated frost damage is not met during the displayed time window.

These results, together with similar time series for the other wall constructions, were used to calculate daily integrals for the frost damage index $\Delta n$ from Equation (1). Recognizing that the maximum temperature gradients, minimum temperatures, and highest total water contents are achieved close to exterior wall surfaces, we focus our attention on this region to generate index predictions that are indicative of the most severe frost damage encountered. Referring to the data presented in Figure 4 as an example, we use only the surface T in Figure 4a along with the surface $RH$ and $\partial T/\partial z$ at 1.84 mm (obtained as the difference between T at the surface and at 3.67 mm depth into the wall divided by that distance) in Figure 4b as inputs to our calculations. As anticipated, Figure 5a reveals that appreciable damage (interpreted from high values of $\Delta n$) accumulates during numerous days over this three month time span, with a maximum of $\Delta n\approx 0.7\%$ for concrete on 1 February. Under saturated conditions, Equation (1) predicts a finite damage index on any day that $T<T_c$, with higher magnitude $\partial T/\partial z$ promoting greater $\Delta n$, and the inverse power-law weighting on $T_m-T$ limiting damage accumulation under very cold conditions, reflecting dramatic restrictions to the liquid transport needed for ice growth to propagate cracks.

The four materials behave differently, with concrete tending to exhibit the largest values of $\Delta n$ on days during which each material accumulates some damage, but stabilized rammed earth and compressed stabilized earth blocks each undergo damage on several days during which it does not become cold enough to damage concrete The solid brick masonry appears to perform best under these saturated conditions, with a maximum value during this time span of $\Delta n<0.04\%$. Further comparison between the damage accumulation in earth blocks and the conventional brick masonry is instructive, as each are modeled with the same cracking threshold of $T_c=-2{}^{\circ }$C. Table 1 indicates that the water transport parameter C that is defined by Equation (2) is a factor of 3 lower for the earth blocks than the brick masonry, yet Figure 5a indicates that the latter material consistently exhibits a lower damage index. The cause of this behavior can be traced to the permeability exponent $\alpha$, with the higher value for brick masonry reflecting an enhanced temperature dependence of the permeability, which regulates the liquid supply needed for crack growth. Hence, although the upper temperature limits to the frost-cracking window for brick masonry and earth blocks are the same ($-2{}^{\circ }$C), the temperature range over which the damage index can grow effectively is much narrower for the masonry. A similar picture emerges upon examining the contrast between the saturated damage of concrete, with $T_c=-3{}^{\circ }$C, and stabilized rammed earth, with $T_c=-1{}^{\circ }$C. As noted above, there are several days during which the surface temperature is cold enough to cause frost damage to rammed earth, but remains too warm for cracking in concrete. On most days where the temperature is cold enough for cracking in both materials; however, $\Delta n$ for concrete is higher than for rammed earth. Once again, the difference reflects the greater permeability exponent $\alpha$ for rammed earth, which restricts the lower limit to the temperature range over which significant damage accumulates. In contrast, the higher $\Delta n$ values predicted in rammed earth than in earth blocks can be traced to the factor of 5 difference between their respective C values (see Equation (2)), with the lower value for earth blocks caused primarily by the smaller temperature offset $T_m-T_f$ at which the first pore ice forms and begins to restrict liquid transport (see Table 1).

To summarize these findings, susceptibility to saturated frost damage is more severe for a material with: (a) a warmer cracking threshold $T_c$ (e.g., due to weaker matrix bonding or larger incipient crack sizes); (b) a smaller permeability exponent $\alpha$ (e.g., due to more widely distributed pore sizes that enable more conductive residual liquid pathways to persist over a broader temperature range); and (c) a higher water transport parameter C (e.g., due to a higher liquid-saturated permeability $k_0$ or a larger temperature depression for initial ice formation $T_f$; note, however that materials with larger pore sizes tend to be characterized by both higher $k_0$ and warmer $T_f$). In a given material, damage is expected to be most severe at temperatures just below $T_c$ before liquid transport becomes too restricted. High temperature gradients also promote damage, both because they drive liquid transport and because they cause larger gradients in permeability that are accommodated in part by freezing. The most effective environmental conditions for producing damage involve prolonged time periods at temperatures near $T_c$ while the material is subjected to high temperature gradients; such behavior is characteristic of cyclic variations near the melting transition, including freeze-thaw.

3.2. Environmental Conditions, Material Properties, and Unsaturated Damage

The unsaturated damage index $\Delta n_u$ obtained over the same three-month time period is displayed in Figure 5b; note the order of magnitude reduction in the axis scale. As anticipated from the discussion surrounding the two week interval highlighted in Figure 4, damage under unsaturated conditions is rare in Golden. Even when it is damp and cold enough to produce some damage, $\Delta n_u$ is always at least an order of magnitude smaller than $\Delta n$, which suggests a remarkable decrease in the damage severity. The peak $\Delta n_u\approx 0.05\%$ for this time series takes place on 16 February in concrete, with earth blocks at $\Delta n_u\approx 0.04\%$, rammed earth at $\Delta n_u\approx 0.03\%$, and brick masonry at $\Delta n_u\approx 0.001\%$. Whereas in this climate, saturated damage to earth blocks is generally lower than to rammed earth, the moisture retention curves from Figure 2a indicate that earth blocks have a higher total water content than rammed earth at a given relative humidity. In addition, the lower vapor diffusion resistance factor ${\mu }_0$ and higher $k_0$ (obtained from the saturated limit of the liquid suction function) listed in Table 1 for earth blocks both reflect somewhat enhanced moisture transport. Combined, these effects cause the earth blocks to be somewhat more susceptible to unsaturated damage than the rammed earth on the days in which the largest values of $\Delta n_u$ are obtained. However, days with noticeable $\Delta n_u$ at this scale are rare and tend to be isolated by long intervals in which it is either too warm or too dry for cracks to grow. In fact, recognizing that some degree of volume change can be accommodated elastically, e.g., [56,57], it is conceivable that the few brief positive excursions of $\Delta n_u$ shown in Figure 5b might relax and produce no lasting damage at all.

It would be reasonable to expect that the same factors that enhance damage in saturated conditions should also tend to enhance damage in unsaturated conditions. However, the sensitivity to water content S that Equation (7) predicts for $T_{cu}$ is notably much greater for materials with lower saturation exponents $\beta$ (see Figure 3a), which tend to reflect more broadly distributed pore sizes. For a given time series of temperature variations, this can cause a reversal of the damage susceptibility under saturated vs. unsaturated conditions for two different materials. The 16 February values shown in Figure 5 for $\Delta n$ and $\Delta n_u$ of compressed stabilized earth blocks and stabilized rammed earth are an example of such behavior (i.e., $\Delta n$ is greater for the stabilized rammed earth under the same temperature forcing for which $\Delta n_u$ is greater for the compressed stabilized earth blocks). In terms of environmental conditions, it is important to emphasize that the susceptibility of a given material to unsaturated frost damage does not depend only on the temperature and its gradient, but also on the pore space relative humidity, which must approach values near unity for the $T_{cu}$ threshold to be reached.

3.3. Damage Variations between Different Cities

Figure 6 shows $\Delta n$ predicted by Equation (1) assuming saturated conditions in each of the cities listed in Table 2 during the earlier range of years; a summary of average daily frost damage indices is given in

Table A2. Average daily damage indices from January–March (note that $\Delta \overline{n}$ values are in %, whereas $\Delta {\overline{n}}_u$ values are in units of ${10}^{-3}\%$). Regular text values represent the earlier range of years listed in Table 2, displayed as time series in Figure 6 and Figure 8. In parentheses, values for the later range of years listed in Table 2 are given, these data correspond to the time series displayed in Figure 10 and Figure 11.

City	Concrete	Compressed Stabilized Earth Blocks	Stabilized Rammed Earth	Solid Brick Masonry
Golden $\Delta \overline{n}$ (%)	0.074 (0.080)	0.063 (0.051)	0.069 (0.056)	0.0064 (0.0049)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	1.1 (0)	0.80 (0)	0.64 (0.13)	0.016 (0)
Tongliao $\Delta \overline{n}$ (%)	0.21 (0.21)	0.12 (0.12)	0.13 (0.13)	0.011 (0.012)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (0)	0.10 (0.78)	0.45 (2.6)	0 (0.11)
Philadelphia $\Delta \overline{n}$ (%)	0.061 (0.056)	0.043 (0.040)	0.046 (0.042)	0.0049 (0.0046)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0.92 (0.080)	1.3 (0.035)	3.0 (0.088)	0.15 (0.0093)
Copenhagen $\Delta \overline{n}$ (%)	0.0084 (0.014)	0.017 (0.014)	0.019 (0.014)	0.0019 (0.0015)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (0)	0 (0.39)	0.029 (2.8)	0 (0.17)
Stockholm $\Delta \overline{n}$ (%)	0.066 (0.12)	0.038 (0.064)	0.037 (0.062)	0.0034 (0.0061)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (0.46)	0.046 (9.4)	0.69 (29)	0.0012 (2.0)
Ankara $\Delta \overline{n}$ (%)	0.020 (0)	0.023 (0.0072)	0.026 (0.0066)	0.0024 (0.00095)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (0)	0 (0)	0 (0)	0 (0)
Toronto $\Delta \overline{n}$ (%)	0.15 (0.097)	0.087 (0.087)	0.087 (0.096)	0.0082 (0.0093)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0.13 (0)	0.26 (0.60)	3.5 (10)	0.24 (0.12)
Helsinki $\Delta \overline{n}$ (%)	0.074 (0.14)	0.057 (0.082)	0.059 (0.077)	0.0054 (0.0071)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (2.6)	0.33 (6.4)	0.68 (20)	0.0082 (1.8)
Montreal $\Delta \overline{n}$ (%)	0.18 (0.15)	0.10 (0.10)	0.10 (0.11)	0.0094 (0.010)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	1.6 (0.80)	2.7 (0.62)	4.0 (0.87)	0.0067 (0.013)
Oslo $\Delta \overline{n}$ (%)	0.031 (0)	0.044 (0)	0.046 (0)	0.0050 (0)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (0)	0.38 (0)	0.62 (0)	0.0030 (0)
Winnipeg $\Delta \overline{n}$ (%)	0.14 (0.17)	0.081 (0.10)	0.079 (0.10)	0.0072 (0.0095)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0.56 (0.30)	1.5 (2.6)	4.5 (6.5)	0.21 (0.28)
Anchorage $\Delta \overline{n}$ (%)	0.14 (0.09)	0.096 (0.067)	0.10 (0.069)	0.0098 (0.0065)
$\Delta {\overline{n}}_u$ ($\times {10}^{-3}\%$)	0 (0)	0.0018 (0.099)	0.24 (0.58)	0 (0)

. As shown in Figure 7, the general patterns of predicted damage accumulation correspond with episodes of low subzero surface temperatures. However, as anticipated from modeled restrictions to liquid transport at very low temperatures, close examination reveals that the days on which the greatest changes in $\Delta n$ take place are not the coldest. Over the entire three month period, for example, Figure 7 indicates that Winnipeg is most frigid, whereas Figure 6 shows that Tongliao has larger average daily $\Delta n$, as do Montreal and Anchorage (see Table A2). Examining particular dates, the largest $\Delta n$ in Montreal takes place in early January when the temperature stays above $-5{}^{\circ }$C. In Anchorage, much more damage is predicted during the relatively mild weather of late February and early March than in the coldest stretches of January.

Comparing the different material behaviors displayed in Figure 6, consistent with the results already discussed for Golden (shown enlarged in Figure 5), concrete exhibits the largest overall $\Delta n$ in most of these cities. In the milder climates of Copenhagen, Ankara, and Oslo, however, temperatures become sufficiently cold to crack concrete on only a few days over this three month period, whereas stabilized rammed earth is damaged more frequently, followed by compressed stabilized earth blocks, with the solid brick masonry consistently accumulating the smallest $\Delta n$ values (see Table A2). Once again, these differences in material performance reflect differences in the temperature dependence of liquid supply, gauged by $\alpha$, the minimum ice pressure needed for cracking to begin, gauged by $T_c$, and the background pore liquid transport rate, gauged by the water transport parameter C (see Table 1).

Figure 8 shows predicted $\Delta n_u$ time series obtained with $T_{cu}$ adjusted following Equation (7) to reflect the more realistic case of frost damage during unsaturated conditions (note the order of magnitude reduction in scale compared to Figure 6). Because of moisture limitations, the correlation between $\Delta n_u$ and the temperature time series in Figure 7 appears weak. The milder climates, including Ankara and Copenhagen, register no frost damage at all, but much colder locations like Tongliao and Anchorage also accumulate negligible $\Delta n_u$. These findings are consistent with expectations based on the surface relative humidity time series shown in Figure 9. During this entire three month time period, the relative humidity on a south-facing stabilized rammed earth wall in Tongliao never reaches 80%, implying low surface water contents (see Figure 2) and correspondingly reduced values of $T_{cu}$ (see Figure 3). Philadelphia, Toronto, Montreal, and Winnipeg each experience brief episodes where $\Delta n_u$ spikes above the maximum scale displayed (reaching peaks of $0.17\%$ on 8 February in Philadelphia; $0.13\%$ on 8 February in Toronto; $0.13\%$ on 6 January in Montreal; and $0.20\%$ on 3 March in Winnipeg, highlighted with arrows in Figure 7, Figure 8 and Figure 9); the surface relative humidity during each of these episodes approaches 100%. More modest periods of vulnerability in Golden, Stockholm, Helsinki and Oslo also correlate with periods of high surface relative humidity.

3.4. Changing Damage Patterns over Time

To gauge potential temporal changes in the patterns and severity of damage as climate changes, we repeated the index calculations using weather files that represent the later time periods listed for each city in italics in Table 2. Figure 10 (see also Table A2) reveals that weather patterns representative of the period from 2003–2017 in Oslo have warmed sufficiently that the saturated damage index has become negligible over the first three months of the year, whereas Figure 8 indicates significant damage during these months in the earlier 1983–1998 interval (see Table 2). Total frost damage in Ankara is also reduced under more recent weather conditions, and significant decreases take place in Toronto, Montreal, Anchorage, and to a lesser extent, Golden. Under both sets of weather files, similar saturated damage indices were predicted for Tongliao and Philadelphia. In Copenhagen, damage is generally reduced on average during the later climate interval (see Table A2), but while the peak $\Delta n$ for concrete is slightly lower, the peak damage to both stabilized rammed earth and compressed stabilized earth blocks are slightly higher. Helsinki and Stockholm both experience more damage under the more recent 2003–2017 interval than they do during the earlier interval. The damage index for Winnipeg is also slightly higher using weather for 2016 than it was for the weather patterns representative of 1961–1990.

The frost damage index for unsaturated conditions under more recent weather conditions is shown in Figure 11. A reduction to negligible damage takes place in Golden, Philadelphia, and Oslo, while Ankara remains too warm and dry for unsaturated cracking and Anchorage experiences a slight increase compared to predictions for earlier years, shown in Figure 8. A substantial reduction in the damage index is also predicted for Montreal, but the index values rise in Tongliao, Copenhagen, Toronto and Winnipeg, predicting significantly greater damage to rammed earth and slightly greater damage to compressed stabilized earth blocks in these climates.

Strikingly, simulations with the most recent weather files available (Table 2) indicate that frost vulnerability is currently increasing in Helsinki and Stockholm (Figure 11). This finding is consistent with recent reports expressing concerns about increasing vulnerability to frost damage in these areas as climate change progresses [45,46]. The underlying causes appear to be closely related in the two cities. In both climates, the combination of warmer winter outdoor air with greater cloudiness, i.e., less direct solar radiation, causes near-freezing (∼−3–$0{}^{\circ }$C) outdoor air to coexist with high (90–100%) relative humidity much more frequently in more recent weather. As a result, near-surface pore spaces more often have high relative humidities at temperatures slightly above freezing, especially during daytimes when solar radiation warms south-facing wall surfaces to temperatures above those of ambient air. When a wall surface at such conditions cools rapidly due to increasing cloudiness or sunset, or from an increase in convective heat loss due to a change in wind speed or direction, pore space relative humidities are then likely to reach 100% as the wall surface drops into freezing temperatures, entering the frost-cracking window.

For Helsinki, the contrast between conditions of the recent past represented by the TMYx.2003-2017 file (Table 2), and those of thirty years ago represented by the IWEC file, is shown in Figure 12, using rammed earth as the material and focusing on the first six weeks of the year (this interval is highlighted with horizontal blue lines beneath the Helsinki panels in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11). Hours during which the surface relative humidity (“Surface RH”) reaches 100% are found within the frost-cracking window during this interval (shaded areas). In particular, high humidities and low surface temperatures coincide over much of 6 January, 18 January and 5 February; these are the three days marked by arrows in Figure 11 that exhibit dramatic peaks in $\Delta n_u$. As the graphs in Figure 12 show, this combination of environmental conditions is predicted to occur much more frequently under more recent conditions (upper panel). In addition, the wall maintains much higher pore space relative humidity overall under the more recent conditions because the frequency of rapid, extensive solar surface heating is much lower; this is visible in the correspondence between peaks in wall surface temperatures (“Surface T”) and dips in pore space relative humidity. This surface heating, which warms the wall well above outdoor air temperatures on numerous occasions in the earlier weather file (lower panel), diminishes the relative humidity in wall surface pores significantly. With far fewer sunny hours, however, this periodic warming and dehumidification cannot occur, causing the wall surface to enter the frost-vulnerable region much more frequently and for more hours each time.

3.5. Interpreting the Damage Index

Our analysis of frost cracking vulnerability makes extensive use of modeled values of the damage index defined by Equation (1). Following the hypothesis of McGreevy and Whalley [59] that “the degree of frost damage (to porous materials) can be equated with the amount of ice (that) forms in them during freezing”, for saturated conditions $\Delta n$ was originally developed to represent the increase in porosity and ice content that occurs when the temperature is sufficiently cold for the stresses exerted by ice on pore walls to propagate cracks [67]. Nevertheless, the process of crack propagation and the partitioning between recoverable (i.e., elastic) and unrecoverable deformation is not directly assessed and, as with other proposed macroscopic indices [63,64,65,66], further efforts are needed to connect calculated values of $\Delta n$ with observed damage severity. The choice to evaluate Equation (1) over daily time periods was made to facilitate comparisons between the predicted accumulation of damage between different materials and weather conditions. In many cases, the surface temperature crosses the threshold $T_c$ on a daily basis, so that melting can take place and allow the stresses on pore walls to relax before the next freezing episode occurs. However, many of the climates we investigated also include conditions during which the material surface was held at $T<T_c$ for several days and hence the daily $\Delta n$ values that we report may be considered to accumulate on top of each other. By this reasoning, a given sequence of daily $\Delta n$ values would be expected to cause more severe damage if the temperature never rose above $T_c$ than if there were mitigating warmer excursions that allowed matrix stresses to relax. The strong dependence of $\Delta n$ on the magnitude of the temperature gradient complicates matters somewhat, since the rapid warming and cooling that is often associated with excursions above and below $T_c$ also tend to produce larger temperature gradients and hence larger values of $\Delta n$ during individual freezing episodes.

For the unsaturated conditions that are expected to apply most frequently in building walls, $\Delta n_u$ cannot strictly be interpreted in terms of absolute increases to the entire pore space volume, but instead as a measure of water redistribution by cryosuction that supplies crack growth in the most damage-prone air-free pores. The large reductions we demonstrate for $\Delta n_u$ in comparison with $\Delta n$ are consistent with the expected reduced frost vulnerability when insufficient moisture is available to freeze and cause damage. The degree to which a given material can accommodate the volume changes implied by particular values of $\Delta n$ or $\Delta n_u$ must depend on matrix mechanical properties and pore characteristics. Further assessment of frost resilience awaits quantitative comparison with field and laboratory observations. In particular, detailed monitoring studies on specific well-characterized materials with measured environmental and in situ variables are needed for improved model validation of both the damage index and the phase distribution predictions that underlie its determination.

4. Conclusions

The low embodied energy of earth building materials, as well as their humidity-buffering properties and thermal stability, are increasing their attractiveness in green building design in climates where frost damage is a concern. Our assessment of a physically-based frost damage index [67] in several of these climates suggests that frost resilience properties of stabilized rammed earth and compressed stabilized earth blocks compare favorably with those of conventional concrete and brick masonry constructions. A key finding is that in most climates, from cold semi-arid Tongliao to subarctic Anchorage, the frequency of winter days that are sufficiently cold for frost cracking under saturated conditions show little consequence for realistic conditions because wall moisture levels remain too low. This highlights the importance in future research of developing laboratory tests that evaluate material performance under the unsaturated conditions most likely to prevail, rather than the saturated conditions approached in many freeze-thaw testing procedures [89,90,91]. In particular, time spent in the frost-cracking window is expected to be more relevant to understanding a material’s freeze-thaw resilience than the frequency of cycling through temperature extremes. A second central prediction is that climate change will affect frost vulnerability of earth materials in northern climates differently depending on coincident changes in temperature, cloud cover, and humidity. In cool coastal cities such as Helsinki and Stockholm, where increasing winter cloud cover is diminishing the solar radiation that tends to maintain drier walls, frost vulnerability is predicted to increase substantially. In those where temperature rise is the dominant effect; however, such as Montreal and Philadelphia, frost damage potential is expected to be reduced or virtually eliminated.