Estimates of Soil Renewal Rates: Applications for Anti-Erosion Arrangement of the Agricultural Landscape
Abstract
1. Introduction
2. Material and Methods
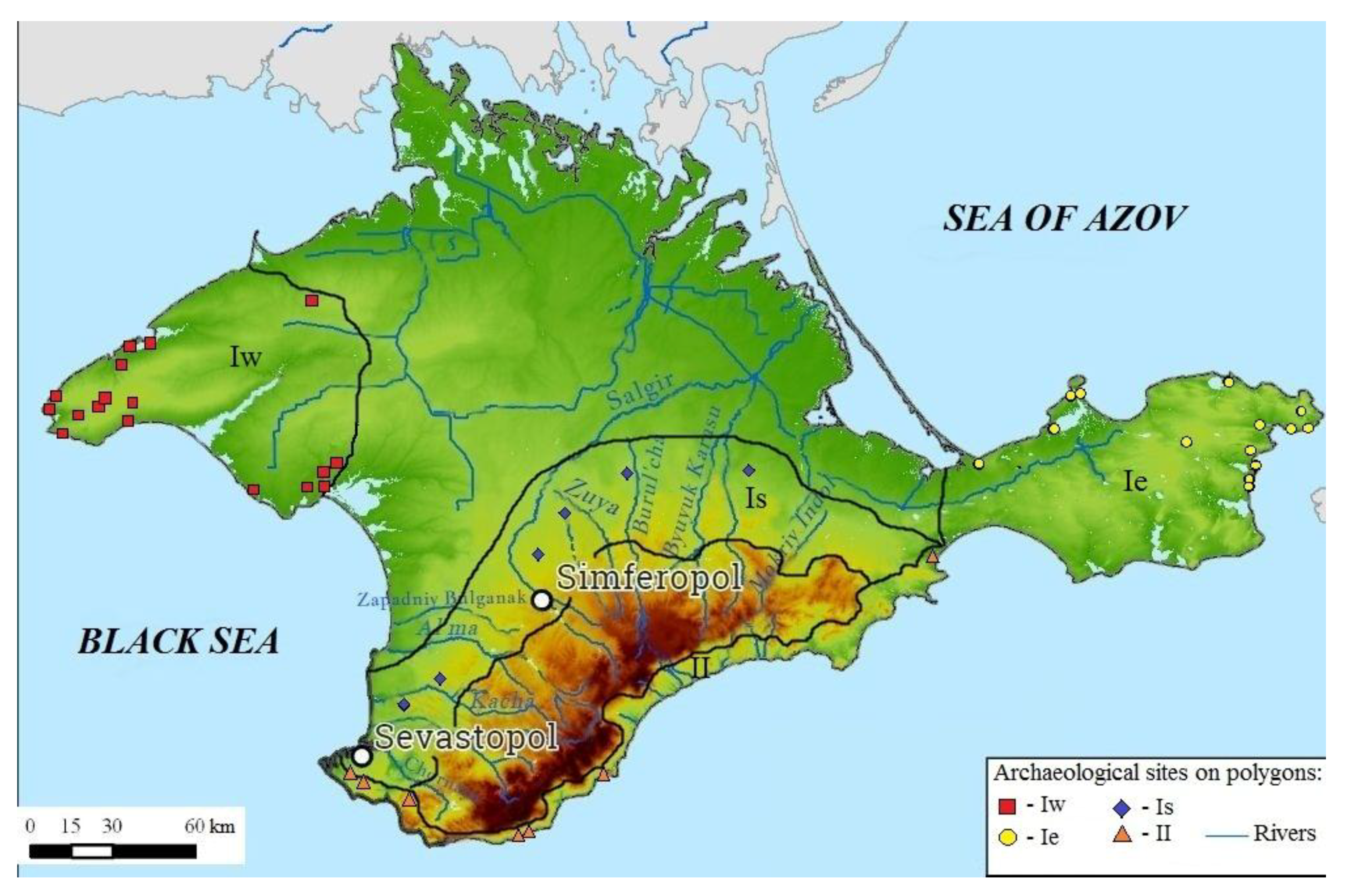
2.1. Different-Time Soils of Archaeological Sites
2.2. The Climatic Features of the Study Area
3. Results
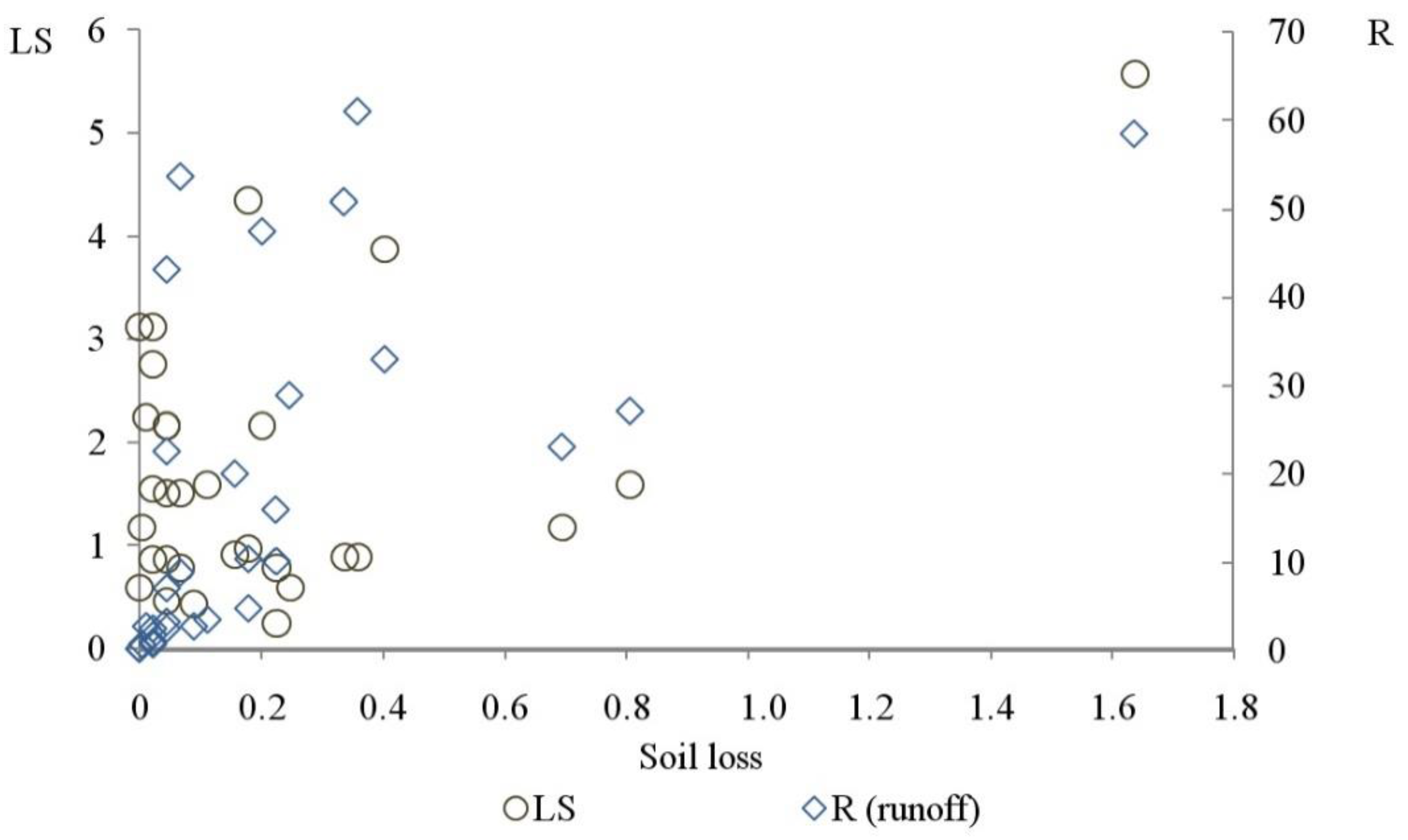
3.1. T-values and the Rate of Soil Formation
3.2. Summarized Rates of Soil Formation
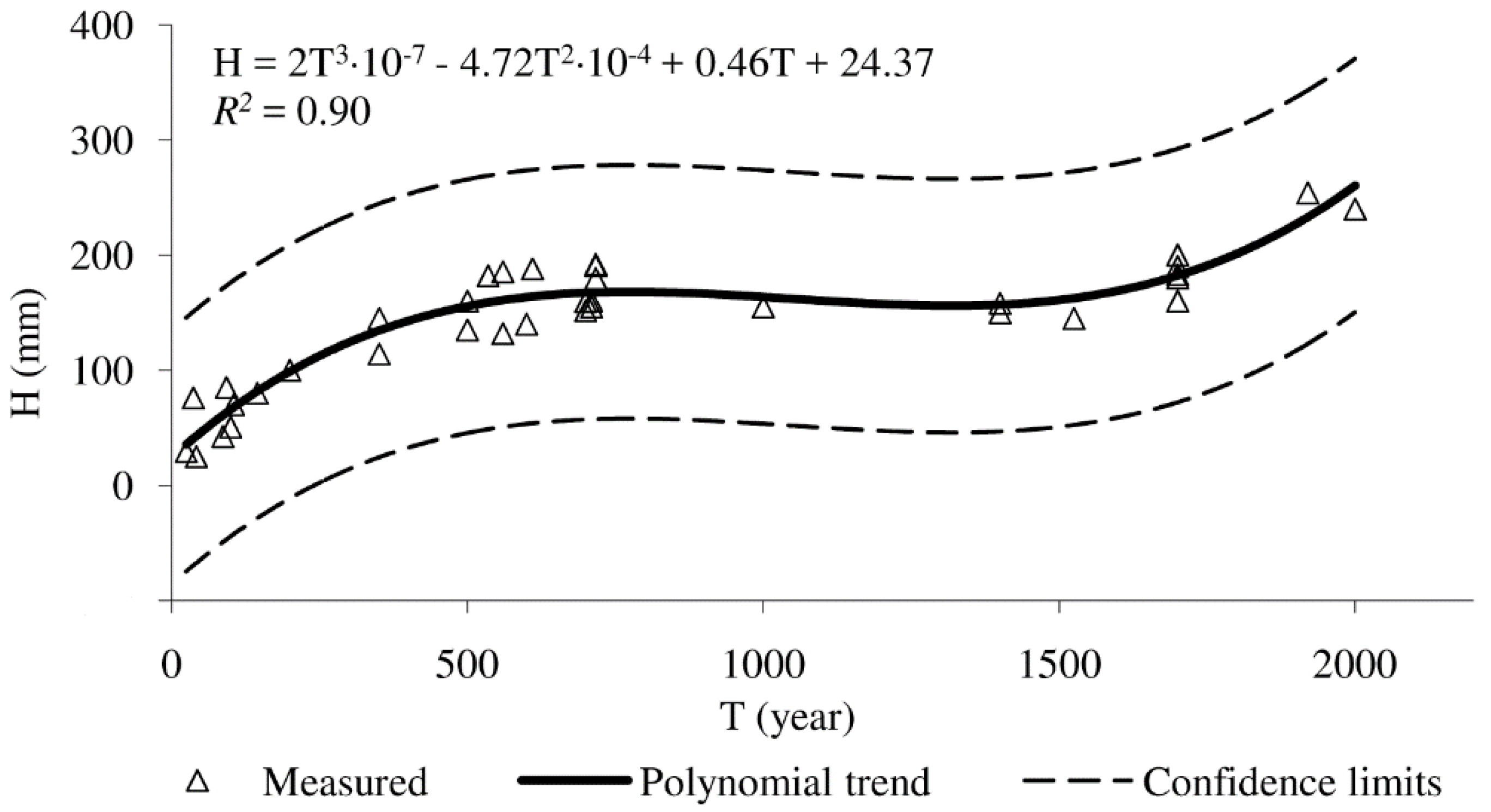
3.3. Regional Chronofunctions of Changes of the Humus Horizon
4. Discussion
4.1. Stages of Engineering and Geographical Arrangement of the Agricultural Landscape
4.2. The Determine of T-values for Agricultural Landscapes
4.3. Use of Pedochronological Data for Land Restoration and Soil Quality
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Litvin, L.F.; Zorina, Y.F.; Sidorchuk, A.Y.; Chernov, A.V.; Golosov, V.N. Erosion and sedimentation on the Russian Plain, part 1: Contemporary processes. Hydrol. Process. 2003, 17, 3335–3346. [Google Scholar] [CrossRef]
- Dolgilevich, M.I. Dust Storms and Agroforestry Activities; Kolos: Moscow, Russia, 1978. [Google Scholar]
- Kirkby, M.J. A basis for soil profile modelling in a geomorphic context. J. Soil Sci. 1985, 36, 97–121. [Google Scholar] [CrossRef]
- Skidmore, E.L. Soil loss tolerance. In Determinants of Soil Loss Tolerance, special publication 45; American Society of Agronomy and Soil Science Society of America: Madison, WI, USA, 1982; pp. 87–93. [Google Scholar]
- Shvebs, H.I. The Theoretical Bases of Erosion Science; Vyisshaya Shkola: Kiev, Ukraine, 1981. [Google Scholar]
- Lisetskii, F.N.; Svetlitchnyi, A.A.; Chornyy, S.G. Recent Developments in Erosion Science; Konstanta: Belgorod, Russia, 2012; ISBN 978-5-9786-0248-7. [Google Scholar] [CrossRef]
- Elwell, H.; Stocking, M. Estimating soil life-span for conservation planning. Trop. Agric. 1984, 61, 148–150. [Google Scholar]
- Lisetskii, F.N.; Muntian, A.N.; Zholumskaya, K.V. Duration estimating spending soil under active development of erosion processes. Biogeosyst. Tech. 2016, 7, 49–64. [Google Scholar]
- Doe, W.W., III; Harmon, R.S. Introduction to soil erosion and landscape evolution modelling. In Landscape Erosion and Evolution Modeling; Kluwer Academic/Plenum Publisher: New York, NY, USA, 2001; pp. 1–14. [Google Scholar]
- Jetten, V.G.; Govers, G.; Hessel, R. Erosion models: Quality of spatial predictions. Hydrol. Process. 2003, 17, 887–900. [Google Scholar] [CrossRef]
- Lenz, J.; Fritz, M.; Schirrmeister, L.; Lantuit, H.; Wooller, M.J.; Pollard, W.H.; Wetterich, S. Periglacial landscape dynamics in the western Canadian arctic: Results from a thermokarst lake record on a push moraine (Herschel island, Yukon territory). Palaeogeogr. Palaeoclimatol. Palaeoecol. 2013, 381, 15–25. [Google Scholar] [CrossRef]
- Griffith, M.A. A pedological investigation of an archaeological site in Ontario, Canada, I. An examination of the soils in and adjacent to a former village. Geoderma 1980, 24, 327–336. [Google Scholar] [CrossRef]
- Ivanov, I.V.; Aleksandrovsky, A.L. Investigation methods of soil evolution. Pochvovedenie 1987, 1, 112–121. [Google Scholar]
- Demkin, V.A.; Dergacheva, M.I.; Borisov, A.V.; Ryskov, Y.G.; Oleinik, S.A. Soil evolution and climate change in the semidesert zone of Eastern Europe during the late Holocene. Eur. Soil Sci. 1998, 2, 133–143. [Google Scholar]
- Chichagova, O.A.; Krenke, N.A.; Alexandrovskiy, A.L.; Glasko, M.P. Buried soils of floodplains and paleoenvironmental changes in the Holocene. Rev. Mex. Cienc. Geológicas 2004, 21, 9–17. [Google Scholar]
- Goleusov, P.V.; Lisetskii, F.N. Soil development in anthropogenically disturbed forest-steppe landscapes. Eur. Soil Sci. 2008, 41, 1480–1486. [Google Scholar] [CrossRef]
- Walkington, H. Soil science applications in archaeological contexts: A review of key challenges. Earth Sci. Rev. 2010, 103, 122–134. [Google Scholar] [CrossRef]
- Alexandrovskiy, A.L. Holocene development of soils in response to environmental changes: The Novosvobodnaya archaeological site, North Caucasus. Catena 2000, 41, 237–248. [Google Scholar] [CrossRef]
- Maher, B.A.; Alekseev, A.; Alekseeva, T. Magnetic mineralogy of soils across the Russian steppe: Climatic dependence of pedogenic magnetite formation. Palaeogeogr. Palaeoclimatol. Paleoecol. 2003, 201, 321–341. [Google Scholar] [CrossRef]
- Prikhod’ko, V.E.; Ivanov, I.V.; Manakhov, D.V.; Gerasimenko, N.P.; Inubushi, K.; Nagano, K.; Kawahigashi, M.; Sugihara, S. Soils, vegetation, and climate of the southern transural region in the middle bronze age (by the example of the Arkaim fortress). Eur. Soil Sci. 2013, 9, 925–934. [Google Scholar] [CrossRef]
- Peters, S.; Borisov, A.V.; Reinhold, S.; Korobov, D.S.; Thiemeyer, H. Microbial characteristics of soils depending on the human impact on archaeological sites in the Northern Caucasus. Quat. Int. 2014, 324, 162–171. [Google Scholar] [CrossRef]
- Saláta, D.; Krausz, E.; Reményi, L.; Kenéz, A.; Peto, Á. Combining historical land-use and geoarchaeological evidence to support archaeological site detection. Agrokem. Talajt. 2014, 1, 99–108. [Google Scholar] [CrossRef]
- Chernysheva, E.V.; Korobov, D.S.; Khomutova, T.E.; Borisov, A.V. Urease activity in cultural layers at archaeological sites. J. Archaeol. Sci. 2015, 57, 24–31. [Google Scholar] [CrossRef]
- Kern, D.C.; Costa, J.A.; da Silveira, M.I.; de Oliveira, E.R.; Lima Frazão, F.J.; Berredo, J.F.; da Costa, M.L.; Kämpf, N. Pedo-geochemical signatures of archeological sites in the tapirapé-aquiri national forest in Marabá, Amazonia, Brazil. Geoarchaeology 2015, 5, 430–451. [Google Scholar] [CrossRef]
- Golyeva, A.; Khokhlova, O.; Lebedeva, M.; Shcherbakov, N.; Shuteleva, I. Micromorphological and chemical features of soils as evidence of bronze age ancient anthropogenic impact (Late Bronze Age Muradymovo settlement, Ural region, Russia). Geosciences (Switz.) 2018, 9, 313. [Google Scholar] [CrossRef]
- Mitusov, A.V.; Mitusova, O.E.; Pustovoytov, K.; Lubos, C.C.-M.; Dreibrodt, S.; Bork, H.-R. Palaeoclimatic indicators in buried soils under archaeological monuments in the Eurasian steppe: A review. Holocene 2009, 19, 1153–1160. [Google Scholar] [CrossRef]
- Gladfelter, B.G. Developments and directions in geoarchaeology. Adv. Archaeol. Method Theory 1981, 4, 343–364. [Google Scholar]
- Opolot, E.; Yu, Y.Y.; Finke, P.A. Modeling soil genesis at pedon and landscape scales: Achievements and problems. Quat. Int. 2015, 376, 34–46. [Google Scholar] [CrossRef]
- Birkeland, P.W. Holocene soil chronofunctions, Southern Alps, New Zealand. Geoderma 1984, 34, 115–134. [Google Scholar] [CrossRef]
- Heimsath, A.M.; Dietrich, W.E.; Nishiizumi, K.; Finkel, R.C. The soil production function and landscape equilibrium. Nature (Lond.) 1997, 388, 358–388. [Google Scholar] [CrossRef]
- Lisetskii, F.N.; Stolba, V.F.; Goleusov, P.V. Modeling of the evolution of steppe chernozems and development of the method of pedogenetic chronology. Eur. Soil Sci. 2016, 49, 846–858. [Google Scholar] [CrossRef]
- Lisetskii, F.N.; Stolba, V.F.; Marininа, O.A. Indicators of agricultural soil genesis under varying conditions of land use. Geoderma 2015, 239, 304–316. [Google Scholar] [CrossRef]
- Cordova, C. Crimea and the Black Sea: An Environmental History; I.B. Tauris: London, UK; New York, NY, USA, 2016. [Google Scholar]
- Lisetskii, F.N.; Stolba, V.F.; Pichura, V.I. Late-holocene palaeoenvironments of southern Crimea: Soils, soil-climate relationship and human impact. Holocene 2017, 27, 1859–1875. [Google Scholar] [CrossRef]
- Lisetskii, F.; Zelenskaya, E.; Rodionova, M. Geochemical features of fallow land in ancient plots in the chora of Chersonesos. Geosciences (Switz.) 2018, 8, 410. [Google Scholar] [CrossRef]
- Munsell Color Company. Munsell Soil Color Charts: Year 2000 Revised Washable Edition; GretagMacbeth: New Windsor, NY, USA, 2000. [Google Scholar]
- Arinushkina, Е.V. Manual for the Chemical Analysis of Soils; University Press: Moscow, Russia, 1970. (In Russian) [Google Scholar]
- Smith, R.M.; Stamey, W.L. Determining the range of tolerable erosion. Soil Sci. 1965, 100, 414–424. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Agroclimatic Guide to the Crimean Region; Bogatyr, T.K., Ed.; Gidrometeoizdat: Leningrad, Russia, 1959. (In Russian) [Google Scholar]
- Volobuev, V.R. Introduction to Energetics of Soil Formation; Franklin Book Programs: Cairo, Egypt, 1975. [Google Scholar]
- Alexander, E.B. Rates of soil formation: Implications for soil loss tolerance. Soil Sci. 1988, 145, 37–45. [Google Scholar] [CrossRef]
- Li, Y.; Bai, X.Y.; Wang, S.J.; Qin, L.Y.; Tian, Y.C.; Luo, G.J. Evaluating of the spatial heterogeneity of soil loss tolerance and its effects on erosion risk in the carbonate areas of southern China. Solid Earth 2017, 3, 661–669. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, Z.; Govers, G. Soil and water conservation measures reduce soil and water losses in China but not down to background levels: Evidence from erosion plot data. Geoderma 2019, 337, 729–741. [Google Scholar] [CrossRef]
- Buryak, Z.A.; Zelenskaya, E.Y.; Poletaev, A.O.; Tsybenko, V.V. System approach to soil protection and ecological arrangement of watersheds at the regional level, Belgorod oblast. Ecol. Environ. Conserv. 2019, 1, 219–228. [Google Scholar]
- Verheijen, F.G.A.; Jones, R.J.A.; Rickson, R.J.; Smith, C.J.; Bastos, A.C.; Nunes, J.P.; Keizer, J.J. Concise overview of European soil erosion research and evaluation. Acta Agric. Scand. Sect. B Soil Plant Sci. 2012, 62 (Suppl. 2), 185–190. [Google Scholar] [CrossRef]
- Goleusov, P.V. Soil formation under different combinations of substrate and phytocenotic conditions in the forest-steppe zone. Eur. Soil Sci. 2003, 9, 937–945. [Google Scholar]
- Schumm, S.A.; Harvey, M.D. Natural erosion in the USA. In Determinants of Soil Loss Tolerance; special publication 45; American Society of Agronomy and Soil Science Society of America: Madison, WI, USA, 1982; pp. 15–22. [Google Scholar]
- Montgomery, D.R. Soil erosion and agricultural sustainability. Proc. Natl. Acad. Sci. USA 2007, 104, 13268–13272. [Google Scholar] [CrossRef]
- Bennett, H.H. Soil Conservation; McGraw–Hill, Book Company, Inc.: New York, NY, USA, 1939. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water. A Guide to Conservation Planning with the Revised Universal Soil Loss Equation RUSLE; USDA Agriculture Handbook No 703; U.S. Department of Agriculture: Washington, DC, USA, 1997.
- Lal, R. Soil degradation by erosion. Land Degrad. Dev. 2001, 12, 519–539. [Google Scholar] [CrossRef]
- Roloff, G.; Larson, G.A.; Larson, W.E.; Voss, R.P.; Becken, P.W. A dual targeting criterion for soil conservation programs in Minnesota. J. Soil Water Conserv. 1988, 1, 99–102. [Google Scholar]
- Lima, C.G.R.; Carvalho, M.P.; Souza, A.; Costa, N.R.; Montanari, R. Influence of chemical attributes in erodibility and tolerance of soil loss in watershed of low São José of Dourados River [Influência de atributos químicos na erodibilidade e tolerância de perda de solo na bacia hidrográfica do baixo São José dos Dourados]. Geociencias 2016, 1, 63–76. [Google Scholar]
- Di Stefano, C.; Ferro, V. Establishing soil loss tolerance: An overview. J. Agric. Eng. 2016, 3, 127–133. [Google Scholar] [CrossRef]
- Duan, X.; Xie, Y.; Liu, B.; Liu, G.; Feng, Y.; Gao, X. Soil loss tolerance in the black soil region of Northeast China. J. Geogr. Sci. 2012, 4, 737–751. [Google Scholar] [CrossRef]
- Singh, R.K.; Somasundaram, J.; Lakaria, B.L.; Mandal, D.; Sinha, N.K.; Lal, R. Using credible soil loss tolerance value for conservation planning and managing diverse physiographic regions in Rajasthan. Agric. Res. 2017, 2, 169–178. [Google Scholar] [CrossRef]
- Chornyy, S.; Poliashenko, N. Determination of soil-loss tolerance for chernozem of Right-Bank Ukraine. In Soil Science Working for a Living: Applications of Soil Science to Present-Day Problems; Springer: Cham, Switzerland, 2017; pp. 109–119. [Google Scholar]
- Kuznetsov, M.S.; Abdulkhanova, D.R. Soil loss tolerance in the central chernozemic region of the European part of Russia. Eur. Soil Sci. 2013, 7, 802–809. [Google Scholar] [CrossRef]
- Johnson, L.C. Soil loss tolerance: Fact or myth? J. Soil Water Conserv. 1987, 3, 155–160. [Google Scholar]
- Duan, X.; Shi, X.; Li, Y.; Rong, L.; Fen, D. A new method to calculate soil loss tolerance for sustainable soil productivity in farmland. Agron. Sustain. Dev. 2017, 37, 2. [Google Scholar] [CrossRef]
- Buol, S.W.; Hole, F.D.; McCracken, R.J. Soil Genesis and Classification; The Jowa State University Press: Ames, IA, USA, 1973. [Google Scholar]
- Lisetskii, F.N. Evaluation of rate of reproduction of soil resources. Sov. Agric. Sci. 1987, 6, 22–25. [Google Scholar]
- Matsumoto, S.; Ogata, S.; Shimada, H.; Sasaoka, T.; Hamanaka, A.; Kusuma, G.J. Effects of pH-induced changes in soil physical characteristics on the development of soil water erosion. Geosciences (Switz.) 2018, 8, 134. [Google Scholar] [CrossRef]
- Zaimes, G.N.; Ioannou, K.; Iakovoglou, V.; Kosmadakis, I.; Koutalakis, P.; Ranis, G.; Emmanouloudis, D.; Schultz, R.C. Improving soil erosion prevention in Greece with new tools. J. Eng. Sci. Technol. Rev. 2016, 9, 66–71. [Google Scholar] [CrossRef]
- Jenny, H. Factors of Soil Formation: A System of Quantitative Pedology; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Kolmogorov, А.N. Confidence limits for an unknown distribution function. AMS 1941, 12, 461–463. [Google Scholar] [CrossRef]
- Olson, K.R.; Ebelhar, S.A.; Lang, J.M. Effects of 24 years of conservation tillage systems on soil organic carbon and soil productivity. Appl. Environ. Soil Sci. 2013, 2013, 617504. [Google Scholar] [CrossRef]
- Lisetskii, F.N. Soil reproduction in steppe ecosystems of different ages. Contemp. Probl. Ecol. 2012, 5, 580–588. [Google Scholar] [CrossRef]
- Goleusov, P.V. Attractors of humus horizon formation in chernozems. Adv. Curr. Nat. Sci. 2016, 11, 106–110. [Google Scholar]
- Goleusov, P.V.; Lisetskii, F.N.; Chepelev, O.A.; Prisniy, A.V. The rate of soil formation in regenerative ecosystems with various combinations of substratum and vegetation conditions. Int. J. Appl. Eng. Res. 2015, 24, 45413–45416. [Google Scholar]
- Lisetskii, F.N.; Stolba, V.F.; Ergina, E.I.; Rodionova, M.E.; Terekhin, E.A. Post-agrogenic evolution of soils in ancient Greek land use areas in the Herakleian Peninsula, southwestern Crimea. Holocene 2013, 23, 504–514. [Google Scholar] [CrossRef]
- Lisetskii, F.N.; Pavlyuk, Y.V.; Kirilenko, Z.A.; Pichura, V.I. Basin organization of nature management for solving hydroecological problems. Russ. Meteorol. Hydrol. 2014, 39, 550–557. [Google Scholar] [CrossRef]
- Amran, M.A. Mapping seagrass condition using google earth imagery. J. Eng. Sci. Technol. Rev. 2017, 10, 18–23. [Google Scholar] [CrossRef]
- Bazilevich, N.I.; Titlyanova, A.A. International Biological Programme 19; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Shvebs, H.I. Formation Water Erosion, Sediment Runoff and Their Evaluation; Hydrometeoyzdat: Leningrad, Russia, 1974. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; USDA Agriculture Handbook No 537; U.S. Department of Agriculture: Washington, DC, USA, 1978.
- Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 1478, 337–341. [Google Scholar] [CrossRef]
- Kalinitchenko, V.P. Soil dynamics management. Biogeosyst. Tech. 2016, 4, 284–316. [Google Scholar] [CrossRef]
- Fridland, V.M. Chernozems USSR (Ukraine); Kolos: Moscow, Russia, 1981. [Google Scholar]
- Shtompel, Y.A.; Lisetskii, F.N.; Sukhanovskii, Y.P.; Strelnikova, A.V. Soil loss tolerance of brown forest soils of northwestern Caucasus under intensive agriculture. Eur. Soil Sci. 1998, 31, 185–190. [Google Scholar]
- Kalinitchenko, V.P. Status of the Earth’s geochemical cycle in the standard technologies and waste recycling, and the possibilities of its correction by biogeosystem technique method (problem-analytical review). Biogeosyst. Tech. 2016, 2, 115–144. [Google Scholar] [CrossRef]
- Batukaev, A.; Kalinitchenko, V.; Glinushkin, A.; Sokolov, M.; Minkina, T.; Andreev, A.; Zinchenko, V.; Mandzhieva, S.; Sushkova, S.; Il’ina, L.; et al. Carbon and heavy metal turnover in a kastanozem complex of South Russia dry steppe. In Geophysical Research Abstracts. 2019 EGU General Assembly; EGU2019-6022; EGU: Göttingen, Germany, 2019; Volume 21. [Google Scholar]

| Approaches and Methods for Determining T-values | Formulas | Author |
|---|---|---|
| 1. Identification of T-values with the rate of natural and/or anthropogenic soil formation, or as a direct function of these values. | ||
| The tolerable value of soil wash-out is equal to the estimate in the process of natural soil formation of the average annual increase in humus horizons, expressed in fractions of a centimetre (or millimetre) per year. | , where VS is the maximum permissible value of soil erosion (mm year−1) and t is the number of years required to form a humus layer with a thickness of H mm | Dolgilevich [2] |
| 2. Value of sediment yield, which does not lead to a significant reduction in crop yields. | ||
| The formula for the most "acceptable" values of the decrease in the thickness of the soil. | , where D is the intensity of soil erosion losses (t ha−1 year−1) and PS is the soil thickness (m) which is formed due to the processes of weathering and soil formation. | Kirkby [3] |
| 3. Approaches in which the estimates of the rate of soil formation are included in the calculation methods for determining the T-values. | ||
| The equation for defining the tolerable soil degradation at the point (x, y) at initial time (t). | where T1 is the soil renewal rate (mm year−1); T2 is the upper limit of allowable soil loss rate (mm year−1); Z is the present soil depth (m); Z1 is the minimum allowable soil depth; Z2 is the optimum soil depth; and π = 3.14 when calculating in radians (or from 0 to 180° for values in degrees). | Skidmore [4] |
| Erosion tolerance level. | 10⋅T-values⋅γ⋅C0−10) − C⋅V ≈ 0, where H is the thickness of the humus horizon (mm); C is the reserve of humus (Corg) in it (t ha−1); V is the rate of soil formation (mm year−1); T-values is the soil loss tolerance (mm year−1); ΔCar is the input component of the process of humus formation due to plant residues and fertilizers (t ha−1); is the mineralization of humus, which depends on the structure of crop rotation and yield level (t ha−1); is the mineralization of passive humus (t ha−1); C0−10 is the humus reserve in the washable layer (%); and γ is the bulk density in the washable soil layer (t m−3). | Shvebs [5]; Lisetskii et al. [6] |
| Calculation of the indicator for the lifespan of a soil. | where LF is the soil lifespan (years); DE is the depth of available productive soil (cm); DO is the minimum soil depth for a particular crop (cm); γ is the bulk mass of the soil (t m−3); ZF is the estimated rate of soil formation (t ha−1 year−1); and Z is the predicted rate of soil loss (t ha−1 year−1). | Elwell and Stocking [7] (with modifications) |
| Indicator of the potential duration of the expenditure of soil with a constant average annual soil loss rate. | where Hin is the initial (actual) thickness of the humus horizon (mm); Hw is the weighted average value of the optimum thickness of the humus horizon, taking into account the composition of crops in the crop rotation (mm); γ is the bulk density of the soil (t m−3); and VE and Vf are the average perennial (or justified in the proportional availability) rates of erosion and soil formation, respectively (t ha−1). | Lisetskii et al. [8] |
| Polygons | I | II | ||
|---|---|---|---|---|
| Regions | West | East | South | SCC |
| T year (°C) | 9.8–11.0 | 10.4–11.0 | 10.3 | 10–12 |
| Σ T > 10° | 3335–3400 | 3340–3460 | 3160 | 3655 |
| Precipitation (mm) | 355 | 225–375 | 450 | 430 |
| Total evaporation (mm) | 744 | 760 | 855 | 925 |
| Q, (MJ m−2 year−1) | 1062 | 1155 | 1195 | 1380 |
| Basic soils | Calcic Chernozem, Petrocalcic Chernozem, Rendzic Leptosol | Luvic Chernozem | Calcic Chernozem | Calcaric Cambisols |
| Archaeological Site a | Soil Age (years) | Parent Material a | Horizon, Levels (mm) | Munsell Colour (dry) | CаCО3 (%) | pH H2О | Corg (%) | ΔC (% year−1), n∙10 | ΔH (mm year−1) |
|---|---|---|---|---|---|---|---|---|---|
| Kutlak | 25 | L | AC, 0–29 | 10YR 5/3.5 | 4.6 | 7.9 | 3.96 | 1.58 | 1.17 |
| Kharaks | 30 | CaG | AC, 0–77 | 10YR 5/3 | 26.2 | 8.2 | 13.86 | 3.75 | 2.57 |
| Ayu-Dag | 42 | L | AC, 0–25 | 10YR 5/3.5 | – | 7.3 | 3.48 | 0.83 | 0.60 |
| Bol’shoi Lambat | 87 | CaG | AC, 0–50 | 10YR 4/2 | 14.4 | 6.8 | 7.13 | 0.82 | 0.84 |
| AC, 50–73 | 10YR 4/2.5 | 14.8 | 7.5 | 5.87 | 0.67 | ||||
| Ayu-Dag | 100 | L | AC, 0–30 | 10YR 5/3 | 2.5 | 7.2 | 4.11 | 0.41 | 0.51 |
| AC, 30–50 | 10YR 5/3.5 | 2.2 | 7.4 | 3.16 | 0.32 | ||||
| Kharakskii park | 107 | CaG | AC, 0–40 | 10YR 5/3 | 22.5 | 8.4 | 14.74 | 1.58 | 0.79 |
| AC, 40–85 | 10YR 5/5 | 3.8 | 8.7 | 2.87 | 0.31 | ||||
| Ayu-Dag | 316 | L | AC, 0–66 | 10YR 5/4 | 3.4 | 6.3 | 6.35 | 0.18 | 0.41 |
| AC, 66–145 | 10YR 6/3 | 2.5 | 6.1 | 5.51 | 0.16 | ||||
| 316 | CaG | AC, 0–83 | 10YR 6/2.5 | 1.5 | 4.8 | 6.93 | 0.25 | 0.30 | |
| Bol’shoi Lambat | 560 | WC | AU, 0–64 | 10YR 4/2 | 2.8 | 5.9 | 2.35 | 0.04 | 0.33 |
| BCA, 64–185 | 10YR 4/2.5 | 1.8 | 5.6 | 5.86 | 0.10 | ||||
| Isar Gelin-Kaya (Kizil-Tash) | 610 | CaG | AU, 0–188 | 10YR 4/2 | 17.5 | 8.1 | 7.57 | 0.12 | 0.44 |
| B, 0–270 | 10YR 5/3 | 26.6 | 8.3 | 14.36 | 0.24 | ||||
| Uchan-Su-Isar | 700 | WC | AU, 0–60 | 10YR 3/3 | 6.8 | 8.0 | 3.39 | 0.05 | 0.26 |
| AU, 60–182 | 10YR 4/3 | 6.8 | 8.0 | 7.27 | 0.10 | ||||
| 700 | WC | AU, 0–135 | 10YR 3/3 | 6.5 | 7.9 | 3.11 | 0.04 | 0.28 | |
| B, 135–196 | 10YR 4/3 | 6.8 | 7.9 | 7.38 | 0.11 | ||||
| Bol’shoi Lambat | 700 | CaG | AU, 0–46 | 10YR 4/2 | 4.0 | 7.2 | 6.58 | 0.12 | 0.18 |
| AU, 46–103 | 10YR 4/2 | 4.6 | 7.6 | 4.35 | 0.08 | ||||
| Alupka-Isar | 710 | CaG | AU, 0–160 | 10YR 4/2 | 3.8 | 8.3 | 3.12 | 0.04 | 0.32 |
| B, 160–229 | 10YR 6/2 | 12.0 | 8.3 | 8.12 | 0.11 | ||||
| Oreanda-Isar | 717 | CaG | AU, 0–124 | 10YR 3/2 | 10.4 | 7.2 | 7.86 | 0.11 | 0.27 |
| AU, 124–190 | 10YR 4/3 | 18.8 | 8.2 | 4.94 | 0.07 | ||||
| Oreanda-Isar | 717 | WC | AU, 0–180 | 10YR 4/2.5 | 19.1 | 8.0 | 3.90 | 0.05 | 0.25 |
| Kharaks | 1700 | WC | AU, 0–130 | 5YR 3/2 | 4.2 | 7.8 | 2.29 | 0.01 | 0.11 |
| B, 130–183 | 5YR 3/4 | 2.5 | 8.2 | 2.09 | 0.01 | ||||
| Kharaks | 1700 | CaG | AU, 0–152 | 10YR 5/3 | 23.6 | 8.2 | 11.51 | 0.07 | 0.15 |
| AU, 152–260 | 10YR 5/4 | 24.4 | 8.2 | 14.38 | 0.08 | ||||
| B, 260–320 | 10YR 6/3 | 26.2 | 8.4 | 13.97 | 0.08 | ||||
| Bol’shoi Lambat | 1920 | L + [A] | AU, 0–25 | 10YR 4/1 | 3.7 | 6.3 | 8.64 | 0.05 | 0.13 |
| AU, 25–120 | 10YR 5/1.5 | 2.8 | 7.0 | 4.56 | 0.02 | ||||
| B, 120–254 | 10YR 5/1.5 | 3.1 | 7.5 | 2.20 | 0.01 | ||||
| Protected soil (Cape Маrtjan) | >10000 | CaG | AU, 0–60 | 5YR 3/1.5 | 4.8 | 8.0 | 4.35 | 0.004 | – |
| AU, 60–200 | 5YR 4/4 | 2.5 | 7.4 | 2.03 | 0.002 |
| Degree of Erosion Degradation | Chernozems | Cambisols |
|---|---|---|
| Low | 1.26 | 1.86 |
| Average | 2.03 | 1.47 |
| Strong | 4.50 | 4.69 |
| Equilibrium bulk density is 1.25 t m−3. | ||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisetskii, F. Estimates of Soil Renewal Rates: Applications for Anti-Erosion Arrangement of the Agricultural Landscape. Geosciences 2019, 9, 266. https://doi.org/10.3390/geosciences9060266
Lisetskii F. Estimates of Soil Renewal Rates: Applications for Anti-Erosion Arrangement of the Agricultural Landscape. Geosciences. 2019; 9(6):266. https://doi.org/10.3390/geosciences9060266
Chicago/Turabian StyleLisetskii, Fedor. 2019. "Estimates of Soil Renewal Rates: Applications for Anti-Erosion Arrangement of the Agricultural Landscape" Geosciences 9, no. 6: 266. https://doi.org/10.3390/geosciences9060266
APA StyleLisetskii, F. (2019). Estimates of Soil Renewal Rates: Applications for Anti-Erosion Arrangement of the Agricultural Landscape. Geosciences, 9(6), 266. https://doi.org/10.3390/geosciences9060266





