Numerical Simulation of Deformation Band Occurrence and the Associated Stress Field during the Growth of a Fault-Propagation Fold
Abstract
1. Introduction
2. Methods
2.1. Numerical Method
2.2. Model Details
3. Results
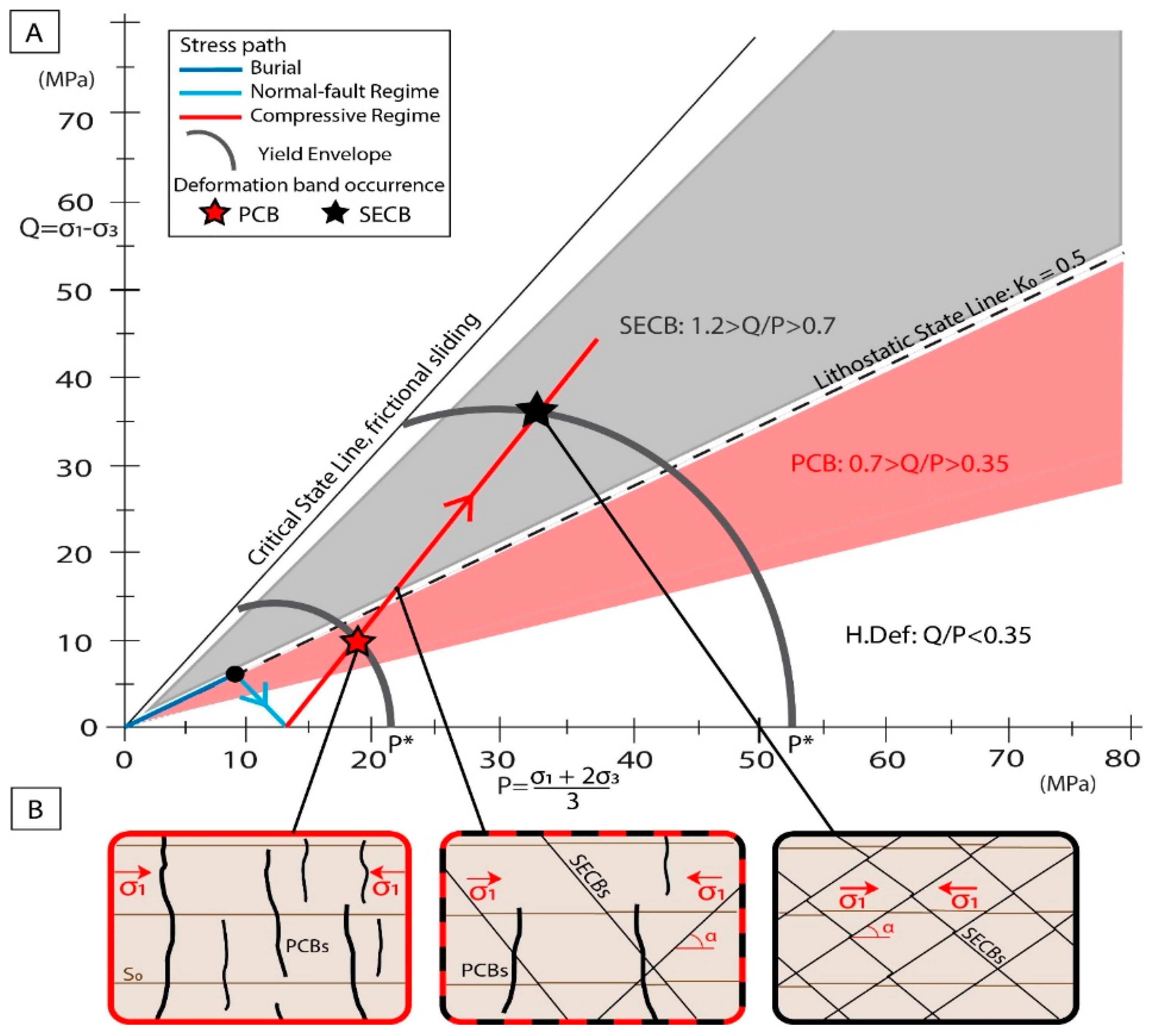
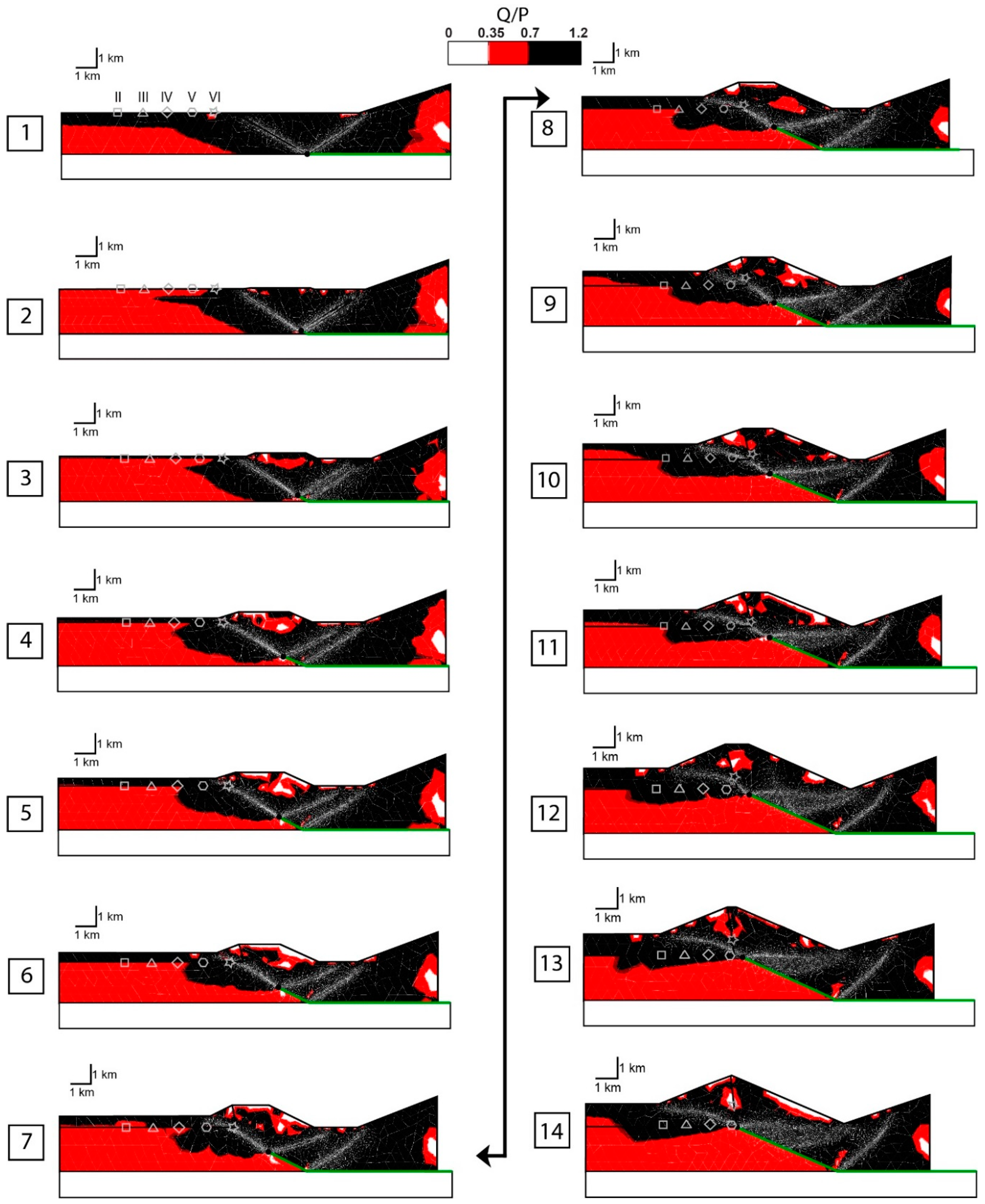
3.1. Q/P Ratios Distribution and Stress Path
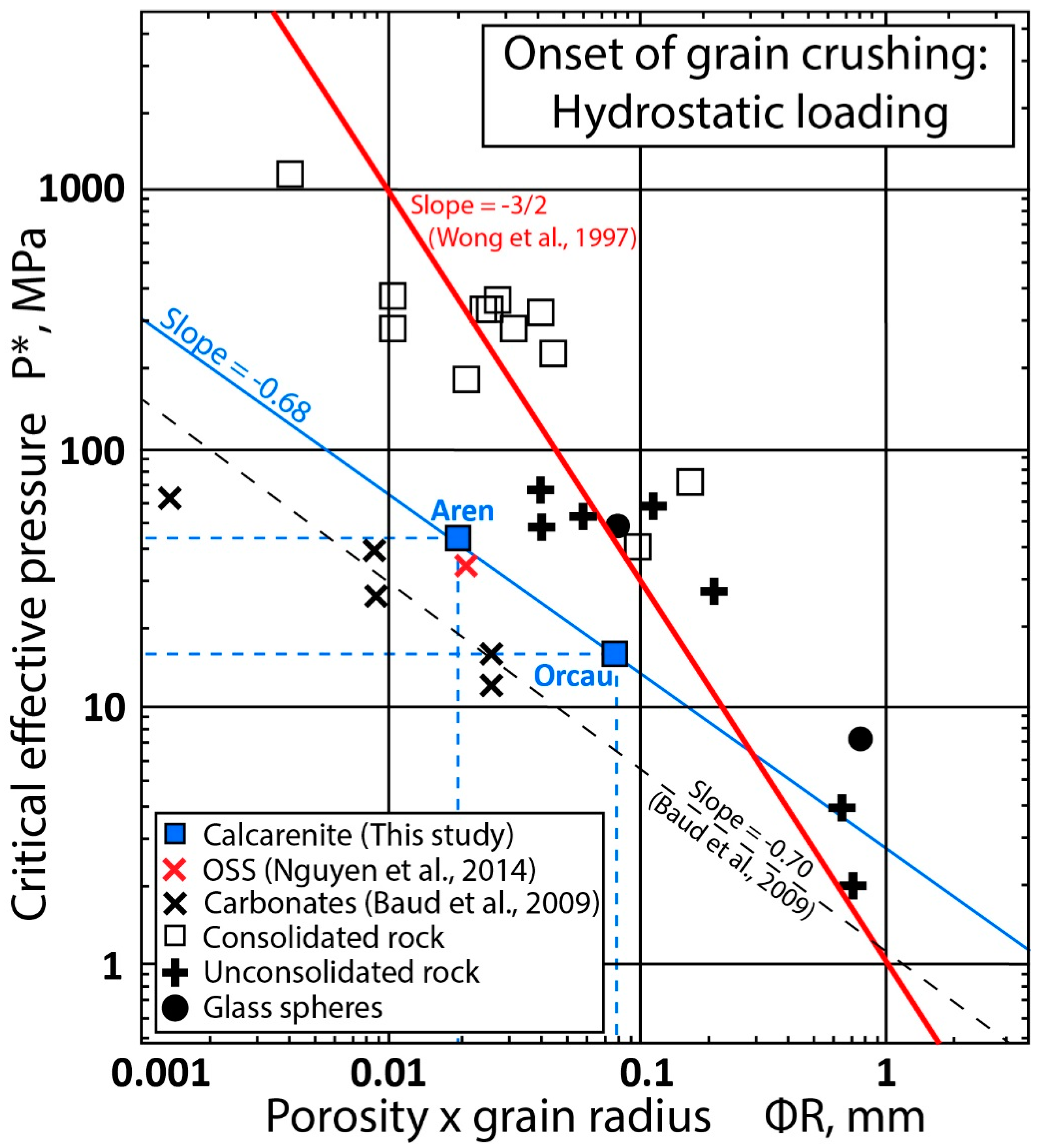
3.2. Failure Envelopes
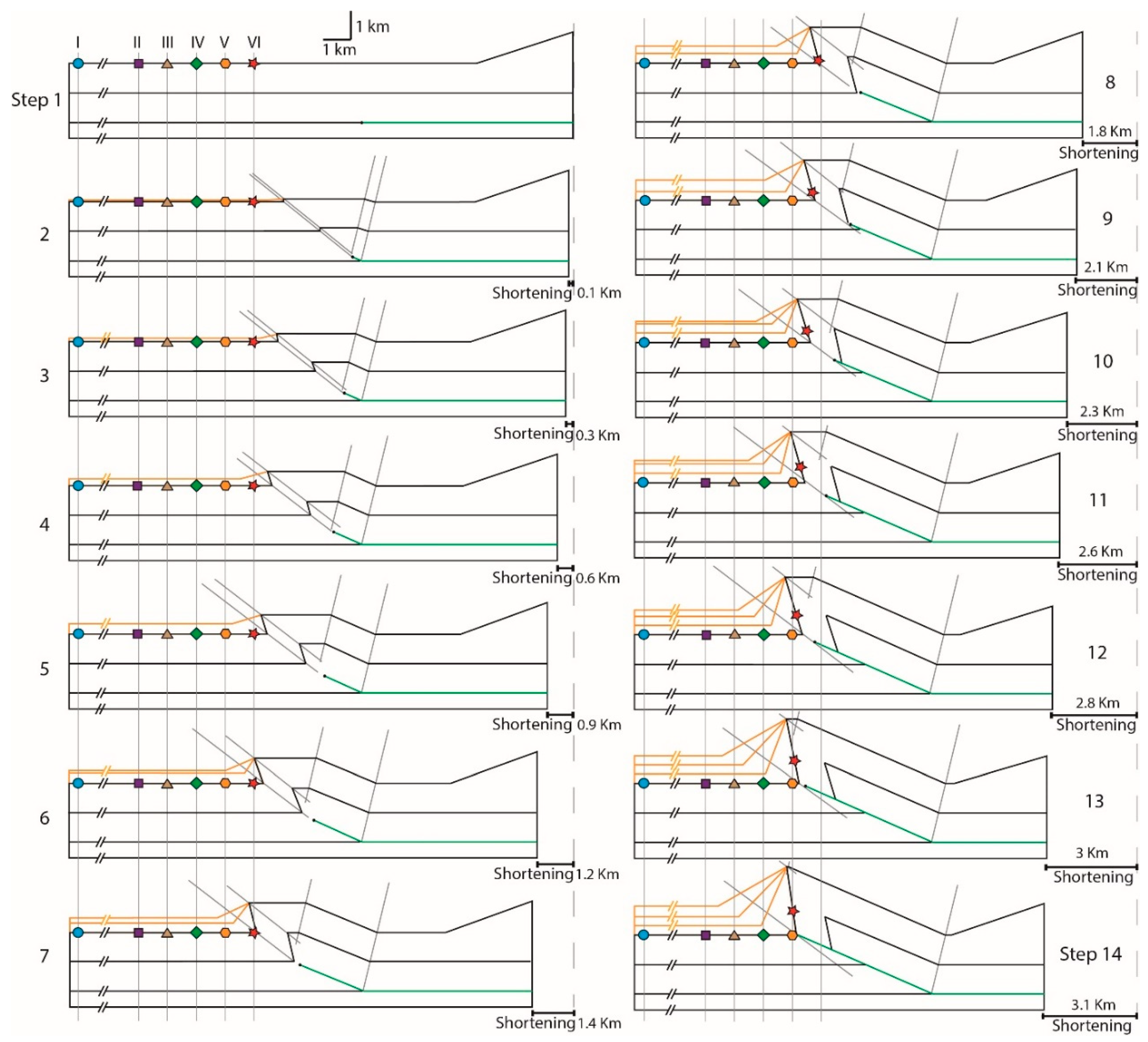
3.3. Band Timing and Distribution
4. Discussion
4.1. Chronology of Band Occurrence
4.2. Deformation Band Occurrence in Heterogeneous Granular Materials
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fossen, H.; Schultz, R.A.; Shipton, Z.K.; Mair, K. Deformation bands in sandstone: A review. J. Geol. Soc. Lond. 2007, 164, 755–769. [Google Scholar] [CrossRef]
- Ballas, G.; Soliva, R.; Sizun, J.-P.; Benedicto, A.; Cavailhes, T.; Raynaud, S.; Cycle, A.N. The importance of the degree of cataclasis in shear bands for fluid flow in porous sandstone, Provence, France. Am. Assoc. Pet. Geol. Bull. 2012, 96, 2167–2186. [Google Scholar] [CrossRef]
- Antonellini, M.A.; Aydin, A.; Pollard, D.D. Microstructure of deformation bands in porous sandstones at Arches National Park, Utah. J. Struct. Geol. 1994, 16, 941–959. [Google Scholar] [CrossRef]
- Schultz, R.A.; Siddharthan, R. A general framework for the occurence and faulting of deformation bands in porous granular rocks. Tectonophysics 2005, 411, 1–18. [Google Scholar] [CrossRef]
- Aydin, A.; Borja, R.I.; Eichhubl, P. Geological and mathematical framework for failure modes in granular rocks. J. Struct. Geol. 2006, 28, 83–98. [Google Scholar] [CrossRef]
- Wibberley, C.A.J.; Petit, J.-P.; Rives, T. The mechanics of fault distribution and localization in high-porosity sands, provence, France. Relatsh. between damage localization. Geol. Soc. Lond. Spec. Publ. 2007, 164, 599–608. [Google Scholar] [CrossRef]
- Eichhubl, P.; Hooker, J.N.; Laubach, S.E. Pure and shear-enhanced compaction bands in Aztec Sandstone. J. Struct. Geol. 2010, 32, 1873–1886. [Google Scholar] [CrossRef]
- Fossen, H. Deformation bands formed during soft-sediment deformation: Observations from SE Utah. Mar. Pet. Geol. 2010, 27, 215–222. [Google Scholar] [CrossRef]
- Saillet, E.; Wibberley, C.A.J. Evolution of cataclastic faulting in high-porosity sandstone, bassin du Sud-Est, Provence, France. J. Struct. Geol. 2010, 32, 1590–1608. [Google Scholar] [CrossRef]
- Schultz, R.A.; Okubo, C.H.; Fossen, H. Porosity and grain size controls on compaction band formation in Jurassic Navajo Sandstone. Geophys. Res. Lett. 2010, 37, L22306. [Google Scholar] [CrossRef]
- Ballas, G.; Soliva, R.; Sizun, J.-P.; Fossen, H.; Benedicto, A.; Skurtveit, E. Shear-enhanced compaction bands formed at shallow burial conditions; implications for fluid flow (Provence, France). J. Struct. Geol. 2013, 47, 3–15. [Google Scholar] [CrossRef]
- Soliva, R.; Schultz, R.A.; Ballas, G.; Taboada, A.; Wibberley, C.; Saillet, E.; Benedicto, A. A model of strain localization in porous sandstone as a function of tectonic setting, burial and material properties; new insight from Provence (southern France). J. Struct. Geol. 2013, 49, 50–63. [Google Scholar] [CrossRef]
- Zhang, J.; Wong, T.-F.; Davis, D.M. Micromechanics of pressure-induced grain crushing in porous rocks. J. Geophys. Res. 1990, 95, 341. [Google Scholar] [CrossRef]
- Wong, T.; David, C.; Zhu, W. The transition from brittle faulting to cataclastic flow in porous sandstones: Mechanical deformation. J. Geophys. Res. Solid Earth 1997, 102, 3009–3025. [Google Scholar] [CrossRef]
- Fossen, H.; Soliva, R.; Ballas, G.; Trzaskos, B.; Cavalcante, C.; Schultz, R.A. A review of deformation bands in reservoir sandstones: Geometries, mechanisms and distribution. Geol. Soc. Lond. Spec. Publ. 2018, 459, 9–33. [Google Scholar] [CrossRef]
- Ballas, G.; Soliva, R.; Benedicto, A.; Sizun, J.-P. Control of tectonic setting and large-scale faults on the basin-scale distribution of deformation bands in porous sandstone (Provence, France). Mar. Pet. Geol. 2014, 55, 142–159. [Google Scholar] [CrossRef]
- Baud, P.; Zhu, W.; Wong, T. Failure mode and weakening effect of water on sandstone. J. Geophys. Res. 2000, 105, 16371–16389. [Google Scholar] [CrossRef]
- Baud, P.; Klein, E.; Wong, T. Compaction localization in porous sandstones: Spatial evolution of damage and acoustic emission activity. J. Struct. Geol. 2004, 26, 603–624. [Google Scholar] [CrossRef]
- Baud, P.; Vajdova, V.; Wong, T. Shear-enhanced compaction and strain localization: Inelastic deformation and constitutive modeling of four porous sandstones. J. Geophys. Res. Solid Earth 2006, 111, B12401. [Google Scholar] [CrossRef]
- Klein, E.; Reuschlé, T. A pore crack model for the mechanical behaviour of porous granular rocks in the brittle deformation regime. Int. J. Rock Mech. Min. Sci. 2004, 41, 975–986. [Google Scholar] [CrossRef]
- Tembe, S.; Baud, P.; Wong, T. Stress conditions for the propagation of discrete compaction bands in porous sandstone. J. Geophys. Res. 2008, 113, B09409. [Google Scholar] [CrossRef]
- Rutter, E.H.; Glover, C.T. The deformation of porous sandstones; are Byerlee friction and the critical state line equivalent? J. Struct. Geol. 2012, 44, 129–140. [Google Scholar] [CrossRef]
- Philit, S. Elaboration of a Structural, Petrophysical and Mechanical Model of Faults in Porous Sandstones; Implication for Migration and Fluid Entrapment. Ph.D. Thesis, Université de Montpellier, Montpellier, France, 2017. [Google Scholar]
- Robert, R.; Robion, P.; Souloumiac, P.; David, C.; Saillet, E. Deformation bands, early markers of tectonic activity in front of a fold-and-thrust belt: Example from the Tremp-Graus basin, southern Pyrenees, Spain. J. Struct. Geol. 2018, 110, 65–85. [Google Scholar] [CrossRef]
- Heynekamp, M.R.; Goodwin, L.B.; Mozley, P.S.; Haneberg, W.C. Controls on fault-zone architecture in poorly lithified sediments, Rio Grande Rift, New Mexico: Implications for fault-zone permeability and fluid flow. In Faults and Subsurface Fluid Flow in the Shallow Crust; Haneberg, W.C., Mozley, P.S., Moore, J.C., Goodwin, L.B., Eds.; Washington DC American Geophysical Union Geophysical Monograph Series: Washington, DC, USA, 1999; pp. 27–49. [Google Scholar]
- Cashman, S.; Cashman, K. Cataclasis and deformation-band formation in unconsolidated marine terrace sand, Humboldt County, California. Geology 2000, 28, 111–114. [Google Scholar] [CrossRef]
- Bense, V.F.; Van den Berg, E.H.; Van Balen, R.T. Deformation mechanisms and hydraulic properties of fault zones in unconsolidated sediments; the Roer Valley Rift System, The Netherlands. Hydrogeol. J. 2003, 11, 319–332. [Google Scholar] [CrossRef]
- Rawling, G.C.; Goodwin, L.B. Cataclasis and particulate flow in faulted, poorly lithified sediments. J. Struct. Geol. 2003, 25, 317–331. [Google Scholar] [CrossRef]
- Balsamo, F.; Storti, F. Grain size and permeability evolution of soft-sediment extensional sub-seismic and seismic fault zones in high-porosity sediments from the Crotone basin, southern Apennines, Italy. Mar. Pet. Geol. 2010, 27, 822–837. [Google Scholar] [CrossRef]
- Beke, B.; Fodor, L.; Millar, L.; Petrik, A. Deformation band formation as a function of progressive burial: Depth calibration and mechanism change in the Pannonian Basin (Hungary). Mar. Pet. Geol. 2019, 105, 1–16. [Google Scholar] [CrossRef]
- Puigdefàbregas, C.; Souquet, P. Tecto-sedimentary cycles and depositional sequences of the Mesozoic and Tertiary from the Pyrenees. Tectonophysics 1986, 129, 173–203. [Google Scholar] [CrossRef]
- Berastegui, X.; Garcia-Senz, J.M.; Losantos, M. Tecto-sedimentary evolution of the Organya extensional basin (central south Pyrenean unit, Spain) during the Lower Cretaceous. Bull. Soc. Géol. Fr. 1990, 6, 251–264. [Google Scholar] [CrossRef]
- Puigdefàbregas, C.; Muñoz, J.A.; Vergés, J. Thrusting and foreland basin evolution in the Southern Pyrenees. In Thrust Tectonics; Springer: Dordrecht, The Netherlands, 1992; pp. 247–254. [Google Scholar]
- Bond, R.M.G.; McClay, K.R. Inversion of a Lower Cretaceous extensional basin, south central Pyrenees, Spain. Geol. Soc. Lond. Spec. Publ. 1995, 88, 415–431. [Google Scholar] [CrossRef]
- Garcia-Senz, J.M. Cuencas Extensivas del Cretácico Inferior en Los Pirineos Centrales, Formación y Subsecuente Inversión; Universitat de Barcelona: Barcelona, Spain, 2002. [Google Scholar]
- Muñoz, J.A. Evolution of a continental collision belt: ECORS-Pyrenees crustal balanced cross-section. In Thrust Tectonics; Springer: Dordrecht, The Netherlands, 1992; pp. 235–246. [Google Scholar]
- Deramond, J.; Souquet, P.; Fondecave-Wallez, M.-J.; Specht, M. Relationships between thrust tectonics and sequence stratigraphy surfaces in foredeeps: Model and examples from the Pyrenees (Cretaceous-Eocene, France, Spain). Geol. Soc. Lond. Spec. Publ. 1993, 71, 193–219. [Google Scholar] [CrossRef]
- Vergés, J. Studi Geològic del Vessant Sud del Pirineu Oriental i Central. Evolució Cinemàtica en 3D. Ph.D. Thesis, Universitet de Barcelona, Barcelona, Spain, 1993. [Google Scholar]
- Vergés, J.; Fernàndez, M.; Martìnez, A. The Pyrenean orogen: Pre-, syn-, and post-collisional evolution. J. Virtual Explor. 2002, 8, 55–74. [Google Scholar]
- Shackleton, J.R.; Cooke, M.L.; Vergés, J.; Simó, T. Temporal constraints on fracturing associated with fault-related folding at Sant Corneli anticline, Spanish Pyrenees. J. Struct. Geol. 2011, 33, 5–19. [Google Scholar] [CrossRef]
- Erickson, G.S.; Jamison, W.R. Viscous-plastic finite-element models of fault-bend folds. J. Struct. Geol. 1995, 17, 561–573. [Google Scholar] [CrossRef]
- Erickson, S.G.; Strayer, L.M.; Suppe, J. Initiation and reactivation of faults during movement over a thrust-fault ramp: Numerical mechanical models. J. Struct. Geol. 2001, 23, 11–23. [Google Scholar] [CrossRef]
- Cooke, M.L.; Mollema, P.N.; Pollard, D.D.; Aydin, A. Interlayer slip and joint localization in the East Kaibab Monocline, Utah: Field evidence and results from numerical modelling. Geol. Soc. Lond. Spec. Publ. 1999, 169, 23–49. [Google Scholar] [CrossRef]
- Guiton, M.L.E.; Sassi, W.; Leroy, Y.M.; Gauthier, B.D.M. Mechanical constraints on the chronology of fracture activation in folded Devonian sandstone of the western Moroccan Anti-Atlas. J. Struct. Geol. 2003, 25, 1317–1330. [Google Scholar] [CrossRef]
- Casey, M.; Butler, R.W. Modelling approaches to understanding fold development: Implications for hydrocarbon reservoirs. Mar. Pet. Geol. 2004, 21, 933–946. [Google Scholar] [CrossRef]
- Reber, J.E.; Schmalholz, S.M.; Burg, J.-P. Stress orientation and fracturing during three-dimensional buckling: Numerical simulation and application to chocolate-tablet structures in folded turbidites, SW Portugal. Tectonophysics 2010, 493, 187–195. [Google Scholar] [CrossRef]
- Frehner, M. The neutral lines in buckle folds. J. Struct. Geol. 2011, 33, 1501–1508. [Google Scholar] [CrossRef]
- Sassi, W.; Guiton, M.L.E.; Leroy, Y.M.; Daniel, J.M.; Callot, J.P. Constraints on bed scale fracture chronology with a FEM mechanical model of folding: The case of Split Mountain (Utah, USA). Tectonophysics 2012, 576–577, 197–215. [Google Scholar] [CrossRef]
- Liu, X.; Eckert, A.; Connolly, P. Stress evolution during 3D single-layer visco-elastic buckle folding: Implications for the initiation of fractures. Tectonophysics 2016, 679, 140–155. [Google Scholar] [CrossRef]
- Peace, A.L.; Dempsey, E.; Schiffer, C.; Welford, J.; McCaffrey, K.J.W.; Imber, J.; Phethean, J.J.J. Evidence for basement reactivation during the Province, Labrador, Canada: Insights from field data. Geosciences 2018, 8, 308. [Google Scholar] [CrossRef]
- Sanz, P.F.; Pollard, D.D.; Allwardt, P.F.; Borja, R.I. Mechanical models of fracture reactivation and slip on bedding surfaces during folding of the asymmetric anticline at Sheep Mountain, Wyoming. J. Struct. Geol. 2008, 30, 1177–1191. [Google Scholar] [CrossRef]
- Albertz, M.; Lingrey, S. Critical state finite element models of contractional fault-related folding: Part 1. Structural analysis. Tectonophysics 2012, 576–577, 133–149. [Google Scholar] [CrossRef]
- Smart, K.J.; Ferrill, D.A.; Morris, A.P.; McGinnis, R.N. Geomechanical modeling of stress and strain evolution during contractional fault-related folding. Tectonophysics 2012, 576, 171–196. [Google Scholar] [CrossRef]
- Albertz, M.; Sanz, P.F. Critical state finite element models of contractional fault-related folding: Part 2. Mechanical analysis. Tectonophysics 2012, 576, 150–170. [Google Scholar] [CrossRef]
- Maillot, B.; Leroy, Y.M. Kink-fold onset and development based on the maximum strength theorem. J. Mech. Phys. Solids 2006, 54, 2030–2059. [Google Scholar] [CrossRef]
- Cubas, N.; Leroy, Y.M.; Maillot, B. Prediction of thrusting sequences in accretionary wedges. J. Geophys. Res. 2008, 113, B12412. [Google Scholar] [CrossRef]
- Souloumiac, P.; Leroy, Y.M.; Maillot, B.; Krabbenhøft, K. Predicting stress distributions in fold-and-thrust belts and accretionary wedges by optimization. J. Geophys. Res. 2009, 114, B09404. [Google Scholar] [CrossRef]
- Mary, B. Au delà du Prisme Critique de Coulomb par L’analyse Séquentielle et Contributions Expérimentales. Ph.D. Thesis, Université de Cergy-Pontoise, Cergy, France, 2012. [Google Scholar]
- Pons, A. Surpressions de Fuide et Stabilité des Prismes D’accrétion: Théorie et Validation Numérique et Expérimentale. Ph.D. Thesis, Université Paris Diderot, Paris, France, 2012. [Google Scholar]
- Caër, T. Interprétation Structurale et Équilibre Mécanique: Le Calcul à la Rupture Appliqué aux Chaînes D’avant-Pays. Ph.D. Thesis, Université de Cergy-Pontoise, Cergu, France, 2016. [Google Scholar]
- Yuan, X.P. Extensional Collapses in the Overpressured Frictional Upper Crust Based on Limit Analysis. Ph.D. Thesis, PSL Research University, Paris, France, 2016. [Google Scholar]
- Salençon, J. De L’élasto-Plasticité au Calcul à la Rupture; Editions Ecole Polytechnique: Paris, France, 2002. [Google Scholar]
- Souloumiac, P.; Krabbenhøft, K.; Leroy, Y.M.; Maillot, B. Failure in accretionary wedges with the maximum strength theorem: Numerical algorithm and 2D validation. Comput. Geosci. 2010, 14, 793–811. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Lyamin, A.V. Optum G2 (2014). Available online: https://optumce.com (accessed on 5 June 2019).
- Krabbenhøft, K.; Damkilde, L. A general non-linear optimization algorithm for lower bound limit analysis. Int. J. Numer. Methods Eng. 2003, 56, 165–184. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Lyamin, A.V.; Hjiaj, M.; Sloan, S.W. A new discontinuous upper bound limit analysis formulation. Int. J. Numer. Methods Eng. 2005, 63, 1069–1088. [Google Scholar] [CrossRef]
- Lyamin, A.V.; Sloan, S.W.; Krabbenhøft, K.; Hjiaj, M. Lower bound limit analysis with adaptive remeshing. Int. J. Numer. Methods Eng. 2005, 63, 1961–1974. [Google Scholar] [CrossRef]
- Suppe, B.J.; Medwedeff, D.A. Geometry and kinematics of fault-propagation folding. Eclogae Geol. Helv. 1990, 454, 409–454. [Google Scholar]
- Mencos, J.; Munoz, J.A.; Hardy, S. Three-Dimensional Geometry and Forward Numerical Modeling of the Sant Corneli Anticline (Southern Pyrenees, Spain). In Thrust Fault-Related Folding (AAPG Memoir); AAPG Special Publications: Tulsa, OK, USA, 2011; pp. 283–300. [Google Scholar]
- Mencos, J.; Carrera, N.; Muñoz, J.A. Influence of rift basin geometry on the subsequent postrift sedimentation and basin inversion: The Organyà Basin and the Bóixols thrust sheet (south central Pyrenees). Tectonics 2015, 34, 1452–1474. [Google Scholar] [CrossRef]
- Fillon, C.; Gautheron, C.; Van, P.; Beek, D. Oligocene-Miocene burial and exhumation of the Southern Pyrenean foreland quantified by low-temperature thermochronology. J. Geol. Soc. Lond. 2013, 107, 67–77. [Google Scholar] [CrossRef]
- Mollema, P.N.; Antonellini, M.A. Compaction bands: A structural analog for anti-mode I cracks in aeolian sandstone. Tectonophysics 1996, 267, 209–228. [Google Scholar] [CrossRef]
- Schultz, R.A. Scaling and paleodepth of compaction bands, Nevada and Utah. J. Geophys. Res. 2009, 114, B03407. [Google Scholar] [CrossRef]
- Fossen, H.; Schultz, R.A.; Torabi, A. Conditions and implications for compaction band formation in the Navajo Sandstone, Utah. J. Struct. Geol. 2011, 33, 1477–1490. [Google Scholar] [CrossRef]
- Fossen, H.; Zuluaga, L.F.; Ballas, G.; Soliva, R.; Rotevatn, A. Contractional deformation of porous sandstone: Insights from the Aztec Sandstone, SE Nevada, USA. J. Struct. Geol. 2015, 74, 172–184. [Google Scholar] [CrossRef]
- Baud, P.; Vinciguerra, S.; David, C.; Cavallo, A.; Walker, E.; Reuschlé, T. Compaction and failure in high porosity carbonates: Mechanical data and microstructural observations. Pure Appl. Geophys. 2009, 166, 869–898. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Gland, N.; Dautriat, J.; David, C.; Wassermann, J.; Guélard, J. Compaction, permeability evolution and stress path effects in unconsolidated sand and weakly consolidated sandstone. Int. J. Rock Mech. Min. Sci. 2014, 67, 226–239. [Google Scholar] [CrossRef]
- Tondi, E.; Antonellini, M.; Aydin, A.; Marchegiani, L.; Cello, G. The role of deformation bands, stylolites and sheared stylolites in fault development in carbonate grainstones of Majella Mountain, Italy. J. Struct. Geol. 2006, 28, 376–391. [Google Scholar] [CrossRef]
- Tondi, E.; Cilona, A.; Agosta, F.; Aydin, A.; Rustichelli, A.; Renda, P.; Giunta, G. Growth processes, dimensional parameters and scaling relationships of two conjugate sets of compactive shear bands in porous carbonate grainstones, Favignana Island, Italy. J. Struct. Geol. 2012, 37, 53–64. [Google Scholar] [CrossRef]
- Rustichelli, A.; Tondi, E.; Agosta, F.; Cilona, A.; Giorgioni, M. Development and distribution of bed-parallel compaction bands and pressure solution seams in carbonates (Bolognano Formation, Majella Mountain, Italy). J. Struct. Geol. 2012, 37, 181–199. [Google Scholar] [CrossRef]
- Cilona, A.; Baud, P.; Tondi, E.; Vinciguerra, S.; Rustichelli, A.; Spiers, C.J. Deformation bands in porous carbonate grainstones: Field and laboratory observations. J. Struct. Geol. 2012, 45, 137–157. [Google Scholar] [CrossRef]
- Cilona, A.; Faulkner, D.R.; Tondi, E.; Agosta, F.; Mancini, L.; Rustichelli, A.; Baud, P.; Vinciguerra, S. The effects of rock heterogeneity on compaction localization in porous carbonates. J. Struct. Geol. 2014, 67, 75–93. [Google Scholar] [CrossRef]
- Rotevatn, A.; Thorsheim, E.; Bastesen, E.; Fossmark, H.S.S.; Torabi, A.; Sælen, G. Sequential growth of deformation bands in carbonate grainstones in the hangingwall of an active growth fault: Implications for deformation mechanisms in different tectonic regimes. J. Struct. Geol. 2016, 90, 27–47. [Google Scholar] [CrossRef]
- Tavani, S.; Granado, P.; Balsamo, F.; Pizzati, M.; Cantarero, I.; Corradetti, A.; Muñoz, J.A. Shear-enhanced compaction-solution bands in quartz-rich calcarenites of the Cotiella Massif (Spanish Pyrenees). J. Struct. Geol. 2017, 114, 274–279. [Google Scholar] [CrossRef]
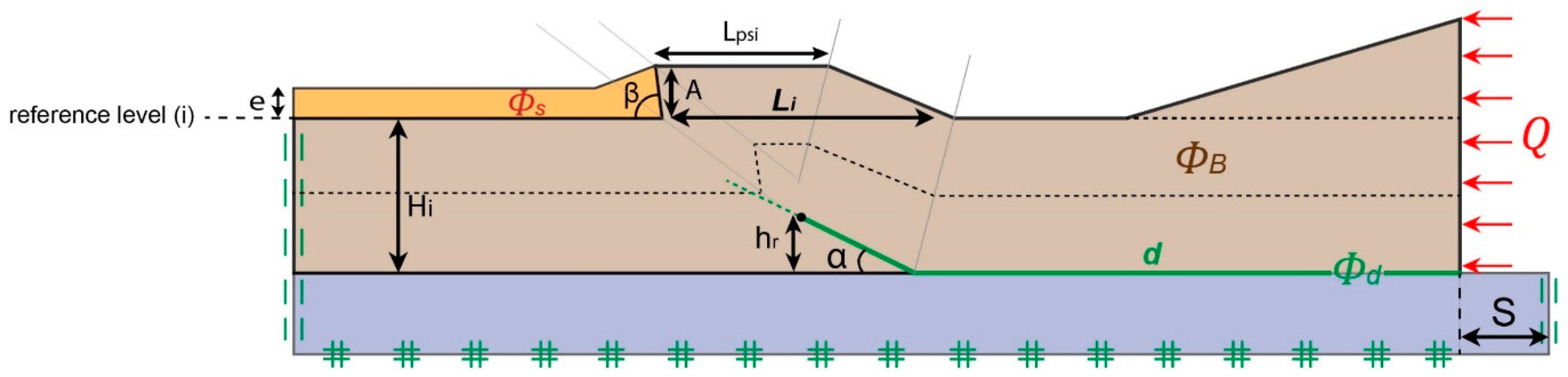

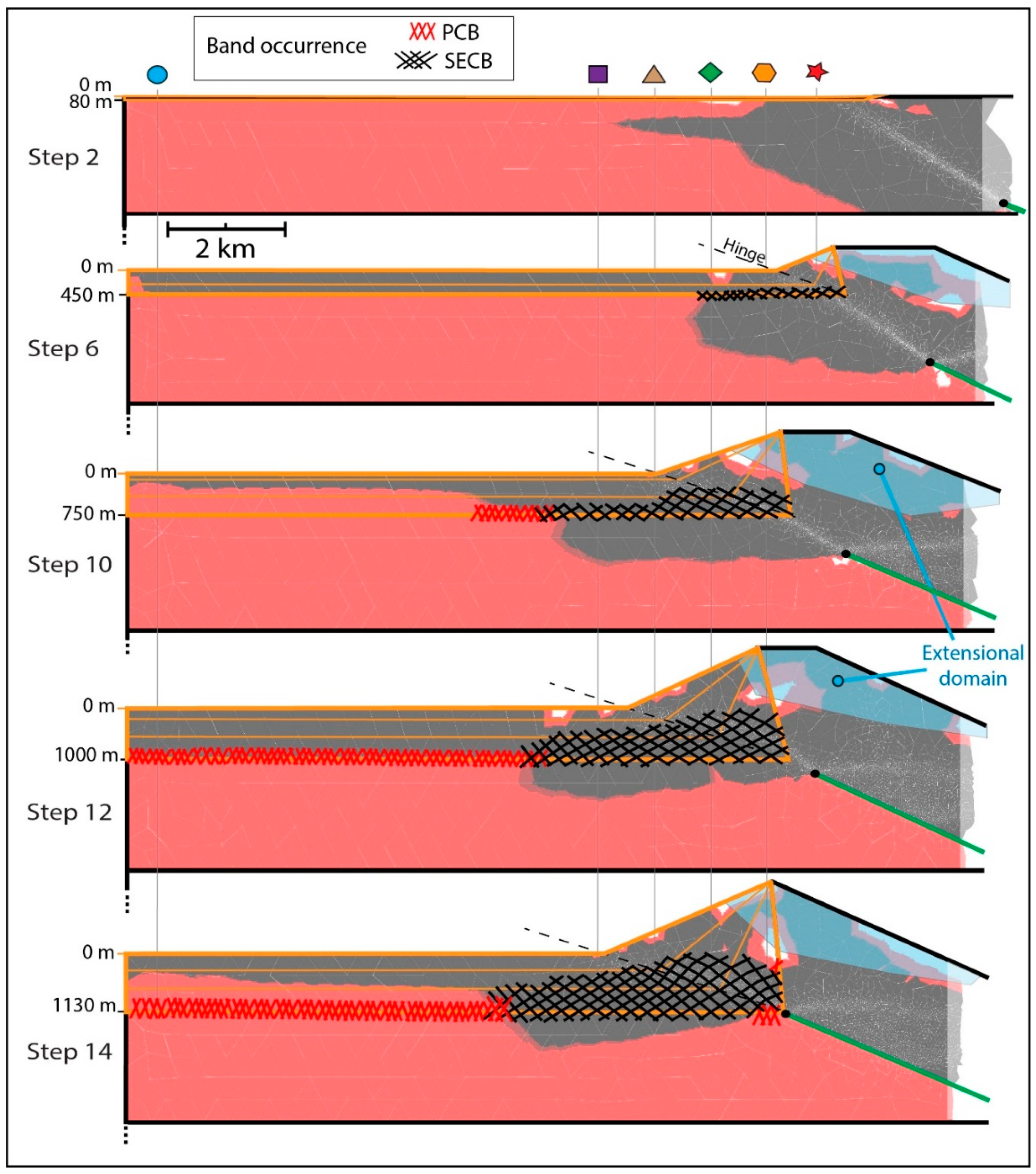
| Exp. | Hi (km) | Lpsi (km) | Li (km) | A (km) | hr (km) | α (°) | β (°) | S (km) | e (m) | φB (°) | φd (°) | φs (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 4 | 30 |
| Step 2 | 2 | 3.1 | 3.2 | 0.1 | 0.15 | 23 | 75 | 0.1 | 70 | 30 | 4 | 30 |
| Step 3 | 2 | 2.7 | 3.3 | 0.25 | 0.25 | 23 | 75 | 0.3 | 125 | 30 | 4 | 30 |
| Step 4 | 2 | 2.6 | 3.6 | 0.5 | 0.45 | 23 | 75 | 0.6 | 250 | 30 | 4 | 30 |
| Step 5 | 2 | 2.4 | 3.7 | 0.6 | 0.55 | 23 | 75 | 0.9 | 325 | 30 | 4 | 30 |
| Step 6 | 2 | 2.1 | 3.9 | 0.9 | 0.75 | 23 | 75 | 1.2 | 450 | 30 | 4 | 30 |
| Step 7 | 2 | 1.9 | 4.1 | 1 | 0.85 | 23 | 75 | 1.4 | 500 | 30 | 4 | 30 |
| Step 8 | 2 | 1.8 | 4.3 | 1.2 | 1.05 | 23 | 75 | 1.8 | 540 | 30 | 4 | 30 |
| Step 9 | 2 | 1.6 | 4.4 | 1.4 | 1.15 | 23 | 75 | 2.1 | 700 | 30 | 4 | 30 |
| Step 10 | 2 | 1.3 | 4.5 | 1.5 | 1.35 | 23 | 75 | 2.3 | 750 | 30 | 4 | 30 |
| Step 11 | 2 | 1.15 | 4.8 | 1.7 | 1.5 | 23 | 75 | 2.6 | 850 | 30 | 4 | 30 |
| Step 12 | 2 | 1 | 5 | 2 | 1.7 | 23 | 75 | 2.8 | 1000 | 30 | 4 | 30 |
| Step 13 | 2 | 0.5 | 5.1 | 2.2 | 1.9 | 23 | 80 | 3 | 1080 | 30 | 4 | 30 |
| Step 14 | 2 | 0 | 5.2 | 2.3 | 2 | 23 | 85 | 3.1 | 1130 | 30 | 4 | 30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robert, R.; Souloumiac, P.; Robion, P.; David, C. Numerical Simulation of Deformation Band Occurrence and the Associated Stress Field during the Growth of a Fault-Propagation Fold. Geosciences 2019, 9, 257. https://doi.org/10.3390/geosciences9060257
Robert R, Souloumiac P, Robion P, David C. Numerical Simulation of Deformation Band Occurrence and the Associated Stress Field during the Growth of a Fault-Propagation Fold. Geosciences. 2019; 9(6):257. https://doi.org/10.3390/geosciences9060257
Chicago/Turabian StyleRobert, Romain, Pauline Souloumiac, Philippe Robion, and Christian David. 2019. "Numerical Simulation of Deformation Band Occurrence and the Associated Stress Field during the Growth of a Fault-Propagation Fold" Geosciences 9, no. 6: 257. https://doi.org/10.3390/geosciences9060257
APA StyleRobert, R., Souloumiac, P., Robion, P., & David, C. (2019). Numerical Simulation of Deformation Band Occurrence and the Associated Stress Field during the Growth of a Fault-Propagation Fold. Geosciences, 9(6), 257. https://doi.org/10.3390/geosciences9060257





