Composite Anchors for Slope Stabilisation: Monitoring of their In-Situ Behaviour with Optical Fibre
Abstract
1. Introduction
- The same mechanical properties at a lower cost.
- Higher ultimate tensile strength and lower elongation in the serviceability state.
- Greater durability (reduced cracking, better protection from corrosion).
- Easier transportation and quick installation.
- Length adaptability to different geological and geotechnical in-situ conditions.
- Higher flexural inertia and better continuity given by the strands to the full reinforcement when compared to a simple coupling sleeve.
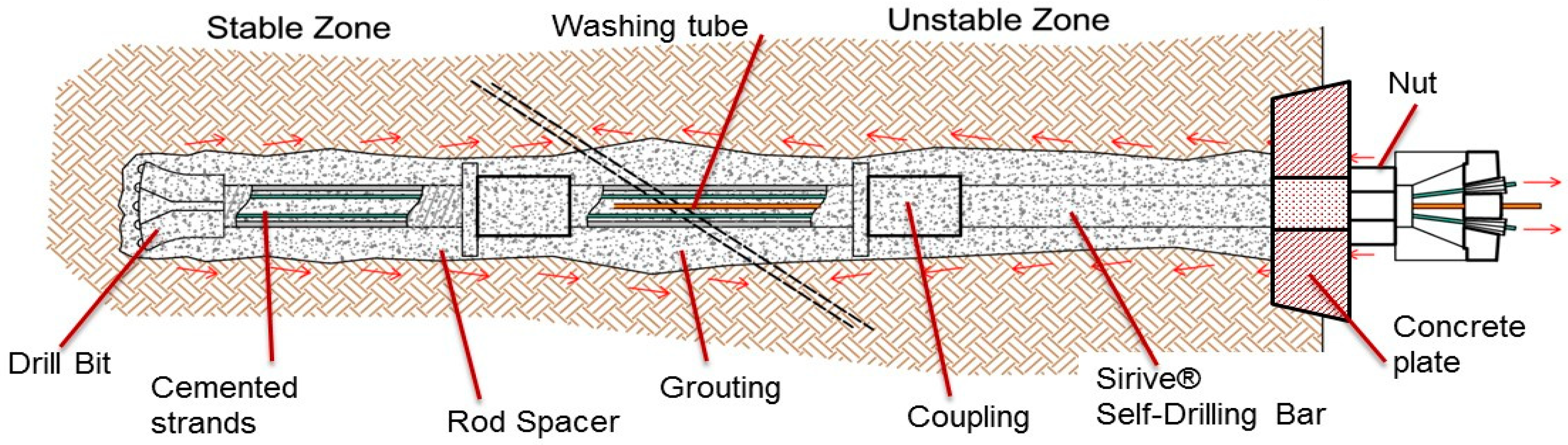
2. Coupling the Fibre to the Composite Bars
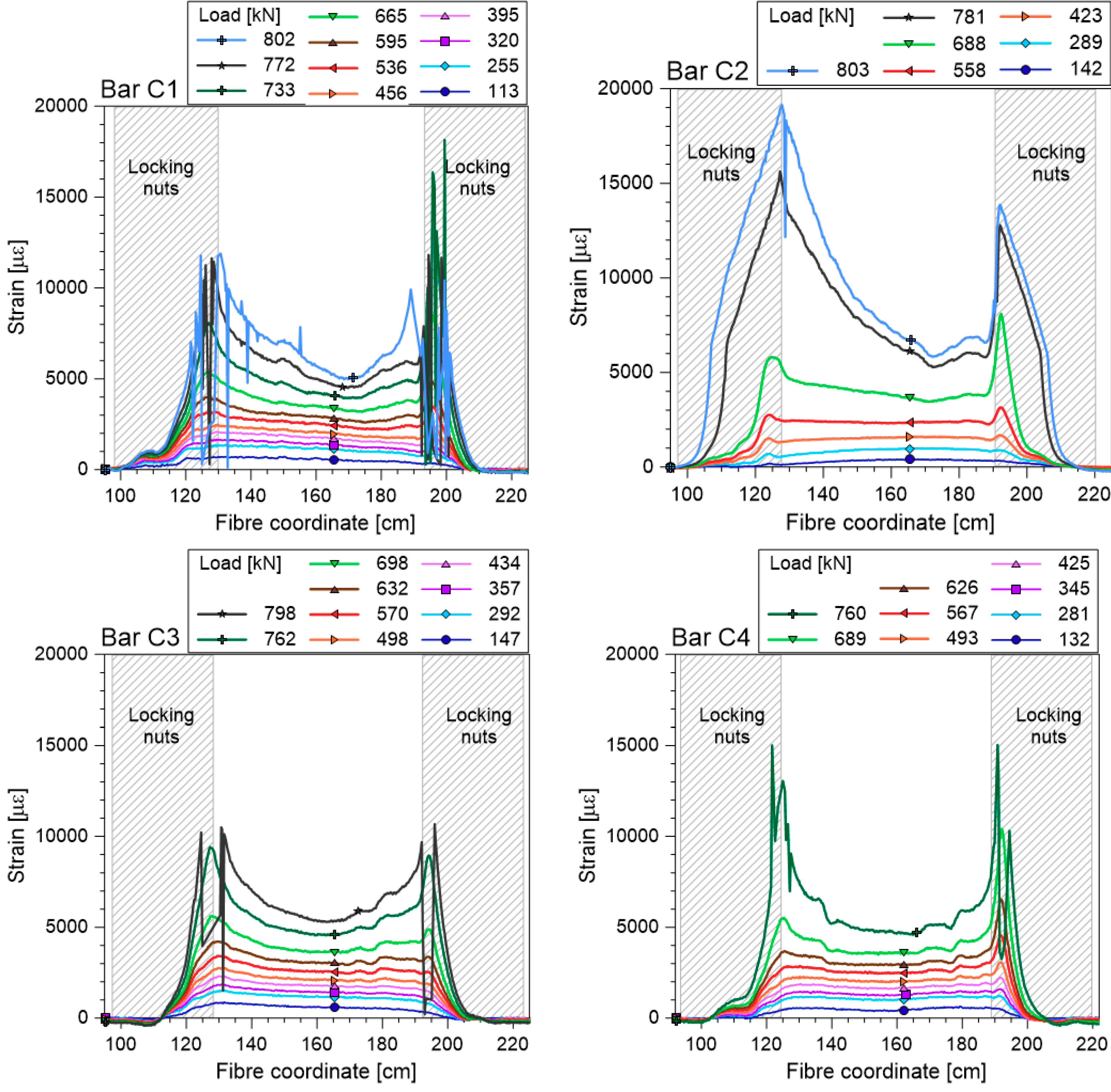
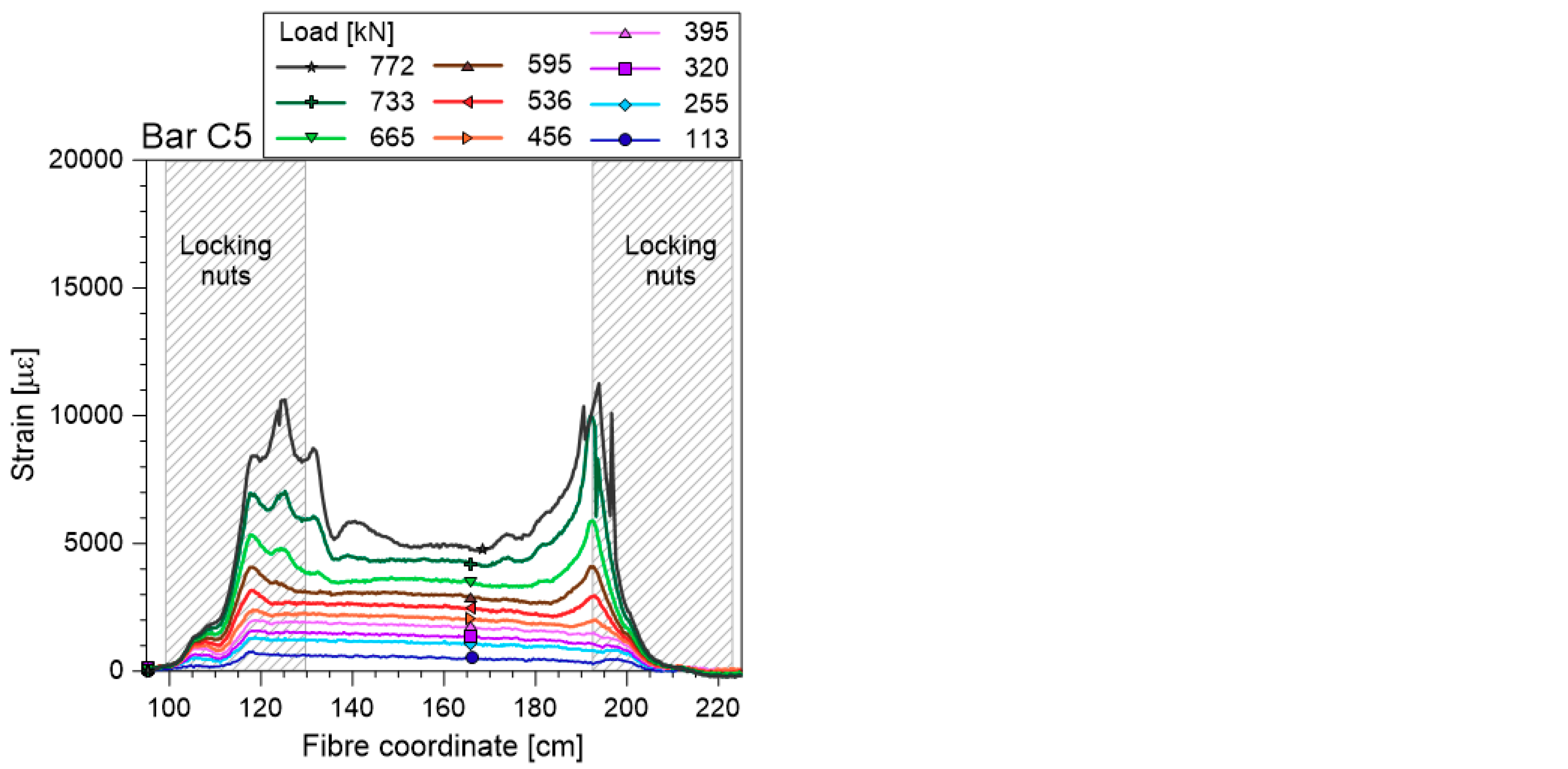
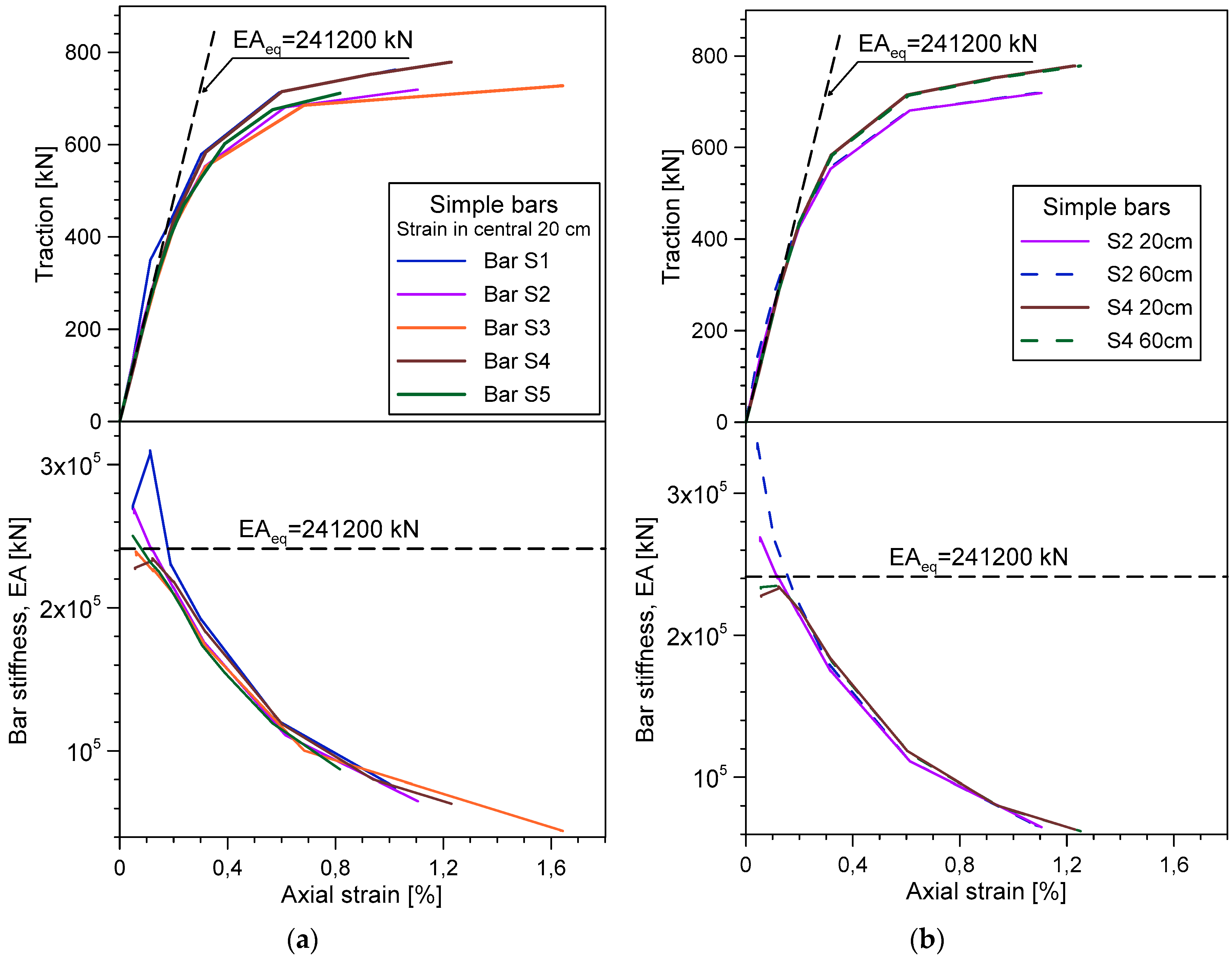
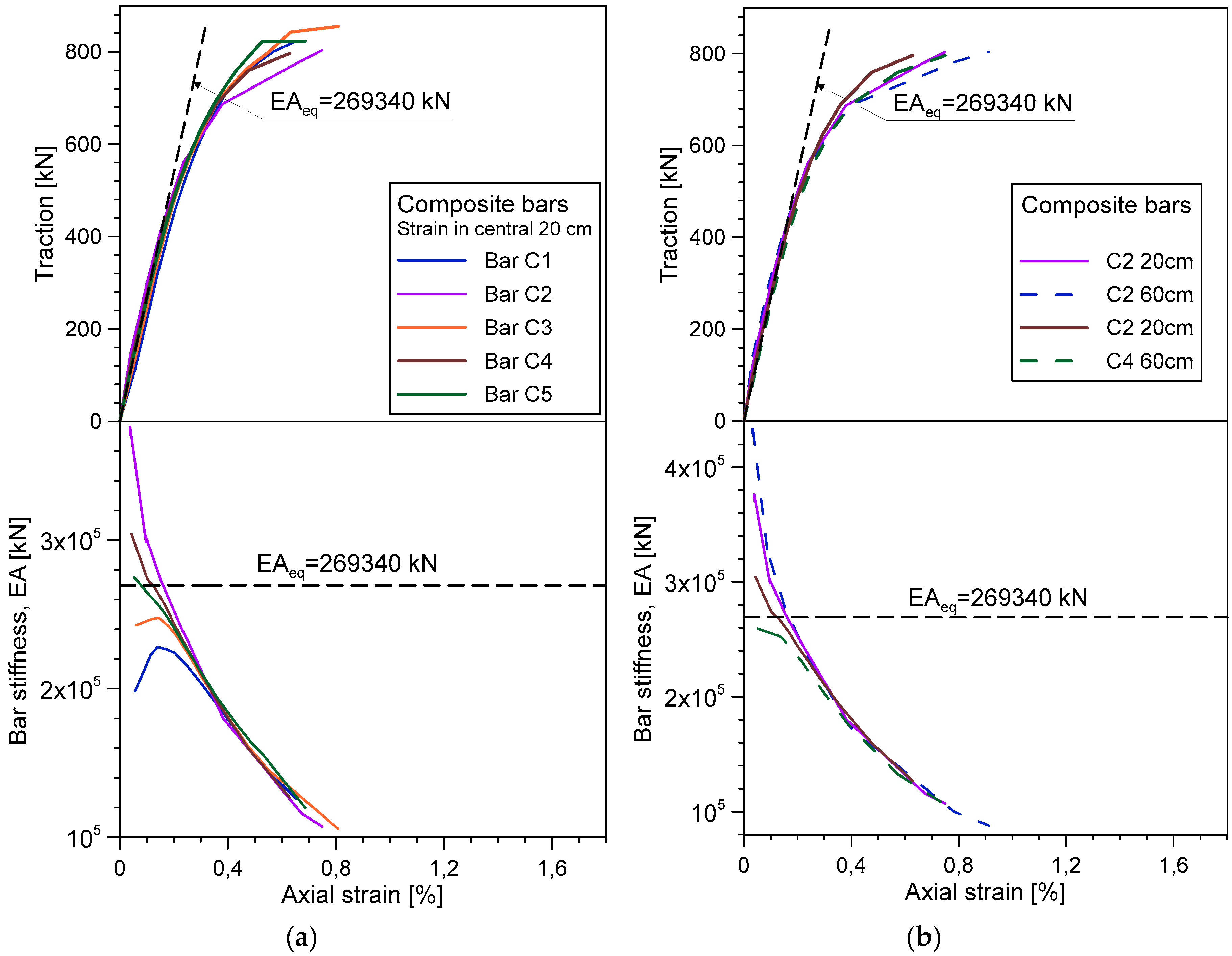
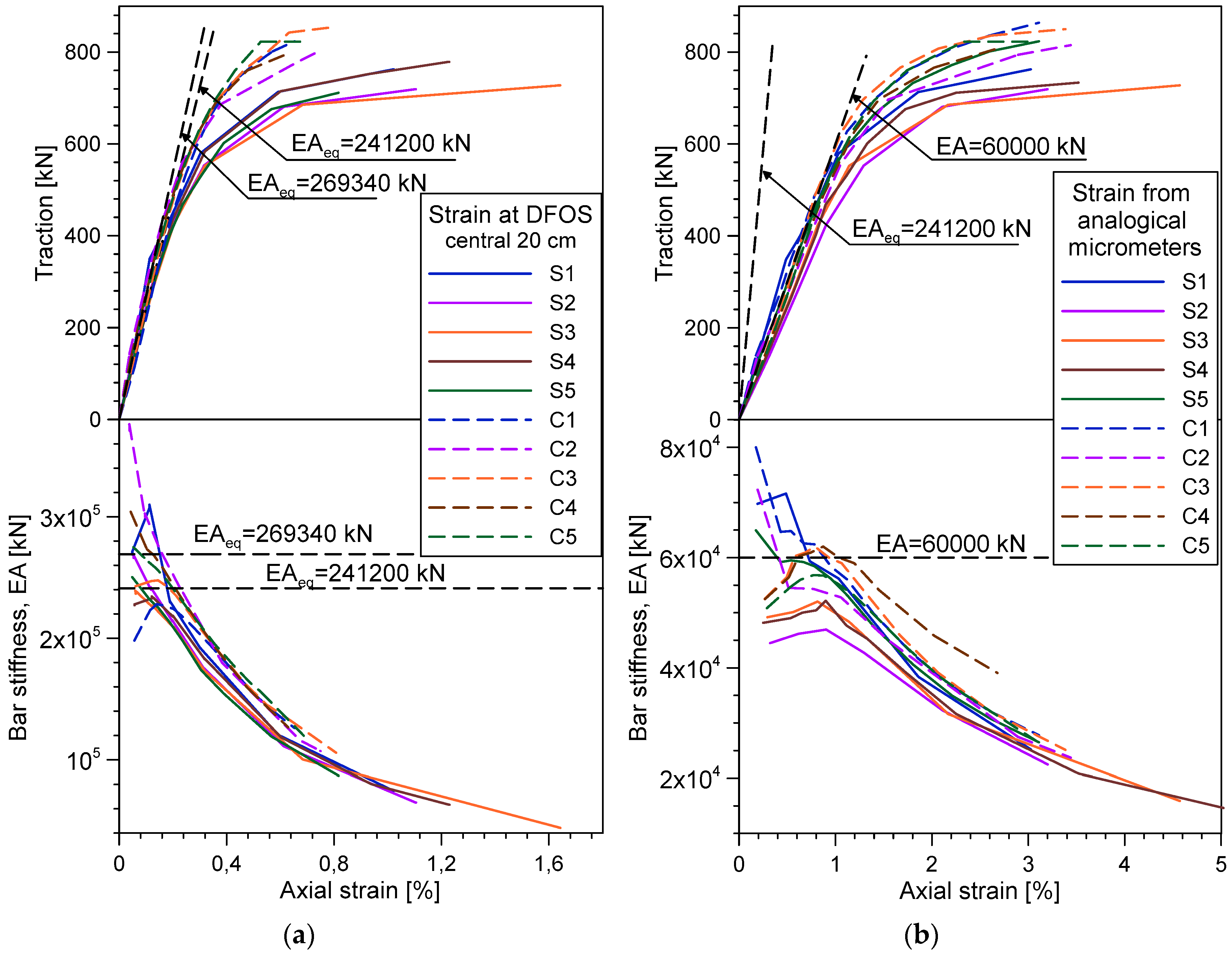
3. Laboratory Tests
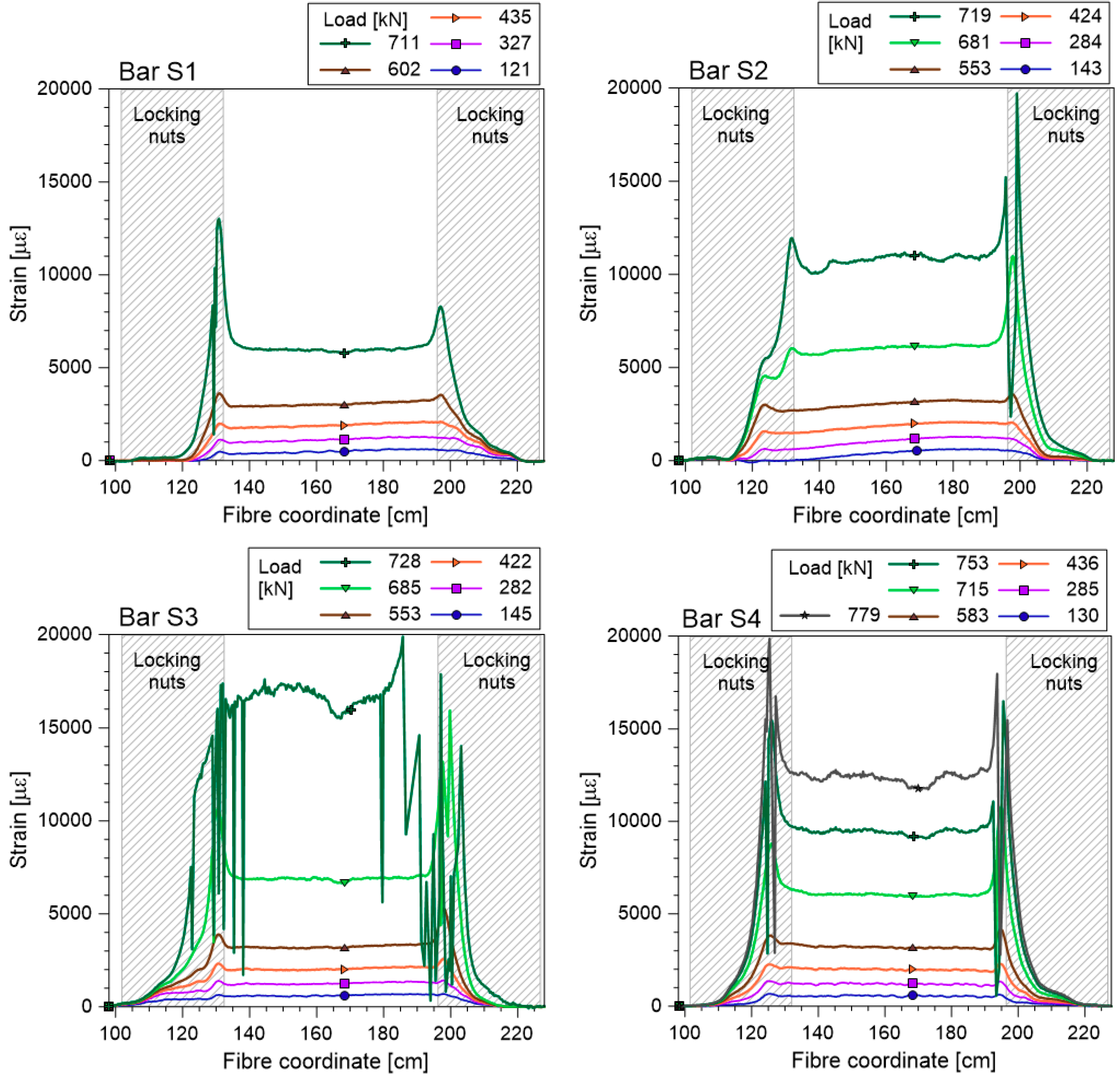
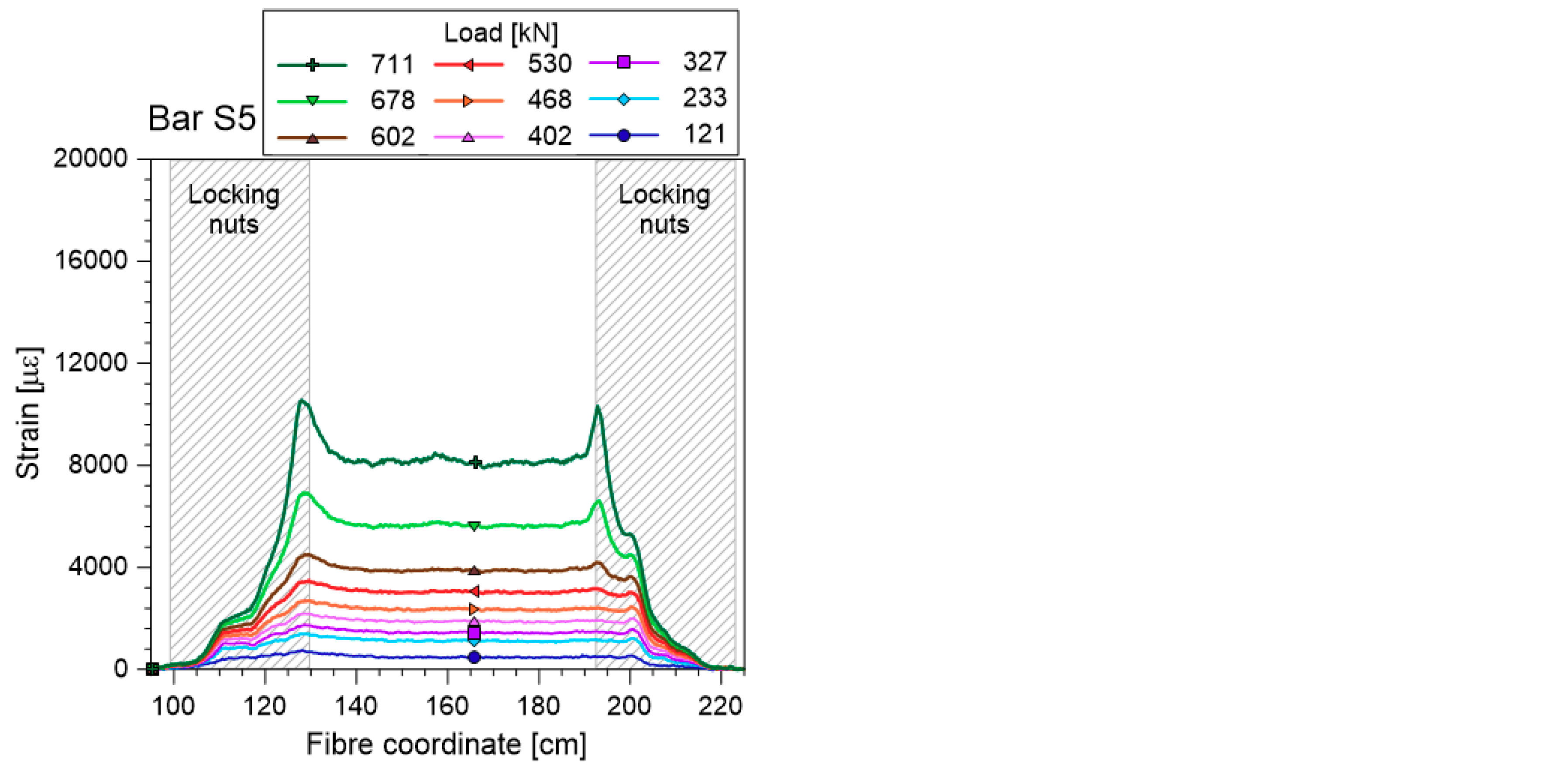
Results
- The coupling of the soil-nailing bars with strands, inserted in the inner cavity, increments the tensile resistance of the bars and their elastic range, thanks to a partial redistribution of the tensile force to the internal strand. This synergy is not achieved in the initial portion of the composite bars because a part of the force applied to the bars from external constraints needs to be redistributed to the strand along the anchorage length. From these tests, the anchorage length seems to increase with the applied load, up to about 25 cm long for traction close to the yielding load of the bar.
- The optical fibres adopted in this measurement system are suitable for monitoring the strain of composite bars in the elastic region, as long as the local strain remains less than 1.2%. The ribbed cover of the fibre guarantees effective interaction between the fibre cable and the cement, thus ensuring a reliable measurement of very small strain up to 1 µε, precision that cannot be obtained with traditional sensors.
4. On-Site Installation
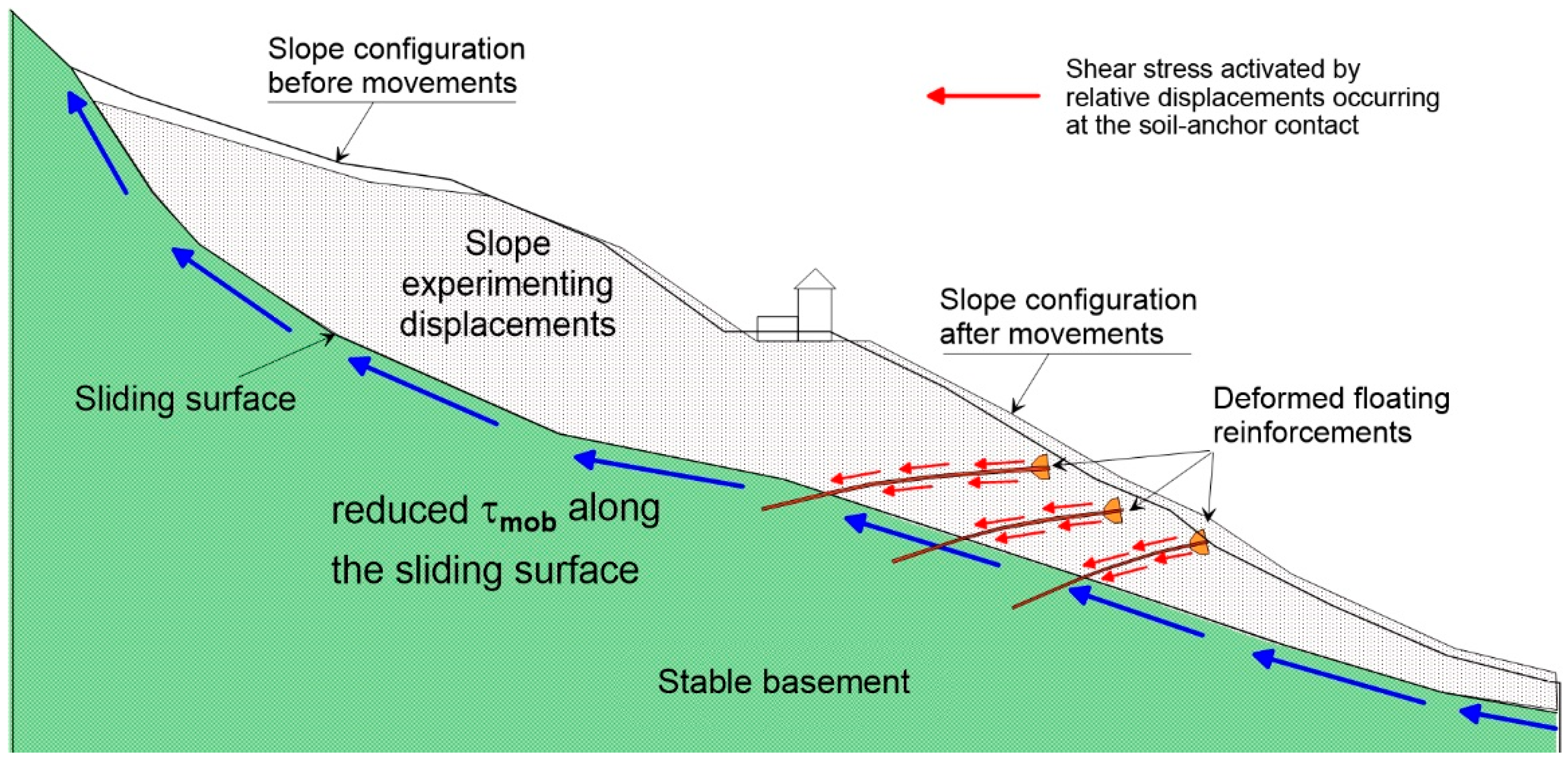
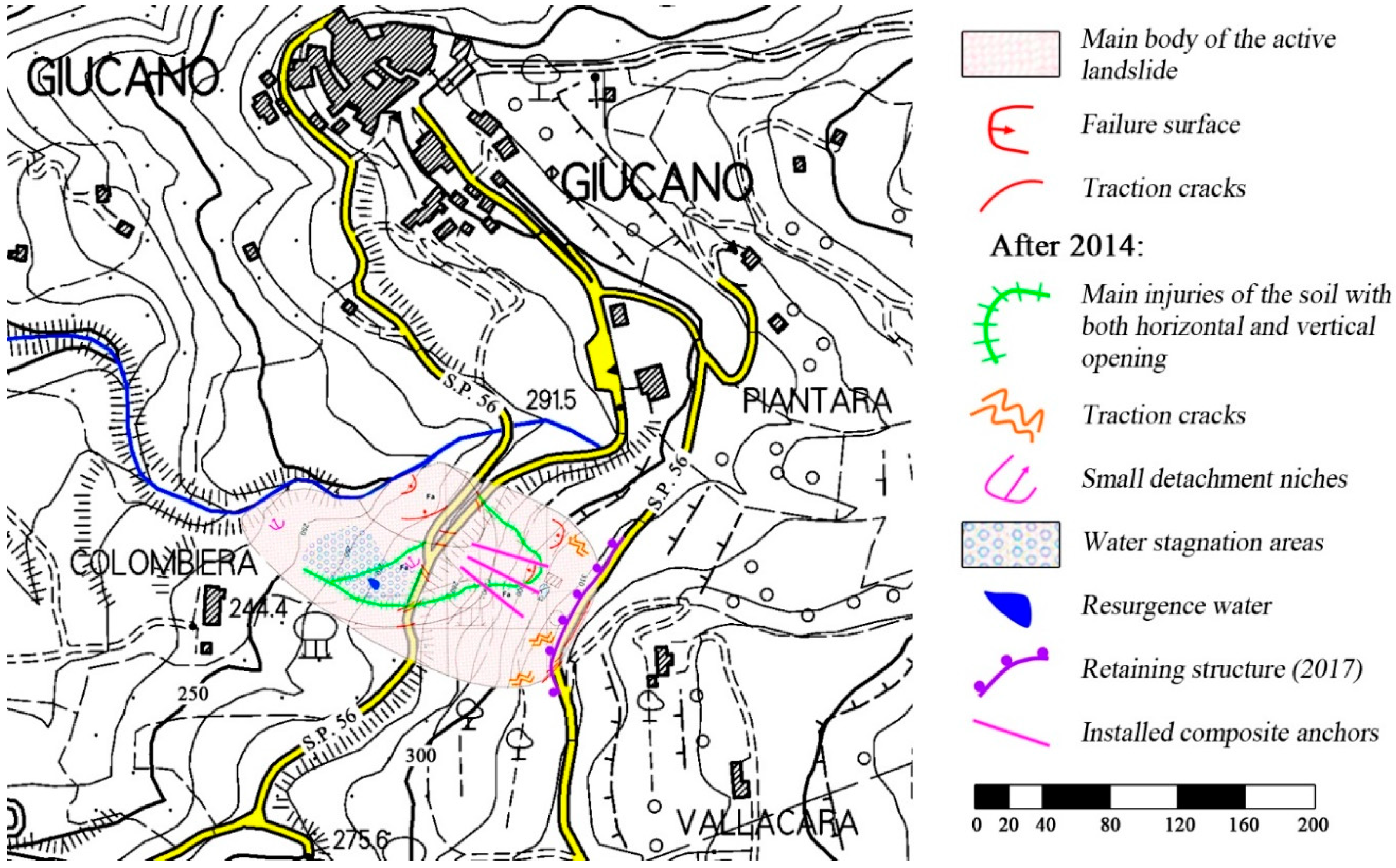
4.1. Landslide Features
- A line of drilled piles, having a diameter of 1 m, an interspace of about 5 m, and a length of 22 m.
- A line of Tub-fix type micropiles, inclined 45° and having a nominal diameter of 250 mm, an interspace of about 5 m, and a length of 24 m with an anchorage length of 12 m in the rock base.
- A reinforced concrete horizontal beam, 50 cm thick and 7.20 m wide, founded on piles on the downhill side and on micropiles on the uphill side.
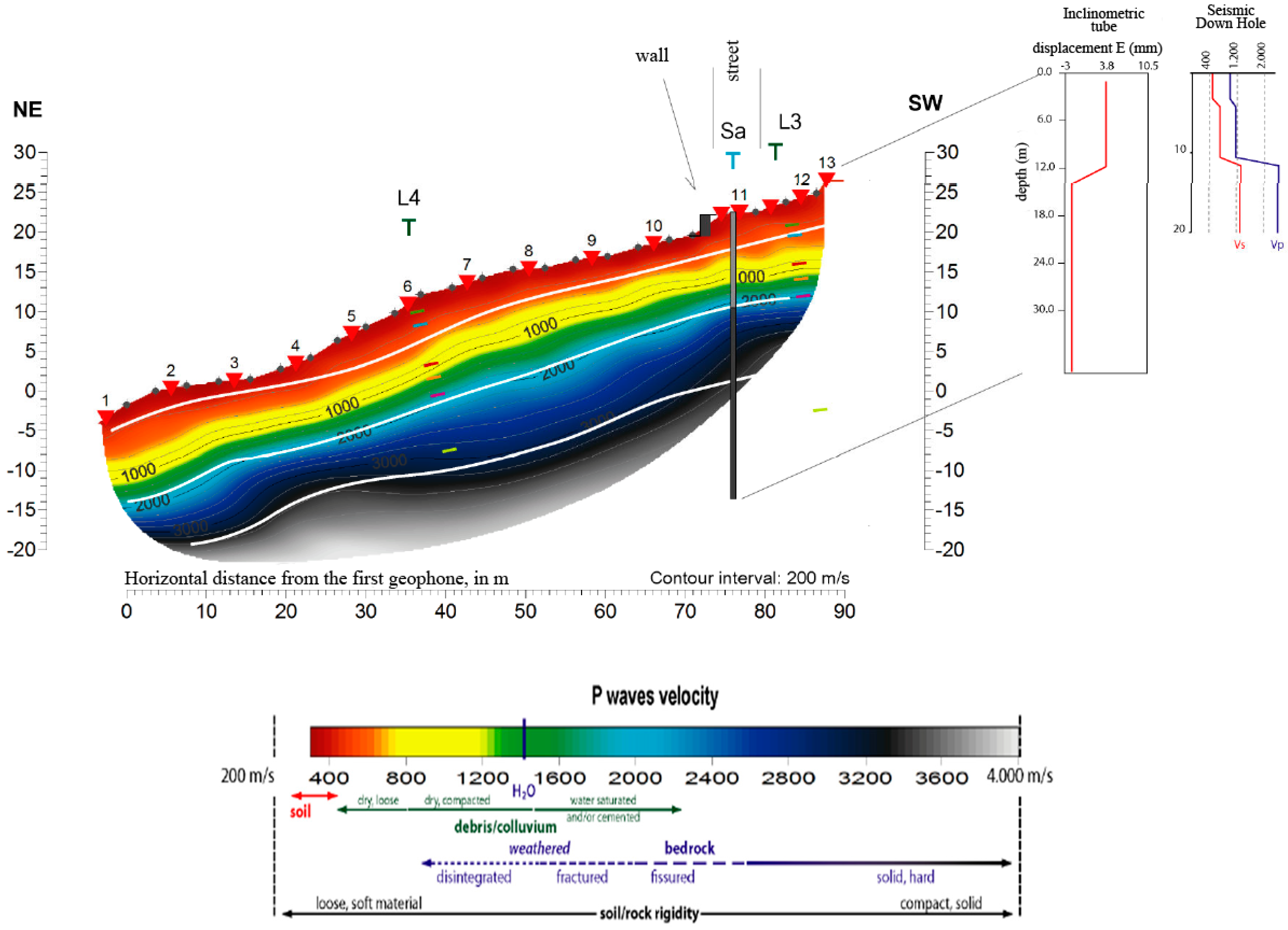
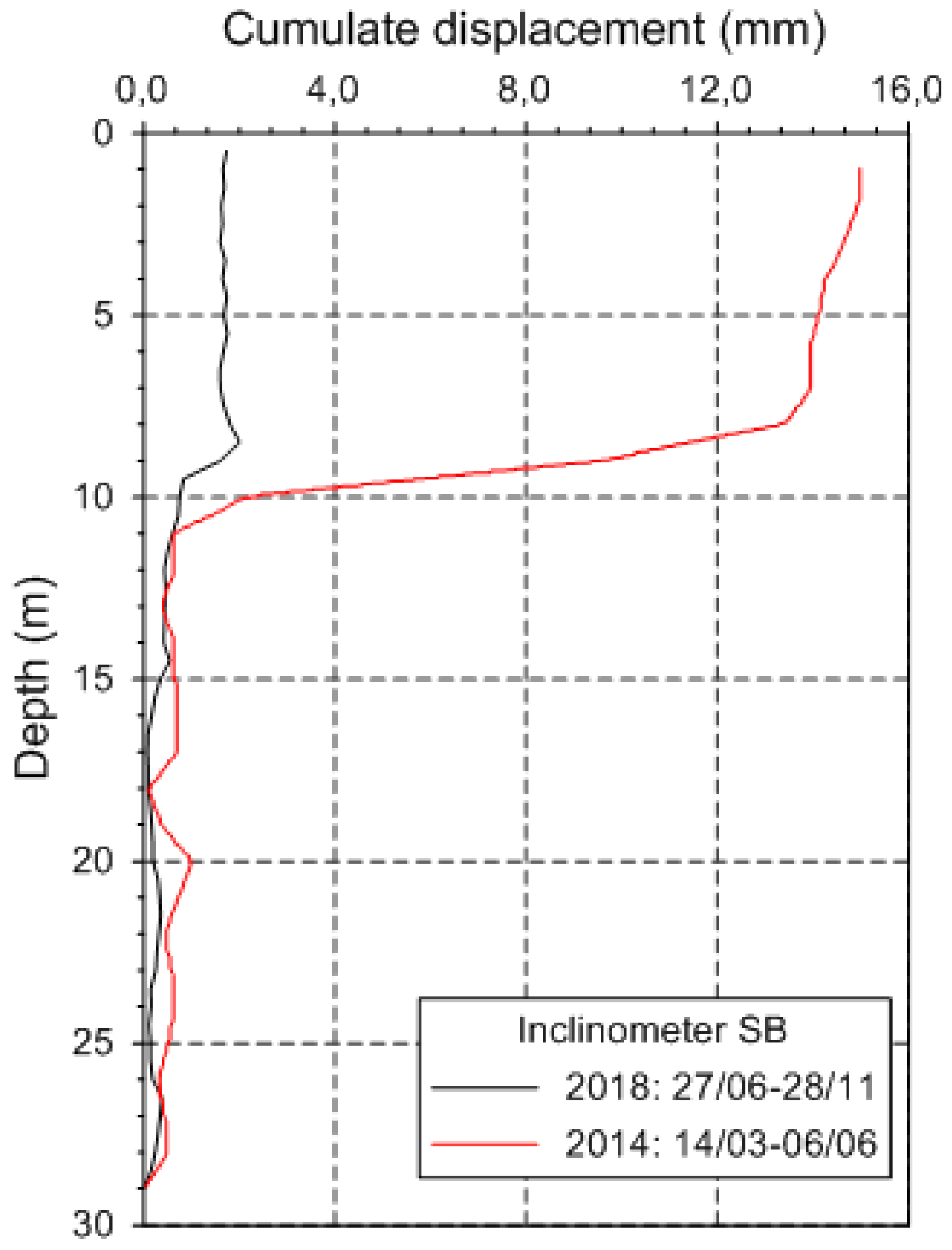
4.2. Testing Site
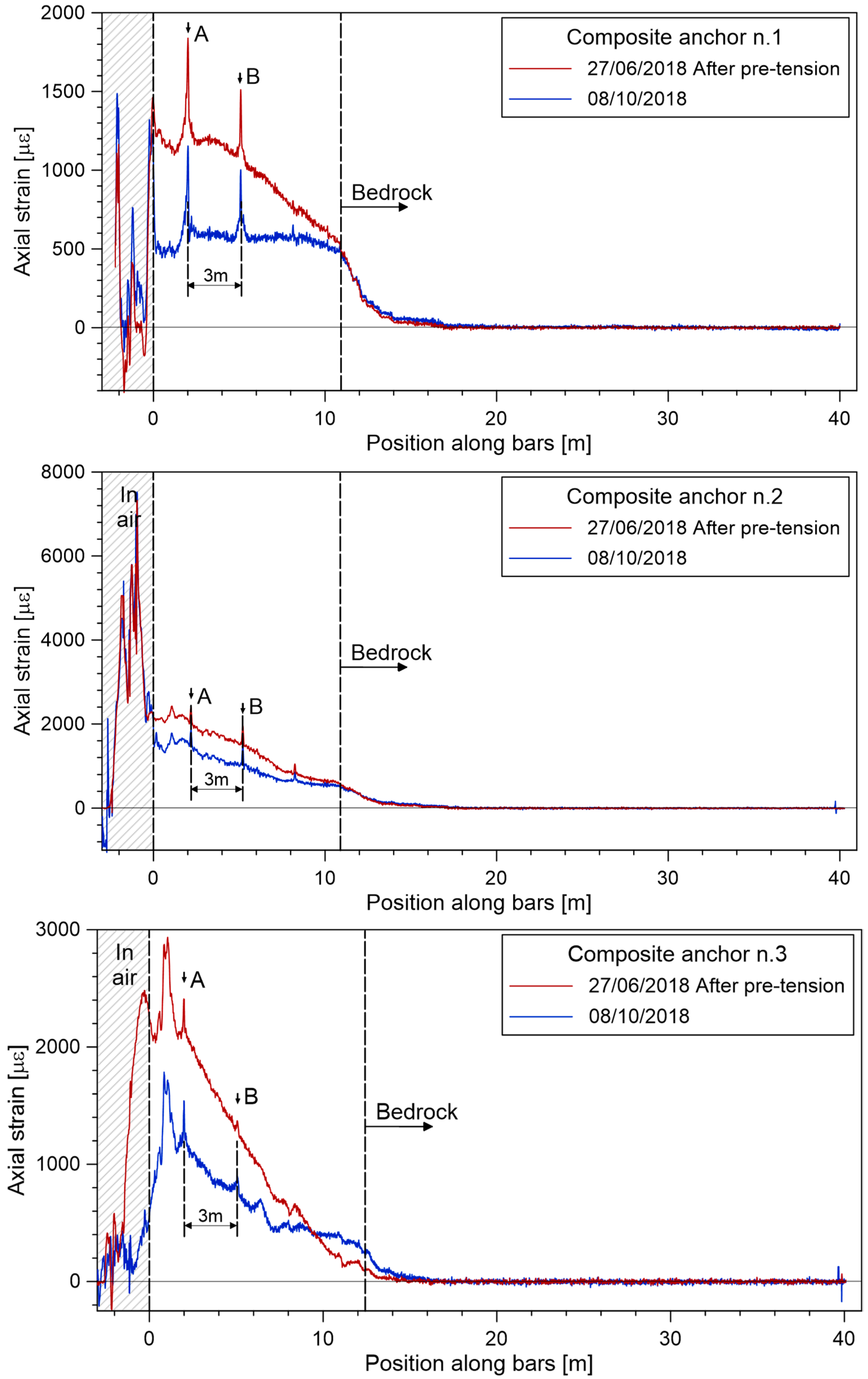
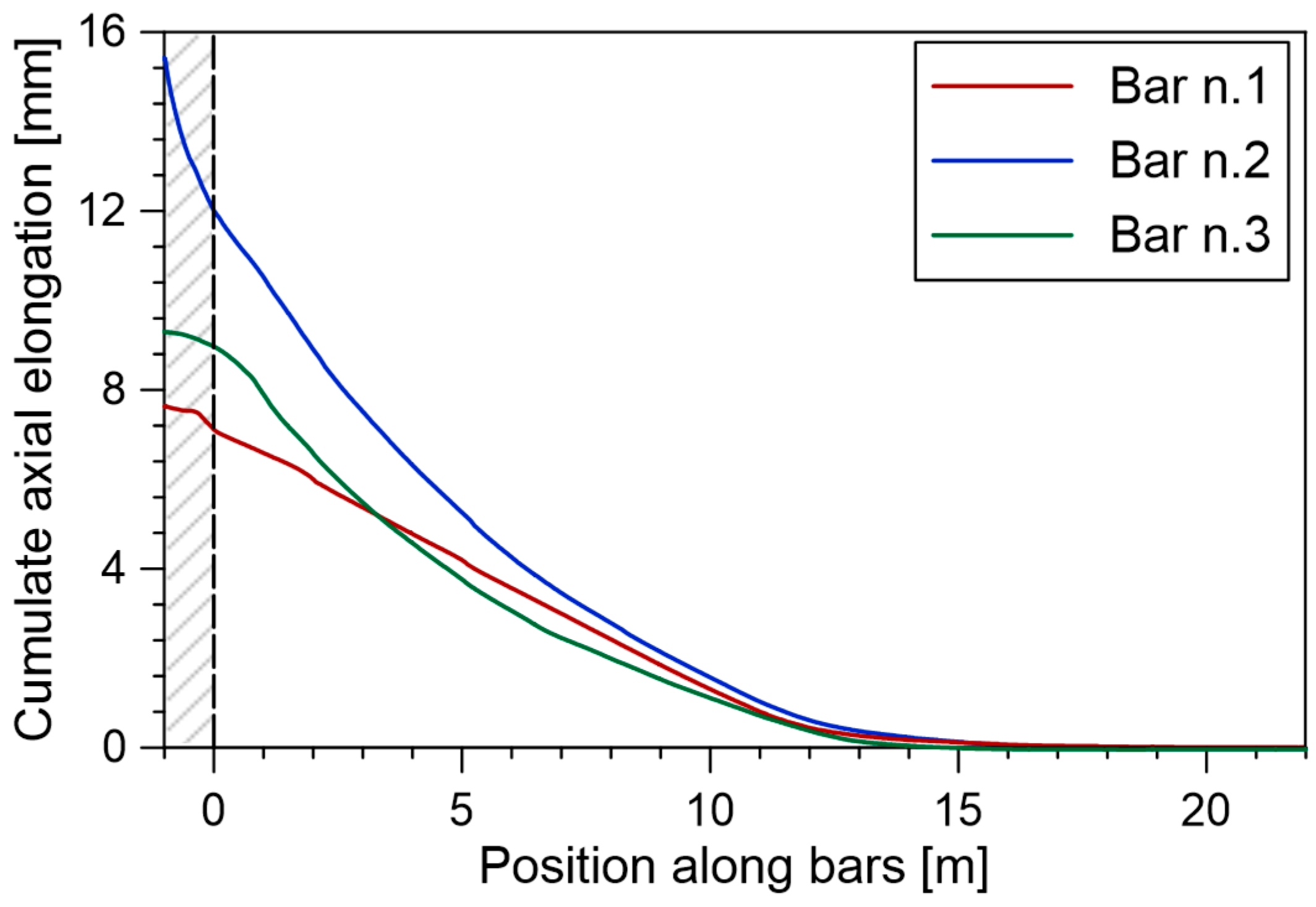
4.3. Results from the Testing Site
- Up to 3.9 m, in which the F-s curve is almost constant, i.e., the shear stress is almost zero.
- s in the range of 3.9 to 10.8 m, in which the slope of the F-s curve is constant and the mobilised shear stress is equal to τmob = 88 kPa.
- s in the range of 10.8 to 12.0 m, characterised by a τmob ≈ 225 kPa.
- From 12.0 to 17.5 m, in which the gradient reduces gradually to zero.
- From 1.5 to 9.5 m for bar n.2 and from 2 m to 7 m for bar n.3, in which the slope of the F-s curve is constant, and the mobilised shear stress is τmob ≈ 225 and 260 kPa, respectively.
- The deepest part in which the gradient gradually reduces to zero.
5. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Bisson, A.; Cola, S.; Tessari, G.; Floris, M. Floating anchors in landslide stabilization: The Cortiana case in North-Eastern Italy. In Engineering Geology for Society and Territory; Lollino, G., Giordan, D., Crosta, G.B., Corominas, J., Azzam, R., Wasowski, J., Sciarra, N., Eds.; Springer: Cham, Switzerland, 2015; Volume 2, pp. 2083–2087. [Google Scholar]
- Bisson, A.; Cola, S. Floating anchors for the stabilization of Cischele landslide in the Venetian Prealps. In Proceedings of the 13th Congress INTERPRAEVENT, Lucerne, Switzerland, 30 May–2 June 2016; pp. 288–289. [Google Scholar]
- Bisson, A.; Cola, S.; Baran, P.; Zydroń, T.; Gruchot, A.T.; Murzyn, R. Passive composite anchors for landslide stabilization: An Italian-Polish research program. In Proceedings of the In Landslides and Engineered Slopes. Experience, Theory and Practice: Proceedings of the 12th International Symposium on Landslides, Napoli, Italy, 12–19 June 2016; p. 433. [Google Scholar]
- Bisson, A. Sirive® Floating Anchor for Landslide Stabilization. Ph.D. Thesis, University of Padova, Padua, Italy, January 2015. [Google Scholar]
- UNI EN 14490:2010 Execution of special geotechnical works-Soil nailing. Italian. Available online: https://infostore.saiglobal.com/en-au/standards/uni-en-14490-2010-1093491_SAIG_UNI_UNI_2544990/ (accessed on 25 May 2019).
- FHWA-IF-03-017 Geotechnical Engineering Circular No. 7. Soil Nail Walls. Available online: https://www.fhwa.dot.gov/engineering/geotech/pubs/nhi14007.pdf (accessed on 25 May 2019).
- Stocker, M.F.; Korber, G.W.; Gassler, G.; Gudehus, G. Soil nailing. In Proceedings of the International Conference on Soil Reinforcement, Paris, France, 20–22 March 1979; pp. 469–474. [Google Scholar]
- Plumelle, C.; Schlosser, F.; Oclage, P.; Knochenmus, G. French national research project on Soil Nailing: Clouterre. Geotech. Spec. Publ. ASCE 1990, 25, 660–675. [Google Scholar]
- Phear, A.; Dew, C.; Ozsoy, B.; Wharmby, N.J.; Judge, J.; Barley, A.D. Soil Nailing: Best Practice Guidance; Report C63.; CIRIA: London, UK, 2005; ISBN 978-0860176374. [Google Scholar]
- Schenato, L. A review of distributed fibre optic sensors for geo-hydrological applications. Appl. Sci. 2017, 7, 896. [Google Scholar] [CrossRef]
- Schenato, L.; Palmieri, L.; Camporese, M.; Bersan, S.; Cola, S.; Pasuto, A.; Galtarossa, A.; Salandin, P.; Simonini, P. Distributed optical fibre sensing for early detection of shallow landslides triggering. Sci. Rep. 2017. [Google Scholar] [CrossRef]
- de Battista, N.; Kechavarzi, C.; Seo, H.; Soga, K.; Pennington, S. Distributed fibre optic sensors for measuring strain and temperature of cast-in-situ concrete test piles. In Proceedings of the International Conference on Smart Infrastructure and Construction (ICSIC), Cambridge, UK, 27–29 June 2016. [Google Scholar] [CrossRef]
- Bersan, S.; Schenato, L.; Rajendran, A.; Palmieri, L.; Cola, S.; Pasuto, A.; Simonini, P. Application of a high resolution distributed temperature sensor in a physical model reproducing subsurface water flow. Meas. J. Int. Meas. Confed. 2017, 98, 321–324. [Google Scholar] [CrossRef]
- Bersan, S.; Bergamo, O.; Palmieri, L.; Schenato, L.; Simonini, P. Distributed strain measurements in a CFA pile using high spatial resolution fibre optic sensors. Eng. Struct. 2018, 160, 554–565. [Google Scholar] [CrossRef]
- Palmieri, L.; Schenato, L. Distribuited optical fibre fensing based on rayleigh scattering. Open Opt. J. 2013, 7, 104–127. [Google Scholar] [CrossRef]
- Milligan, G.W.E.; Tei, K. The pull-out resistance of model soil nails. Soils Found. 1998, 38, 179–190. [Google Scholar] [CrossRef]
- Luo, S.Q.; Tan, S.A.; Yong, K.Y. Pull-out resistance mechanism of a soil nail reinforcement in dilative soils. SOILS Found. 2011, 40, 47–56. [Google Scholar] [CrossRef]
- Hong, Y.-S.; Wu, C.-S.; Yang, S.-H. Pullout resistance of single and double nails in a model sandbox. Can. Geotech. J. 2003, 40, 1039–1047. [Google Scholar] [CrossRef]
- Junaideen, S.M.; Tham, L.G.; Law, K.T.; Lee, C.F.; Yue, Z.Q. Laboratory study of soil–nail interaction in loose, completely decomposed granite. Can. Geotech. J. 2004, 41, 274–286. [Google Scholar] [CrossRef]
- Chu, L.-M.; Yin, J.-H. Comparison of interface shear strength of soil nails measured by both direct shear box tests and pullout tests. J. Geotech. Geoenviron. Eng. 2005, 131, 1097–1107. [Google Scholar] [CrossRef]
- Su, L.-J.; Chan, T.C.F.; Yin, J.-H.; Shiu, Y.K.; Chiu, S.L. Influence of overburden pressure on soil–nail pullout resistance in a compacted fill. J. Geotech. Geoenviron. Eng. 2008, 134, 1339–1347. [Google Scholar] [CrossRef]
- Pradhan, B.; Tham, L.G.; Yue, Z.Q.; Junaideen, S.M.; Lee, C.F. Soil–nail pullout interaction in loose fill materials. Int. J. Geomech. 2006. [Google Scholar] [CrossRef]
- Schroeck, M.; Ecke, W.; Graupner, A. Strain monitoring in steel rock bolts using FBG sensor arrays. Appl. Opt. Fiber Sensors. Int. Soc. Opt. Photonics 2000, 4074, 298–305. [Google Scholar]
- Zhang, B.; Benmokrane, B.; Ebead, U.A.A. Design and evaluation of Fiber-Reinforced Polymer bond-type anchorages and ground anchors. Int. J. Geomech. 2006, 6, 166–175. [Google Scholar] [CrossRef]
- Hong, C.-Y.; Yin, J.-H.; Jin, W.; Wang, C.; Zhou, W.-H.; Zhu, H.-H. Comparative study on the elongation measurement of a soil nail using Optical Lower Coherence Interferometry method and FBG method. Adv. Struct. Eng. 2010, 13, 309–319. [Google Scholar] [CrossRef]
- Pei, H.; Yin, J.; Zhu, H.; Hong, C. Performance monitoring of a glass fiber-reinforced polymer bar soil nail during laboratory pullout test using FBG sensing technology. Int. J. Geomech. 2012, 13, 467–472. [Google Scholar] [CrossRef]
- Zhu, H.-H.; Yin, J.-H.; Jin, W. Soil nail monitoring using Fiber Bragg Grating sensors during pullout test. In Proceedings of the Joint 60th Canadian Geotechnical and 8th Joint CGS/IAH-CNC Groundwater Conferences, Ottawa, ON, Canada, 21–24 October 2007; pp. 821–828. [Google Scholar]
- Zhu, H.H.; Shi, B.; Zhang, J.; Yan, J.F.; Zhang, C.C. Distributed fiber optic monitoring and stability analysis of a model slope under surcharge loading. J. Mt. Sci. 2014, 11, 979–989. [Google Scholar] [CrossRef]
- Weng, X.; Ma, H.; Wang, J. Stress monitoring for anchor rods system in subway tunnel using FBG technology. Adv. Mater. Sci. Eng. 2015. [Google Scholar] [CrossRef]
- Amatya, B.; Bennett, P.; Uchimura, T.; Soga, K.; Ball, P.; Lung, R. Installation of optical fibre strain sensors on soil nails used for stabilising a steep highway cut slope. In Proceedings of the 1st International Conference on Transportation Geotechnics, Nottingham, UK, 25–27 August 2008; pp. 277–282. [Google Scholar]
- Iten, M.; Puzrin, A.M. Monitoring of stress distribution along a ground anchor using BOTDA. Sensors Smart Struct. Technol. Civil, Mech. Aerosp. Syst. 2010 2010, 7647, 76472J. [Google Scholar]
- Hong, C.Y.; Yin, J.H.; Zhang, Y.F. Deformation monitoring of long GFRP bar soil nails using distributed optical fiber sensing technology. Smart Mater. Struct. 2016, 25, 085044. [Google Scholar] [CrossRef]
- Monsberger, C.M.; Lienhart, W.; Caporossi, P. Distributed fiber optic sensing along grouted anchors to assess curvature and bending characteristics. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Lausanne Switzerland, 24–28 September 2018. [Google Scholar]
- Bado, M.F.; Casas, J.R.; Barrias, A. Performance of rayleigh-based distributed optical fiber sensors bonded to reinforcing bars in bending. Sensors 2018, 18, 3125. [Google Scholar] [CrossRef] [PubMed]
- Sirgiovanni, E. Movimento franoso in località Giucano su SP56: Relazione geologico-geomorfologica e geologio-tecnica. Available online: http://www.comune.cereseto.al.it/doc/file/RelazionegeologicadivarianteconIIIfaseefranadefinitiva01-06-2011.pdf (accessed on 25 May 2019).
- Cola, S.; San Vitale, N. Interazione tra rivestimento, barre e terreno nelle pareti sostenute con Soil Nailing. In Proceedings of the XXIV CNG–Innovazione Tecnologica nell’Ingegneria Geotecnica, Napoli, Italy, 22–24 June 2011; Volume 1, pp. 217–230. [Google Scholar]
- Bustamante, M.; Doix, B. Une méthode pour le calcul des tirants et des micropieux injectés. Bull. Liaison Lab. des Ponts Chaussèes 1985, 140, 75–95. [Google Scholar]
- Hong, C.-Y.; Yin, J.-H.; Zhou, W.-H.; Pei, H.-F. Analytical study on progressive pullout behavior of a soil nail. J. Geotech. Geoenviron. Eng. 2011, 138, 500–507. [Google Scholar] [CrossRef]
- Elias, V.; Juran, I. Soil Nailing for Stabilization of Highway Slopes and Excavations; publication FHWA-RD-89-198; Federal Highway Administration: Washington, DC, USA, 1991. [Google Scholar]
- Bisson, A.; Cola, S. Stabilizzazione di movimenti franosi con ancoraggi flottanti: il caso di frana Val Maso (Valli del Pasubio, Vicenza). In Proceedings of the 5° IAGIG. L’Ingegneria geotecnica a servizio delle grandi opere: Necessità e opportunità, Roma, Italy, 22–23 May 2015. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cola, S.; Schenato, L.; Brezzi, L.; Tchamaleu Pangop, F.C.; Palmieri, L.; Bisson, A. Composite Anchors for Slope Stabilisation: Monitoring of their In-Situ Behaviour with Optical Fibre. Geosciences 2019, 9, 240. https://doi.org/10.3390/geosciences9050240
Cola S, Schenato L, Brezzi L, Tchamaleu Pangop FC, Palmieri L, Bisson A. Composite Anchors for Slope Stabilisation: Monitoring of their In-Situ Behaviour with Optical Fibre. Geosciences. 2019; 9(5):240. https://doi.org/10.3390/geosciences9050240
Chicago/Turabian StyleCola, Simonetta, Luca Schenato, Lorenzo Brezzi, Francine Chantal Tchamaleu Pangop, Luca Palmieri, and Alberto Bisson. 2019. "Composite Anchors for Slope Stabilisation: Monitoring of their In-Situ Behaviour with Optical Fibre" Geosciences 9, no. 5: 240. https://doi.org/10.3390/geosciences9050240
APA StyleCola, S., Schenato, L., Brezzi, L., Tchamaleu Pangop, F. C., Palmieri, L., & Bisson, A. (2019). Composite Anchors for Slope Stabilisation: Monitoring of their In-Situ Behaviour with Optical Fibre. Geosciences, 9(5), 240. https://doi.org/10.3390/geosciences9050240







