Impact of Nonzero Intercept Gas Transfer Velocity Parameterizations on Global and Regional Ocean–Atmosphere CO2 Fluxes
Abstract
1. Introduction
2. Materials and Methods
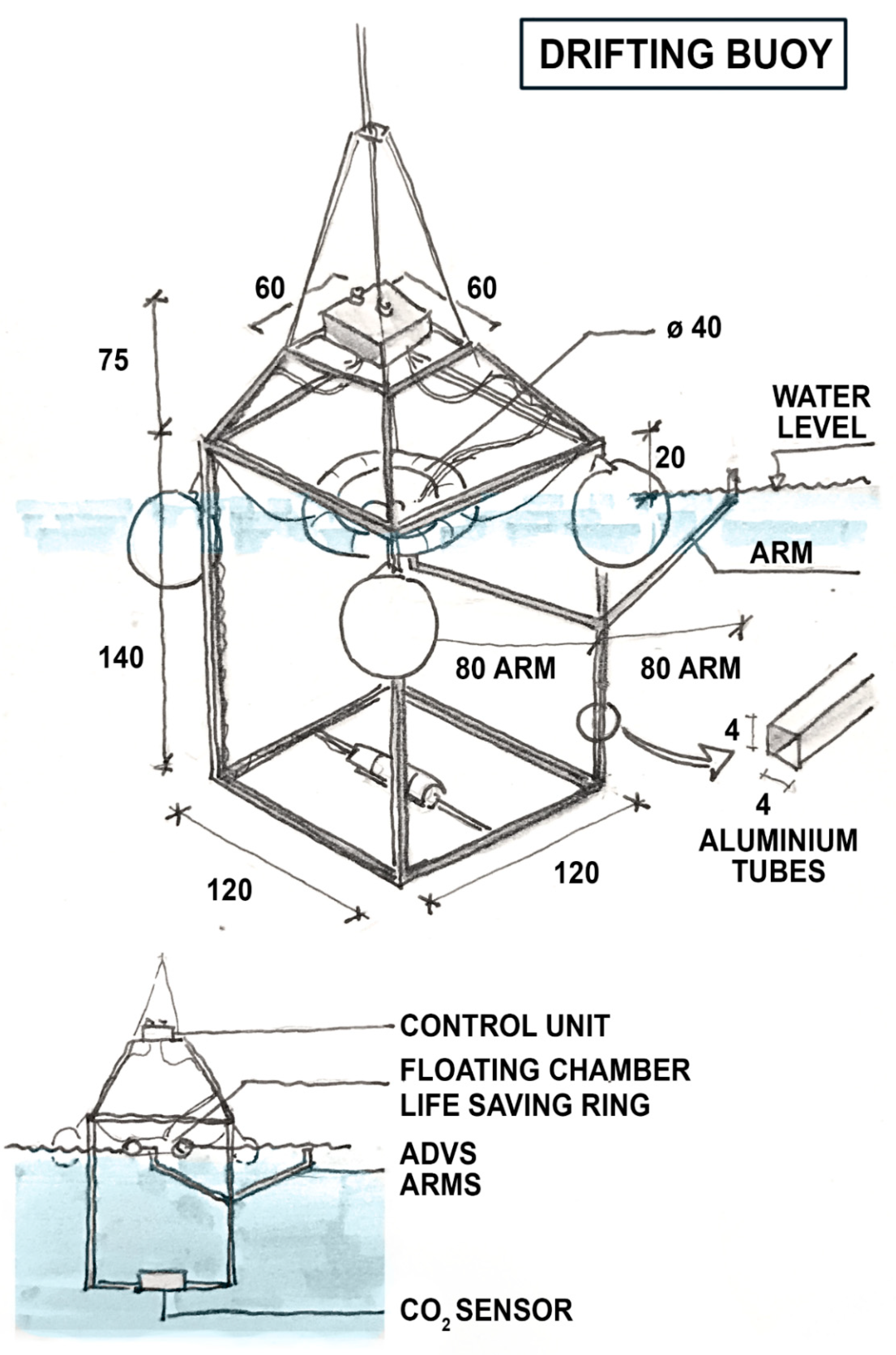
2.1. In Situ Flux Measurements with the Sniffle Floating Chamber
2.2. Global Surface Ocean pCO2-Based Flux Product
2.3. Bern3D Ocean Model
3. Results
3.1. Flux Measurements with Sniffle
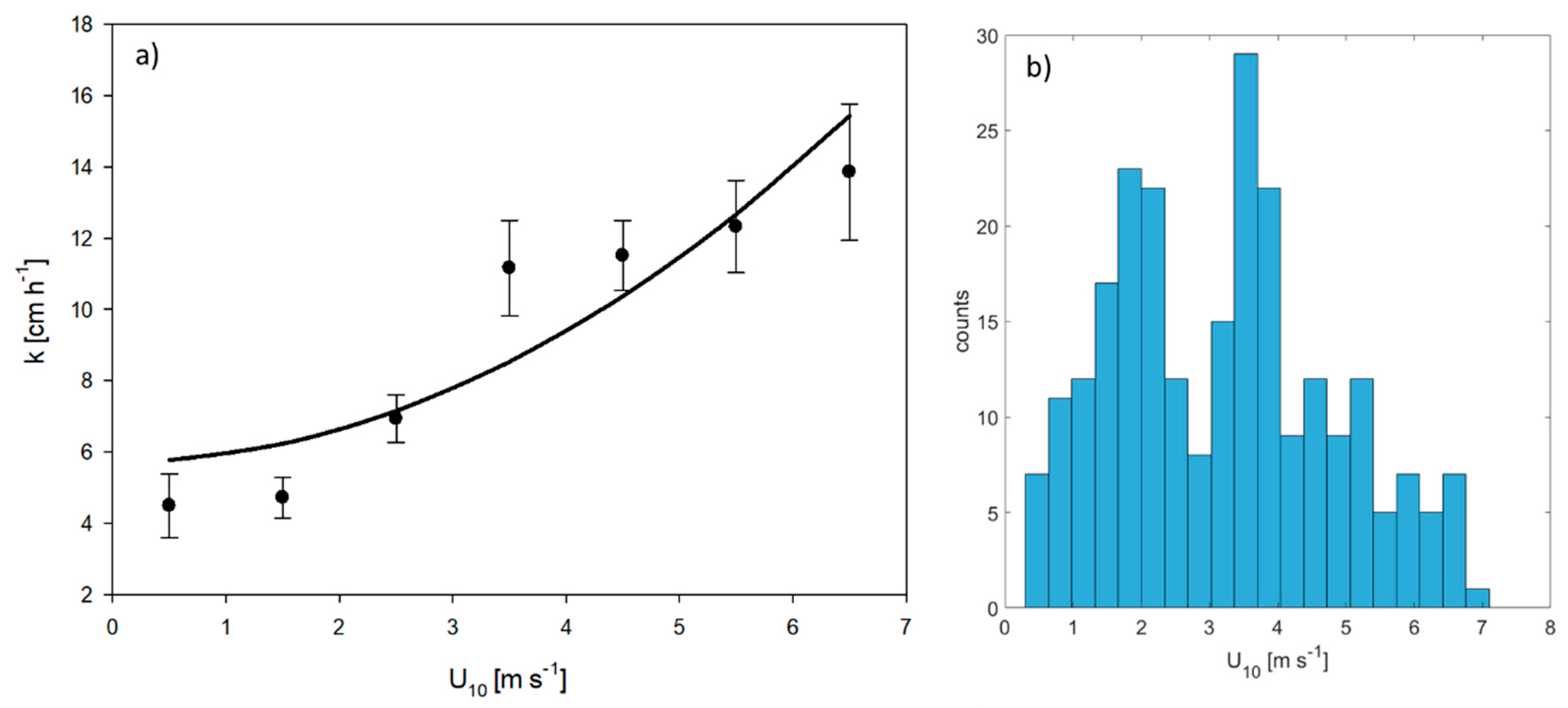
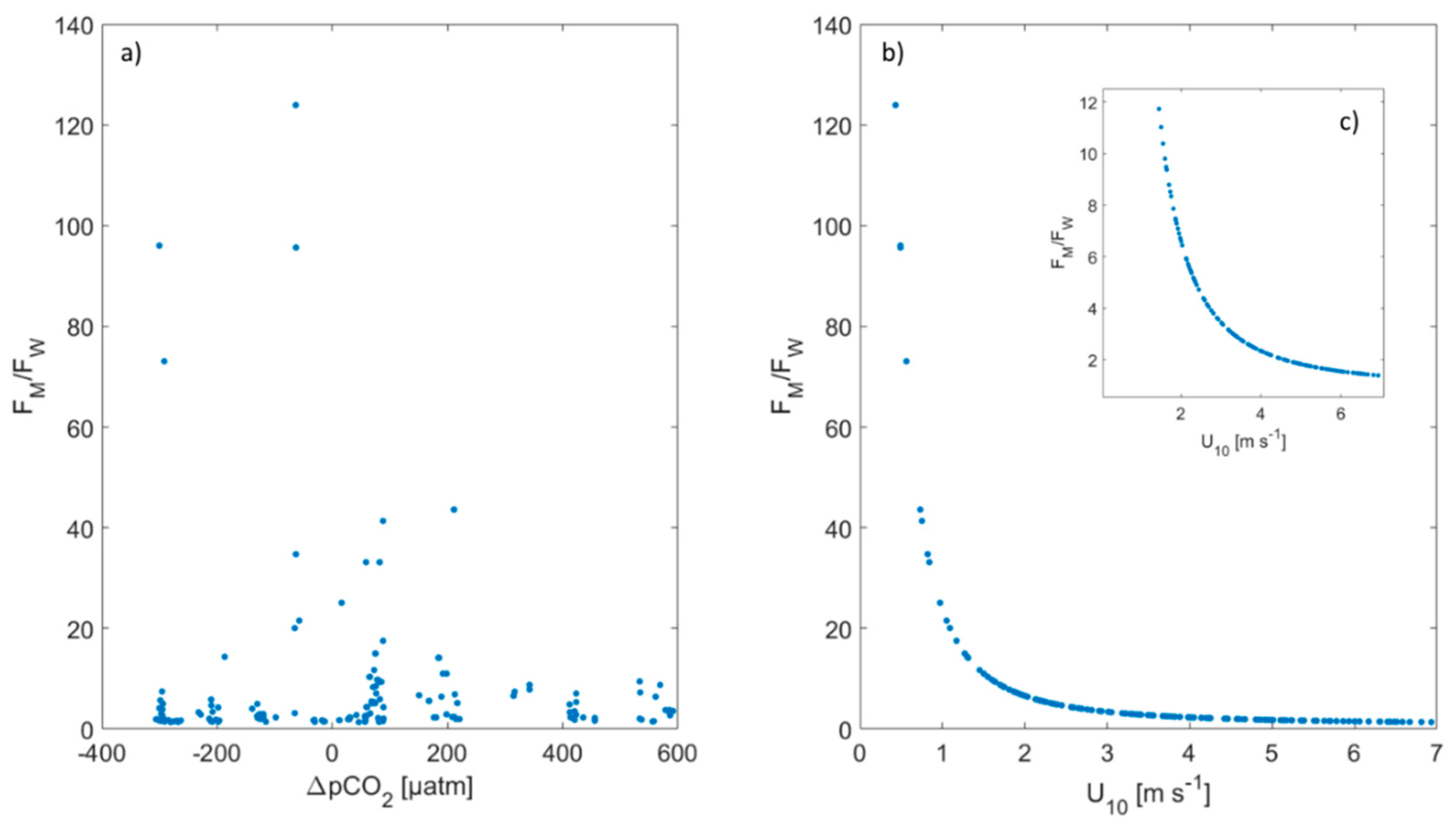
3.1.1. Parameterization
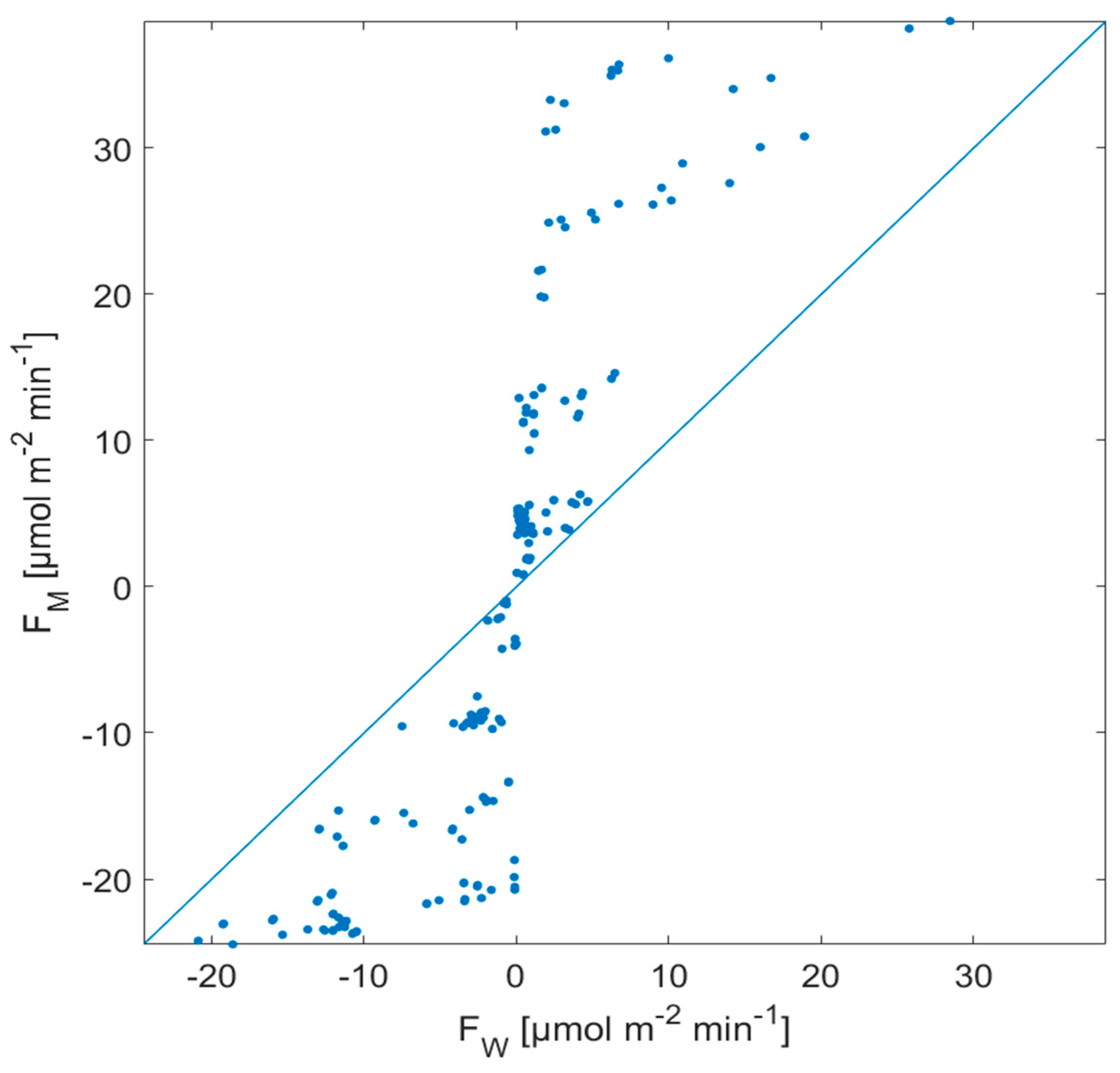
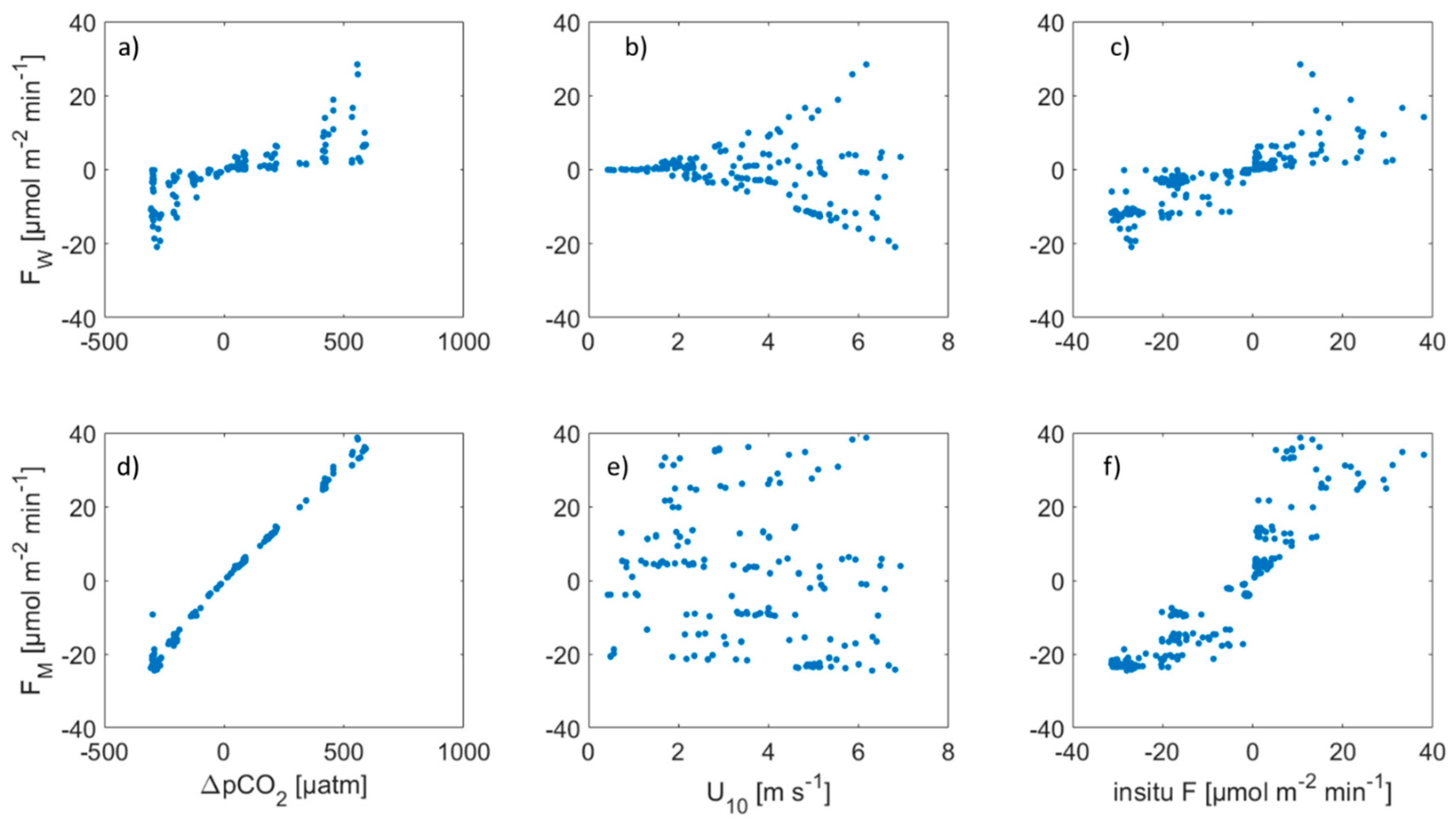
3.1.2. Comparison of Zero Intercept and Nonzero Intercept Parameterizations
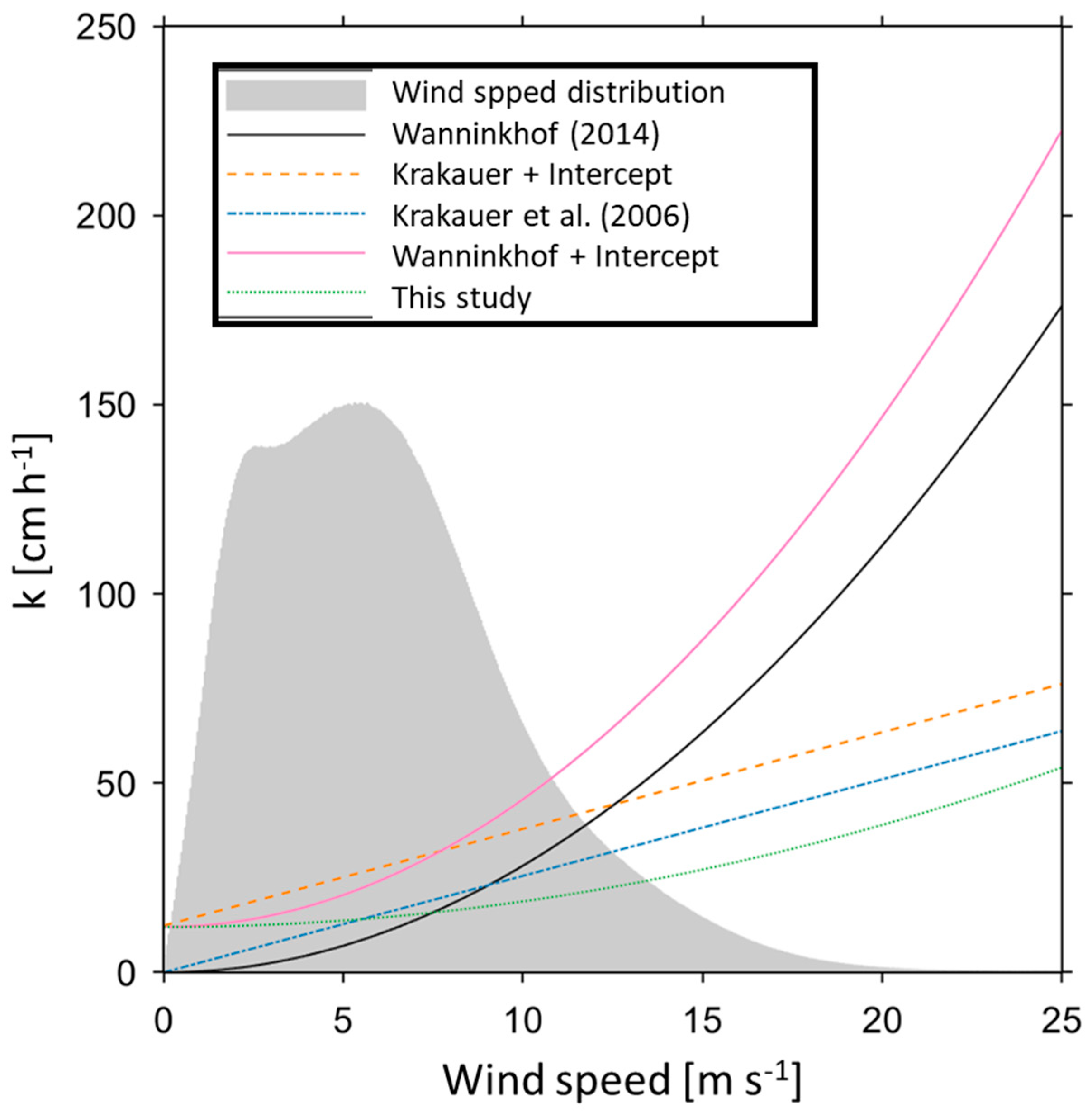
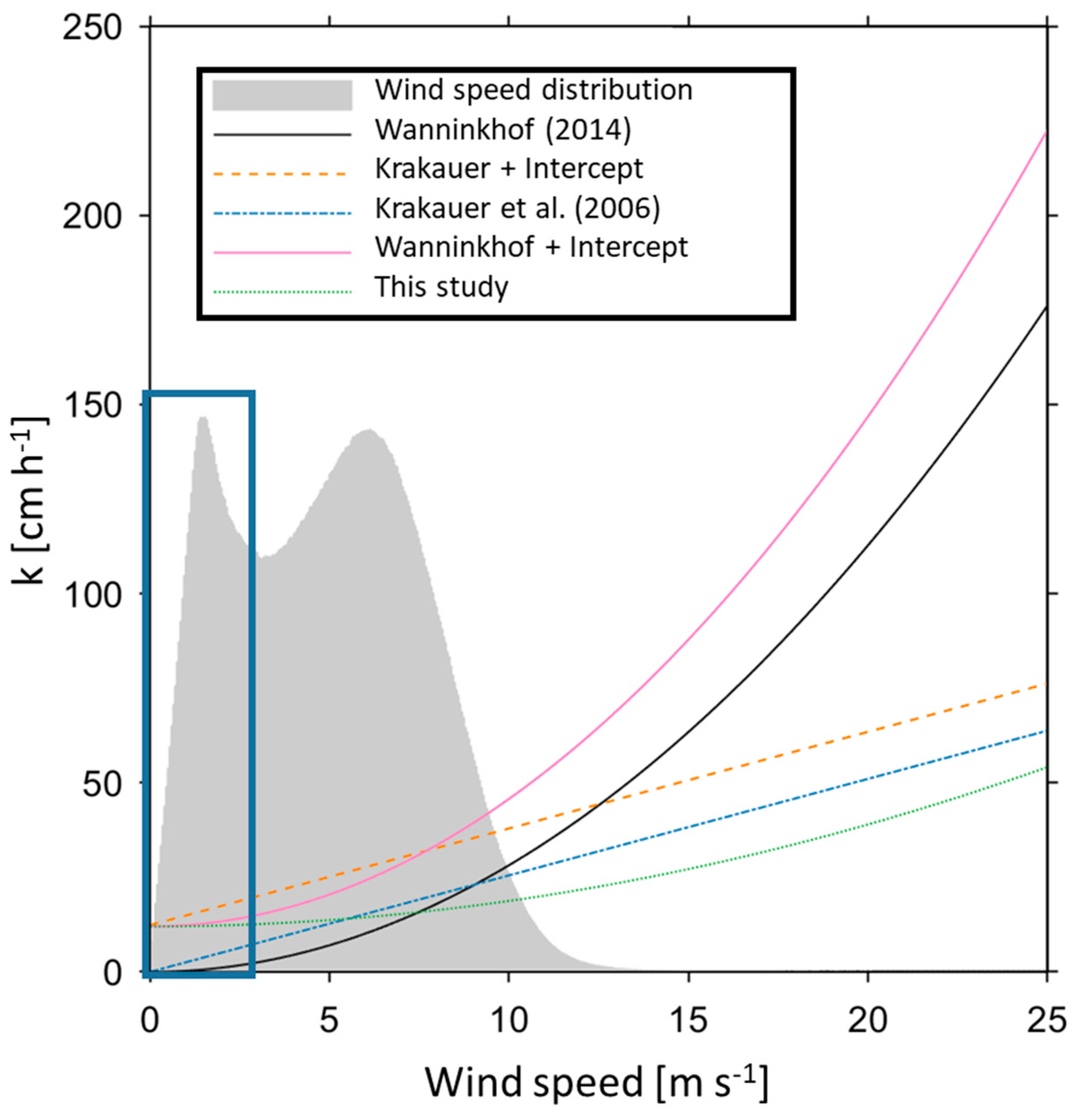
3.2. Application of Nonzero Intercept Parameterizations within Different Frameworks
3.2.1. Use and Description of Parameterizations
- From 0–11 m s−1, parametrizations with a nonzero intercept were similar, and parametrizations without an intercept were similar. This was the wind region for which the implementation of a nonzero intercept was relevant for global FCO2.
- Above 11 m s−1, the groups were quadratic parameterizations with higher slope versus linear or quadratic with lower slope. The nonzero intercept had no impact on FCO2, because bubble-mediated transport may dominate the FCO2. Therefore, this wind regime is not further discussed, and details on gas transfer at the high wind speed regimes can be found in Krall and Jähne [47], McNeil and D’Asaro [48].
3.2.2. Surface Ocean Observation-Based Method
3.2.3. Tropical Ocean
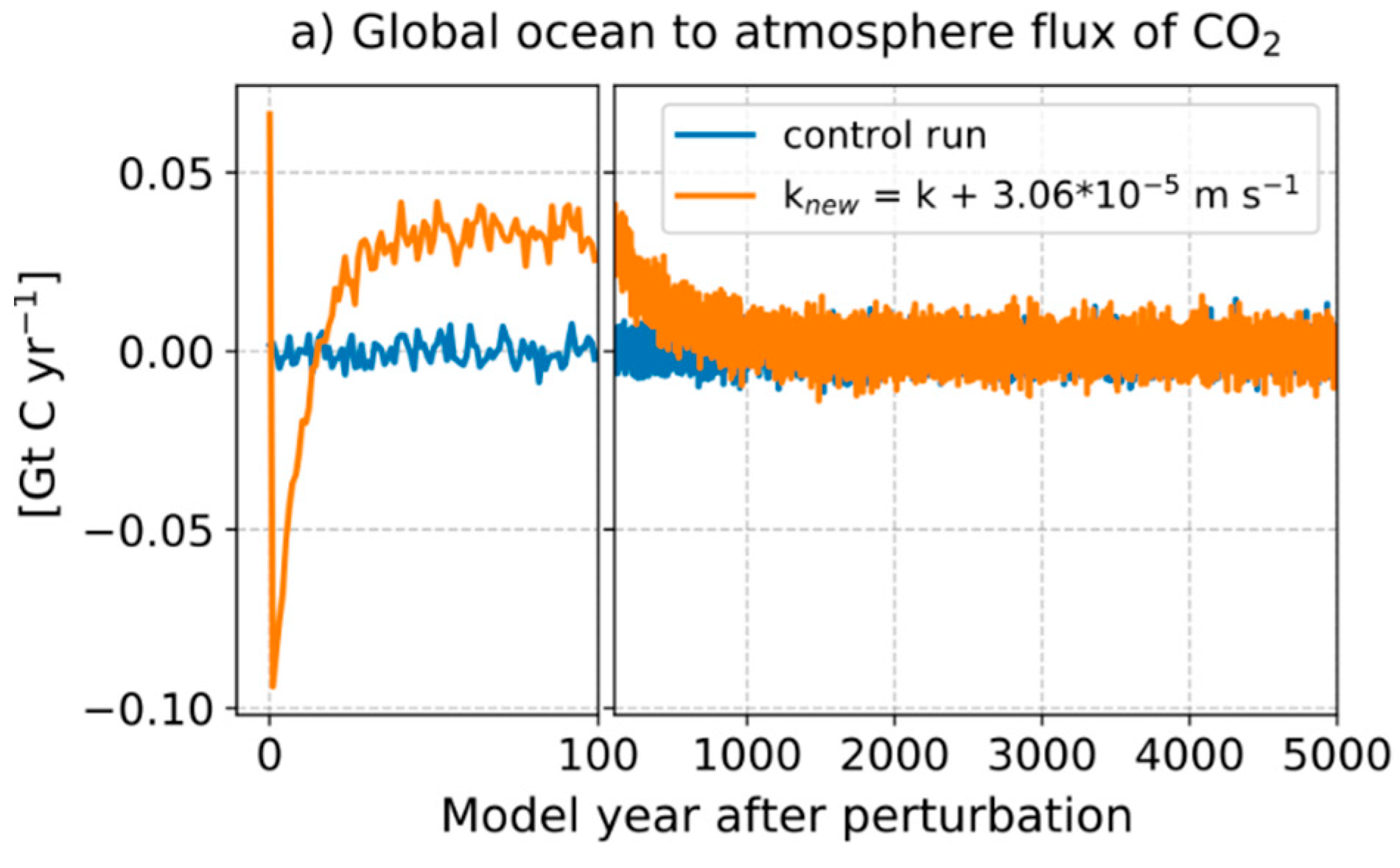
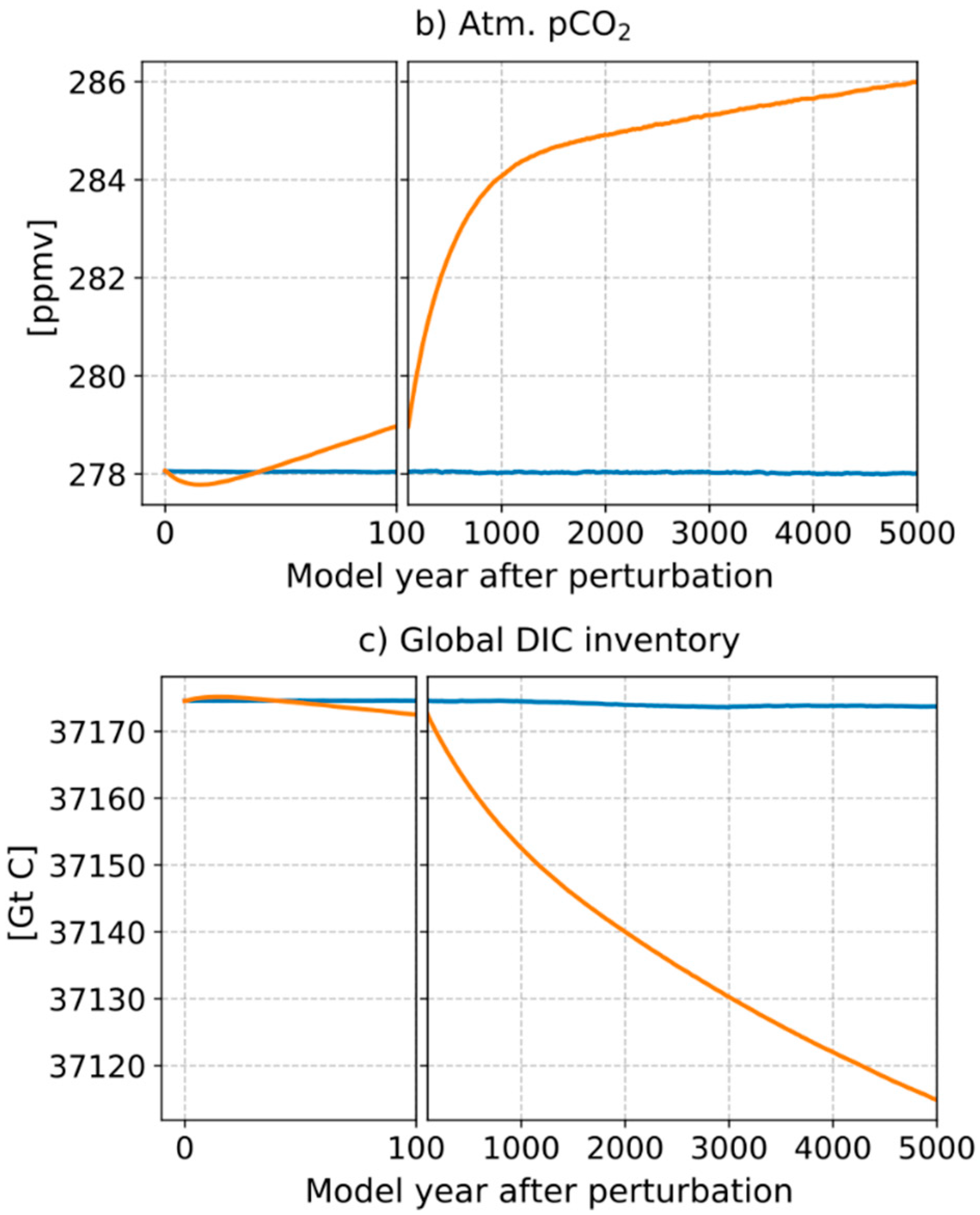
3.2.4. Bern3D Ocean Model
3.2.5. Global Evolution
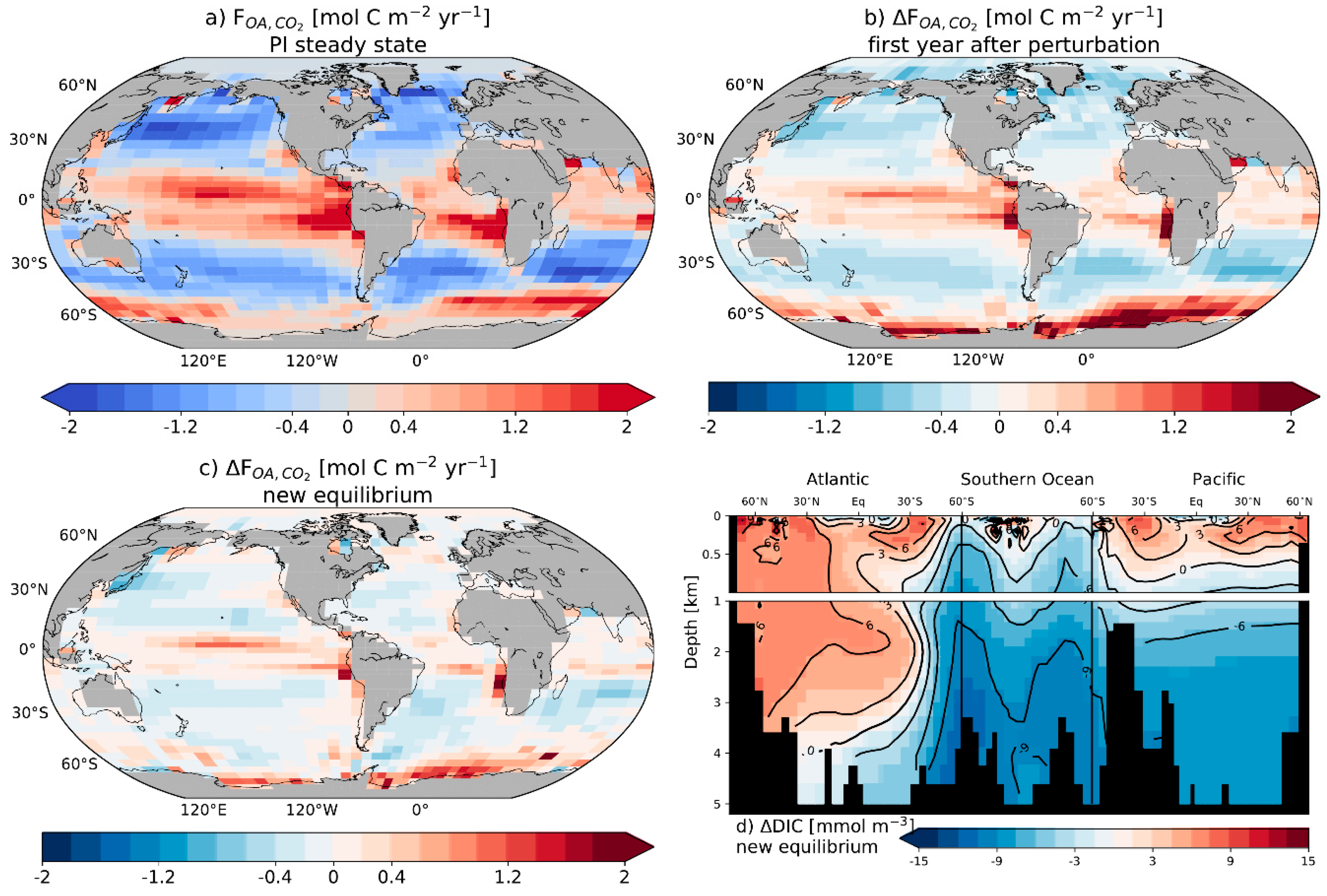
3.2.6. Regional Patterns
4. Discussion
4.1. Global Ocean-Atmospher Carbon Fluxes Based on Observations of pCO2
4.2. Regional Patterns
4.3. Inference of Nonzero Intercept Parameterizations Based on Observations
4.4. Implications in Ocean Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global carbon budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar]
- Weiss, R.F. Carbon dioxide in water and seawater: The solubility of a non–ideal gas. Mar. Chem. 1974, 2, 203–215. [Google Scholar] [CrossRef]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 2014, 12, 351–362. [Google Scholar] [CrossRef]
- Johnson, M.T. A numerical scheme to calculate temperature and salinity dependent air–water transfer velocities for any gas. Ocean Sci. 2010, 6, 913–932. [Google Scholar] [CrossRef]
- Archer, C.L.; Jacobson, M.Z. Evaluation of global wind power. J. Geophys. Res. Atmos. 2005, 110, D12110. [Google Scholar] [CrossRef]
- Wurl, O.; Stolle, C.; Van Thuoc, C.; The Thu, P.; Mari, X. Biofilm-like properties of the sea surface and predicted effects on air-sea CO2 exchange. Prog. Oceanogr. 2016, 144, 15–24. [Google Scholar] [CrossRef]
- Rödenbeck, C.; Bakker, D.C.E.; Gruber, N.; Iida, Y.; Jacobson, A.R.; Jones, S.; Landschützer, P.; Metzl, N.; Nakaoka, S.; Olsen, A.; et al. Data-based estimates of the ocean carbon sink variability – first results of the surface ocean pCO2 mapping intercomparison (socom). Biogeosciences 2015, 12, 7251–7278. [Google Scholar]
- Landschützer, P.; Gruber, N.; Bakker, D.; Schuster, U. Recent variability of the global ocean carbon sink. Global Biogeochem. Cy. 2014, 28, 927–949. [Google Scholar] [CrossRef]
- Mustaffa, N.I.H.; Ribas-Ribas, M.; Banko-Kubis, H.M.; Wurl, O. In situ CO2 transfer velocity reduction by natural surfactants in the sea surface microlayer. in preparation.
- McGillis, W.R.; Edson, J.B.; Zappa, C.J.; Ware, J.D.; McKenna, S.P.; Terray, E.A.; Hare, J.E.; Fairall, C.W.; Drennan, W.; Donelan, M. Air-sea CO2 exchange in the equatorial pacific. J. Geophys. Res. Oceans 2004, 109, C08S02. [Google Scholar] [CrossRef]
- Butterworth, B.J.; Miller, S.D. Air-sea exchange of carbon dioxide in the southern ocean and antarctic marginal ice zone. Geophys. Res. Lett. 2016, 43, 7223–7230. [Google Scholar] [CrossRef]
- Borges, A.V.; Delille, B.; Schiettecatte, L.-S.; Gazeau, F.; Abril, G.; Frankignoulle, M. Gas transfer velocities of CO2 in three european estuaries (randers fjord, scheldt, and thames). Limnol. Oceanogr. 2004, 49, 1630–1641. [Google Scholar] [CrossRef]
- Frankignoulle, M.; Gattuso, J.-P.; Biondo, R.; Bourge, I.; Copin-Montégut, G.; Pichon, M. Carbon fluxes in coral reefs. Ii. Eulerian study of inorganic carbon dynamics and measurement of air-sea CO2 exchanges. Mar. Ecol. Prog. Ser. 1996, 145, 123–132. [Google Scholar] [CrossRef]
- Kremer, J.N.; Reischauer, A.; D’Avanzo, C. Estuary-specific variation in the air-water gas exchange coefficient for oxygen. Estuaries Coasts 2003, 26, 829–836. [Google Scholar] [CrossRef]
- Ribas-Ribas, M.; Helleis, F.; Rahlff, J.; Wurl, O. Air-sea CO2-exchange in a large annular wind-wave tank and the effects of surfactants. Front. Mar. Sci. 2018, 5, 457. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, W.J. On some biases of estimating the global distribution of air-sea CO2 flux by bulk parameterizations. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Soloviev, A.; Schluessel, P. A model of air-sea gas exchange incorporating the physics of the turbulent boundary layer and the properties of the sea surface. In Gas Transfer at Water Surfaces; Donelan, M., Ed.; AGU: Washington, DC, USA, 2002; Volume 127, pp. 141–146. [Google Scholar]
- Monahan, E.C.; Spillane, M.C. The role of oceanic whitecaps in air-sea gas exchange. In Gas Transfer at Water Surfaces; Brutsaert, W., Jirka, G.H., Eds.; Springer: New York, NY, USA, 1984; pp. 495–503. [Google Scholar]
- Asher, W.E.; Jessup, A.T.; Atmane, M.A. Oceanic application of the active controlled flux technique for measuring air-sea transfer velocities of heat and gases. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Banko-Kubis, H.M.; Wurl, O.; Mustaffa, N.I.H.; Ribas-Ribas, M. Gas transfer velocities in norwegian fjords and the adjacent north atlantic waters. Oceanologia 2019, 61. [Google Scholar] [CrossRef]
- Zappa, C.J.; McGillis, W.R.; Raymond, P.A.; Edson, J.B.; Hintsa, E.J.; Zemmelink, H.J.; Dacey, J.W.; Ho, D.T. Environmental turbulent mixing controls on air–water gas exchange in marine and aquatic systems. Geophys. Res. Lett. 2007, 34, L10601. [Google Scholar] [CrossRef]
- Wanninkhof, R.; Asher, W.E.; Ho, D.T.; Sweeney, C.; McGillis, W.R. Advances in quantifying air–sea gas exchange and environmental forcing. Annu. Rev. Marine Sci. 2009, 1, 213–244. [Google Scholar] [CrossRef]
- Ribas-Ribas, M.; Kilcher, L.F.; Wurl, O. Sniffle: A step forward to measure in situ CO2 fluxes with the floating chamber technique. Elem. Sci. Anth. 2018, 6, 14. [Google Scholar] [CrossRef]
- Ribas-Ribas, M.; Mustaffa, N.I.H.; Rahlff, J.; Stolle, C.; Wurl, O. Sea surface scanner (s3): A catamaran for high–resolution measurements of biogeochemical properties of the sea surface microlayer. J. Atmos. Ocean Tech. 2017, 34, 1433–1448. [Google Scholar] [CrossRef]
- Stolle, C.; Ribas-Ribas, M.; Badewien, T.H.; Carpenter, L.J.; Chance, R.; Damgaard, L.R.; Quesada, A.M.D.; Engel, A.; Frka, S.; Galgani, L.; et al. The milan campaign: Studying diel light effects on the air-sea interface. B Am. Meteorol. Soc. under revision.
- Mesarchaki, E.; Kräuter, C.; Krall, K.; Bopp, M.; Helleis, F.; Williams, J.; Jähne, B. Measuring air–sea gas-exchange velocities in a large-scale annular wind–wave tank. Ocean Sci. 2015, 11, 121–138. [Google Scholar] [CrossRef]
- Taylor, J. Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements; University Science Book: Sausalito, CA, USA, 1997. [Google Scholar]
- Rödenbeck, C.; Keeling, R.F.; Bakker, D.C.E.; Metzl, N.; Olsen, A.; Sabine, C.; Heimann, M. Global surface-ocean pCO2 and sea–air CO2 flux variability from an observation-driven ocean mixed-layer scheme. Ocean Sci. 2013, 9, 193–216. [Google Scholar] [CrossRef]
- Bakker, D.C.E.; Pfeil, B.; Landa, C.S.; Metzl, N.; O’Brien, K.M.; Olsen, A.; Smith, K.; Cosca, C.; Harasawa, S.; Jones, S.D.; et al. A multi-decade record of high-quality fCO2 data in version 3 of the surface ocean CO2 atlas (socat). Earth Syst. Sci. Data 2016, 8, 383–413. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P. The era-interim reanalysis: Configuration and performance of the data assimilation system. QJ Roy. Meteor. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Rödenbeck, C.; Bakker, D.C.E.; Metzl, N.; Olsen, A.; Sabine, C.; Cassar, N.; Reum, F.; Keeling, R.F.; Heimann, M. Interannual sea–air CO2 flux variability from an observation-driven ocean mixed-layer scheme. Biogeosciences 2014, 11, 4599–4613. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Randerson, J.T.; Primeau, F.W.; Gruber, N.; Menemenlis, D. Carbon isotope evidence for the latitudinal distribution and wind speed dependence of the air–sea gas transfer velocity. Tellus 2006, 58B, 390–417. [Google Scholar] [CrossRef][Green Version]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 1992, 97, 7373–7382. [Google Scholar] [CrossRef]
- Müller, S.; Joos, F.; Edwards, N.; Stocker, T. Water mass distribution and ventilation time scales in a cost-efficient, three-dimensional ocean model. J. Clim. 2006, 19, 5479–5499. [Google Scholar] [CrossRef]
- Griffies, S.M. The gent–mcwilliams skew flux. J. Phys. Oceanogr. 1998, 28, 831–841. [Google Scholar] [CrossRef]
- Ritz, S.P.; Stocker, T.F.; Joos, F. A coupled dynamical ocean–energy balance atmosphere model for paleoclimate studies. J. Clim. 2011, 24, 349–375. [Google Scholar] [CrossRef]
- Tschumi, T.; Joos, F.; Gehlen, M.; Heinze, C. Deep ocean ventilation, carbon isotopes, marine sedimentation and the deglacial CO2 rise. Clim. Past 2011, 6, 1895–1958. [Google Scholar] [CrossRef]
- Parekh, P.; Joos, F.; Müller, S.A. A modeling assessment of the interplay between aeolian iron fluxes and iron-binding ligands in controlling carbon dioxide fluctuations during antarctic warm events. Paleoceanography 2008, 23. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The ncep/ncar 40-year reanalysis project. B Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Roth, R. Modeling forcings and responses in the global carbon cycle-climate system: Past, present and future. Verlag nicht ermittelbar, 2013. Available online: http://work.bergophil.ch/roth13phd.pdf (accessed on 15 May 2019).
- Roth, R.; Ritz, S.P.; Joos, F. Burial-nutrient feedbacks amplify the sensitivity of atmospheric carbon dioxide to changes in organic matter remineralisation. Earth Syst. Dyn. 2014, 5, 321–343. [Google Scholar] [CrossRef]
- Battaglia, G.; Steinacher, M.; Joos, F. A probabilistic assessment of calcium carbonate export and dissolution in the modern ocean. Biogeosciences 2016, 13, 2823–2848. [Google Scholar] [CrossRef]
- Najjar, R.; Orr, J. Biotic—howto, Internal Ocmip Report; LSCE/CEA Saclay: Gifsur-Yvette, France, 1999. [Google Scholar]
- Orr, J.; Najjar, R.; Sabine, C.; Joos, F. Abiotic-howto, Internal Ocmip Report; LSCE/CEA Saclay: Gifsur-Yvette, France, 1999. [Google Scholar]
- Orr, J.; Epitalon, J.-M. Improved routines to model the ocean carbonate system: Mocsy 2.0. Geosci. Model Dev. 2015, 8, 485–499. [Google Scholar] [CrossRef]
- Müller, S.; Joos, F.; Plattner, G.K.; Edwards, N.; Stocker, T. Modeled natural and excess radiocarbon: Sensitivities to the gas exchange formulation and ocean transport strength. Global Biogeochem. Cy. 2008, 22. [Google Scholar] [CrossRef]
- Krall, K.E.; Jähne, B. First laboratory study of air–sea gas exchange at hurricane wind speeds. Ocean Sci. 2014, 10, 257–265. [Google Scholar] [CrossRef]
- McNeil, C.; D’Asaro, E. Parameterization of air–sea gas fluxes at extreme wind speeds. J. Marine Syst. 2007, 66, 110–121. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Orr, J.C.; Siegenthaler, U. A perturbation simulation of CO2 uptake in an ocean general circulation model. J. Geophys. Res. Oceans 1992, 97, 3621–3645. [Google Scholar] [CrossRef]
- Graven, H.D.; Gruber, N.; Key, R.; Khatiwala, S.; Giraud, X. Changing controls on oceanic radiocarbon: New insights on shallow-to-deep ocean exchange and anthropogenic CO2 uptake. J. Geophys. Res. Oceans 2012, 117, C10005. [Google Scholar] [CrossRef]
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.G.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Carbon and other biogeochemical cycles. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group i to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Landschützer, P.; Gruber, N.; Haumann, F.A.; Rödenbeck, C.; Bakker, D.C.; Van Heuven, S.; Hoppema, M.; Metzl, N.; Sweeney, C.; Takahashi, T. The reinvigoration of the southern ocean carbon sink. Science 2015, 349, 1221–1224. [Google Scholar] [CrossRef]
- Takahashi, T.; Sutherland, S.C.; Wanninkhof, R.; Sweeney, C.; Feely, R.A.; Chipman, D.W.; Hales, B.; Friederich, G.; Chavez, F.; Sabine, C. Climatological mean and decadal change in surface ocean pCO2, and net sea–air CO2 flux over the global oceans. Deep Sea Res. Part. II: Top. Stud. Oceanogr. 2009, 56, 554–577. [Google Scholar] [CrossRef]
- McNeil, B.I.; Metzl, N.; Key, R.M.; Matear, R.J.; Corbiere, A. An empirical estimate of the southern ocean air-sea CO2 flux. Global Biogeochem. Cy. 2007, 21. [Google Scholar] [CrossRef]
- Donelan, M.; Wanninkhof, R. Gas transfer at water surfaces—concepts and issues. In Gas Transfer at Water Surfaces; Donelan, M., Drennan, W.M., Saltzman, E.S., Eds.; American Geophysical Union: Washington, DC, USA, 2001; pp. 1–10. [Google Scholar]
- Crusius, J.; Wanninkhof, R. Gas transfer velocities measured at low wind speed over a lake. Limnol. Oceanogr. 2003, 48, 1010–1017. [Google Scholar] [CrossRef]
- Crill, P.M.; Bartlett, K.B.; Wilson, J.O.; Sebacher, D.I.; Harriss, R.C.; Melack, J.M.; MacIntyre, S.; Lesack, L.; Smith-Morrill, L. Tropospheric methane from an amazonian floodplain lake. J. Geophys. Res. Atmos. 1988, 93, 1564–1570. [Google Scholar] [CrossRef]
- Wanninkhof, R.; Knox, M. Chemical enhancement of CO2 exchange in natural waters. Limnol. Oceanogr. 1996, 41, 689–697. [Google Scholar] [CrossRef]
- Frew, N.M.; Bock, E.J.; Schimpf, U.; Hara, T.; Haußecker, H.; Edson, J.B.; McGillis, W.R.; Nelson, R.K.; McKenna, S.P.; Uz, B.M. Air–sea gas transfer: Its dependence on wind stress, small–scale roughness, and surface films. J. Geophys. Res. Oceans 2004, 109, C08S17. [Google Scholar] [CrossRef]
- Ho, D.T.; Asher, W.E.; Bliven, L.F.; Schlosser, P.; Gordan, E.L. On mechanisms of rain-induced air-water gas exchange. J. Geophys. Res. Oceans 2000, 105, 24045–24057. [Google Scholar] [CrossRef]
- MacIntyre, S.; Eugster, W.; Kling, G.W. The critical importance of buoyancy flux for gas flux across the air-water interface. Geophysical Monograph-American Geophysical Union 2002, 127, 135–140. [Google Scholar]
- Fairall, C.; Hare, J.; Edson, J.; McGillis, W. Parameterization and micrometeorological measurement of air–sea gas transfer. Boundary Layer Meteorol. 2000, 96, 63–106. [Google Scholar] [CrossRef]
- Chen, C.-T.A.; Borges, A.V. Reconciling opposing views on carbon cycling in the coastal ocean: Continental shelves as sinks and near-shore ecosystems as sources of atmospheric CO2. Deep Sea Res. Part. II: Top. Stud. Oceanogr. 2009, 56, 578–590. [Google Scholar] [CrossRef]
- Raymond, P.A.; Cole, J.J. Gas exchange in rivers and estuaries: Choosing a gas transfer velocity. Estuaries 2001, 24, 312–317. [Google Scholar] [CrossRef]
- Borges, A.V.; Vanderborght, J.-P.; Schiettecatte, L.-S.; Gazeau, F.; Ferrón-Smith, S.; Delille, B.; Frankignoulle, M. Variability of the gas transfer velocity of CO2 in a macrotidal estuary (the scheldt). Estuaries 2004, 27, 593–603. [Google Scholar] [CrossRef]
- Cole, J.J.; Caraco, N.F. Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of sf6. Limnol. Oceanogr. 1998, 43, 647–656. [Google Scholar] [CrossRef]
- McGillis, W.R.; Edson, J.B.; Hare, J.E.; Fairall, C.W. Direct covariance air-sea CO2 fluxes. J. Geophys. Res. Oceans 2001, 106, 16729–16745. [Google Scholar] [CrossRef]
- Broecker, W.S.; Peng, T.H. Tracers in the Sea; Lamont-Doherty Geological Observatory: Palisades, NY, USA, 1982. [Google Scholar]
| Cruise ID | Research Vessels | Start Date | End Date | Year | Area | # obs | Ref. |
|---|---|---|---|---|---|---|---|
| M117 | Meteor | 1 August | 12 August | 2015 | Baltic Sea | 19 | |
| FK161010 | Falkor | 12 October | 6 November | 2016 | Timor Sea | 60 | [9] |
| HE491 | Heincke | 10 July | 25 July | 2017 | Norwegian fjords & coastal North Atlantic | 47 | [9,20] |
| EMB184 | Elisabeth Mann Borgese | 1 June | 10 June | 2018 | Baltic Sea | 56 | |
| 31 March | 2 August | 2016 | Jade Bay * | 34 | [23] | ||
| 3 April | 4 September | 2017 | Jade Bay * | 29 | [25] |
| Parameterization Name | Reference | Used in: | |
|---|---|---|---|
| Wanninkhof (W) | [3] | kW = 0.251 U102 | Sniffle & SOCAT |
| This study | kM = 5.7 + 0.23 U102 | Sniffle & SOCAT | |
| Wanninkhof + Intercept (W+I) | [15] | kW+I = 10.7 + 0.30 U102 | SOCAT |
| Krakauer (K) | [32] | kK = 2.275 * U10 | SOCAT & Bern3D |
| Krakauer + Intercept (K+I) | kK+I = 11 + 2.275 * U10 | SOCAT & Bern3D |
| Comparison Statistics | FX = P1 * F Insitu + P2 | ||||
|---|---|---|---|---|---|
| r | RMSE | R-Squared | P1 | P2 | |
| FM | 0.9122 | 6.9142 | 0.832 | 0.881 (0.831, 0.931) | 2.928 (2.165, 3.691) |
| FW | 0.8262 | 10.2064 | 0.682 | 0.398 (0.364, 0.432) | 0.657 (0.133, 1.180) |
| Areas | FW | FK | FM | FW+I | FK+I | FW-FM | |
|---|---|---|---|---|---|---|---|
| Global | −2.56 | −2.27 | −1.83 | −4.28 | −3.52 | −0.73 | |
| Southern | 60° S – 80° S | −0.02 | −0.02 | −0.02 | −0.03 | −0.04 | 0.00 |
| 180° W – 180° E | |||||||
| North Atlantic | 65° N – 30° N | −0.18 | −0.17 | −0.15 | −0.32 | −0.28 | −0.03 |
| 55° W – 15° W | |||||||
| Tropical | 14° N – 14° S | 0.28 | 0.41 | 0.43 | 0.70 | 0.78 | −0.16 * |
| 180° W – 180° E | |||||||
| South Atlantic | 20° S – 40° S | −0.15 | −0.15 | −0.13 | −0.27 | −0.25 | −0.01 |
| 40° W – 10° E | |||||||
| South Pacific | 20° S – 40° S | −0.34 | −0.36 | −0.31 | −0.64 | −0.59 | −0.03 |
| 155° W – 80° E |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribas-Ribas, M.; Battaglia, G.; Humphreys, M.P.; Wurl, O. Impact of Nonzero Intercept Gas Transfer Velocity Parameterizations on Global and Regional Ocean–Atmosphere CO2 Fluxes. Geosciences 2019, 9, 230. https://doi.org/10.3390/geosciences9050230
Ribas-Ribas M, Battaglia G, Humphreys MP, Wurl O. Impact of Nonzero Intercept Gas Transfer Velocity Parameterizations on Global and Regional Ocean–Atmosphere CO2 Fluxes. Geosciences. 2019; 9(5):230. https://doi.org/10.3390/geosciences9050230
Chicago/Turabian StyleRibas-Ribas, Mariana, Gianna Battaglia, Matthew P. Humphreys, and Oliver Wurl. 2019. "Impact of Nonzero Intercept Gas Transfer Velocity Parameterizations on Global and Regional Ocean–Atmosphere CO2 Fluxes" Geosciences 9, no. 5: 230. https://doi.org/10.3390/geosciences9050230
APA StyleRibas-Ribas, M., Battaglia, G., Humphreys, M. P., & Wurl, O. (2019). Impact of Nonzero Intercept Gas Transfer Velocity Parameterizations on Global and Regional Ocean–Atmosphere CO2 Fluxes. Geosciences, 9(5), 230. https://doi.org/10.3390/geosciences9050230







