1. Introduction
It has been observed that soil pipes are often located at the sites of landslides [
1,
2,
3,
4]. Based on field observations at the sites of landslides in previous studies, it has been suggested that there is a relationship between the presence of soil pipes and the incidence of landslides. Moreover, Uchida et al. [
5] reported that soil pipes have been observed in natural vegetated hillslopes with a variety of soil types, such as brown forest soil, clay loam decomposed granite, silt and loam soil, peaty podzol, etc. In particular, it has been pointed out that soil pipes influence hillslope hydrological processes, such as runoff from soil pipe outlets [
4,
6]. For example, Kitahara [
4] and Jones [
6] indicated that the amount of pipe flow plays a large role in the runoff from the side hillslopes on river discharge, thus influencing river flow in first order streams. Numerical simulations have been carried out to elucidate the roles of soil pipes in landslides and the hydrological processes of hillslopes. Kosugi et al. [
7] showed that the pore water pressure increases with the length of clogged soil pipes. Tsutsumi et al. [
8] carried out numerical simulations to verify the effect of soil pipe roughness on the hydrological features of soil pipes using finite element methods (FEMs), and showed that locations where the pipe is very rough affect the flow through the soil pipe and piezometric head. Moreover, Uchida and Mizuyama [
9] carried out field observations and numerical simulations, and concluded that the buildup of pore water pressure and decreasing slope safety factor caused by the clogging of the soil pipes supports the hypothesis that soil pipes affect landslides induced by peak rainfall.
However, there are several limitations to understanding the influence of soil pipes on landslides and hydrological processes through only the use of field investigations and numerical simulations. In field observations, it can be very difficult to comprehend the hydraulic conditions during the landslide process such as the build-up of pore water pressure using piezometers, owing to a lack of prior spatial information with regard to its occurrence. In the numerical simulation, it is also quite difficult to estimate the parameters such as hydraulic conductivity or flow discharge of the soil pipes in hill slopes. Hence, model experiments have been carried out to clarify the influence of soil pipes on runoff generation during and after rainfall, fluctuations in groundwater levels, and buildup of pore water pressure on landslide occurrence [
1,
10,
11,
12,
13,
14,
15]. Pierson [
1] found that the pore water pressure is higher when the end of a pipe is closed. Tada et al. [
10] carried out model experiments with a valve representing a clog, and found that although pipes stabilize model slopes when their lower ends are open to air, soil pipes destabilize model slopes when they become clogged. Similar results have been reported in other experiments [
1,
11,
15].
Recently, Yamasaki et al. [
16] discussed the influence of the air in the soil pipe on the water flow in a closed pipe. They also indicated that the soil pipe flow occurs only when soil air can escape freely from the soil pipe to the atmosphere, and air entrapment in the soil pipes may be affected by soil water and air flow in the soil matrix around the soil pipe. Moreover, several researchers argued about the effects of entrapped air in the soil layer on hydrological processes (e.g., [
16,
17,
18,
19,
20,
21]). These studies revealed that the entrapped air contributed rapid increase of pore water pressure and enhanced hillslope discharge through field observation and laboratory experiments.
So, it has been considered that the entrapped pore air in the soil layer could induce slope instability, because of a quick and large groundwater table increase [
19,
20,
21]. For example, Liu et al. [
21] pointed that pore air pressure by rainfall infiltration can increase sharply at difference locations and that the pore air pressure can also cause a rapid decrease in the slope safety factor by numerical simulation. They also indicated that pore air pressure throughout the whole unsaturated zone has the same value, which means that the air pressure could spread quickly to the whole sample by laboratory experiment.
Thus, to understand the influence of soil pipe on the build-up of the pore water pressure, we need to discuss the effects of soil pipe and entrapped air together on the build-up of the pore water pressure.
However, it is difficult to confirm whether previous model experiments perfectly describe the features of soil pipes that have been observed in field research. Hence, we focus on three main factors in this paper. The first factor is the form of the soil pipe. Most previous model experiments were carried out with straight pipes. However, soil pipes in mountain slopes branch and merge repeatedly [
4,
22,
23]. The second factor is whether the flow in the soil pipe is under pressure. To understand the effects of pipes on the build-up of pore water pressure, we need to consider the pressured flow. There has been one study showing that the pressure in a pipe flow depends on the pipe drainage capacity [
22]. Moreover, it has been pointed out that pipe flow discharge depends on the water content of the surrounding soil and upstream of the pipe [
24,
25]. However, previous experiments were carried out with model slopes that were up to one to two metres in length, and the water supply system consisted of an artificial rainfall simulator, or supplied a fixed amount of water to the top of the model slope. Hence, it is difficult to determine whether the water content upstream of the soil pipe affects the flow in the soil pipe or the build-up of pore water pressure. The third factor to consider is the entrapped air. Previous reports have noted that entrapped air in the soil layer can increase the pore water pressure [
16,
17,
18,
19,
20,
21]. As Yamasaki et al. [
16] noted, soil pipes usually contain relatively large voids. However, there have been few experiments on the interactions between the build-up of pore water pressure between soil pipes and entrapped air.
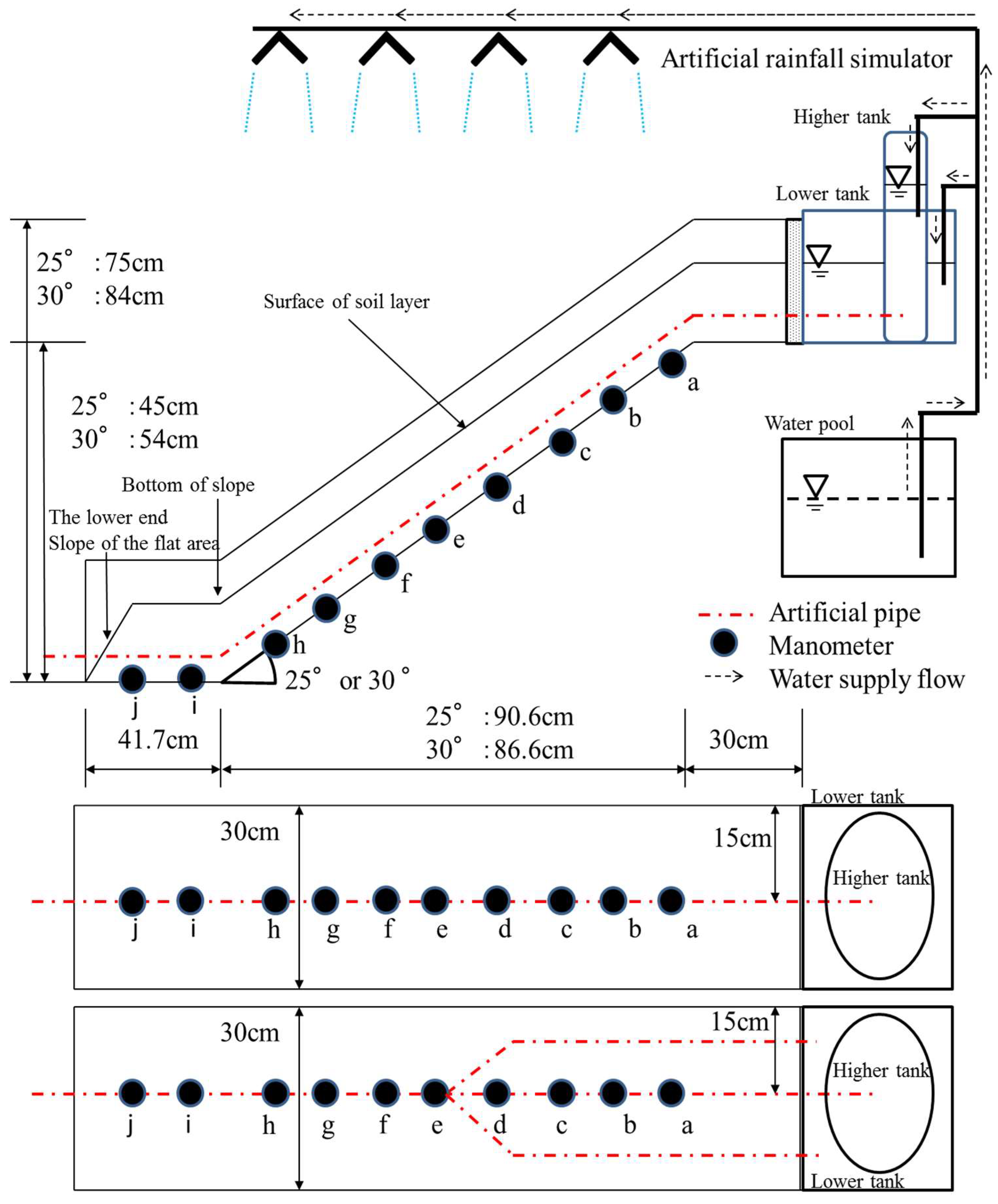
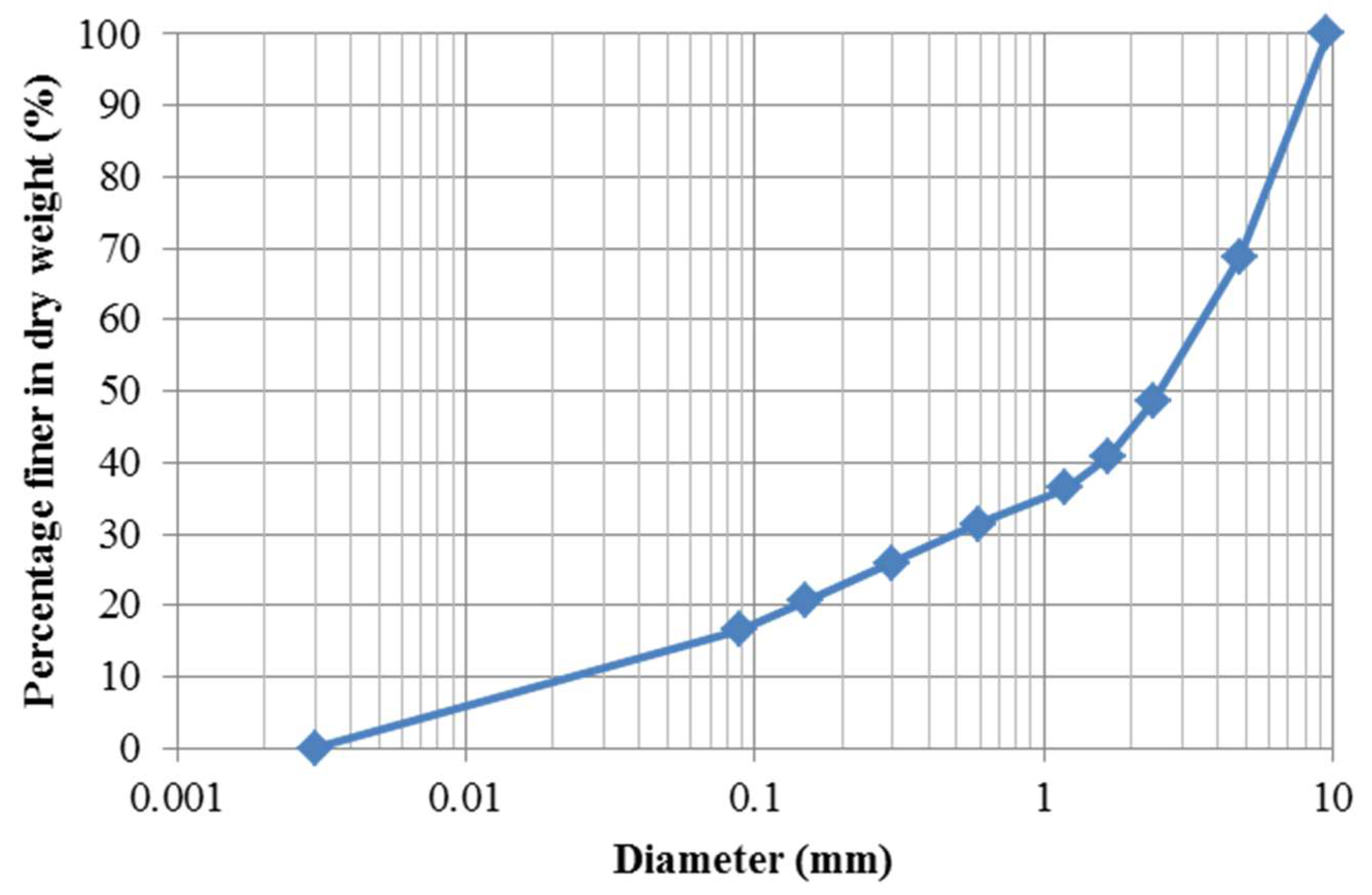
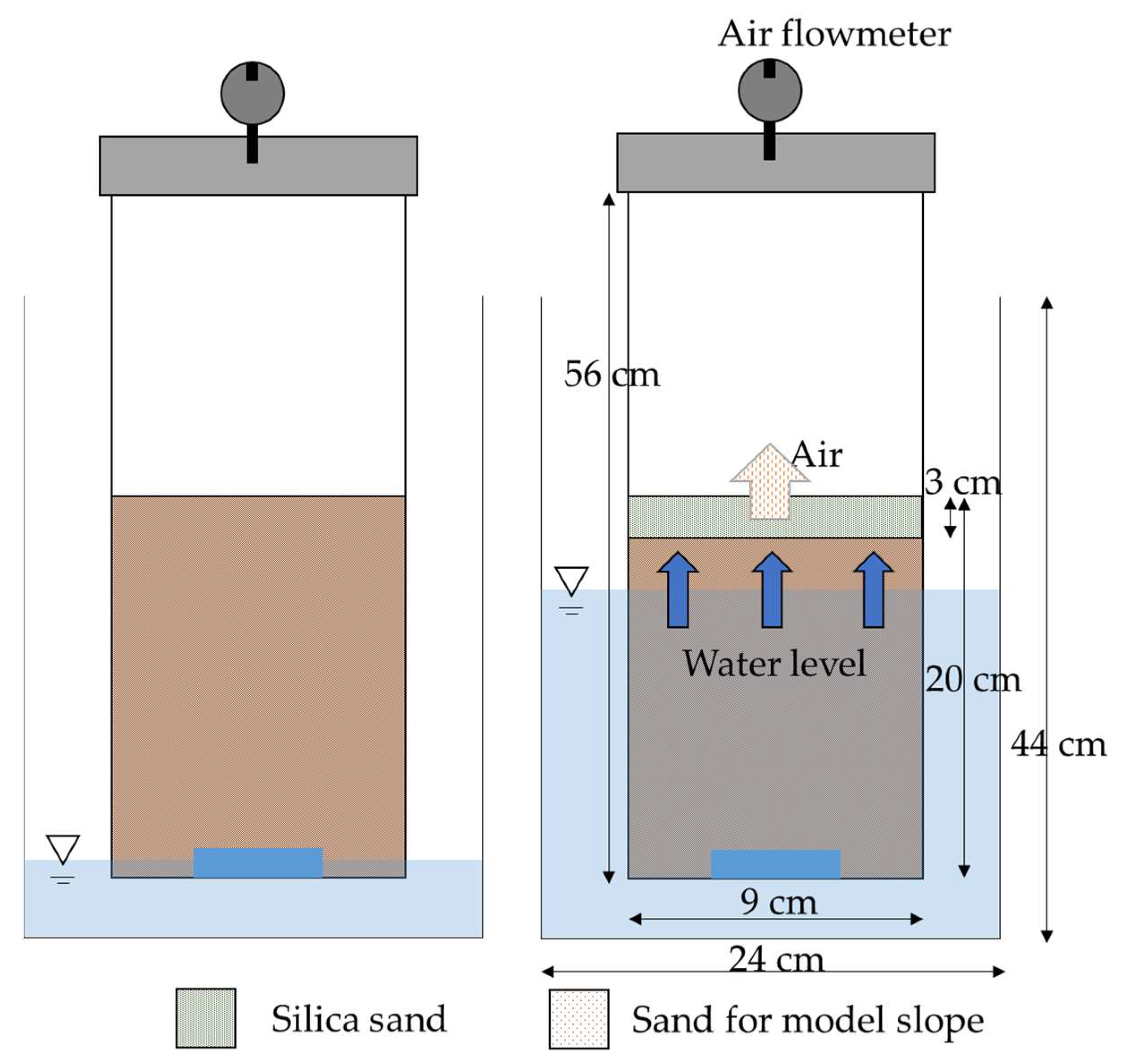
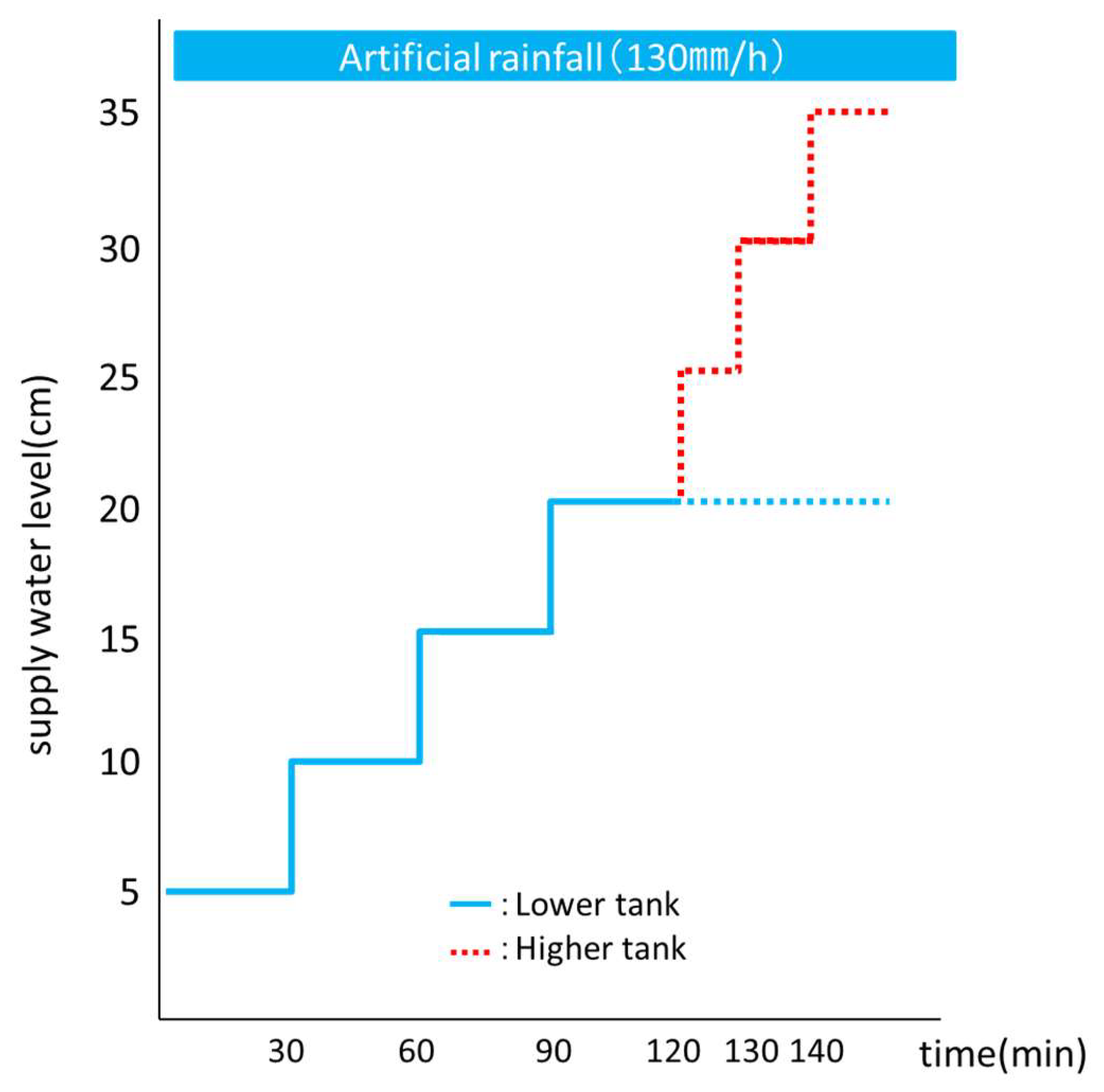
Based on the above, we tested cases with branching and merging pipes so that we could investigate the influence of the confluence of pipes. We also installed a tank to supply water to the pipe and considered the influence of the pressured flow through the pipe on the build-up of pore water pressure. Furthermore, we used finer sand on the model slope to investigate the influence of air trapped in the soil on the build-up of pore water pressure.
4. Discussion
4.1. Influence of Pipes and Entrapped Air on Buildup of Pore Water Pressure
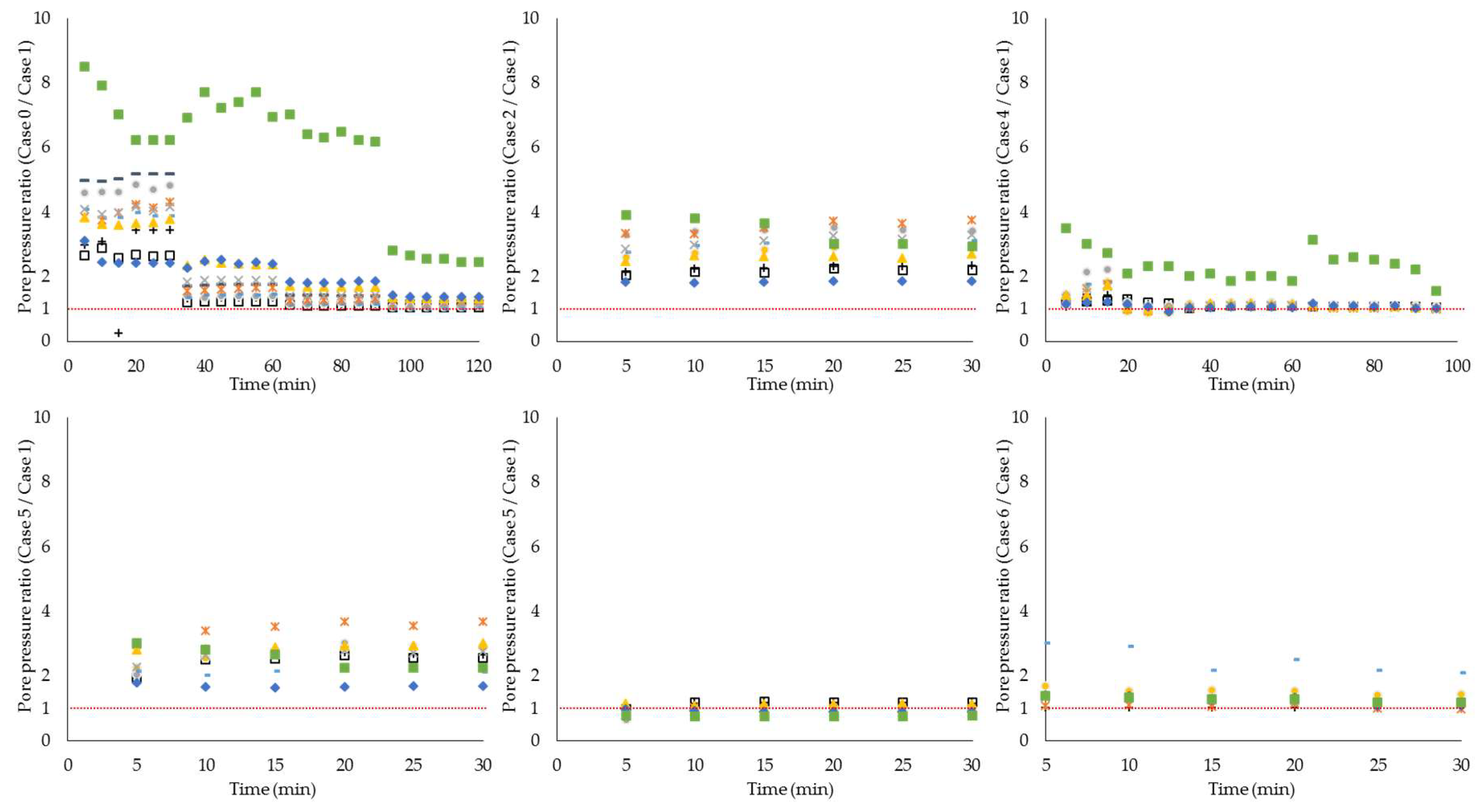
In this experiment, we observed that the drainage capacity of soil pipes varied between the flat area below the slope and the confluence of pipes. Hence, the soil pipe drainage capacity decreased at the bottom of the slope, where the longitudinal gradient of the soil pipes decreased significantly. In Case 1, we used the higher tank. The results obtained from manometers f to h in Case 1, and from manometers g and h in Case 3, suggested that the drainage capacity of the soil pipe was lower in the flat area than halfway down the slope. Hence, the pore water pressure increased more readily in the lower part of the hillslope. Moreover, for the confluence pipe, total drainage capacity became small at the confluence due to a decrease of number of soil pipes. Although the area above the confluence of pipes have a high drainage capacity and decrease pore water pressure, the pore water pressure can become high in this area, as seen in the results of manometers e and f in Case 2 and manometers c to f in Case 5. This trend is especially clear when the water supply level is high as seen in the results of manometer e in Case 2 when the water supply level was 10 cm, and manometers c to e in Case 5 when the water supply level was 10 cm. From these results, it can be thought that the flow in the pipe was pressured by the change of longitudinal gradient and the junction of pipe. Consequently, the pore water pressure in the soil was affected by the high pressure in the pipe.
Based on the results obtained from manometers e to i when using the higher tank to pressure the flow in the pipe, the result imply that the pore water pressure can be directly influenced by the flow from the upper hillslope through the soil pipe, apart from at specific locations influenced by the pipes, even though the pore water pressure in the area immediately upstream of the slope from a given location did not change. Hence, the pressure of the flow in the pipe, enhanced the buildup of pore water pressure.
It has been observed that when the end of the soil pipe is open to the air, the pore water pressure is lower than when there is no soil pipe [
1,
7,
10,
11,
13,
15]. In contrast, the pore water pressure increases when the pipes get clogged, or the ends of the pipes are not open to the air. In these cases, the pore water pressure is higher than in the case without pipes for the same water supply level [
7,
10,
13,
15]. In this experiment, we found that a decrease in the longitudinal gradient of the artificial pipe, and that a confluence of soil pipes has a similar effect to clogged soil pipes. We conjecture that this is because the effect of the area with a relatively low drainage capacity can propagate increases in the pore water pressure.
Moreover, we carried out experiments with slopes with gradients of 25 and 30 degrees, and we observed that it was easier to increase the pore water pressure in the cases with slopes of 30 degrees rather than 25 degrees. Although there are several possible explanations about the processes of this result, we consider that the longitudinal change of drainage capacity of soil pipe should be a key factor of this result. The longitudinal change of drainage capacity of soil pipe in 30 degree slope was larger than that of 25 degree slope. Thus, pore water pressure easily increased in a 30 degree slope, because the flow in the pipe was easily pressured by a relatively large change of drainage capacity of the soil pipe. In the downstream flat area (manometers f to i) in Case 4, and near the confluence of pipes (manometers c to e) in Case 5, the pore water pressure increased more than in other areas. It has been suggested that when the surface of the soil layer is saturated, the pore water pressure is higher than under unsaturated conditions due to the entrapped air [
16,
17,
18,
19,
20,
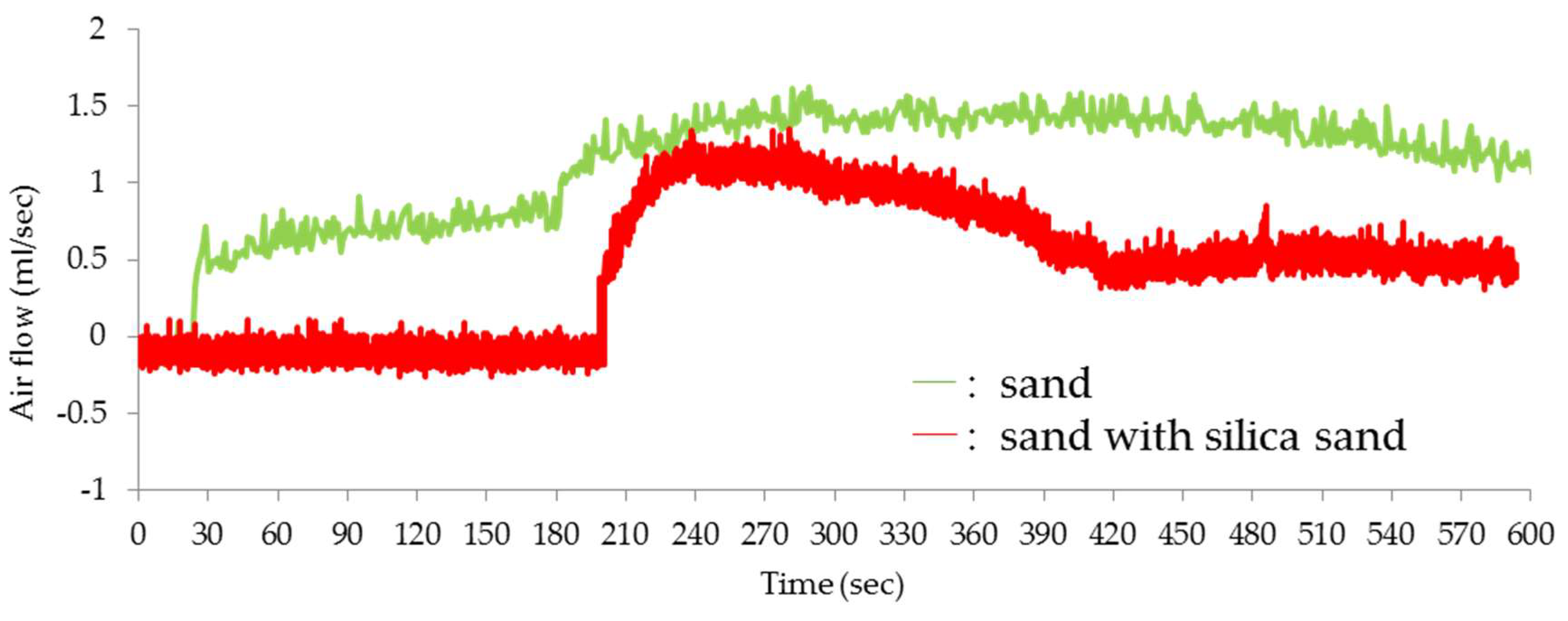
21]. There is a possibility that entrapped air increases the pore water pressure, where we observed increases in the pore water pressure in Cases 4, 5, and 6, which had poor permeability due to the layer of silica sand on the surface of the model slope. The effect of the entrapped air was clear in areas with relatively low drainage capability. This may be due to the fact that the air in the soil layer is compressed, which increases the pore water pressure. In turn, this increases the pressure in the pipe and the amount of water entering the soil layer from the pipe.
It was easier to increase the pore water pressure in the cases with the confluence pipe, than in the cases with the straight pipe. It has been mentioned previously that soil pipes often have merges and branches. Based on these observations, we believe that, in addition to clogs in pipes, it is necessary to analyze the safety of hillslopes based on the confluence of pipes. However, it is also necessary to investigate the influence of confluence of pipes on the buildup of pore water pressure in the field. We do not have enough data to discuss these effects, so a detailed field investigation is necessary.
4.2. Influence of Soil Pipes on the Timing and Geometry of Landslides
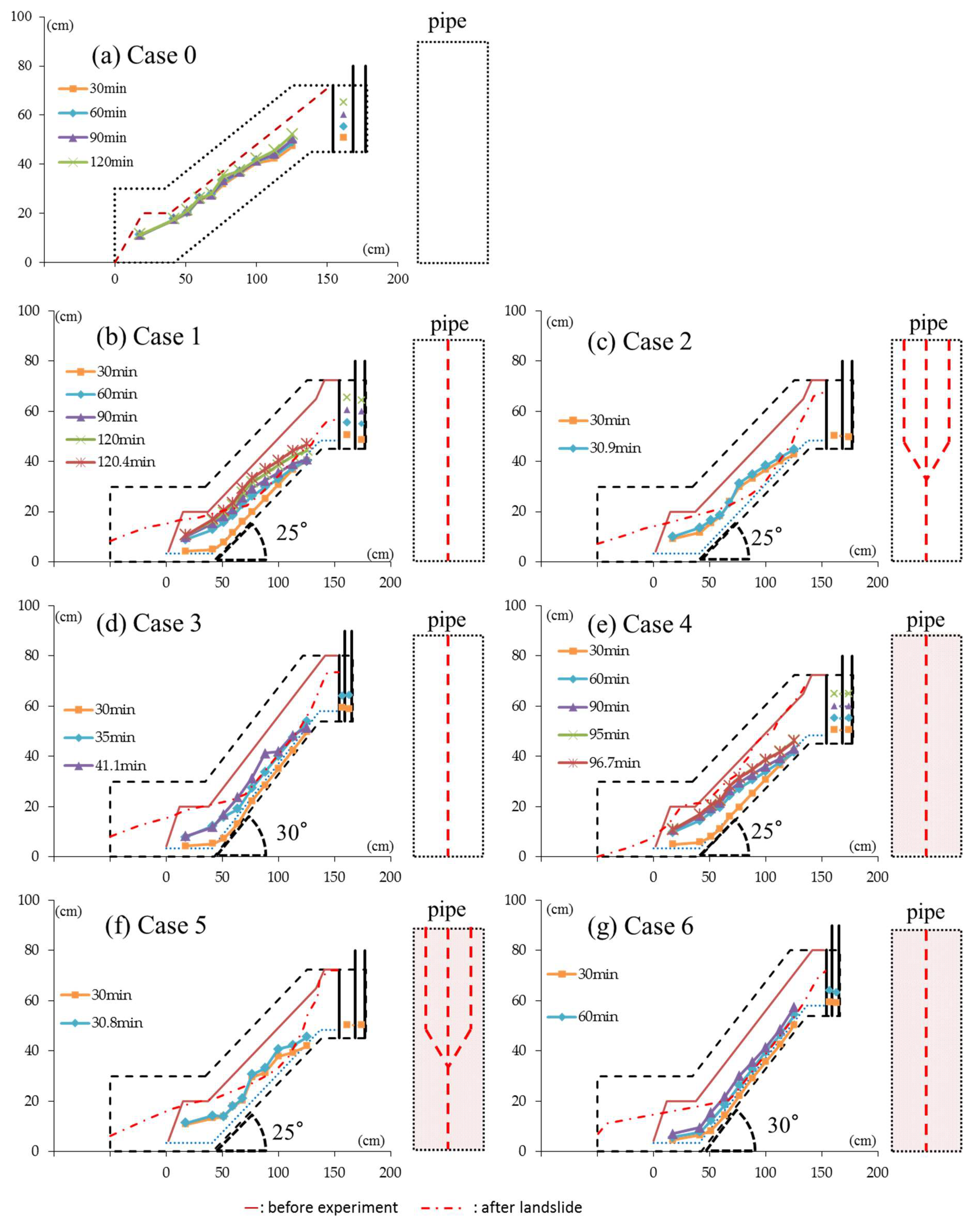
First, we discuss the effect of the pipe on landslide timing and form by comparing Case 0 to Case 1. In these cases, no clear displacement or landslide occurred until the water supply level reached 20 cm. However, in Case 1, when we set the water supply level in the higher tank to 25 cm, a landslide occurred. Here, when we used a higher tank, we expected the pressure in the pipe to increase. This implies that the presence of pipes in the soil layer has an effect on landslide occurrence.
Second, we discuss the effects of the soil pipe structure, i.e., straight pipe or confluence pipe. The results of our comparison between Cases 1 and 2, and Cases 4 and 5, show that landslides occurred when the water supply level was lower in the cases with confluence pipes than in the cases with straight pipes. These results imply that the confluence of soil pipes has a significant effect on the deterioration of the stability of the slope. Although in Cases 2 and 5 the landslide was rotational, and was deepest upstream of the confluence of pipes, in Cases 1 and 6 the surface of the landslide was generally planar. Therefore, the structure of the soil pipe can give impacts on not only the timing, but also the geometry of landslides.
It has been suggested that the clogging of a soil pipe induced the decrease of the time taken to induce a landslide, and the increase of the depth of the landslide, near a clog [
10]. This is similar to our results indicating that the role of confluence of a soil pipe and the longitudinal change of drainage capacity of soil pipe gave similar impacts on landslide occurrence.
4.3. Influence of Entrapped Air on the Timing and Form of Landslides
The water supply level was 10 cm when landslides occurred in Cases 2 and 5, which can be included by the confluence of pipes. There was no clear difference between these cases in terms of water supply level. However, we believe that a displacement occurred when the water supply level reached 5 cm in Case 5, as the air entrapped by the silica sand destabilized the surface of the model slope early. Based on a comparison between Cases 3 and 6, which were both 30-degree slopes with only one straight pipe, landslides occurred when the water supply level was 15 cm in Case 3, and 10 cm in Case 6, and the silica sand on the surface of the model slope destabilized earlier in Case 6 than in Case 3. Although it is difficult to compare Case 1 to Case 4, which both had 25-degree slopes with only one straight pipe, it is conceivable that entrapped air destabilized the model slope early, in which case we regard the gully erosion observed in Case 4 as destabilization. The difference in the landslide forms between Cases 2 and 5, and Cases 3 and 6, are not clear. Based on the above, although entrapped air may contribute to destabilizing the slopes, it seems to have little effect on the form of the landslide.
Continued seepage was observed to compress the air in an experiment with a uniform layer of soil and no pipe. The entrapped air increased the pore water pressure, especially around the flat area of the model slope, thus inducing a landslide [
19].
As landslides occurred earlier in Cases 5 and 6, which included silica sand, than in Cases 1 and 2, which did not have silica sand, it is possible that entrapped air increased the pore water pressure. In terms of the form of the landslide, a previous study only used an artificial rainfall simulator as a water supply system. In this case, a small landslide occurred at the toe of the model slope, where the pore water pressure was high, and then the landslide propagated upstream [
19]. In our experiments, all the landslides occurred all at once, although prior displacement was observed in Case 5. This suggests that the air in the soil layer compacted rapidly due to the pipe. The entrapped air contributed to the increase in pore water pressure and thus affected the occurrence of landslides.
4.4. Landslide Mechanisms
In this experiment, we found that the pipe’s ability to drain water affects whether landslides occur. In short, when less water is supplied, the pipe can drain all of the water, as in the early stages of Case 1, where the pore water pressure is low and thus the pipe contributes to stabilizing the model slope. On the other hand, the pore water pressure is higher around flat areas downstream of model slopes, such as in Case 0. However, the slope destabilizes when more water is supplied than the pipe can drain, such as in the final stages of Case 1. The increase in the pore water pressure propagated upstream to the transition area, which was downstream of the model slope, where less water could drain.
We believe that the entire model slope will also destabilize if the flow in the pipe is pressurized directly by the higher tank and the pore water pressure increases, as in Case 1. This suggests that a mountainous slope can be destabilized by soil pipes, as pipes are often connected to other pipes some distance away [
22,
23,
24,
25].
In Cases 2 and 5, in which we used three pipes (although, we would expect the three pipes to contribute to the stabilization of the slope when the amount of supplied water was smaller than their drainage capacity), the pore water pressure increased rapidly around the confluence of pipes. This is because three pipes supply more water to one downstream pipe than a single pipe. At this point, the pore water pressure increased locally around the confluence of pipes (manometers c–e), but did not increase in other areas. This is why the landslide was deeper in this area than in other areas. It has been noted that soil pipes repeatedly merge and branch [
4,
22,
23], and mountainous slopes can be destabilized by this merging and branching.
5. Conclusions
We investigated the effects of the confluence of pipes and entrapped air on landslides by measuring the pore water pressure just prior to landslides, and by assessing the form and timing of landslides. Planar landslides were observed in cases with one straight pipe, whereas rotational landslides occurred in cases with a confluence of three pipes; these were deepest around the confluence of pipes. This demonstrates that the confluence of pipes leads to locally high pore water pressure, thus influencing landslides.
The time taken for a landslide to occur was considerable with only one pipe, because the drainage of the pipe helped to stabilize the slope in the early stages of the increasing water levels. However, there were many cases in which landslides occurred as soon as the water supply level was raised.
The pore water pressure was high near the transition area downstream of the model slope in the cases where air was trapped in the soil layer. Furthermore, we observed that the pore water pressure was high near the confluences of pipes in Case 2. However, we also observed high pore water pressures in other areas in Case 5. This implies that water in the soil layer collects in the pipe, thus increasing the pore water pressure.
This experiment implies the importance of the drainage capacity of pipes. In the future, it will be necessary to investigate the relationship between the conditions of the soil layers (soil pipes and entrapped air), the water supply conditions, and landslide occurrences.
We should also consider the effect of storage discharge in soil layers, as this influences the saturation and destabilization of the soil layer. In the future, we would like to investigate the stabilization effects of storage discharge in soil layers and the effects of soil pipes and entrapped air on landslides.