1. Introduction
Residential real estate plays an important role in the spatial structure of a town or a city, and it is an important element of the urban management system which considerably influences economic development, in particular decision-making processes. Housing constitutes a large subsector of the real estate market, and the majority of market transactions involve residential real estate. This segment of the real estate market is characterised by high levels of activity that are reflected in the number of conducted transactions. The demand for housing is affected by numerous factors, where residential needs play the key role. The supply of housing is determined by the existing resources and new development projects. The real estate market is a complex system that is characterised by broad spatial coverage, a large number of transactions, highly dynamic market phenomena, and large amounts of data. At the same time, the real estate market is highly diverse due to the location and physical attributes of real estate, political factors, information flow, macroeconomic and microeconomic factors, as well as global and national shocks. As a result, the real estate market is difficult to analyze [
1,
2,
3,
4]. The variability of prices over time and real estate values cannot be easily identified due to the low frequency of transactions in a specific location (the overall number of transactions is high, but the number of transactions in a specific location can be very low). Depending on the purpose of the analysis, real estate value can be determined in the past, present or future. The variability of real estate prices over time has been analyzed by numerous authors [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. Such analyses involve time series methods, fuzzy logic methods, time trends, multiple regression, hedonistic regression, spatiotemporal forecasting, spatiotemporal autoregression, price modelling, and indicators of variation in real estate prices. The absence of sufficiently long time series of data relating to real estate prices in a selected location prevents accurate analyses and the development of precise forecasts that are important in a market economy. New methods and solutions are being sought to address this problem. In this study, the GRID method was used to prepare data for spatiotemporal analysis based on a complete network of nodes. The proposed approach supports the determination of time intervals at any point in the analyzed space (node) as well as the approximation of changes that occur over time in every epoch with the use of a polynomial with an automatically determined degree.
Spatial Information Systems (SIS) support the acquisition, collection, processing, and sharing of spatial and descriptive data relating to various objects [
18,
19,
20,
21,
22,
23]. Therefore, these systems are increasingly often used to perform operations where the location and identity of objects in a spatial frame of reference play the main role. Spatial information systems are commonly used to describe, analyze, explain, interpret, and predict different kinds of spatial phenomena [
24,
25,
26]. Due to the growing demand for information, the applicability of modern SIS is determined mainly based on their ability to collect large amounts of data in the shortest possible time as well as their dynamic updating, processing and data-sharing capabilities. Various types of data change dynamically within a relatively short time. Such changes can be identified through multiple analyses of the data relating to the same area in successive measurement epochs. In this approach, the studied object (or economic and physical phenomena) is measured at different points in time, which leads to a rapid increase in the volume of the processed data. The above applies particularly to situations where various aspects of reality are measured (not only spatial coordinates of objects, but also their quality attributes), and analyses are conducted in real time [
27,
28]. Therefore, the requirements for SIS continue to increase with a growing volume of collected and processed data (especially data collected during several measurement epochs at various points in time). Data gathering methods and processing techniques have to evolve to meet those requirements.
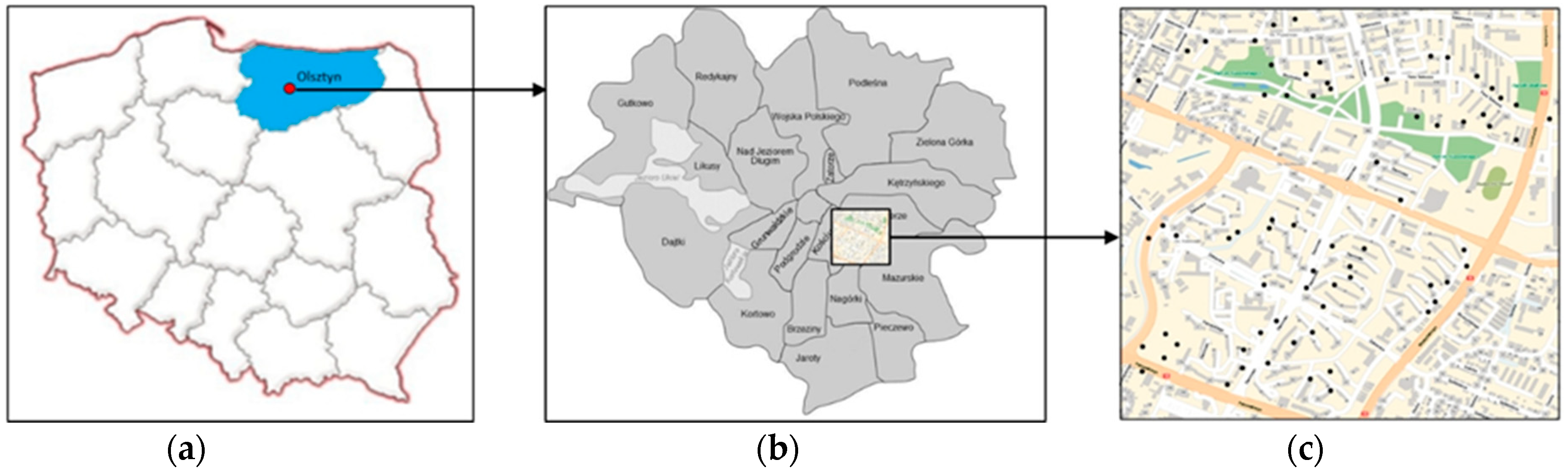
This paper proposes a method for reconstructing, forecasting and archiving data relating to the values of residential property in successive years of measurements in a selected object (measurement epochs which denote successive years of data registration). In this study, the term “reconstruction” denotes the search for missing data (in nodes or epochs) based on the values recorded in nodes or in the neighbouring epochs. “Measurement points” denote the geometric centre of a building where the analyzed transaction took place (
Section 3.1). Modelling and calculations were performed with the use of dedicated software developed by the authors. In the proposed approach, one of the many interpolation methods was deployed to generate a GRID network and extract the values allocated to individual network nodes in successive measurement epochs.
Irregularly distributed measurement data (real estate prices) acquired in successive years are transformed into a regular GRID structure to develop digital surface models. The models describe the distribution of prices in an object in each epoch. In the simplest terms, real estate prices constitute points whose spatial distribution can be interpolated. This approach is based on the assumption that space is continuous, and that real estate is an element of space; therefore, the surface of a variable (the price of real estate) is also continuous (in consequence, the value can be estimated at each point). A variable is also space-dependent (the value in a specific location is associated with the values in adjacent locations). The data (prices) which make up a time series are described by the coefficients of polynomials whose degree is determined automatically. The description of GRID nodes with the coefficients of approximating polynomials supports the reconstruction and prediction of real estate value at any point in time in the measurement epoch. As a result, the number of points stored in a database can be reduced without compromising the precision of spatial models generated in the process. The size of the datasets to be incorporated into SIS is optimized, and data are archived effectively, which considerably facilitates analysis.
The proposed method relies on GRID structures generated in successive measurement epochs to prepare data for time-series analysis. The data from each measurement epoch are used to generate a GRID structure with a complete network of nodes. This approach generates a full set of data in every epoch (node), which supports the determination of specific time intervals at every point in the analyzed space. Values that change over time are selected in each node (at the same point in each epoch), and they are approximated with the use of a polynomial with an automatically determined degree. The polynomial supports the description of changes over time with the use of coefficients that are allocated to each node. The data recorded in multiple measurement epochs are stored in a single file, which reduces the volume of the resulting dataset. The above improves the effectiveness of archiving operations, accelerates data exchange and facilitates resource management. In each node, the coefficients of approximating polynomials contain information about changes in real estate value, and they can also be used to generate surfaces that are allocated to a selected epoch and to reconstruct values at any point in time.
The coefficients of approximating polynomials are used to reconstruct the value of nodes with the same location (x, y) based on individually determined polynomials. This approach supports the reconstruction of the time series in each node. The coefficients are generated independently for each node in every epoch, and they are influenced by the degree of the polynomial describing changes in node values over time. The time interval between the reconstructed epochs can be freely set, which supports the determination of intermediate epochs. As a result, data can be reconstructed at any point in time without the need to archive the entire dataset, which reduces the volume of data required for the recreation of a complete GRID structure for a given point in time. The resulting database contains only the coefficients of approximating polynomials which describe changes in the examined phenomenon, which supports comprehensive analyses.
4. An Analysis of the Fit between Reconstructed and Original Values
The fit between the reconstructed surface and the reference surface (based on market data) can be analyzed with the use of the RMS (root mean square) coefficient (3) [
41,
42,
43]. In this approach, the fit between two surfaces is presented by a single numerical coefficient. The smaller the value of RMS, the better the fit between both surfaces (between the points that create both surfaces).
where:
ri—value of a node in the reconstructed network,
pi—value of a node in the original network,
n—number of node points.
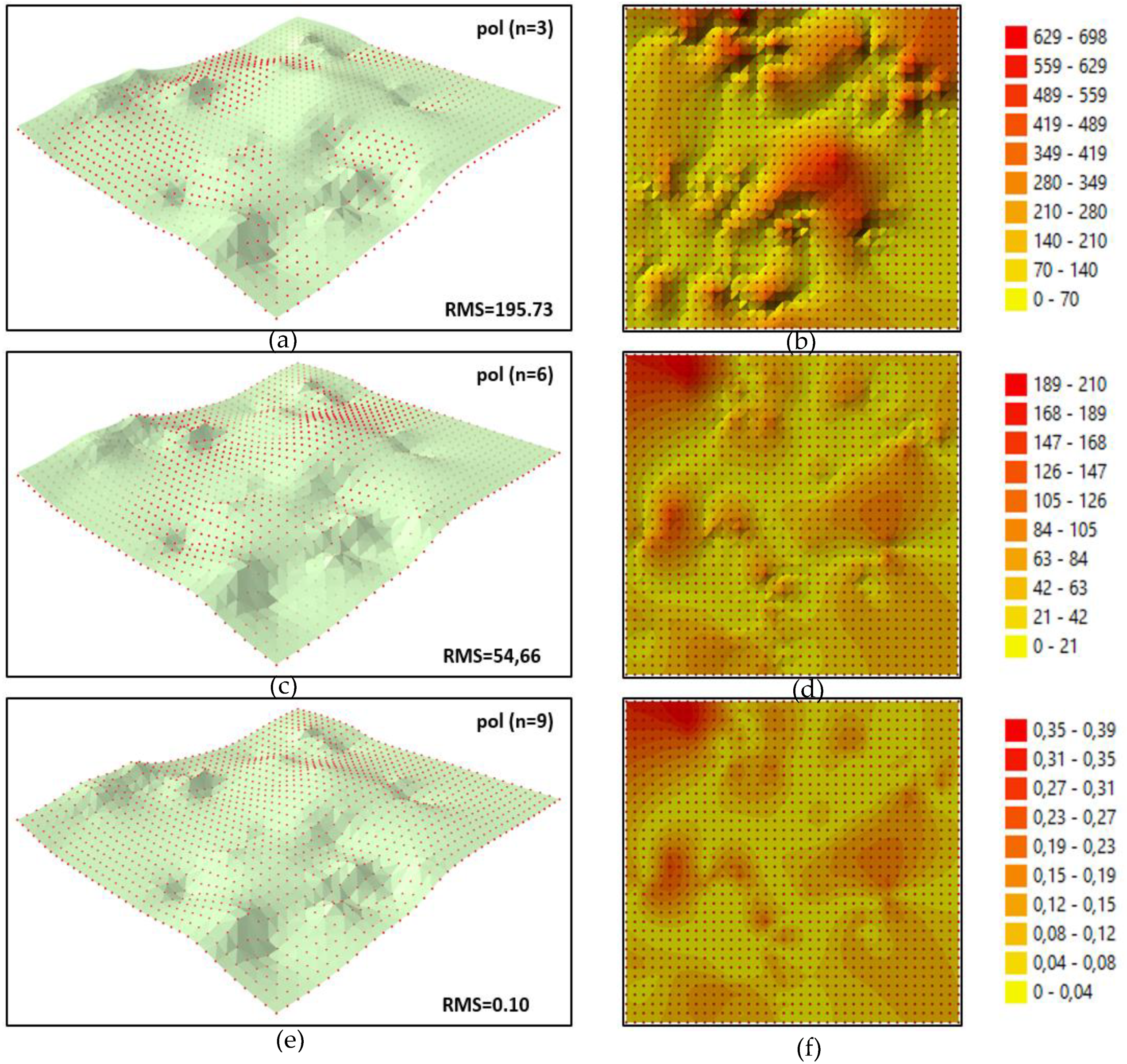
In the presented example, the original surface was created with the use of a GRID structure (t) generated directly from measurement points. The reconstructed surface was generated based on the GRID structure (r) calculated from polynomial coefficients. The differences in node values in both structures were used to determine the RMS. These differences were also used to create differential diagrams presenting the degree of fit between both surfaces. The accuracy with which the reconstructed nodes of the GRID structure were fit to the original surface (2012 data) for different degrees (n) of polynomials generated with the use of all measurement epochs is presented in
Figure 5a,c,e.
Differential diagrams generated based on the absolute differences |r
i − p
i| (3) in each node are presented on the right hand side of each diagram. The differences were divided into 10 class intervals. Class intervals differ between diagrams due to considerable differences in the presented values. The RMS coefficient and the presented diagrams support an assessment of the degree of fit between both surfaces and the accuracy with which a given epoch was reconstructed. For nodes that were reconstructed with the coefficient of an approximating polynomial of the 3rd degree (
Figure 5a; n = 3), the surfaces were characterised by the worst fit, and the coefficient was the highest (RMS = 195.73). In
Figure 5, several reconstructed nodes are positioned above the original surface, whereas other nodes are located under that surface. In the corresponding differential diagram, the digital surface is most deformed at measurement points and in the central part of the model. Most of the presented values are situated within the 0 to 210 interval, which can be attributed to the considerable generalisation of the values reconstructed with the use of the n = 3 polynomial (cf.
Figure 4a, b).
The approximating polynomial of the 6th degree (
Figure 5; n = 6) better fits reconstructed nodes to the original surface; the RMS is smaller (RMS = 54.66). The differences presented in
Figure 5d are three times smaller than in the previous case, and their distribution is similar to interpolation values (
Figure 5). Most of the values in
Figure 5d are positioned in the 0 to 63 interval, which can be attributed to the smaller generalisation of the values reconstructed in individual nodes of the model (cf.
Figure 4d,c). The best fit was achieved for the nodes reconstructed by the interpolating polynomial of the 9th degree (
Figure 5e; n = 9), and the differences were within the round-off error. The RMS for the entire object was determined at RMS = 0.10. In the differential diagram for the interpolating polynomial, the distribution of deformations is similar to that observed in the previous case, but most of the presented values are located within the 0 to 0.12 interval. The values determined with the coefficients of the interpolating polynomial can be regarded as error-free (within the range of computational error).
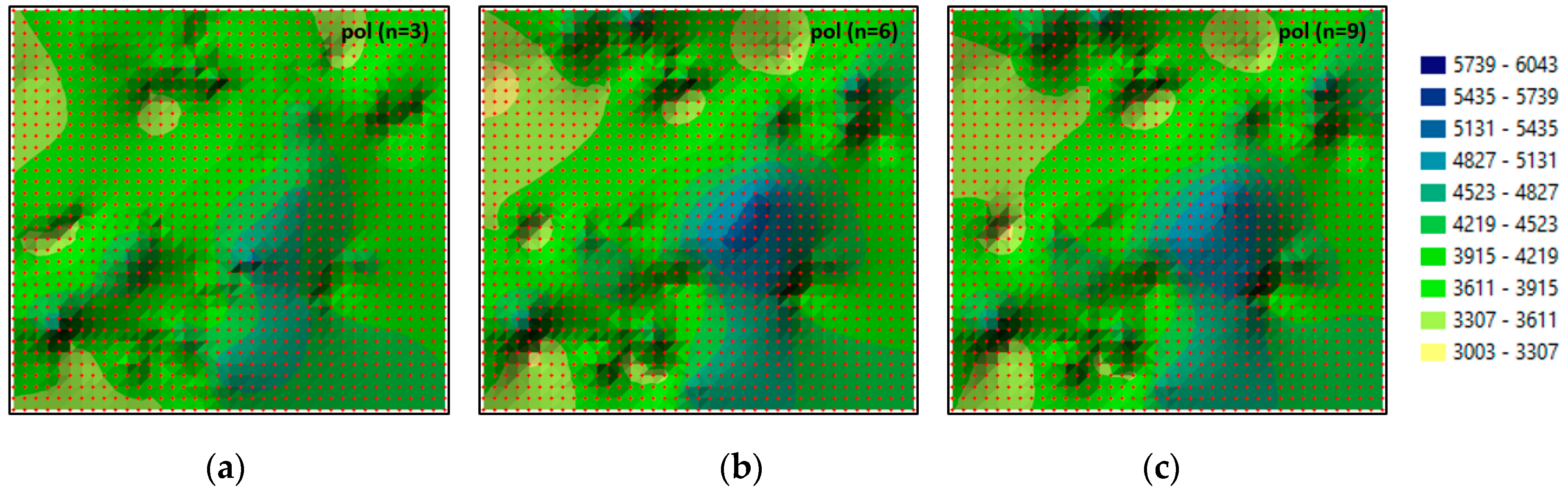
The interpolation surfaces of real estate prices reconstructed for 2012 based on GRID nodes generated for various degrees (n) of polynomials for all measurement epochs are presented in
Figure 6. In the presented example (
Figure 6), the original surface (
Figure 3b) is reconstructed with increasing accuracy based on the nodes generated with the use of polynomials of increasing degree. The original surface (
Figure 3b) and the reconstructed surfaces (
Figure 6) are presented for identical class intervals. Successive surfaces are increasingly less generalised. The 2012 surface created based on the interpolating polynomial (
Figure 6c; n = 9) does not differ from the original 2012 surface (
Figure 3b).
An interpolating polynomial also supports the lossless reconstruction of values in all GRID nodes in each epoch. The same surface (reconstructed from a GRID structure) can be generated in a selected epoch (as the original GRID structure) based on measurement data. This approach can be used to reconstruct values in each measurement epoch with the desired accuracy, and the generated values do not have to be saved in separate files. The creation of a single dataset cuts data carrier costs by 25% and speeds up data transfer.
5. Time Series Forecasting for a Selected Measurement Epoch
Individual polynomial coefficients are allocated to each GRID node; therefore, the coefficients saved in a single file can be used to forecast complete GRID structures at any point in time (in any measurement epoch or between epochs). In the predicted structure, each point is determined by solving a system of equations for a curve described by the coefficients of a polynomial (2) and a straight line intersecting the epoch on the time axis (t). In general, the number of generated epochs depends on the time interval adopted for the differences between epochs, which does not have to be identical for individual epochs. If the number of epochs is identical to the number of epochs for determining polynomial coefficients, successive epochs are forecast at the same intervals as the source intervals. A time interval can be freely adjusted, which supports the generation of any number of intermediate epochs or a specific epoch at a given point on the time line (
Figure 4 and
Figure 7). This missing intermediate structure can be generated based on the nodes created in the neighbouring measurement epochs.
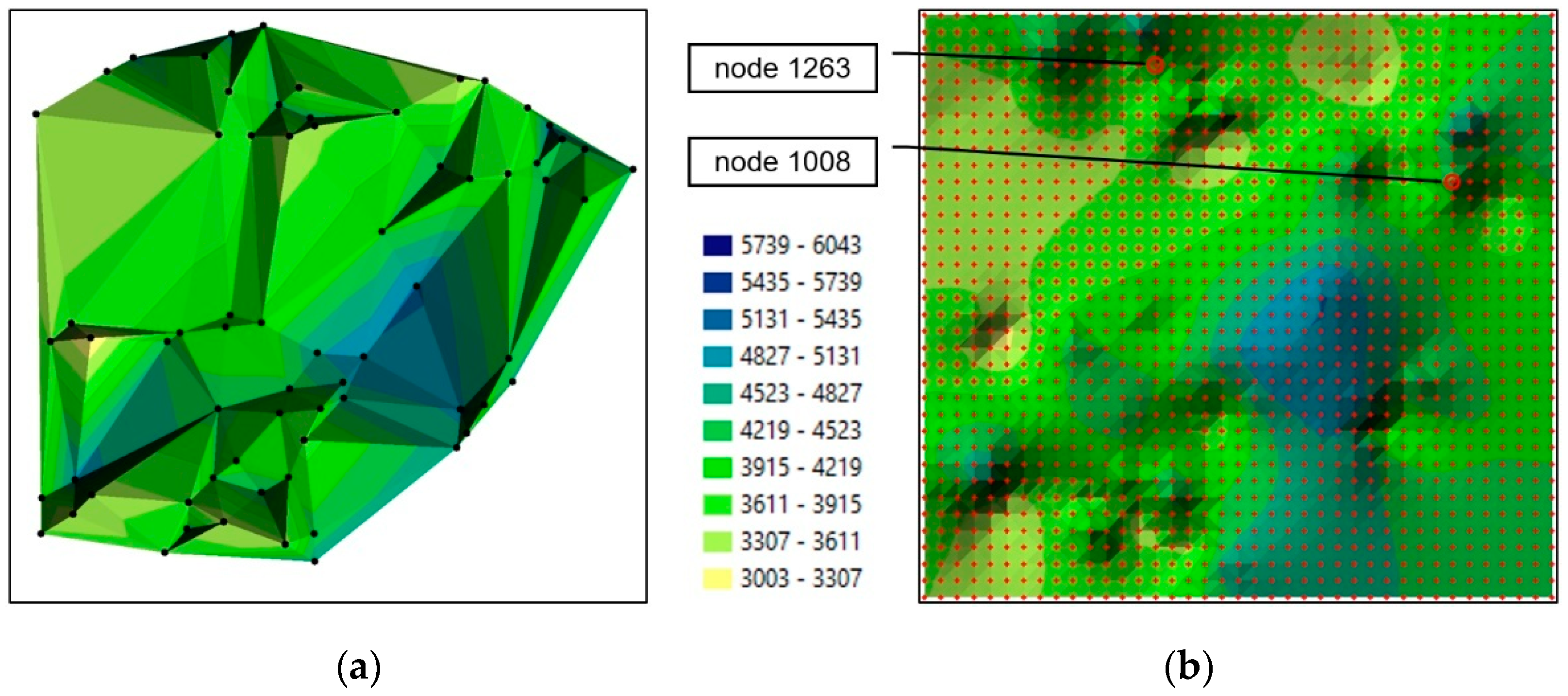
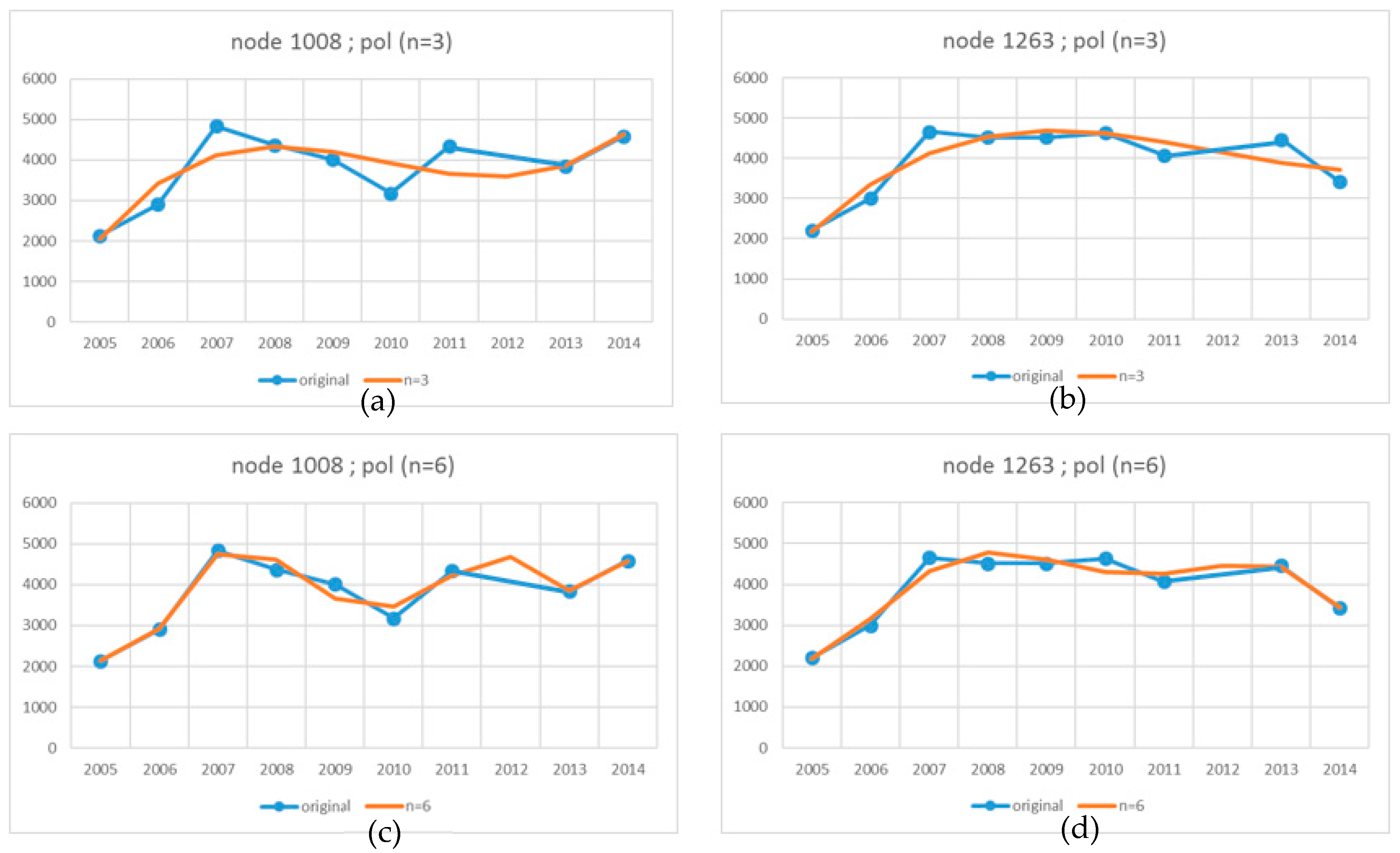
The procedure of forecasting a missing GRID structure is presented on the example of the two nodes that were used in the previous case (
Figure 2b and
Figure 3b). The missing structure was created with the use of the same measurement data acquired in the 10 epochs, but the 2012 epoch was randomly eliminated. The previously described procedure was used to allocate data from each epoch to all nodes and create a time series (without the 2012 epoch). The selected values were used to calculate the coefficients of polynomials of various degrees (n = 3; n = 6 and n = 8). According to the presented set of equations (1), an interpolating polynomial of the highest degree (n = 8) could be created based on the nine available measurement epochs (E = 9). Individually calculated polynomial coefficients were allocated to each node in a complete GRID structure and saved in a single file. The file containing polynomial coefficients was used to generate all nodes in the measured epochs and in the missing 2012 epoch. The value of (t) was substituted into equation (2) of the polynomial described by the coefficients, and node values were determined in each epoch.
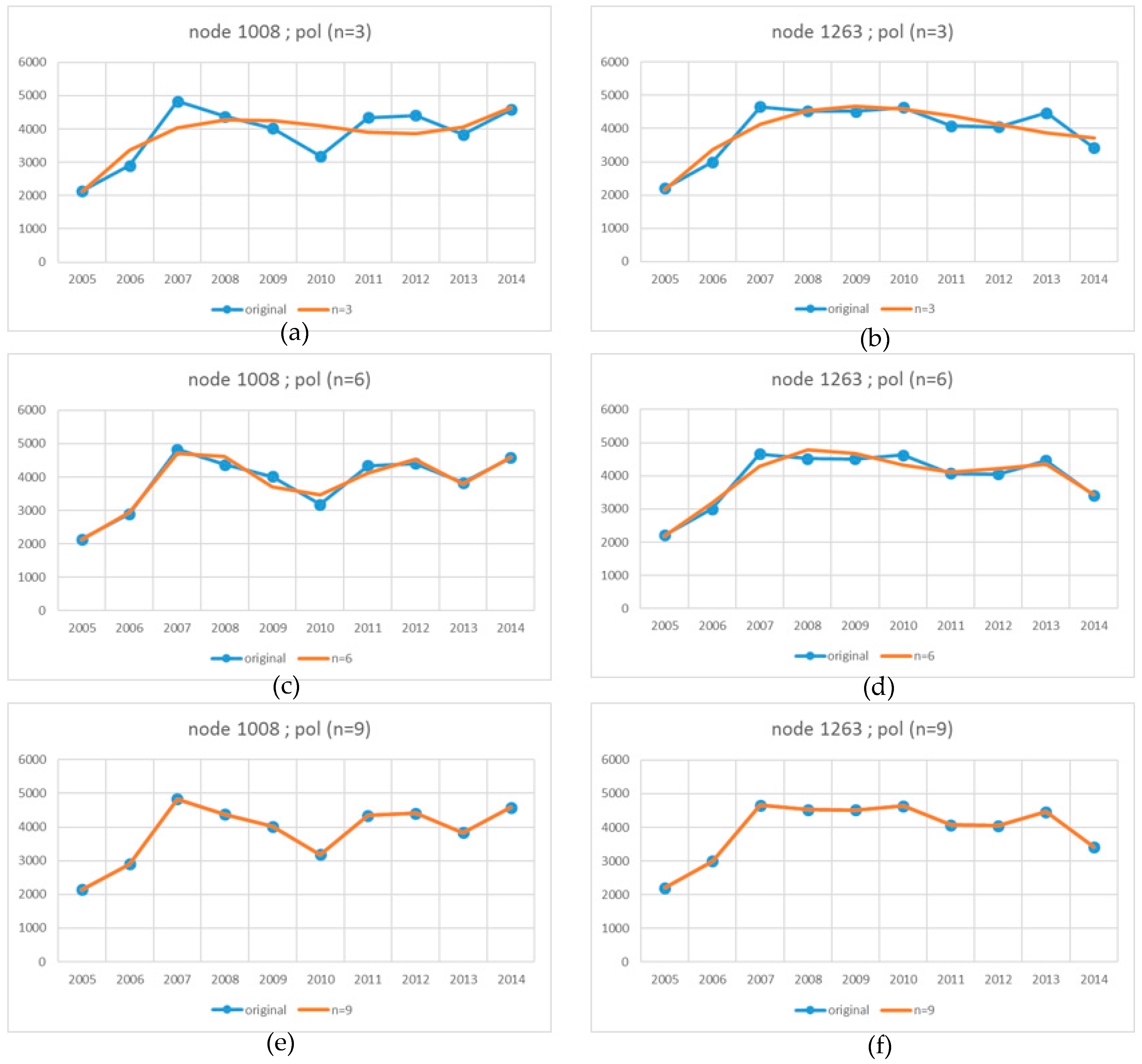
The set of nodes generated for a specific intermediate epoch constitutes an intermediate forecast GRID structure which enables the generation of an intermediate surface at a given point in time. The changes in the original and forecast values in two selected nodes in successive measurement epochs for different degrees (n) of polynomials generated in the absence of the 2012 epoch are compared in
Figure 7 (refer to
Figure 4 for the legend). Despite the absence of the 2012 epoch, the forecast values are characterised by similar relationships to those in
Figure 4 in all cases. Similarly to the previous case, the RMS (3) was calculated and differential diagrams were generated to analyze the accuracy with which the missing 2012 epoch was forecast. The diagrams present the fit between the original surface created based on the measurement points for 2012 and the surface forecast based on the coefficients of polynomials determined in the absence of the 2012 epoch. The accuracy with which the forecast nodes of the GRID structure fit the theoretical surface generated with the use of various methods in the absence of the 2012 epoch is compared in
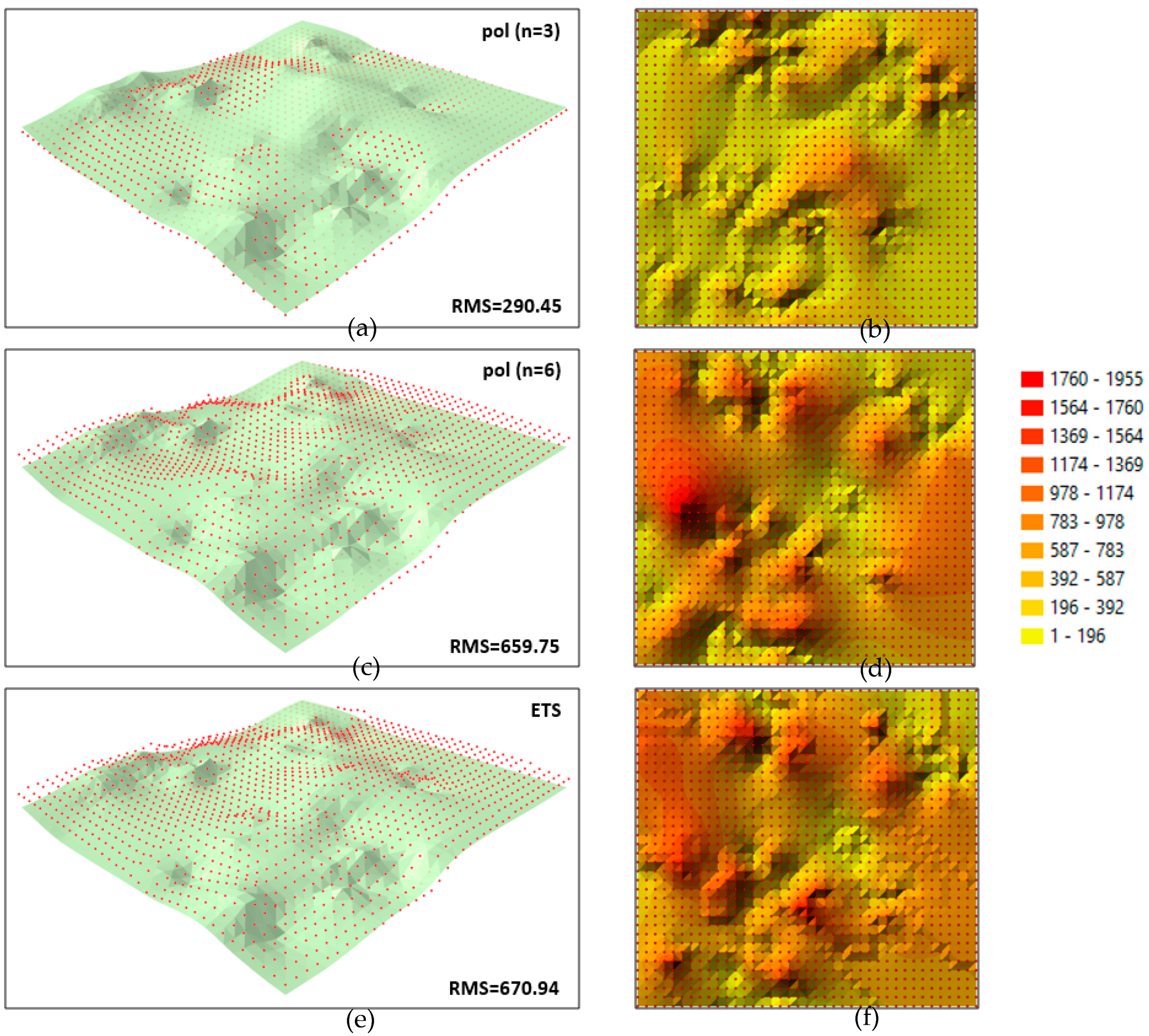
Figure 8. The same interval classification was applied to compare all cases. For the 3rd degree polynomial (
Figure 8 a; n = 3), the fit between the forecast surface and the theoretical surface was similar to that presented in
Figure 5a. The location of nodes relative to the theoretical surface was similar, and the RMS coefficient was not significantly higher (RMS = 290.45). The differential diagram (
Figure 8b) generated for this case was also characterised by a similar pattern of deformations to that presented in
Figure 5b. In turn, the 6th degree polynomial produced a less satisfactory fit than when all the measurement epochs were used to determine polynomial coefficients. The majority of the forecast nodes are situated above the original surface (
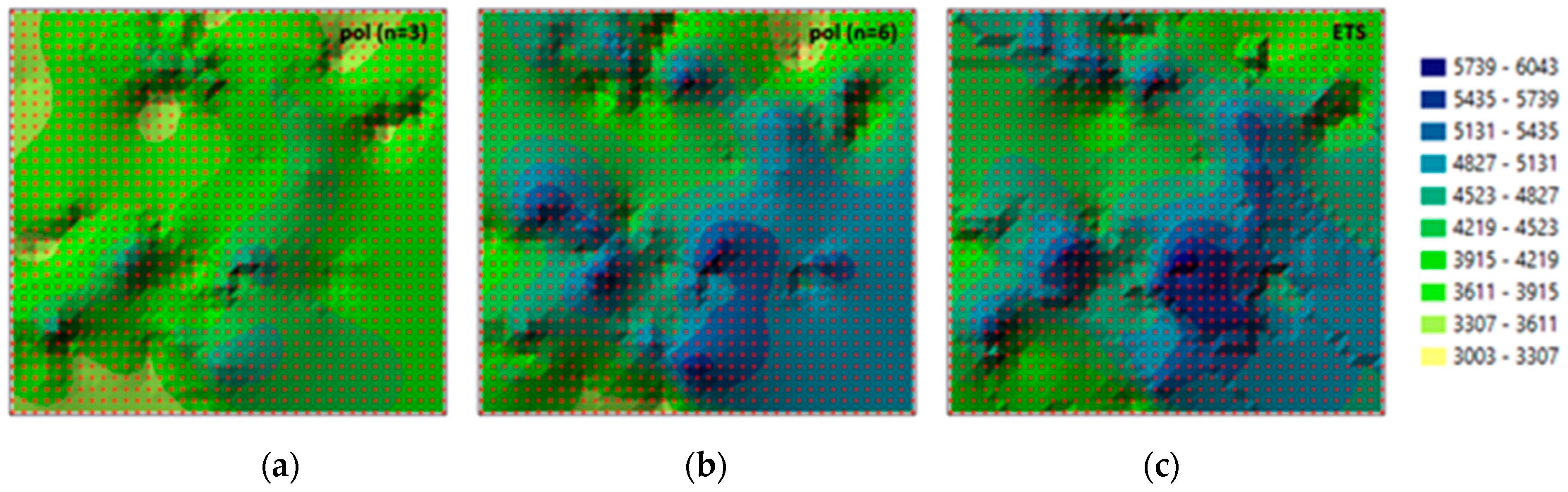
Figure 8c). The RMS for the forecast epoch increased to RMS = 659.75. The differential diagram generated for this case (
Figure 8d) is characterised by extreme local deformations which also affect the value of the RMS. Node values were forecast with even lower accuracy when the interpolating polynomial (n = 8) was used. The RMS coefficient was determined at RMS = 2050.63 when this polynomial was applied to forecast the missing 2012 epoch, which makes it unsuitable for use.
The values forecast with the REGLINX.ETS function in MS Excel were also forecast for comparative purposes (REGLINX.ETS calculates or predicts a future value based on historical values by using the AAA version of the Exponential Smoothing (ETS) algorithm.). This function forecasts time series, and it supports the prediction of values based on historical data. The function relies on Exponential Triple Smoothing (ETS) which is an advanced machine learning algorithm. A forecast value is a continuation of historical values on a specified target date which extends the time axis [
44,
45].
The fit between the nodes generated by ETS and the original surface created for the 2012 epoch based on measurement data is presented in
Figure 8e. Similarly to the polynomial (n = 6), the majority of the forecast nodes are situated above the original surface. The value of the RMS is also similar at RMS = 670.94. However, unlike in the previous cases, the differential diagram generated based on ETS results (
Figure 8f) is characterized by local stepped surface deformations.
The interpolation surfaces of real estate prices forecast for 2012 based on the GRID nodes generated with the use of various methods (in the absence of the 2012 epoch) are presented in
Figure 9. The classification of the forecast real estate prices was identical to that applied to the original surface. The generated surface differs from the original surface (
Figure 3b) in all cases (
Figure 9). The smallest differences are observed when the 3rd degree polynomial is used (
Figure 9a). These differences are similar to the values forecast with the use of the coefficients of the 3rd degree polynomial based on all measurement epochs (
Figure 6a).
The surfaces forecast with the use of the 6th degree polynomial (n = 6) and ETS are comparable. In both cases, extreme forecast values have identical locations in the model. Local stepped deformations of the surface model are additionally encountered in the ETS approach. A comparison of the models indicates that the highest forecast values have an identical location to the values in the original model in all cases.
6. Conclusions
The determination of real estate value is of key importance for all operations on the real estate market. Real estate values are the main criterion in investment decisions, and they have an informative role in the economy and real estate management. The appraisal of real estate values requires a thorough knowledge of selling prices and trends in a given time interval; therefore, it is similar to forecasting. In most cases, real estate values are forecast on a local (residential estate, city), regional or national scale, but the results do not contribute information on a given scale. The above can be attributed to the fact that observations at a given “point” are not continuous—real estate transactions are not conducted in a given location at constant time intervals. The proposed methodology can be used to forecast real estate value at a given point in time in a given location, which is of particular importance in real estate market analyses.
An interpolation algorithm is used during the generation of a GRID structure to determine real estate values at regular network intervals based on irregularly distributed measurement points. One of the greatest weaknesses of GRID structures is that unlike TIN structures, they do not support surface modelling based on the original measurements. However, the desired accuracy can be achieved by selecting the appropriate GRID resolution and the appropriate interpolation parameters. When a TIN structure has a small number of measurement points, the generated digital terrain model (DTM) is characterized by low resolution and low quality. This is not always the case when a GRID structure is applied, because the resolution of nodes in the generated network exceeds the density of measurement points (
Figure 3). The above task is not easily accomplished in other structures (TIN, linear models). The resulting model is more accurate in selected locations when surface nodes have higher resolution. An increase in the model’s resolution supports more accurate analyses in selected points, and a complete node network can be used to analyse successive measurement epochs. At the same time, the selected spatial elements can be excluded from interpolation because the resolution of GRID structures is scalable, and therefore, selected nodes can be excluded from analyses.
The solutions presented in this paper can be used to identify data for comparing the prices of real estate registered in various epochs, reconstructing and forecasting price changes over time, and effectively archiving data resources. Data that support the creation of time series for each GRID node can be used to analyze and compare changes in the measured space at selected points of the examined object. The generation of uniform structures in each epoch enables the selection of the values that change over time in each node (located at the same point in each epoch) and the approximation of the observed changes with the use of polynomials of any degree. The information about changes in values in each node is stored in the form of polynomial coefficients, and it can be used to generate the surface of a model allocated to any epoch and to reconstruct and forecast the searched values at any point in time with the required precision. Interpolating polynomials support data reconstruction without loss. A complete GRID structure can be generated in each epoch, and the measured values can be reconstructed and forecast in a given base field with minimum error. Approximating polynomials of a lower degree produce better results in the absence of the forecast measurement epoch. In turn, approximating polynomials of a higher degree generate results that are comparable with the ETS approach, whereas interpolating polynomials are not useful in practice. Polynomial approximation supports the description of changes over time in each node by deploying a series of coefficients that are allocated to each node, which are stored in a single file. The volume of stored data can be reduced by organizing the records from multiple measurement epochs and storing them in a single file. The information stored in databases can be used dynamically with the minimum processing time when the volume of the stored data is minimized. The reduction in the size of the archived datasets speeds up data access and supports real-time analysis. These considerations are particularly important during mass appraisals that rely on extensive sets of data about real estate transactions and prices in analyses covering large areas and long time intervals.