An Improved Strength Reduction-Based Slope Stability Analysis
Abstract
1. Introduction
2. Fundamental Theories
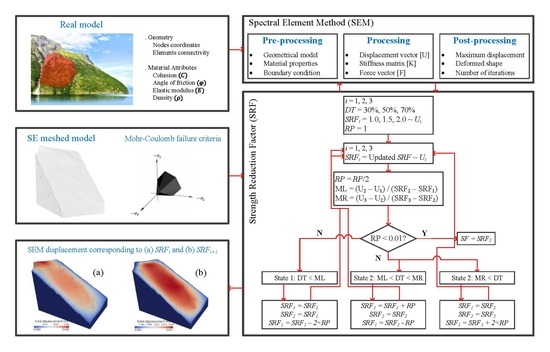
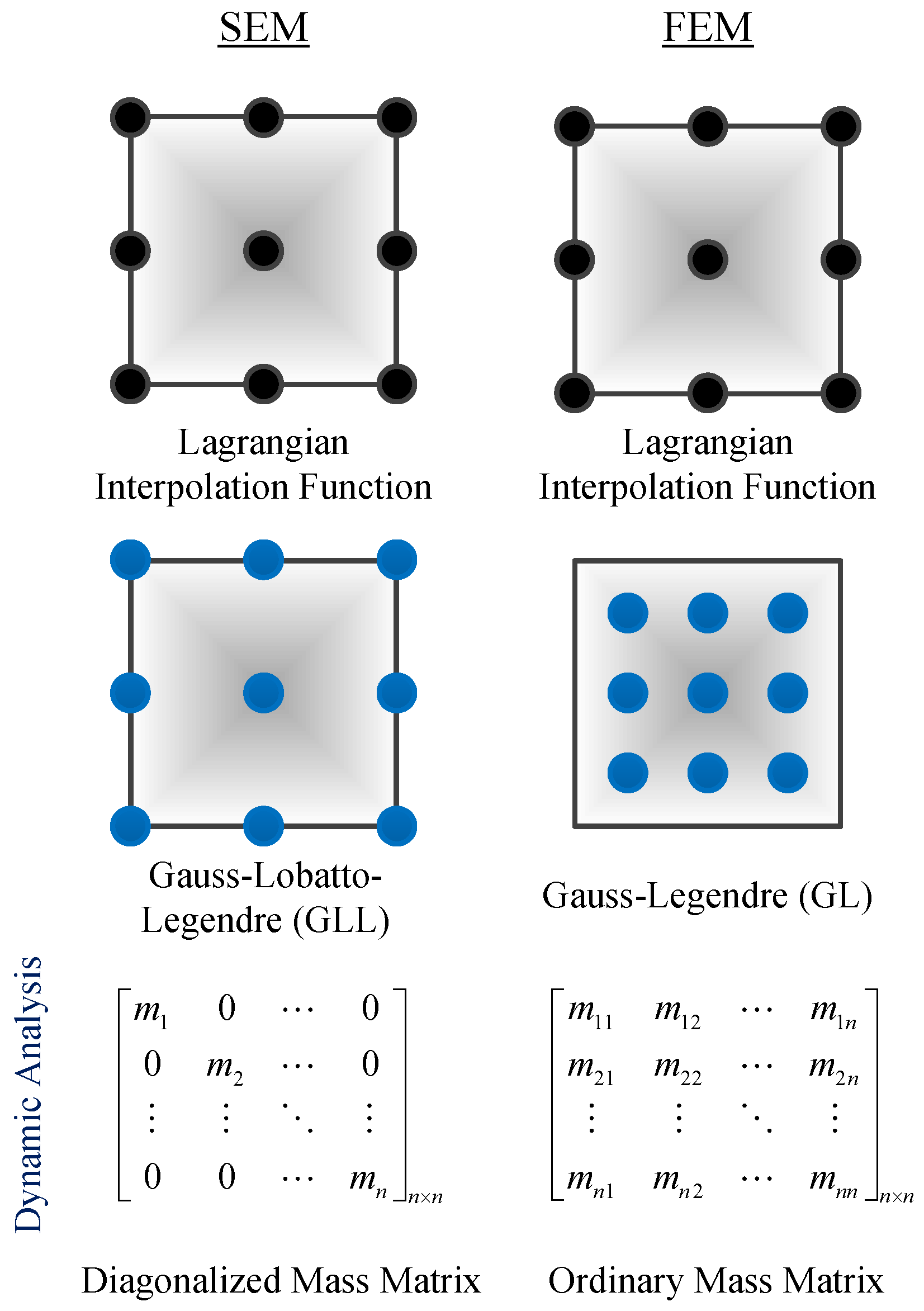
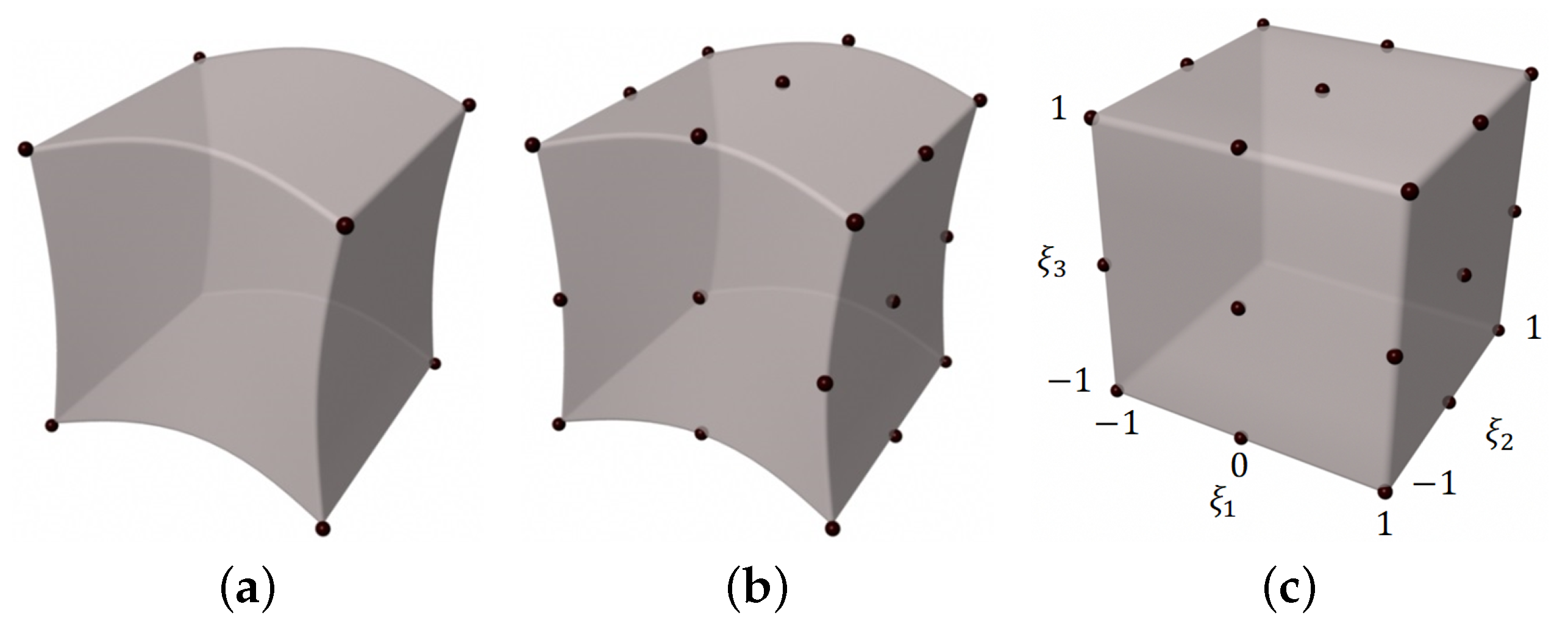
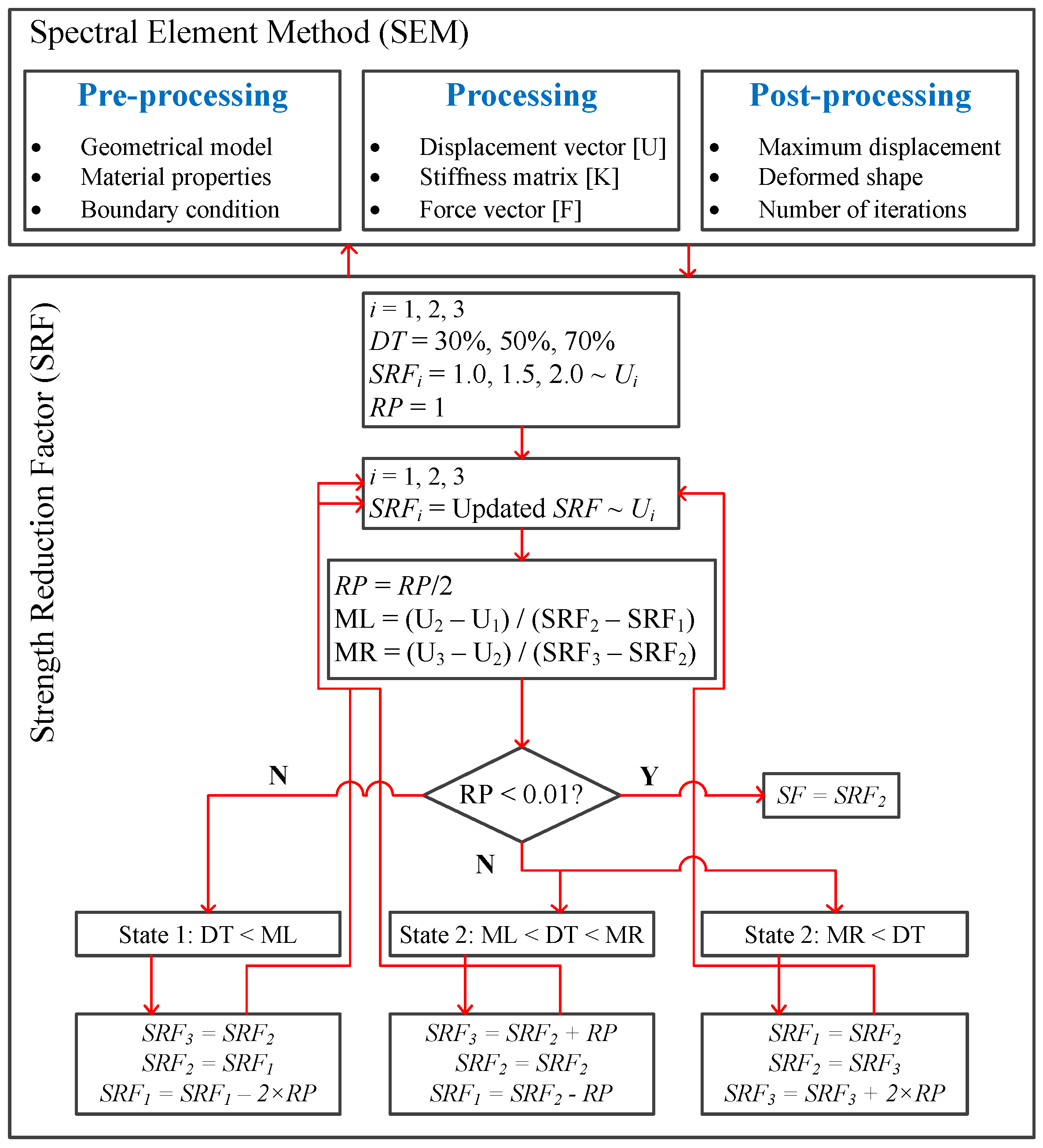
2.1. Spectral Element Method
2.2. Strength Reduction Method
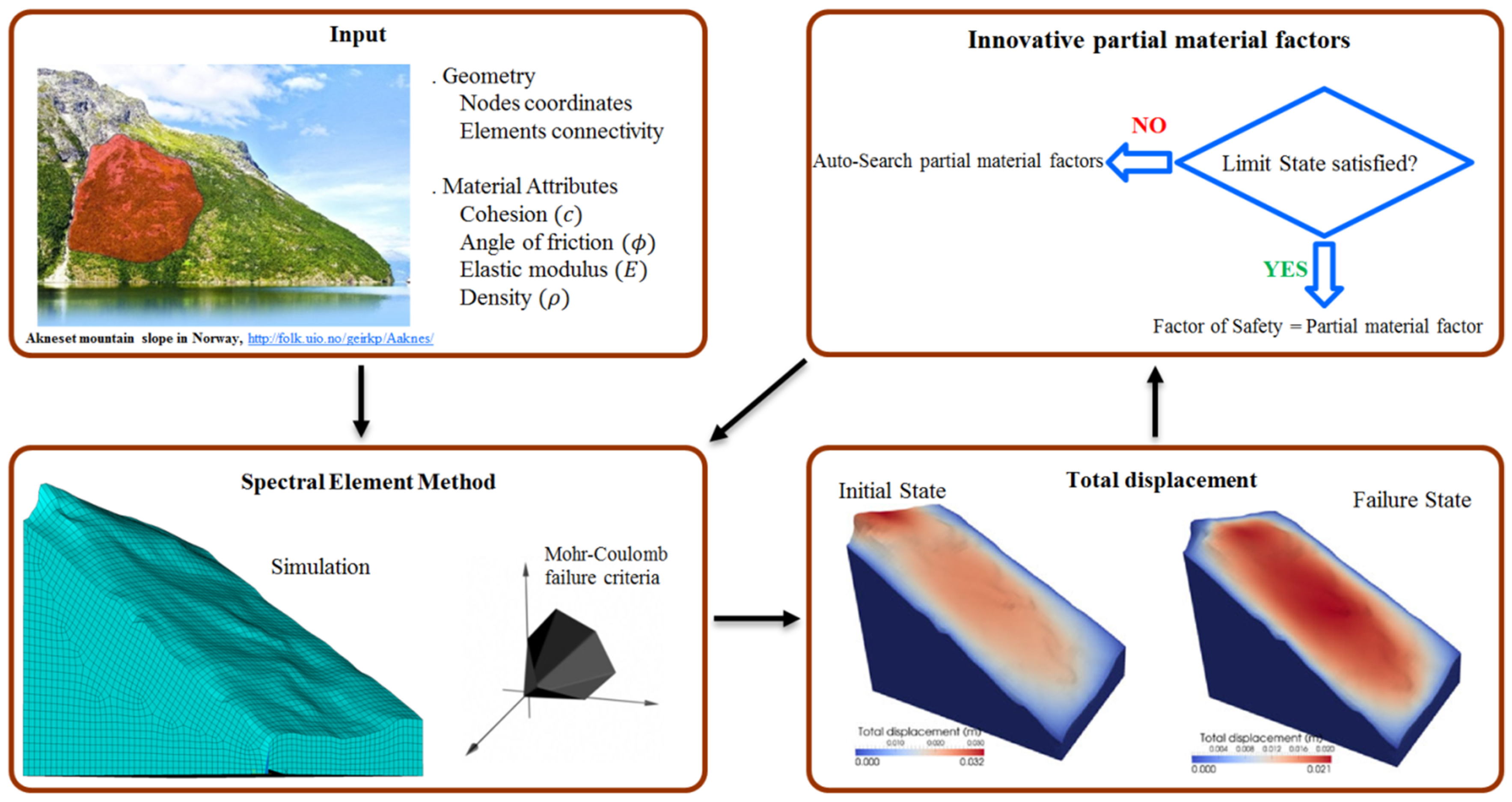
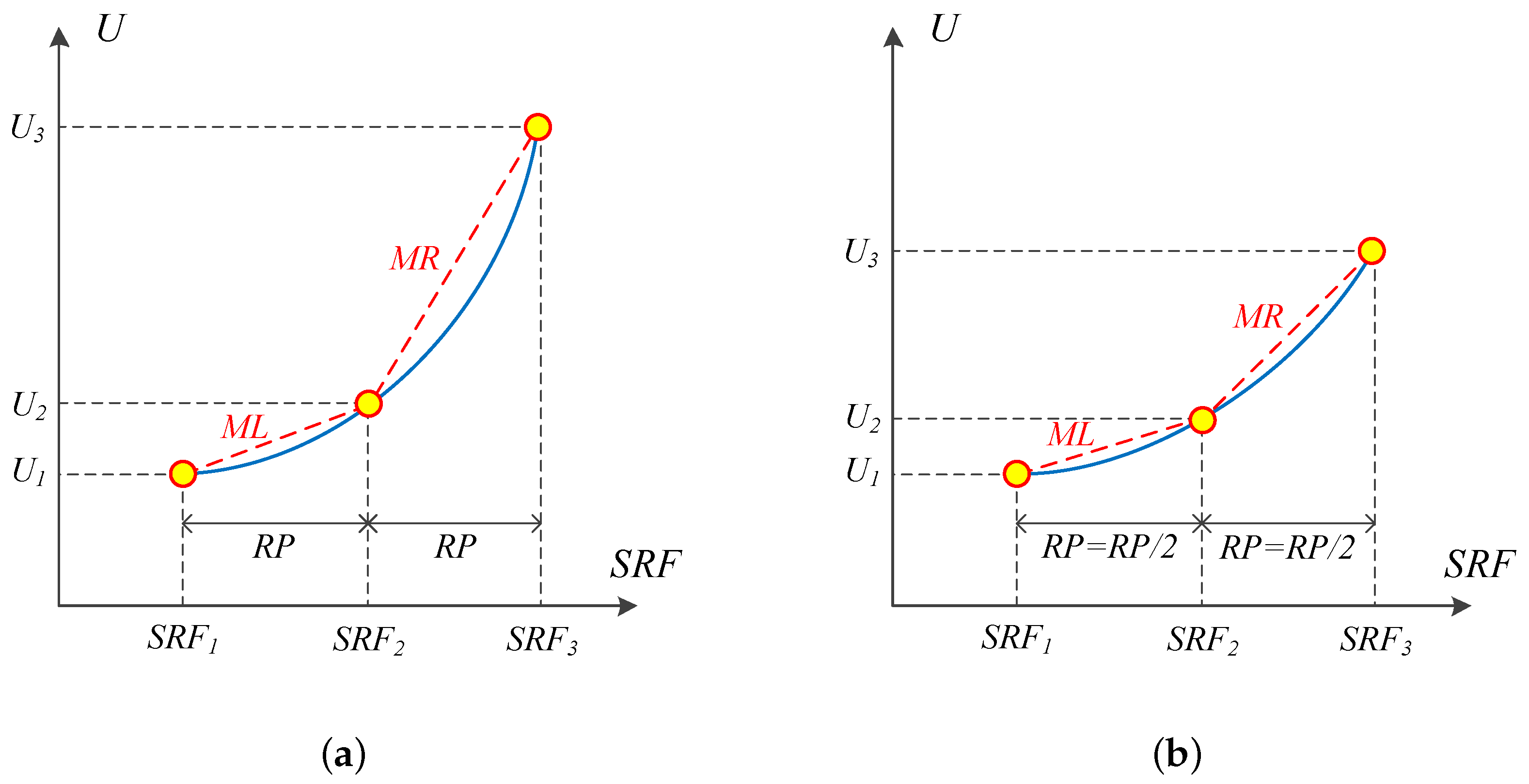
3. Methodology
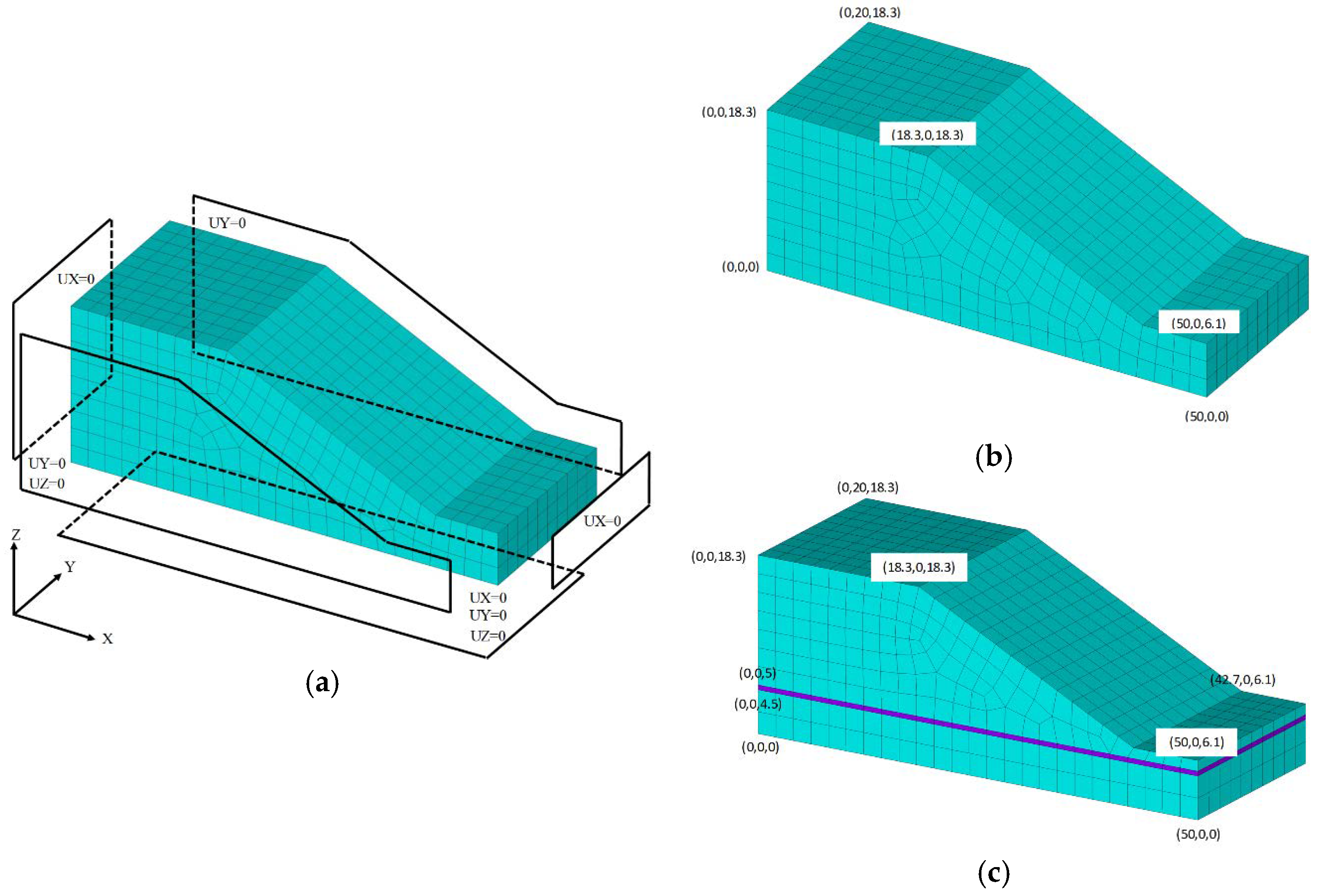
4. Case Study Models
5. Results and Discussion
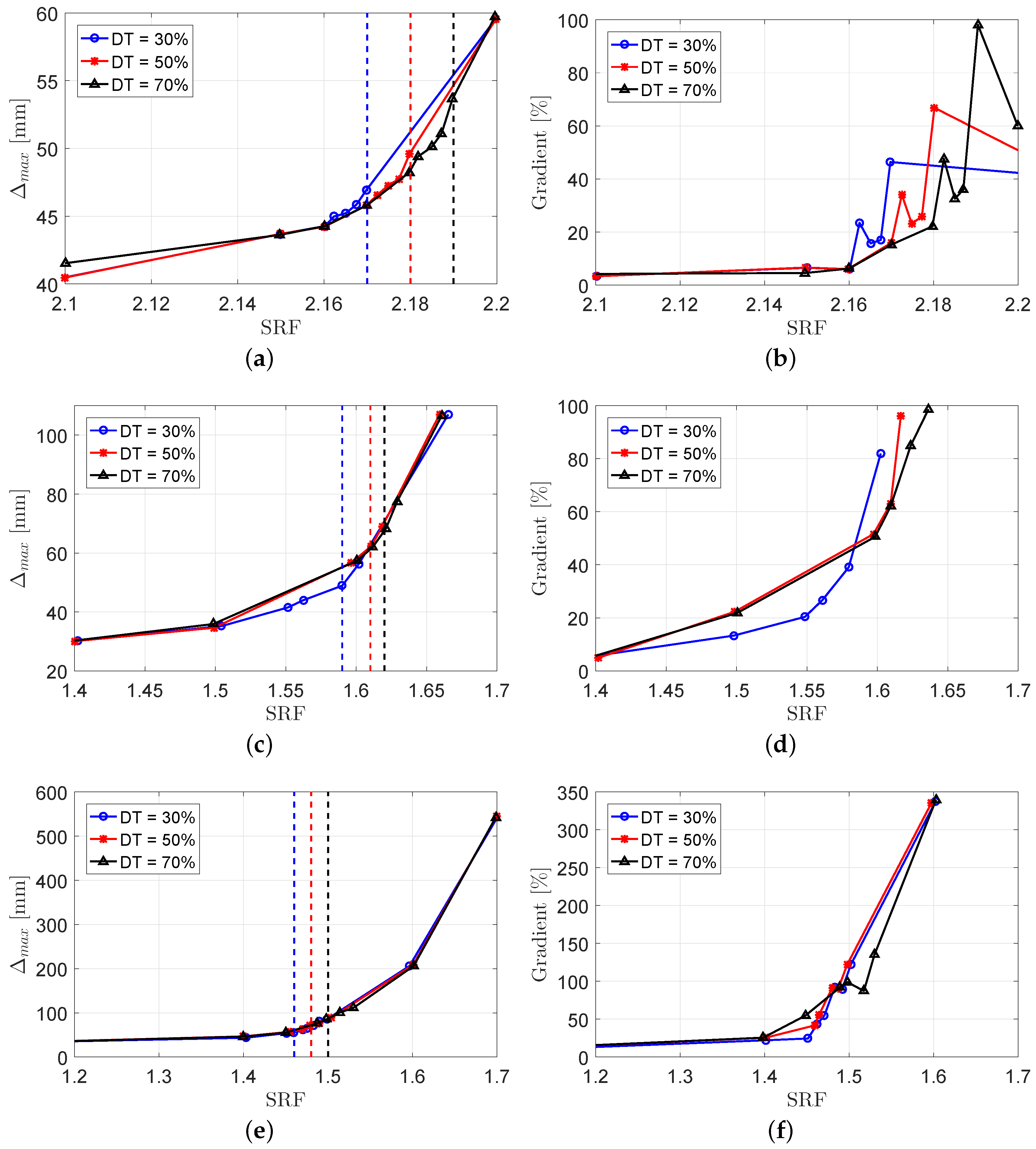
5.1. Case 1
5.2. Cases 2 and 3
5.3. Safety Factor Determination
- The displacement-based curves were smoother than the gradient-based ones.
- In displacement-based curves, the three plots resulting from three DT values were very close to each other. However, they had meaningful differences in the gradient-based plots.
- The range of SRF in which the system moved from the linear to plastic phase was longer for Cases 2 and 3 than Case 1.
- In all case studies, the safety factor for the system with DT = 30% was the minimum, and for the system with DT = 70%, it was the maximum.
- The safety factor of the homogeneous model (i.e., Case 1) was more than the two other cases (with a weak layer). This is consistent with the physics of the problem.
- Comparing Cases 2 and 3 revealed that the safety factor of the dry model (Case 2) was higher than the partially-wet slope (i.e., Case 3).
- The number of required simulations depended on the LS and pre-defined accuracy.
5.4. Validation
- The SFs obtained by Gharti et al. [14] were approximately equal to the proposed hybrid SEM-SRM with DT of 50%, 10%, and 60% for Case Studies 1, 2, and 3, respectively. This indicates that the inconsistency in SF resulted from the conventional SRM.
- The differences between SFs were equal to 0.02, 0.03, and 0.04 within DT of 30–70% for Case Studies 1, 2, and 3, respectively. This reveals that the influence of DT on SF was numerically significant for multilayer soil slopes. One should note that from the practical point of view, these differences are negligible.
- The number of required analyses to evaluate a particular example that considered both design and precision parameters was about 10 using the proposed method. However, it was a considerable number in other methods (depending on the technique).
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Tang, W.H.; Zhang, L.; Huang, H. Characterising geotechnical model uncertainty by hybrid Markov Chain Monte Carlo simulation. Comput. Geotech. 2012, 43, 26–36. [Google Scholar] [CrossRef]
- Kurowicka, D.; Cooke, R.M. Uncertainty Analysis with High Dimensional Dependence Modelling; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Spencer, E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Sarma, S. Stability analysis of embankments and slopes. Geotechnique 1973, 23, 423–433. [Google Scholar] [CrossRef]
- Krahn, J. The 2001 RM Hardy Lecture: The limits of limit equilibrium analyses. Can. Geotech. J. 2003, 40, 643–660. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Pourkamali-Anaraki, F. Simplified reliability analysis of multi hazard risk in gravity dams via machine learning techniques. Arch. Civ. Mech. Eng. 2018, 18, 592–610. [Google Scholar] [CrossRef]
- Chowdhury, R.; Rao, B. Probabilistic stability assessment of slopes using high dimensional model representation. Comput. Geotech. 2010, 37, 876–884. [Google Scholar] [CrossRef]
- Dawson, E.; Roth, W.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Griffiths, D.; Lane, P. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Matsui, T.; San, K.C. Finite element slope stability analysis by shear strength reduction technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Ugai, K. A method of calculation of total safety factor of slope by elasto-plastic FEM. Soils Found. 1989, 29, 190–195. [Google Scholar] [CrossRef]
- Huang, M.; Wang, H.; Sheng, D.; Liu, Y. Rotational–translational mechanism for the upper bound stability analysis of slopes with weak interlayer. Comput. Geotech. 2013, 53, 133–141. [Google Scholar] [CrossRef]
- Xu, Q.; Yin, H.; Cao, X.; Li, Z. A temperature-driven strength reduction method for slope stability analysis. Mech. Res. Commun. 2009, 36, 224–231. [Google Scholar] [CrossRef]
- Gharti, H.N.; Komatitsch, D.; Oye, V.; Martin, R.; Tromp, J. Application of an elastoplastic spectral-element method to 3D slope stability analysis. Int. J. Numer. Methods Eng. 2012, 91, 1–26. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Zheng, L.; Li, Y.; Zhuang, X. Effects of geometries on three-dimensional slope stability. Can. Geotech. J. 2013, 50, 233–249. [Google Scholar] [CrossRef]
- Tiwari, R.; Bhandary, N.; Yatabe, R.; Bhat, D. Evaluation of factor of safety for vegetated and barren soil slopes with limit equilibrium computations. Geomech. Geoeng. 2013, 8, 254–273. [Google Scholar] [CrossRef]
- Tiwari, R.; Bhandary, N.; Yatabe, R. 3-D elasto-plastic SEM approach for pseudo-static seismic slope stability charts for natural slopes. Indian Geomech. J. 2014, 44, 305–321. [Google Scholar] [CrossRef]
- Tiwari, R.C.; Bhandary, N.P.; Yatabe, R. Spectral element analysis to evaluate the stability of long and steep slopes. Acta Geotech. 2014, 9, 753–770. [Google Scholar] [CrossRef]
- Zheng, L.; Zhao, Q.; Milkereit, B.; Grasselli, G.; Liu, Q. Spectral-element simulations of elastic wave propagation in exploration and geotechnical applications. Earthq. Sci. 2014, 27, 179–187. [Google Scholar] [CrossRef]
- Shen, J.; Karakus, M. Three-dimensional numerical analysis for rock slope stability using shear strength reduction method. Can. Geotech. J. 2013, 51, 164–172. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.; Saouma, V. Single and multi-hazard capacity functions for concrete dams. Soil Dyn. Earthq. Eng. 2017, 101, 234–249. [Google Scholar] [CrossRef]
- Snitbhan, N.; Chen, W.F. Elastic-plastic large deformation analysis of soil slopes. Comput. Struct. 1978, 9, 567–577. [Google Scholar] [CrossRef]
- Dunlop, P.; Duncan, J.M. Development of failure around excavated slopes. J. Soil Mech. Found. Div 1970, 96, 471–493. [Google Scholar]
- Chen, J.X.; Ke, P.Z.; Zhang, G. Slope stability analysis by strength reduction elasto-plastic FEM. Key Eng. Mater. 2007, 345, 625–628. [Google Scholar]
- Luan, M.; Wu, Y.; Nian, T. An alternating criterion based on development of plastic zone for evaluating slope stability by shear strength reduction FEM. In Proceedings of the Sina-Japanese Symposium on Geotechnical Engineering, Beijing, China, 29–30 October 2003; pp. 181–188. [Google Scholar]
- Zheng, H.; Liu, D.; Li, C. Slope stability analysis based on elasto-plastic finite element method. Int. J. Numer. Methods Eng. 2005, 64, 1871–1888. [Google Scholar] [CrossRef]
- Duan, Q.; Wang, Y.; Zhang, P. Study on deformation parameter reduction technique for the strength reduction finite element method. In Landslides and Engineered Slopes. From the Past to the Future, Two Volumes+ CD-ROM; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- MATLAB, version 9.1 (R2016b); The MathWorks Inc.: Natick, MA, USA, 2016.
- Chen, J.; Yin, J.H.; Lee, C. Upper bound limit analysis of slope stability using rigid finite elements and nonlinear programming. Can. Geotech. J. 2003, 40, 742–752. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Haberfield, C.; Yin, J.H.; Wang, Y. A three-dimensional slope stability analysis method using the upper bound theorem: Part I: Theory and methods. Int. J. Rock Mech. Min. Sci. 2001, 38, 369–378. [Google Scholar] [CrossRef]
- Lam, L.; Fredlund, D. A general limit equilibrium model for three-dimensional slope stability analysis. Can. Geotech. J. 1993, 30, 905–919. [Google Scholar] [CrossRef]
- Xing, Z. Three-dimensional stability analysis of concave slopes in plan view. J. Geotech. Eng. 1988, 114, 658–671. [Google Scholar] [CrossRef]
- Griffiths, D.; Marquez, R. Three-dimensional slope stability analysis by elasto-plastic finite elements. Geotechnique 2007, 57, 537–546. [Google Scholar] [CrossRef]
| Methods | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Xing [32] | 2.122 | 1.553 | 1.441 |
| Bishop’s modified method (Lam and Fredlund [31]) | - | 1.607 | 1.511 |
| Janbu’s simplified method (Lam and Fredlund [31]) | - | 1.558 | 1.481 |
| CLARA (Lam and Fredlund [31]) | - | 1.62 | 1.54 |
| CLE (Lam and Fredlund [31]) | - | 1.603 | 1.508 |
| Chen et al. [30] | 2.262 | 1.717 | - |
| Chen et al. [30] | 2.187 | 1.603 | - |
| FEM (Griffiths and Marquez [33]) | 2.17 | 1.58 | - |
| SEM (Gharti et al. [14]) | 2.18 | 1.57 | 1.49 |
| SEM (DT = 30%)—present study | 2.17 | 1.59 | 1.46 |
| SEM (DT = 50%)—present study | 2.18 | 1.61 | 1.48 |
| SEM (DT = 70%)—present study | 2.19 | 1.62 | 1.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyed-Kolbadi, S.M.; Sadoghi-Yazdi, J.; Hariri-Ardebili, M.A. An Improved Strength Reduction-Based Slope Stability Analysis. Geosciences 2019, 9, 55. https://doi.org/10.3390/geosciences9010055
Seyed-Kolbadi SM, Sadoghi-Yazdi J, Hariri-Ardebili MA. An Improved Strength Reduction-Based Slope Stability Analysis. Geosciences. 2019; 9(1):55. https://doi.org/10.3390/geosciences9010055
Chicago/Turabian StyleSeyed-Kolbadi, S. M., J. Sadoghi-Yazdi, and M. A. Hariri-Ardebili. 2019. "An Improved Strength Reduction-Based Slope Stability Analysis" Geosciences 9, no. 1: 55. https://doi.org/10.3390/geosciences9010055
APA StyleSeyed-Kolbadi, S. M., Sadoghi-Yazdi, J., & Hariri-Ardebili, M. A. (2019). An Improved Strength Reduction-Based Slope Stability Analysis. Geosciences, 9(1), 55. https://doi.org/10.3390/geosciences9010055