Selective Aggregation Experiments on Planetesimal Formation and Mercury-Like Planets
Abstract
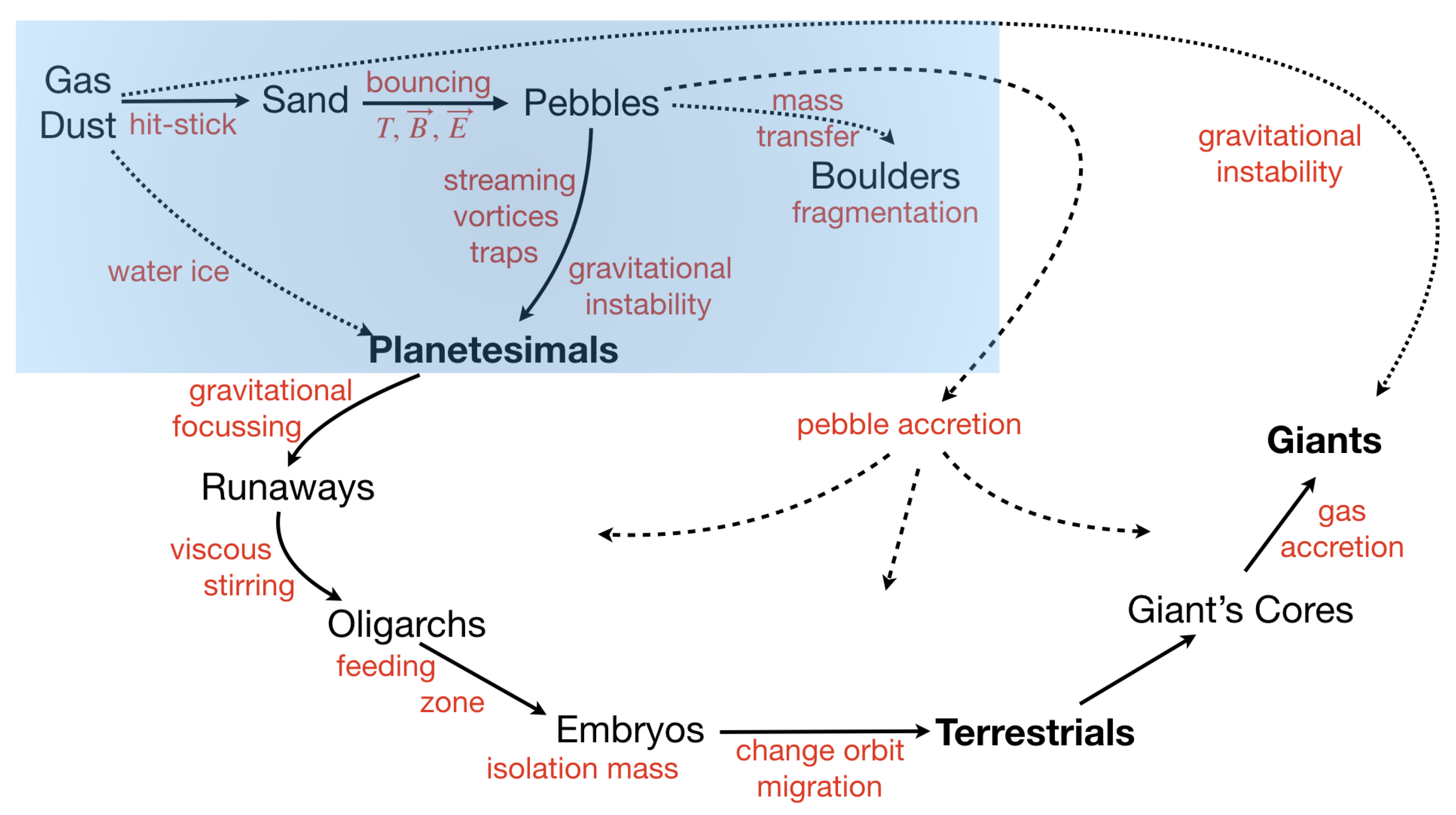
1. Planet Formation
The Red Lines of Planet Formation
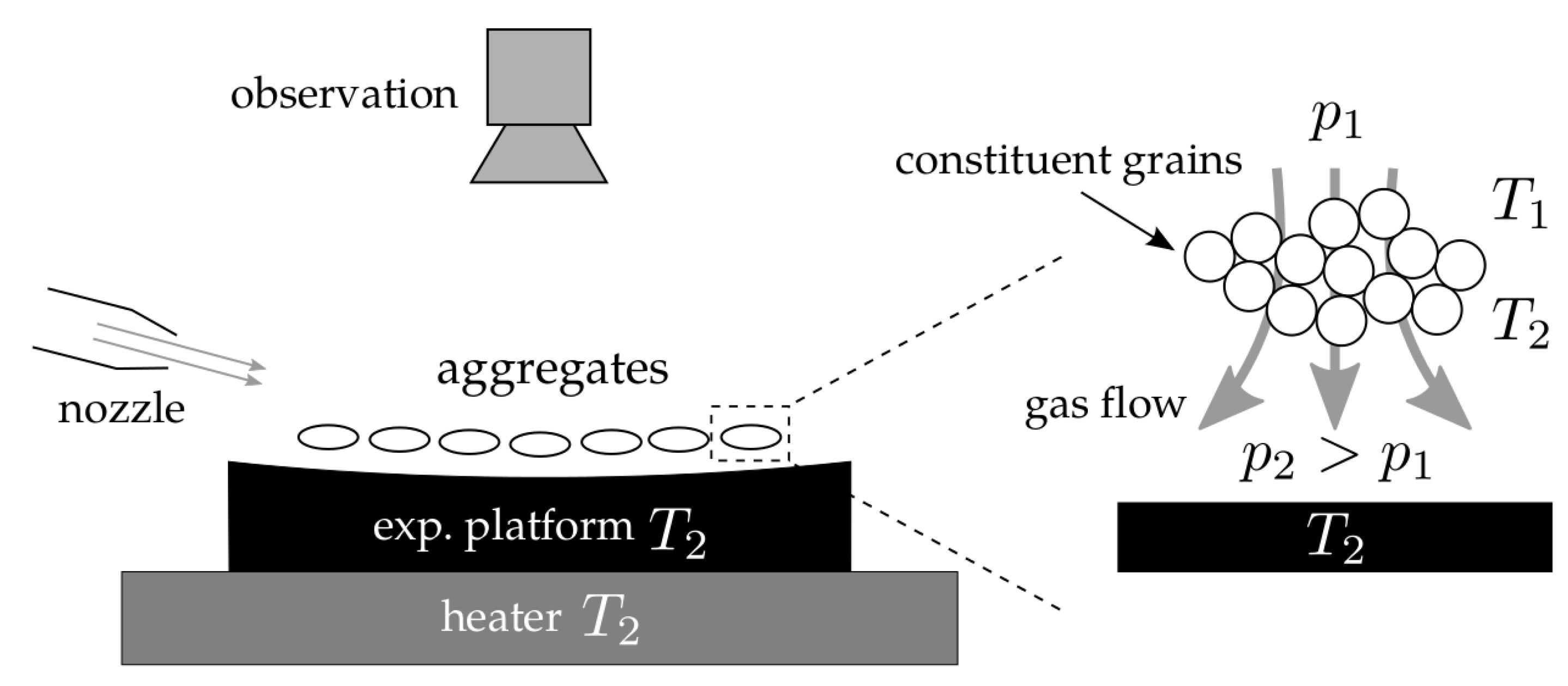
2. Experiments with Levitated Grains
Evolution beyond Bouncing
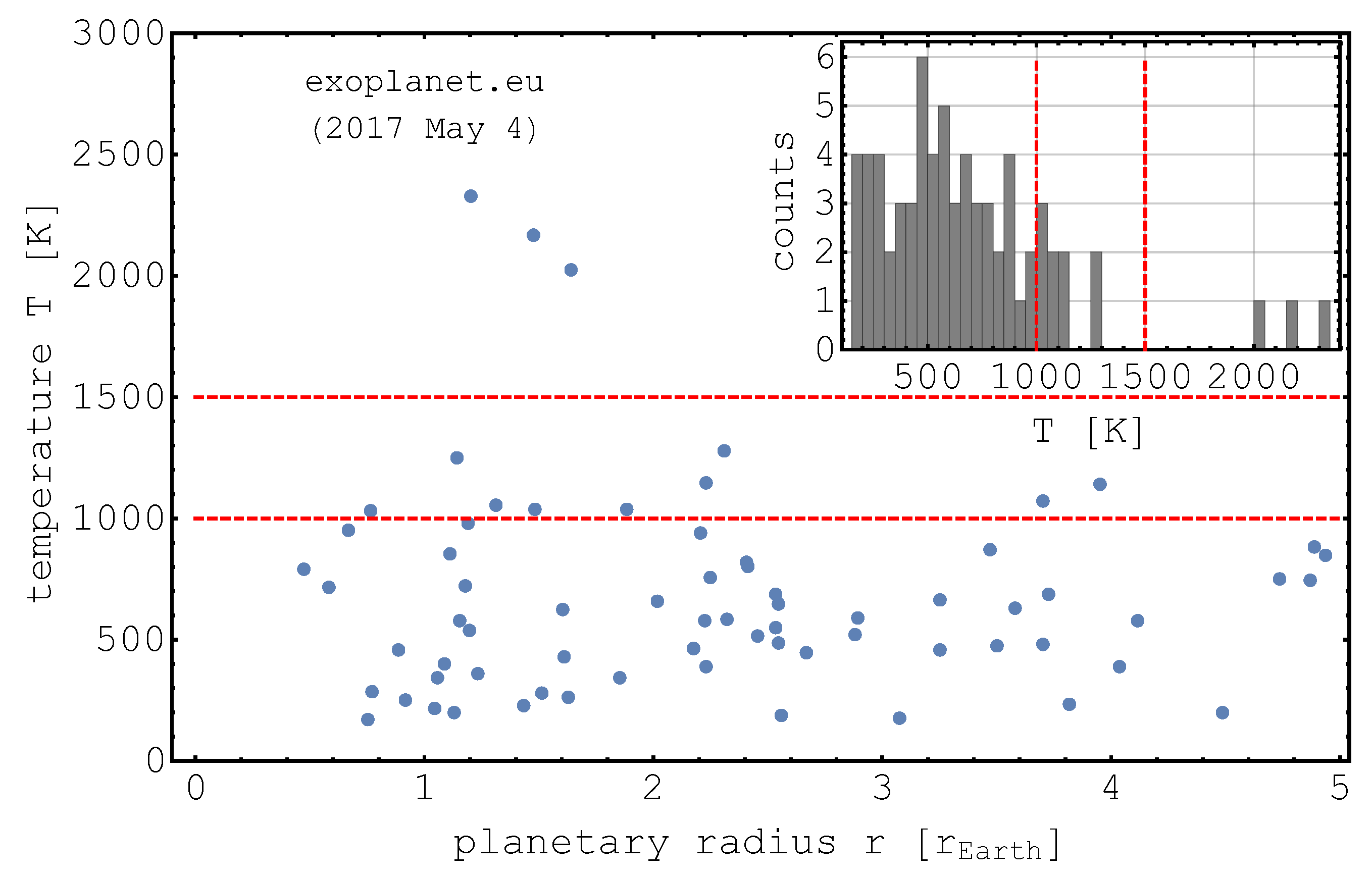
3. Mercury-Like Planets
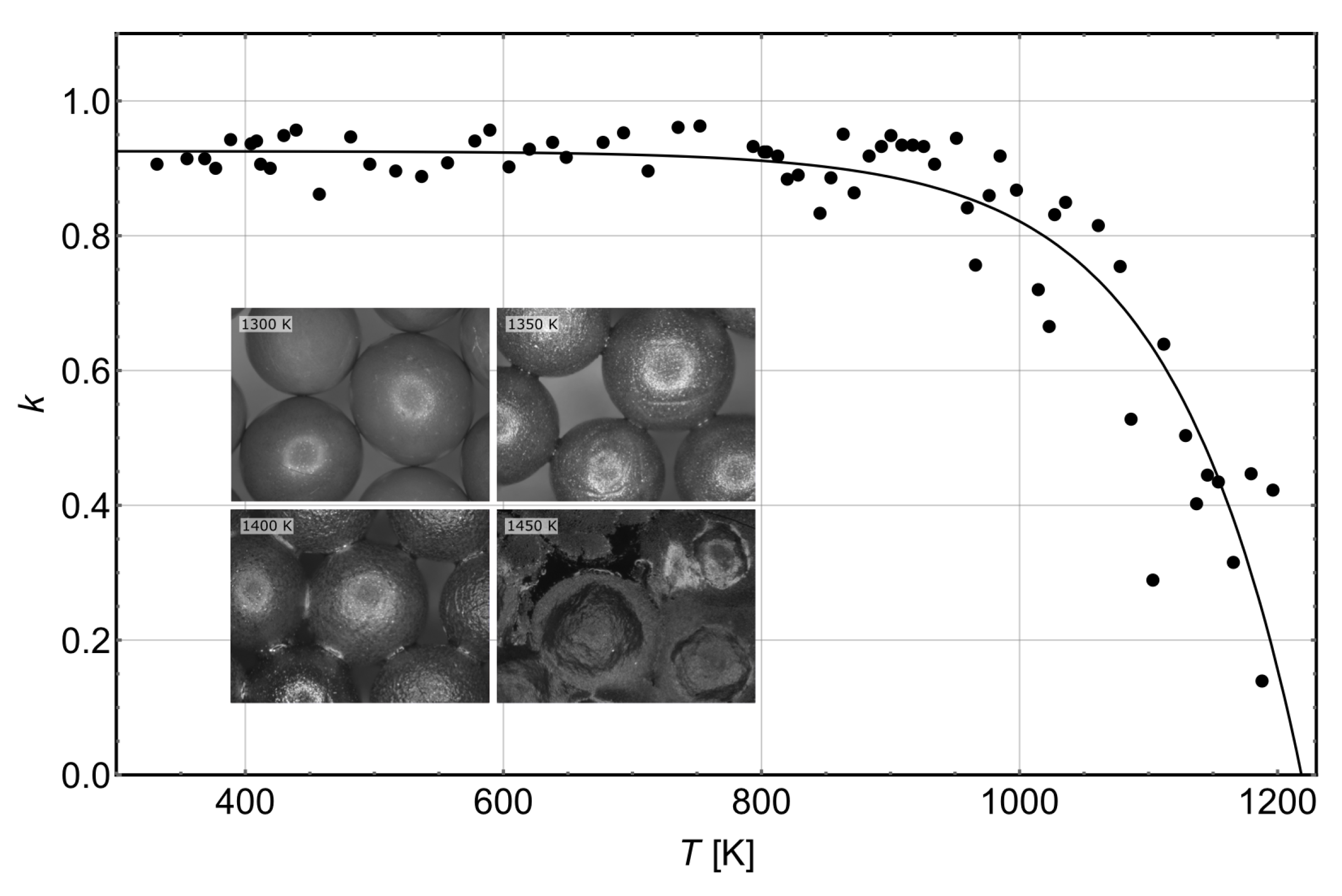
3.1. Temperature and Collisional Growth
3.2. Photophoresis
3.3. Thermoluminescent Erosion of Pre-Planetary Surfaces
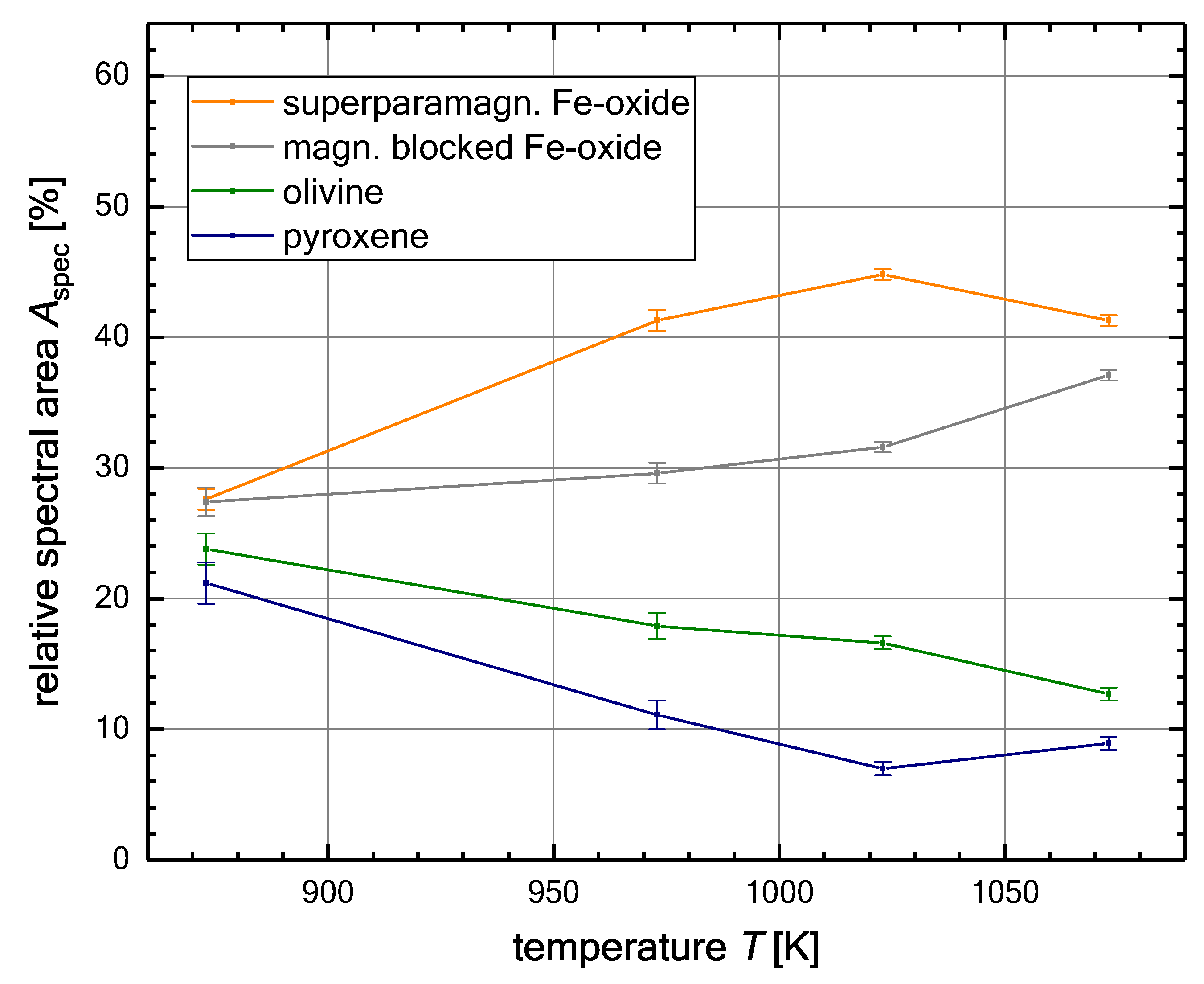
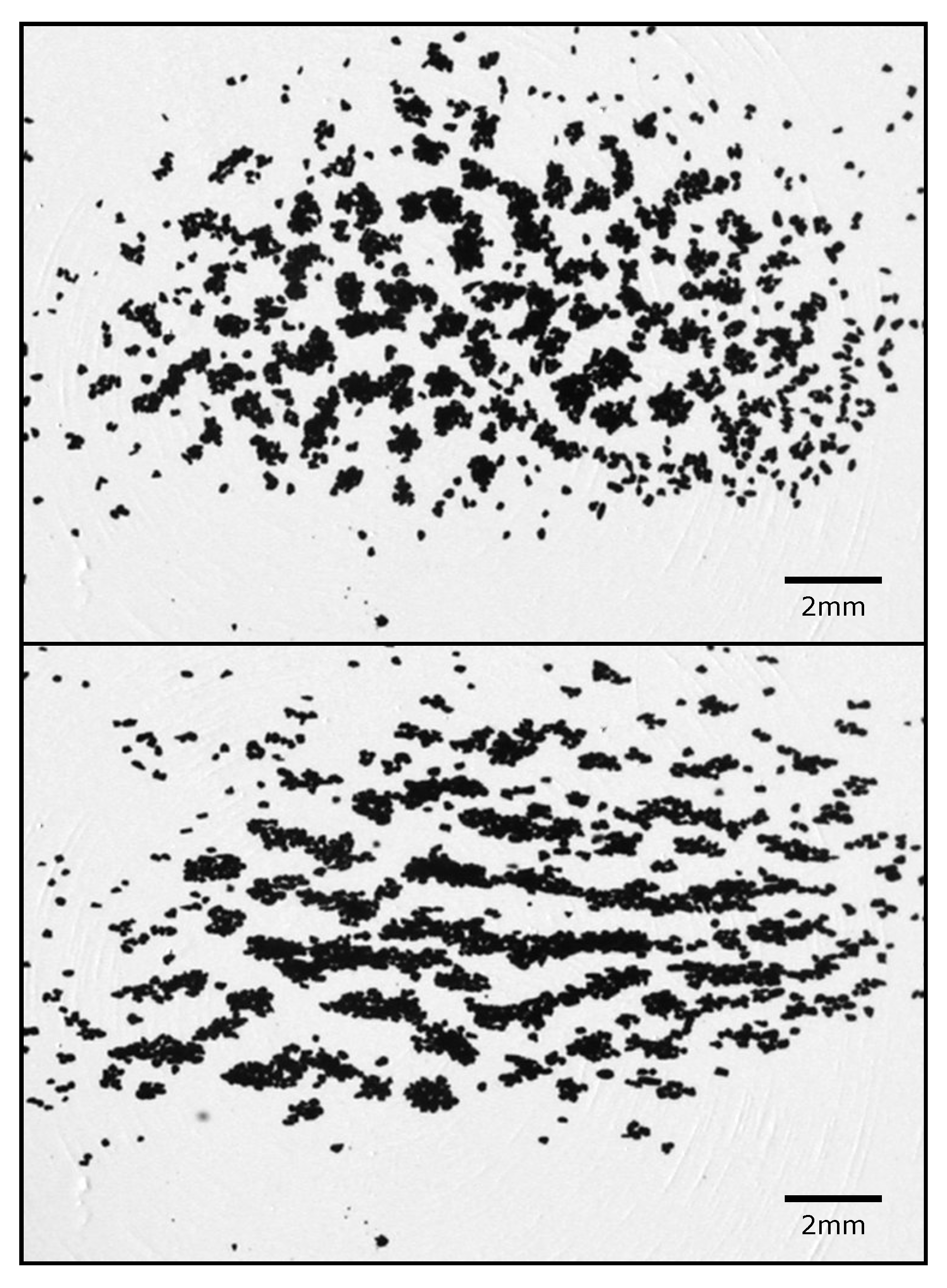
3.4. Magnetic Aggregation
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Blum, J. Dust Evolution in Protoplanetary Discs and the Formation of Planetesimals. What Have We Learned from Laboratory Experiments? Space Sci. Rev. 2018, 214, 52. [Google Scholar] [CrossRef]
- Wyatt, M.C. Debris Disks: Probing Planet Formation. arXiv, 2018; arXiv:1804.08636. [Google Scholar]
- Kley, W. Planet formation and disk-planet interactions. arXiv, 2017; arXiv:1707.07148. [Google Scholar]
- Morbidelli, A.; Raymond, S.N. Challenges in planet formation. J. Geophys. Res. (Planets) 2016, 121, 1962–1980. [Google Scholar] [CrossRef]
- Pfalzner, S.; Davies, M.B.; Gounelle, M.; Johansen, A.; Münker, C.; Lacerda, P.; Portegies Zwart, S.; Testi, L.; Trieloff, M.; Veras, D. The formation of the solar system. Phys. Scr. 2015, 90, 068001. [Google Scholar] [CrossRef]
- Johansen, A.; Blum, J.; Tanaka, H.; Ormel, C.; Bizzarro, M.; Rickman, H. The Multifaceted Planetesimal Formation Process. In Protostars and Planets VI; The University of Arizona Press: Tucson, AZ, USA, 2014; pp. 547–570. [Google Scholar]
- Armitage, P.J. Astrophysics of Planet Formation; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Blum, J.; Wurm, G. The Growth Mechanisms of Macroscopic Bodies in Protoplanetary Disks. Ann. Rev. Astron. Astrophys. 2008, 46, 21–56. [Google Scholar] [CrossRef]
- Leinhardt, Z.M. Terrestrial Planet Formation: A Review and Current Directions. In Extreme Solar Systems, Proceedings of the Astronomical Society of the Pacific Conference (ASP), Santorini Island, Greece, 25–29 June 2007; Fischer, D., Rasio, F.A., Thorsett, S.E., Wolszczan, A., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2008; Volume 398, p. 225. [Google Scholar]
- Richert, A.J.W.; Getman, K.V.; Feigelson, E.D.; Kuhn, M.A.; Broos, P.S.; Povich, M.S.; Bate, M.R.; Garmire, G.P. Circumstellar Disk Lifetimes In Numerous Galactic Young Stellar Clusters. arXiv, 2018; arXiv:1804.05076. [Google Scholar]
- Haisch, K.E., Jr.; Lada, E.A.; Lada, C.J. Disk Frequencies and Lifetimes in Young Clusters. Astrophys. J. 2001, 553, L153–L156. [Google Scholar] [CrossRef]
- Pollack, J.B.; Hubickyj, O.; Bodenheimer, P.; Lissauer, J.J.; Podolak, M.; Greenzweig, Y. Formation of the Giant Planets by Concurrent Accretion of Solids and Gas. Icarus 1996, 124, 62–85. [Google Scholar] [CrossRef]
- Alibert, Y. Maximum mass of planetary embryos that formed in core-accretion models. Astron. Astrophys. 2017, 606, A69. [Google Scholar] [CrossRef]
- Weidenschilling, S.J.; Cuzzi, J.N. Formation of Planetesimals in the Solar Nebula. In Protostars and Planets III; Levy, E.H., Lunine, J.I., Eds.; The University of Arizona Press: Tucson, AZ, USA, 1993; pp. 1031–1060. [Google Scholar]
- Goldreich, P.; Ward, W.R. The Formation of Planetesimals. Astrophys. J. 1973, 183, 1051–1062. [Google Scholar] [CrossRef]
- Blum, J.; Wurm, G.; Kempf, S.; Poppe, T.; Klahr, H.; Kozasa, T.; Rott, M.; Henning, T.; Dorschner, J.; Schräpler, R.; et al. Growth and Form of Planetary Seedlings: Results from a Microgravity Aggregation Experiment. Phys. Rev. Lett. 2000, 85, 2426–2429. [Google Scholar] [CrossRef] [PubMed]
- Blum, J.; Wurm, G.; Kempf, S.; Henning, T. The Brownian Motion of Dust Particles in the Solar Nebula: An Experimental Approach to the Problem of Pre-planetary Dust Aggregation. Icarus 1996, 124, 441–451. [Google Scholar] [CrossRef]
- Paszun, D.; Dominik, C. The influence of grain rotation on the structure of dust aggregates. Icarus 2006, 182, 274–280. [Google Scholar] [CrossRef]
- Wurm, G.; Blum, J. Experiments on Preplanetary Dust Aggregation. Icarus 1998, 132, 125–136. [Google Scholar] [CrossRef]
- Paszun, D.; Dominik, C. Collisional evolution of dust aggregates. From compaction to catastrophic destruction. Astron. Astrophys. 2009, 507, 1023–1040. [Google Scholar] [CrossRef]
- Weidling, R.; Güttler, C.; Blum, J.; Brauer, F. The Physics of Protoplanetesimal Dust Agglomerates. III. Compaction in Multiple Collisions. Astrophys. J. 2009, 696, 2036–2043. [Google Scholar] [CrossRef]
- Blum, J.; Wurm, G. Experiments on Sticking, Restructuring, and Fragmentation of Preplanetary Dust Aggregates. Icarus 2000, 143, 138–146. [Google Scholar] [CrossRef]
- Zsom, A.; Ormel, C.W.; Güttler, C.; Blum, J.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? II. Introducing the bouncing barrier. Astron. Astrophys. 2010, 513, A57. [Google Scholar] [CrossRef]
- Whizin, A.D.; Blum, J.; Colwell, J.E. The Physics of Protoplanetesimal Dust Agglomerates. VIII. Microgravity Collisions between Porous SiO2 Aggregates and Loosely Bound Agglomerates. Astrophys. J. 2017, 836, 94. [Google Scholar] [CrossRef]
- Brisset, J.; Colwell, J.; Dove, A.; Maukonen, D. NanoRocks: Design and performance of an experiment studying planet formation on the International Space Station. Rev. Sci. Instrum. 2017, 88, 074502. [Google Scholar] [CrossRef] [PubMed]
- Jankowski, T.; Wurm, G.; Kelling, T.; Teiser, J.; Sabolo, W.; Gutiérrez, P.J.; Bertini, I. Crossing barriers in planetesimal formation: The growth of mm-dust aggregates with large constituent grains. Astron. Astrophys. 2012, 542, A80. [Google Scholar] [CrossRef]
- Demirci, T.; Teiser, J.; Steinpilz, T.; Landers, J.; Salamon, S.; Wende, H.; Wurm, G. Is There a Temperature Limit in Planet Formation at 1000 K? Astrophys. J. 2017, 846, 48. [Google Scholar] [CrossRef]
- Kruss, M.; Teiser, J.; Wurm, G. Growing into and out of the bouncing barrier in planetesimal formation. Astron. Astrophys. 2017, 600, A103. [Google Scholar] [CrossRef]
- Kruss, M.; Demirci, T.; Koester, M.; Kelling, T.; Wurm, G. Failed Growth at the Bouncing Barrier in Planetesimal Formation. Astrophys. J. 2016, 827, 110. [Google Scholar] [CrossRef]
- Kelling, T.; Wurm, G.; Köster, M. Experimental Study on Bouncing Barriers in Protoplanetary Disks. Astrophys. J. 2014, 783, 111. [Google Scholar] [CrossRef]
- Yoshimatsu, R.; Araújo, N.A.M.; Wurm, G.; Herrmann, H.J.; Shinbrot, T. Self-charging of identical grains in the absence of an external field. Sci. Rep. 2017, 7, 39996. [Google Scholar] [CrossRef] [PubMed]
- Kothe, S.; Blum, J.; Weidling, R.; Güttler, C. Free collisions in a microgravity many-particle experiment. III. The collision behavior of sub-millimeter-sized dust aggregates. Icarus 2013, 225, 75–85. [Google Scholar] [CrossRef]
- Güttler, C.; Blum, J.; Zsom, A.; Ormel, C.W.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? I. Mapping the zoo of laboratory collision experiments. Astron. Astrophys. 2010, 513, A56. [Google Scholar] [CrossRef]
- Brisset, J.; Heißelmann, D.; Kothe, S.; Weidling, R.; Blum, J. Submillimetre-sized dust aggregate collision and growth properties. Experimental study of a multi-particle system on a suborbital rocket. Astron. Astrophys. 2016, 593, A3. [Google Scholar] [CrossRef]
- Blum, J.; Wurm, G.; Poppe, T. The CODAG sounding rocket experiment to study aggregation of thermally diffusing dust particles. Adv. Space Res. 1999, 23, 1267–1270. [Google Scholar] [CrossRef]
- Musiolik, G.; Steinpilz, T.; Kruss, M.; Jungmann, F.; Demirci, T.; Aderholz, M.; Teiser, J.; Wurm, G. ARISE: Building Planetary Seedlings on the ISS. In Proceedings of the IAC Conference, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Kelling, T.; Wurm, G. Self-Sustained Levitation of Dust Aggregate Ensembles by Temperature-Gradient- Induced Overpressures. Phys. Rev. Lett. 2009, 103, 215502-1–215502-4. [Google Scholar] [CrossRef] [PubMed]
- Knudsen, M. Thermischer Molekulardruck der Gase in Röhren and porösen Körpern. Ann. Phys. 1909, 336, 633–640. [Google Scholar] [CrossRef]
- Kelling, T.; Wurm, G.; Dürmann, C. Ice particles trapped by temperature gradients at mbar pressure. Rev. Sci. Instrum. 2011, 82, 115105. [Google Scholar] [CrossRef] [PubMed]
- Fung, F.; Usatyuk, M.; DeSalvo, B.J.; Chin, C. Stable thermophoretic trapping of generic particles at low pressures. Appl. Phys. Lett. 2017, 110, 034102. [Google Scholar] [CrossRef]
- Aumatell, G.; Wurm, G. Ice aggregate contacts at the nm-scale. Mon. Not. R. Astron. Soc. 2014, 437, 690–702. [Google Scholar] [CrossRef]
- Aumatell, G.; Wurm, G. Breaking the ice: Planetesimal formation at the snowline. Mon. Not. R. Astron. Soc. 2011, 418, L1–L5. [Google Scholar] [CrossRef]
- Saito, E.; Sirono, S.i. Planetesimal Formation by Sublimation. Astrophys. J. 2011, 728, 20. [Google Scholar] [CrossRef]
- Schoonenberg, D.; Ormel, C.W. Planetesimal formation near the snowline: In or out? Astron. Astrophys. 2017, 602, A21. [Google Scholar] [CrossRef]
- Dra̧żkowska, J.; Alibert, Y. Planetesimal formation starts at the snow line. Astron. Astrophys. 2017, 608, A92. [Google Scholar] [CrossRef]
- Morbidelli, A.; Bitsch, B.; Crida, A.; Gounelle, M.; Guillot, T.; Jacobson, S.; Johansen, A.; Lambrechts, M.; Lega, E. Fossilized condensation lines in the Solar System protoplanetary disk. Icarus 2016, 267, 368–376. [Google Scholar] [CrossRef]
- Muntz, E.P.; Sone, Y.; Aoki, K.; Vargo, S.; Young, M. Performance analysis and optimization considerations for a Knudsen compressor in transitional flow. J. Vacuum Sci. Technol. Vac. Surf. Films 2002, 20, 214–224. [Google Scholar] [CrossRef]
- De Beule, C.; Wurm, G.; Kelling, T.; Küpper, M.; Jankowski, T.; Teiser, J. The martian soil as a planetary gas pump. Nat. Phys. 2014, 10, 17–20. [Google Scholar] [CrossRef]
- Koester, M.; Kelling, T.; Teiser, J.; Wurm, G. Gas flow within Martian soil: Experiments on granular Knudsen compressors. Astrophys. Space Sci. 2017, 362, 171. [Google Scholar] [CrossRef]
- Musiolik, G.; de Beule, C.; Wurm, G. Analog Experiments on Tensile Strength of Dusty and Cometary Matter. Icarus 2017, 296, 110–116. [Google Scholar] [CrossRef]
- Husmann, T.; Loesche, C.; Wurm, G. Self-sustained Recycling in the Inner Dust Ring of Pre-transitional Disks. Astrophys. J. 2016, 829, 111. [Google Scholar] [CrossRef]
- Ormel, C.W.; Cuzzi, J.N. Closed-form expressions for particle relative velocities induced by turbulence. Astron. Astrophys. 2007, 466, 413–420. [Google Scholar] [CrossRef]
- Weidenschilling, S.J. The distribution of mass in the planetary system and solar nebula. Astrophys. Space Sci. 1977, 51, 153–158. [Google Scholar] [CrossRef]
- Deckers, J.; Teiser, J. Colliding Decimeter Dust. Astrophys. J. 2013, 769, 151. [Google Scholar] [CrossRef]
- Beitz, E.; Güttler, C.; Blum, J.; Meisner, T.; Teiser, J.; Wurm, G. Low-velocity Collisions of Centimeter-sized Dust Aggregates. Astrophys. J. 2011, 736, 34. [Google Scholar] [CrossRef]
- Schräpler, R.; Blum, J.; Seizinger, A.; Kley, W. The Physics of Protoplanetesimal Dust Agglomerates. VII. The Low-velocity Collision Behavior of Large Dust Agglomerates. Astrophys. J. 2012, 758, 35. [Google Scholar] [CrossRef]
- Birnstiel, T.; Dullemond, C.P.; Brauer, F. Gas- and dust evolution in protoplanetary disks. Astron. Astrophys. 2010, 513, A79. [Google Scholar] [CrossRef]
- Birnstiel, T.; Klahr, H.; Ercolano, B. A simple model for the evolution of the dust population in protoplanetary disks. Astron. Astrophys. 2012, 539, A148. [Google Scholar] [CrossRef]
- Wurm, G.; Paraskov, G.; Krauss, O. Growth of planetesimals by impacts at 25 m/s. Icarus 2005, 178, 253–263. [Google Scholar] [CrossRef]
- Teiser, J.; Wurm, G. High-velocity dust collisions: Forming planetesimals in a fragmentation cascade with final accretion. Mon. Not. R. Astron. Soc. 2009, 393, 1584–1594. [Google Scholar] [CrossRef]
- Meisner, T.; Wurm, G.; Teiser, J.; Schywek, M. Preplanetary scavengers: Growing tall in dust collisions. Astron. Astrophys. 2013, 559, A123. [Google Scholar] [CrossRef]
- Windmark, F.; Birnstiel, T.; Güttler, C.; Blum, J.; Dullemond, C.P.; Henning, T. Planetesimal formation by sweep-up: How the bouncing barrier can be beneficial to growth. Astron. Astrophys. 2012, 540, A73. [Google Scholar] [CrossRef]
- Drążkowska, J.; Windmark, F.; Dullemond, C.P. Modeling dust growth in protoplanetary disks: The breakthrough case. Astron. Astrophys. 2014, 567, A38. [Google Scholar] [CrossRef]
- Youdin, A.N.; Goodman, J. Streaming Instabilities in Protoplanetary Disks. Astrophys. J. 2005, 620, 459–469. [Google Scholar] [CrossRef]
- Simon, J.B.; Armitage, P.J.; Li, R.; Youdin, A.N. The Mass and Size Distribution of Planetesimals Formed by the Streaming Instability. I. The Role of Self-gravity. Astrophys. J. 2016, 822, 55. [Google Scholar] [CrossRef]
- Schneider, N.; Wurm, G.; Teiser, J.; Klahr, H.; Carpenter, V. Streaming in laboratory experiments. Astrophys. J. 2018. submitted. [Google Scholar]
- Spohn, T. Planetologie. In Erde und Planeten; Raith, W., Ed.; Walter de Gruyter: Berlin, Germany, 2001; pp. 427–525. [Google Scholar]
- Trieloff, M.; Palme, H. The Origin of Solids in the Early Solar System. In Planet Formation; Klahr, H., Brandner, W., Eds.; Cambridge University Press: Cambridge, UK, 2006; p. 64. [Google Scholar]
- Rappaport, S.; Sanchis-Ojeda, R.; Rogers, L.A.; Levine, A.; Winn, J.N. The Roche Limit for Close-orbiting Planets: Minimum Density, Composition Constraints, and Application to the 4.2 hr Planet KOI 1843.03. Astrophys. J. 2013, 773, L15. [Google Scholar] [CrossRef]
- Sinukoff, E.; Howard, A.W.; Petigura, E.A.; Fulton, B.J.; Crossfield, I.J.M.; Isaacson, H.; Gonzales, E.; Crepp, J.R.; Brewer, J.M.; Hirsch, L.; et al. K2-66b and K2-106b: Two Extremely Hot Sub-Neptune-size Planets with High Densities. Astron. J. 2017, 153, 271. [Google Scholar] [CrossRef]
- Santerne, A.; Brugger, B.; Armstrong, D.J.; Adibekyan, V.; Lillo-Box, J.; Gosselin, H.; Aguichine, A.; Almenara, J.M.; Barrado, D.; Barros, S.C.C.; et al. An Earth-sized exoplanet with a Mercury-like composition. Nat. Astron. 2018, 2, 393–400. [Google Scholar] [CrossRef]
- Guenther, E.W.; Barragán, O.; Dai, F.; Gandolfi, D.; Hirano, T.; Fridlund, M.; Fossati, L.; Chau, A.; Helled, R.; Korth, J.; et al. K2-106, a system containing a metal-rich planet and a planet of lower density. Astron. Astrophys. 2017, 608, A93. [Google Scholar] [CrossRef]
- Benz, W.; Slattery, W.L.; Cameron, A.G.W. Collisional stripping of Mercury’s mantle. Icarus 1988, 74, 516–528. [Google Scholar] [CrossRef]
- Cameron, A.G.W. The partial volatilization of Mercury. Icarus 1985, 64, 285–294. [Google Scholar] [CrossRef]
- Peplowski, P.N.; Blewett, D.T.; Denevi, B.W.; Evans, L.G.; Lawrence, D.J.; Nittler, L.R.; Rhodes, E.A.; Selby, C.M.; Solomon, S.C. Mapping iron abundances on the surface of Mercury: Predicted spatial resolution of the MESSENGER Gamma-Ray Spectrometer. Planet. Space Sci. 2011, 59, 1654–1658. [Google Scholar] [CrossRef]
- Gundlach, B.; Blum, J. The Stickiness of Micrometer-sized Water-ice Particles. Astrophys. J. 2015, 798, 34. [Google Scholar] [CrossRef]
- Deckers, J.; Teiser, J. Collisions of solid ice in planetesimal formation. Mon. Not. R. Astron. Soc. 2016, 456, 4328–4334. [Google Scholar] [CrossRef]
- Musiolik, G.; Teiser, J.; Jankowski, T.; Wurm, G. Ice Grain Collisions in Comparison: CO2, H2O, and Their Mixtures. Astrophys. J. 2016, 827, 63. [Google Scholar] [CrossRef]
- Kataoka, A.; Tanaka, H.; Okuzumi, S.; Wada, K. Fluffy dust forms icy planetesimals by static compression. Astron. Astrophys. 2013, 557, L4. [Google Scholar] [CrossRef]
- Okuzumi, S.; Tanaka, H.; Kobayashi, H.; Wada, K. Rapid Coagulation of Porous Dust Aggregates outside the Snow Line: A Pathway to Successful Icy Planetesimal Formation. Astrophys. J. 2012, 752, 106. [Google Scholar] [CrossRef]
- Musiolik, G.; Teiser, J.; Jankowski, T.; Wurm, G. Collisions of CO2 Ice Grains in Planet Formation. Astrophys. J. 2016, 818, 16. [Google Scholar] [CrossRef]
- Pinilla, P.; Pohl, A.; Stammler, S.M.; Birnstiel, T. Dust Density Distribution and Imaging Analysis of Different Ice Lines in Protoplanetary Disks. Astrophys. J. 2017, 845, 68. [Google Scholar] [CrossRef]
- Schäfer, C.; Riecker, S.; Maindl, T.I.; Speith, R.; Scherrer, S.; Kley, W. A smooth particle hydrodynamics code to model collisions between solid, self-gravitating objects. Astron. Astrophys. 2016, 590, A19. [Google Scholar] [CrossRef]
- Geretshauser, R.J.; Meru, F.; Speith, R.; Kley, W. The four-population model: A new classification scheme for pre-planetesimal collisions. Astron. Astrophys. 2011, 531, A166. [Google Scholar] [CrossRef]
- Geretshauser, R.J.; Speith, R.; Kley, W. Collisions of inhomogeneous pre-planetesimals. Astron. Astrophys. 2011, 536, A104. [Google Scholar] [CrossRef]
- Blum, J.; Schraepler, R. Structure and Mechanical Properties of High-Porosity Macroscopic Agglomerates Formed by Random Ballistic Deposition. Phys. Rev. Lett. 2004, 93, 115503. [Google Scholar] [CrossRef] [PubMed]
- Meisner, T.; Wurm, G.; Teiser, J. Experiments on centimeter-sized dust aggregates and their implications for planetesimal formation. Astron. Astrophys. 2012, 544, A138. [Google Scholar] [CrossRef]
- De Beule, C.; Landers, J.; Salamon, S.; Wende, H.; Wurm, G. Planetesimal Formation in the Warm, Inner Disk: Experiments with Tempered Dust. Astrophys. J. 2017, 837, 59. [Google Scholar] [CrossRef]
- Zanda, B. Chondrules. Earth Planet. Sci. Lett. 2004, 224, 1–17. [Google Scholar] [CrossRef]
- Connolly, H.C., Jr.; Hewins, R.H.; Atre, N.; Lofgren, G.E. Compound chondrules: An experimental investigation. Meteoritics 1994, 29, 458. [Google Scholar]
- Bodgan, T.; Teiser, J.; Fischer, N.; Kruss, M.; Wurm, G. Constrains on compound chondrule formation from laboratory high temperature collisions. Icarus 2018. submitted. [Google Scholar]
- Krauss, O.; Wurm, G. Photophoresis and the Pile-up of Dust in Young Circumstellar Disks. Astrophys J. 2005, 630, 1088–1092. [Google Scholar] [CrossRef]
- Wurm, G.; Krauss, O. Concentration and sorting of chondrules and CAIs in the late Solar Nebula. Icarus 2006, 180, 487–495. [Google Scholar] [CrossRef]
- Herrmann, F.; Krivov, A.V. Effects of photophoresis on the evolution of transitional circumstellar disks. Astron. Astrophys. 2007, 476, 829–839. [Google Scholar] [CrossRef]
- Takeuchi, T.; Krauss, O. Photophoretic Structuring of Circumstellar Dust Disks. Astrophys. J. 2008, 677, 1309–1323. [Google Scholar] [CrossRef]
- Rohatschek, H. Semi-empirical model of photophoretic forces for the entire range of pressures. J. Aerosol Sci. 1995, 26, 717–734. [Google Scholar] [CrossRef]
- Cordier, D.; Prada Moroni, P.G.; Tognelli, E. Dust photophoretic transport around a T Tauri star: Implications for comets composition. Icarus 2016, 268, 281–294. [Google Scholar] [CrossRef]
- Beresnev, S.A.; Kovalev, F.D.; Kochneva, L.B.; Runkov, V.A.; Suetin, P.E.; Cheremisin, A.A. On the possibility of particle’s photophoretic levitation in the stratosphere. Atmos. Ocean. Opt. 2003, 16, 44–48. [Google Scholar]
- Matthews, L.S.; Kimery, J.B.; Wurm, G.; de Beule, C.; Kuepper, M.; Hyde, T.W. Photophoretic force on aggregate grains. Mon. Not. R. Astron. Soc. 2016, 455, 2582–2591. [Google Scholar] [CrossRef]
- Loesche, C.; Wurm, G. Thermal and photophoretic properties of dust mantled chondrules and sorting in the solar nebula. Astron. Astrophys. 2012, 545, A36. [Google Scholar] [CrossRef]
- Wurm, G.; Trieloff, M.; Rauer, H. Photophoretic Separation of Metals and Silicates: The Formation of Mercury-like Planets and Metal Depletion in Chondrites. Astrophys. J. 2013, 769, 78. [Google Scholar] [CrossRef]
- Cuello, N.; Gonzalez, J.F.; Pignatale, F.C. Effects of photophoresis on the dust distribution in a 3D protoplanetary disc. Mon. Not. R. Astron. Soc. 2016, 458, 2140–2149. [Google Scholar] [CrossRef]
- Krauss, O.; Wurm, G.; Mousis, O.; Petit, J.M.; Horner, J.; Alibert, Y. The photophoretic sweeping of dust in transient protoplanetary disks. Astron. Astrophys. 2007, 462, 977–987. [Google Scholar] [CrossRef]
- Mousis, O.; Petit, J.M.; Wurm, G.; Krauss, O.; Alibert, Y.; Horner, J. Photophoresis as a source of hot minerals in comets. Astron. Astrophys. 2007, 466, L9–L12. [Google Scholar] [CrossRef]
- Moudens, A.; Mousis, O.; Petit, J.M.; Wurm, G.; Cordier, D.; Charnoz, S. Photophoretic transport of hot minerals in the solar nebula. Astron. Astrophys. 2011, 531, A106. [Google Scholar] [CrossRef]
- Haack, H.; Wurm, G. Life on the Edge—Formation of CAIs and Chondrules at the Inner Edge of the Dust Disk. Meteorit. Planet. Sci. Suppl. 2007, 42, 5157. [Google Scholar]
- Wurm, G.; Haack, H. Outward transport of CAIs during FU-Orionis events. Meteorit. Planet. Sci. 2009, 44, 689–699. [Google Scholar] [CrossRef]
- McNally, C.P.; McClure, M.K. Photophoretic Levitation and Trapping of Dust in the Inner Regions of Protoplanetary Disks. Astrophys. J. 2017, 834, 48. [Google Scholar] [CrossRef]
- Loesche, C.; Wurm, G.; Kelling, T.; Teiser, J.; Ebel, D.S. The motion of chondrules and other particles in a protoplanetary disc with temperature fluctuations. Mon. Not. R. Astron. Soc. 2016, 463, 4167–4174. [Google Scholar] [CrossRef]
- McNally, C.P.; Hubbard, A. Photophoresis in a Dilute, Optically Thick Medium and Dust Motion in Protoplanetary Disks. Astrophys. J. 2015, 814, 37. [Google Scholar] [CrossRef]
- Wurm, G.; Teiser, J.; Bischoff, A.; Haack, H.; Roszjar, J. Experiments on the photophoretic motion of chondrules and dust aggregates—Indications for the transport of matter in protoplanetary disks. ICARUS 2010, 208, 482–491. [Google Scholar] [CrossRef]
- Loesche, C.; Teiser, J.; Wurm, G.; Hesse, A.; Friedrich, J.M.; Bischoff, A. Photophoretic Strength on Chondrules. 2. Experiment. Astrophys. J. 2014, 792, 73. [Google Scholar] [CrossRef]
- Kuepper, M.; de Beule, C.; Wurm, G.; Matthews, L.S.; Kimery, J.S.; Hyde, T.W. Photophoresis on polydisperse basalt microparticles under microgravity. J. Aerosol Sci. 2014, 76, 126–137. [Google Scholar] [CrossRef]
- von Borstel, I.; Blum, J. Photophoresis of dust aggregates in protoplanetary disks. Astron. Astrophys. 2012, 548, A96. [Google Scholar] [CrossRef]
- Beresnev, S.A.; Kochneva, L.B.; Suetin, P.E. Photophoresis of Aerosols in the Earth Atmosphere. Thermophys. Aeromech. 2003, 10, 287–301. [Google Scholar]
- van Eymeren, J.; Wurm, G. The implications of particle rotation on the effect of photophoresis. Mon. Not. R. Astron. Soc. 2012, 420, 183–186. [Google Scholar] [CrossRef]
- Loesche, C.; Wurm, G.; Jankowski, T.; Kuepper, M. Photophoresis on particles hotter/colder than the ambient gas in the free molecular flow. J. Aerosol Sci. 2016, 97, 22–33. [Google Scholar] [CrossRef]
- Loesche, C.; Husmann, T. Photophoresis on particles hotter/colder than the ambient gas for the entire range of pressures. J. Aerosol Sci. 2016, 102, 55–71. [Google Scholar] [CrossRef]
- Cheremisin, A.A.; Vassilyev, Y.V.; Horvath, H. Gravito-photophoresis and aerosol stratification in the atmosphere. J. Aerosol Sci. 2005, 36, 1277–1299. [Google Scholar] [CrossRef]
- Cheremisin, A.A.; Shnipov, I.S.; Horvath, H.; Rohatschek, H. The global picture of aerosol layers formation in the stratosphere and in the mesosphere under the influence of gravito-photophoretic and magneto-photophoretic forces. J. Geophys. Res. (Atmos.) 2011, 116, 19204. [Google Scholar] [CrossRef]
- Rohatschek, H. Über die Kräfte der reinen Photophorese und der Gravitophotophorese (On the forces of pure and gravito-photophoresis). Acta Phys. Austriaca 1956, 10, 267–286. [Google Scholar]
- Rohatschek, H. Direction, magnitude and causes of photophoretic forces. J. Aerosol Sci. 1985, 16, 29–42. [Google Scholar] [CrossRef]
- Rohatschek, H. Photophoretic levitation of carbonaceous aerosols. J. Aerosol Sci. 1989, 20, 903–906. [Google Scholar] [CrossRef]
- Wurm, G. Light-induced disassembly of dusty bodies in inner protoplanetary discs: Implications for the formation of planets. Mon. Not. R. Astron. Soc. 2007, 380, 683–690. [Google Scholar] [CrossRef]
- Wurm, G.; Krauss, O. Dust Eruptions by Photophoresis and Solid State Greenhouse Effects. Phys. Rev. Lett. 2006, 96, 134301. [Google Scholar] [CrossRef] [PubMed]
- De Beule, C.; Kelling, T.; Wurm, G.; Teiser, J.; Jankowski, T. From Planetesimals to Dust: Low-gravity Experiments on Recycling Solids at the Inner Edges of Protoplanetary Disks. Astrophys. J. 2013, 763, 11. [Google Scholar] [CrossRef]
- Kelling, T.; Wurm, G. A Mechanism to Produce the Small Dust Observed in Protoplanetary Disks. Astrophys. J. 2011, 733, 120–125. [Google Scholar] [CrossRef]
- Kocifaj, M.; Klačka, J.; Wurm, G.; Kelling, T.; Kohút, I. Dust ejection from (pre-)planetary bodies by temperature gradients: Radiative and heat transfer. Mon. Not. R. Astron. Soc. 2010, 404, 1512–1518. [Google Scholar] [CrossRef]
- Schmidt, F.; Andrieu, F.; Costard, F.; Kocifaj, M.; Meresescu, A.G. Formation of recurring slope lineae on Mars by rarefied gas-triggered granular flows. Nat. Geosci. 2017, 10, 270–273. [Google Scholar] [CrossRef]
- De Beule, C.; Wurm, G.; Kelling, T.; Koester, M.; Kocifaj, M. An insolation activated dust layer on Mars. Icarus 2015, 260, 23–28. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Balme, M.R.; Esposito, F.; Kelling, T.; Klose, M.; Kok, J.F.; Marticorena, B.; Merrison, J.; Patel, M.; Wurm, G. Particle Lifting Processes in Dust Devils. Space Sci. Rev. 2016, 203, 347–376. [Google Scholar] [CrossRef]
- Nuth, J.A.; Berg, O.; Faris, J.; Wasilewski, P. Magnetically enhanced coagulation of very small iron grains. Icarus 1994, 107, 155. [Google Scholar] [CrossRef] [PubMed]
- Nübold, H.; Poppe, T.; Rost, M.; Dominik, C.; Glassmeier, K.H. Magnetic aggregation. II. Laboratory and microgravity experiments. Icarus 2003, 165, 195–214. [Google Scholar] [CrossRef]
- Dominik, C.; Nübold, H. Magnetic Aggregation: Dynamics and Numerical Modeling. Icarus 2002, 157, 173–186. [Google Scholar] [CrossRef]
- Dudorov, A.E.; Khaibrakhmanov, S.A. Fossil magnetic field of accretion disks of young stars. Astrophys. Space Sci. 2014, 352, 103–121. [Google Scholar] [CrossRef]
- Brauer, R.; Wolf, S.; Flock, M. Magnetic fields in circumstellar disks. The potential of Zeeman observations. Astron. Astrophys. 2017, 607, A104. [Google Scholar] [CrossRef]
- Hubbard, A. Explaining Mercury’s density through magnetic erosion. Icarus 2014, 241, 329–335. [Google Scholar] [CrossRef]
- Kruss, M.; Wurm, G. Seeding the formation of Mercurys: An iron sensitive bouncing barrier in disk magnetic fields. Icarus 2018. submitted. [Google Scholar]




© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wurm, G. Selective Aggregation Experiments on Planetesimal Formation and Mercury-Like Planets. Geosciences 2018, 8, 310. https://doi.org/10.3390/geosciences8090310
Wurm G. Selective Aggregation Experiments on Planetesimal Formation and Mercury-Like Planets. Geosciences. 2018; 8(9):310. https://doi.org/10.3390/geosciences8090310
Chicago/Turabian StyleWurm, Gerhard. 2018. "Selective Aggregation Experiments on Planetesimal Formation and Mercury-Like Planets" Geosciences 8, no. 9: 310. https://doi.org/10.3390/geosciences8090310
APA StyleWurm, G. (2018). Selective Aggregation Experiments on Planetesimal Formation and Mercury-Like Planets. Geosciences, 8(9), 310. https://doi.org/10.3390/geosciences8090310



