Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy
Abstract
:1. Introduction
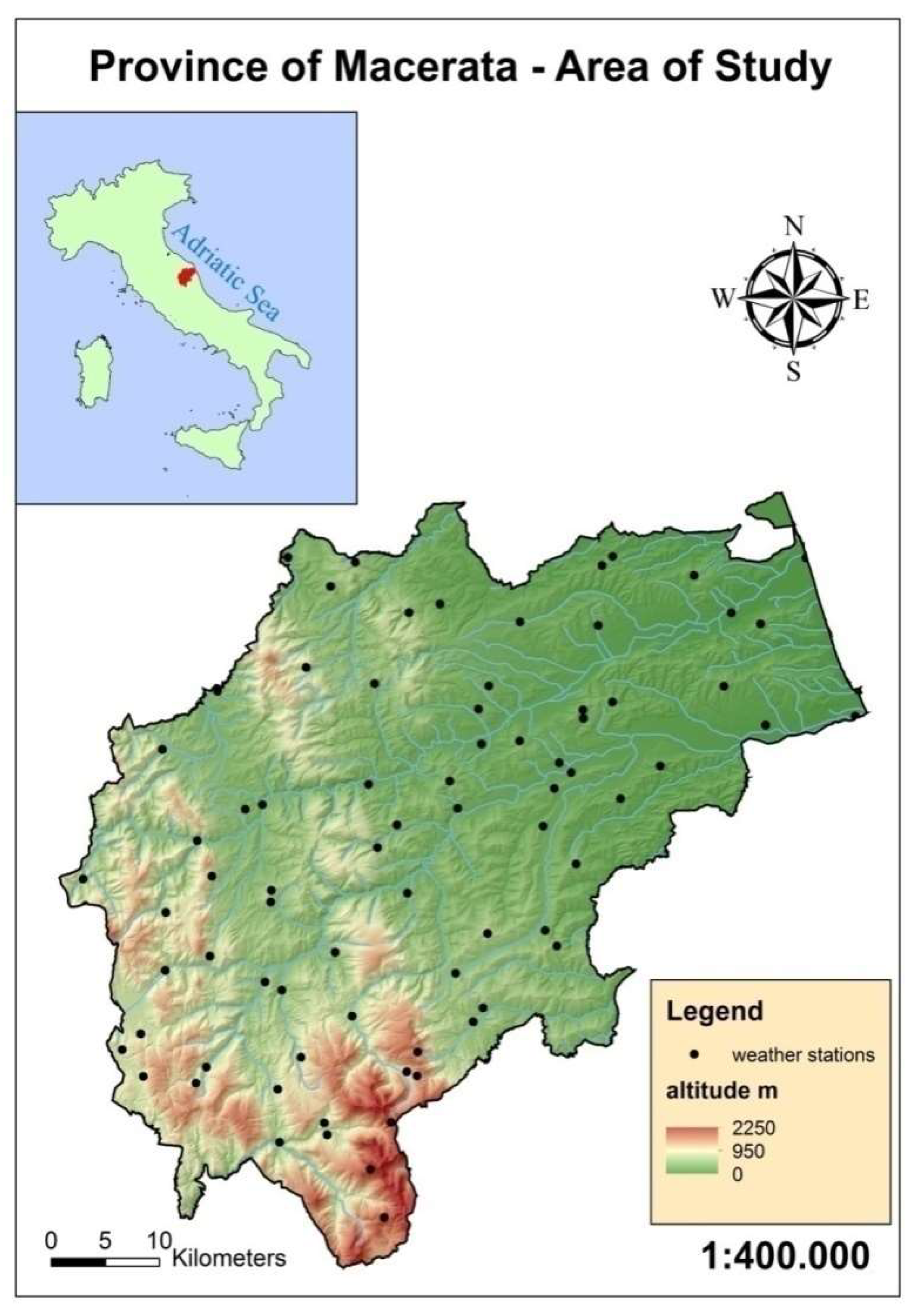
Geographical Boundaries of the Analysis
2. Methodology
2.1. Climate Data
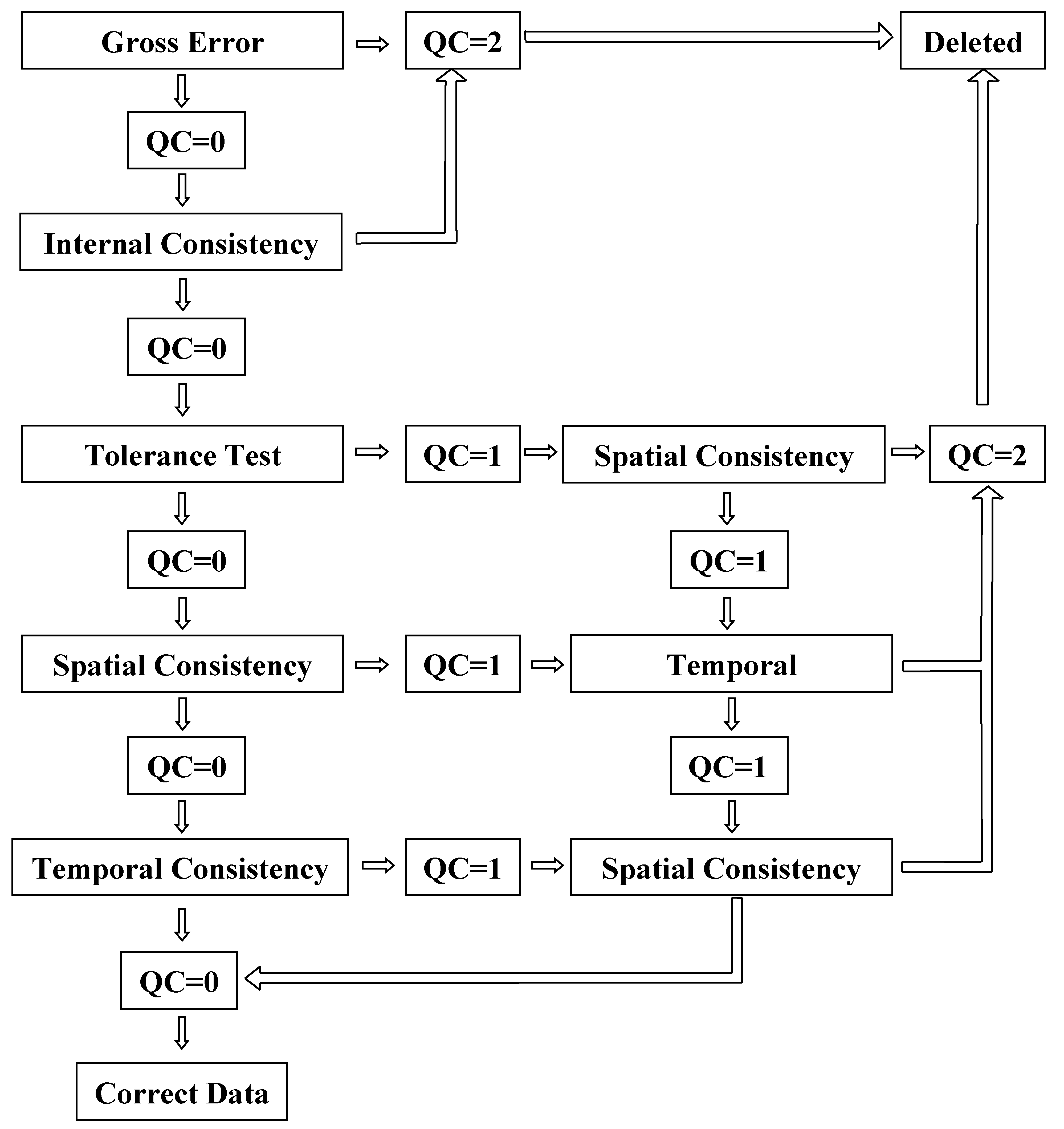
2.2. Data Analysis
- Gross error checking
- Internal consistency check
- Tolerance test
- Temporal consistency
- Spatial consistency
- 1.
- The rain gauges that show QC = 1 after the spatial consistency because of very low precipitation were analysed through a test composed by the calculation of the squared correlation coefficient (R2) [33]:
- R2 > 0.7: the rain gauge value is accepted for all months only if it is above its minimum limit as calculated by the time series, for at least 9 out of 12 months;
- R2 < 0.7: the months below the lower threshold of the time series are removed only if at least 9 out of 12 months are above this limit;
- If there are less than nine months above the lower limit but the value of R2 is greater than 0.7; it is necessary to calculate the median of each month and of each year in the five nearby rain gauges in the lifetime of the investigated one and subtract 1.5 times the standard deviation, thus obtaining another threshold value. When the rain recording station shows three years or more below the lower threshold the whole year is deleted, otherwise it is accepted completely without removing any months;
- When there are less than nine months above the minimum limit and R2 < 0.7 the whole suspect year is deleted.
- 2.
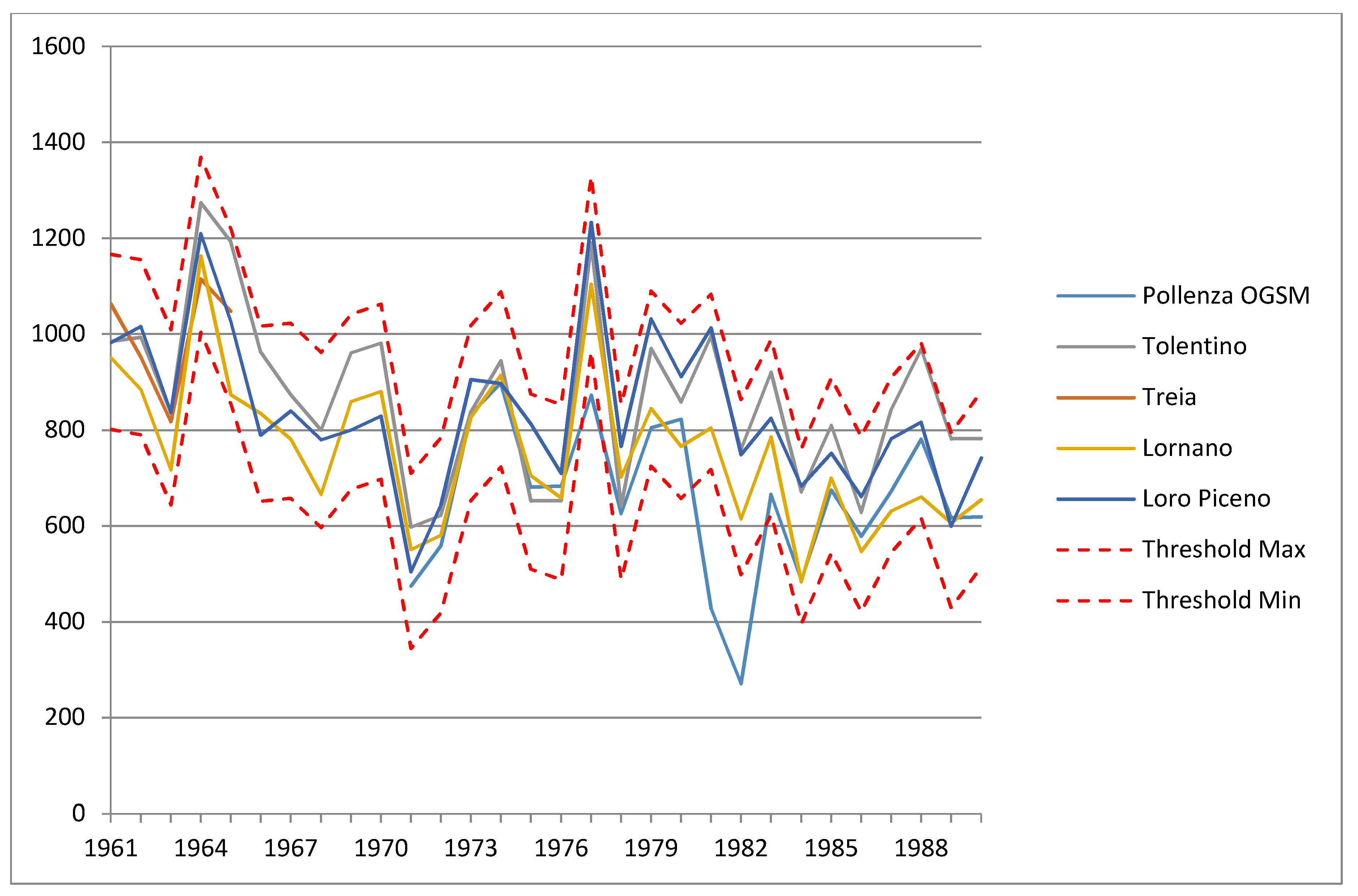
- The rain gauges, which had a QC = 1 after the spatial consistency analysis due to the exceeding of 3σ threshold for annual values, required use of a procedure slightly different from the gauges with very little precipitation. The monthly data of the weather station under investigation were analysed with its historical time series and accepted if they were lower than 2σ + µ (QC = 0), investigated if they were between 2σ + µ and 3σ + µ (QC = 1), or removed if they were above 3σ + µ (QC = 3). The suspect rainfall stations with at least 10 years of observations and no more than 20, were analysed in comparison with the neighbouring stations through the following procedure:
- If the similarity is greater than 0.7 (R2), the rain gauges would remain for all the months if they are below the threshold value for at least 9 out of 12 months. If the threshold value is above the limit for more than four months, it should be compared with five nearby rain gauges. This comparison allowed calculation of a median that should be multiplied by two times the standard deviation: Th.Max.Neigh.pt = Me + 2σ. When the record exceeded this limit for more than three months the whole year is removed (QC = 3): otherwise, only the months above the threshold would be deleted (QC = 3);
- When R2 was < 0.7, the records were deleted for all the values above the set limit if at least 9 out of 12 months were below the limit (Th.Max.Neigh.pt = Me + 2σ); however, if there were four months above the limit, data were removed for the whole year.
2.3. Reconstruction of Missing Data
- inverse distance weighted (IDW) [37]:
- Empirical Bayesian Kriging(EBK) allows an automatic estimate of the semivariogram through GIS software. It is possible to set the number of attempts, 1000 in this case with 60 points in each subset and an overlap factor equal to 1 (empirically demonstrated assessing the greatest minimization of the error). This method is very convenient when the data are non-stationary and with a great extension in the territory, because it uses a local model and, with 1000 attempts, it is possible to obtain the best fit for each value [38].
- ordinary co-kriging method [37]:
3. Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Zahumenský, I. Guidelines on Quality Control Procedures for Data from Automatic Weather Stations; WMO (World Meteorological Organization): Geneva, Switzerland, 2004. [Google Scholar]
- Filippov, V.V. Quality Control Procedures for Meteorological Data; Tech. Rep. 26; WMO (World Meteorological Organization): Geneva, Switzerland, 1968. [Google Scholar]
- Eischeid, J.K.; Bruce Baker, C.; Karl, T.R.; Diaz, H.F. The Quality Control of Long-Term Climatological Data Using Objective Data Analysis. J. Appl. Meteorol. 1995, 34, 2787–2795. [Google Scholar] [CrossRef] [Green Version]
- Boyer, T.; Levitus, S. Quality Control and Processing of Historical Oceanographic Temperature, Salinity, and Oxygen Data; NOAA Technical Report NESDIS 81: Washington, DC, USA, 1994. [Google Scholar]
- Peterson, T.C.; Vose, R.; Schmoyer, R.; Razuvaëv, V. Global historical climatology network (GHCN) quality control of monthly temperature data. Int. J. Climatol. 1998, 18, 1169–1179. [Google Scholar] [CrossRef] [Green Version]
- Meek, D.W.; Hatfield, J.L. Data quality checking for single station meteorological databases. Agric. For. Meteorol. 1994, 36, 85–109. [Google Scholar] [CrossRef]
- Cheng, A.R.; Lee, T.H.; Ku, H.I.; Chen, Y.W. Quality Control Program for Real-Time Hourly Temperature Observation in Taiwan. J. Atmos. Ocean. Technol. 2016, 33, 953–976. [Google Scholar] [CrossRef]
- Qi, Y.; Martinaitis, S.; Zhang, J.; Cocks, S. A Real-Time Automated Quality Control of Hourly Rain Gauge Data Based on Multiple Sensors in MRMS System. J. Hydrometeor. 2016, 17, 1675–1691. [Google Scholar] [CrossRef]
- Svensson, P.; Björnsson, H.; Samuli, A.; Andresen, L.; Bergholt, L.; Tveito, O.E.; Agersten, S.; Pettersson, O.; Vejen, F. Quality Control of Meteorological Observations. Available online: https://www.researchgate.net/publication/238738578_Quality_Control_of_Meteorological_Observations_Description_of_potential_HQC_systems (accessed on 3 June 2018).
- Boulanger, J.P.; Aizpuru, J.; Leggieri, L.; Marino, M. A procedure for automated quality control and homogenization of historical daily temperature and precipitation data (APACH): Part 1: Quality control and application to the Argentine weather service stations. Clim. Chang. 2010, 98, 471–491. [Google Scholar] [CrossRef]
- Acquaotta, F.; Fratianni, S.; Venema, V. Assessment of parallel precipitation measurements networks in Piedmont, Italy. Int. J. Climatol. 2016, 36, 3963–3974. [Google Scholar] [CrossRef]
- Mekis, E.; Vincent, L. An overview of the second generation adjusted daily precipitation dataset for trend analysis in Canada. Atmos. Ocean 2011, 2, 163–177. [Google Scholar] [CrossRef]
- Sciuto, G.; Bonaccorso, B.; Cancelliere, A.; Rossi, G. Probabilistic quality control of daily temperature data. Int. J. Climatol. 2013, 33, 1211–1227. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New techniques for the detection and adjustment of shifts in daily precipitation data series. J. Appl. Meteorol. Climatol. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Alexander, L.; Yang, H.; Perkins, S. ClimPACT—Indices and Software in User Manual. In Guide to Climatological Practices; WMO (World Meteorological Organization): Geneva, Switzerland, 2009; Available online: http://www.wmo.int/pages/prog/wcp/ccl/opace/opace4/meetings/documents/ETCRSCI_software_documentation_v2a.doc (accessed on 3 June 2018).
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.C.; Wieringa, J. Guidance on Metadata and Homogenization; WMO (World Meteorological Organization): Geneva, Switzerland, 2003. [Google Scholar]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Coulibaly, P.; Evora, N.D. Comparison of neural network methods for infilling missing daily weather records. J. Hydrol. 2007, 341, 27–41. [Google Scholar] [CrossRef]
- Eccel, E.; Cau, P.; Ranzi, R. Data reconstruction and homogenization for reducing uncertainties in high-resolution climate analysis in Alpine regions. Theor. Appl. Climatol. 2012, 110, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Mitchel, A. The ESRI Guide to GIS analysis, volume 2: Spatial measurements and statistics. In ESRI Guide GIS Analysis; FAO: Rome, Italy, 2005. [Google Scholar]
- Kolahdouzan, M.; Shahabi, C. Voronoi-based k nearest neighbor search for spatial network databases. In Proceedings of the Thirtieth International Conference on Very Large Data Bases-Volume 30; VLDB Endowment: San Jose, CA, USA, 2004; pp. 840–851. [Google Scholar]
- Köppen, W. Versuch einer Klassifikation der Klimate, vorzugsweise nach ihren Beziehungen zur Pflanzenwelt. Geogr. Zeitschr. 1900, 6, 593–611. [Google Scholar]
- Geiger, R. Landolt-Börnstein—Zahlenwerte und Funktionenaus Physik, Chemie, Astronomie, Geophysik und Technik; alte Serie Vol. 3; der Klimatenach, C.K., Köppen, W., Eds.; Springer: Berlin, Germany, 1954; pp. 603–607. [Google Scholar]
- Fratianni, S.; Acquaotta, F. Landscapes and Landforms of Italy; Marchetti, M., Soldati, M., Eds.; Springer: Berlin, Germany, 2017; pp. 29–38. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Grykałowska, A.; Kowal, A.; Szmyrka-Grzebyk, A. The basics of calibration procedure and estimation of uncertainty budget for meteorological temperature sensors. Meteorol. Appl. 2015, 22, 867–872. [Google Scholar] [CrossRef] [Green Version]
- Martin, W.B.; Gnanadesikan, R. Probability plotting methods for the analysis for the analysis of data. Biometrika 1968, 55, 1–17. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Hae-Young, K. Statistical notes for clinical researchers: Assessing normal distribution (2) using skewness and kurtosis. Restor. Dent. Endod. 2013, 38, 52–54. [Google Scholar]
- Hackshaw, A. Statistical Formulae for Calculating Some 95% Confidence Intervals. In A Concise Guide to Clinical Trials; Wiley-Blackwell: West Sussex, UK, 2007; pp. 205–207. [Google Scholar]
- Omar, M.H. Statistical Process Control Charts for Measuring and Monitoring Temporal Consistency of Ratings. J. Educ. Meas. 2010, 47, 18–35. [Google Scholar] [CrossRef]
- Schönwiese, C.D. Praktische Methoden für Meteorologen und Geowissenschaftler; Schweizerbart Science Publishers: Stuttgart, Germany, 2006; pp. 232–234. [Google Scholar]
- Bono, E.; Noto, L.; La Loggia, G. Tecniche di analisi spaziale per la ricostruzione delle serie storiche di dati climatici. In Atti del Convegno 9a Conferenza Nazionale ASITA; CINECA IRIS: Catania, Italy, 2005. [Google Scholar]
- Easterling, D.R.; Peterson, T.C. A new method for detecting undocumented discontinuities in climatological time series. Int. J. Clim. 1995, 15, 369–377. [Google Scholar] [CrossRef]
- Jung-Woo, K.; Pachepsky, Y.A. Reconstructing missing daily precipitation data using regression trees and artificial neural networks for SWAT stream flow simulation. J. Hydrol. 2010, 394, 305–314. [Google Scholar]
- Johnston, K.; VerHoef, J.M.; Krivoruchko, K.; Lucas, N. Appendix A. In Using ArcGIS Geostatistical Analyst; ESRI: Redlands, CA, USA, 2001; pp. 247–273. [Google Scholar]
- Krivoruchko, K. Empirical Bayesian Kriging; Esri: Redlands, CA, USA, 2012. [Google Scholar]
- Gentilucci, M.; Bisci, C.; Burt, P.; Fazzini, M.; Vaccaro, C. Interpolation of Rainfall Through Polynomial Regression in the Marche Region (Central Italy). In Lecture Notes in Geoinformation and Cartography; Mansourian, A., Pilesjö, P., Harrie, L., van Lammeren, R., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.; García-Vera, M.A.; Stepanek, P. A complete daily precipitation database for northeast Spain: Reconstruction, quality control, and homogeneity. Int. J. Climatol. 2010, 30, 1146–1163. [Google Scholar] [CrossRef] [Green Version]
- Robinson, T.P.; Metternicht, G. Testing the performance of spatial interpolation techniques for mapping soil properties. Comput. Electron. Agric. 2006, 50, 97–108. [Google Scholar] [CrossRef]
| St. N. | PDA | Sensor | Weather Station | Lat. | Long. | Altitude (m) |
|---|---|---|---|---|---|---|
| 1 | 1931–2007 | P | Acquasanta | 42°46′ | 13°25′ | 392 |
| 2 | 1931–2014 | P | Amandola | 42°59′ | 13°22′ | 550 |
| 3 | 1931–2012 | P | Amatrice | 42°38′ | 13°17′ | 954 |
| 4 | 1951–2014 | P | Ancona Baraccola | 43°34′ | 13°31′ | 37 |
| 5 | 1931–2014 | P | Ancona Torrette | 43°36′ | 13°27′ | 6 |
| 6 | 1931–2009 | P | Apiro | 43°23′ | 13°8′ | 516 |
| 7 | 2009–2014 | P-T | Apiro 2 | 43°25′ | 13°5′ | 270 |
| 8 | 1931–1956 | P | Appennino | 42°59′ | 13°5′ | 798 |
| 9 | 1931–1976 | P | Appignano | 43°22′ | 13°21′ | 199 |
| 10 | 1999–2014 | P | Appignano 2 | 43°22′ | 13°20′ | 195 |
| 11 | 1931–2014 | P | Arquata del Tronto | 42°46′ | 13°18′ | 720 |
| 12 | 1931–2013 | P | Ascoli Piceno | 42°51′ | 13°36′ | 136 |
| 13 | 1931–2006 | P | Bolognola Paese | 42°59′ | 13°14′ | 1070 |
| 14 | 1967–2014 | P-T | Bolognola Pintura RT201 | 43°00′ | 13°14′ | 1352 |
| 15 | 1931–1950 | P | Caldarola | 43°8′ | 13°13′ | 314 |
| 16 | 1931–1996 | P | Camerino | 43°8′ | 13°4′ | 664 |
| 17 | 1999–2014 | P-T | Camerino 2 | 43°8′ | 13°4′ | 581 |
| 18 | 1931–2014 | P | Campodiegoli | 43°18′ | 12°49′ | 507 |
| 19 | 1931–2007 | P | Capo il Colle | 42°50′ | 13°28′ | 539 |
| 20 | 1931–2007 | P | Capodacqua | 42°44′ | 13°14′ | 817 |
| 21 | 1931–2014 | P | Case San Giovanni | 43°23′ | 13°2′ | 620 |
| 22 | 1999–2014 | P-T | Castelraimondo | 43°13′ | 13°2′ | 410 |
| 23 | 1931–1963 | P | Castelraimondo | 43°13′ | 13°2′ | 307 |
| 24 | 1931–1963 | P | Chiaravalle | 43°36′ | 13°20′ | 25 |
| 25 | 1931–2008 | P-T | Cingoli | 43°22′ | 13°13′ | 631 |
| 26 | 1999–2014 | P-T | Cingoli 2 | 43°25′ | 13°10′ | 494 |
| 27 | 1999–2014 | P-T | Cingoli 3 | 42°23′ | 13°15′ | 265 |
| 28 | 1997–2014 | P | Civitanova Marche OGSM | 43°17′ | 13°44′ | 10 |
| 29 | 1931–2009 | P | Civitella del Tronto | 42°46′ | 13°40′ | 589 |
| 30 | 1931–1976 | P | Corridonia | 43°15′ | 13°30′ | 255 |
| 31 | 1951–2014 | P | Croce di Casale | 42°55′ | 13°26′ | 657 |
| 32 | 1931–2007 | P | Cupramontana | 43°27′ | 13°7′ | 506 |
| 33 | 1934–2007 | P | Diga di Carassai | 43°2′ | 13°41′ | 130 |
| 34 | 1967–2006 | P | Diga di Talvacchia | 42°47′ | 13°31′ | 515 |
| 35 | 1931–1951 | P | Dignano | 43°1′ | 12°56′ | 873 |
| 36 | 1931–1976 | P | Elcito | 43°19′ | 13°5′ | 824 |
| 37 | 1999–2014 | P-T | Esanatoglia | 43°15′ | 12°56′ | 608 |
| 38 | 1931–2008 | P-T | Fabriano RM1810 | 43°20′ | 12°54′ | 357 |
| 39 | 1964–1989 | P | FalconaraAeroporto | 43°38′ | 13°22′ | 9 |
| 40 | 1933–2007 | P-T | Fermo RM2220 | 43°10′ | 13°43′ | 280 |
| 41 | 1931–2007 | P | Filottrano | 43°26′ | 13°21′ | 270 |
| 42 | 1999–2014 | P | Fiastra | 43°02′ | 13°16′ | 747 |
| 43 | 1931–2007 | P | Fiume di Fiastra | 43°2′ | 13°10′ | 618 |
| 44 | 1931–2014 | P | Gelagna Alta | 43°5′ | 13°0′ | 711 |
| 45 | 1931–1989 | P | Grottazzolina | 43°6′ | 13°36′ | 200 |
| 46 | 1931–1949 | P-T | GualdoTadino | 43°14′ | 12°47′ | 535 |
| 47 | 1931–2007 | P-T | Jesi | 43°31′ | 13°15′ | 96 |
| 48 | 1932–2008 | P | Loreto RM1940 | 43°26′ | 13°36′ | 127 |
| 49 | 1932–2008 | P-T | Lornano | 43°17′ | 13°25′ | 232 |
| 50 | 1931–2007 | P | Loro Piceno | 43°10′ | 13°25′ | 435 |
| 51 | 1970–2014 | P-T | Macerata OGSM | 43°18′ | 13°25′ | 303 |
| 52 | 1999–2014 | P-T | Macerata Montalbano | 43°18′ | 13°25′ | 294 |
| 53 | 1999–2014 | P-T | Macerata 3 | 43°14′ | 13°24′ | 146 |
| 54 | 1999–2014 | P-T | Matelica | 43°18′ | 13°0′ | 325 |
| 55 | 1951–2013 | P-T | Moie | 43°30′ | 13°8′ | 110 |
| 56 | 1999–2014 | P-T | Monte BoveSud | 42°55′ | 13°11′ | 1917 |
| 57 | 1931–2007 | P | Montecarotto | 43°31′ | 13°4′ | 388 |
| 58 | 1931–2006 | P | Montecassiano | 43°22′ | 13°26′ | 215 |
| 59 | 1999–2014 | P-T | Montecavallo | 42°59′ | 12°59′ | 960 |
| 60 | 1999–2014 | P-T | Montecosaro | 43°17′ | 13°38′ | 45 |
| 61 | 1999–2014 | P | Montecosaro 2 | 43°17′ | 13°38′ | 50 |
| 62 | 1931–1951 | P-T | Montefano | 43°24′ | 13°26′ | 242 |
| 63 | 1999–2014 | P | Montefano 2 | 43°25′ | 13°27′ | 144 |
| 64 | 1999–2014 | P | Montelupone | 43°22′ | 13°35′ | 29 |
| 65 | 1931–2007 | P-T | Montemonaco RM2230 | 42°54′ | 13°19′ | 987 |
| 66 | 1999–2014 | P-T | Monteprata | 42°54′ | 13°13′ | 1813 |
| 67 | 1931–2007 | P | Monterubbiano | 43°5′ | 13°43′ | 463 |
| 68 | 1931–2014 | P | Morrovalle | 43°19′ | 13°35′ | 246 |
| 69 | 1999–2014 | P-T | Muccia | 43°4′ | 13°4′ | 430 |
| 70 | 1931–2014 | P-T | Nocera Umbra | 43°07′ | 12°47′ | 535 |
| 71 | 1931–2014 | P-T | Norcia | 42°48′ | 13°06′ | 691 |
| 72 | 1931–2012 | P | Osimo città RM1920 | 43°29′ | 13°29′ | 265 |
| 73 | 1931–2007 | P | Pedaso | 43°6′ | 13°51′ | 4 |
| 74 | 1932–2002 | P | Petriolo | 43°13′ | 13°28′ | 271 |
| 75 | 1931–2007 | P | Pié del Sasso | 42°59′ | 13°0′ | 711 |
| 76 | 1931–2013 | P | Pievebovigliana | 43°3′ | 13°5′ | 451 |
| 77 | 1931–2013 | P | Pioraco RM1970 | 43°11′ | 12°59′ | 441 |
| 78 | 1931–1957 | P-T | PoggioSorifa | 43°9′ | 12°52′ | 552 |
| 79 | 1970–2014 | P | Pollenza OGSM | 43°15′ | 13°24′ | 158 |
| 80 | 1999–2014 | P-T | Pollenza 2 | 43°16′ | 13°19′ | 170 |
| 81 | 1999–2014 | P-T | Porto Recanati | 43°25′ | 13°40′ | 0 |
| 82 | 1936–2007 | P-T | Porto Sant’Elpidio RM2160 | 43°15′ | 13°46′ | 3 |
| 83 | 1931–1984 | P | Preci | 42°53′ | 13°02′ | 907 |
| 84 | 1935–1991 | P | Ragnola | 42°55′ | 13°53′ | 10 |
| 85 | 1975–2014 | P | Recanati OGSM ITIS | 43°25′ | 13°32′ | 243 |
| 86 | 1931–2006 | P | Recanati RM2020 | 43°24′ | 13°33′ | 235 |
| 87 | 1931–2014 | P | Ripatransone | 43°00′ | 13°46′ | 494 |
| 88 | 1931–1946 | P | San Gregorio di Camerino | 43°9′ | 13°0′ | 754 |
| 89 | 1931–1961 | P | San Maroto | 43°5′ | 13°8′ | 555 |
| 90 | 1953–2002 | P | San Martino | 42°44′ | 13°27′ | 783 |
| 91 | 1931–1963 | P | San Severino Marche RM1998 | 43°14′ | 13°11′ | 344 |
| 92 | 1964–1984 | P | San Severino OGSM | 43°15′ | 13°14′ | 180 |
| 93 | 1931–1989 | P | Sant’Angelo in Pontano RM2150 | 43°6′ | 13°24′ | 473 |
| 94 | 1999–2014 | P-T | Sant’Angelo in Pontano 2 | 43°6′ | 13°23′ | 373 |
| 95 | 1931–2008 | P | Santa Maria di Pieca | 43°4′ | 13°17′ | 467 |
| 96 | 1931–2007 | P-T | Sarnano | 43°2′ | 13°18′ | 539 |
| 97 | 1999–2014 | P | Sassotetto | 43°1′ | 13°14′ | 1365 |
| 98 | 1931–2014 | P | Sassoferrato | 43°26′ | 12°52′ | 312 |
| 99 | 1950–1987 | P | Sellano | 42°53′ | 12°55′ | 604 |
| 100 | 1933–2000 | P | Serralta RM2000 | 43°19′ | 13°11′ | 546 |
| 101 | 1938–1976 | P-T | Serrapetrona | 43°11′ | 13°11′ | 450 |
| 102 | 1999–2014 | P | Serrapetrona 2 | 43°11′ | 13°13′ | 437 |
| 103 | 1931–2008 | P | Serravalle di Chienti RM2030 | 43°4′ | 12°57′ | 647 |
| 104 | 1999–2014 | P-T | Serravalle di Chienti 2 | 43°0′ | 12°54′ | 925 |
| 105 | 1932–2014 | P-T | Servigliano RM2190 | 43°5′ | 13°30′ | 215 |
| 106 | 1931–2008 | P | Sorti | 43°7′ | 12°57′ | 672 |
| 107 | 1931–2008 | P | Tolentino RM2090 | 43°12′ | 13°17′ | 244 |
| 108 | 1999–2014 | P-T | Tolentino 2 | 43°14′ | 13°23′ | 183 |
| 109 | 1998–2014 | P | Tolentino 3 | 43°13′ | 13°17′ | 224 |
| 110 | 1931–1964 | P-T | Treia | 43°17′ | 13°18′ | 230 |
| 111 | 1999–2014 | P | Treia 2 | 43°18′ | 13°18′ | 342 |
| 112 | 1931–1951 | P | Urbisaglia | 43°12′ | 13°22′ | 311 |
| 113 | 1931–1979 | P | Ussita | 42°57′ | 13°08′ | 744 |
| 114 | 2000–2014 | P-T | Ussita 2 | 42°57′ | 13°08′ | 749 |
| 115 | 2000–2014 | P | Villa Potenza | 43°20′ | 13°26′ | 133 |
| 116 | 1931–2007 | P | Ville Santa Lucia | 43°11′ | 12°51′ | 664 |
| 117 | 1931–1971 | P | Visso | 42°56′ | 13°05′ | 607 |
| 118 | 1999–2014 | P-T | Visso 2 | 43°0′ | 13°07′ | 978 |
| IDW | EBK | Co-Kriging | |
|---|---|---|---|
| Regression function | 0.6221x + 6.8366 | 0.6813x + 5.7113 | 0.9400x + 1.2166 |
| Mean | 0.0119 | 0.0311 | 0.0566 |
| Root-mean-square | 1.6870 | 1.6429 | 1.2465 |
| Mean standardized | −0.0002 | 0.0237 | |
| Rootmeansquarestandardized | 0.9514 | 0.9890 | |
| Average standard error | 1.7366 | 1.5278 |
| Weather Station | QC = 2 T | QC = 2 P | Weather Station | QC = 2 T | QC = 2 P |
|---|---|---|---|---|---|
| Amandola | 1 | Nocera Umbra | 10 | 14 | |
| Apiro 2 | 11 | 1 | Norcia | 11 | 1 |
| Appennino | 1 | Osimo città RM1920 | 3 | ||
| Arquata del Tronto | 2 | Petriolo | 1 | ||
| Bolognola Paese | Pievebovigliana | 2 | |||
| Bolognola Pintura RT201 | 1 | Pioraco | 2 | ||
| Camerino | 7 | Pollenza OGSM | 4 | ||
| Cingoli | 9 | Pollenza 2 | 3 | ||
| Cingoli 2 | 1 | 12 | Sant’Angelo in Pontano | 1 | |
| Civitanova Marche OGSM | 2 | Recanati | 1 | ||
| Dignano | 3 | Sarnano | 1 | ||
| Fabriano RM1810 | 3 | 12 | S. Severino M. RM1998 | 1 | |
| Fermo | 5 | 11 | Sellano | 5 | |
| Gualdo Tadino | 1 | Serravalle di C. RM2030 | 1 | ||
| Jesi | 9 | 4 | Serravalle di C. 2 | 2 | |
| Loro Piceno | 1 | Servigliano RM2190 | 12 | ||
| Lornano | 10 | 1 | Sorti | 1 | |
| Matelica | 3 | Tolentino OGSM | 4 | ||
| M. Bove Sud RT207 | 5 | 1 | Tolentino 2 | 4 | |
| Montecassiano | 25 | Urbisaglia | 6 | ||
| Montefano | 2 | Ussita 2 | 5 | 1 | |
| Montemonaco | 6 | 1 | Ville Santa Lucia | 1 | |
| Monteprata RT206 | 8 | 1 | Visso | 4 | |
| Muccia ST26 | 6 | Visso 2 | 9 |
| QC = 0 T | QC = 1 T | QC = 2 T | QC = 0 P | QC = 1 P | QC = 2 P | |
|---|---|---|---|---|---|---|
| Gross error | 1,821,039 | - | 15 | 76,981 | - | 40 |
| Internal consistency | 1,821,007 | - | 32 | 76,869 | - | 112 |
| Tolerance Test | 1,820,925 | 82 | - | 76,662 | 207 | - |
| Temporal consistency | 1,820,767 | 240 | - | 76,489 | 380 | - |
| Spatial Consistency | 1,820,679 | - | 328 | 75,735 | - | 1134 |
| 1931–1960 | 1961–1990 | 1991–2014 | |
|---|---|---|---|
| Deleted temperature data | 78 (0.017%) | 137 (0.023%) | 160 (0.021%) |
| Deleted precipitation data | 351 (1.52%) | 363 (1.34%) | 572 (1.89%) |
| ME | RMSE | ASE | MSE | RMSSE | |
|---|---|---|---|---|---|
| Temperature | −0.15 | 1.46 | 1.62 | −0.021 | 0.97 |
| Precipitation | −0.22 | 9.77 | 10.01 | −0.013 | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gentilucci, M.; Barbieri, M.; Burt, P.; D’Aprile, F. Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy. Geosciences 2018, 8, 202. https://doi.org/10.3390/geosciences8060202
Gentilucci M, Barbieri M, Burt P, D’Aprile F. Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy. Geosciences. 2018; 8(6):202. https://doi.org/10.3390/geosciences8060202
Chicago/Turabian StyleGentilucci, Matteo, Maurizio Barbieri, Peter Burt, and Fabrizio D’Aprile. 2018. "Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy" Geosciences 8, no. 6: 202. https://doi.org/10.3390/geosciences8060202
APA StyleGentilucci, M., Barbieri, M., Burt, P., & D’Aprile, F. (2018). Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy. Geosciences, 8(6), 202. https://doi.org/10.3390/geosciences8060202







