Abstract
We consider the effect of global warming on the coupled plankton-oxygen dynamics in the ocean. The net oxygen production by phytoplankton is known to depend on the water temperature and hence can be disrupted by warming. We address this issue theoretically by considering a mathematical model of the plankton-oxygen system. The model is generic and can account for a variety of biological factors. We first show that sustainable oxygen production by phytoplankton is only possible if the net production rate is above a certain critical value. This result appears to be robust to the details of model parametrization. We then show that, once the effect of zooplankton is taken into account (which consume oxygen and feed on phytoplankton), the plankton-oxygen system can only be stable if the net oxygen production rate is within a certain intermediate range (i.e., not too low and not too high). Correspondingly, we conclude that a sufficiently large increase in the water temperature is likely to push the system out of the safe range, which may result in ocean anoxia and even a global oxygen depletion. We then generalize the model by taking into account the effect of environmental stochasticity and show that, paradoxically, the probability of oxygen depletion may decrease with an increase in the rate of global warming.
1. Introduction
Global warming, i.e. the tendency of the average Earth surface temperature to increase with time [1,2], is a major threat to the environment worldwide, which can lead to a number of adverse consequences to ecology, agriculture, health and society [3]. Perhaps the best known and widely-discussed result of climate change is the expected increase in the ocean level because of melting of polar ice, which would lead to flooding of many coastal areas [4,5], hence resulting in huge economic losses, devastating effects on ecology and, possibly, the loss of human lives. Somewhat less publicized in the media, but perhaps even more dangerous is the observed decrease in the concentration of dissolved oxygen in the ocean [6]. It is predicted that in the worst case scenario, the amount of ocean oxygen could fall almost twice [7], which would lead to disastrous consequences for the ocean ecosystems by suffocating most of marine life [8].
The currently-observed oxygen decrease is attributed to a variety of hydrological and geophysical factors such as lower oxygen solvability in warmer water and slower ocean overturning and mixing [6,7]. However, a decrease in the oxygen concentration can also occur for a different reason, i.e., not because of changes in oxygen transport and/or consumption rate, but as a result of disruption in oxygen production. Indeed, oxygen is consumed through several different processes, e.g., by breathing of marine fauna and in biochemical reactions (e.g., remineralization), but is mostly produced in one process, i.e., by phytoplankton photosynthesis. (The second largest flux of O emerges from the pyrite regeneration by bacteria in the ocean [9], which we do not consider here.) Meanwhile, it is a well-established fact that the net production of oxygen by marine phytoplankton (i.e., the difference between the amount of oxygen produced in photosynthesis during daytime and the amount consumed through breathing during the night-time) depends on the water temperature [10,11,12]. It has been observed that the rate of oxygen production by some plankton species decrease monotonously along with an increase in the water temperature and even can become negative when the temperature increases by about 5–6 C: phytoplankton then start consuming oxygen instead of producing it [13]. Arguably, this may lead to a widespread marine anoxia.
We mention here that the potential disruption of the oxygen production by phytoplankton can have negative consequences on a global scale. The oxygen produced inside phytoplankton cells diffuses into the ocean water. A part of the dissolved oxygen enters the atmosphere through the ocean surface, thus contributing to the global oxygen budget. It is estimated that more than one half of the atmospheric stock of oxygen is produced in the ocean through phytoplankton photosynthesis [14]. Correspondingly, should the production stop (e.g., because of the negative effect of global warming), the amount of atmospheric oxygen would eventually fall more than twice, with apparently devastating effect on animals and humans.
Whilst empirical research into this issue remains meagre, it has recently been studied theoretically by considering a novel model of coupled plankton-oxygen dynamics [15,16,17]. The model is simple (`conceptual’), but it has been shown to provide an upper bound for more realistic models [15] so that, whenever oxygen depletion and plankton extinction happen in the conceptual model, these will necessarily happen in a more realistic model. Interestingly, the model predicts two different types of oxygen catastrophe as a result of global warming. One of them would be preceded by a slow, gradual decrease in the O concentration to very small values and is reversible if global warming stops and the temperature returns to its pre-change values. The other happens suddenly, almost without warning; once the parameters (e.g., the O net production rate and/or the phytoplankton growth rate) surpass certain critical values, the system starts a free fall to a zero-oxygen state. This type of the catastrophe is irreversible and hence much more dangerous [15].
The above studies left several open questions. Firstly, it remained unclear how robust the prediction of oxygen depletion in response to a sufficiently large increase in water temperature is to the details of parametrization of the coupling between phytoplankton and oxygen. Indeed, model prediction can only be regarded as meaningful if it does not depend strongly on the specific choice of functional feedbacks [18,19,20]. However, the details of the coupling in a real-world plankton-oxygen system are largely unknown. In this paper, we consider several different models of the phytoplankton-oxygen system and show that the prediction of oxygen depletion does not depend on the details of parameterizations. Since different parameterizations account for somewhat different ecological situations, this broadens the generality of our results.
Secondly, previous theoretical studies on the plankton-oxygen dynamics have mostly been done using deterministic models [15,16,17,21,22,23]. Meanwhile, the high variability of the ocean environment, in particular due to the inherently stochastic marine turbulent flows [24] and weather conditions [25], can make such an approach somewhat questionable. Moreover, the process of global warming itself exhibits clear irregular fluctuations around the general trend [1]. A more realistic modelling approach should therefore include some form of the environmental stochasticity or noise [26,27]. Remarkably, the systems’ dynamical properties can differ significantly under the effect of noise [27,28,29]. Therefore, our second goal in this paper is to consider how the earlier modelling predictions of oxygen depletion may change if the model includes environmental noise.
2. Parametrization of the Oxygen-Phytoplankton System
Our conceptual model of coupled phytoplankton-oxygen dynamics is shown in Figure 1. Phytoplankton (u) produce oxygen (c) with the per capita rate during the daytime photosynthesis. Function describes the rate of oxygen decrease due to different processes such as its consumption by phytoplankton during the night-time, breathing of marine fauna, decay in the oxygen concentration due to (bio)chemical reactions in the water (e.g., decay and remineralization of detritus) [22,30,31,32,33,34], etc. The phytoplankton growth rate is known to be correlated with the rate of photosynthesis [35]. The mechanisms resulting in this correlation are poorly understood; here, we assume that the growth rate depends on the amount of available oxygen. This is in agreement with the general biological observation that all living beings (except for those relatively rare species, e.g. some bacteria, the metabolism of which is not based on oxygen), animals and plants alike, need oxygen for their normal functioning. The term is the phytoplankton mortality rate that includes its natural mortality and its consumption by zooplankton and planktivorous fish. Note that, in the general case, it may depend on the oxygen concentration, e.g., because the efficiency of zooplankton feeding may depend on the oxygen (see Section 3).
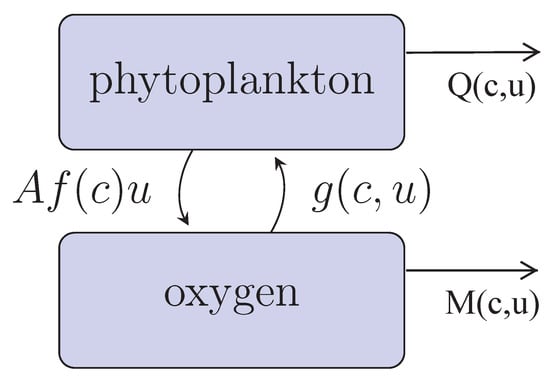
Figure 1.
Flowchart diagram of mass flows between the components of the system (quantified by the growth rates and ) and losses of oxygen and phytoplankton due to their flows out of the system (quantified by and , accordingly); see the details in the text.
The corresponding mathematical model that describes the processes and mass flows shown in Figure 1 is given by the following equations:
where c is the concentration of the dissolved oxygen, u is the density of phytoplankton and t is time. Function describes the combined effect of the oxygen production inside the phytoplankton cells and its transport from the cells to the surrounding water. Note that, since the transport through the cell membrane depends on the concentration in the vicinity of the cell, f appears to be a monotonously-decreasing function of c; see [17] for details. Parameter A takes into account the effect of the environmental factors (such as the water temperature) on the rate of oxygen production inside the phytoplankton cells. We assume that both plankton and oxygen are distributed approximately uniformly in the upper layer of the ocean (the so-called approximation of a well-mixed layer, cf. [36,37]); hence, Equations (1) and (2) do not include space.
Note that Equations (1) and (2) are extremely simple, much simpler than `realistic’ ecological models [38] or climate models (e.g., [39]). However, we want to emphasize here that the model given by Equations (1) and (2) is not just a mathematical toy as it provides an upper bound for a family of realistic marine ecosystem models; see Section 5 for details.
In order to further specify the model, we use the standard assumption that phytoplankton exhibit logistic growth so that:
where B is the maximum phytoplankton per capita growth rate in the large oxygen limit, is a half-saturation constant and is the intensity of the intraspecific competition. For function , assuming that the transport through the cell membrane is described by the Fick law, it can be parameterized as follows [17]:
where is a parameter.
Specific parametrization of functions M and Q can be different depending on the biological processes taken into account. Correspondingly, the system (1) and (2) can attain somewhat different properties, in particular in terms of the existence and stability of its steady states. Below, we consider several different parameterizations of M and Q to reveal that, in fact, the qualitative properties of model Equations (1) and (2) are robust to the choice of M and Q.
2.1. Model 1
We begin with the baseline case where functions M and Q are linear with respect to their arguments. Although this assumption of linearity is not entirely realistic in the general case, in particular because it apparently assumes that the per capita amount of oxygen consumed by phytoplankton and the per capita amount of phytoplankton consumed by its predators are unbounded, the linear approximation of nonlinear population dynamics models is known to work well in a certain parameter range; see [40], also Section 2 in [41].
Correspondingly, Equation (1) takes the following form (in appropriately chosen dimensionless variables, cf. [17]):
where the term accounts for oxygen losses for reasons other than plankton breathing.
For phytoplankton, the density-independent mortality rate (so that Q is linear with respect to u) not only takes into account the natural, age-related mortality, but can also account for other processes resulting in phytoplankton losses, in particular the effect of a terminal (lytic) viral infection [42,43], which is known to be an important factor controlling phytoplankton abundance [44]. Equation (2) turns into the following:
where parameter is the (constant) mortality rate of the phytoplankton.
Equations (5) and (6) contain several parameters. Since our main goal is to reveal how the system properties can change depending on the rate of oxygen production A (which is known to depend on water temperature and hence is affected by global warming), in this paper, we only consider explicitly the effect of A and fix all other parameters at some hypothetical values.
For any parameter values, the extinction state is a steady state of the system. Having analysed the direction of the phase flow, it can be shown that it is always stable [17]. In order to understand how the existence of positive (coexistence) steady states depends on A, it is convenient to consider the isoclines of the system, which are given by the following equations:
Figure 2a shows the relative position of the isoclines in the phase plane of the system. Any intersection between the two isoclines (i.e., between the red and black curves) is a steady state. It is readily seen that the positive steady states only exist if A is not too small. In case A is smaller than a certain critical value, say , there are no positive steady states. This can be summarized as a bifurcation curve showing the steady state values of oxygen vs. A; see Figure 2b. For any , there are two steady states, as shown by the two branches of the curve (where corresponds to the right-most point in the dotted red curve). It can be shown [17] that the upper steady state is stable and the lower steady state is unstable. At , the two branches merge.
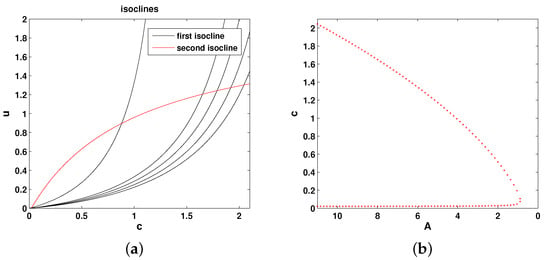
Figure 2.
(a) The (null)-isoclines of the oxygen-phytoplankton system for Model 1. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equations (5) and (6) shown as functions of A. Other parameters are , , , and .
These properties of Equations (5) and (6) mean that, for , the system is likely to be found in the vicinity of the upper (stable) steady state (unless the initial state is close to extinction). For , regardless of the initial state of the system, in the long-term run, the system will converge to the extinction state . In this case, the extinction of plankton and the depletion of oxygen are the only possible results.
Having considered the properties of the curve in Figure 2b, one readily reveals the generic response of the system to a decrease in A (due to the temperature increase, e.g., due to global warming). Presumably, before the change, the system is in a `safe’ parameter range, i.e., . The system is then in its upper steady state, i.e., at a point on the upper branch of the bifurcation curve in Figure 2b. With a decrease in A, the point is pushed to the right. For any , the system is in a state of sustainable oxygen production. However, once the system is pushed beyond the bifurcation point , sustainable functioning of the system is not possible any more, and the extinction/depletion is the only possible outcome.
Now, we are going to check whether the properties of the system and its bifurcation curve (in particular, the existence of the critical value and the depletion catastrophe for ) remain similar for different assumptions leading to different M and Q.
2.2. Model 2
Now, we take into account that, in the case where the phytoplankton mortality term Q is linked to its consumption by a species from a higher trophic level, e.g., zooplankton, the Holling Type II density-dependent predator response is more realistic than a linear response. Considering as above M to be a linear function with respect to its arguments, Equations (1) and (2) take the following form:
where v is the zooplankton density (regarded as a parameter; a more general model where v is a dynamical variable will be considered in Section 3).
The isoclines of Equations (8) and (9) are, respectively, as follows:
Figure 3a shows the relative position of the isoclines given by Equations (10) in the phase plane of Equations (8) and (9), and Figure 3b shows the corresponding bifurcation curve. It is readily seen that the properties of the system are essentially the same as for Model 1, and hence, all conclusions about the system properties are exactly the same as for Model 1.
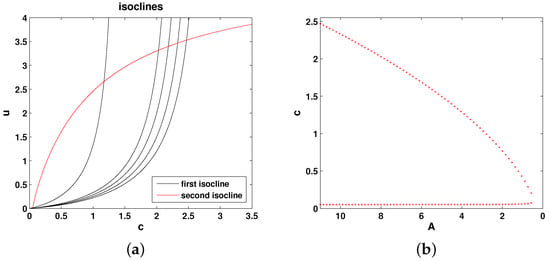
Figure 3.
(a) The (null-)isoclines of the oxygen-phytoplankton system for Model 2. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equations (8) and (9) shown as functions of A. Here, , and other parameters are the same as in Figure 2.
2.3. Model 3
We keep as a bilinear function. For function Q, we combine the density-dependent Holling Type II response to account for the effect of predation with the density-independent linear response to account for the natural mortality and the effect of viruses. Equations (1) and (2) take the following form:
Note that in the special case , Equations (11) and (12) coincide with Model 1.
The isoclines of Equations (11) and (12) are as follows:
Figure 4 shows the relative position of the isoclines and the corresponding bifurcation diagram (the steady state values of oxygen as a function of parameter A). Thus, the system properties are qualitatively the same as in Models 1 and 2.
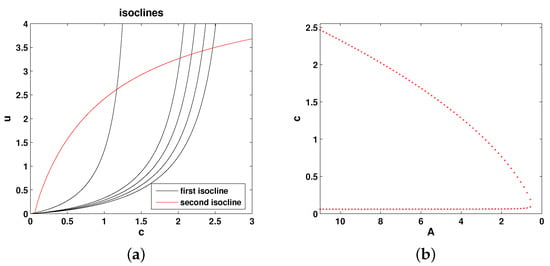
Figure 4.
(a) The (null-)isoclines of the oxygen-phytoplankton system for Model 3. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equations (11) and (12) shown as functions of A. Here, and , and other parameters are the same as in Figure 2.
2.4. Model 4
Now, we consider Holling Type II predation for the consumption of phytoplankton (e.g., by zooplankton) and neglect the linear term in Q, thus assuming that the phytoplankton losses due to their predation are more important than losses due to their natural mortality or viral infection. For the rate of oxygen consumption by marine flora and fauna, we change the bilinear term in M to a more realistic Monod-type response, which accounts for the general observation that the per capita rate of consumption of oxygen is bounded. Equations (1) and (2) take the following form:
The isoclines of Equations (14) and (15) are, respectively, as follows:
Figure 5 shows the relative position of the isoclines and the corresponding bifurcation diagram of Equations (14) and (15). The system properties therefore remain the same as above.
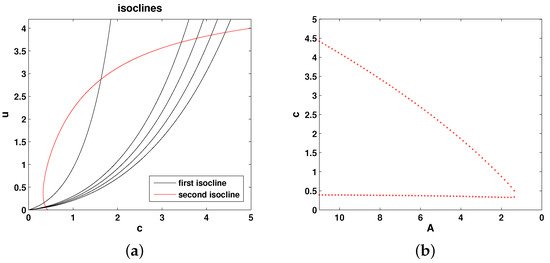
Figure 5.
(a) The (null-)isoclines of the oxygen-phytoplankton system for Model 4. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equations (14) and (15) shown as functions of A. Here , other parameters are the same as in Figure 4.
2.5. Model 5
For this model, we use the same function M as in Model 4. For function Q, we keep the Holling Type II predation term and add the linear term, hence assuming that phytoplankton losses occur due to a combined action of the density-dependent predation, viruses and natural mortality. Equations (1) and (2) now take the following form:
The isoclines of the system are as follows:
Figure 6 shows the relative position of the isoclines and the corresponding bifurcation diagram. It is readily seen that the system properties are the same as above.
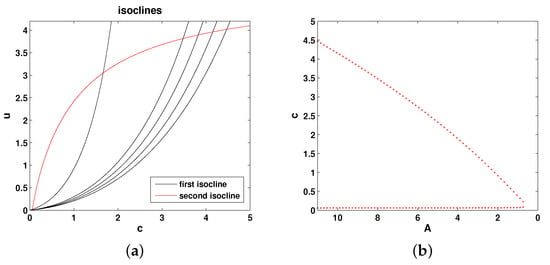
Figure 6.
(a) The (null-)isoclines of the oxygen-phytoplankton system for Model 5. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equations (17) and (18) shown as functions of A. Here, , other parameters are the same as in Figure 4.
2.6. Model 6
We consider the same function M as in Models 4 and 5 (i.e., a combination of the linear term and Monod kinetics). For the losses of phytoplankton, we neglect the density-dependent predation and only consider the linear term. This correspond to a situation where the phytoplankton abundance is mostly controlled by its natural mortality and possibly viruses, but not by predation. Equations (1) and (2) then take the following form:
The isoclines of the system are as follows:
Figure 7 shows the relative position of the isoclines and the steady state values of oxygen as a function of parameter A (bifurcation diagram). The properties are the same as in the previous models.
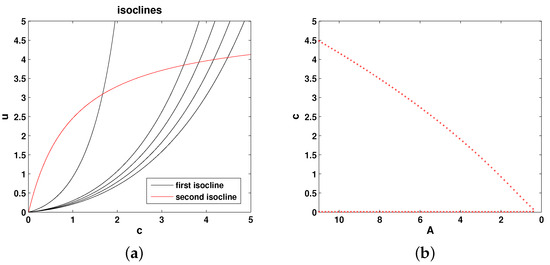
Figure 7.
(a) The (null-)isoclines of the oxygen-phytoplankton system for Model 6. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equations (20) and (21) shown as functions of A. Parameters are the same as in Figure 6.
2.7. Model 7
This model considers the most general case (within the given framework), which combines all the specific cases above. Function M now takes into account the oxygen losses due to its consumption by phytoplankton (during the night-time) and due to breathing by marine fauna (e.g., zooplankton), both terms described by Monod kinetics. It also includes the linear term to account for oxygen losses due to other reasons, which include losses due to oxygen diffusion through the ocean surface. Function Q includes both the linear term (that takes into account the natural mortality and the virulence in the case of a viral infection) and Holling Type II predation. Equations (1) and (2) then take the following form:
In the special case , Equations (23) and (24) coincide with Model 6.
The isoclines of Equations (23) and (24) are, respectively, as follows:
Figure 8 shows the relative position of the isoclines in the phase plane of the system and the corresponding bifurcation diagram, which are apparently similar to those in the previous models.
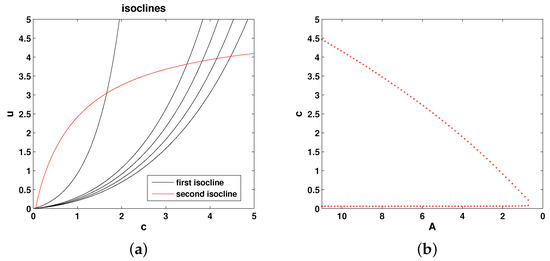
Figure 8.
(a) The (null-)isoclines of the oxygen-phytoplankton system for Model 7. Black curves show the oxygen isocline () for and 11 (from left to right, respectively), and the red curve shows the phytoplankton isocline (). (b) Positive steady states of Equation (23) and (24) shown as functions of A. Here, and , and other parameters are the same as in Figure 6.
A brief inspection of the bifurcation diagrams obtained for Models 1–7 immediately reveals that they are qualitatively the same; in particular, they all predict that sustainable functioning of the plankton-oxygen system can only occur if the rate of oxygen production is not too low. A summary of the processes taken into account by different models is given in Table 1. It is readily seen that the critical behaviour (disappearance of the positive steady states) in response to a decrease in A is shown by all models, although the parametrization of functions M and Q varies significantly. We therefore conclude that this is a relatively general property of the phytoplankton-oxygen dynamics and not an artefact of a specific parametrization. In the case that the rate of oxygen production decreases with an increase in the water temperature (as was observed for some phytoplankton species [10,11,13]), the generic Equations (1) and (2) predict an ecological catastrophe resulting in oxygen depletion and plankton extinction when the temperature exceeds a certain critical value.

Table 1.
Summary of the biological factors accounted for and of the types of nonlinear responses used in Models 1–7.
Arguably, from the range of models considered above, the most realistic is Model 7, as it accounts for the largest number of relevant factors. Thus, we will use it in the rest of the paper.
3. Oxygen-Phyto-Zooplankton Model
The baseline oxygen-phytoplankton model given by Equations (1) and (2) considered in the previous section is very simple and obviously disregards many factors that may affect the system properties. Arguably, one of the most important factors is zooplankton. Indeed, zooplankton are often present in high densities and hence may consume a considerable amount of the dissolved oxygen through their breathing. Furthermore, zooplankton are known to control phytoplankton growth, hence indirectly damping the oxygen production.
An extension of Equations (1) and (2) (which we now consider in a more specific form given by Model 7) to include zooplankton is readily obtained by taking into account the two processes mentioned above along with zooplankton’s own growth. Considering the Holling Type II functional response for the zooplankton feeding on phytoplankton, we arrive at the following system [17]:
where v is the zooplankton density (now a dynamical variable), is the zooplankton feeding efficiency, and are the maximum per capita respiration rates for phytoplankton and zooplankton, respectively, is the zooplankton mortality rate (which can also take into account the effect of animals from higher trophic levels who feed on zooplankton [45,46]), is the maximum predation rate and h, and are half saturation constants of the Monod-type kinetics. Other parameters have the same meaning as above. Due to their biological meaning, all parameters are nonnegative. Note that in the special `zooplankton-free’ case where , Equations (26)–(28) coincide with Models 6 and 7 from Section 2.
There are some generic biological arguments suggesting that the zooplankton feeding efficiency should depend on the availability of oxygen, and this dependence should be of a sigmoidal shape, i.e., being approximately constant for the oxygen concentrations above a certain threshold, but promptly decaying to zero for the concentration below the threshold [22,47,48]. Correspondingly, we consider it as follows:
where is thus the maximum zooplankton feeding efficiency achieved in the high-oxygen limit and is the half saturation constant.
Equations (26)–(28) are complemented with the initial conditions:
where , and are nonnegative constants with obvious meaning.
Equations (26) and (28) are known to have at most four steady states [17]. The trivial equilibrium always exists and is stable. Depending on the parameter values, there may be two semi-trivial zooplankton-free states, , where . One of them, say, , is a saddle (hence unstable), and the other one, , can be either stable or unstable. Under some constraints on the parameter values, there also exists the positive “coexistence” steady state , which also can be either stable or unstable [17]. In the case where the coexistence state is unstable, it can be surrounded by a stable limit cycle, so that in that parameter range, the system shows sustainable oscillations. The non-trivial positive and boundary (zooplankton-free) steady states and/or the limit cycle only exist for some intermediate values of A; thus, the sustainable dynamics of the system not resulting in the extinction/depletion of all species only appears possible for values of A not too large and not too small; see [15] for details.
4. Effect of Environmental Stochasticity: Simulations
Equations (26) and (28) are known to predict a catastrophic response of the plankton-oxygen system to a sufficiently large change in parameters A or [17]. In case A and/or change with time, e.g., as a result of global warming, the plankton densities and oxygen concentration would first show a slow decrease that eventually turns into a fast decay to the extinction/depletion state [15,17]. However, Equations (26) and (28) are deterministic: as long as the parameters and the initial conditions are known precisely, their solution gives the state of the system at any given time t. This is not entirely realistic, in particular because the environment is never exactly stationary, which means that at least some of the parameters in Equations (26)–(28) may not be constant, but change with time. The environment often changes or fluctuates in a complicated manner, which is loosely referred to as the environmental stochasticity or environmental noise (Figure 9). It is well known that the environmental stochasticity can affect the corresponding population dynamics significantly [49]; in particular, under certain conditions, it may lead to species extinction [50,51].
Figure 9.
A sketch of oxygen-phyto-zooplankton dynamics affected by noise of different origins.
As for any other species or ecological community, the oxygen-plankton system is affected by environmental noise of various origins, e.g., due to the inherent stochasticity of the weather conditions; see Figure 9. Mathematically, the stochasticity can be taken into account in different ways [27,52,53]. Since our deterministic model is described by a system of ordinary differential equations, in order to account for the environmental stochasticity, we consider its generalization to become a system of stochastic differential equations where some of the parameters change randomly over the course of time. In this paper, we assume that the stochasticity only affects the oxygen production through parameter A and/or the phytoplankton growth through parameter by turning A and into random variables:
where is the pre-change net oxygen production rate (i.e., before global warming started at ), is the rate of change in the oxygen production as a response to global warming, is the noise intensity and is a normally-distributed random variable with zero mean and unit variance. Parameters , and have similar meaning. If (e.g. because of the normally-distributed random values ), then ; similarly for .
Equations (31) therefore takes into account two different processes, i.e. the general trend (as given by the terms and ) and the effect of environmental stochasticity (as given by the stochastic terms). Note that, generally speaking, and , which reflect the fact that the oxygen production rate and the phytoplankton growth rate may respond differently to the increase in the water temperature.
Equations (26)–(29) with Equation (31) were studied by means of extensive numerical simulations. The numerical scheme was carefully checked and tested in order to avoid numerical artefacts. To reveal the effect of noise on the system’s dynamics, we first consider a special case where the stochasticity only affects , but not A, so that . Furthermore, we consider that there is now global change, i.e., . We choose the value of other parameters such as the system without noise exhibits periodic oscillations due to the limit cycle (see [15,17]), namely and . Typical simulation results are shown in Figure 10 (obtained for the initial conditions and ). We readily observe that, due to the effect of noise, the solution becomes quasi-periodical rather than periodical. Note that, due to the randomness in , each simulation run is different: the apparently different solutions shown in Figure 10a,b are obtained for exactly the same parameters and initial conditions.
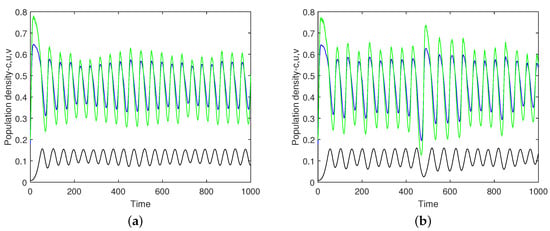
Figure 10.
Oxygen concentration (blue), phytoplankton density (green) and zooplankton density (black) vs. time obtained for , , and . The presence of noise distorts the otherwise periodical oscillations. Results shown in (a,b) are obtained in different simulation runs performed for the same parameters and initial conditions; hence, the apparent difference between (a,b) is the effect of the stochasticity.
The average amplitude of the oscillations appears to increase with an increase in the noise intensity. Figure 11 shows the zooplankton density (considered here as a proxy of the system state) averaged over ten simulation runs obtained for several different values of . Interestingly, the dependence of the average amplitude on is described very well by a cubic polynomial; see the black dashed curve in Figure 11.
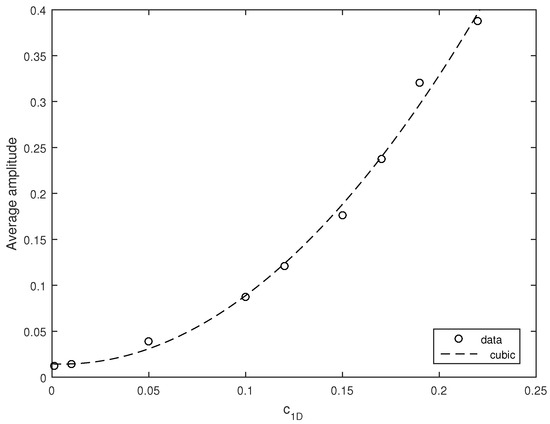
Figure 11.
Average amplitude of the oscillations of the zooplankton density obtained for different values of ; other parameters are the same as in Figure 10. The black dashed line shows the best-fit of the data by a cubic polynomial, .
The effect of noise on the system’s dynamics is seen particularly well for the parameter values close to the boundary of the system’s sustainability range (cf. the end of Section 3). One example is shown in Figure 12 (obtained in the zooplankton-free case, , for parameters , , , , , and the initial conditions , ). We first notice that the generic prediction of the deterministic Equations (26)–(28) remains valid: over the course of time, a gradual decrease in the oxygen concentration and plankton density changes to a fast decay resulting in the extinction/depletion catastrophe. Figure 12a,b shows two simulation runs performed for exactly the same parameters and initial conditions; hence, any difference is attributed to the inherent stochasticity of the system. In the case shown in Figure 12a, the average values of the oxygen concentration and the phytoplankton density decrease slowly up to when this slow dynamics changes to a fast decay, resulting in the plankton extinction and oxygen depletion at . In the case shown in Figure 12b, the dynamics exhibits similar features, but the timing is different; in particular, the extinction/depletion occurs at .
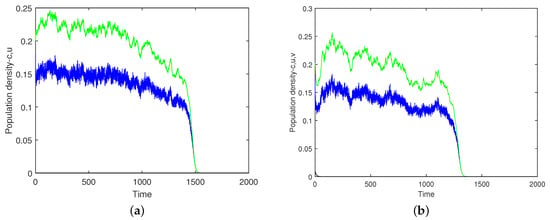
Figure 12.
Phytoplankton density (green) and the concentration of oxygen (blue) vs. time obtained for parameters , , , , and . (a,b) show two simulation runs obtained for the same parameters and the initial conditions.
Since the effect of noise is apparent, a question arises as to how the dynamics may differ for different intensities of noise. This question was addressed by means of numerical simulations having varied the intensity of noise and keeping other parameters the same as in Figure 12. The black circles in Figure 13 show the average extinction time (averaged over ten simulation runs) obtained for several values of in the zooplankton-free system. It is readily seen that the extinction time increases approximately linearly. In order to reveal the effect of zooplankton, simulations were also performed with the initial zooplankton density , other initial conditions and parameters being the same as in Figure 12. The average extinction time thus obtained in the full three-component system is shown in Figure 13 by red circles. We therefore observe that in the presence of zooplankton, the extinction time slightly decreases, but altogether, zooplankton have a relatively small effect. This is perhaps not surprising given that, for these parameter values, in the system without noise the zooplankton are not viable as the positive steady state does not exist [17], so that the system quickly converges to the zooplankton-free boundary state .
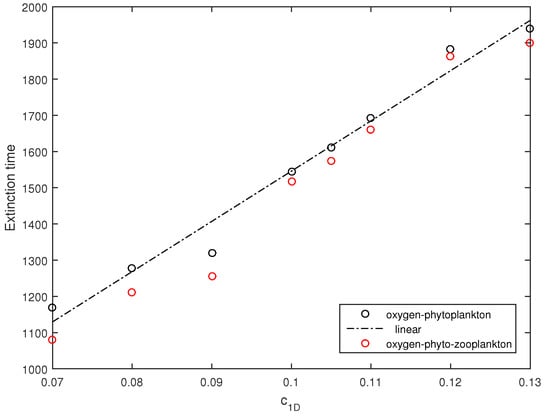
Figure 13.
Average extinction time calculated for different values of for the oxygen-phytoplankton model (, black circles) and the full oxygen-phyto-zooplankton model (, red circles). Other parameters are the same as in Figure 12. The black dashed-and-dotted straight line shows the best-fit of the data by a linear function.
An interesting question is what could be the interplay between the rate of decrease in the oxygen production rate and the relevant noise intensity quantified by . Let us consider parameter values to be sufficiently close to the boundary of the parameter range where the dynamics is sustainable in the absence of noise, i.e., the system is close to the extinction/depletion disaster. In case A is close to its upper critical value, a decrease in A obviously takes the system away from the catastrophic transition. However, the stochastic fluctuations, especially if the noise intensity is sufficiently large, can yet randomly push the system out of the safe range. One can therefore expect that the outcome of the system’s dynamics (extinction or persistence) is essentially random and will differ between different realizations of the process, i.e., between different simulation runs.
This intuitive expectation is confirmed by simulations. Figure 14 shows the oxygen concentration and the plankton densities versus time obtained for , (this value of being very close to the upper boundary of the safe parameter range), and . Panels (a) and (b) correspond to different simulation runs performed for exactly the same values of the parameters and initial conditions. It is readily seen that, whilst for the simulation run shown in Figure 14a, the system quickly converges to the extinction/depletion state, for the run shown in Figure 14b, the system’s dynamics is sustainable (exhibiting a decay in the zooplankton density, but keeping safe numbers for oxygen and phytoplankton), at least over the given time interval.
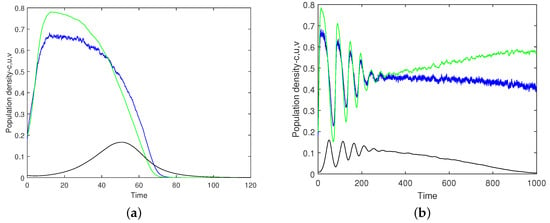
Figure 14.
Population densities of phytoplankton (green), zooplankton (black) and the oxygen concentration (blue) vs. time obtained for parameters , , , , and . Results shown in (a,b) are obtained in different simulation runs performed for the same parameters and initial conditions.
The outcome of stochastic dynamics can be quantified by the probability of different events. In order to achieve this, for every point in a grid of parameter values and , we performed fifty simulation runs and counted the probability of extinction (e.g., a probability of 2% means that the extinction was observed only once). The results are shown in Figure 15. It is therefore readily seen that the probability of oxygen depletion shows a clear tendency to increase with a decrease in and with an increase in , i.e., from the right bottom corner to the left top corner. Although this dependence on the rate of change may look somewhat counterintuitive at first sight, a heuristic explanation is straightforward: the slower the change, the longer the system stays in the vicinity of the critical value of A before being taken sufficiently far away, and hence, the higher is the probability that the noise pushes the system to catastrophe.
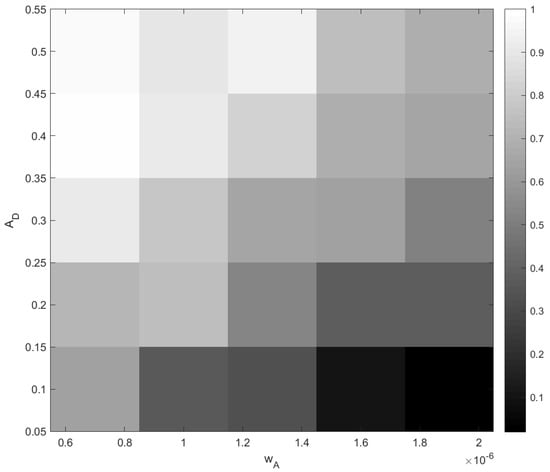
Figure 15.
Probability of the oxygen depletion and plankton extinction shown as a map in the parameter plane . Parameters are the same as in Figure 14.
5. Discussion and Concluding Remarks
Understanding the consequences of global climate change is a highly important issue. A variety of adverse effects have been identified [3]; however, because of the scale and complexity of the phenomenon, the list of potential problems is unlikely to be complete, and more research is needed to make mankind better informed about the arguably worst danger that it has ever faced. It has been shown that global warming can lead to a significant reduction in the amount of oxygen stocked in the ocean [6], in particular by reducing the oxygen solvability and slowing down the ocean upturning and mixing [7]. If this happens, it could have a devastating effect on marine life [8]. More recently, it has been shown that the effect of warming on the total oxygen budget in the ocean can be even worse, as a sufficiently large increase in the water temperature can disrupt the net oxygen production by phytoplankton’s photosynthesis [15,17]. Should the oxygen production stop (and insights from a relevant empirical study suggest that it may happen if the temperature increases by 5–6C [13]), the global ocean would experience a regime shift to eventually become anoxic. Moreover, since the oxygen produced in the ocean adds up to more than one half of the total atmospheric budget [14], such global ocean anoxia or “panoxia” would likely lead to a depletion of atmospheric oxygen as well.
In studies aiming to understand the consequences of global warming, mathematical modelling has long been used as a powerful research tool [2,54,55,56]. Models of climate dynamics are usually very complicated [39] (but see [57]): indeed, a predictive model should account for many factors and processes occurring in the environment. In contrast, our model is very simple; however, it is by no means just a mathematical toy. It has been shown in [15] that the three-component oxygen-phyto-zooplankton model given by Equations (26)–(28) provides an upper bound for a class of much more complicated (and much more realistic) food web-type marine ecosystem models. This means that, whenever the plankton extinction/oxygen depletion happens in the simple model (26)–(28), it necessarily happens in the more realistic model (Figure 16). Therefore, although Equations (26)–(28) do not have the power to predict the details of the ecosystem dynamics, they do have the power to predict the possibility of an extreme event such as a global oxygen crisis due to the disruption in the oxygen production. Moreover, using the same mathematical technique (called the comparison principle for differential equations; see [15] for details), it is readily seen that the extremely simple model given by Equations (1) and (2) actually provides a further upper bound limiting the solutions of the three-component model Equations (26)–(28); see Figure 16.
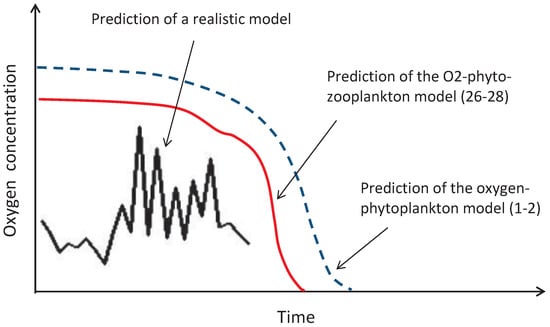
In this paper, we have shown that the oxygen catastrophe predicted by the baseline oxygen-phytoplankton model (Equations (1) and (2)) is robust to the details of the parametrization of the system feedbacks, which points out that the prediction is robust to the specifics of a given ecological situation. Whenever the oxygen production rate falls below a certain critical value, sustainable dynamics becomes impossible, and the system experiences a free fall to the extinction/depletion state. Interestingly and rather counter-intuitively, in the somewhat more realistic three-component system Equations (26)–(28), a similar change happens in the case that the oxygen production rate becomes too high [15,17]. Here, we showed that the latter remains true in the somewhat more realistic system given by Equations (26)–(28) with Equation (31) that takes into account the environmental stochasticity (see Figure 14 and Figure 15).
Apparently, our study leaves many open questions. Arguably, the main question is whether the predicted global anoxia due to plankton photosynthesis disruption can actually happen in reality. Even though our study clearly indicates it (and the relation of our simple models to more realistic models is explained above), this indication should be verified by empirical studies before it can become a firmly-established scientific fact. Whilst investigation into this issue through field and/or laboratory experiments is likely to be technically challenging and hence will take a long time to accomplish, there is an alternative way to link our findings to the real-world dynamics by checking the available palaeontological records [58]: indeed, whatever bio-geophysical event may happen in the future, there is a possibility that it has already happened in the past over the millions of years of Earth’s history. There have been many mass extinction events in the past when more than one half of the total Earth biota disappeared [59]. Mass extinction is a complex event and hence is likely to be a result of the joint effect of different factors, yet the existence of a single, universal physical mechanism responsible for this phenomenon is thought to be plausible [60]. A global anoxia or “panoxia” is believed to be a possibility [61,62]. It is indeed well known that oxygen has played a very important role in palaeoecology and biological evolution [63]. In particular, the geological records show that several of the mass mortality events coincided with a significant decrease in the oxygen level [61,63]. Moreover, it has been proven that some of the mass extinction events were preceded by a considerable increase in the average Earth temperature (by several degrees or even more [64]). The decrease in the global oxygen budget is thought to be a result of a global ocean deoxygenation, but whether it happened largely because of the temperature effects on the ocean ventilation and mixing (cf. [7]) or was a combined effect of some other factors remains unclear. Here, we argue that slowing down the ocean mixing and/or decreasing oxygen solvability are unlikely to have a prolonged effect as long as the rate of oxygen production is maintained. Instead, we hypothesize that, at least in some of the cases, the mass extinctions in the past might have resulted from the mechanism that we investigated here (see also [15,17]), i.e., due to the disruption of phytoplankton photosynthesis.
Author Contributions
S.P. designed the research. Y.S. and S.P. considered and analysed the mathematical models. Y.S. performed numerical simulations. S.P. and Y.S. wrote the manuscript.
Acknowledgments
Useful discussion of the problem with Ezio Venturino (Torino, Italy), Mark Puttick (Bath, UK.). and Scott Denning (Colorado, USA) is acknowledged and appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K.; Lea, D.W. Medina-Elizade M Global temperature change. Proc. Natl. Acad. Sci. USA 2006, 103, 14288–14293. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Sato, M.; Ruedy, R.; Kharecha, P.; Lacis, A.; Miller, R.; Nazarenko, L.; Lo, K.; Schmidt, G.A.; Russell, G.; et al. Climate simulations for 1880–2003 with GISS model E. Clim. Dyn. 2007, 29, 661–696. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate change 2014: Synthesis report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Team CoreWriting; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Najjar, R.G.; Walker, H.A.; Anderson, P.J.; Barron, E.J.; Bord, R.J.; Gibson, J.R.; Kennedy, V.S.; Knight, C.G.; Megonigal, J.P.; O’Connor, R.E.; et al. The potential impacts of climate change on the mid-Atlantic coastal region. Clim. Res. 2000, 14, 219–233. [Google Scholar] [CrossRef]
- Najjar, R.G.; Pyke, C.R.; Adams, M.B.; Breitburg, D.; Hershner, C.; Kemp, M.; Howarth, R.; Mulholland, M.R.; Paolisso, M.; Secor, D.; et al. Potential climate-change impacts on the Chesapeake Bay. Estuar. Coast. Shelf Sci. 2010, 86, 1–20. [Google Scholar] [CrossRef]
- Breitburg, D.; Levin, L.A.; Oschlies, A.; Grégoire, M.; Chavez, F.P.; Conley, D.J.; Garçon, V.; Gilbert, D.; Gutiérrez, D.; Isensee, K.; et al. Declining oxygen in the global ocean and coastal waters. Science 2018, 359, eaam7240. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, G.; Olsen, S.M.; Pedersen, J.O.P. Long-term ocean oxygen depletion in response to carbon dioxide emissions from fossil fuels. Nat. Geosci. 2009, 2, 105–109. [Google Scholar] [CrossRef]
- Battaglia, G.; Joos, F. Hazards of decreasing marine oxygen: the near-term and millennial-scale benefits of meeting the Paris climate targets. Earth Syst. Dyn. Discuss. 2017. [Google Scholar] [CrossRef]
- Catling, D.C.; Zahnle, K. Evolution of Atmospheric Oxygen. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Pyle, J., Curry, J.A., Eds.; Academic Press Inc.: San Diego, CA, USA, 2003; pp. 754–761. [Google Scholar]
- Hancke, K.; Glud, R.N. Temperature effects on respiration and photosynthesis in three diatom-dominated benthic communities. Aquat. Microb. Ecol. 2004, 37, 265–281. [Google Scholar] [CrossRef]
- Jones, R.I. The importance of temperature conditioning to the respiration of natural phytoplankton communities. Br. Phycol. J. 1977, 12, 277–285. [Google Scholar] [CrossRef]
- Li, W.; Smith, J.; Platt, T. Temperature response of photosynthetic capacity and carboxylase activity in arctic marine phytoplankton. Mar. Ecol. Prog. Ser. 1984, 17, 237–243. [Google Scholar] [CrossRef]
- Robinson, C. Plankton gross production and respiration in the shallow water hydrothermal systems of Milos, Aegean Sea. J. Plankton Res. 2000, 22, 887–906. [Google Scholar] [CrossRef]
- Harris, G.P. Phytoplankton Ecology: Structure, Function and Fluctuation; Springer: Berlin, Germany, 1986. [Google Scholar]
- Petrovskii, S.V.; Sekerci, Y.; Venturino, E. Regime shifts and ecological catastrophes in a model of plankton-oxygen dynamics under the climate change. J. Theor. Biol. 2017, 424, 91–109. [Google Scholar] [CrossRef] [PubMed]
- Sekerci, Y.; Petrovskii, S. Mathematical modelling of spatiotemporal dynamics of oxygen in a plankton system. Math. Mod. Nat. Phenom. 2015, 10, 96–114. [Google Scholar] [CrossRef]
- Sekerci, Y.; Petrovskii, S. Mathematical modelling of plankton-oxygen dynamics under the climate change. Bull. Math. Biol. 2015, 77, 2325–2353. [Google Scholar] [CrossRef] [PubMed]
- Cordoleani, F.; Nerini, D.; Gauduchon, M.; Morozov, A.; Poggiale, J.C. Structural sensitivity of biological models revisited. J. Theor. Biol. 2011, 283, 82–91. [Google Scholar] [PubMed]
- Maynard Smith, J. Models in Ecology; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Petrovskii, S.V.; Petrovskaya, N.B. Computational ecology as an emerging science. Interface Focus 2012, 2, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Chapelle, A.; Ménesguen, A.; Deslous-Paoli, J.M.; Souchu, P.; Mazouni, N.; Vaquer, A.; Millet, B. Modelling nitrogen, primary production and oxygen in a Mediterranean lagoon. Impact of oysters farming and inputs from the watershed. Ecol. Mod. 2000, 127, 161–181. [Google Scholar] [CrossRef]
- Hull, V.; Parrella, L.; Falcucci, M. Modelling dissolved oxygen dynamics in coastal lagoons. Ecol. Mod. 2008, 211, 468–480. [Google Scholar] [CrossRef]
- Misra, A.K. Modeling the depletion of dissolved oxygen in a lake due to submerged macrophytes. Nonlinear Anal. Model. Control 2010, 15, 185–198. [Google Scholar]
- Benzi, R.; Paladin, G.; Parisi, G.; Vulpiani, A. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A Math. Gen. 1984, 17, 3521–3531. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmospheric Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Garcia-Ojalvo, J.; Sancho, J.M. Noise in Spatially Extended Systems; Springer: New York, NY, USA, 1999. [Google Scholar]
- Haken, H. Synergetics; Springer-Verlag: Berlin, Germany, 1978. [Google Scholar]
- Haken, H. Advanced Synergetics; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Horsthemke, W.; Lefever, R. Noise-Induced Transitions in Physics, Chemistry, and Biology; Springer-Verlag: Berlin, Germany, 1984. [Google Scholar]
- De Vries, I.D.; Duin, R.; Peeters, J.; Los, F.; Bokhorst, M.; Laane, R. Patterns and trends in nutrients and phytoplankton in Dutch coastal waters: comparison of time-series analysis, ecological model simulation, and mesocosm experiments. ICES J. Mar. Sci. J. 1998, 55, 620–634. [Google Scholar] [CrossRef]
- Keller, K.; Slater, R.D.; Bender, M.; Key, R.M. Possible biological or physical explanations for decadal scale trends in north pacific nutrient concentrations and oxygen utilization. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 49, 345–362. [Google Scholar] [CrossRef]
- Kemp, W.M.; Boynton, W.R.; Adolf, J.E.; Boesch, D.F.; Boicourt, W.C.; Brush, G.; Cornwell, J.C.; Fisher, T.R.; Glibert, P.M.; Hagy, J.D.; et al. Eutrophication of chesapeake bay: historical trends and ecological interactions. Mar. Ecol. Prog. Ser. 2005, 303, 1–29. [Google Scholar] [CrossRef]
- Moloney, C.L.; Bergh, M.O.; Field, J.G.; Newell, R.C. The effect of sedimentation and microbial nitrogen regeneration in a plankton community: a simulation investigation. J. Plankt. Res. 1986, 8, 427–445. [Google Scholar] [CrossRef]
- Voinov, A.; Tonkikh, A. Qualitative model of eutrophication in macrophyte lakes. Ecol. Mod. 1987, 35, 211–226. [Google Scholar] [CrossRef]
- Franke, U.; Hutter, K.; Johnk K, A. physical-biological coupled model for algal dynamics in lakes. Bull. Math. Biol. 1999, 61, 239–272. [Google Scholar] [CrossRef] [PubMed]
- Fasham, M.J.R.; Ducklow, H.W.; McKelvie, S.M. A nitrogen-based model of plankton dynamics in the oceanic mixed layer. J. Mar. Res. 1990, 48, 591–639. [Google Scholar] [CrossRef]
- Huisman, J.; Weissing, F.J. Competition for nutrients and light in a mixed water column: A theoretical analysis. Am. Nat. 1995, 146, 536–564. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. A consumers guide to phytoplankton primary productivity models. Limnol. Oceanogr. 1997, 42, 1479–1491. [Google Scholar] [CrossRef]
- Shaffer, G.; Olsen, S.M.; Pedersen, J.O.P. Presentation, calibration and validation of the low-order, DCESS Earth System model. Geosci. Model Dev. 2008, 1, 17–51. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology I: An introduction. In Interdisciplinary Applied Mathematics; Springer: Berlin, Germany, 2002; Volume 17. [Google Scholar]
- Lewis, M.A.; Petrovskii, S.V.; Potts, J. The Mathematics Behind Biological Invasions. In Interdisciplinary Applied Mathematics; Springer: Berlin, Germany, 2016; Volume 44. [Google Scholar]
- Beltrami, E.; Carroll, T. Modelling the role of viral disease in recurrent phytoplankton blooms. J. Math. Biol. 1994, 32, 857–863. [Google Scholar] [CrossRef]
- Malchow, H.; Hilker, F.M.; Petrovskii, S.V.; Brauer, K. Oscillations and waves in a virally infected plankton system, I. The lysogenic stage. Ecol. Compl. 2004, 1, 211–223. [Google Scholar] [CrossRef]
- Fuhrman, J. Marine viruses and their biogeochemical and ecological effects. Nature 1999, 399, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Edwards, A.M.; Yool, A. The role of higher predation in plankton population models. J. Plankt. Res. 2000, 22, 1085–1112. [Google Scholar] [CrossRef]
- Steele, J.H.; Henderson, E.W. The role of predation in plankton model. J. Plankt. Res. 1992, 14, 157–172. [Google Scholar] [CrossRef]
- Devol, A.H. Vertical distribution of zooplankton respiration in relation to the intense oxygen minimum zones in two British Columbia fjords. J. Plankton Res. 1981, 3, 593–602. [Google Scholar] [CrossRef]
- Prosser, C.L. Oxygen: Respiration and Metabolism. In Comparative Animal Physiology; Prosser, C.L., Brown, F.A., Eds.; WB Saunders: Philadelphia, PA, USA, 1961; pp. 165–211. [Google Scholar]
- Vakulenko SA Sudakov, I.; Mander, L. The influence of environmental forcing on biodiversity and extinction in a resource competition model. Chaos 2018, 28, 031101. [Google Scholar] [CrossRef] [PubMed]
- Feldman, M.W.; Roughgarden, J. A population’s stationary distribution and chance of extinction in a stochastic environment with remarks on the theory of species packing. Theor. Pop. Biol. 1975, 7, 197–207. [Google Scholar] [CrossRef]
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 1973; Volume 6. [Google Scholar]
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, and Simulation; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Renshaw, E. Modelling Biological Populations in Space and Time; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Bender, M.A.; Knutson, T.R.; Tuleya, R.E.; Sirutis, J.J.; Vecchi, G.A.; Garner, S.T.; Held, I.M. Modeled Impact of Anthropogenic Warming on the Frequency of Intense Atlantic Hurricanes. Science 2010, 327, 454–458. [Google Scholar] [CrossRef] [PubMed]
- Broecker, W.S. Climatic change: Are we on the brink of a pronounced global warming? Science 1975, 189, 460–463. [Google Scholar] [CrossRef] [PubMed]
- Millar, R.J.; Fuglestvedt, J.S.; Friedlingstein, P.; Rogelj, J.; Grubb, M.J.; Matthews, H.D.; Skeie, R.B.; Forster, P.M.; Frame, D.J.; Allen, M.R. Emission budgets and pathways consistent with limiting warming to 1.5 ∘C. Nat. Geosci. 2017, 10, 741–748. [Google Scholar] [CrossRef]
- Quinn, C.; Sieber, J.; von der Heydt, A.S.; Lenton, T.M. The Mid-Pleistocene Transition induced by delayed feedback and bistability. ArXiv, 2017; arXiv:1712.07614v1. [Google Scholar]
- Flessa, K.; Jackson, S. (Eds.) The Geological Records of Ecological Dynamics: Understandding the Biotic Effects of Future Environmental Change; Committee on the Geological Records of Biosphere Dynamics, The Nstional Academic Press: Washington, DC, USA, 2005. [Google Scholar]
- Bambach, R.K. Phanerozoic biodiversity mass extinctions. Annu. Rev. Earth Planet. Sci. 2006, 34, 127–155. [Google Scholar] [CrossRef]
- Quinn, J.F.; Signor, P.W. Death stars, ecology, and mass extinctions. Ecology 1989, 70, 824–834. [Google Scholar] [CrossRef]
- Bond, D.P.G.; Grasby, S.E. On the causes of mass extinctions. Palaeogeography, Palaeoclimatology. Palaeoecology 2017, 478, 3–29. [Google Scholar] [CrossRef]
- Andrew, J.; Watson, A.J.; Lenton, T.M.; Mills, B.J.W. Ocean deoxygenation, the global phosphorus cycle and the possibility of human-caused large-scale ocean anoxia. Phil. Trans. R. Soc. A 2017, 375, 20160318. [Google Scholar]
- Berner, R.A.; Vanden Brooks, J.M.; Ward, P.D. Oxygen and evolution. Science 2007, 316, 557–558. [Google Scholar] [CrossRef] [PubMed]
- Aze, T.; Pearson, P.N.; Dickson, A.J.; Badger, M.P.; Bown, P.R.; Pancost, R.D.; Gibbs, S.J.; Huber, B.T.; Leng, M.J.; Coe, A.L.; et al. Extreme warming of tropical waters during the Paleocene-Eocene Thermal Maximum. Geology 2014, 42, 739–742. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).