Temperature and Conductivity as Indicators of the Morphology and Activity of a Submarine Volcano: Avyssos (Nisyros) in the South Aegean Sea, Greece
Abstract
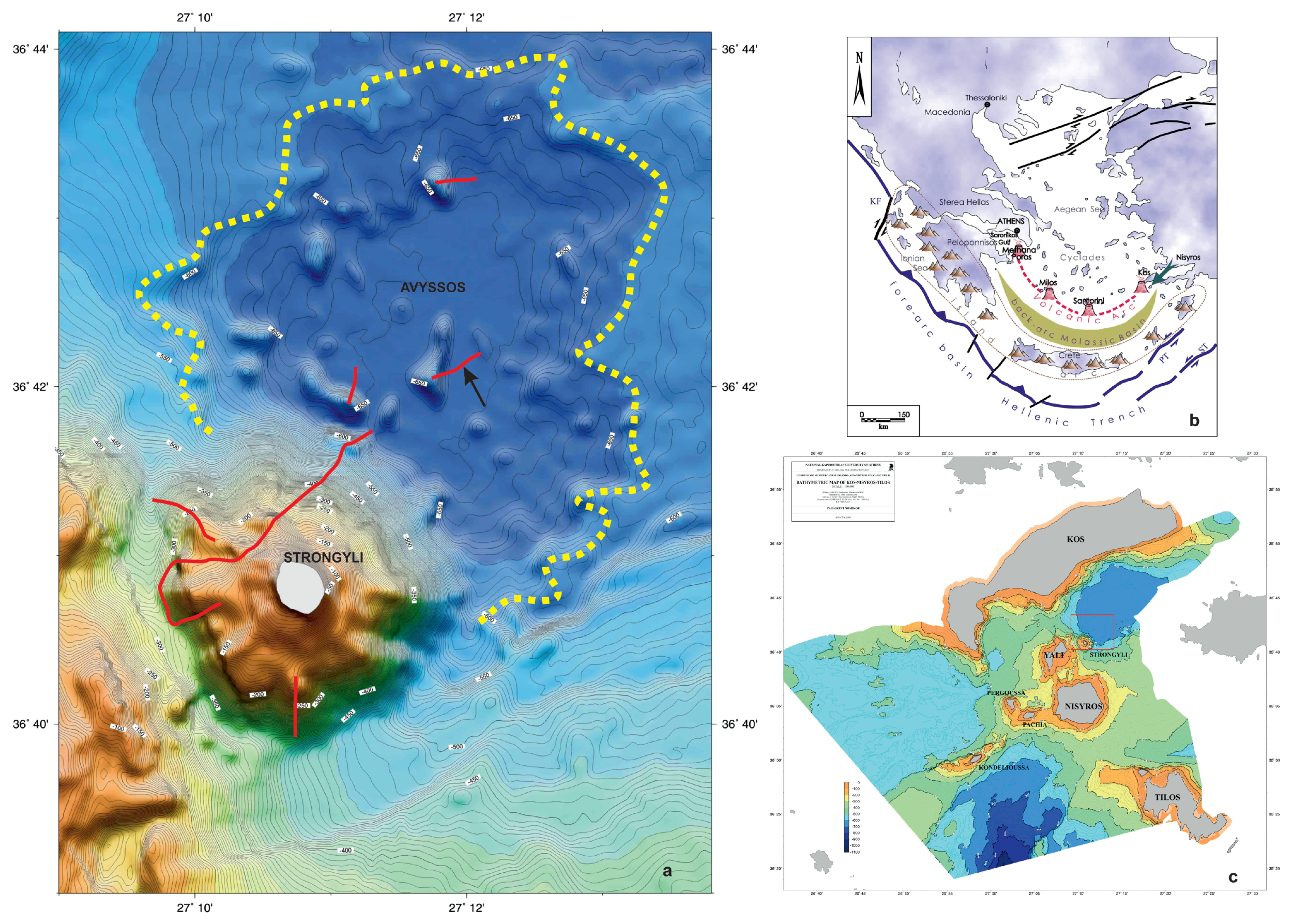
:1. Introduction
2. Methodology
- Step 1: Construction of time series with different lag times.
- Step 2: Estimate of the statistical moments.
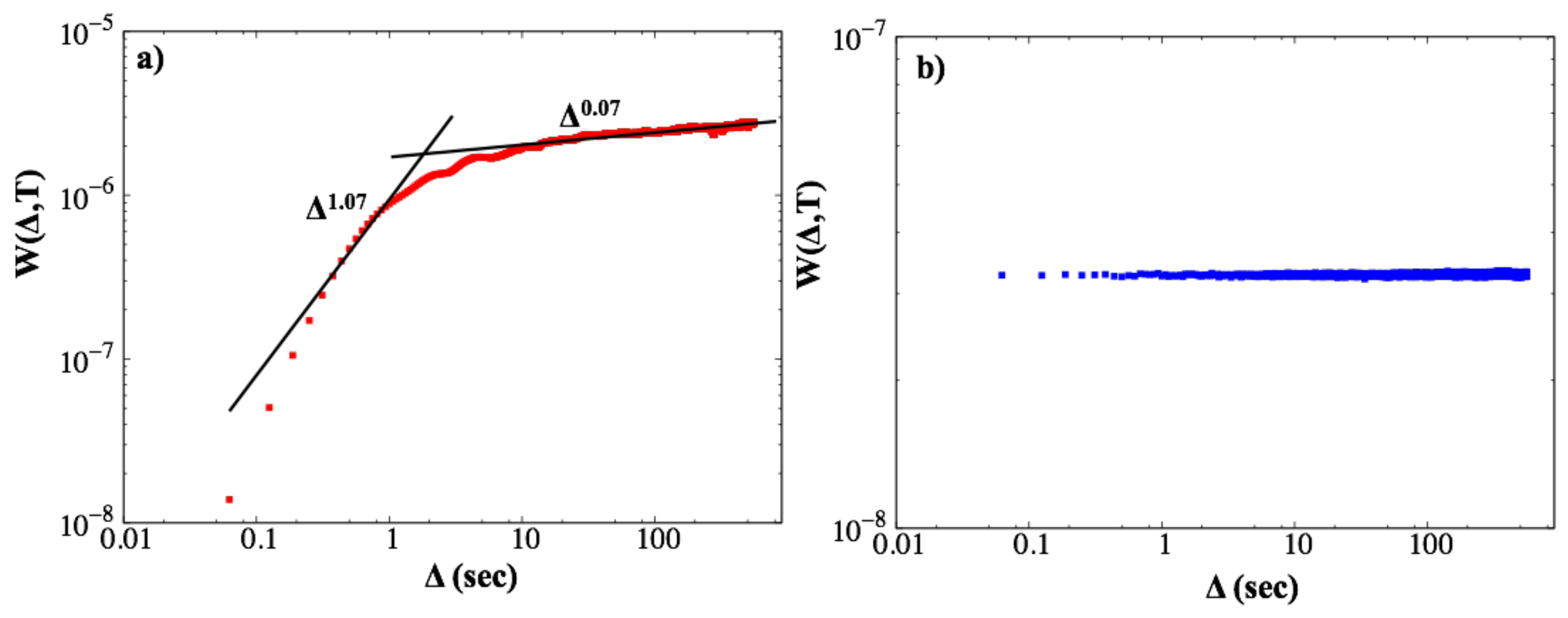
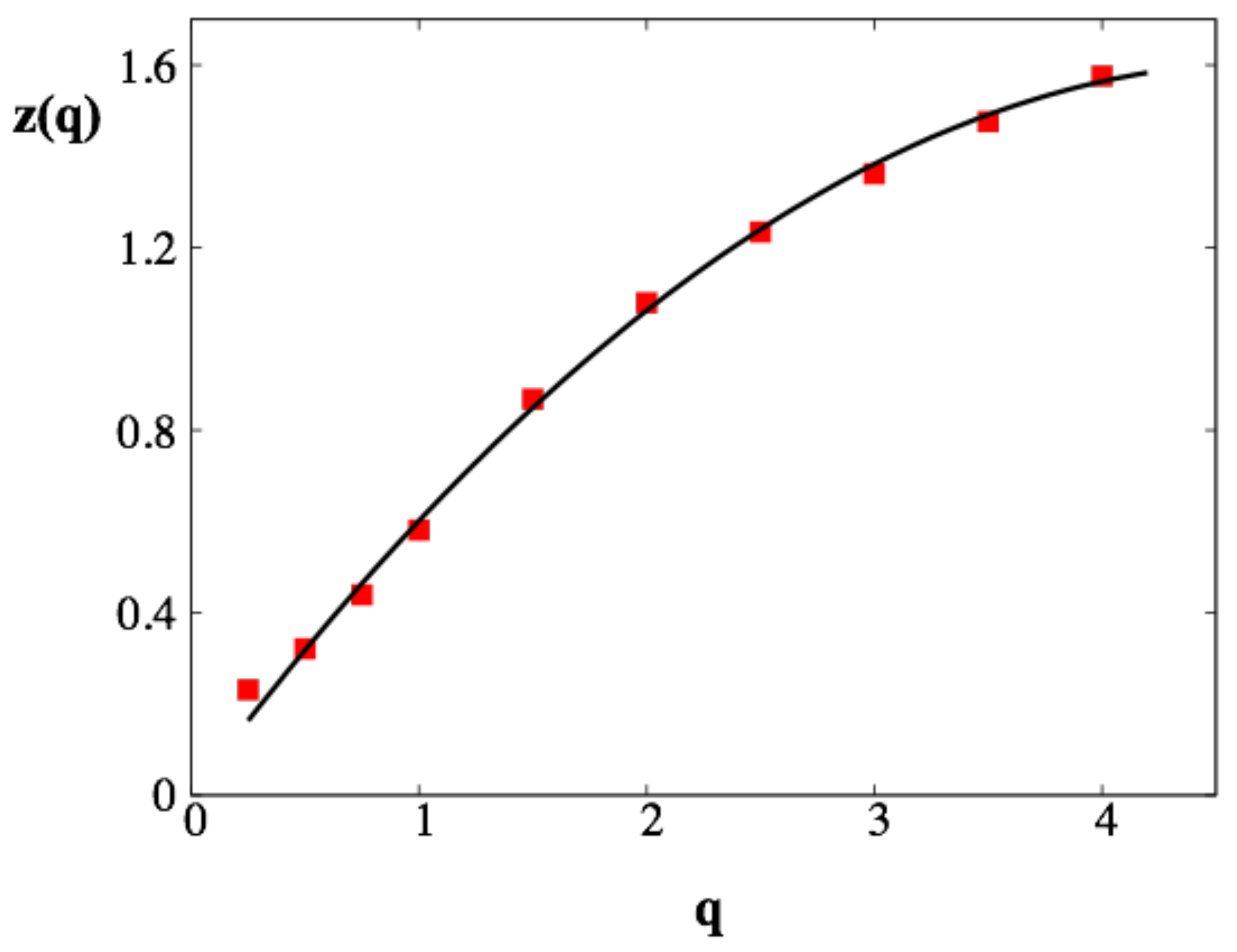
- Step 3: In general, the moments will scale according to Equation (4).
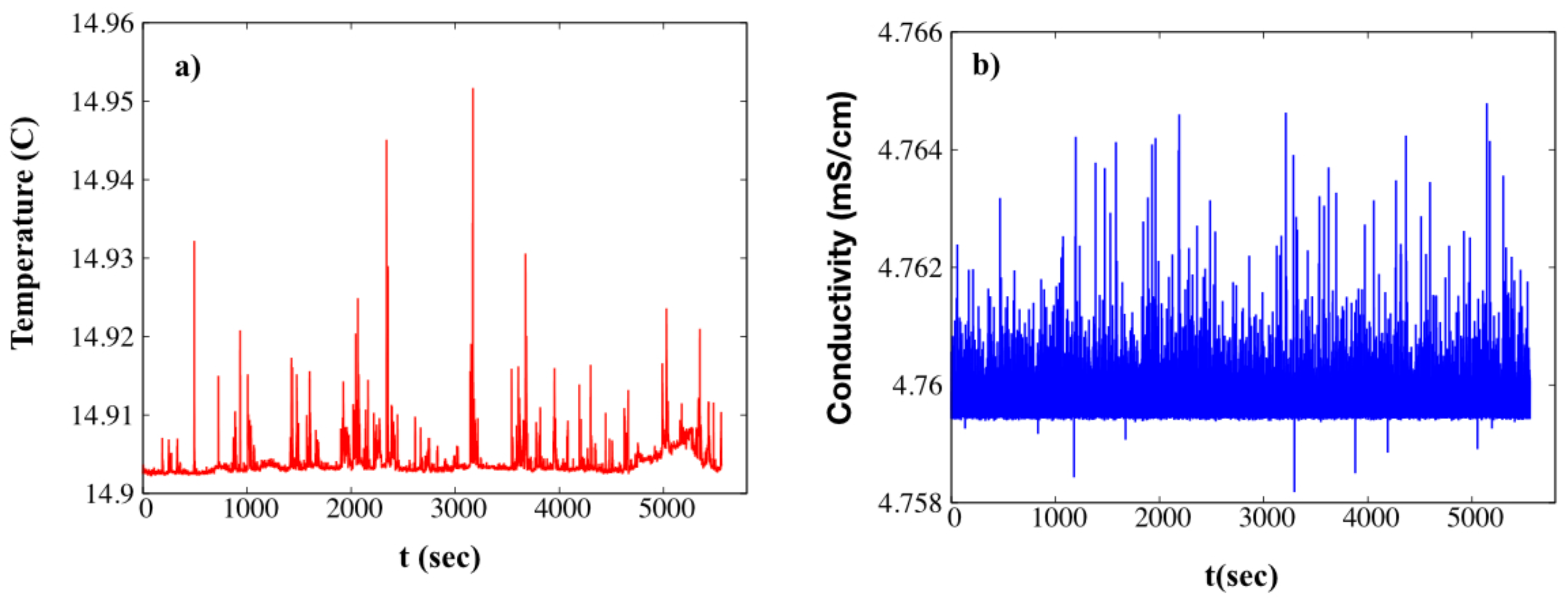
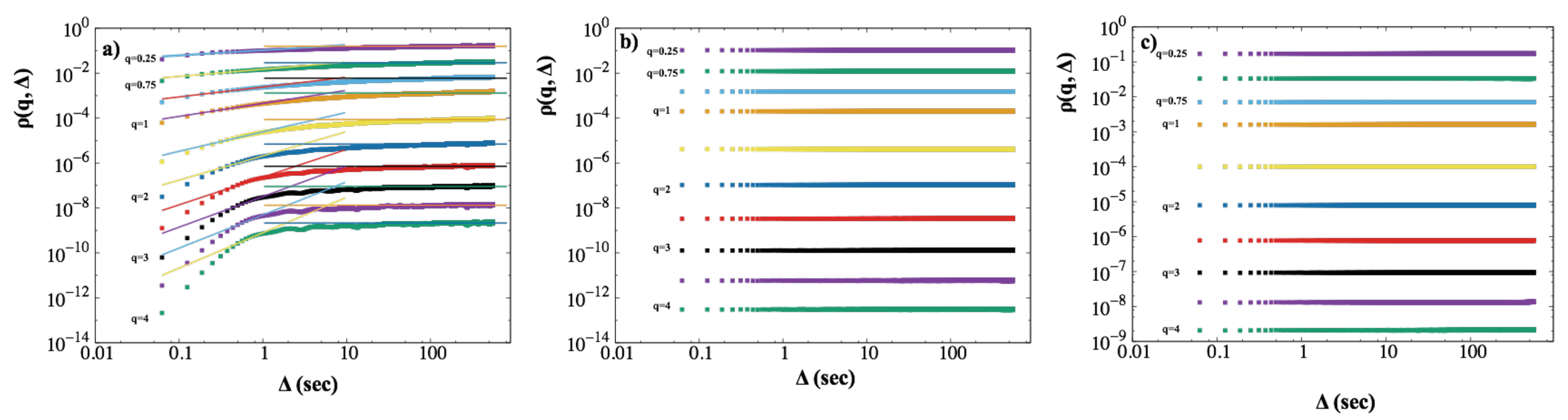
3. Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Papanikolaou, D.; Nomikou, P. Tectonic structure and volcanic centres at the eastern edge of the Aegean volcanic arc around Nisyros Island. Bull. Geol. Soc. Greece 2001, 34, 289–296. [Google Scholar]
- Nomikou, P.; Papanikolaou, D.; Dietrich, V. Geodynamics and Volcanism in the Kos-Yali-Nisyros Volcanic Field; Dietrich, V., Lagios, E., Eds.; Springer: Berlin, Germany, 2018; pp. 13–56. [Google Scholar]
- Nomikou, P.; Papanikolaou, D. Extension of active fault zones on Nisyros volcano across the Yali-Nisyros Channel based on onshore and offshore data. Mar. Geophys. Res. 2011, 32, 181–192. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Sachpazi, M.; Panopoulou, G.; Stavrakakis, G. The volcanoseismic crisis of 1996–1997 in Nisyros, SE Aegean Sea, Greece. Terra Nova 1998, 10, 151–154. [Google Scholar] [CrossRef]
- Longchamp, C.; Bonadonna, C.; Bachmann, O.; Skopelitis, A. Characterization of tephra deposits with limited exposure: The example of the two largest explosive eruptions at Nisyros volcano (Greece). Bull. Volcanol. 2011, 73, 1337–1352. [Google Scholar] [CrossRef]
- Bachmann, O.; Deering, C.D.; Ruprecht, J.S.; Huber, C.; Skopelitis, A.; Schnyder, C. Evolution of silicic magmas in the Kos-Nisyros volcanic center, Greece: A petrological cycle associated with caldera collapse. Contrib. Mineral. Petrol. 2012, 163, 151–166. [Google Scholar] [CrossRef]
- Brombach, T.; Caliro, S.; Chiodini, G.; Fiebig, J.; Hunziker, J.C.; Raco, B. Geochemical evidence for mixing of magmatic fluids with seawater, Nisyros hydrothermal system, Greece. Bull. Volcanol. 2003, 65, 505–516. [Google Scholar] [CrossRef]
- Nomikou, P.; Bell, K.; Vougioukalakis, G.; Livanos, I.; Martin Fero, J. Exploring the Nisyros Volcanic Field. In New Frontiers in Ocean Exploration: The E/V Nautilus 2010 Field Season; Bell, K.L.C., Fuller, S.A., Eds.; The Oceanography Society: Rockville, MD, USA, 2011; Volume 24, p. 27. [Google Scholar]
- Sigurdsson, H.; Carey, S.; Alexandri, M.; Vougioukalakis, G.; Croff, K.; Roman, C.; Sakellariou, D.; Anagnostou, C.; Rousakis, G.; Ioakim, C.; et al. Marine investigations of Greece’s Santorini Volcanic Field. EOS 2006, 87, 337–342. [Google Scholar] [CrossRef]
- Nomikou, P.; Carey, S.; Papanikolaou, D.; Bell, K.C.; Sakellariou, D.; Alexandri, M.; Bejelou, K. Submarine volcanoes of the Kolumbo volcanic zone {NE} of Santorini Caldera, Greece. Glob. Planet. Chang. 2012, 90-91, 135–151. [Google Scholar] [CrossRef]
- Kilias, S.P.; Nomikou, P.; Papanikolaou, D.; Polymenakou, P.N.; Godelitsas, A.; Argyraki, A.; Carey, S.; Gamaletsos, P.; Mertzimekis, T.J.; Stathopoulou, E.; et al. New insights into hydrothermal vent processes in the unique shallow-submarine arc-volcano, Kolumbo (Santorini), Greece. Sci. Rep. 2013, 3, 2421. [Google Scholar] [CrossRef] [PubMed]
- Christopoulou, M.E.; Mertzimekis, T.J.; Nomikou, P.; Papanikolaou, D.; Carey, S.; Mandalakis, M. Influence of hydrothermal venting on water column properties in the crater of the Kolumbo submarine volcano, Santorini volcanic field (Greece). Geo-Mar. Lett. 2016, 36, 15–24. [Google Scholar] [CrossRef]
- Parks, M.; Biggs, J.; England, P.; Mather, T.; Nomikou, P.; Palamartchouk, K.; Papanikolaou, X.; Paradissis, D.; Parsons, B.; Pyle, D.; et al. Evolution of Santorini Volcano dominated by episodic and rapid fluxes of melt from depth. Nat. Geosci. 2012, 5, 749–754. [Google Scholar] [CrossRef]
- Bakalis, E.; Mertzimekis, T.J.; Nomikou, P.; Zerbetto, F. Breathing modes of Kolumbo submarine volcano (Santorini, Greece). Sci. Rep. 2017, 7, 46515. [Google Scholar] [CrossRef] [PubMed]
- E/V “Nautilus” Cruise logs NA007 and NA011. unpublished work. 2010.
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Hansen, L.P. Large Sample Properties of Generalized Method of Moments Estimators. Econometrica 1982, 50, 1029–1054. [Google Scholar] [CrossRef]
- Andersen, K.; Castiglione, P.; Mazzino, A.; Vulpiani, A. Simple stochastic models showing strong anomalous diffusion. Eur. Phys. J. B 2000, 18, 447–452. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Scafetta, N.; Grigolini, P. Scaling detection in time series: Diffusion entropy analysis. Phys. Rev. E 2002, 66, 036130. [Google Scholar] [CrossRef] [PubMed]
- Barunik, J.; Kristoufek, L. On Hurst exponent estimation under heavy-tailed distributions. Physica A 2010, 389, 3844–3855. [Google Scholar] [CrossRef]
- Bakalis, E.; Hofinger, S.; Venturini, A.; Zerbetto, F. Crossover of two power laws in the anomalous diffusion of a two lipid membrane. J. Chem. Phys. 2015, 142, 215102. [Google Scholar] [CrossRef] [PubMed]
- Sändig, N.; Bakalis, E.; Zerbetto, F. Stochastic analysis of movements on surfaces: The case of {C60} on Au(1 1 1). Chem. Phys. Lett. 2015, 633, 163–168. [Google Scholar] [CrossRef]
- Parent, L.R.; Bakalis, E.; Ramirez-Hernandez, A.; Kammeyer, J.K.; Park, C.; de Pablo, J.; Zerbetto, F.; Patterson, J.P.; Gianneschi, N.C. Directly Observing Micelle Fusion and Growth in Solution by Liquid- Cell Transmission Electron Microscopy. J. Am. Chem. Soc. 2017, 139, 17140–17151. [Google Scholar] [CrossRef] [PubMed]
- Parent, L.R.; Bakalis, E.; Proetto, M.; Li, Y.; Park, C.; Zerbetto, F.; Gianneschi, N.C. Tackling the Challenges of Dynamic Experiments Using Liquid-Cell Transmission Electron Microscopy. Acc. Chem. Res. 2018, 51, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Barabasi, A.L.; Vicsek, T. Multifractality of self-affine fractals. Phys. Rev. A 1991, 44, 2730–2733. [Google Scholar] [CrossRef] [PubMed]
- Flandrin, P. On the Spectrum of Fractional Brownian Motions. IEEE Trans. Inf. Theory 1989, 35, 197–199. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Universal Multifractals Do Exist! Comments on “A Statistical Analysis of Mesoscale Rainfall as a Random Cascade”. J. Appl. Meteorol. 1997, 36, 1296–1303. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Multifractals and rain. In New Uncertainty Concepts in Hydrology and Water Resources; Cambridge University Press: Cambridge, UK, 1995; pp. 61–103. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakalis, E.; Mertzimekis, T.J.; Nomikou, P.; Zerbetto, F. Temperature and Conductivity as Indicators of the Morphology and Activity of a Submarine Volcano: Avyssos (Nisyros) in the South Aegean Sea, Greece. Geosciences 2018, 8, 193. https://doi.org/10.3390/geosciences8060193
Bakalis E, Mertzimekis TJ, Nomikou P, Zerbetto F. Temperature and Conductivity as Indicators of the Morphology and Activity of a Submarine Volcano: Avyssos (Nisyros) in the South Aegean Sea, Greece. Geosciences. 2018; 8(6):193. https://doi.org/10.3390/geosciences8060193
Chicago/Turabian StyleBakalis, Evangelos, Theo J. Mertzimekis, Paraskevi Nomikou, and Francesco Zerbetto. 2018. "Temperature and Conductivity as Indicators of the Morphology and Activity of a Submarine Volcano: Avyssos (Nisyros) in the South Aegean Sea, Greece" Geosciences 8, no. 6: 193. https://doi.org/10.3390/geosciences8060193
APA StyleBakalis, E., Mertzimekis, T. J., Nomikou, P., & Zerbetto, F. (2018). Temperature and Conductivity as Indicators of the Morphology and Activity of a Submarine Volcano: Avyssos (Nisyros) in the South Aegean Sea, Greece. Geosciences, 8(6), 193. https://doi.org/10.3390/geosciences8060193







